Test de hipótesis
Objetivos
Que el alumno:
- Aprenda un procedimiento de gran aplicación para hacer inferencias, que le permita tomar decisiones referentes a afirmaciones a las que se da el nombre de hipótesis.
- Conozca la diferencia entre los distintos tipos de errores.
- Adquiera conocimientos básicos en el campo del diseño de experimentos.
- Aprenda a aplicar el test chi-cuadrado de KolmogorovSmirnov (KS).
- Conozca el análisis de varianza (ANOVA) para un factor y descubra las posibilidades que le ofrece la programación de una planilla de cálculo para su aplicación.
- Comprenda la importancia de la aplicación del método de la diferencia mínima significativa, como complemento del ANOVA.
9.1. Introducción
Supongamos que uno de los insumos empleado por una empresa son las bolsas plásticas que emplea para la comercialización de su producto. La resistencia a la tracción de dichas bolsas será entonces una de las características que debe controlar periódicamente.
El fabricante de dichas bolsas asegura que la resistencia a la tracción de estas es de 0,002 kPa. Sin embargo, el ensayo de rutina de uno de los lotes recibidos indica que la resistencia promedio de una muestra de cuatro bolsas es de solo 0,0018 kPa.
Surgen entonces las siguientes inquietudes: ¿es posible que, a pesar de que la media de la muestra sea 0,0018 kPa, esta corresponda a un lote cuya resistencia sea 0,002 kPa? ¿O, efectivamente, la resistencia del lote recibido es inferior a la que garantizaba el proveedor del insumo?
No se trata de preguntas triviales: de la respuesta dependerá que el lote sea aceptado o rechazado.
9.1.1. Hipótesis nula e hipótesis alternativa
Ante el problema planteado, se proponen dos hipótesis estadísticas sobre el valor del parámetro, es decir, la resistencia a la tracción de las bolsas.
La primera (a la que denominaremos hipótesis nula y expresaremos como \(H_0\)) es que, a pesar de que la resistencia a la tracción de la muestra haya resultado inferior al valor garantizado, la resistencia promedio del lote es efectivamente 0,002 kPa.
La segunda hipótesis (a la que denominaremos hipótesis alternativa y expresaremos como \(H_1\)) es que la resistencia promedio del lote es inferior a la garantizada, tal como lo indica la media de la muestra.
Todo esto habrá de resumirse escribiendo:
\[\large{ H_0: \mu= 0,002 }\]
\[\large{ H_1: \mu < 0,002 }\]
A partir de este planteo habrán de seguirse una serie de pasos ordenados que nos permitirán aceptar o rechazar la hipótesis nula. Pero antes de detallarlos, detengámonos en los tipos de riesgos que plantea adoptar una decisión a partir de este procedimiento estadístico.
9.1.2. Tipos de errores
Una vez planteadas las dos hipótesis, nos enfrentamos a cuatro posibilidades que se indican en el cuadro de la imagen 9.1.

Tipos de errores.
Es evidente que si se acepta la hipótesis nula siendo esta verdadera, se habrá tomado una decisión correcta. Lo mismo sucede si se rechaza la hipótesis nula, siendo esta falsa.
El problema se presenta cuando la hipótesis nula resulta ser verdadera pero, puesto que no contamos con elementos estadísticos que nos lo aseguren, terminamos rechazándola. En este caso, diremos que se comete un error de tipo I. La probabilidad de que ello suceda recibe el nombre de riesgo del fabricante y se representa por la letra griega \(\alpha\).
También podría suceder que la hipótesis nula no fuera rechazada a pesar de ser falsa. En ese caso, se dice que se trata de un error de tipo II. En este caso, la probabilidad de que ello suceda recibe el nombre de riesgo del consumidor y se representa mediante la letra griega β.
El error de tipo I, entonces, estará vinculado con una acción que no debería haberse llevado a cabo; el fabricante del insumo se ve perjudicado cuando se rechaza su producto a pesar de que cumplía con las especificaciones garantizadas.
El error de tipo II, en cambio, se relaciona con una falta de respuesta por parte de quien ha llevado a cabo el examen de la muestra: se acepta al insumo como adecuado sin que este lo sea.
En general, se asume que el error de tipo I es más grave, de modo que es el que trata de evitarse. Entonces, para minimizar este tipo de error, adoptaremos un valor de \(\alpha\) que sea lo menor posible. Dicho valor recibe el nombre de nivel de significancia de la prueba.
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México. pp. 370 a 380.
Gutiérrez Pulido, H.; De La Vara Salazar, R.(2008), Análisis y Diseño de Experimentos, Mc Graw Hill, México, pp.30 a 39.
Volvamos a la situación planteada en la introducción de la presente unidad: buscamos evidencia estadística para aceptar (o rechazar) la afirmación del fabricante de bolsas plásticas respecto de la resistencia a la tracción de su producto. Él asegura que la resistencia a la tracción es de 0,002 kPa, pero el ensayo de rutina de uno de los lotes recibidos indica que la resistencia promedio de una muestra de cuatro bolsas es de solo 0,0018 kPa.
El test consiste en una serie de pasos ordenados, que detallaremos a continuación:
Definir la variable aleatoria en estudio que, en nuestro caso, será la resistencia a la tracción de las bolsas.
Plantear claramente la situación problemática.
Necesitamos alguna evidencia estadística para decidir si, a pesar de que la resistencia promedio obtenida a partir de la resultara inferior a 0,02 kPa, el valor de la variable aleatoria en estudio es en realidad el garantizado por el proveedor.
Hacer las suposiciones necesarias.
Supongamos que el proveedor no solo garantiza una resistencia promedio sino que, además, nos asegura que dicha variable sigue una distribución normal y que la desviación estándar de esta es 0,001 kPa. Entonces:
\[\large{ X\sim N (\mu=0,002 KPa,\sigma=0,001KPa) }\]
Es decir, podemos suponer que la distribución de probabilidades de nuestra variable aleatoria es normal, con media 0,002 kPa y desviación estándar 0,001 kPa.
Plantear matemáticamente las hipótesis.
Tal como lo anticipamos:
\[\large{ H_0: \mu = 0,002 }\]
\[\large{ H_1: \mu < 0,002 }\]
Definir el estadístico de prueba.
Recordemos que se define como estadístico o medida estadística a una función de los datos muestrales que no contiene datos desconocidos. Al hablar de estadístico de prueba nos referimos en este caso a \(\Large{ E=\frac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}} }\)
Adoptar la distribución para el caso de que el estadístico de prueba sea verdadero. En nuestro ejemplo emplearemos la distribución normal estándar, a la que expresamos como
\[\large{ E \sim N(0,1) }\]
Establecer la región de rechazo de la prueba fijado.
Adoptaremos \(\alpha=5\%\), que es un valor usualmente empleado.
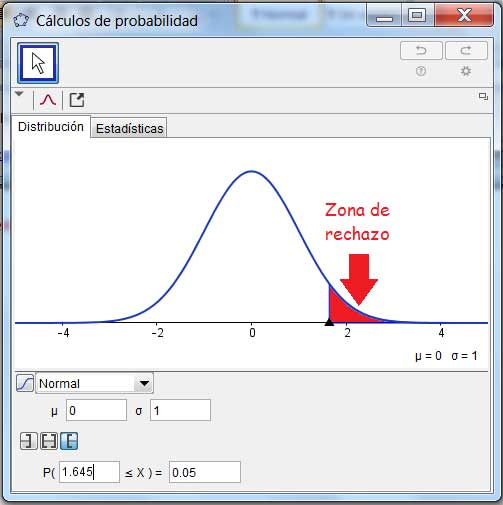
Para hallar el valor de Z correspondiente, podemos emplear una de las funciones que nos brinda la planilla de cálculo, tal como se observa en las imágenes 9.2 y 9.3.
De acuerdo con lo que se observa en la imagen 9.3, el valor de Z correspondiente al nivel de significancia del 5 % para una prueba de una sola cola como la de nuestro ejemplo es aproximadamente -1,645. En general, a dicho valor de Z se le agrega un subíndice que se corresponde con el nivel de significancia. En nuestro caso, corresponde escribir \(Z_{0,05}\).
Calcular el estadístico observado E.
Según lo planteado anteriormente, tenemos:
\[\Large{ E=\frac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}} = \frac{0,0018-0,002}{\frac{0,001}{\sqrt{4}}} =-0,4}\]
Interpretar los resultados.
El valor del estadístico observado resulta ser superior al de Z, razón por la cual aquel se encuentra dentro de lo que llamaremos zona de aceptación. No existe entonces evidencia estadística para que rechacemos la hipótesis nula.
Utilizamos ahora el GeoGebra para interpretar con mayor claridad la situación. En la imagen 9.4 se ve claramente que \(Z_{0,05}=-1,645\) representa el extremo superior de la región de rechazo de la hipótesis nula. Dado que el estadístico observado adopta un valor superior al de Z, se encuentra fuera de dicha región.
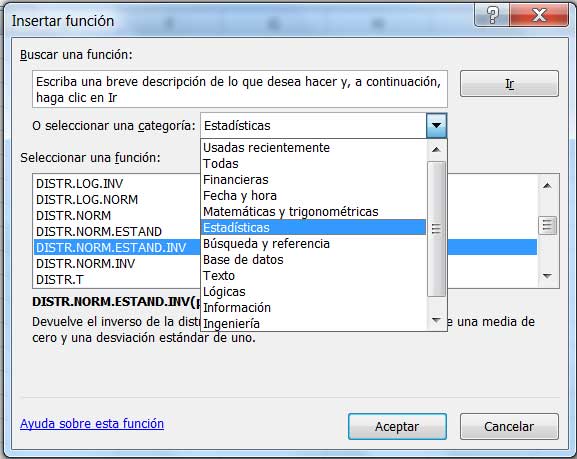
Selección de la función que ofrece la planilla de cálculo.
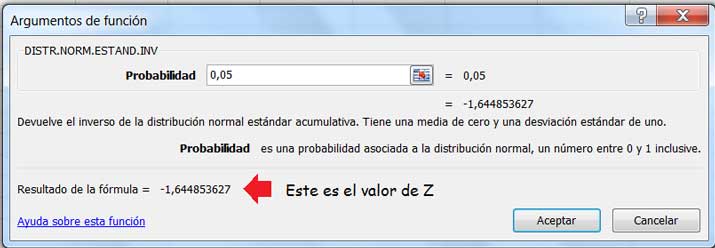
Ingresando el valor de la probabilidad correspondiente al nivel de significancia, obtenemos el valor de Z correspondiente.
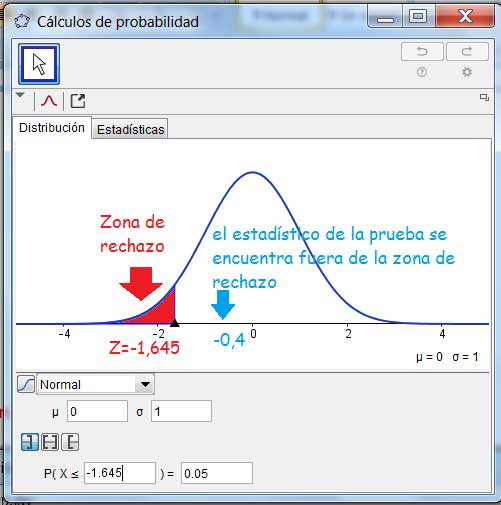
El estadístico observado se encuentra fuera de la zona de rechazo, de modo que no existe evidencia estadística que nos permita rechazar la hipótesis nula.
9.2. El p-valor
Debemos tener en cuenta que el nivel de significancia corresponde a una probabilidad y que esta, desde el punto de vista gráfico, no es otra cosa que un área.
El siguiente ejemplo nos ofrecerá una nueva herramienta para llevar adelante el test de hipótesis.
La cantidad de sodio que contiene un paquete de leche instantánea en polvo de 200 g es de 96 mg. Sin embargo, de un lote de producción se extraen 4 paquetes y se determina que el contenido medio de sodio en ellos resulta ser de 98 mg. Sabiendo que la varianza poblacional es de 9 mg2 y que se puede suponer una distribución normal para esta variable, se pide poner a prueba la hipótesis de que el contenido medio de sodio de cada paquete en el lote es efectivamente de 96 mg, como lo indica el envase del producto, y no superior a dicho valor, adoptando para la prueba un nivel de significancia del 5 %.
En este caso, la variable X es el contenido de sodio en cada paquete de leche en polvo y la distribución de probabilidades de dicha variable resulta ser normal, \(X\sim N(\mu=96,\sigma=3)\).
En este ejemplo \(H_0:\mu=96;H_1:\mu>96\) y el nivel de significancia es 0,05. Entonces, a diferencia del problema anterior, la región de rechazo se encuentra en el extremo superior. Por ese motivo, al buscar el valor de Z mediante la planilla de cálculo hemos ingresado una probabilidad de 0,95 (ver imagen 9.5), siendo entonces la región de rechazo de la hipótesis nula la que aparece claramente indicada en la imagen 9.6.
Calculamos seguidamente el estadístico observado E para este problema:
\[\Large{ E=\frac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}} = \frac{98-96}{\frac{3}{\sqrt{4}}} \cong 1,33}\]
Puesto que el valor de E es inferior al de Z (1,33 < 1,645) no existe evidencia estadística para rechazar la hipótesis nula.
Para verificar esta afirmación, podemos igualmente comparar el nivel de significancia con el área (o probabilidad, según cuál sea el criterio con el que queramos manejarnos) determinada por el E observado. El p-valor será, en este problema, el área de rechazo para dicho estadístico observado. Es decir, se trata de P(Z>1,33)=1-P(Z<1,33).
En la imagen 9.7 se observa cómo calculamos el p-valor para nuestro problema. Dado que su valor es superior al nivel de significancia, concluimos que no existe evidencia estadística que nos permita rechazar la hipótesis nula.
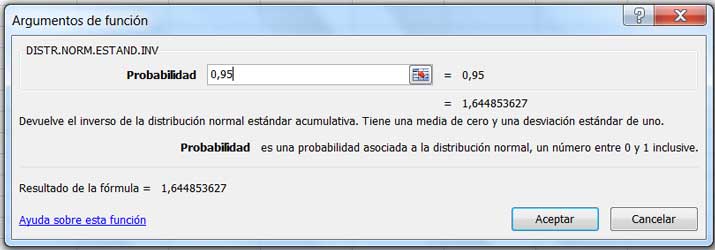
Obtención de Z empleando la planilla de cálculo.
Región de rechazo
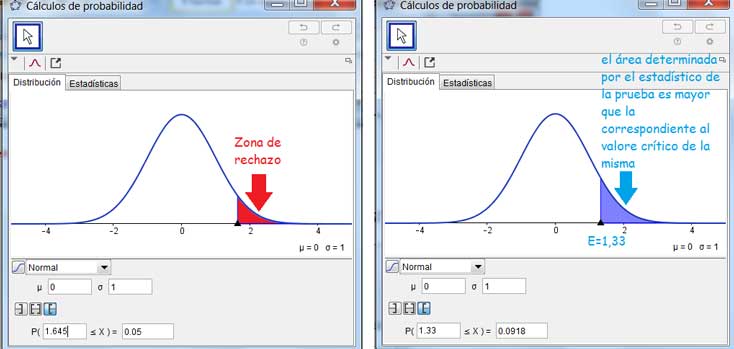
La primera de las dos imágenes vuelve a mostrarnos la zona de rechazo, a la que le corresponde un área de valor 0,05 (con Z=1,645). La segunda de las imágenes muestra, en cambio, el área correspondiente al estadístico de la prueba, de valor 0,0918 (es decir, superior al anterior), en correspondencia con E=1,33. Entonces, como E es menor que Z, decimos que no existe evidencia estadística para rechazar la hipótesis nula.
Un fabricante de equipos de prevención de incendios asegura que la temperatura de activación promedio de sus rociadores de agua es de 130 °C. Sin embargo, se lleva a cabo una prueba con nueve rociadores, obteniéndose una temperatura de activación promedio de 131 °C. Si la temperatura de activación resulta ser una variable que se distribuye normalmente, con una desviación estándar de 1,5 °C, analizar si los resultados de la prueba contradicen las afirmaciones del fabricante. Emplear un nivel de significancia para la prueba del 1%.
El tiempo de proceso de un producto en una cadena de montaje puede describirse como una variable normal, con media de 75 minutos y desviación estándar de 9 minutos. Se realiza un cambio en la disposición de las máquinas, mejorando de ese modo las condiciones ergonómicas del personal afectado a dicho proceso. Se pone a prueba dicho cambio, tomándose 25 mediciones. El tiempo de proceso promedio obtenido en dicha prueba resultó ser de 73 minutos. Se pide efectuar un adecuado test de hipótesis, con el fin de obtener evidencia estadística del efecto que sobre el tiempo de proceso pueda tener el cambio descripto. Adoptar como nivel de significancia de la prueba el 5%.
9.3. Test de hipótesis para muestras con varianzas desconocidas
En los problemas anteriores, se conocía el valor de la varianza poblacional. Veamos a través del siguiente ejemplo de qué modo tenemos que actuar cuando la varianza es desconocida.
Un fabricante de lámparas eléctricas ha desarrollado un nuevo proceso de producción mediante el cual espera aumentar la iluminación de estas, que hasta ese momento era de 9,50 lúmenes. Se lleva a cabo un experimento con 10 lámparas, obteniéndose los siguientes resultados:
9,97 11,46 12,05 9,87 10,85 9,28 10,25 11,52 13,02 11,58
Se desea saber entonces si existe evidencia estadística de que efectivamente la iluminación de las lámparas aumentó, tomando 0,05 como nivel de significancia de la prueba.
En esta oportunidad, \(H_0:\mu_0=9,5;\ H_1:\mu_0>9,5\).
No conocemos la media de la muestra ni la desviación poblacional.
El estadístico observado, entonces, recibirá el nombre de t9 y estará relacionado con la distribución t de Student de grado de libertad 9.
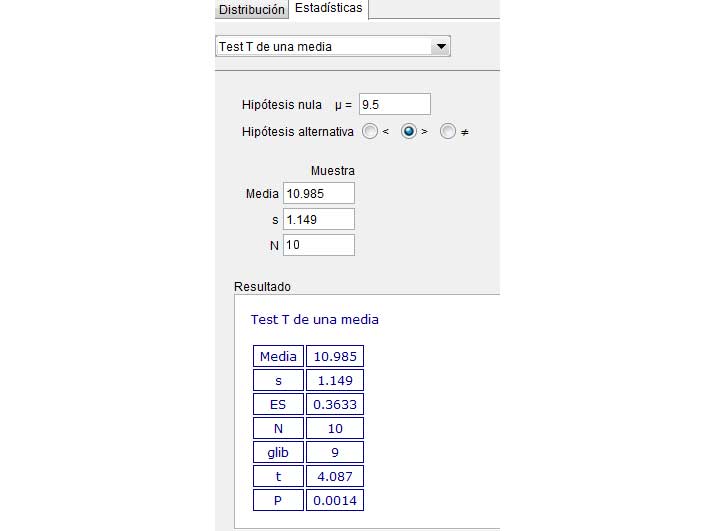
En primer lugar, volcamos los datos correspondientes a la muestra en una planilla de cálculo y, seleccionando y utilizando la función PROMEDIO (Imágenes 9.8 y 9.9), obtenemos la media de la muestra (cuyo valor resulta ser 10,985 lúmenes).
Seguidamente y empleando la misma planilla de cálculo, seleccionamos y aplicamos la función DESVEST (imágenes 9.10 y 9.11), obteniendo de ese modo el valor de la desviación estándar de la muestra.
Calculamos seguidamente el estadístico observado:
\[\Large{ E=\frac{\overline{X}-\mu_0}{\frac{S}{\sqrt{n}}} = \frac{10,985-9,5}{\frac{1,149}{\sqrt{10}}} = 4,087}\]
En la imagen 9.12 se observa cómo obtuvimos el valor del estadístico correspondiente al nivel de significancia adoptado. Puesto que el valor del estadístico correspondiente al nivel de significancia de la prueba (1,833) resulta ser inferior al del estadístico observado, concluimos que existe evidencia estadística para rechazar la hipótesis nula.
En la imagen 9.13 graficamos empleando el GeoGebra. Se observa claramente que el estadístico observado se encuentra a la derecha respecto del t0,05;9, estadístico correspondiente al nivel de significancia de nuestro problema.
Finalmente, observemos la imagen 9.14, en la que reproducimos los resultados de la prueba t llevada a cabo con el GeoGebra. Se observa que el p-valor (0,0014) es inferior al nivel de significancia de la prueba; eso significa que el área de rechazo para este último es superior al del estadístico observado, confirmándose entonces la conclusión respecto de la hipótesis nula a la que habíamos llegado anteriormente.
Se selecciona la función PROMEDIO
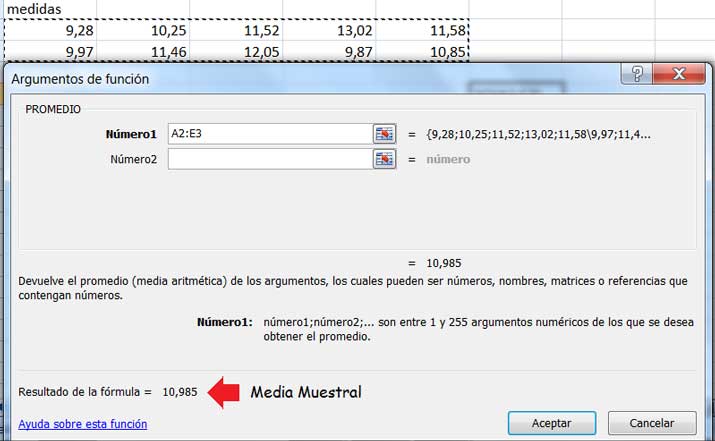
Una vez que en la ventana reproducida en la imagen 9.8 hacemos clic en “Aceptar”, obtenemos de inmediato el valor de la media de la muestra.
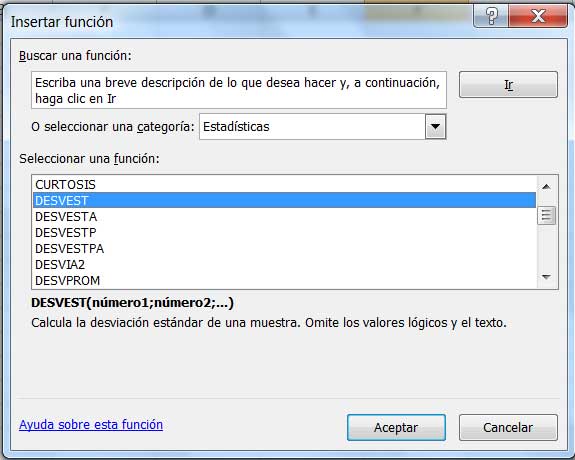
Se selecciona la función DESVEST.
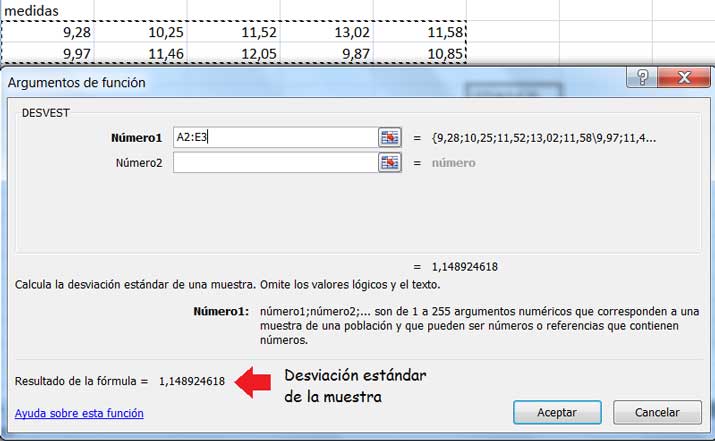
Una vez que en la ventana reproducida en la imagen 9.10, hacemos clic en “Aceptar”, obtenemos de inmediato el valor de la desviación estándar S de la muestra.
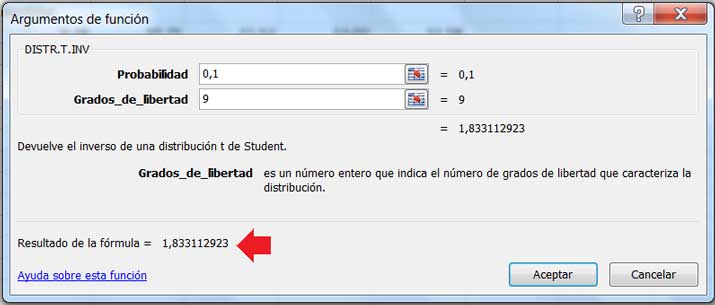
Obtenemos, mediante la planilla de cálculo, el valor del estadístico correspondiente al nivel de significancia de la prueba. En la ventana correspondiente a la probabilidad hemos escrito “0,1” en lugar de “0,05” porque la planilla de cálculo nos devuelve el inverso de una distribución de dos colas (y en nuestro caso trabajábamos solo con una cola).
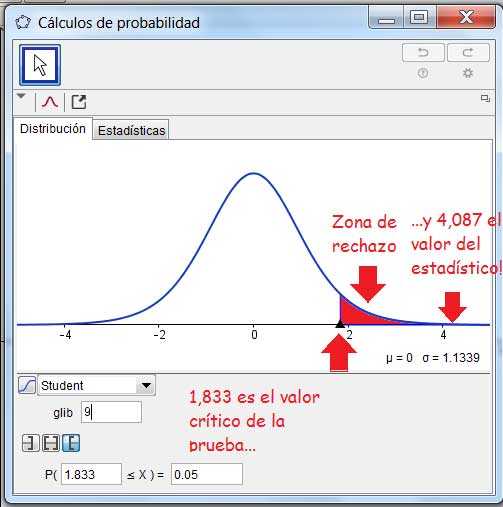
Utilizamos el GeoGebra para representar gráficamente la situación correspondiente a nuestro problema.
Verificación de los resultados obtenidos para la prueba t.
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México. pp. 404 a 408.
Para aplicar la sierra que corta las losas de hormigón de calles recién pavimentadas, la resistencia del material debe ser menor a 30 libras sobre pulgada cuadrada. Se toma la siguiente muestra:
14,1 14,5 15,5 16,0 16,0 16,7 16,9 17,1 17,5 17,8
17,8 18,1 18,2 18,3 18,3 19,0 19,2 19,4 20,0 20,0
20,8 20,8 21,0 21,5 23,5 27,5 28,0 28,3 28,7 30,0
30,0 31,6 31,7 31,7 31,7 32,5 33,5 33,9 35,0 35,0
36,7 40,0 40,0 41,3 41,7 47,5 50,0 51,0 51,8 54,4
A partir de estos valores, decidir si el pavimento del que se ha tomado dicha muestra se encuentra en condiciones de ser cortado por las sierras para la ejecución de las juntas de dilatación. Enunciar para ello las hipótesis nula y alternativa apropiadas. Adoptar como nivel de significancia el 5 %.
El nivel histórico de producción de una planta de productos químicos es de 880 toneladas diarias. Sin embargo, durante 20 días consecutivos se registra dicho nivel de producción, obteniéndose un valor promedio de solo 871 toneladas diarias, con una desviación estándar muestral de 12 toneladas.
El gerente de producción opina entonces que el nivel ha disminuido respecto del estándar histórico. Tomando un nivel de significancia del 5 %, diseñar un test de hipótesis que brinde evidencia estadística para confirmar o refutar la opinión del gerente.
9.4. Diseño de experimentos
Supongamos que en un proceso dado necesitamos determinar cuáles son las variables que más influyen en las características del producto que estemos fabricando; que busquemos cuáles son las condiciones de operación que optimicen el rendimiento de un proceso dado, o que quisiéramos obtener las características de un nuevo material. En estas y otras situaciones, el diseño estadístico de experimentos será el modo más eficiente para lograr nuestro objetivo, pues nos ayudará a determinar cuáles son las pruebas que deben llevarse a cabo y de qué modo debemos hacerlo.
Para obtener los datos que nos permitan mejorar un proceso existente, existen dos estrategias posibles. La primera consiste en monitorear dicho proceso hasta detectar alguna variable o condición de operación particular que resulte conveniente para alcanzar nuestro objetivo. Este procedimiento recibe el nombre de estrategia pasiva.
El otro camino consiste en llevar a cabo en forma deliberada una serie de pequeños cambios en el proceso, alguno de los cuales podrá brindar las señales favorables buscadas. Este tipo de estrategia, a diferencia de la anterior, recibe el nombre de activa y el conjunto de técnicas de este tipo que se desarrollan para la mejora del proceso reciben el nombre de diseño de experimentos.
9.4.1. Definiciones básicas para el diseño de experimentos
Experimento: alteración deliberada de las condiciones habituales de operación de un proceso que permite medir el efecto de aquellas sobre este.
Variable de respuesta: característica del producto o variable cuyo valor numérico habrá de medirse para determinar el éxito o no del experimento.
Factores controlables: son las variables del proceso cuyos valores fijamos deliberadamente al llevar a cabo cada uno de los experimentos. Se las conoce también como variables de entrada, variables del proceso o, simplemente, factores. Debe diferenciárselas de los factores no controlables o ruido, que son aquellas variables que no pueden controlarse durante el experimento.
Niveles y tratamientos: los diferentes valores que se asignen a uno de los factores reciben el nombre de niveles. Si, por ejemplo, realizamos un experimento en el cual la temperatura sea uno de los factores y fijamos una temperatura de 120 grados para llevarlo a cabo, dicha temperatura representará el nivel del factor en cuestión.
Un tipo de experimento muy común es el que recibe el nombre de diseño factorial 22, en el que se trabaja con dos factores que habrán de ser fijados en dos niveles cada uno. En este tipo de experimento se define como tratamiento a la combinación de niveles y factores estudiados. Volviendo al caso que mencionamos en el párrafo anterior, supongamos que los dos factores de nuestro experimento fuesen la temperatura y el tiempo durante el cual se lleva a cabo el experimento. Si la temperatura se fija en 120 y en 130 grados, y el tiempo en dos y tres horas de tratamiento, la combinación de esos dos factores a esos niveles nos permitirá llevar a cabo cuatro ensayos que conformarán un tratamiento.
El diseño experimental tiene varias etapas, entre las cuales se encuentra la de análisis. Es importante en esta recordar que los resultados obtenidos experimentalmente son observaciones hechas a partir de muestras, de modo que deberán aplicarse métodos inferenciales que garanticen que las diferencias entre los experimentos y el proceso (que representa a la población) sean pequeñas. El análisis de varianza (conocido por su acrónimo inglés, ANOVA) representa la técnica estadística principal en el análisis de los experimentos. En una de las siguientes secciones mostraremos cómo aplicar dicha técnica al estudiar un factor. Pero, previamente, nos detendremos en la prueba de bondad de ajuste de KolmogorovSmirnov.
9.4.2. Test chi-cuadrado Kolmogorov Smirnov (KS)
Se realiza para comprobar si los resultados de la variable de respuesta corresponden a los de una población normal. Su aplicación se puede generalizar a otras distribuciones y las hipótesis a contrastar son las siguientes:
H0: los datos analizados corresponden a una distribución de tipo M.
H1: los datos analizados no corresponden a dicha distribución.
Se define un estadístico de contraste D, siendo el criterio para la toma de decisión respecto de las dos hipótesis el siguiente:
Si \( D \le D_{\alpha} \to \text{ se acepta } H_0 \)Si, en cambio, \( D > D_{\alpha} \to \text{ se rechaza } H_0 \)
El valor \( D_{\alpha} \) corresponde al nivel \(\alpha\) de significación de la prueba y representa la probabilidad de rechazar la hipótesis nula sabiendo que dicha hipótesis es verdadera, es decir:
\[\large{ P \left( \frac{\text{rechazar } H_0}{H_0 \text{ es cierta}} \right) = P \left( \frac{D\ >\ D{\alpha}}{\text{los datos siguen una distribución M}} \right) = \alpha }\]
El valor de \( D_{\alpha} \) depende del tipo de distribución M que se desee contrastar. En general, \( D_{\alpha}= \frac{C_{\alpha}}{k(n)} \) , donde \( C_{\alpha} \) y k(n) están tabulados. Por ejemplo, para la distribución normal y un \(\alpha\) de valor \( 0,05,C_{\alpha}=0,895 \). Por otro lado, el valor de k(n) depende del tamaño de la muestra y del tipo de distribución. Para el caso de la distribución normal,
\[\large{ k(n)=\sqrt{n}-0,01+\frac{0,85}{\sqrt{n}} }\]
Determinar si la siguiente muestra corresponde a una distribución normal:
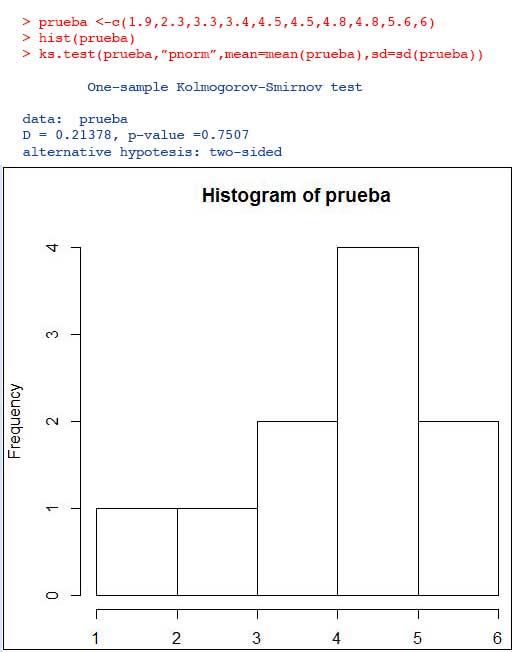
1,9 ; 2,3 ; 3,3 ; 3,4 ; 4,5 ; 4,5 ; 4,8 ; 4,8 ; 5,6 ; 6,0
Para su resolución utilizaremos el software R, que empleamos en la unidad 2 para construir histogramas. Primeramente, definimos un vector al que damos el nombre de prueba dentro del cual incluimos a los datos. Hemos dibujado el histograma correspondiente (con la instrucción HIST, tal como se observa en la segunda línea, para finalmente llevar adelante la prueba (como se observa en la tercera instrucción).
En la imagen 9.15 se observa la captura de pantalla correspondiente a la resolución de nuestro ejemplo. En color rojo se observan las tres instrucciones empleadas: en primer lugar, definimos un vector al que denominamos “prueba”, dentro del cual ingresamos los datos de nuestra muestra. Seguidamente, la instrucción HIST nos permite obtener el histograma correspondiente.
Finalmente, la tercera de las líneas corresponde a la instrucción que hemos de emplear para obtener el valor de D.
Seguidamente, obtenemos \( D_{\alpha} \):
\[\large{ D_{\alpha} = \frac{0,895}{\sqrt{10}-0,01+ \frac{0,85}{\sqrt{10}}}= \frac{0,895}{3,42}= 0,262 }\]
Dado que \( D_{\alpha}=0,213<0,262 \), no existe evidencia estadística para rechazar la hipótesis nula y se acepta que los datos se distribuyen normalmente.
9.4.3. Empleo del p-valor en el Test KS
Un método alternativo para llevar a cabo la prueba de KolmogorovSmirnov consiste en emplear el p-valor asociado al estadístico D. El p-valor se define en este caso como
\[ p-valor = P\ (D\ >\ D_{obs} \text{ sabiendo que } H_0 \text{ es cierta}) \]
Si el p-valor es grande, no existe evidencia estadística para rechazar la hipótesis nula; si, en cambio, el p-valor es pequeño, se pone en duda la validez de la hipótesis nula, razón por la cual habrá de ser rechazada. Para un nivel de significancia \(\alpha\), entonces, la regla de decisión es la siguiente:
\[\text{Si el }p-valor \ge \alpha \to \text{ se acepta }H_0\]
\[\text{Si el }p-valor < \alpha \to \text{ se rechaza }H_0\]
La obtención del p-valor exige conocer la distribución de D. En nuestro ejemplo, el cálculo se obtuvo con el R, como se observa en la imagen 9.15. Como el p-valor es 0,75 y el nivel de significancia 0,05, confirmamos el resultado de la prueba obtenido previamente, es decir, que no existe evidencia estadística para rechazar la hipótesis nula, de modo que nuestra muestra proviene de una población normal.
9.4.4. El diagrama Q-Q
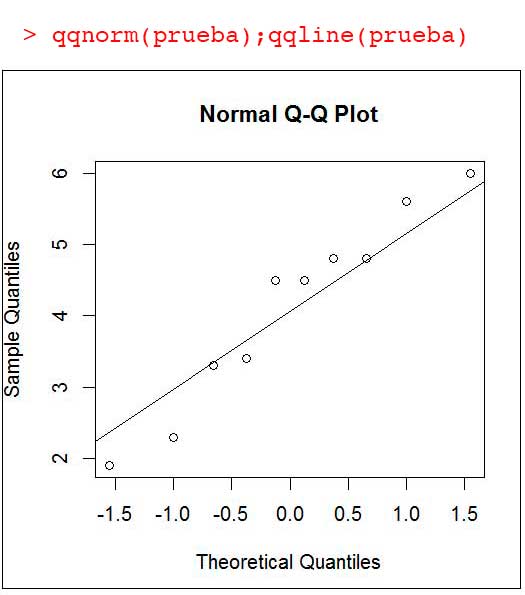
El gráfico cuantil-cuantil (conocido como diagrama Q-Q) representa los cuantiles de la distribución teórica supuesta respecto de los de la distribución experimental. Si el ajuste es bueno, la mayoría de estos últimos puntos deberían situarse sobre la recta, de pendiente uno (es decir, la recta y = x).
En la imagen 9.16 se observa la captura de pantalla correspondiente al empleo del software R. En primer lugar, las instrucciones QQNORM y QQLINE aplicadas al vector prueba que contiene a los datos de la muestra. Debajo de la instrucción, el diagrama Q-Q correspondiente a nuestro ejemplo.
Los siguientes datos corresponden a una muestra obtenida en un estudio de control de calidad. Determinar si existe evidencia estadística de que esta corresponda a una distribución lineal, empleando el test KS, el p-valor y el diagrama Q-Q.

Los siguientes datos corresponden a una muestra obtenida al calibrar las tensiones de los motores de los cabezales de una impresora en 3D. Determinar si existe evidencia estadística de que la variable se comporte normalmente, empleando para ello el test KS, el p-valor y el diagrama Q-Q.

9.5. Análisis de varianza para un factor
Supongamos que un laboratorio medicinal estudia un nuevo analgésico. En una etapa preliminar, lleva a cabo un estudio donde la variable de interés es el tiempo que tarda en hacer efecto su producto —una de las características que se supone que lo diferenciaría en el futuro de los que ya se comercian en el mercado—. Para ello, se trabaja con varios grupos de personas. A uno de ellos se le suministra el producto en cuestión, mientras en cada uno de los demás grupos se suministra alguno de los analgésicos de la competencia. El objetivo es estudiar si el tiempo promedio en que se manifiesta el efecto del nuevo producto es el mismo o resulta menor que el de los productos de otros laboratorios.
Desde el punto de vista estadístico, la hipótesis fundamental cuando se comparan diversos tratamientos será:
\[\large{ H_0:\mu_1=\mu_2=\cdots=\mu_k=\mu }\]
\[\large{ H_A=\mu_i \ne \mu_j \text{ para algún }i \ne j }\]
Es decir, se busca evidencia estadística de que todos los tratamientos son iguales, frente a la alternativa de que al menos dos de ellos presentan medias distintas.
Este tipo de estudio se lleva a cabo en base al diseño completamente al azar (que en la bibliografía suele expresarse como DCA), el más simple de todos los que se utilizan para comparar dos o más tratamientos. Las dos únicas fuentes de variabilidad serán entonces los mismos tratamientos y los errores aleatorios; la idea de llevar a cabo las corridas experimentales de este modo se basa en que los posibles efectos ambientales o externos se distribuyan equitativamente entre dichos tratamientos.
En general, se supone que existen k poblaciones o tratamientos independientes, con medias desconocidas \(\mu_1,\ \mu_2, \dots,\ \mu_k\), cuyas varianzas \(\sigma^2_1,\ \sigma^2_2, \dots,\ \sigma^2_k\) también son desconocidas, pero se suponen iguales. Las medias, tal como lo plantea el ejemplo con el que comenzamos la presente sección, corresponden a la variable de respuesta de nuestro estudio.
Se recomienda que el número de repeticiones para cada uno de los tratamientos sea siempre la misma, a menos que existiese una razón muy particular para no hacerlo. Cuando la condición recomendada se verifica, decimos que el diseño es balanceado.
El número de tratamientos dependerá del problema particular que se trate (en nuestro ejemplo, el número de productos similares que ya se comercializan más el que el laboratorio piensa lanzar al mercado). En lo que respecta a n, el número de observaciones por tratamiento, dependerá de la variabilidad que se espera observar en los datos y de la mínima diferencia que el investigador desee detectar. En general, se recomiendan entre cinco y treinta mediciones, adoptándose un número mayor a medida que el comportamiento esperado sea menos consistente (es decir, se espere mayor variabilidad).
Si las pruebas son muy costosas o demandan demasiado tiempo, de modo que el investigador decide llevar a cabo un reducido número de ensayos, solo se podrán detectar diferencias grandes entre los distintos tratamientos.
La imagen 9.17 corresponde a la captura de pantalla de la planilla de cálculo que programamos para resolver este tipo de problema. El alumno podrá construir dicha planilla después de leer la bibliografía obligatoria, siguiendo los pasos detallados en la imagen 9.18.
Se compara el estadístico de la prueba con el valor crítico de esta, que se obtiene empleando la distribución F. En la imagen 9.19 se observa el resultado de nuestro estudio: puesto que el estadístico de la prueba se encuentra dentro de la zona de rechazo, disponemos de evidencia estadística para concluir que al menos dos de las muestras que componían nuestro estudio poseían medias distintas.
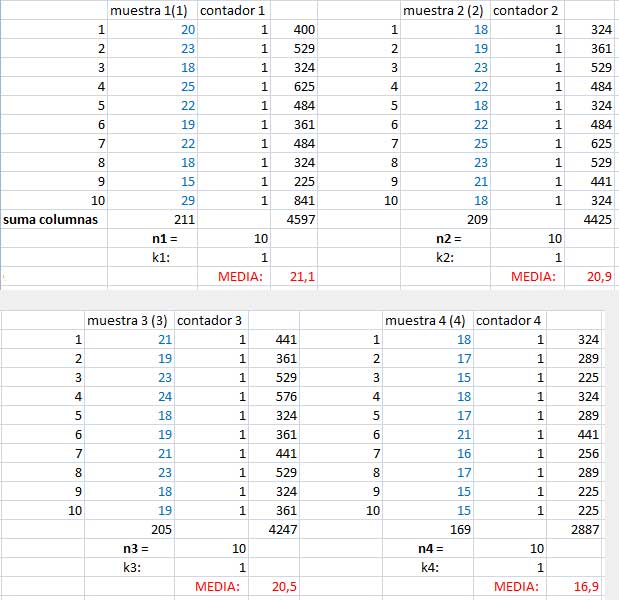
Captura de pantalla correspondiente a la planilla de cálculo que utilizamos para resolver nuestro problema. Las columnas en color azul corresponden a los datos de las muestras tomadas en nuestro estudio. Las tres primeras muestras corresponden a los productos que ya se comercian en el mercado, en tanto que la cuarta muestra se tomó con las personas a las que se suministró el medicamento bajo estudio.
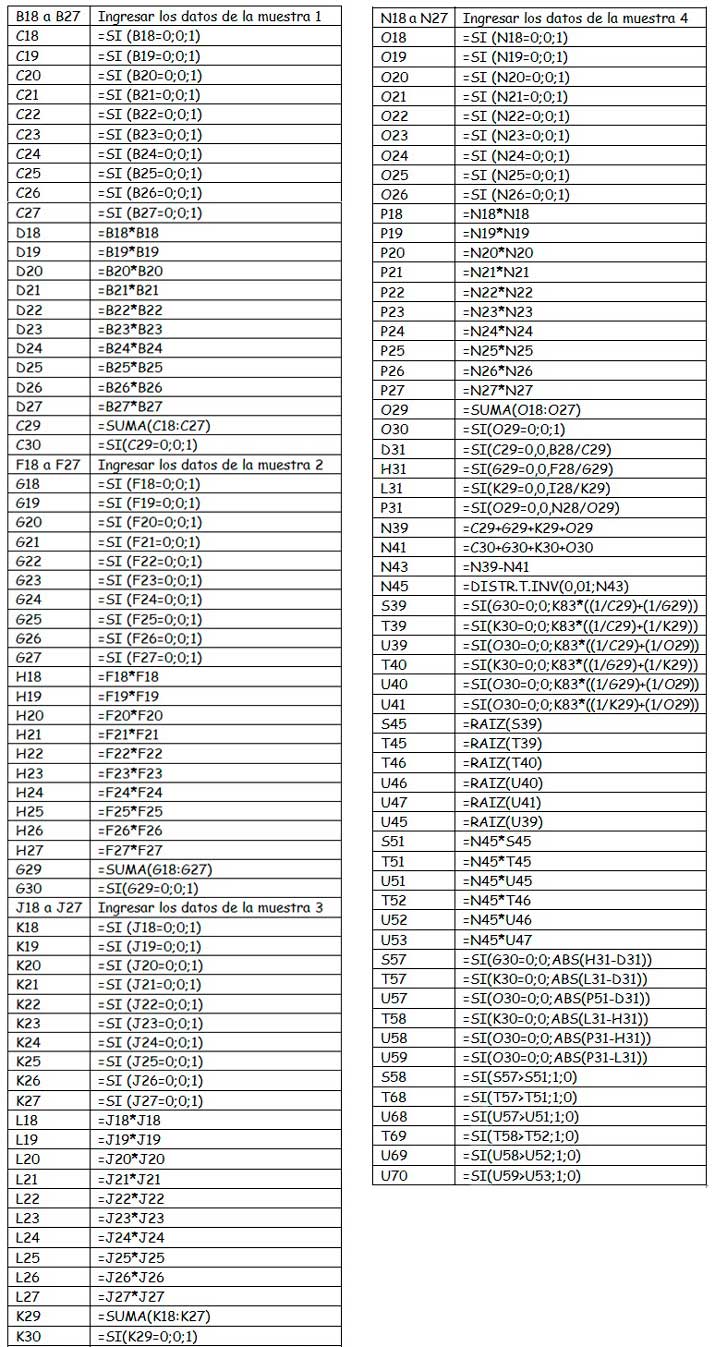
Instrucciones para construir una planilla de cálculo mediante la cual podemos efectuar un análisis de varianza (ANOVA) para un solo factor, para un máximo de cuatro muestras que, como máximo, contengan diez lecturas cada una.
Weimer, R. (2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 589 a 613.
9.6. Diagrama de cajas simultáneas
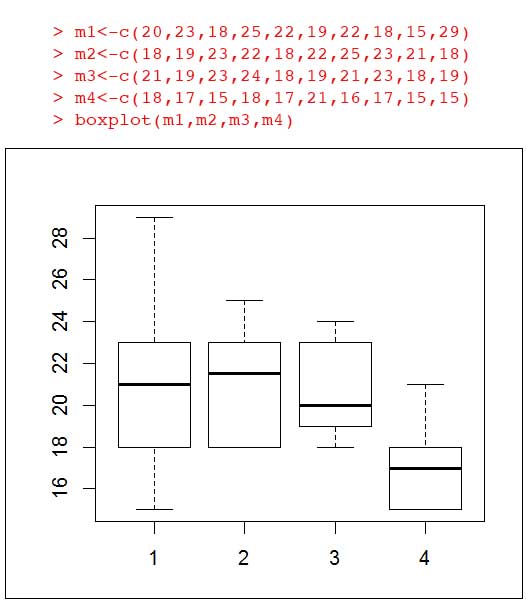
Una forma gráfica de describir lo que sucede con los distintos tratamientos consiste en construir los diagramas de cajas simultáneas. El empleo del software resulta adecuado para dicho fin. En la imagen 9.20 reproducimos la captura de pantalla correspondiente a la aplicación del software R en nuestro problema. Se observa claramente el resultado del análisis de varianza: una de las muestras se diferencia claramente de las restantes.
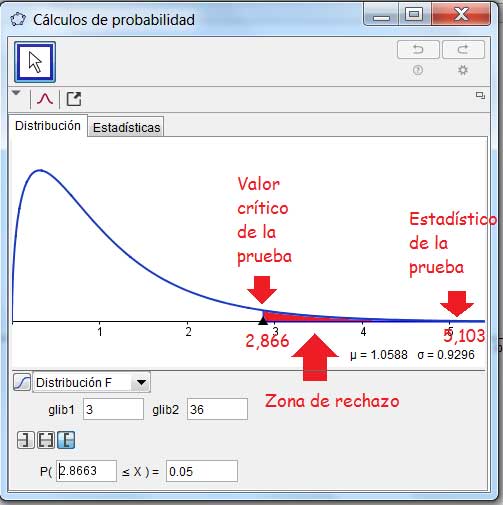
El valor del estadístico de la prueba (5,103) es superior al valor crítico de la prueba (2,866), lo que significa que contamos con evidencia estadística para rechazar la hipótesis nula.
9.7. Pruebas de rango múltiples: método de la diferencia mínima significativa (LSD)
Cuando la hipótesis nula se rechaza en un análisis de varianza, es necesario determinar cuál o cuáles de los tratamientos resultan distintos de los restantes. Existen varios métodos para hacerlo y nosotros aplicaremos uno de los más comunes: el método de la diferencia mínima significativa (más conocido por su acrónimo en inglés, LSD o least significant difference).
El problema consiste en probar para todos los posibles pares de medias la hipótesis:
\[\large{ H_0:\mu_i=\mu_j }\]
\[\large{ H_1:\mu_i \ne \mu_j }\]
Se rechaza la hipótesis nula mediante la cantidad LSD, que es la mínima diferencia que debe existir entre dos medias muestrales para considerar que los correspondientes tratamientos son significativamente diferentes.
La planilla de cálculo empleada en la sección 9.5 nos permite llevar a cabo este análisis. En la imagen 9.21 reproducimos la captura de pantalla que nos permite confirmar que la media correspondiente al producto es distinta a la de los otros que se comercializaban en el mercado.
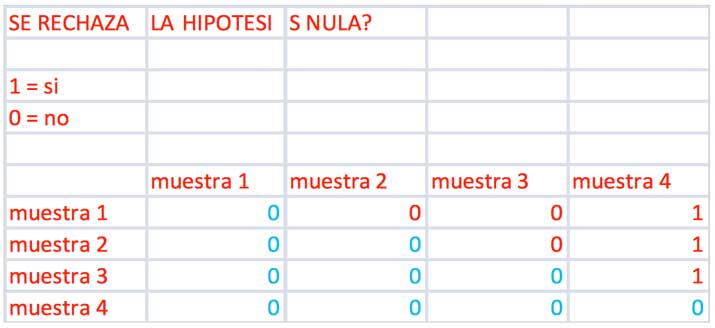
La matriz de la imagen muestra que la media de la muestra difiere de las demás. Los tres números uno que aparecen en la última columna indican justamente que existe evidencia estadística para rechazar las hipótesis nulas al comparar la media del tratamiento 4 con la de los tres restantes, lo que se puede expresar como \(\mu_1 \ne \mu_4,\ \mu_2 \ne \mu_4\ y\ \mu_3 \ne \mu_4\).
Gutiérrez Pulido, H.; De La Vara Salazar, R. (2008), Análisis y Diseño de Experimentos, Mc Graw Hill, México, pp.74 a 76.

