Introducción a la probabilidad elemental
Objetivos
Que el alumno:
- Conozca el concepto de probabilidad, que resulta fundamental para comprender conceptos como distribución de probabilidad y función de distribución de probabilidad
- Aprenda las reglas elementales de la probabilidad y sea capaz de diferenciar sucesos dependientes de sucesos independientes, aplicando en cada caso las expresiones adecuadas para el cálculo.
- Comprenda la importancia del Teorema de Bayes y sepa aplicarlo, dado su valor en el momento de profundizar en el estudio de la probabilidad condicionada.
- Adquiera conocimientos básicos de combinatoria, que habrán de permitirle resolver diversos problemas.
4.1. Experimentos y espacios muestrales
Puede definirse como experimento a cualquier proceso creado que permita llevar a cabo observaciones o recolectar datos. Por ejemplo, si arrojamos un dado, podemos observar y registrar qué número quedó en la cara superior de este. Dicho experimento tendría seis resultados posibles (justamente, los números que van del uno al seis). También podríamos preguntarnos si el número que se observa en la cara superior es par o impar; si es un as; o si es menor o igual a tres.
Otro ejemplo se correspondería con un caso frecuente en la industria, el de controlar una línea de producción para determinar si un producto determinado es o no defectuoso. En este caso, los dos únicos resultados posibles son éxito (paradójicamente, si el producto es defectuoso) o fracaso (cuando el producto no lo es). Aun cuando resulte curioso el planteo, dado que buscamos detectar artículos que no se adecúen a las especificaciones de producción, hemos de considerar que el éxito consiste en encontrar uno de ellos.
Todos los experimentos tienen resultados, cuyo resultado es en general incierto y depende del azar. En este tipo de experimento, el conjunto de los posibles resultados recibe el nombre de espacio muestral.
Supongamos que nuestro experimento consistiese en arrojar dos veces un dado, registrando si sale un as o no. Podemos escribir \( A_i\) si sale as en el i‑ésimo tiro (ya sea el primero o el segundo), y \( \overline{A_i}\) si en el mismo tiro no sale un as. Así \( A_1 A_2\)representaría al caso en que se obtuviera un as en ambos tiros, y \( A_1 \overline{A_2}\) al caso en que se obtuviera un as en el primer tiro pero no se lo obtuviera en el segundo. El espacio muestral correspondiente a este experimento se representaría de la siguiente manera:
\[{\large S = \{A_1 A_2, \text{ }A_1\overline{A_2}, \text{ }\overline{A_1}A_2, \text{ }\overline{A_1}\overline{A_2}\} }\]
4.1.1. Concepto de probabilidad
Ahora bien: siguiendo con el experimento descripto en la sección anterior (arrojar dos veces un dado para registrar los resultados obtenidos), se observa que, al repetírselo reiteradas veces, resultará poco frecuente que los dos tiros nos permitan obtener un as. En cambio, en muchas de las oportunidades notaremos que no habrá de obtenerse un as en ninguno de los dos tiros.
Diremos entonces que es poco probable obtener dos ases, en tanto que es bastante probable no obtener un as en ninguno de los dos tiros.
Cuantificaremos entonces nuestras aseveraciones definiendo como probabilidad de obtener un determinado resultado en nuestro experimento (\(P (E)\)) al cociente entre el número de casos en los que dicho resultado hubiera de obtenerse (casos favorables) y el número total de casos posibles. Es decir:
\[ {\large P (E) = \frac{\text{número de casos favorables}}{\text{número de casos posibles}} }\]
En la tabla de la imagen 4.1 reproducimos todos los posibles resultados del experimento propuesto. Obsérvese que las columnas impares de dicha tabla contienen los resultados posibles para el primer tiro, en tanto que en las columnas pares se crean las combinaciones correspondientes, a partir de los posibles resultados en el segundo tiro.
En la tabla de la imagen 4.2 reprodujimos la misma matriz, pero utilizando diversos colores para representar los distintos casos. Vemos que existen 36 casos posibles y que los cuatro resultados descriptos al definir el espacio muestral no resultan ser equiprobables (es decir, la probabilidad de que, por ejemplo, se obtengan dos ases es muy distinta a la probabilidad de que no se obtenga ninguno).
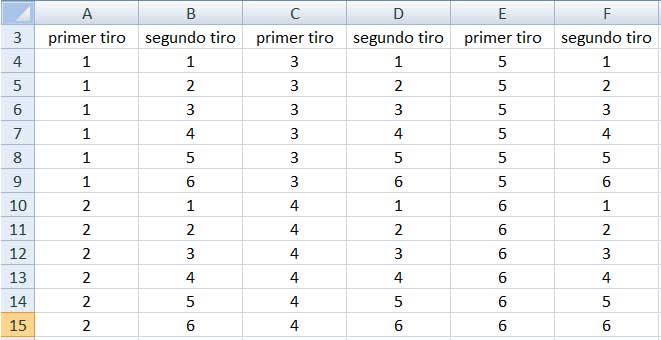
Matriz que contiene todos los posibles resultados de nuestro experimento.
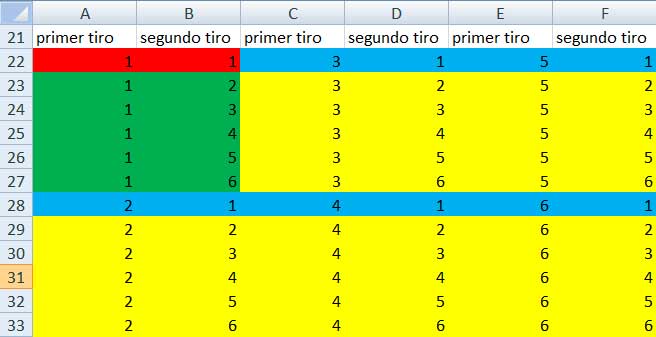
Con distintos colores indicamos los cuatro posibles resultados de nuestro experimento. Con rojo, sale as en ambos tiros; con verde, sale as en el primer tiro y no sale as en el segundo; con azul, no sale as en el primer tiro, pero sale as en el segundo; y finalmente, en amarillo, no sale as en ninguno de los dos tiros.
De acuerdo con la definición de probabilidad expresada anteriormente, la probabilidad de obtener ases en ambos tiros sería igual a:
\[{\large P(A_1 A_2) = \frac {1}{36} }\]
En cambio, la probabilidad de no obtener ases en ninguno de los dos tiros será:
\[{\large P (\overline{A_1} \overline{A_2}) = \frac {25}{36} }\]
En la tabla de la imagen 4.3 resumimos los valores de las probabilidades correspondientes a cada uno de los casos de nuestro espacio muestral. En la imagen 4.4 dichos valores se grafican en un diagrama de distribución de probabilidades.
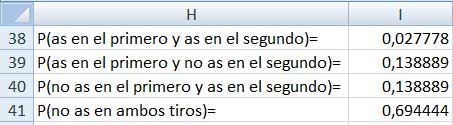
Probabilidad asignada a cada uno de los posibles resultados del experimento.
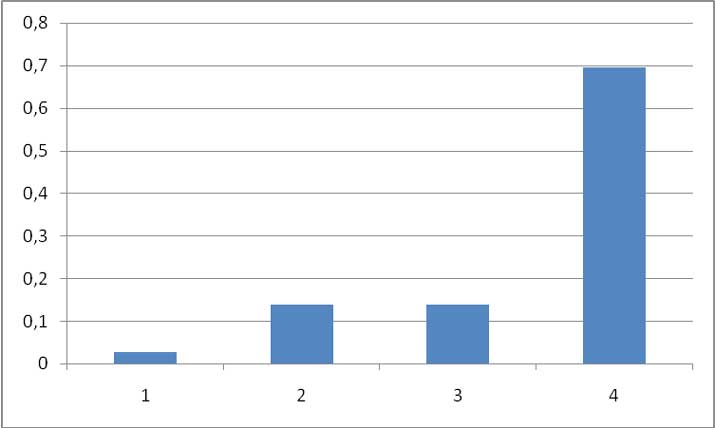
Diagrama de distribución de probabilidades para el experimento de arrojar un dado dos veces.
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México. pp. 61 a 66.
4.1.2. Propiedades de la probabilidad
De acuerdo con la expresión matemática que define la probabilidad, se observa que esta quedará representada por un número mayor que cero y menor que la unidad.
Si la probabilidad de que se produjera algún evento fuese cero, ello significaría que dicho evento es imposible. Si, en cambio, la probabilidad de que un suceso valiese uno, ello significaría que tenemos la certeza de que eso habrá de suceder.
Ninguna de dichas situaciones extremas entra dentro de nuestro campo de interés, puesto que en ambas poseemos certeza acerca de lo que está sucediendo.
Un ejemplo de interés se presenta cuando estudiamos la estructura del átomo. Por ejemplo, sabemos que en el caso del hidrógeno, la probabilidad de encontrar el único electrón de dicho átomo sobre algún punto de una superficie esférica con centro en el núcleo y radio 5,2. 10-11 metros es igual a uno (es decir, estamos seguros de que sobre dicha superficie esférica habrá de encontrarse el electrón). Pero, paralelamente, la probabilidad de encontrar en un instante determinado al electrón en un punto en particular de dicha superficie vale cero.
Por otro lado, si sumamos las probabilidades de ocurrencia de todos los resultados correspondientes a nuestro espacio muestral, el resultado de dicha suma debe ser uno. Ello es esperable: siempre dentro del experimento consistente en arrojar dos veces un dado y determinar cuántas veces sale un as, es esperable que salgan dos, uno o ninguno. La suma de los valores correspondientes en la columna derecha de la tabla de la imagen 4.3 efectivamente es igual a la unidad.
Se arroja dos veces un dado y se registra el número que se observa en la cara superior de este. Calcular la probabilidad de que dicho número sea:
- ambas veces par;
- par en el caso del primer tiro e impar en el segundo;
- impar en ambos tiros.
Ayuda: Aplicar la tabla de la imagen 4.1.
De un mazo de cartas españolas (cuarenta cartas) se extrae una carta al azar. Calcular la probabilidad de que:
- dicha carta sea un as;
- dicha carta sea de basto.
Montgomery, D.; Runger, G.(2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México, pp. 69 a 73.
4.1.3. Sucesos independientes
Supongamos que disponemos de una moneda y de un dado. Proponemos entonces un experimento consistente en arrojar al aire la moneda y el dado y observar qué número queda en la cara superior de este y si la moneda muestra cara o ceca.
Podríamos entonces preguntarnos cuál es la probabilidad de que salga un as en el dado y cara en la moneda. Como pedimos que ambas cosas sucedan simultáneamente, utilizando notación de conjuntos, podemos decir que buscamos:
\[{\large P(as \cap cara) }\]
Ahora bien: el resultado de cada uno de los dos sucesos es independiente del otro (el hecho de que salga cara en el tiro de la moneda en nada influye en el número que quede en la cara superior del dado, por ejemplo). Entonces, cuando dos sucesos sean independientes, la probabilidad de que ambos ocurran simultáneamente se calculará directamente como el producto de ambas probabilidades por separado, es decir:
\[{\large P(as \cap cara) = P (as) \cdot P (cara) = \frac {1}{6} \ast \frac {1}{2} = \frac {1}{12} }\]
Ahora propongamos otro experimento. Por ejemplo, dentro de una bolsa tenemos tres bolas azules y dos rojas. Supongamos que se extraen al azar dos bolas y se nos pregunta cuál es la probabilidad de que la primera sea azul y la segunda roja.
Antes de responder a dicha pregunta, debemos conocer exactamente de qué modo se llevó a cabo el experimento. No es lo mismo extraer la primera bola y registrar de qué color era antes de volver a introducirla en la bolsa para efectuar la segunda extracción (en cuyo caso decimos que el experimento se llevó a cabo con reposición) que sacar una primera bola sin devolverla a la bolsa antes de extraer la segunda (es decir, sin reposición).
En el primer caso, el resultado de la segunda extracción es independiente del de la primera (el número de bolas es el mismo antes de que se produzca cada una de las extracciones), y la respuesta será la siguiente:
\[P(\text{azul primera} \cap \text{roja segunda}) = P (\text{azul primera}) \cdot P (\text{roja segunda}) = \frac {3}{5} \ast \frac {2}{5} = \frac {6}{25} \]
Ahora bien: ¿qué sucedería si el experimento hubiera consistido en extraer una primera bola, tomar nota de cuál es su color y, sin devolverla a la bolsa, extraer una segunda?
4.1.4. Probabilidad condicionada y sucesos dependientes
Continuando con el experimento que estamos estudiando (es decir, la extracción de dos bolas del interior de una bolsa que contiene a tres de color azul y dos de color rojo), vemos que no resultaría difícil calcular, por ejemplo, la probabilidad de que la segunda bola extraída fuera roja sabiendo que la primera de ellas fue azul. Es decir, condicionamos el resultado de la segunda extracción a un posible resultado de la primera.
Podemos entonces escribir:
\[{\large P = \left(\frac{\text{segunda roja}}{\text{primera azul}}\right) = \frac {2}{4} }\]
Es decir, si sabemos que la primera bola extraída era de color azul, solo habrán quedado cuatro bolas en la bolsa, dos de las cuales son rojas.
Las dos extracciones son en este caso sucesos dependientes, y para responder a la pregunta inicial (“¿cuál es la probabilidad de que la primera bola sea azul y la segunda roja?”) ya no podremos operar como lo hicimos anteriormente. La expresión que hemos de aplicar al efectuar la extracción sin reposición será:
\[ P (\text{primera azul} \cap \text{segunda roja})= P\left(\frac{\text{segunda roja}}{\text{primera azul}}\right) \cdot P(\text{primera azul}) \]
Es decir:
\[{\large P (\text{primera azul} \cap \text{segunda roja})= \frac {2}{4} \ast \frac {3}{5} = \frac {3}{10} }\]
En general, dados dos sucesos dependientes A y B, diremos que la expresión de la probabilidad condicionada es:
\[{\large P (B/A)= P(A \cap B)\cdot P(A) }\]
- Con un mazo de cartas españolas (cuarenta cartas) se propone como experimento extraer dos cartas al azar. Calcular la probabilidad de que la primera de ellas sea el as de espadas y la segunda el siete de espadas, si la extracción se lleva a cabo sin reposición.
- Volver a calcular el valor pedido, pero suponiendo que la segunda extracción se efectúa después de volver a colocar la primera carta.
Una bolsa contiene dos bolas amarillas, tres rojas y cinco azules. Se propone extraer sin reposición tres bolas, y se pide calcular:
- la probabilidad de que las tres sean rojas;
- la probabilidad de que las tres sean azules;
- la probabilidad de que la primera sea azul, la segunda amarilla y la tercera azul.
Responder las mismas tres preguntas suponiendo que las extracciones se llevan a cabo con reposición.
Los exámenes finales de algunas materias del Ciclo Básico Común de la UBA constaban de veinte preguntas de elección múltiple. Cada una de ellas presentaba cuatro respuestas posibles y, para aprobar, el alumno debía responder correctamente un mínimo de ocho preguntas. ¿Cuál era la probabilidad de que un alumno, sin haber estudiado, aprobase un examen de esas características respondiendo únicamente ocho preguntas?
4.2. Reglas fundamentales de la probabilidad
4.2.1. Regla de la suma
Supongamos ahora que contamos con un mazo de cartas españolas y que el experimento consistiese simplemente en extraer una carta al azar y observar de qué carta se trata.
Si nos pidieran entonces calcular la probabilidad de que la carta extraída fuera un as o un oro, debemos expresar la consigna como:
\[{\large P(as \cup oro) }\]
La carta que nos interesa debe ser un as, un oro… ¡o el as de oros! Es decir, existe la probabilidad de que una de las cuarenta cartas cumpla con ambas condiciones simultáneamente.
Entonces, la forma de responder a la pregunta que se nos hizo será:
\[{\large P(as \cup oro) = P(as) + P(oro) - P(as \cap oro) }\]
Si reemplazamos por los valores correspondientes:
\[{\large P(as \cup oro) = \frac{4}{40} + \frac{10}{40} - \frac{1}{40} = \frac{13}{40}}\]
Si, en cambio, se nos preguntara cuál es la probabilidad de que la carta sea un oro o una espada, nuestra respuesta sería:
\[{\large P(oro \cup espada) = P(oro) + P(espada) }\]
Es decir:
\[{\large P(oro \cup espada) = \frac{10}{40} + \frac{10}{40} = \frac{1}{2} }\]
En este caso, P(oro ∩espada)=0, puesto que los sucesos de ser un oro o ser una espada son mutuamente excluyentes.
Podemos entonces decir que, dados dos sucesos A y B, se cumple que \(P (A\cup B) = P (A) + P (B) - P(A\cap B)\), siempre y cuando dichos sucesos no sean mutuamente excluyentes (en cuyo caso \( P(A\cap B) = 0\).
4.2.2. Probabilidad de un suceso complementario \(\overline{E}\)
Supongamos que tenemos una bolsa con tres bolillas azules, dos rojas, cuatro blancas y seis negras. Proponemos como experimento extraer una de las bolillas y observar de qué color es.
Si se nos preguntara cuál es la probabilidad de que la bolilla extraída fuera azul, definiríamos entonces como evento E al hecho de que la bolilla que se extraiga sea de ese color.
En ese caso:
(4.1)\[{\large P (E) = \frac {\text{número de bolillas azules}}{\text{número total de bolillas}} = \frac {3}{15} = \frac {1}{5} = 0,2 }\]
Si seguidamente se nos preguntara cuál es la probabilidad de que la bolilla extraída no fuese azul, podríamos entonces responder que:
\[{\large P (\overline{E}) = P(roja) + P(blanca) + P(negra) }\]
Es decir:
(4.2)\[{\large P (\overline{E}) = \frac {2}{15} + \frac {4}{15} + \frac {6}{15} = \frac {12}{15} = \frac {4}{5} = 0,8 }\]
Sin embargo, puesto que los dos eventos definidos (“que la bolilla sea azul” y “que la bolilla no sea azul”) son mutuamente excluyentes, la probabilidad de que ambos sucedan simultáneamente vale cero, es decir:
(4.3)\[{\large P (E \cap \overline{E}) = 0 }\]
Además, tengamos en cuenta que:
(4.4)\[{\large P (E \cup \overline{E}) = 1 }\]
Ello se debe a que, independientemente del color que tenga la bolilla, tenemos la certeza de haber extraído alguna.
Si aplicamos la regla de la suma a nuestro experimento, veremos que:
(4.5)\[{\large P (E \cup \overline{E}) = P(E) + P(\overline{E}) - P (E \cap \overline{E}) }\]
Reemplazando (4.3) y (4.4) en (4.5), obtenemos:
(4.6)\[{\large 1 = P(E) + P (\overline{E}) - 0 \to P (\overline{E}) = 1 -P(E) }\]
Dicho en lenguaje coloquial, la probabilidad de que no sea azul es igual a uno (que representa la certeza de haber extraído alguna bolilla) menos la probabilidad de extraer una bolilla azul.
Es evidente que de este modo llevamos a cabo muchos menos cálculos que los expresados en (4.2); simplemente, basta con restarle a la unidad el valor calculado en (4.1):
\[{\large P(\overline{E}) = 1 - P(E) = 1 -0,2 =0,8 }\]
De un mazo de cartas españolas se extrae una carta al azar. Calcular la probabilidad de que dicha carta sea espada o que sea una figura (es decir, un diez, un once o un doce).
Se arroja un dado y se observa cuál es el número que aparece en su cara superior. Calcular la probabilidad de que dicho número sea seis o sea par.
Se arroja un dado cargado, en el cual la probabilidad de que quede un seis en la cara superior vale 0,25. ¿Cuál será la probabilidad de que, una vez que se lo arroje, el número que pueda leerse sea uno, dos, tres, cuatro o cinco?
4.3. Empleo de diagramas de Venn
Se nos plantea ahora la siguiente situación: dentro de una empresa, el 45 % de los empleados habla inglés, el 15 % de ellos habla alemán y un 5 % de los empleados ha declarado que habla ambos idiomas.
A partir de lo que expresa la regla de la suma, podríamos escribir:
\[{\large P (inglés \cup alemán) = P (inglés) + P(alemán) - P(inglés \cap alemán) }\]
En números:
\[{\large P (inglés \cup alemán) = 0,45 + 0,15 - 0,05 = 0,55 }\]
El dato puede resultar útil, pues si aplicamos la expresión (4.6) podremos saber qué porcentaje de empleados de la empresa no habla ni inglés ni alemán. Es decir:
\[{\large P (\overline{inglés} \cup \overline{alemán}) = 1 - 0,55 = 0,45 }\]
Toda esta información puede volcarse en un tipo de diagrama empleado frecuentemente en la teoría de conjuntos denominado Diagrama de Venn.
En la imagen 4.5 presentamos la forma de construir el diagrama correspondiente a nuestro problema. Lo primero que debemos definir, para poder construir nuestra tabla, es el número de clases en las que agruparemos nuestros datos.
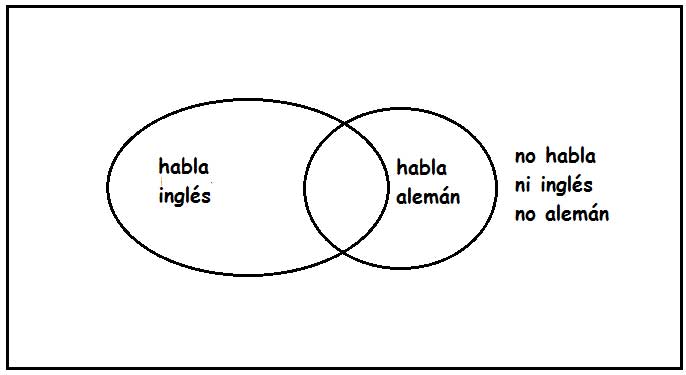
Diagrama de Venn para el problema propuesto en la presente sección.
El rectángulo representa el denominado conjunto universal, que contiene a todos los casos posibles. El globo de la izquierda incluye a todos los empleados que hablan inglés; el de la derecha, a todos los que hablan alemán. El área encerrada entre ambos (coloreada en verde en la imagen 4.6) corresponde a los empleados que hablan ambos idiomas.
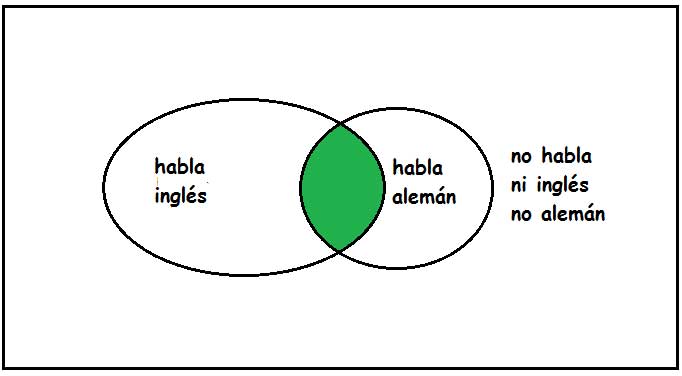
El área en color verde representa a aquellos empleados que hablan ambos idiomas.
Finalmente, en la imagen 4.7 agregamos los datos del enunciado y los calculados a partir de aquellos.
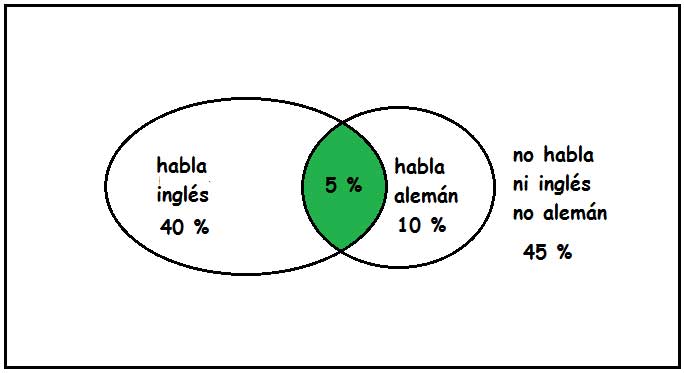
Volcamos los datos en el diagrama de Venn
Ciento cincuenta operarios trabajan en el área de producción de una empresa. De ellos, el 50 % opera reactores. Se sabe que, además, 50 operarios han sido capacitados para realizar controles de calidad, y que 15 operarios operan reactores y además fueron capacitados para realizar controles de calidad. Se pide:
- Representar la situación construyendo el Diagrama de Venn correspondiente. Expresar los datos en cantidad de operarios.
- ¿Cuál es la probabilidad de que un operario tomado al azar no sepa operar reactores ni haya sido capacitado para llevar a cabo tareas de control de calidad?
El Ministerio de Transporte lleva a cabo una encuesta, a partir de una muestra conformada por 2500 personas. De ellas, la mitad informa que debe tomar tren o subte para llegar desde sus hogares hasta su lugar de trabajo. Otras 300 personas responden que solo toman subte para llegar a sus empleos, en tanto que 400 personas dicen que solo toman tren para efectuar dicho viaje.
El resto de los entrevistados informa que emplea otro tipo de medio de transporte para movilizarse desde su casa hasta su trabajo. Construir el Diagrama de Venn y responder:
¿Cuál es la probabilidad de que una de las personas entrevistadas tomada al azar haga el viaje mencionado tomando solamente tren y subte?
4.4. Teorema de Bayes
En la presente unidad hemos hablado acerca de la probabilidad condicionada. Pero vamos a avanzar sobre el concepto, a partir del siguiente ejemplo.
Supongamos que, en víspera de elecciones, un partido político efectúa un estudio, del que se desprende que el 75 % de las mujeres encuestadas votarían al candidato A (que encabeza las listas de dicho partido), mientras que la intención de voto hacia dicho candidato por parte de los hombres resulta ser solamente del 45 %.
Es decir, la probabilidad de que un voto dado sea para el candidato A, sabiendo que dicho voto fue emitido por una mujer, es del 75 %; asimismo, la probabilidad de que un voto dado sea para el candidato A, sabiendo que dicho voto fue emitido por un hombre, es del 45 %.
Entonces, podríamos escribir:
\[{\large P(\text{voto para A} \text{ / } \text{vota una mujer}) = 0,75 }\]
\[\large P(\text{voto para A} \text{ / } \text{vota un hombre}) = 0,45\]
Podemos expresar en forma reducida dichas probabilidades condicionadas escribiendo:
\[{\large P(A \text{ / } mujer) = 0,75 }\] y \[{\large P(A \text{ / } hombre) = 0,45 }\]
Supongamos, por otro lado, que el 52 % del padrón está conformado por mujeres y el 48 % restante por hombres. Es decir:
\[{\large P(mujer) = 0,52 }\] y \[{\large P(hombre) = 0,48 }\]
Ahora bien: supongamos que el día de la elección se extrae de una de las urnas un voto para el candidato A y por alguna razón nos interesa saber cuál es la probabilidad de que dicho voto hubiera sido emitido por una mujer.
Es decir, deseamos saber si el voto fue depositado por una mujer sabiendo que le corresponde al candidato A.
O sea, nos interesa conocer:
\[{\large P(\text{voto de una mujer} \text{ / } \text{vota para A}) }\]
O, en forma reducida:
\[{\large P(mujer \text{ / } A) }\]
Como vemos, se ha invertido el orden de la condicionalidad.
Ahora bien, de acuerdo con lo dicho anteriormente respecto de la probabilidad condicionada, podemos escribir:
(4.7)\[{\large P(mujer \text{ / } A) = \frac {P (\text{mujer } \cap \text{ A})}{P(A)} }\]
Además, sabemos que:
(4.8)\[{\large P(A \text{ / } mujer) = \frac {P (\text{A } \cap \text{ mujer})}{P(mujer)} = \frac {P (\text{mujer } \cap \text{ A})}{P(mujer)} }\]
De acuerdo con lo expresado en (4.8), podemos escribir:
(4.9)\[{\large P (\text{mujer } \cap \text{ A}) = P (A \text{ / }mujer \cdot P(mujer)) }\]
Por otro lado, a partir de los datos que nos ofrece el problema, sabemos que:
(4.10)\[{\large P (A) = P (A \text{ / }mujer) \cdot P(mujer) + P(A \text{ / }hombre) \cdot P(hombre) }\]
Si entonces reemplazamos las expresiones (4.10) y (4.9) en la (4.7), obtendremos:
\[{\large P (mujer \text{ / }A) = \frac {P (A \text{ / }mujer) \cdot P(mujer)}{P(A \text{ / }mujer) \cdot P(mujer) + P(A \text{ / }hombre) \cdot P(hombre)} }\]
Dicha expresión, mediante la cual llegamos a calcular una probabilidad condicionada invirtiendo el sentido de la condicionalidad, se corresponde con lo que enuncia el Teorema de Bayes.
El Teorema de Bayes puede expresarse en forma genérica como:
\[{\large P(A_j \text{ / } B) = \frac {P(B \text{ / } A_j) P(A_j)}{\sum P(B \text{ / }A_k) P(A_k)} }\]
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México, pp. 91 y 92.
Una pyme tiene tres máquinas (la I, la II y la III) con las que produce arandelas de presión. El 1 % de las piezas que salen de la máquina I resultan defectuosas. Lo mismo sucede con el 2 % de las que salen de la máquina II y con el 1,5 % de las que produce la máquina III. Por otro lado, el 40 % de la producción recae sobre la máquina I, en tanto que las máquinas II y III fabrican en igual proporción las arandelas restantes.
Si durante una inspección de rutina se detecta una arandela defectuosa, ¿cuál es la probabilidad de que haya sido fabricada por la máquina II?
4.5. Combinatoria
No queremos finalizar la presente unidadsin hacer mención a una de las herramientas que en muchos casos resulta fundamental para el cálculo de probabilidades.
4.5.1. Permutaciones sin repetición
Supongamos que seis amigos deciden reservar una mesa en un restaurante para cenar. El local dispone de mesas redondas en las que ellos pueden ubicarse cómodamente y nos podemos preguntar, por ejemplo, cuál es la probabilidad de que dos de ellos (digamos Nahuel y Francisco) se sienten juntos. Sabemos que para ello deberíamos conocer, por empezar, de cuántas formas distintas podrían sentarse los seis amigos.
Tenemos entonces seis elementos (cada uno de los amigos) y seis posiciones a cubrir (los lugares que habrán de ocupar en la mesa reservada). Cada una de las posibles distribuciones de los lugares habrá de diferir de las otras solo por el modo en que los comensales se ubiquen.
Cuando esto suceda, diremos que estamos en presencia de una permutación de n elementos.
El cálculo del número de permutaciones posibles (al que expresaremos como Pn) se obtiene haciendo:
\[{\large P_n = n! }\]
En la expresión que acabamos de presentar, n!recibe el nombre de factorial de n, y se define como el producto de todos los números naturales entre uno y n.
Para resolver el problema que propone el ejemplo, debemos hacer el siguiente razonamiento: tratándose de seis personas, el número de formas distintas en las que podrían tomar asiento será igual a:
\[{\large P_6 = 6! = 1.2.3.4.5.6 = 720 }\]
Una vez calculados todos los casos posibles, nos interesa obtener el número de casos favorables (es decir, aquellos en los que Nahuel y Francisco habrán de sentarse uno al lado del otro). Para ello, podemos hacer un razonamiento sencillo: en lugar de pensar en seis elementos, tomemos a los dos amigos como si solo fuesen un elemento, con lo que la cantidad de formas en las que los seis comensales habrán de tomar asiento —con la condición de que dos de ellos estén uno al lado del otro—, se podrá calcular como:
\[{\large 2.P_5 = 2.5! = 2.1.2.3.4.5 = 240 }\]
Obsérvese que al factorial hemos de multiplicarlo por dos, puesto que habrá que contemplar que, aun sentándose juntos, Nahuel podrá sentarse a la izquierda de Francisco o viceversa.
Así, finalmente, la probabilidad de que estos dos amigos se sienten juntos ante la mesa del restaurante será:
\[{\large P(\text{Nahuel junto a Francisco}) = \frac {2.P_5}{P_6} = \frac{1}{3} }\]
¿Cuál es la probabilidad de que al colocar en el estante de una biblioteca tres libros de química, cuatro de física y cinco de matemática sin criterio determinado, queden acomodados de tal modo que se encuentren separados por materia?
4.5.2. Variaciones sin repetición
En una bolsa tenemos nueve bolillas numeradas (del uno al nueve). Nos proponemos entonces extraer sin reposición tres de ellas, de modo de generar un número de tres cifras. La primera bolilla corresponderá a las centenas, la segunda a las decenas y la tercera a las unidades.
Nos preguntamos, entonces, cuál será la probabilidad de que el número obtenido mediante este procedimiento sea menor que 312.
A diferencia de lo que sucedía en el ejemplo propuesto en la sección anterior, contamos ahora con nueve elementos, de los cuales solo habremos de seleccionar tres. Por otro lado, el orden en el que los elementos sean extraídos nos interesa: aun cuando las tres bolillas extraídas fuesen las mismas, el 312, el 213 o el 123 resultan ser diferentes entre sí, como consecuencia de que las mismas bolillas salieron de la bolsa en distinto orden.
Cuando el número de elementos de que se dispone es superior al de los que habrán de interesarnos en el problema en cuestión, y el orden en que dichos elementos se encuentren diferencie un resultado posible de otro, diremos que el número total de resultados habrá de calcularse como variaciones de n elementos tomados de a m. En símbolos:
\[{\large V^n_m = \frac {n!}{(n-m)!} }\]
Así, la cantidad total de ternas posibles será igual a las variaciones de nueve elementos tomados de a tres.
Calculamos entonces:
\[{\large V^9_3 = \frac {9!}{(9-3)!} = \frac {9.8.7.6!}{6!} = 504 }\]
Para conocer el número de casos favorables (es decir, aquellos en los que el número sea menor que el 312) debemos tener en cuenta que ese es el menor número comenzado en tres que podemos generar con las cifras disponibles. Es decir, lo que en definitiva se nos pide es determinar la probabilidad de que el número en cuestión corresponda a la primera o la segunda centena.
Si la primera bola extraída fuese el uno, quedarían entonces otras ocho bolas en la bolsa, que permitirían generar:
\[{\large V^8_2 = \frac {8!}{(8-2)!} = \frac {8.7.6!}{6!} = 56 }\]
Lo mismo sucedería si la primera bolilla extraída fuese el dos (en cuyo caso los números obtenidos corresponderían a la segunda centena).
Entonces, aplicando la definición de probabilidad, escribimos:
\[{\large P (\text{número menor que 312}) = \frac {2.V^8_2}{V^9_3} = \frac {112}{504} }\]
Durante los Juegos Olímpicos, un atleta argentino resulta ser uno de los seis finalistas en la competencia de lanzamiento de disco. Teniendo en cuenta que solo tres de ellos habrán de ser galardonados con las consabidas medallas de oro, bronce y plata, ¿cuál es la probabilidad de que nuestro compatriota reciba la primera de ellas?
4.5.3. Combinaciones sin repetición
La Comisión Directiva de un club vecinal está conformada por quince miembros. Se decide conformar una Subcomisión de Juegos de Salón, conformada por tres miembros de la propia Comisión Directiva. El mecanismo de selección de sus miembros es elemental: dentro de una bolsa se coloca un papel con el nombre de cada uno de los quince miembros, y se extraen tres de dichos papeles. Si el Señor López es uno de las quince personas, ¿cuál es la probabilidad de que forme parte de la subcomisión?
Como hay quince personas y solo tres cargos a cubrir, doce de ellas terminarán fuera de la selección. Sin embargo, a diferencia de lo que sucedía en el caso de las variaciones, aun cuando los elegidos fuesen, por ejemplo, los señores López, Pérez y García, el orden en el que los papelitos fuesen retirados de la bolsa no distinguiría a una de las posibilidades de las restantes. Es decir, a los fines prácticos, da lo mismo que el papel en el que aparecía el nombre de López aparezca en primer, segundo o tercer lugar: para el caso, lo único que importa es que el habrá de conformar la subcomisión.
Cuando el número de elementos sea inferior al de posiciones a ocupar (como en el caso de lasvariaciones) pero no importe el orden en que se encuentren los elementos seleccionados, diremos que se trata de una combinación de n elementos tomados de a m, que habrá de calcularse mediante la expresión:
\[{\large c^n_m = \frac{n!}{(n-m)!.m!} }\]
Entonces, para la resolución de nuestro problema, podemos razonar prácticamente del modo en que lo hicimos en el caso de las variaciones. Los casos posibles serán ahora combinaciones de quince elementos tomados de a tres, en tanto que los casos favorables serán combinaciones de catorce elementos tomados de a dos (ya que debemos considerar que uno de los tres cargos ya ha quedado en manos del señor López). Escribimos entonces:
\[{\Large P (\text{López en Subcomisión}) = \frac {C^{14}_2}{C^{15}_3} = \frac {\frac{14!}{(14-2)!.2!}}{\frac{15!}{(15-3)!.3!}} = \frac{1}{5} }\]
Teniendo en cuenta que un hexágono es un polígono de seis lados y que se define como diagonal de un polígono al segmento que une dos de sus vértices no consecutivos, se pide calcular cuántas diagonales tiene un hexágono.
Walpole, R.; Myers, R; Myers, S.; Keying Ye(2007), Probabilidad y Estadística para Ingeniería y Ciencias, Pearson Education, México, pp. 31 a 46.
Devore, J.(2008), Probabilidad y Estadística para Ingeniería y Ciencias, CengageLearning, México, pp. 51 a 56.

