Teoría del muestreo
Objetivos
Que el alumno:
- Comprenda porqué cualquier estadístico puede pensarse como una variable aleatoria.
- Se familiarice con la distribución de Student y aprenda a aplicarla en aquellos casos en que las condiciones del problema lo exijan.
- Conozca el Teorema Central del Límite y comprenda la importancia de su aplicación.
7.1. Distribuciones muestrales
Al tomar distintas muestras de una misma población nos encontramos con que sus estadísticos puedenadoptar distintos valores. Por ejemplo, en la imagen 7.1 reproducimos las tablas de valores correspondientes a tres muestras que fueron tomadas de una misma población.
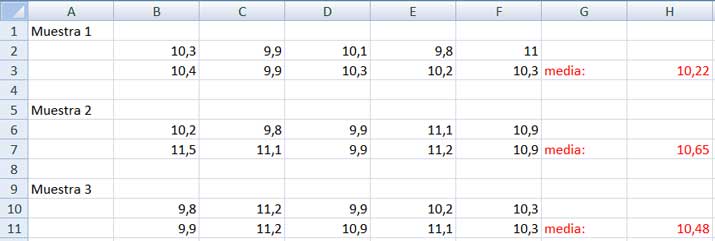
Teniendo en cuenta que el campo de la inferencia estadística tiene por objetivo obtener conclusiones sobre una población a partir de una o más muestras de esta, necesitamos entonces estudiar la distribución de todos los valores posibles de un estadístico dado.
Dado que entonces los valores de cualquier estadístico suelen cambiar de una muestra a otra, puede considerarse a dicho estadístico como una variable aleatoria a la que, como tal, habrá de corresponderle una determinada distribución de frecuencias. Llamaremos entonces distribución muestral a la distribución de frecuencias del estadístico en cuestión.
La distribución muestral de un estadístico, como veremos seguidamente, habrá de obtenerse a partir de muestras del mismo tamaño.
Weimer, R. (2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 353 a 356.
7.2. Media de la distribución muestral de las medias y desviación estándar para poblaciones de pequeño y gran tamaño
La media de la distribución muestral de la media de un grupo de muestras tomadas de una población dada es igual a la media de dicha población, lo que se expresa como:
\[\large{\mu_{\overline{x}}=\mu }\]
En lo que respecta a la desviación estándar de una media, tendremos que diferenciar dos situaciones. Por un lado, diremos que una muestra es de gran tamaño cuando N, el número de elementos que componen a dicha población, sea al menos veinte veces mayor a n, número de elementos que componen a cada una de las muestras.
Hecha esta aclaración, calcularemos la desviación estándar de una media para poblaciones de gran tamaño empleando la siguiente expresión:
\[\large{ \sigma_{\overline{x}}=\frac{\sigma}{\sqrt{n}} }\]
Aquí, \(\sigma\) representa la desviación estándar poblacional y n el tamaño de la muestra.
En cambio, cuando el tamaño de la población N resulte ser menor que veinte veces el tamaño de la muestra, la desviación estándar de la media se obtendrá empleando la expresión:
\[\large{ \sigma_{\overline{x}}=\frac{\sigma}{\sqrt{n}}\sqrt{\frac{N-n}{N-1}} }\]
Weimer, R. (2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 359 a 367.
7.3. Muestreo en poblaciones normales
Cuando las muestras de tamaño n provienen de una población normal, la distribución muestral de la media también será normal.
Entonces, si el muestreo se hace a partir de una población de gran tamaño (como vimos anteriormente, como mínimo mayor que veinte veces el tamaño de la muestra) cuya media es \(\mu\), entonces:
\[\large{\mu_{\overline{x}}=\mu }\]
Por otro lado, en lo que respecta a la deviación estándar muestral, tendremos:
\[\large{ \sigma_{\overline{x}}=\frac{\sigma}{\sqrt{n}}\sqrt{\frac{N-n}{N-1}} }\]
Por ejemplo, supongamos que el peso promedio de cierto tipo de arandela de presión fuese de 1,75 gramos, con una desviación estándar de valor 0,065 gramos. Si se seleccionaran muestras de tamaño 25, la distribución muestral de la media se distribuiría normalmente, siendo \(\mu_{\overline{x}}=1,75\) gramos y \(\sigma_{\overline{x}}=0,065\ /\sqrt{25}=0,013\) gramos. La imagen 7.2 nos permite comparar la distribución de la población (a la izquierda) con la distribución de la media muestral (a la derecha de la imagen).
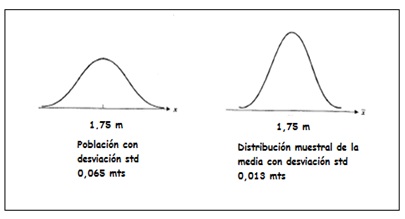
Comparación entre la distribución poblacional y la muestral.
¿Cuál es la probabilidad de que la media muestral de una muestra de tamaño 9 proveniente de una población normal con media 25 y desviación 6 sea mayor que 28?
La desviación estándar de la muestra será igual al cociente entre la desviación de la población (6, de acuerdo con el enunciado) y la raíz cuadrada del tamaño de la muestra (3, para una muestra de tamaño 9). Entonces
\[\large{\sigma_{\overline{x}}=2. }\]
Entonces:
\[\large{P(\overline{X} > 28)=1-P(\overline{X} \le 28)}\]
Este cálculo podrá efectuarse con nuestra planilla, tal como se muestra en la imagen 7.3.
El valor obtenido (0,0668) se ha verificado posteriormente utilizando el GeoGebra, tal como puede observarse en la imagen 7.4.
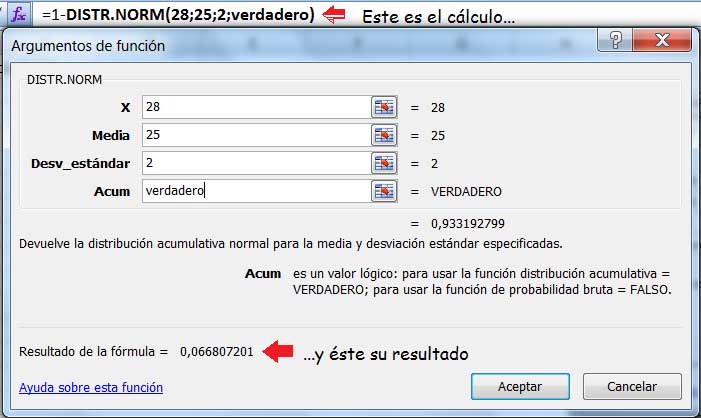
El valor que aparece en la parte inferior de la imagen corresponde al resultado de la pregunta
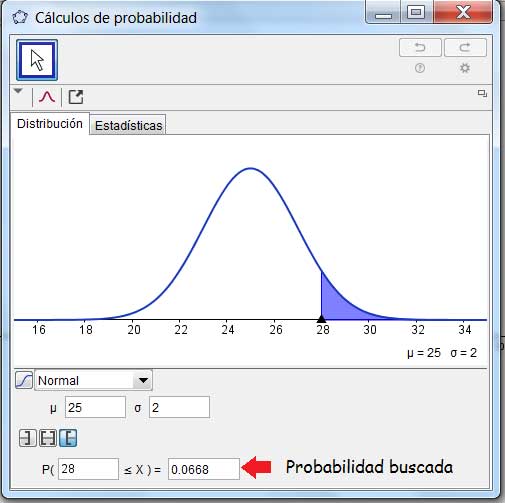
Verificamos el resultado del ejemplo obtenido mediante la planilla de cálculo utilizando el GeoGebra.
Los siguientes dos ejemplos ayudarán al estudiante a comprender en qué caso es necesario emplear la distribución muestral de la media.
(i) Encontrar la probabilidad de que la duración de una llamada telefónica recibida por una oficina de información supere los 3,5 minutos, sabiendo que la duración de las llamadas recibidas por dicha oficina se distribuye normalmente, con una media de 3,4 minutos y una desviación estándar de 0,30 minutos.
En este caso, estamos tomando al azar una llamada de todas las que recibe dicha oficina, de modo que basta con calcular:
\[\large{P(X > 3,5)=1-P(X \le 3,5)}\]
De acuerdo con la expresión matemática que nos define la probabilidad, se observa que esta quedará representada por un número mayor que cero y menor que la unidad.
Aquí tenemos \(\mu = 3,4\) y \(\sigma = 0,3\), de modo que basta con emplear nuestra planilla de cálculo con estos valores, tal como se observa en la imagen 7.5. El resultado obtenido fue verificado empleando el GeoGebra, tal como puede observarse en la imagen 7.6.
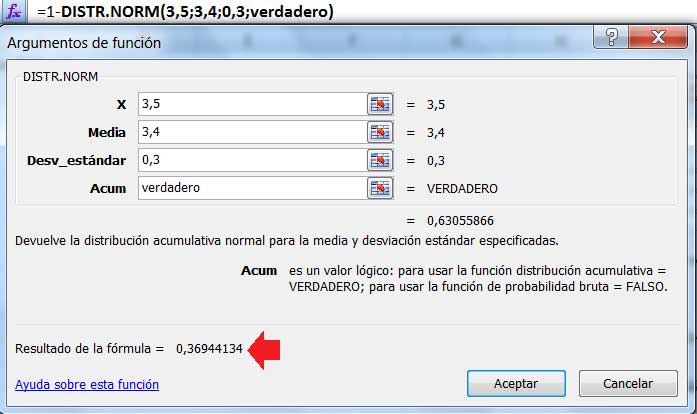
La probabilidad de que una llamada tomada al azar tenga una duración superior a los 3,5 minutos es del 2,27 %.
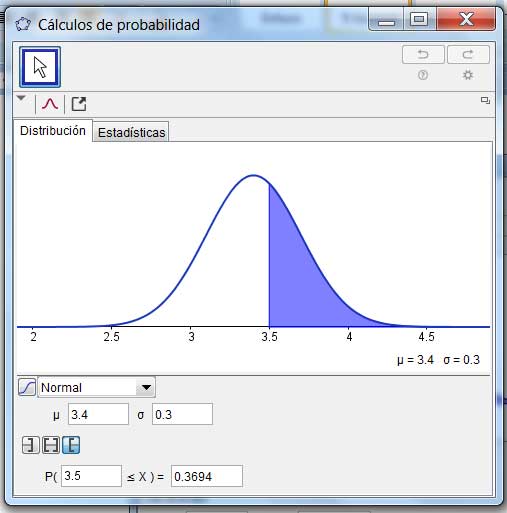
Verificamos los resultados obtenidos mediante la planilla de cálculo y graficamos con el GeoGebra.
(ii) Teniendo en cuenta que la duración promedio de una llamada recibida por la oficina de informes se distribuye normalmente, con una media de 3,4 minutos y una desviación estándar de 0,3 minutos, hallar la probabilidad de que la duración promedio de una muestra de 16 llamadas exceda los 3,5 minutos.
En este caso se requiere calcular una media muestral dentro de una muestra. Tendremos entonces que trabajar con la distribución muestral de la media. De modo que, aun cuando la media siga siendo de 3,4 minutos, la desviación estándar tomará valor:
\[\large{ \sigma_\overline{X}=\frac{0,3}{\sqrt{16}}=0,075 }\]
La respuesta, 0,0912, se obtuvo nuevamente empleando la planilla de cálculo, como puede observarse en la imagen 7.7. El resultado fue verificado, tal como lo hicimos en el caso anterior, empleando el programa GeoGebra, tal como puede verse en la imagen 7.8.
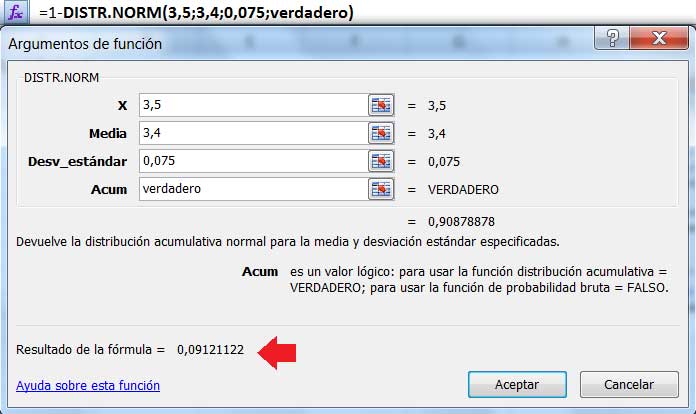
Cálculo de la probabilidad de que la duración promedio de una llamada dentro de una muestra de tamaño 16 supere los 3,5 minutos.
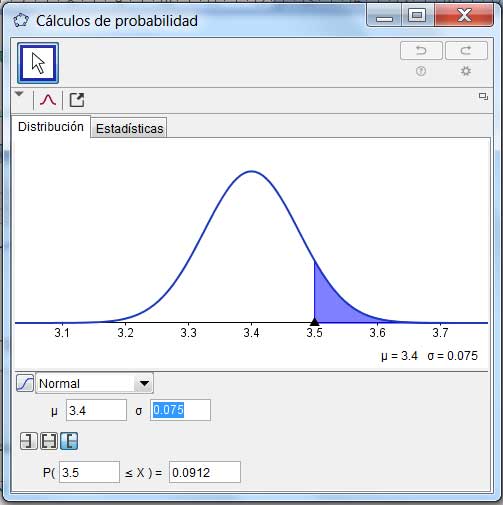
Verificación del resultado obtenido mediante la planilla de cálculo.
Weimer, R. (2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 369 a 373.
La temperatura de activación de un equipo contra incendios se distribuye normalmente, con una media de 130 grados y una desviación estándar de 2 grados. Una empresa compra veinte de esos equipos para instalarlos en una planta que está a punto de inaugurar. Calcular la probabilidad de que la media de la temperatura de activación de los equipos comprados por la empresa supere los 132 grados.
7.4. Distribución t de Student
Es frecuente que se tomen muestras de una población normal, para la cual la distribución muestral de la media también sea normal, pero donde no se conozca la desviación estándar de la población.
En estos casos se emplea un estadístico que recibe el nombre de estadístico t y que se calcula empleando la siguiente expresión:
\[\Large{ t=\frac{\overline{X}-\mu}{\frac{s}{\sqrt{n}}} }\]
Dado que ignoramos el valor de la desviación estándar poblacional, en la expresión utilizamos la desviación estándar de la muestra, s.
La gráfica correspondiente a la distribución t es muy similar a la de la distribución normal, puesto que ambas son de forma acampanaday simétricas respecto de sus medias. Sin embargo, en el caso de la distribución normal estándar, \(\overline{X}\) es la única cantidad que varía entre las distintas muestras, en tanto que en el caso de t varían tanto como s. La forma exacta de la distribución t dependerá entonces de un parámetro conocido como número de grados de libertad, que se suele expresar como gl y que es igual al tamaño de la muestra disminuido en una unidad.
En la imagen 7.9 pueden observarse superpuestas las gráficas de la distribución normal estándar y de dos posibles distribuciones t. Estas últimas, además de ser simétricas, tienen siempre por media al valor cero. Por otro lado, cabe recalcar que se van haciendo cada vez más parecidas a la normal a medida que aumentan los grados de libertad.
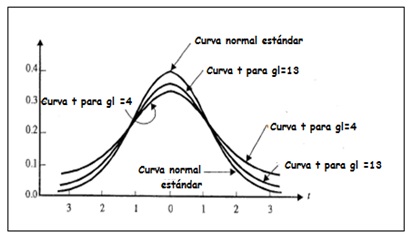
Comparación entre la distribución normal estándar y dos distribuciones t.
Weimer, R. (2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 373 a 376.
7.5. Muestreo de poblaciones no normales. Teorema Central del Límite
Hemos visto anteriormente que cuando la población de la que se extraían las muestras era normal, la distribución muestral de las medias también lo era. Sin embargo, en muchos casos se trabaja con muestras de poblaciones grandes cuya forma exacta y parámetros ignoramos.
Cuando el tamaño de la muestra es grande (en la práctica, superior a las treinta unidades) se observa que la distribución muestral de la media tiene forma acampanada.
Además, cuanto mayor sea el tamaño de la muestra, más se aproximará a la curva característica de la distribución normal.
Para interpretar lo que acabamos de decir, consideramos adecuado partir de un ejemplo desarrollado por Box, Hunter y Hunter (1978) al que accedimos a través de Montgomery y Runger (2003).
Box, G. E. P.; Hunter, W. G.; Hunter, J. S. (1978),Statistics for Experiments, John Wiley and Sons, New York.
Montgomery, D.;Runger, G. (2003), "Chapter 7.Point estimation of Parameters".En: Applied Statistics and Probability for Engineers, Wiley and Sons, New York, pp. 239 a 241.
Supongamos que arrojamos al aire un dado y definimos como variable aleatoria el valor que queda en la cara superior de este una vez que cae. Suponiendo que dicho dado no esté cargado, sabemos que dicha variable adoptará valores enteros mayores o iguales a uno y menores o iguales a seis. La probabilidad correspondiente a cada uno de los seis valores de la variable es la misma, siendo el gráfico correspondiente a la distribución de probabilidades el que se observa en la imagen 7.10.
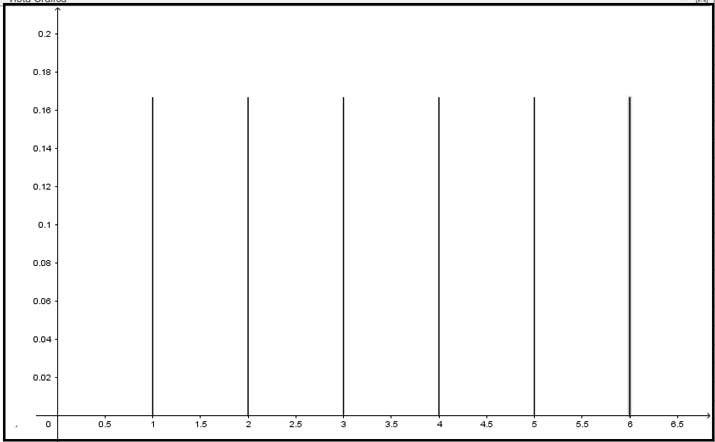
Distribución de probabilidades para el caso del lanzamiento de un dado
Supongamos ahora que el experimento consiste en lanzar simultáneamente al aire dos dados, siendo la variable aleatoria en este caso el promedio de los dos valores obtenidos.
En este caso, la obtención de las probabilidades para cada una de las variables nos demandará un poco más de trabajo. Para comenzar, existen 36 casos posibles, que habrán de contemplarse. En la imagen 7.10 reproducimos la modalidadque utilizamos para determinar todos los casos posibles. La primera fila y la primera columna aparecen en rojo y corresponden al valor que se podría obtener respectivamente al arrojar el primero y el segundo de los dados. En la imagen 7.11 dividimos por dos a cada uno de los valores de la matriz anterior, quedando así definidos los posibles valores de la variable aleatoria para este segundo caso. Gracias a la información obtenida, construimos la tabla de distribución de probabilidades, que se reproduce en la imagen 7.13. Finalmente, la imagen 7.14 nos muestra el gráfico correspondiente a la distribución de probabilidades para el promedio del tiro de dos dados.
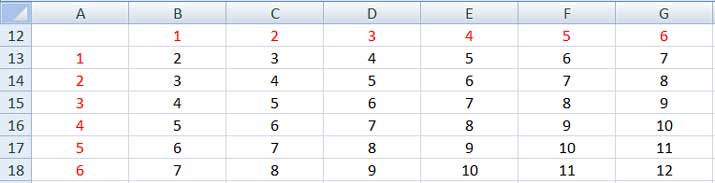
La primera columna de la matriz representa al valor que puede salir para el primero de los dados, en tanto que la primera fila al que puede salir en el segundo. Los restantes valores corresponden a la suma de ambos.
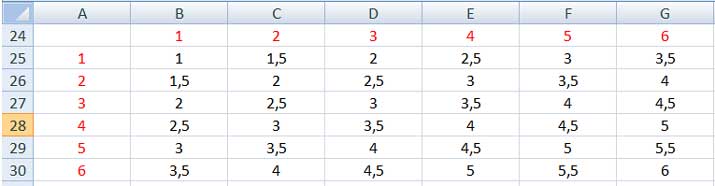
En este caso, los valores en negro dentro de la tabla representan a los promedios de las sumas de valores obtenidos. Se observa que los valores de la variable aleatoria ya no son solo enteros, sino que habrán de incluirse 1,5; 2,5; 3,5; 4,5; y 5,5.
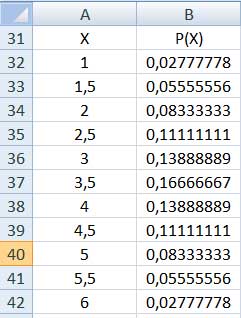
Con la información que ofrece la matriz de la imagen 7.12 construimos la tabla de distribución de probabilidades para la variable aleatoria promedio obtenido a partir del tiro de dos dados.
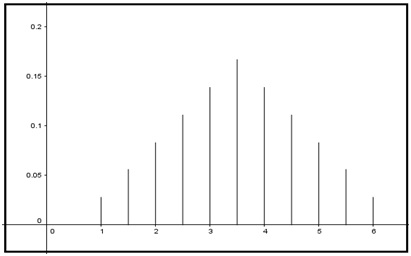
Distribución de probabilidades para el promedio del valor obtenido al arrojar dos dados.
Finalmente, suponemos que el experimento consiste en arrojar ahora tres dados, de modo que la variable aleatoria asociada al mismo habrá de ser el promedio de los valores obtenidos con los tres dados en cada tiro.
En la imagen 7.10 se pudo observar la matriz que generamos oportunamente para evaluar el caso anterior, es decir, el de la obtención del promedio obtenido con solo dos dados. Sin embargo, en este caso nos vemos obligados a manejar mucha más información. Para ello construimos la matriz que se reproduce en la imagen 7.15: la primera columna corresponde a los valores que podrían obtenerse al tirar los dos primeros dados, mientras que la primera fila indica los valores que podrían resultar al arrojar el tercero de los tiros. En la matriz figuran las sumas de los posibles valores obtenidos al lanzar tres dados.
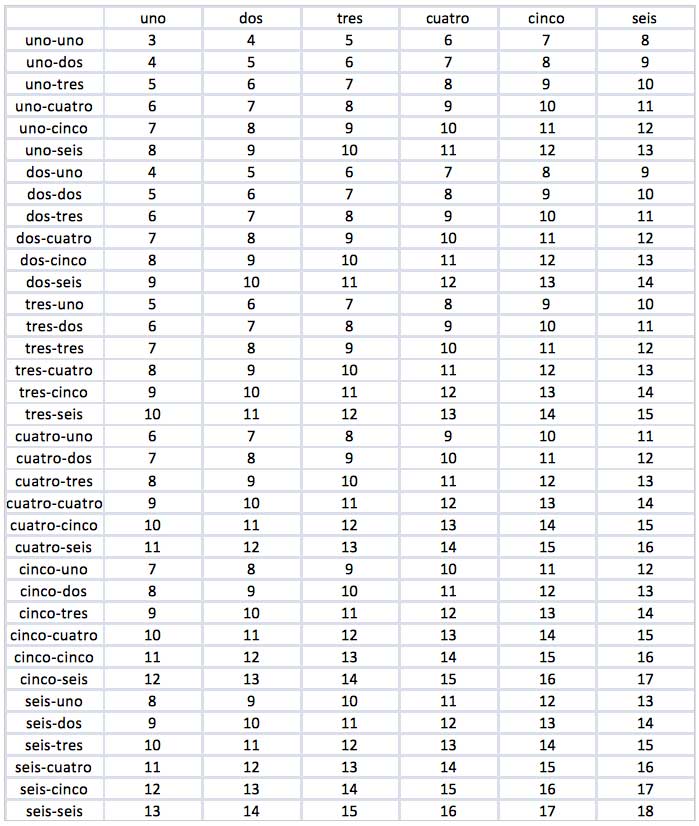
Matriz que contiene la suma de los valores obtenidos al arrojar tres dados para todos los casos posibles. En la primera columna figuran los valores de los números que salen en los primeros dos dados, en tanto que la primera fila escribimos el valor del número que sale en el tercer dado. Los restantes números de la matriz corresponden a las sumas de los valores obtenidos en cada uno de los 216 casos posibles.
Para obtener, como en los casos anteriores, el diagrama de distribución de probabilidades correspondiente, desarrollamos un programa de computadora con el Matlab, que se observa en la imagen 7.16. Mediante dicho programa obtuvimos la tabla de distribución de probabilidades (que, como captura de pantalla, puede verse en la imagen 7.17) y el diagrama de distribución. A este último lo hemos representado dos veces. En la imagen 7.18 con el mismo formato que empleamos en la Imágenes 7.10 y 7.14, para el tiro de uno y dos dados, respectivamente.

Programa de computadora desarrollado para procesar la información correspondiente al experimento consistente en lanzar tres dados.

Tabla de distribución de probabilidades obtenida mediante nuestro programa de computadora. En la primera fila aparecen los valores correspondientes a la variable aleatoria, promedio del tiro de tres dados; en la segunda fila, las probabilidades correspondientes.
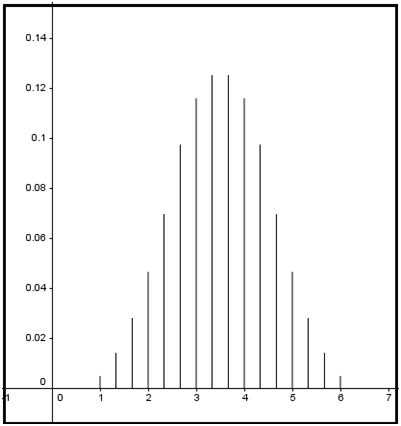
Distribución de probabilidades para el promedio del valor obtenido al arrojar tres dados.
En cambio, en la imagen 7.19, reproducimos el diagrama de distribución de probabilidades tal como se obtuvo empleando el programa de computadora. Como en él los valores de la probabilidad correspondiente a cada uno de los valores de la variable aleatoria aparecen unidos por pequeños segmentos, se hace evidente que el diagrama comienza a adoptar una forma acampanada y simétrica, característica de la distribución normal de probabilidades.
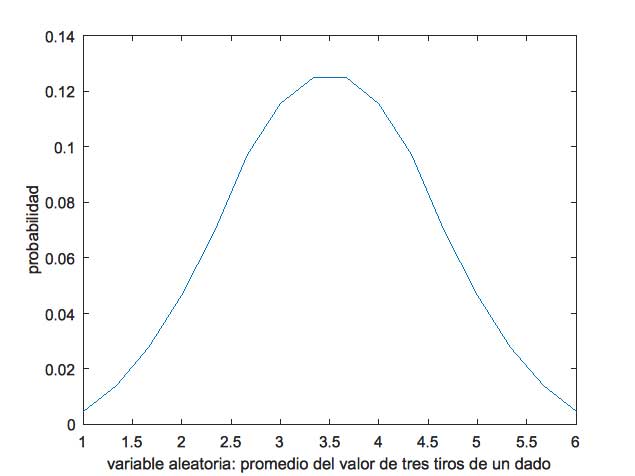
Diagrama de distribución de probabilidades para el promedio del tiro de tres dados obtenido mediante nuestro programa de computadora.
En la imagen 7.20 reproducimos los diagramas de distribución de probabilidades de las imágenes 7.10, 7.14 y 7.18, de modo que pueda compararse lo que sucede a medida que el tamaño de la muestra (es decir, el número de veces que arrojamos el dado) va aumentando. El trabajo de Box, Hunter y Hunter (1978) va mucho más allá de lo que acabamos de plantear, ya que allí aparecen además losdiagramas de distribución de probabilidades correspondientes al promedio del tiro de cinco y diez dados. Lo expresado al principio de esta sección, en el sentido de que cuanto mayor sea el tamaño de la muestra, más se aproximará el diagrama de distribución de probabilidades a la curva característica de la distribución normal, se hace evidente al observar los diagramas mencionados.
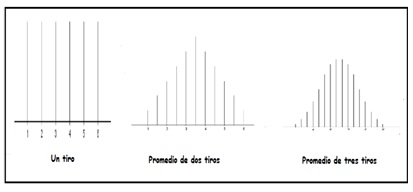
Comparación de las gráficas de distribución de probabilidades para un tiro, promedio de dos tiros y promedio de tres tiros.
Lo expuesto hasta aquí nos habilita a enunciar uno de los teoremas más útiles en Estadística, el Teorema Central del Límite.
Si \(X_1,\ X_2, \dots X_n\) es una muestra tomada al azar tomada de una población (ya sea finita o infinita) que tenga media \(\mu\) y varianza \(\sigma^2\) , siendo \(\overline{X}\) la media de la muestral, la distribución de:
\[\Large{ Z=\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}} }\]
será la distribución normal estándar, en la medida que el valor del tamaño muestraln tienda a infinito. Enunciamos así el Teorema Central del Límite.
Montgomery, D.; Runger, G. (2003), Applied Statistics and Probability for Engineers, John Wiley & Sons Inc., New York, pp. 301 a 303.
Weimer, R. (2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 378 a 387.
7.6. Distribución chi-cuadrado
Como veremos en las próximas unidades, una de las distribuciones de muestreo que habremos de utilizar con frecuencia es la distribución chi-cuadrado o ji cuadrado, según algunos autores. Tal denominación proviene de las denominaciones latina y castellana, respectivamente, de la letra griega c.
Para comenzar, definamos a la función gamma:
Se define a la función gamma como
\[\large{ \Gamma(r)=\int^\infty_0 x^{r-1}e^{-x} dx \text{ con }r > 0 }\]
Se trata de una función finita, que, para valores enteros de r verifica la condición:
\[\large{ \Gamma(r)=(r-1)! }\]
Conocida la función gamma, estamos en condiciones de presentar a la distribución chi-cuadrado:
Sean
\[\large{ Z_1,\ Z_2, \dots Z_k }\]
variables aleatorias distribuidas normal e independientemente, de modo que la media de cada una de ellas valga cero y la varianza sea en todos los casos igual a uno, puede definirse una variable aleatoria:
\[\large{ X= Z^2_1 + Z^2_2 + \dots + Z^2_k }\]
cuya función de densidad de probabilidad será:
\[\Large{ f(x)=\frac{1}{2^{k/2}\Gamma (\frac{k}{2})} e^{-(x/2)}x^{-(k/2)-1}\text{ para }x>0 }\]
Diremos entonces que la variable aleatoria X sigue una distribución chi-cuadrado con k grados de libertad, lo que generalmente se escribe como \(X^2_k\).
En la imagen 7.21 puede observarse la representación gráfica de la función de distribución de probabilidades de la distribución chi-cuadrado para k = 3. La variable aleatoria que estamos estudiando es no negativa y presenta sesgo hacia la derecha. Sin embargo, a medida que el parámetro k va aumentando, la distribución se hace más simétrica, asemejándose a la normal. Comparar la gráfica de la imagen 7.21 con la de la imagen 7.22, donde la variable k adopta valor 50.
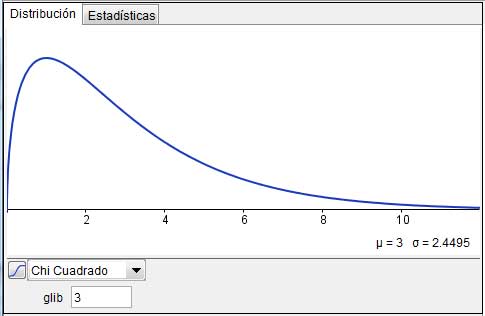
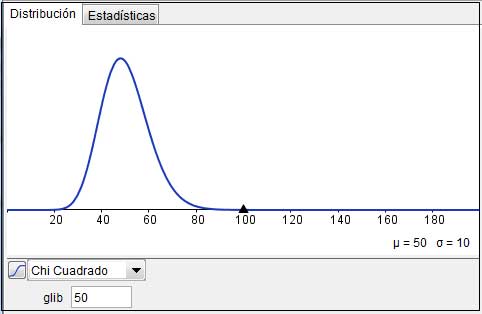
7.7. Distribución F
Otra de las distribuciones con las que trabajaremos en las últimas dos unidades es la distribución F, cuya variable aleatoria se define como el cociente entre dos variables chi-cuadrado independientes entre sí, cada una de las cuales deberá dividirse a su vez por su correspondiente grado de libertad. Así, siendo \(W\) e \(Y\) las variables independientes chi-cuadrado y \(u\) y \(\gamma\) sus respectivos grados de libertad, la variable aleatoria F podrá expresarse como:
\[\large{ F=\frac{W/u}{Y/\gamma} }\]
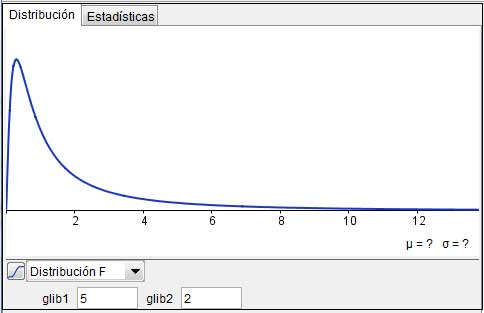
La distribución F depende entonces de dos variables (los grados de libertad de las variables aleatorias de su numerador y de su denominador) y su representación gráfica presenta sesgo hacia la derecha, tal como puede observarse en la imagen 7.23.
Montgomery, D.;Runger, G. (2003), Applied Statistics and Probability for Engineers, John Wiley & Sons Inc., New York, pp. 308 a 318.

