Distribuciones discretas
Objetivos
Que el alumno:
- Comprenda el concepto de distribución discreta y su importancia en las aplicaciones prácticas.
- Conozca dos de las distribuciones más frecuentemente empleadas, la binomial y la Poisson.
- Aprenda a resolver problemas concretos en las que dichas distribuciones sean aplicadas empleandosoftware.
5.1. Variable aleatoria y distribución de probabilidad
En la sección 4.1 de la unidad anterior propusimos un experimento consistente en arrojar dos veces un dado para registrar en cada caso si salía o no un as y dijimos que el espacio muestral correspondiente podía expresarse como:
\[{\large S= \{A_1A_2,A_1\overline{A_2},\overline{A_1}A_2,\overline{A_1}\overline{A_2}\} }\]
Recordemos que habíamos definido como \(A_i\) al suceso consistente en que se obtuviese un as en el i-ésimo tiro, mientras que escribíamos \(\overline{A_i}\) en caso de que no saliera as en ese mismo tiro.
A cada elemento del espacio muestral le podemos entonces asignar un valor numérico, en correspondencia con el número de veces que se hubiese obtenido un as. Esos valores (0, 1 o 2) son cantidades que quedan determinadas en función del resultado del experimento.
Llamaremos variable aleatoria X a la función que le asigna un número real a cada uno de los valores de un espacio muestral dado.
En nuestro ejemplo, la variable aleatoria X representa el número de veces que se obtuvo un as al arrojar dos veces un dado, mientras que x corresponde a cada uno de los valores que aquella variable pueda adoptar. Es decir, con una letra mayúscula habrá de indicarse la variable aleatoria, mientras que con su correspondiente minúscula se expresará cada uno de los valores de aquella. Así, por ejemplo, la variable aleatoria X tomaría valor uno para los elementos del subconjunto E del espacio muestralS definido como:
\[{\large E = \{A_1\overline{A_2},\overline{A_1}A_2\} }\]
En el ejemplo que acabamos de analizar, la variable aleatoria solo podía adoptar tres valores. Sin embargo, otros experimentos, como por ejemplo registrar la estatura de una persona, pueden ofrecernos, en teoría, infinitos resultados posibles.
El resultado numérico obtenido al medir la estatura de una persona es un número real, mientras que el número de veces que se obtiene un as al arrojar dos veces un dado será un número natural no mayor que 2.
Como veremos más adelante, sin embargo, como la altura de la persona habrá de obtenerse en centímetros, los posibles valores de la variable aleatoria serán muchísimos, aunque no infinitos. La mínima unidad del instrumento de medición utilizado limitará así la cantidad de valores que habrá de adoptar la variable aleatoria.
Observamos entonces que las variables aleatorias podrán clasificarse en dos categorías, en función del número de valores que puedan adoptar.
Cuando la variable aleatoria adopte un número finito de valores, (número que pertenezca al conjunto de los números naturales) diremos que se trata de una variable de tipo discreta.
5.1.1. Función de probabilidad
En muchas ocasiones resulta conveniente expresar la relación entre los valores de una variable aleatoria y sus probabilidades asociadas a partir de una función, a la que denominaremos función de probabilidad o función de distribución de probabilidad.
Se arroja al aire un dado y se observa cuál es el número que queda en la parte superior de este en el momento en que cae. Se sabe que el dado no está cargado, de modo que existe la misma probabilidad de que se obtenga cualquiera de los seis valores posibles.
Podemos entonces construir en primer lugar una tabla de probabilidad para X (siendo X nuestra variable aleatoria, el número que se obtiene después de cada tiro). La imagen 5.1 reproduce dicha tabla.
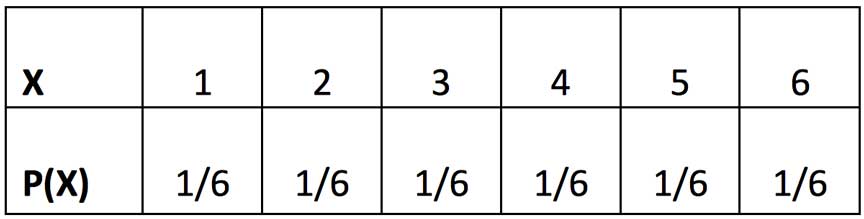
Tabla de probabilidades correspondiente al experimento de arrojar un dado
Si para el ejemplo anterior definimos como g(x) a la función que vincula a los valores de la variable aleatoria con sus correspondientes probabilidades, podremos escribir:
\[ {\large g(x) = \left \{ \begin{matrix} \frac{1}{6} \mbox{ si } x = 1,2,3,4,5,6 \\ 0 \mbox{ para cualquier otro valor de }x\end{matrix}\right. }\]
La función g(x) será entonces la función de distribución de probabilidad correspondiente a la variable aleatoria X, número que se obtiene después de cada tiro.
Se cuenta con un dado cargado. Como en el ejemplo que acabamos de estudiar, se adopta como variable aleatoria al número que aparece en la cara superior del dado después de que se la arroje.
La tabla de probabilidades que se obtiene en este caso es la siguiente:

Escribir la expresión correspondiente a la función de probabilidad f(x) que vincula a los valores de la variable aleatoria con sus correspondientes probabilidades.
5.1.2. Gráficas de probabilidad
Las tablas de probabilidades pueden representarse gráficamente, recibiendo dichas representaciones el nombre de gráficas deprobabilidad. Para el caso de variables aleatorias discretas, a cada valor de la variable aleatoria (que habrá de aparecer sobre el eje de abscisas) le corresponderá un segmento vertical, cuya longitud será igual a su probabilidad. En la imagen 5.2 puede observarse la gráfica correspondiente a la función g(x) definida en la sección anterior.
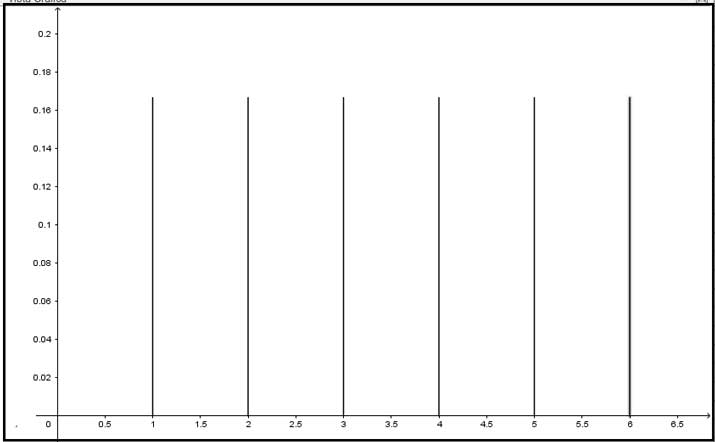
Gráfica de probabilidades correspondiente al ejemplo propuesto en 5.1.2, cuyos datos se presentaban en la imagen 5.1.
Walpole, R.; Myers, R; Myers, S.; Keying Ye (2007), Probabilidad y Estadística para Ingeniería y Ciencias, Pearson Education, México, pp. 80 a 84.
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México, pp. 99 a 106.
Devore, J. (2008), Probabilidad y Estadística para Ingeniería y Ciencias,CengageLearning, México, pp. 971 a 109.
5.2. Distribuciones binomiales
Se arroja una moneda al aire tres veces, y se registra el número de veces que se obtiene cara.
El experimento que acabamos de proponer se caracteriza por lo siguiente:
- En los tres casos, lanzamos una moneda al aire.
- El resultado de cada lanzamiento tiene solo dos resultados posibles.
- El resultado de cada lanzamiento es independiente del que se obtuviera en el o los anteriores.
- La probabilidad de obtener cara es la misma en cada uno de los lanzamientos.
Definamos como variable aleatoria X a la cantidad de veces que se puede obtener cara cada vez que se lleva a cabo el experimento y expresemos como Ca al caso de obtener “cara” en un lanzamiento y como Ce al caso de obtener “ceca”. El diagrama de la imagen 5.3, entonces, nos permite calcular la probabilidad correspondiente a cada uno de los posibles valores de X. Estos serán cero (ninguna cara), uno (una cara y dos cecas), dos (dos caras y una ceca) y tres (obtener cara en cada uno de los tres lanzamientos).
La tabla de distribución de probabilidades correspondiente será entonces la que reproducimos bajo estas líneas:
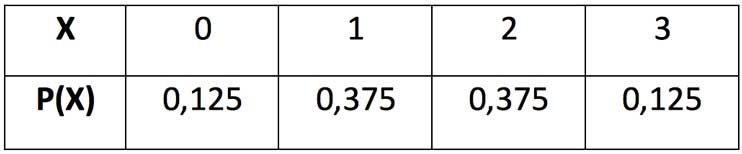
El experimento que acabamos de analizar resulta ser un clásico ejemplo de lo que se denomina un experimento binomial, cuyas características se detallan en la siguiente sección.
5.2.1. Propiedades de un experimento binomial
Las características del experimento propuesto que se enumeraron anteriormente resultan ser comunes a todos los experimentos que se clasifican como binomiales. Generalizaremos seguidamente dichas características:
- El experimento consiste en n ensayos o intentos idénticos.
- Cada intento tiene solo dos resultados posibles, a los que denominamos “éxito” o “fracaso”.
- Losn intentos son independientes.
- La probabilidad p de éxito permanece constante de un intento a otro.
En el ejemplo analizado en la sección anterior, consideramos como éxito al hecho de que el resultado del lanzamiento de la moneda nos brinde una cara. La probabilidad de éxito (suponiendo que se trata de una moneda que no esté “cargada”) vale p = 0,5.
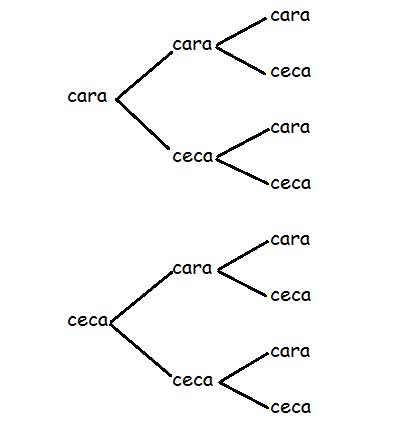
Mediante el diagrama podemos calcular los valores a asignar a la variable aleatoria definida en nuestro experimento.
5.2.2. Fórmula de la probabilidad binomial
Tomemos otro clásico ejemplo para este tipo de experimento. Supongamos ahora que cambiamos el lanzamiento de la moneda por el de un dado y que también lo arrojamos tres veces. En este caso registraremos la cantidad de veces que sale el número uno. Es decir, consideraremos que el éxito en cada uno de los lanzamientos consiste en que se obtenga un uno, siendo entonces la probabilidad de éxito p = 1/6. La variable aleatoria X nos indicaría el número de unos que se pudieran obtener en los tres tiros.
La probabilidad de fracaso (es decir, de que no salga un uno como resultado del lanzamiento del dado) será entonces igual a 1 – p, o sea 5/6. Teniendo en cuenta que el resultado de cada lanzamiento es independiente de los restantes, calculamos la probabilidad de que solo salga un uno en el primero de los tres tiros. Representando con una letra E al éxito y con una F al fracaso, podemos entonces expresar:
\[{\large P(EFF) = \left(\frac{1}{6}\right) \left(\frac{5}{6}\right) \left(\frac{5}{6}\right) = \left(\frac{1}{6}\right)^1 \left(\frac{5}{6}\right)^2 }\]
Si, en cambio, quisiéramos conocer la probabilidad de que solo salga un uno en el tercer tiro, escribiríamos:
\[{\large P(FFE) = \left(\frac{5}{6}\right) \left(\frac{5}{6}\right) \left(\frac{1}{6}\right) = \left(\frac{1}{6}\right)^1 \left(\frac{5}{6}\right)^2 }\]
Finalmente, calculemos la probabilidad de que solo salga un uno en el segundo de los tiros:
\[{\large P(FEF) = \left(\frac{5}{6}\right) \left(\frac{1}{6}\right) \left(\frac{5}{6}\right) = \left(\frac{1}{6}\right)^1 \left(\frac{5}{6}\right)^2 }\]
No debe sorprendernos que el valor obtenido en los tres casos sea el mismo, teniendo en cuenta que el resultado de cada uno de los tiros es independiente del que se obtuviera en los restantes. Pero, entonces, calculemos a continuación la probabilidad de que la variable aleatoria adopte valor uno, es decir, de que al arrojar tres veces un dado, solo aparezca uno en una oportunidad:
\[{\large P(X=1) = P(EFF) + P(FEF) + P(FFE) = 3\left(\frac{1}{6}\right)^1 \left(\frac{5}{6}\right)^2 }\]
En la expresión obtenida se observa que la probabilidad de éxito p aparece elevada al número de veces en que dicho éxito se produce. De igual modo, la probabilidad de fracaso (1–p) está elevada al número de veces que en los tres tiros no salió el uno.
Si ahora quisiéramos calcular la probabilidad de que en los tres tiros saliera el uno (lo que también podría expresarse como la probabilidad de que la variable aleatoria adoptada para el caso tome valor tres) escribiríamos:
\[{\large P(X=3) = P(EEE) = \left(\frac{1}{6}\right) \left(\frac{1}{6}\right) \left(\frac{1}{6}\right) = \left(\frac{1}{6}\right)^3 }\]
Desde el punto de vista matemático, podríamos igualmente escribir:
\[{\large P(X=3) = P(EEE) = \left(\frac{1}{6}\right) \left(\frac{1}{6}\right) \left(\frac{1}{6}\right) = \left(\frac{1}{6}\right)^3 \left(\frac{5}{6}\right)^0 }\]
De este modo, volvemos a observar que p vuelve a aparecer elevada al número de éxitos y (1–p) al número de fracasos (en este caso cero, ninguno).
A partir de lo antedicho, podremos interpretar entonces la fórmula de la probabilidad binomial, que nos permite calcular la probabilidad de obtener x éxitos en n ensayos, cuya probabilidad de éxito sea p.
Dicha fórmula expresa lo siguiente:
\[{\large P(X=x) = \left(^n_x\right) p^x (1-p)^{n-x} }\]
Cabe aclarar que \( \left(^n_x\right) \) representa lo que se conoce como número combinatorio, que se calcula de la siguiente manera:
\[{\Large \left(^n_x\right) = \frac{n!}{(n-x)!x!} }\]
Además, vimos en la unidad anterior que n!recibía el nombre de factorial del número n, y que se definía como la productoriade todos los números naturales desde el uno hasta el n.
A partir de todo lo dicho hasta el momento y siempre teniendo en cuenta el experimento propuesto en el que lanzamos tres veces al aire un dado, calculemos la probabilidad de que se obtenga exactamente dos veces el número uno. Escribimos entonces:
\[{\large P(X=2) = \left(\frac{3}{2}\right) \left(\frac{1}{6}\right)^2 \left(\frac{5}{6}\right)^1 = \frac{15}{216} }\]
5.2.3. Empleo de la planilla de cálculo
Podemos verificar este resultado utilizando nuestra planilla de cálculo. Para ello bastará con emplear la función DISTR.BINOM, como se muestra en la imagen 5.4.
Haciendo clic en “Aceptar”, aparece la ventana que se observa en la imagen 5.5. En la primera casilla debemos ingresar la cantidad de éxitos (x); en la segunda, el número de ensayos (n) y en la tercera, la probabilidad de éxito (p).
Nos detenemos en la última de las casillas que aparece en la ventana. En nuestro caso, en el que deseamos saber la probabilidad de obtener exactamente dos éxitos, debemos escribir “falso”. La otra opción consiste en escribir “verdadero”, en cuyo caso la respuesta que se obtendría correspondería a la probabilidad de que en los tres tiros se obtengan a lo sumo dos ases.
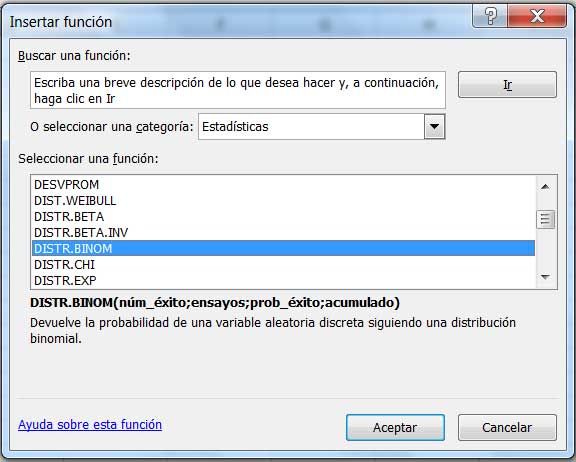
Seleccionamos la función DISTR BINOM
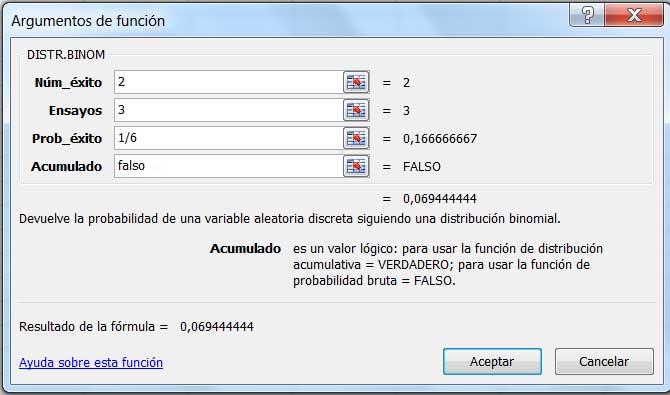
Cálculo de la probabilidad de obtener x éxitos en n ensayos, cuya probabilidad de éxito sea p.
El resultado de la fórmula es, de acuerdo con lo que se observa en la parte inferior de la ventana, 0,0694, que equivale a la fracción 15/216 que habíamos obtenido al final de la sección anterior.
Para estos cálculos también podemos emplear el GeoGebra, un valioso software del que podemos disponer libremente. En la imagen 5.6 se observa el modo de acceder a las aplicaciones estadísticas del software. Basta con seleccionar “Vista” y hacer clic en “Cálculos de probabilidad”.
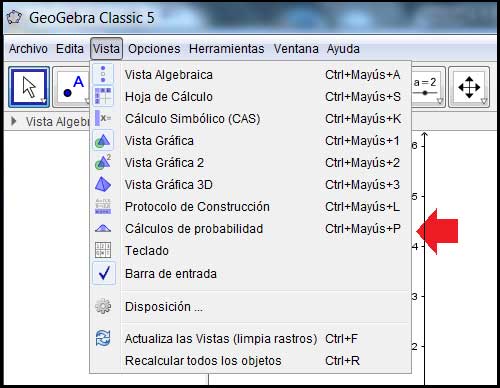
Forma de acceder a las aplicaciones de probabilidad y estadística del GeoGebra.
En la ventana que se abre inmediatamente después debemos seleccionar “Binomial”, como se observa en la imagen 5.7.
Una vez seleccionada dicha distribución, aparece la ventana de la imagen 5.8. En esta se deben ingresar los valores de n y p, y aparecerá de inmediato el diagrama de barras que se observa en la imagen. Cada una de dichas barras verticales representa la probabilidad que le corresponde a cada uno de los valores de la variable aleatoria.
A la derecha de la ventana se observan los valores numéricos de dichas probabilidades. Es decir, se trata de la tabla de distribución de probabilidades para nuestra variable aleatoria.
En la parte inferior se ha seleccionado el cálculo de la probabilidad de que la variable aleatoria adopte un valor menor o igual a dos.
Verificamos dicho valor utilizando nuevamente nuestra planilla de cálculo. Para ello, a diferencia de lo que se observaba en la ventana de la Figura 5.6, hemos de seleccionar verdadero en el casillero correspondiente a Acumulado (ver imagen 5.9).
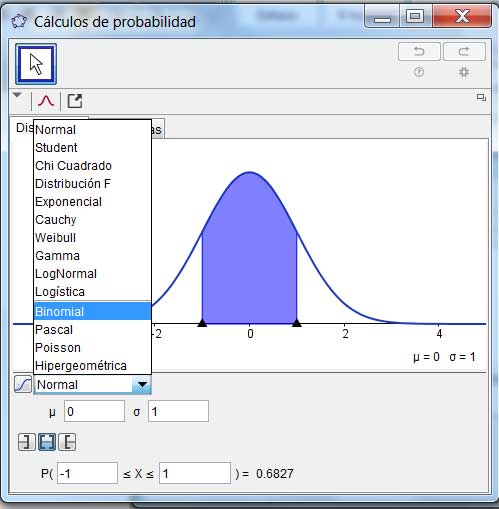
Buscar la ventana que aparece a la izquierda y seleccionar “Binomial”.
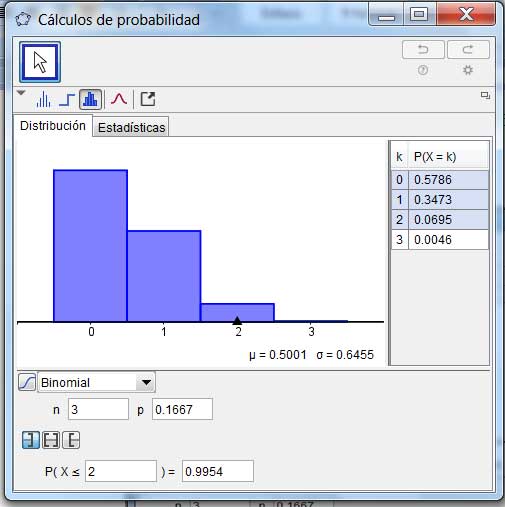
Resultados obtenidos mediante el GeoGebra
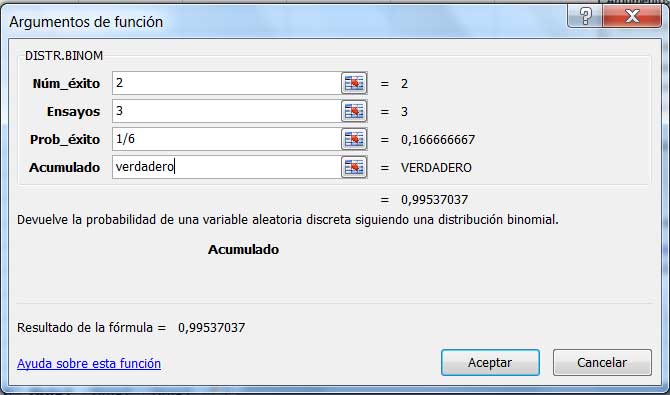
El resultado de la fórmula que nos ofrece la planilla de cálculo es 0,99537037, verificándose así el valor que habíamos obtenido utilizando el GeoGebra.
Entre las contraindicaciones de un determinado medicamento se menciona una leve reacción alérgica, que de acuerdo con un estudio llevado a cabo por el Ministerio de Salud, solo se presenta en el 10 por ciento de los casos. Si se toman al azar quince personas a las que se le ha recetado dicho medicamento, se pregunta:
- ¿Cuál es la probabilidad de que ninguna de ellas haya presentado reacción alérgica?
- ¿Cuál es la probabilidad de que diez de las personas entrevistadas hayan presentado dicha reacción alérgica?
- ¿Cuál es la probabilidad de que menos de diez personas dentro del grupo hayan presentado reacción alérgica?
Devore, J.(2008), Probabilidad y Estadística para Ingeniería y Ciencias, CengageLearning, México, pp. 120 a 124.
Montgomery, D.; Runger, G.(2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México, pp. 122 a 128.
5.2.4. Cálculo de la media y la varianza de una distribución binomial
Los parámetros característicos de toda distribución binomial son la probabilidad de éxito p y el tamaño de la muestra n. A partir de ellos, podemos definir:
Media de una distribución binomial \(\mu\):
\[{\large \mu = n.p }\]
Varianza de una distribución binomial \(\sigma^2\):
\[{\large \sigma^2 = np (1-p) }\]
Se observa que la media y la varianza dependen de los parámetros de la distribución. Para interpretar mejor de qué modo lo hacen, volvamos al sencillo experimento de arrojar al aire una moneda. Supongamos entonces que la arrojamos diez veces al aire y que consideramos como éxito que salga cara. La probabilidad de éxito p será entonces 0,5 y n será igual a 10. La imagen 5.10 muestra gráficamente la distribución de probabilidades.
El valor de la media es:
\[{\large \mu = n.p = 10.0,5 = 5 }\]
En cuanto a la varianza, su valor es:
\[{\large \sigma^2 = np (1-p) = 10.0,5.(1-0,5) =2,5}\]
En la parte inferior de la ventana que aparece en la imagen 5.10 se observa,coloreado en celeste, el valor de la probabilidad de que en cinco de los diez tiros salga cara. Además, la simetría de la distribución se manifiesta en forma inmediata a partir del diagrama de barras.
Si en cambio la moneda estuviese “cargada” y la probabilidad de que al arrojarla al aire saliera cara fuera 0,8, la media también cambiaría (y su valor sería 8 en lugar de 5), en tanto que su varianza sería 1,6. La imagen 5.11 grafica la situación que acabamos de describir.
Nuevamente, el valor de la media coincide con el de la variable aleatoria cuya probabilidad de ocurrencia es mayor. La asimetría, por otro lado, se hace manifiesta en la gráfica que aparece a la izquierda en la imagen.
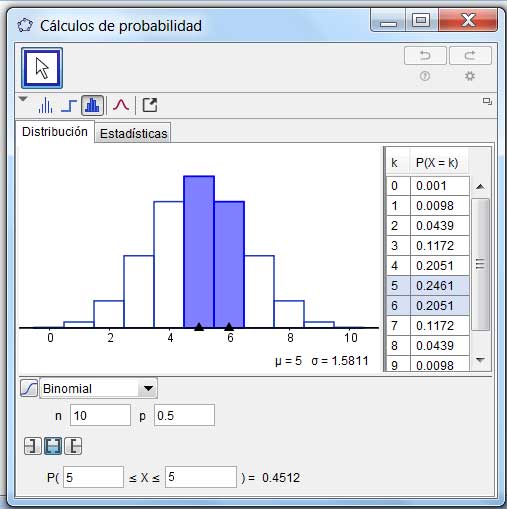
Tabla y gráfica de distribución de probabilidades para el caso de p = 0,5.
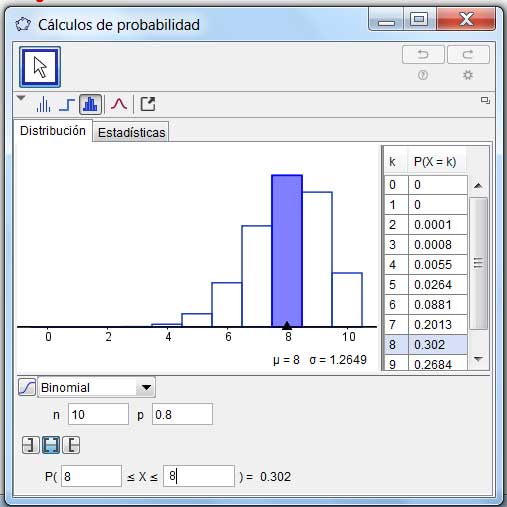
Tabla y gráfica de distribución de probabilidades para el caso de p = 0,8.
El 0,2 % de los circuitos integrados que produce la empresa X resulta ser defectuoso. Si la empresa Y recibe un lote de 1000 circuitos integrados por la empresa X, calcular:
- ¿Cuál es la probabilidad de que exactamente seis de ellos resulten defectuosos?
- ¿Cuál es la probabilidad de que a lo sumo seis de ellos resulten defectuosos?
- ¿Cuál es la probabilidad de que más de nueve circuitos resulten ser defectuosos?
5.3. Distribución de Poisson
Supongamos ahora que nos interesa saber cuál es la probabilidad de que exista un determinado número de bacterias en un volumen dado de una sustancia orgánica líquida. O que queremos estimar la probabilidad de que, en un cierto período de tiempo, se desintegre una cantidad especificada de partículas.
Estamos entonces observando la probabilidad de ocurrencia de un suceso dado en un volumen dado o dentro de un cierto intervalo de tiempo, es decir, dentro de un continuo.
En estos casos aplicaremos otro tipo de distribución, que recibe el nombre de distribución de Poisson (en honor al matemático francés Simeón Denis Poisson). En ella la variable aleatoria indica el número de éxitos por unidad de medida (ya sea longitud, superficie, volumen o tiempo) y el parámetro (que es un número real positivo y se expresa comúnmente con la letra griega lambda, λ) representa justamente al número de ocurrencias dentro de dicha unidad de medida.
Las características condiciones que debe cumplir entonces un proceso de Poisson son las siguientes:
- En intervalos de igual tamaño del continuo en cuestión, el promedio del número de ocurrencias debe ser el mismo.
- La probabilidad de sucesos en diferentes intervalos resulta ser independiente.
La función de distribución de probabilidades correspondiente a este tipo de distribución tiene la forma:
\[ {\Large P(k) = p(X=k) = \frac{e^{-\lambda}\lambda^k}{k!} \text{ con k } = 0,1,2,\cdots}\]
Para ejemplificar todo lo dicho hasta el momento, supongamos que ante una muestra de sustancia radioactiva dada, un contador Geiger detecta un promedio de cinco partículas en un minuto. Nos proponemos calcular la probabilidad de que en un minuto dado se detecten solo tres partículas.
El parámetro correspondiente a nuestro problema será λ = 5 (número de partículas que en promedio se detectan en un minuto) y el valor de la variable aleatoria deberá ser tres (cantidad de partículas que se estiman para el intervalo de tiempo). Entonces:
\[{\Large P(X=3) = \frac{e^{-5}5^3}{3!} = 0,14037}\]
ste valor puede verificarse gracias a las funciones presentes en nuestra planilla de cálculo. Para ello, comenzamos seleccionando la función POISSON, como se observa en la imagen 5.12
Seleccionamos la función POISSON.
Una vez que hacemos clic en “Aceptar”, aparece la ventana que se observa en la imagen 5.13. Debemos entonces ingresar el valor de la variable aleatoria y el valor del parámetro (que en la ventana aparece indicado como “media”). Tal como nos sucediera con la ventana correspondiente a la distribución binomial, debemos, en último lugar, escribir “falso” en el casillero correspondiente a “Acumulado”, de modo de obtener la probabilidad de que se detecten exactamente tres partículas. De escribir “verdadero”, el resultado obtenido correspondería a la probabilidad de detectar tres o menos partículas durante un minuto (imagen 5.14).
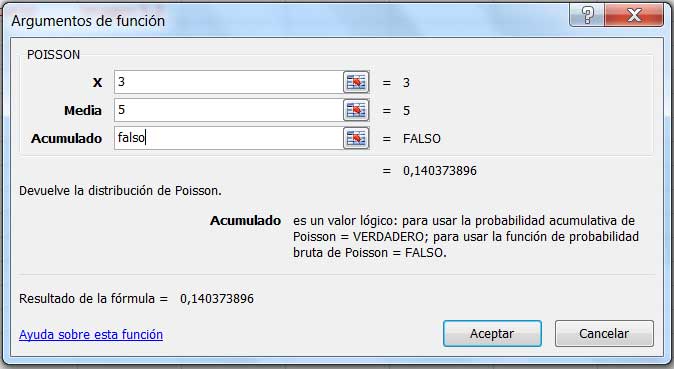
Resolución del problema propuesto empleando la planilla de cálculo.
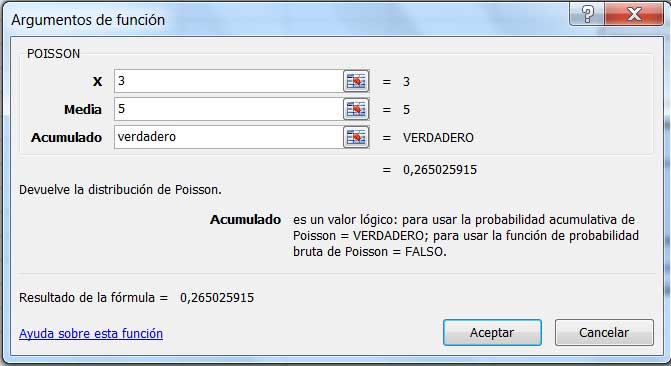
El resultado de la fórmula indica en este caso la probabilidad de que en un minuto sean detectadas tres o menos partículas.
También podemos emplear el GeoGebra para responder a la consigna del problema planteado. En la imagen 5.15 se observa el diagrama de distribución de probabilidades junto con la correspondiente tabla, tal como sucedía para la distribución binomial. Aquí solo basta con indicar el valor del parámetro (que nuevamente aparece indicado como media, expresada con la letra \(\mu\)). En la tabla del extremo derecho, en correspondencia con el valor de la variable aleatoria k = 3, se verifica el valor de la probabilidad que habíamos obtenido previamente con la planilla de cálculo. Por otro lado, en el extremo inferior de la imagen se observa la probabilidad acumulada, cuyo valor permite verificar además el resultado obtenido según lo que se observa en la imagen 5.14.
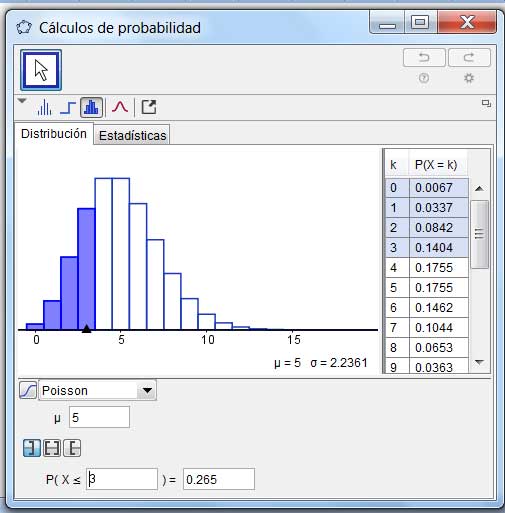
Resolución del problema propuesto empleando el GeoGebra.
¿Qué sucedería ahora si nos preguntáramos cuál es la probabilidad de que nuestro contador Geiger detecte diez partículas durante un intervalo de tiempo de tres minutos?
Teniendo en cuenta las características de esta distribución, recomendamos considerar que nuestra nueva unidad de tiempo son esos tres minutos y que, en intervalos de igual tamaño del continuo en cuestión, el promedio del número de ocurrencias debe ser el mismo. Basta con multiplicar por tres (minutos) el número de ocurrencia conocido. De este modo, el parámetro característico lambda adopta para el problema valor 15.
En la imagen 5.16 se obtuvo el resultado del problema empleando la planilla de cálculo. Dicho valor se puede verificar empleando el GeoGebra, tal como se observa en la imagen 5.17.
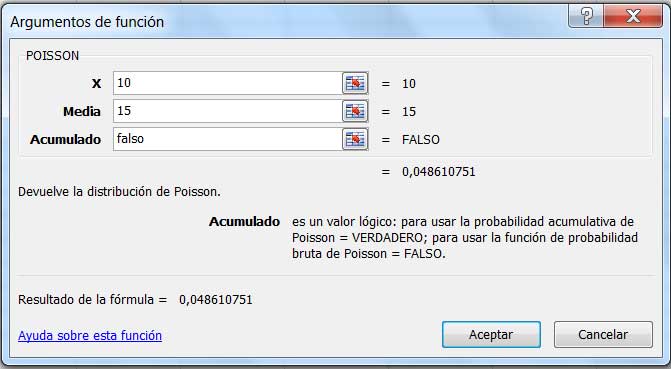
Cálculo de la probabilidad de que el contador Geiger detecte exactamente diez partículas en un lapso de tres minutos.
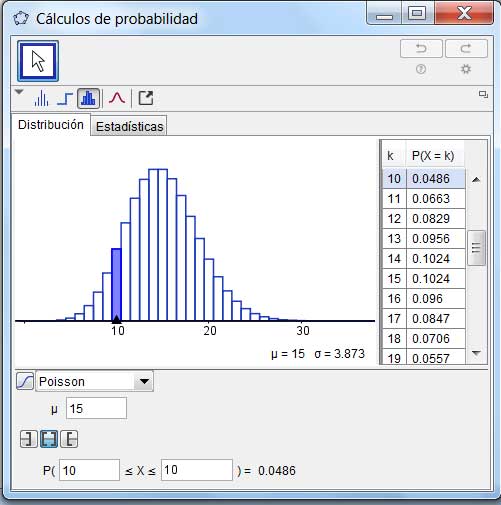
Verificación del resultado obtenido con la planilla de cálculo empleando el GeoGebra.
La media de errores de impresión en la superficie de las planchas que emplea una envasadora automática de lácteos es de dos por metro cuadrado (ver imagen 5.18). Dichas fallas no solo alteran la presentación del producto sino que, en algunos casos, pueden provocar a la empresa otro tipo de inconvenientes (el hecho de que la tabla de contenidos nutricionales no pueda leerse podría afectar a clientes celíacos o que sufriesen algún otro tipo de problema de salud).
En un control de calidad se analiza una plancha de diez metros cuadrados de superficie y se desea saber cuál es la probabilidad de que presente menos de quince errores de impresión.

La plancha acaba de ser introducida en la máquina envasadora de lácteos.
Fuente: “Cómo se mete la leche en el cartón”, Tetra PakSpain. Disponible en <https://www.youtube.com/watch?v=-P-zgAheFjc> [Consulta: 3 noviembre 2017]
Se considera que el número de llamadas que recibe una pequeña empresa de remises se puede estudiar como una variable aleatoria del tipo Poisson. En días de semana, por la mañana y con buen tiempo, la telefonista atiende una media de veinte llamados por hora. Calcular la probabilidad que una mañana cualquiera, durante un período de media hora, se reciban más de quince llamadas.
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México. pp. 146 a 150.
Devore, J. (2008), Probabilidad y Estadística para Ingeniería y Ciencias, CengageLearning, México, pp. 135 a 138.
5.4. Aproximación de una distribución binomial empleando una distribución de Poisson
Es frecuente encontrarse con problemas en los cuales la distribución de probabilidades adecuada resulta ser la binomial, pero el número de veces que se repite el experimento resulte ser muy grande.
Por ejemplo, la probabilidad de que una persona sufra una leve inflamación cutánea al inyectársele una determinada vacuna vale 0,001. Se desea conocer cuál es la probabilidad de que exactamente dos personas, de un total de quinientas a las que lesfuera suministrada dicha vacuna, pudiesen presentar inflamación cutánea.
Puesto que la probabilidad de que una persona sufra alguna reacción nociva es independiente de lo que pueda sucederle a otra y que la probabilidad de ocurrencia es la misma para todas las personas, el fenómeno debe estudiarse a partir de una distribución de tipo binomial. Se considera como éxito el hecho de que una persona se vea afectada ante la inoculación (convengamos que el sentido del éxito en este tipo de experimento es puramente matemático y carece de relación alguna con lo que pudiera indicar el sentido común).
Determinar entonces cuántas de las 500 personas podrían ser afectadas se reduce a repetir 500 veces el experimento de determinar si una persona dada sufre o no efectos indeseados, considerando que si ello sucede el experimento es exitoso. Entonces, el cálculo que debemos llevar a cabo es el siguiente:
\[{\large P(X=2) = \left( \begin{matrix}500\\2\end{matrix} \right) 0,001^2(1-0,001)^{498} = \frac{500!}{2!498!}0,001^20,999^{498} }\]
Aun cuando en el cálculo en forma manual del resultado pudieran aplicarse las propiedades de los factoriales para simplificar la expresión, se buscó un camino alternativo para la resolución, a partir de que puede demostrarse que:
\[{\Large \begin{matrix}\text{lim } n \to \infty \\p \to 0\\np \to \lambda \end{matrix} \left( ^n_k \right) p^k(1-p)^{n-k} = \frac{e^{-\lambda}\lambda^k}{k!} }\]
Es decir, si el número de experimentos que se llevan a cabo es muy grande y la probabilidad de ocurrencia es muy pequeña, la distribución binomial puede asimilarse a una de tipo Poisson, en la que el parámetro lambda no es otra cosa que la media, es decir, el producto entre el número de experimentos (o tamaño de la muestra adoptada) y la probabilidad de éxito.
Así, en nuestro caso:
\[{\large P(X=2) = \left( \begin{matrix}500\\2\end{matrix} \right) 0,001^2(1-0,001)^{498} \cong P(Y=2) = \frac{e^{-0,5}0,5^2}{2!} }\]
Obsérvese que hemos utilizado dos variables aleatorias distintas, X e Y. Ello se debe a que la primera se corresponde con la distribución binomial original, en tanto que la segunda está vinculada con la distribución de Poisson que empleamos como alternativa.
En las imágenes 5.19 y 5.20 reproducimos los resultados obtenidos aplicando la distribución binomial y la de Poisson, respectivamente, para resolver nuestro problema. Obsérvese que los resultados no difieren en forma significativa.
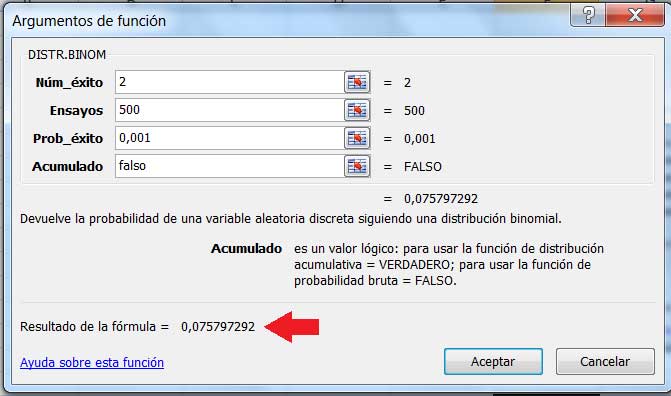
Probabilidad de que exactamente 2 de las 500 personas que tomaron parte en el experimento sufriesen daños colaterales al aplicársele la vacuna, obtenida teniendo en cuenta que la distribución de probabilidades es binomial.
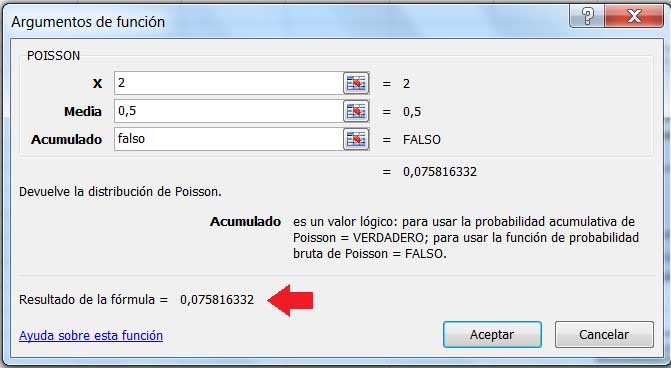
Efectuamos el mismo cálculo pero empleando la aproximación por distribución Poisson. Se observa que la diferencia entre ambos resultados obtenidos no resulta ser significativa.
Aun cuando al efectuar el cálculo empleando software evitamos las complicaciones del cálculo manual, consideramos oportuno que el alumno sea capaz de aplicar la aproximación descripta en este apartado.

