Análisis descriptivos bivariados
Objetivos
Que el alumno:
- Comprenda la importancia que el análisis multivariado posee dentro del campo de la investigación.
- Aprenda a reconocer la existencia de una relación de tipo lineal entre dos variables dadas como medio para ratificar o rectificar alguna hipótesis dentro de su estudio.
- Descubra la importancia de métodos matemáticos como el de cuadrados mínimos y la utilidad de herramientas algebraicas como la regla de Cramer.
3.1. Dependencia lineal y covarianza
En muchos estudios estadísticos se analizan simultáneamente dos o más variables. En algunos de ellos se trata de determinar si existe o no relación entre ellas y, en caso afirmativo, cuál es el tipo de relación que las vincula.
Los datos bivariados pueden expresarse como un conjunto de pares ordenados (x,y). En la imagen 3.1 reproducimos los datos de un estudio llevado a cabo con una pequeña muestra, en la que se consignan la cantidad de horas que cada estudiante empleó para la preparación de un examen (que se representa con la variable x) y la calificación obtenida por el estudiante, a la que se le asigna la variable y. El par ordenado (22,8) indicaría entonces que un estudiante dado dedicó 22 horas a la preparación del examen, obteniendo como calificación 8 puntos.
Aun cuando entre dos variables dadas pueden existir distintos tipos de relaciones, en la presente unidad pondremos particular énfasis en las de tipo lineal, es decir, aquellas que presentan una proporcionalidad directa entre las variables involucradas y que, por esa razón, pueden representarse gráficamente mediante una recta.
En este tipo de relación, cuando la variable y adopte valores mayores a medida que crezcan los valores de x, diremos que la dependencia entre ambas variables es positiva. Si, en cambio, a medida que x adopta valores cada vez más grandes se observa que los valores de la variable y disminuyen, decimos que la dependencia entre ambas variables es negativa.
Una medida que nos permite determinar si dicha dependencia lineal existe o no es la covarianza muestral, que se obtiene como
(3.1)\[{\large cov (x, y) = S_{xy} = \frac {\sum^n_{i=1} (x_i - \overline{x}) (y_i - \overline{y})}{n - 1}}\]
En la expresión, xi e yi representan los valores de cada una de las variables en una de las mediciones, en tanto que \(\overline {x}\) e \(\overline {y}\) son las medias de cada una de dichas variables, para una muestra de tamaño n.
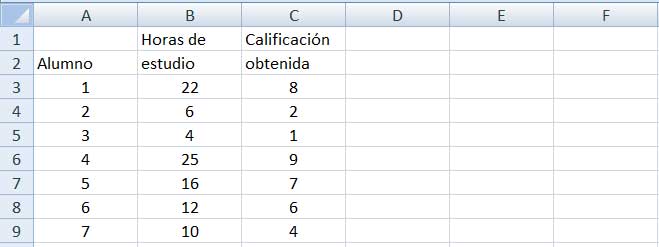
Calificación obtenida por un grupo de alumnos en un examen vs.cantidad de horas dedicadas a la preparación de este.
Si las dos variables no son linealmente dependientes, la covarianza vale cero (o es muy próxima a cero). Sin embargo, puesto que la relación entre dichas variables podría existir aun sin ser lineal, el hecho de que la covarianza valga cero no implica que las variables sean independientes.
Vamos a determinar si existe o no una relación directa entre las variables “cantidad de horas dedicadas al estudio” y “calificación obtenida” a partir de los datos que figuran en la tabla de laimagen 3.1. Utilizaremos una planilla de cálculo para ver de qué modo se aplica la expresión (3.1) en este tipo de problema. Como se observa en la imagen 3.2, una vez que los datos fueron volcados a la planilla de cálculo, procedemos a obtener las medias de cada una de las variables, utilizando para ello la función PROMEDIO.
Seguidamente calculamos la diferencia entre cada uno de los valores de las variables y el promedio de cada una de ellas, como se observa en la imagen 3.3.
En la columna F multiplicaremos para cada una de las muestras las diferencias que aparecen en las columnas D y E (imagen 3.4), para luego obtener la suma de todos esos productos (mediante la instrucción SUMA, tal como puede observarse en la imagen 3.5). Dividiendo a dicha suma por el tamaño de la muestra disminuido en una unidad, tal como lo indica la expresión (3.1), obtenemos finalmente la covarianza (imagen 3.6).
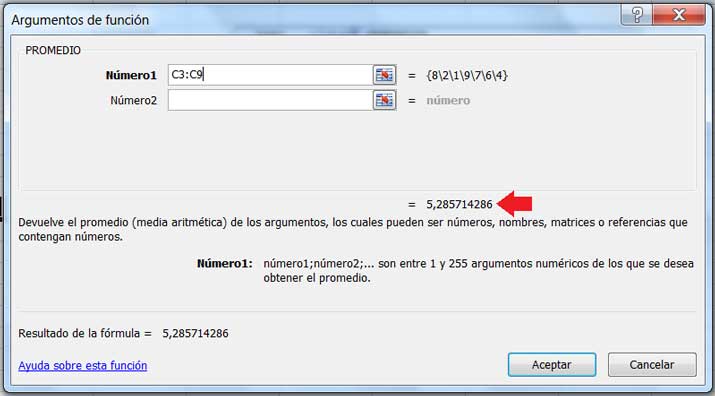
Con una flecha roja hemos señalado el valor de dicho promedio (5,28), que aparecerá en dicha casilla una vez que hagamos click en Aceptar.
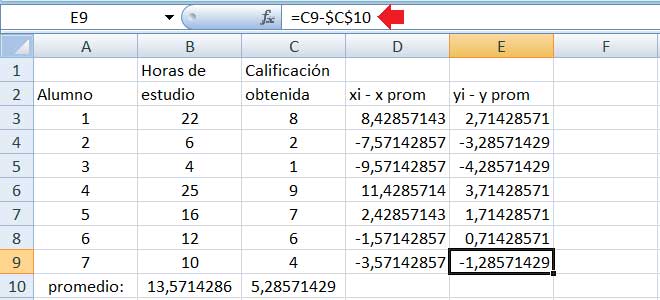
La flecha roja indica cuál es la operación mediante la cual se obtiene el valor de la casilla E9. C9 representa el valor de la calificación del último de los seis alumnos, en tanto que $C$10 corresponde a la calificación promedio del grupo. Los signos $ que acompañan a esta última variable deben agregarse porque, al apoyar el cursor sobre la cruz que aparece en el extremo inferior derecho de la casilla E3 para luego llevarla hasta la E9, todas las diferencias tendrán como sustraendo al mismo valor, es decir, la media de la variable.
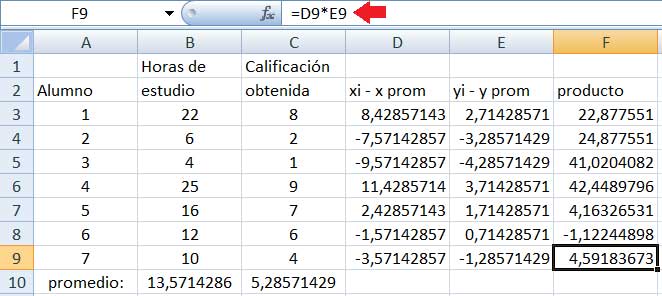
La flecha roja señala, en esta oportunidad, el cálculo llevado a cabo para obtener el resultado de la casilla F9.
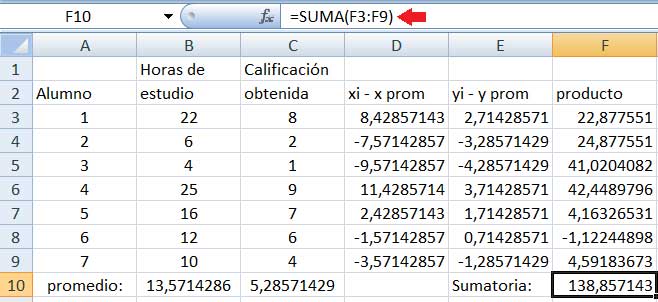
El cálculo que llevamos a cabo en la casilla F10 es el que resalta la flecha roja. La función SUMA es la que nos permite operar en este caso.
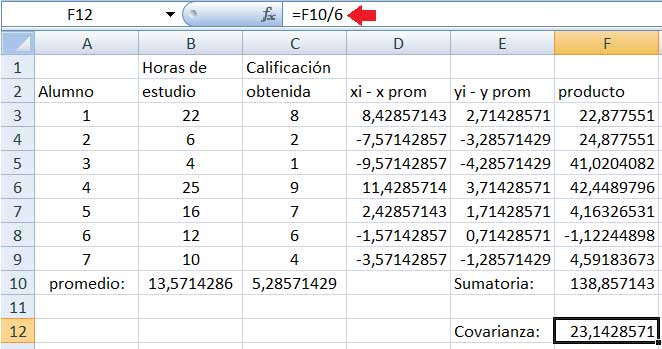
Finamente, calculamos la covarianza como el cociente entre la sumatoria obtenida en F10 y la cantidad de pares ordenados de datos menos uno (de ahí que se divide por seis y no por siete).
Se observa en la casilla F12 de la imagen 3.6 que el valor de la covarianza obtenido es distinto de cero y positivo. Ello indica que la dependencia entre ambas variables es positiva (es decir, ambas aumentan o disminuyen simultáneamente).
Por otro lado, el resultado obtenido no es próximo a cero, lo que confirma la existencia de una relación lineal entre ambas variables.
Devore, J.(2008), Probabilidad y Estadística para Ingeniería y Ciencias, CengageLearning, México, pp. 198 y 199.
Montgomery, D.; Runger, G.(2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México. pp. 257 a 260.
3.1.1. Obtención de la covarianza aplicando planilla de cálculo
La propia planilla de cálculo contiene una función COVAR, que nos permite obtener la covarianza sin necesidad de efectuar todos los cálculos que hemos descripto anteriormente. En la imagen 3.7 mostramos de qué modo tenemos que utilizar dicha función para obtener el valor de la covarianza.
En la imagen 3.8 puede observarse que el valor de la covarianza que se obtiene con la función COVAR difiere del que habíamos calculado anteriormente. El motivo de dicha diferencia (bastante notable en nuestro ejemplo) es sencillo: la función que emplea la planilla de cálculo divide a la sumatoria de los productos por el número total de pares ordenados, mientras que en el cálculo previo habíamos dividido por el tamaño de la muestra menos uno.
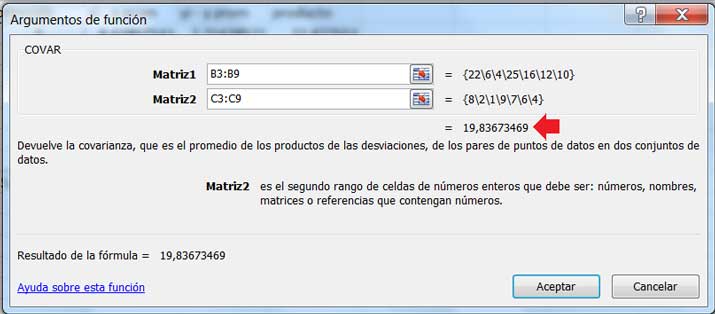
Una vez abierta la ventana correspondiente a la función COVAR se ingresan los valores de las dos variables consideradas como dos Matrices separadas.
La razón por la cual es conveniente dividir por n – 1 en lugar de hacerlo por n se relaciona con una característica de las muestras, el sesgo, sobre el cual nos detendremos más adelante. Limitémonos por el momento a decir que el criterio que hemos empleado en nuestro cálculo hace que el valor obtenidode la covarianza de la muestra se aproxime más al de la covarianza poblacional. El hecho de que la planilla de cálculo esté programada empleando otro criterio se relaciona con que la diferencia entre dividir por n o por n-1 se hace cada vez menos evidente a medida que el tamaño de la muestra sea mayor.
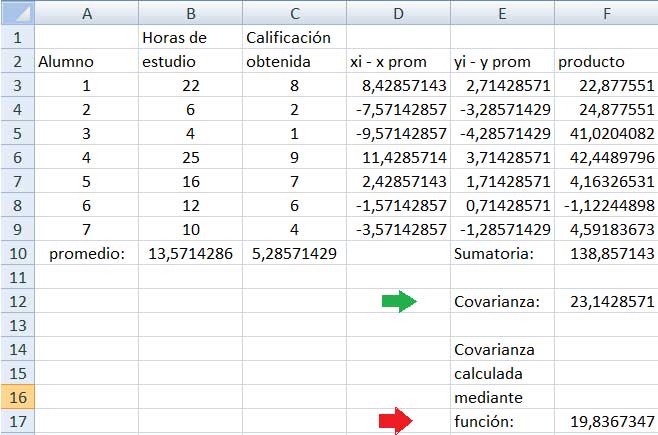
La flecha verde señala el valor de la covarianza que habíamos obtenido anteriormente. La flecha roja, en cambio, señala el valor de la covarianza obtenida mediante la función COVAR. La diferencia entre ambos valores hace aconsejable el empleo de la función solamente en aquellos casos en los que el tamaño de la muestra sea mayor.
3.1.2. Diagramas de dispersión para los datos
La imagen 3.9 reproduce los datos de dos muestras distintas, a las que denominaremos “caso 1” y “caso 2”. En la parte inferior de cada una de las dos tablas aparece el valor de la covarianza de las muestras, que fue obtenida aplicando la función COVAR, aplicada en la sección 3.1.1. Las dos covarianzas resultan ser positivas y significativamente superiores a cero, de modo que en ambos casos podemos decir que la relación entre las variables es lineal y positiva.
Para interpretar gráficamente la información de que disponemos, podemos representar los pares de valores de las dos tablas sobre un sistema de ejes cartesianos. Dichas gráficas reciben el nombre de diagramas de dispersión. En la imagen 3.10 se pueden observar los diagramas correspondientes a las dos muestras que estamos estudiando, que fueron construidos mediante la planilla de cálculo.
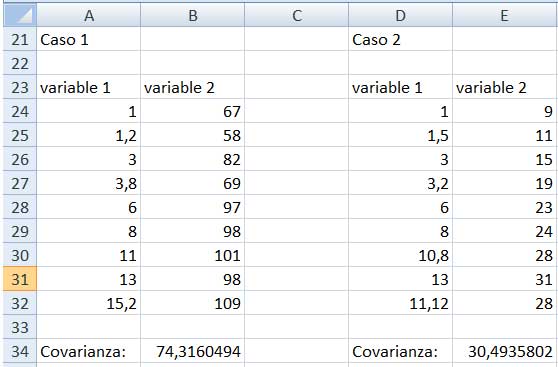
Tablas de valores correspondientes a las muestras “caso 1” y “caso 2”.
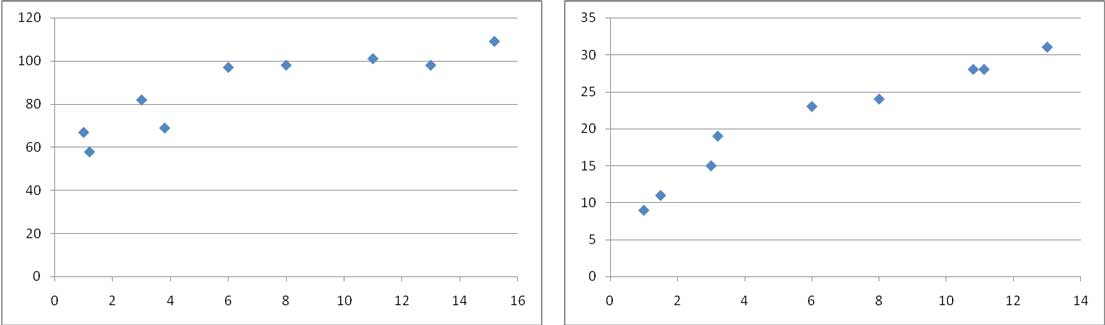
Diagramas de dispersión de los casos 1 y 2.
En próximas secciones buscaremos la recta de regresión, a la que también se conoce como curva de ajuste. Esta segunda denominación nos habla acerca de su significado: es la que más se aproxima a los puntos representativos de la muestra; es aquella donde las distancias entre los valores medidos y los de la propia recta se reduce a la mínima expresión.
En la imagen 3.11 volvemos a reproducir los diagramas de dispersión de ambas muestras, pero, además, mostramos las rectas de regresión correspondientes a cada uno de ellos.
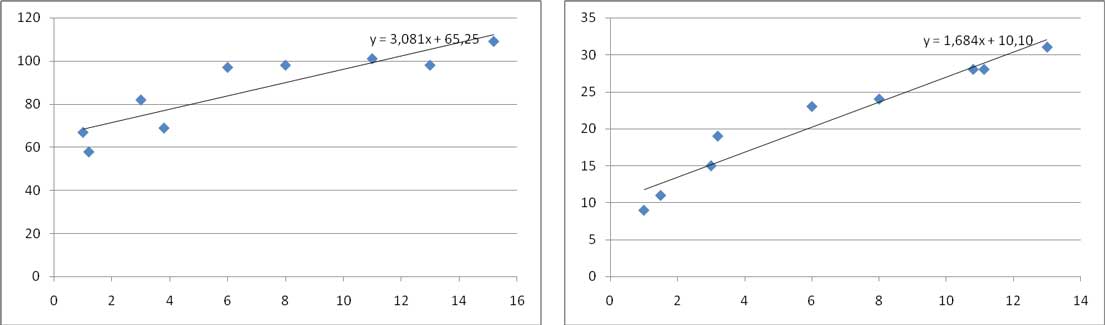
Diagramas de dispersión y rectas de regresión de cada uno de los casos
Aun teniendo en cuenta que las escalas son distintas en ambos casos, se observa que la curva correspondiente al caso 2 se ajusta mejor que la del caso 1 a su respectiva recta, lo que implica que la covarianza nada nos dice respecto de la bondad en el ajuste que pueda presentar nuestra muestra. Esta última característica, sumamente deseable, deberá ponerse entonces de manifiesto de otro modo. Y ello nos llevará entonces a definir el coeficiente de correlación.
3.1.3. Correlación
Uno de los objetivos principales de la Estadística es determinar si entre dos variables dadas existe algún tipo de relación. El análisis de la correlación es el método utilizado para determinar el grado de dependencia lineal que exista entre dos variables.
Para determinar el grado de relación lineal entre las variables se necesita un índice que cumpla con las siguientes cuatro propiedades:
- Debe ser independiente de las unidades de medida de cada una de las variables.
- Su valor habrá de ser igual a uno si los puntos se encontraran sobre una recta con pendiente positiva.
- Su valor habrá de ser menos uno si los puntos se encontraran sobre una recta con pendiente negativa.
- Su valor será cero en caso de que la relación entre las variables no sea lineal.
3.1.4. Coeficiente de correlación de Pearson
El índice que cumple con todas las condiciones que acabamos de expresar recibe el nombre de índice o coeficiente de correlación de Pearson (al que se expresa comúnmente con la letra r) y su expresión matemática es similar a la de la covarianza, obteniéndose de dividir a esta por el producto de las desviaciones estándar muestrales de cada una de las variables. Es decir:
(3.2)\[{\large r = \frac {\sum (x_i - \overline{x}) (y_i - \overline{y})} {(n - 1) S_x S_y}}\]
Recordemos que:
(3.3)\[{\large S_x = \sqrt {\frac {1}{n-1} \sum (x_i - \overline {x})^2} }\]
mientras que
(3.4)\[{\large S_y = \sqrt {\frac {1}{n-1} \sum (y_i - \overline {y})^2} }\]
El valor de r adopta valores entre 1 y -1. Cuando es muy próximo a cero, la relación entre las variables no será de tipo lineal. A medida que se aproxime a 1 la relación entre las variables se hará cada vez más lineal y de tipo directa: es decir, las dos variables crecerán o decrecerán al mismo tiempo, lo que se corresponde con una recta de pendiente positiva.
Cuando r, en cambio, se aproxime a -1, la relación entre ambas variables también será de tipo lineal, pero la recta tendrá pendiente negativa: a medida que una de las variables aumenta, la otra disminuye.
En la imagen 3.12 agregamos a las tablas de la imagen 3.9 los coeficientes de correlación de Pearson. Puede entonces observarse que el correspondiente al “caso 2” resulta aproximarse mucho más a la unidad que el del “caso 1”, lo que confirma nuestra observación previa respecto de la mayor bondad de ajuste de aquella.
El valor de la covarianza está influenciado por los órdenes de magnitud de las variables involucradas y el hecho de que su valor sea muy alto no necesariamente signifique que el ajuste entre los valores de la muestra y la recta de regresión sea muy buena. La normalización de la covarianza, que se obtiene al dividirla por el producto de las desviaciones estándar, será lo que nos permitirá determinar cuando el ajuste de los puntos respecto de la recta de regresión sea mayor.
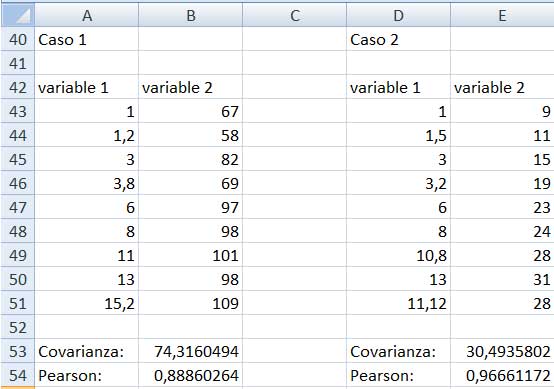
Comparación entre los coeficientes de correlación de Pearson para las dos muestras que estábamos analizando en las últimas tres secciones.
Para cada uno de los siguientes conjuntos de datos bivariados dibujar el diagrama de dispersión y calcular la covarianza. En los casos en que tenga sentido hacerlo, calcular además el coeficiente de correlación de Pearson.
3.2. Regresión y predicción
Definimos como análisis de regresión al método empleado en Estadística para estudiar la relación entre dos o más variables y predecir el valor de una de ellas a partir de la relación existente entre ambas.
Por ejemplo, cuando el coeficiente de Pearson sea muy próximo a uno (o a menos uno), podemos buscar una recta cercana a los puntos del diagrama de dispersión que refleje el tipo de relación entre ambas variables.
La proximidad de los puntos del diagrama de dispersión a la recta que estamos buscando se juzga a partir de los cuadrados de las distancias verticales desde aquellos puntos y la recta. Esta tendrá una ecuación de la forma \(\hat{y} = b + ax\) y recibe el nombre de recta de mejor ajuste o recta de regresión. La letra m representa a la pendiente de dicha recta, en tanto que b no es otra cosa que la ordenada al origen de esta.
Para esta recta, la suma de los cuadrados de las distancias verticales entre los puntos del diagrama de dispersión y la propia recta debe ser mínima. El procedimiento para determinar la recta de mejor ajuste recibe por ello el nombre de método de los cuadrados mínimos y nos permitirá obtener, de todas las posibles rectas que puedan dibujarse a partir del diagrama de dispersión, aquella que cumpla la condición planteada al comenzar el presente párrafo.
3.3. Deducción de la fórmula para el cálculo de la recta de regresión
Seguidamente, nos proponemos deducir las expresiones que habrán de permitirnos calcular la pendiente(a) y la ordenada al origen (b) de la recta de regresión, cuya ecuación tendrá entonces la forma y = a.x+b.
Expresando como (xi, yi) a cada uno de los pares ordenados que contienen a los valores medidos, y como \(( x_i, \hat{y}_i)\) a los pares ordenados donde la segunda de las coordenadas corresponde al valor estimado de la variable, el error que se comete para cada una de dichas mediciones habrá de expresarse como
(3.5)\[{\large e_i = y_i - \hat{y}_i }\]
Puesto que los \(( x_i, \hat{y}_i)\) deben pertenecer a la recta, deberá verificarse para cada uno de ellos la igualdad:
(3.6)\[{\large \hat{y}_i = ax_i + b }\]
En la imagen 3.13 pueden observarse un diagrama de dispersión construido a partir de cuatro puntos, con su respectiva recta de regresión. Hemos señalado claramente las diferencias entre los valores medidos y estimados para cada uno de esos puntos.
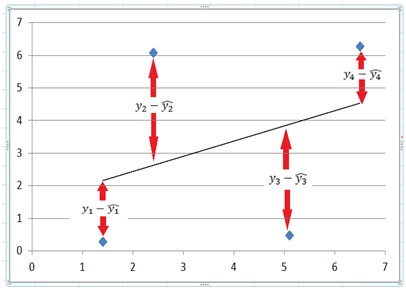
Valores obtenidos y valores estimados para una muestra dada.
En la sumatoria
(3.7)\[{\large \sum^4_{i=1} e_i = (y_1 - \hat{y}_1) + (y_2 - \hat{y}_2) + (y_3 - \hat{y}_3) + (y_4 - \hat{y}_4) }\]
se produce un efecto de compensación que se refleja en el resultado, que es cero. Ello habrá de cumplirse en todos los casos, lo que significa que la suma de los errores cometidos no resulta ser la expresión adecuada para nuestros fines.
Pero dicho efecto de compensación desaparece cuando sumamos los cuadrados de las diferencias entre los valores medidos y los estimados, es decir:
(3.8)\[{\large \sum e^2_i = (y_1 - \hat{y}_1)^2 + (y_2 - \hat{y}_2)^2 + (y_3 - \hat{y}_3)^2 + (y_4 - \hat{y}_4)^2 } \]
Nuestro objetivo, entonces, es minimizar \(\sum e^2_i\). Si operamos con las expresiones (3.5) y (3.6) obtenemos:
(3.9)\[{\large e_i = y_i - (ax_i + b) } \]
Definimos entonces la función D(a,b) como:
(3.10)\[{\large D (a, b) = \sum^n_{i=1} e^2_1 = \sum^n_{i=1} (y_1 - ax_i - b)^2 } \]
Calculamos las derivadas parciales respecto de las variables a y b para igualarlas a cero y encontrar los puntos críticos:
(3.11)\[{\large \frac {\delta D}{\delta a} = 2\sum^n_{i=1} (y_1 - ax_i - b)(-x_i) = 0 } \]
(3.12)\[{\large \frac {\delta D}{\delta b} = 2\sum^n_{i=1} (y_1 - ax_i - b)(-1) = 0 } \]
Operando, obtenemos el siguiente sistema de ecuaciones:
(3.13)\[{\large \sum^n_{i=1} (x_i \text{ }y_i - ax^2_i - bx_i) = 0 } \]
(3.14)\[{\large \sum^n_{i=1} (y_i - ax_i - b) = 0 } \]
De la (3.13):
(3.15)\[\sum^n_{i=1} x_i y_i - a \sum^n_{i=1} x^2_1 - b \sum^n_{i=1} x_i = 0 \to a \sum^n_{i=1} x^2_i + b \sum^n_{i=1} x_i = \sum^n_{i=1} x_i y_i \]
De la (3.14):
(3.16)\[\sum^n_{i=1} y_i - a \sum^n_{i=1} x_1 - nb = 0 \to a \sum^n_{i=1} x_i + nb = \sum^n_{i=1} y_i \]
Las ecuaciones (3.15) y (3.16) conforman un sistema que habremos de resolver por la Regla de Cramer para obtener el valor de a:
(3.17)\[ {\Large a = \frac {\left| \begin{array}{cc} \sum^n_{i=1} x_iy_i & \sum^n_{i=1} x_i\\ \sum^n_{i=1} y_i & n \end{array}\right|} {\left| \begin{array}{cc} \sum^n_{i=1} x^2_i & \sum^n_{i=1} x_i\\ \sum^n_{i=1} x_i & n \end{array}\right|} = \frac {n \sum^n_{i=1} x_iy_i - \sum^n_{i=1} x_i \sum^n_{i=1} y_i} {n \sum^n_{i=1} x^2_i - (\sum^n_{i=1} x_i)^2} } \]
En lo que respecta al valor de b, para obtenerlo bastará con tener en cuenta que
\[{\large \overline{y} = a \overline{x} + b \to b = \overline{y} - a \overline{x} } \]
3.4. Obtención de las curvas de regresión empleando la planilla de cálculo
En la imagen 3.14 reproducimos la tabla correspondiente a una muestra en la que se midieron dos variables que, suponemos, presentan dependencia lineal entre sí.

Tabla de valores correspondiente a la muestra que vamos a estudiar a continuación.
El coeficiente de Pearson resulta ser muy próximo a uno, tal como puede observarse en la imagen 3.15. Allí también se muestra la ventana que abrimos para el cálculo de dicho coeficiente.
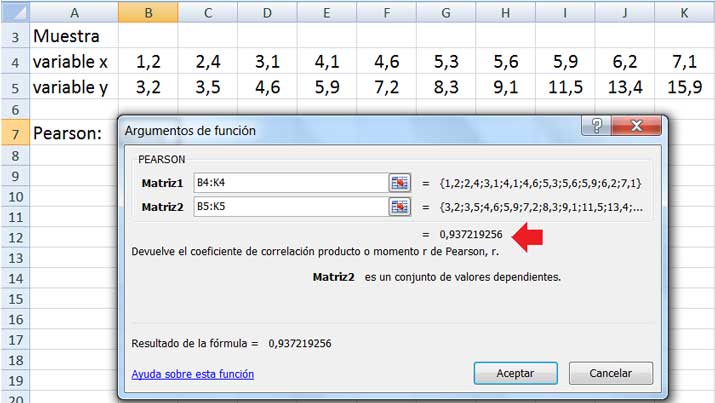
Debajo de la tabla puede observarse la ventana que se abre cuando aplicamos la función PEARSON que nos permite obtener el coeficiente de correlación.
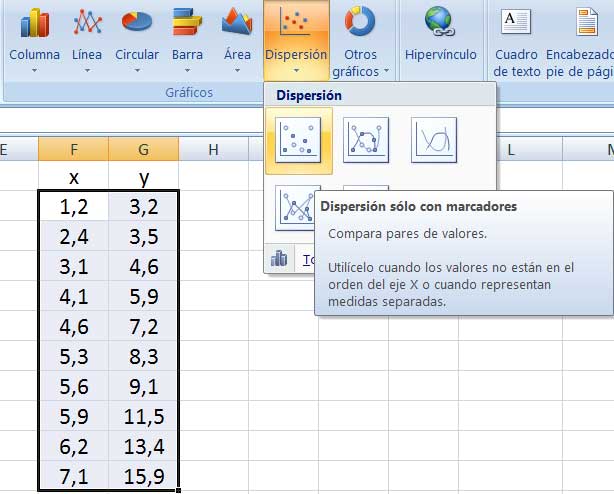
Captura de pantalla donde se indica cómo construir el diagrama de dispersión. Se seleccionan los datos en la tabla de dos columnas, para luego ingresarlos en “Insertar gráficos de dispersión”.
Si con el cursor nos apoyamos en cualquiera de los puntos del diagrama de dispersión y hacemos clic con botón derecho sobre él, se abre otra ventana, como se observa en la imagen 3.17. En esta última ventana debemos seleccionar “Agregar línea de tendencia”.
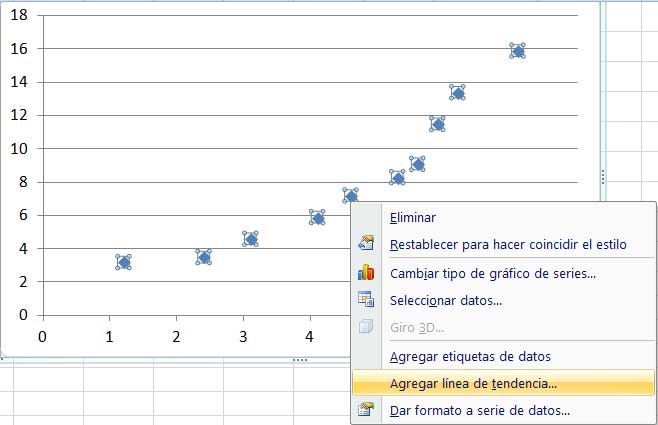
Haciendo clic con botón derecho sobre cualquiera de los puntos del diagrama de dispersión, aparece otra ventana que nos habilitará a dibujar la línea de tendencia.
Se abre una nueva ventana, en la cual, por default, aparece seleccionada la tendencia lineal. Recomendamos hacer clic en “Presentar ecuación en gráfico”, como se observa en la imagen 3.18, para obtener automáticamente la recta de regresión.
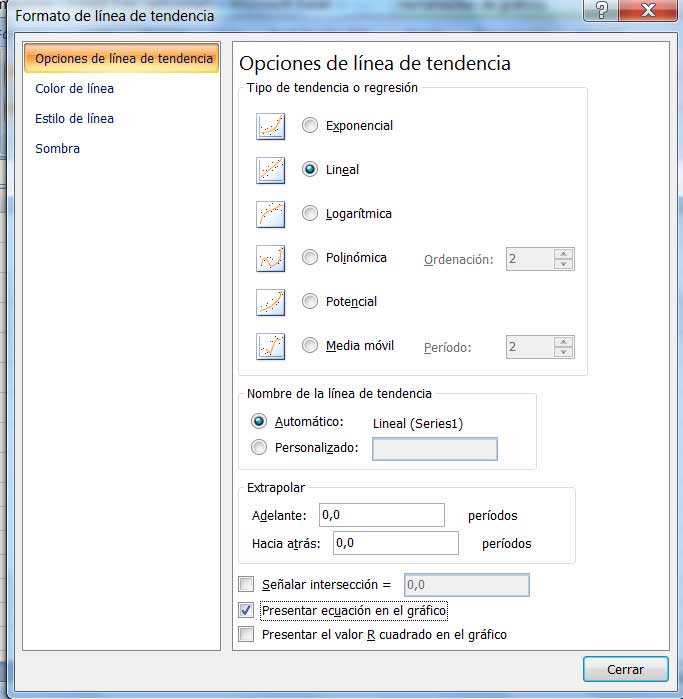
Captura de pantalla correspondiente a la ventana que se abre para seleccionar el tipo de curva a graficar. Recomendamos hacer clic en “Presentar ecuación en gráfico”.
Finalmente, en la imagen 3.19 presentamos la recta de regresión. Obsérvese que en el extremo superior derecho de la curva aparece la ecuación de dicha recta.
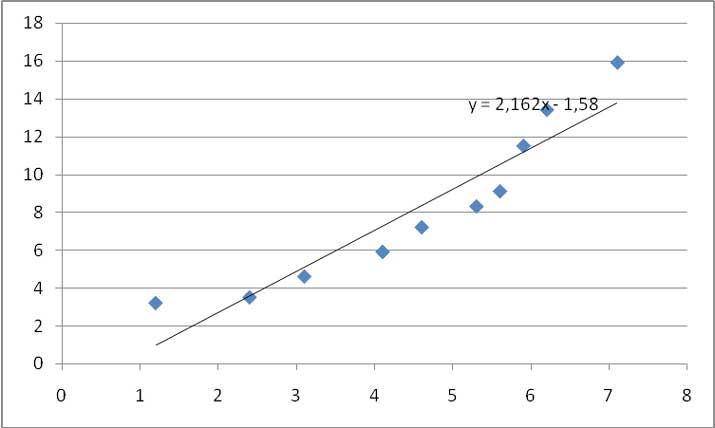
Recta de regresión
El software nos permite, además, obtener curvas de ajuste no lineales. En la imagen 3.20 mostramos nuevamente la ventana que reprodujimos en la imagen 3.18; pero en esta oportunidad, seleccionamos línea de tendencia polinómica.
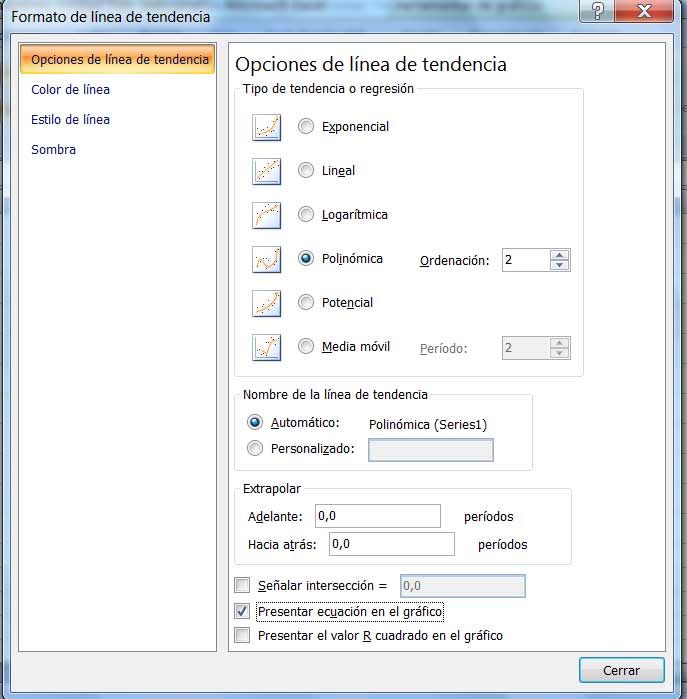
Captura de pantalla para seleccionar curva de tendencia polinómica.
En la imagen 3.21 vemos la curva de tendencia parabólica obtenida mediante el software.
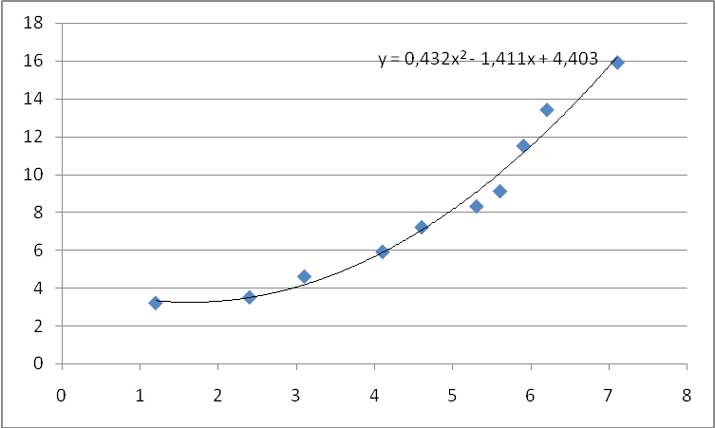
En busca de la mejor curva de ajuste para nuestra muestra, seleccionamos finalmente curva exponencial. La curva correspondiente aparece en la imagen 3.22.
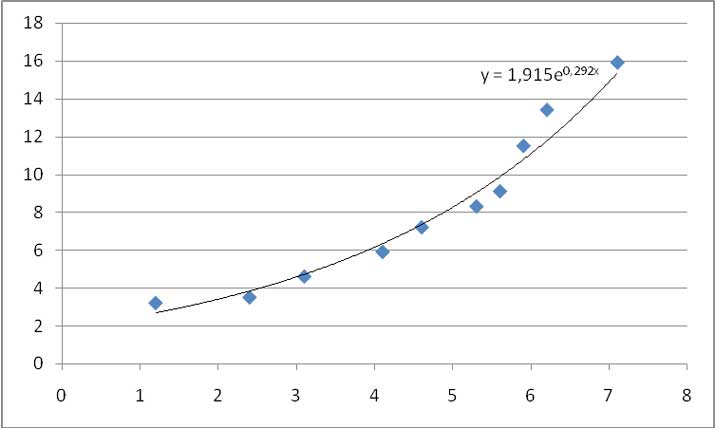
Curva de ajuste exponencial para nuestra muestra.
Finalmente, en la imagen 3.23 reproducimos las tres curvas de ajuste obtenidas. El investigador experimentado podrá aplicar su criterio para decidir cuál de las obtenidas resulta la más adecuada. Sin embargo, a simple vista se observa que, aun cuando el coeficiente de Pearson resultaba muy próximo a la unidad, cualquiera de las otras dos curvas parece ajustarse mejor que la lineal a nuestra muestra.
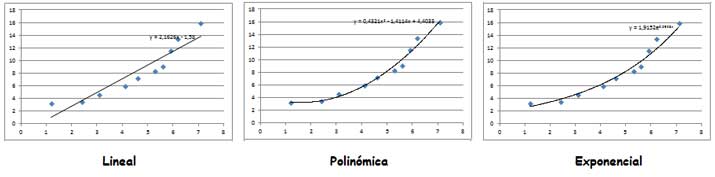
Comparación entre las tres curvas de ajuste obtenidas.
Devore, J. (2008), Probabilidad y Estadística para Ingeniería y Ciencias, CengageLearning, México, pp. 447 a 464.




