Distribuciones continuas
Objetivos
Que el alumno:
- Comprenda los conceptos de función de distribución de probabilidad y de distribución acumulativa, para poder aplicarlas a distribuciones continuas distintas de la normal.
- Aprenda a resolver problemas en los que se aplique la distribución normal, empleando para ello software adecuado.
- Aprenda a aproximar distribuciones binomiales empleando para ello distribuciones normales.
6.1. Introducción
En la unidad anterior trabajamos con variables aleatorias discretas para estudiar cierto tipo de fenómeno. Por ejemplo, al proponer como experimento el lanzamiento al aire de un dado dos veces, definimos como variable aleatoria al número de veces que se obtenía un as. Los únicos valores posibles para dicha variable eran 0, 1 y 2. No tenía sentido asignarle valores como 0,53 o 1,25.
Sin embargo, supongamos que nos proponemos estudiar otro tipo de fenómeno, como el tiempo necesario para que una reacción química dada se complete, medido en milisegundos. Existen diversos factores por los cuales dicho tiempo de reacción puede ser distinto de un ensayo a otro y tal vez nos interese poder saber cuál es la probabilidad de que la reacción se produzca en un tiempo menor a una cierta cantidad demilisegundos. En este caso, dicho tiempo podría ser de 0,199 o de 0,200 segundos. Es decir: la variable aleatoria con la que hemos de trabajar deberá expresarse como un número real.
Cuando los valores que pueda adoptar la variable aleatoria pertenezcan al conjunto de los números reales, diremos que se trata de una variable de tipo continua.
El hecho de que el instrumento de medición empleado para registrar dichos valores los reduzca a un número finito solo debe considerarse como una limitación práctica.
Para este tipo de fenómeno bajo estudio habrán de definirse dos funciones: la de densidad de probabilidad y la de distribución acumulativa.
Para una variable aleatoria continua X existirá una función f(x) que ha de cumplir las siguientes condiciones:
- \(f(x) \ge 0\)
- \(\int^\infty_{-\infty} f(x)dx = 1 \)
- \(P(a \le X \le b) = \int^b_a f(x)dx\)
Es decir, la probabilidad de que la variable aleatoria adopte un valor entre a y b resulta ser igual al área encerrada entre el eje de abscisas y la función f(x) dentro del intervalo definido por dichos valores de X.
Dicha función f(x) es la que recibe el nombre de función de densidad de probabilidad.
Por otro lado, definiremos a la función de distribución acumulativa F(x) de una variable aleatoria X como:
\[F(x) = P(X \le x) = \int^x_{-\infty} f(u)du\]
Es decir, la función de distribución acumulativa nos permite calcular la probabilidad de que la variable aleatoria X adopte un valor menor o igual a x.
Volviendo entonces al ejemplo que mencionamos anteriormente, supongamos entonces que la función de distribución acumulativa correspondiente a una reacción química dada pudiera expresarse aproximadamente como:
\[{\large f(x) = \left\{ \begin{array}{l} 0 \\ 1-e^{-0.01x} \end{array} \right. \begin{array}{l} \text{si } x < 0 \\ \text{si } x \ge 0 \end{array} }\]
Si nos preguntaran entonces cuál es la probabilidad de que una reacción se complete en menos de 200 milisegundos, bastará entonces con calcular:
\[\large{ F(200) = P(X<200) = 1 - e^{-0,01.200}=0,8647 }\]
Si, en cambo se nos pidiera calcular cuál es la probabilidad de que la reacción se complete en un tiempo que oscile entre los 100 y los 200 milisegundos, necesitaremos la función de densidad de probabilidad. Esta, de acuerdo con las definiciones dadas, no es otra cosa que la derivada de la función de probabilidad acumulada, de modo que para el caso sería:
\[{\large f(x) = \left\{ \begin{array}{l} 0 \\ 0,01e^{-0.01x} \end{array} \right. \begin{array}{l} \text{si } x < 0 \\ \text{si } x \ge 0 \end{array} }\]
Entonces:
\[\large{ P(100 \le x \le 200) = \int^{200}_{100} 0,01e^{-0,01x} dx = 0,2325 }\]
Seguidamente, estudiaremos una distribución de variable continua cuya función de distribución permite estudiar gran número de fenómenos reales y naturales.
Devore, J. (2008), Probabilidad y Estadística para Ingeniería y Ciencias, CengageLearning, México, pp. 145 a155
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México, pp. 157 a 162.
6.2. Distribuciones normales
Definimos como variable aleatoria normal \(X\) a aquella cuya función de densidad de probabilidad tenga la forma:
\[\large{ f(x)=\frac{1}{\sqrt{2\pi\sigma}}e^{\frac{(x-\mu)^2}{2\sigma^2}} }\]
Dicha variable estará asociada a una distribución de probabilidades que recibe el nombre de distribución normal, cuyos parámetros característicos son la media \(\mu\) y la varianza \(\sigma^2\) y que suele expresarse como \(N(\mu, \sigma^2)\).
Esta distribución habrá de permitirnos resolver infinidad de problemas. Por ejemplo, se sabe que el tiempo promedio que requiere una célula para dividirse en el proceso de mitosis es de una hora, con una desviación estándar de cinco minutos (recordemos que, matemáticamente, la desviación estándar no era otra cosa que la raíz cuadrada de la varianza). Nos interesará calcular la probabilidad de que una célula cualquiera se divida en menos de 45 minutos.
El tiempo en que se produce la división será nuestra variable aleatoria, variable que habrá de distribuirse normalmente. De acuerdo con la información de que disponemos, su media será de sesenta segundos, en tanto que su varianza valdrá veinticinco segundos al cuadrado. Para determinar entonces la probabilidad de que el proceso se produzca en una célula tomada al azar en menos de 45 minutos, escribimos:
\[\large{ P(X \le 45) = \int^{45}_{-\infty} \frac{1}{\sqrt{2\pi5}}e^{\frac{(x-60)^2}{2.25}}dx }\]
Desde ya, esta integral no habrá de poder resolverse con facilidad. Sin embargo, volveremos a utilizar nuestra planilla de cálculo para alcanzar nuestro objetivo. La función será en este caso DISTR.NORM (ver imagen 6.1). Una vez que se hace clic en “Aceptar” aparece la ventana que se observa en la imagen 6.2. Allí hemos de ingresar el valor de la variable aleatoria, la media y la desviación estándar.
El resultado que acabamos de obtener puede verificarse utilizando el GeoGebra. En la imagen 6.3 se observa no solo el valor de la probabilidad buscada, sino además, la representación gráfica aproximada de la función de densidad de probabilidad característica de toda distribución normal.
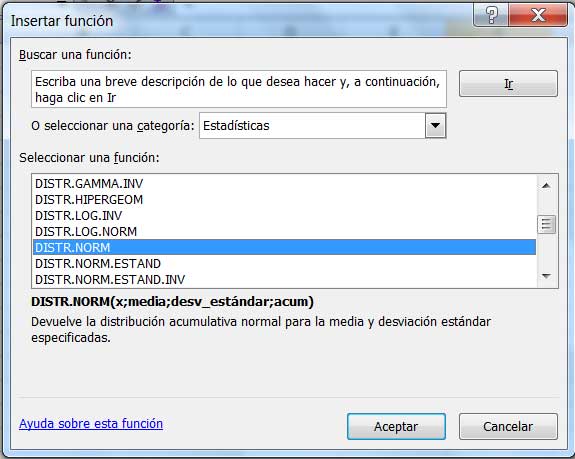
Seleccionamos la función DISTR.NORM para la resolución de nuestro problema.
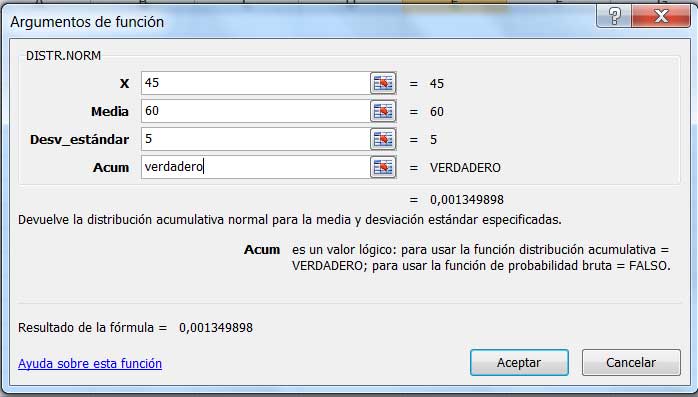
La probabilidad de que una célula se divida en menos de 45 minutos resulta ser del 0,13 %.
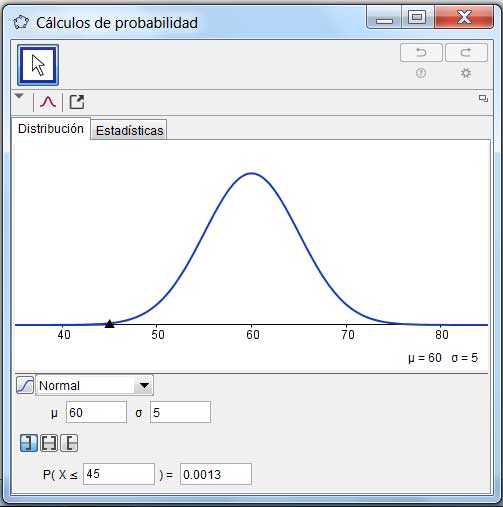
Verificamos el valor obtenido con la planilla de cálculo empleando el GeoGebra
La gráfica que corresponde a la función de densidad de probabilidad de esta distribución (a la que suele conocerse como campana de Gauss) tiene por dominio a todo el campo real, se hace asintótica al eje de abscisas para más y menos infinito y presenta un único máximo en correspondencia con el valor de la media de la distribución.
Si nos preguntáramos cuál es la probabilidad de que una célula tomada al azar tarde entre 55 y 65 segundos en dividirse, podríamos comenzar procediendo de un modo similar al ya aplicado. Sin embargo, en la planilla de cálculo no se contempla la posibilidad de trabajar con un intervalo de extremos finitos. Es decir, el límite inferior de integración será siempre menos infinito, tal como se observa en las imágenes 6.4 y 6.5.
Lo que deberíamos hacer entonces es restarle al valor que acabamos de obtener el correspondiente a la probabilidad de que el tiempo en que se produzca la mitosis sea inferior a 55 minutos, que podemos obtener nuevamente utilizando la planilla de cálculo, tal como se observa en la imagen 6.6.
Dicha diferencia puede llevarse a cabo en un único paso, tal como puede observarse en la ventana del extremo superior de la planilla de cálculo de la imagen 6.8.
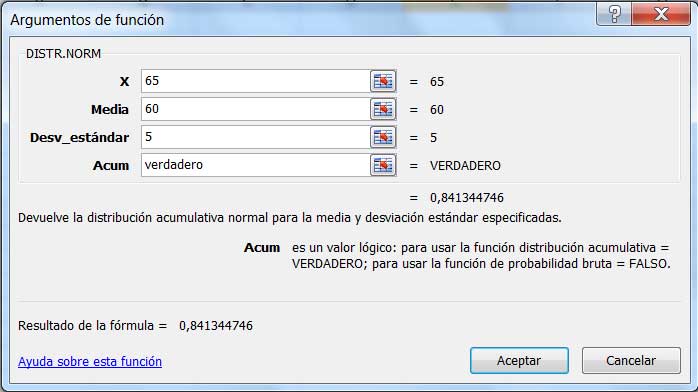
Al asignar como valor de la variable aleatoria el correspondiente al límite superior del intervalo con el que estamos trabajando…
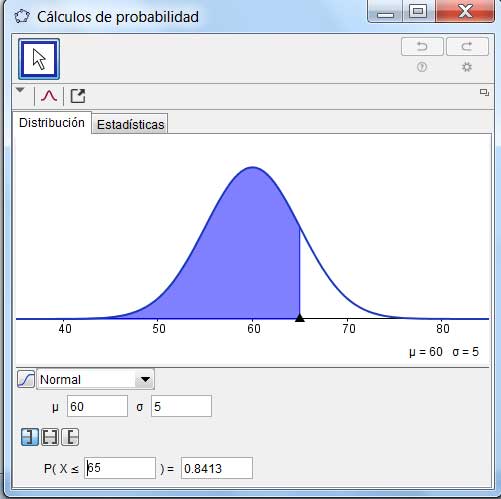
…se observa que la probabilidad resultante es la que corresponde a valores de la variable aleatoria menores a 65 (pero no simultáneamente superiores a 55).
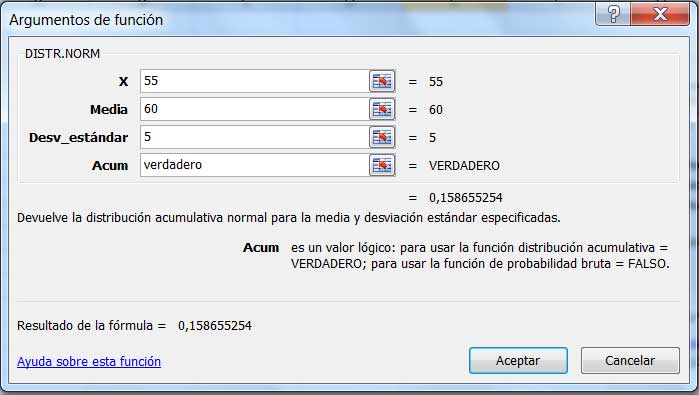
Calculamos la probabilidad de que la mitosis se produzca en un tiempo inferior a los 55 minutos.
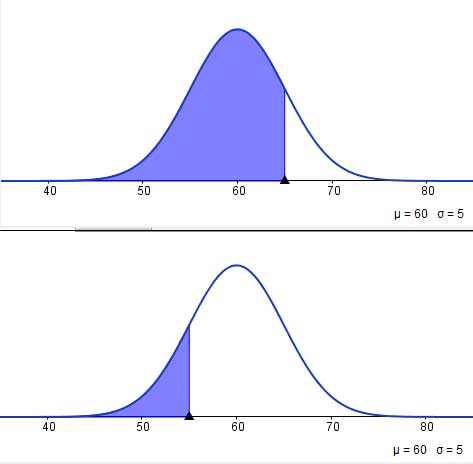
Al restarle al valor de la probabilidad obtenida según la figura 6.4 la que se obtuvo tal como se observa en la imagen 6.6, lo que hacemos es restar al área de arriba la de abajo.
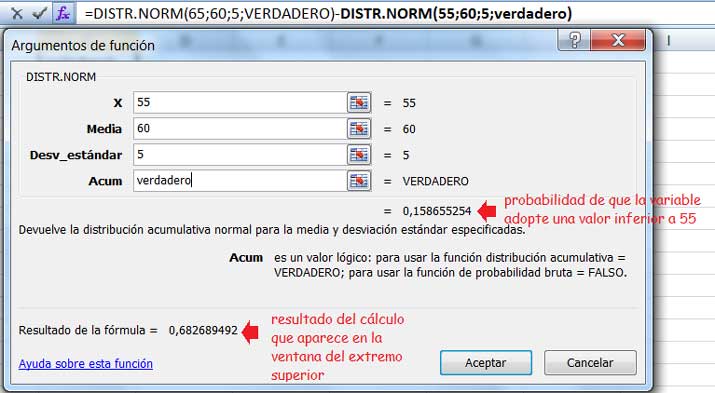
En la parte inferior, la probabilidad de que el tiempo que requiera la célula para dividirse esté entre los 55 y los 65 minutos.
6.2.1. Propiedades de las distribuciones normales
- Como acabamos de ver, la curva que representa a la función de distribución de probabilidad tiene forma de campana.
- El área entre dicha curva y el eje de abscisas vale uno, para todo el dominio de integración de la correspondiente función de densidad de probabilidades.
- La media de la distribución se localiza en el centro de la distribución, en correspondencia con la abscisa del máximo de esta.
- La media, la mediana y la moda coinciden, reflejando la ausencia de sesgo.
- La curva se hace asintótica al eje de abscisas, de modo que nunca corta a dicho eje; ello también es de esperar, si tenemos en cuenta que la función de densidad de probabilidades ha de ser positiva.
- De acuerdo con los valores de la media y de la desviación estándar, el eje de simetría y la forma de la campana habrán de ser distintos (Imágenes 6.9 y 6.10)
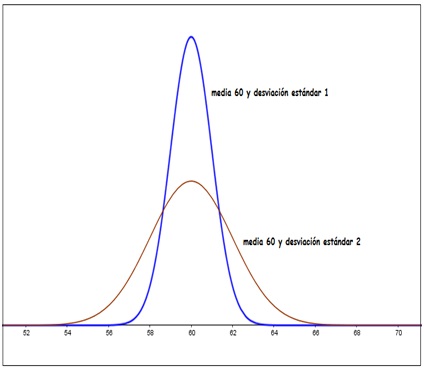
Para un mismo valor de la media, se observa que la forma de la campana cambia según el de la desviación estándar. Cuanto menor sea este valor, más puntiaguda resulta ser la campana.
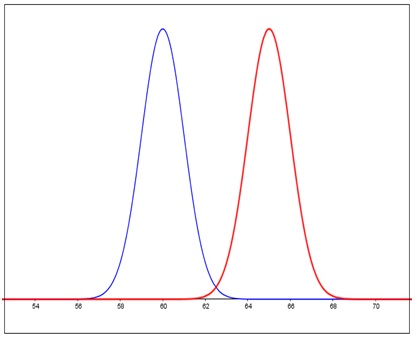
Dos distribuciones que tienen la misma desviación estándar pero distintas medias. La de la izquierda (en color azul) con media 60, en tanto que la de la derecha (en color rojo) con media 65.
6.2.2. Relación entre la desviación estándar y las probabilidades
- El 68,27 % de las medidas distan menos de una desviación estándar respecto de la media.
- El 95,45 % de las medidas distan menos de dos desviaciones estándar respecto de la media.
- El 99,73 % de las medidas distan menos de tres desviaciones estándar respecto de la media.
Para graficar esta situación hemos utilizado el problema analizado anteriormente, en el que se estudiaba el tiempo que requería la célula para dividirse. En las imágenes 6.11, 6.12 y 6.13 representamos dichos intervalos, teniendo en cuenta que la media era de 60 minutos y la desviación estándar de cinco.
En cada caso, definimos los intervalos a los que hacen referencia los puntos (1), (2) y (3), y verificamos los valores de probabilidades mencionados.
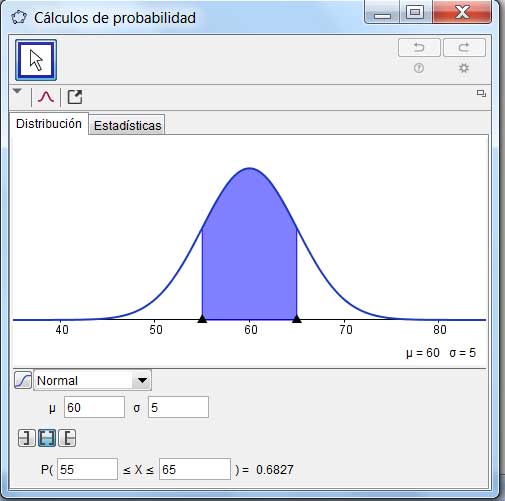
A partir del problema planteado al comenzar el apartado 6.2, donde la
variable era el tiempo promedio requerido por una célula para dividirse
por el proceso de mitosis,se observa que la probabilidad de que la variable
adopte un valor entre \(\mu-\sigma\) y \(\mu+\sigma\) es 0,6827.
( diseño: hacer enlace en el apartado 6.2)
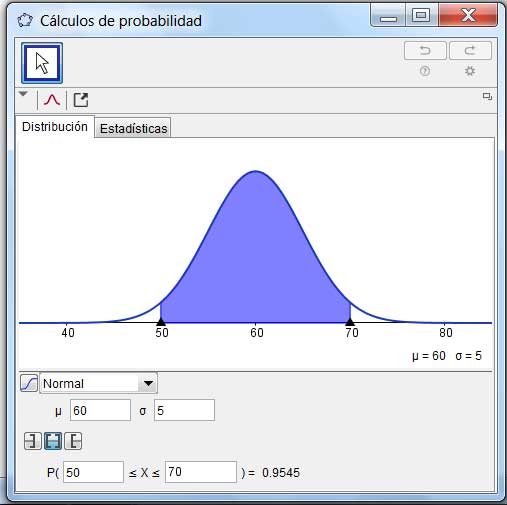
La probabilidad aumenta hasta 0,9545 cuando el intervalo va desde \(\mu-2\sigma\) hasta \(\mu+2\sigma\)
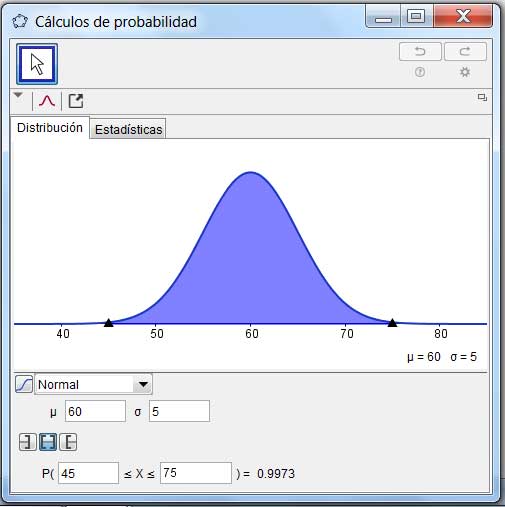
La probabilidad llega hasta 0,9973 cuando el intervalo es \( (\mu-3\sigma,\ \mu+3\sigma) \).
El contenido de una lata de gaseosa es una variable aleatoria normal, con una media de 330 centímetros cúbicos y una desviación estándar de 10 centímetros cúbicos.
- ¿Cuál es la probabilidad de que una lata tomada al azar contenga menos de 315 centímetros cúbicos de gaseosa?
- Si una lata contiene menos de 310 centímetros cúbicos o más de 350, no está en condiciones de poder comercializarse. ¿Cuál es entonces la probabilidad de que una lata tomada al azar sea descartada?
- ¿Entre qué valores deberían fijarse las especificaciones en lo que al contenido de gaseosa respecta para que el 99 % de las latas no fuesen rechazadas?
Sugerencia: utilizar la instrucción DISTR.NORM.INV de la planilla de cálculo y confirmar el resultado obtenido empleando el softwareGeoGebra.
El tiempo de reacción de un conductor a un estímulo visual se distribuye normalmente, con una media de 0,4 segundos y una desviación estándar de 0,05 segundos.
- ¿Cuál es la probabilidad de que un conductor tarde más de 0,5 segundos en reaccionar?
- ¿Cuál es la probabilidad de que un conductor tarde entre 0,4 y 0,5 segundos en reaccionar?
La vida de un circuito integrado se distribuye normalmente, con una media de 7000 horas y una deviación estándar de 600 horas.
- ¿Cuál es la probabilidad de que el circuito falle antes de las 5000 horas de uso?
- Si tres de esos circuitos se encuentran conectados en serie y se puede asumir que la vida útil de cada uno de ellos resulta independiente de la de los restantes, ¿cuál es la probabilidad de que el equipo siga operando después de las 7000 horas?
6.3. Distribución normal estándar
Si X es una variable aleatoria normal, con media \(\mu\) y desviación estándar \(\sigma\), entonces la variable \(Z=(X-\mu)/\sigma\) es una variable estandarizada, cuyas unidades son desviaciones estándar. La variable normal estándar Z, tal como la acabamos de definir, ha sufrido un desplazamiento horizontal y un cambio de escala, razón por la cual su media es cero y su desviación estándar uno. La distribución de probabilidades de Z recibe el nombre de distribución normal estándar.
La función de distribución acumulada correspondiente a una variable aleatoria normal estándar se suele expresar de la siguiente manera:
\[\Phi\ (z) = p\ (Z \le z)\]
Al crear una nueva variable Z a partir de otra X, la variable aleatoria Z representa la distancia desde X hasta su media, medida en desviaciones estándar.
La corriente eléctrica que atraviesa un cable conductor de cobre puede considerarse como una variable aleatoria normal, con media de 10 miliamperes y deviación estándar de 2 miliamperes. ¿Cuál será entonces la probabilidad de que la corriente que circule por un cable supere los 13 miliamperes?
Si X corresponde a la corriente en miliamperes, la probabilidad que hemos de calcular es P (X > 13). Podemos entonces definir Z = ((X - 10)) /2.
\(\text{Si } X= 13,Z =((13-10))/2=1,5 \text{, de manera que:}\)
\(P\ (X>13) = P\ (Z>1,5) = 1-P\ (Z\le1,5)\)
Para calcular P (Z ≤ 1,5) podemos volver a emplear la planilla de cálculo, pero utilizando una nueva función, DISTR.NORM.ESTAN.
En la imagen 6.14 se observa la ventana que se abre en la planilla de cálculo para obtener la probabilidad con la variable aleatoria estandarizada. Teniendo en cuenta toda la información disponible, podemos finalmente responder que:
\[P\ (Z>1,5)=1-P\ (Z\le1,5)=1-0,93319\]
\[P\ (X>13)=P\ (Z>1,5)=0,06681\]
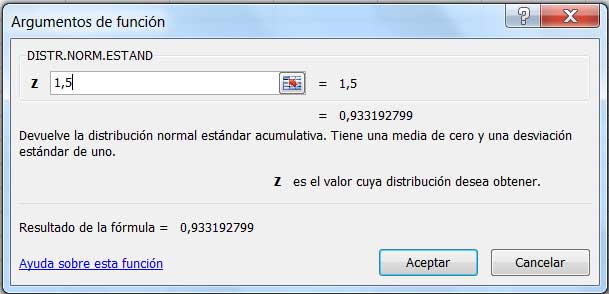
Al utilizar esta nueva función, el único valor que hemos de ingresar es el que corresponde a Z.
En la imagen 6.15 se comparan las distribuciones de la variable original X con la de su variable estandarizada Z.
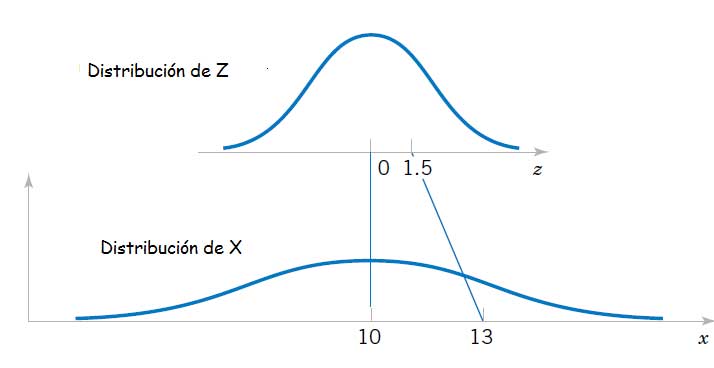
Los segmentos celestes unen los valores de las variables aleatorias, original y estandarizada, para la media y x=13.
El resultado puede obtenerse empleando nuestra planilla de cálculo, tal como se observa en la imagen 6.16.
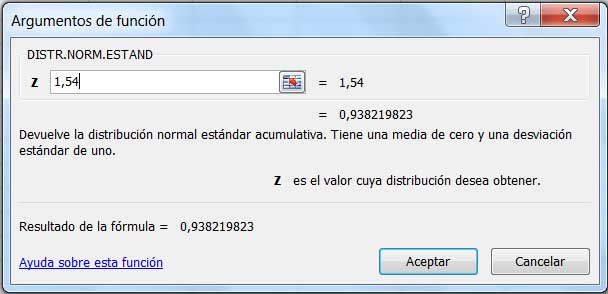
Calculamos el valor de P(Z≤1,54) utilizando la planilla de cálculo.
El alumno puede preguntarse qué necesidad existe de estandarizar una variable aleatoria normal. Entre las razones por las cuales el alumno debe manejar el concepto de estandarización podemos mencionar la siguiente: en control estadístico de procesos, existen diversos métodos para la confección de los diagramas de control para la fracción de artículos disconformes con muestras de tamaño variable. De todos esos métodos, el mejor, desde el punto de vista del ingeniero, es justamente el que estandariza dicha fracción disconforme.
6.4. Empleo de distribuciones normales para aproximar distribuciones binomiales
Existen experimentos binomiales en los que el cálculo manual de probabilidades requiere de un gran número de operaciones largas y tediosas, razón por la cual buscamos algún mecanismo que nos facilite la tarea.
Se observa que cuando una distribución binomial es simétrica o aproximadamente simétrica respecto de su media, su gráfica de barras se asemeja a la campana de Gauss, típica de la distribución normal. En la imagen 6.17 reproducimos los diagramas de barras de un experimento BernoulliN con p = 0,5. Obsérvese que, para un número de experimentos muy elevado, dicho diagrama se confunde con la clásica campana.
Se define como experimento Bernoulli a aquel que solo admite dos resultados posibles. Si, por ejemplo, nuestro experimento consiste en arrojar un dado para obtener un as, en el caso de que ello suceda diremos que obtuvimos un “éxito”; si el número que queda en la cara superior del dado no llegara a ser un uno, diremos que el resultado del experimento fue un “fracaso”.
Los valores de la variable aleatoria correspondiente a una distribución binomial serán entonces la cantidad de “éxitos” que puedan obtenerse al repetirsen experimentos Bernoulli independientes entre sí.
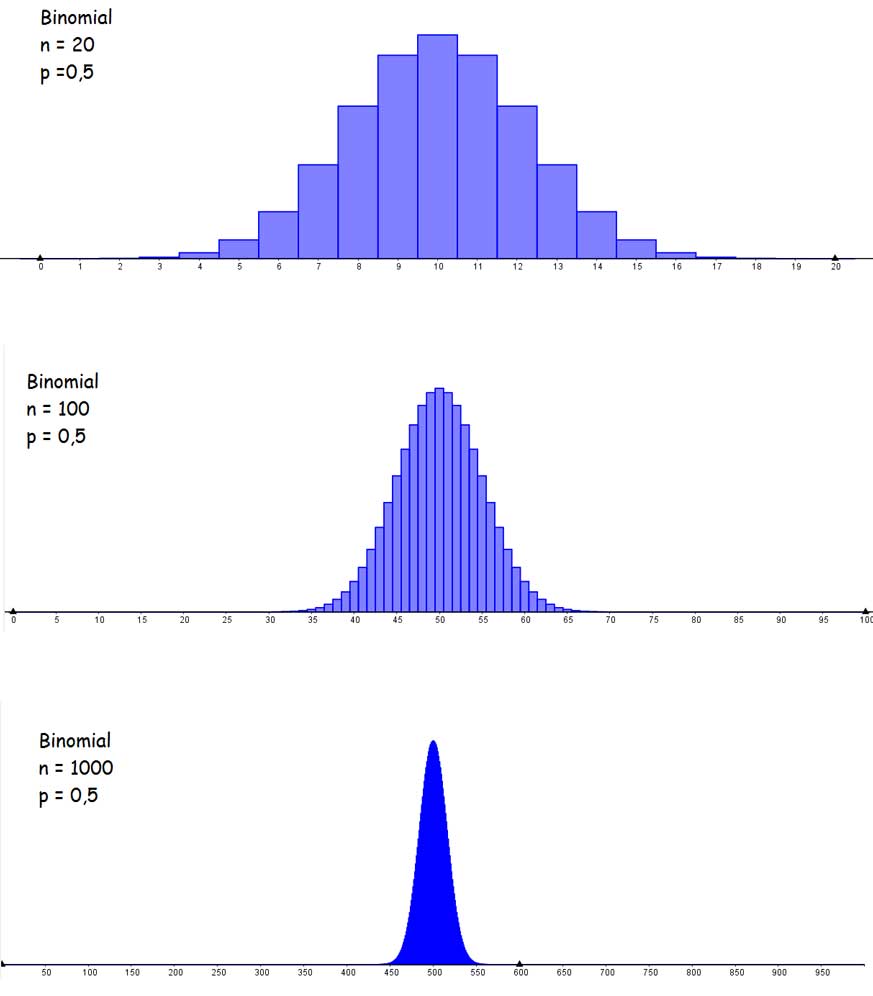
Para una variable aleatoria binomial comparamos los diagramas de barras correspondientes a tres casos distintos, en los que el número de repeticiones del experimento aumenta. Evidentemente, cuando dicho número es muy alto, resulta difícil diferenciar el diagrama escalonado (que se observa claramente para el caso de n = 20) con la forma acampanada típica de la distribución normal (que parece ser representada para el caso en que n = 1000).
Dijimos anteriormente que, en una distribución normal con media \(\mu\) y desviación estándar \(\sigma\), aproximadamente el 99,7 % (es decir, prácticamente toda la distribución) se encontraba entre \(\mu-3\sigma\) y \(\mu+3\sigma\). Si tenemos una distribución binomial cuya media es \(\mu=np\), su desviación estándar será:
\[\large{ \sigma =\sqrt{np(1-p)} }\]
Además, si tenemos en cuenta que los valores de la distribución normal son mayores que cero y menores o iguales a n, entonces deberán cumplirse simultáneamente las siguientes dos condiciones:
\[\large{ 0 \le \mu-3\sigma y \mu + 3\sigma \le n }\]
Es decir:
\[\large{ \begin{gather} \begin{split} & 0 \le np-3\sqrt{np(1-p)}\\ ynp +3 &\sqrt{np(1-p)} \le n \end{split} \end{gather} }\]
Se puede demostrar que, para p≤0,5, ambas desigualdades son equivalentes a np≥4,5 y que, en cambio, sip≥0,5, dichas inecuaciones serán equivalentes a n(1-p)≥4,5.
Teniendo en cuenta lo antedicho, se establece como regla que una distribución binomial se puede aproximar por una distribución normal cuando np≥5 y n(1-p)≥5.
El 80 % del ganado inoculado con un determinado suero queda protegido de la fiebre aftosa. Hallar la probabilidad de que, de 30 vacas inoculadas, 28 no contraigan la enfermedad.
Verificamos que la regla que acabamos de plantear pueda aplicarse, calculando:
\[np=30.0,\ 8=28 \ y \ n(1-p)=30.0,\ 2=6 \]
Entonces:
\[\mu= np =24y\]
\[\sigma= \sqrt{np(1-p)} = \sqrt{30.0,\ 8.0,\ 2}=2,19\]
Tratándose de una distribución continua no podemos asignar a la variable aleatoria un único valor, de modo que calcularemos la probabilidad de que dicha variable adopteun valor entre 27,5 y 28,5.
Las figuras 6.18 y 6.19 nos permiten comparar los resultados obtenidos en forma aproximada y exacta, utilizando la aproximación normal y la distribución binomial, respectivamente.
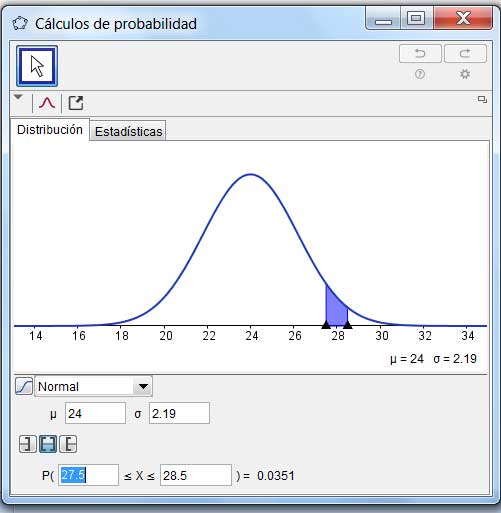
Cálculo aproximado con la distribución normal.
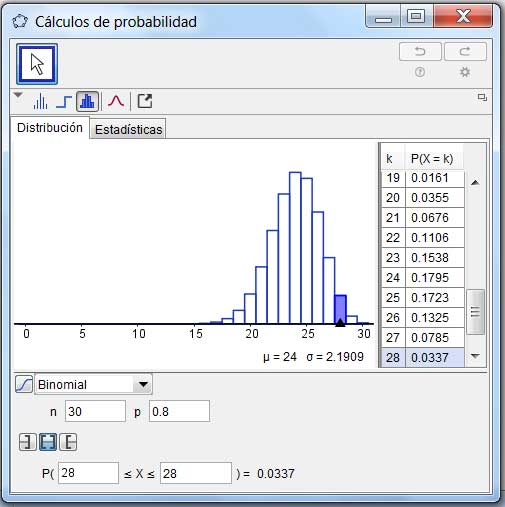
Verificación utilizando la distribución binomial.
Devore, J. (2008), Probabilidad y Estadística para Ingeniería y Ciencias, CengageLearning, México, pp.160 a 171.
Montgomery, D.; Runger,G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México, pp. 173 a 184.
6.5. Distribuciones exponenciales
Estrechamente vinculada con la distribución de Poisson que estudiamos anteriormente, la distribución exponencial se suele usar, por ejemplo, para modelar los tiempos de ocurrencia entre dos eventos sucesivos, cuya distribución resulte ser exponencial. El tiempo entre dos llamadas telefónicas sucesivas que entran a un conmutador o entre dos temblores sucesivos en una determinada región son tan solo dos de los muchos ejemplos de aplicación más comunes para este tipo de distribución.
Diremos que una variable aleatoria X tiene una distribución de tipo exponencial cuando su función de densidad de probabilidad tenga la forma:
\[\large{ f(x)= \lambda e^{-\lambda x} }\]
Este tipo de variable aleatoria se caracteriza por lo siguiente:
(i) Su media vale \(\large{ \mu = \frac{1}{\lambda} }\)
(ii) Su varianza vale \(\large{ \sigma^2 = \frac{1}{\lambda^2} }\)
Nótese que tanto la media como la desviación estándar de esta distribución son iguales entre sí e iguales a la inversa de la constante \(\lambda\). Dicha constante recibe el nombre de parámetro de la distribución.
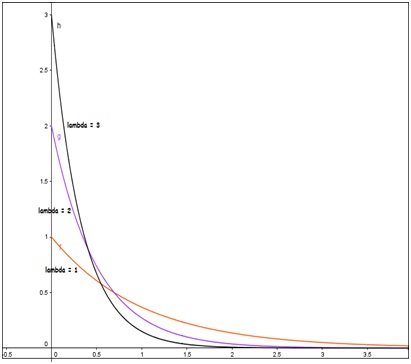
Graficamos comparativas de las funciones de densidad de probabilidad para \( \lambda =1,\ \lambda =2,\ \lambda =3. \)
El tiempo en minutos entre las llamadas telefónicas que llegan a un conmutador se distribuyen exponencialmente, con parámetro \( \lambda =1,8\). Hallar la probabilidad de que haya un tiempo de espera de al menos un minuto entre las dos primeras llamadas que lleguen a dicho conmutador en un día cualquiera.
Si llamamos X a la variable aleatoria que representa al tiempo en minutos entre dos llamadas sucesivas, tendremos que calcular \(P\ (X\ge 1) \).
Al emplear la planilla de cálculo tendremos que utilizar una nueva función, DISTR.EXP. Aplicando las propiedades de las probabilidades estudiadas oportunamente, tenemos que:
\[P\ (X\ge 1)=1-P\ (X<1) \]
En la imagen 6.21 se observa el cálculo llevado a cabo mediante la planilla de cálculo.
Utilizando el GeoGebra no solo verificamos el resultado obtenido sino que, además, podemos observar la gráfica de la función de densidad de probabilidad correspondiente al problema (imagen 6.22).
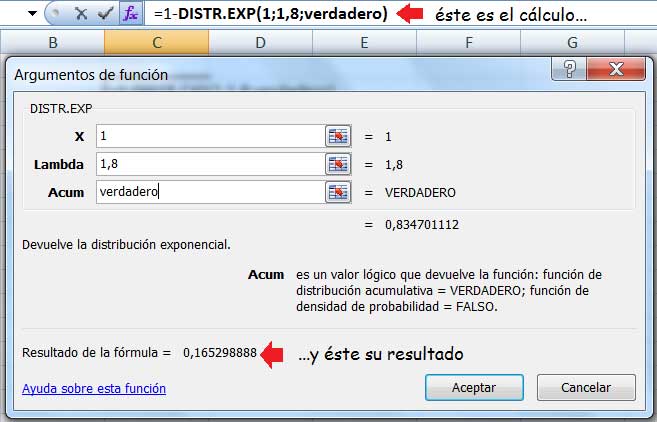
En este caso no solo reproducimos la ventana correspondiente a la función, sino que es interesante atender a la instrucción que nos lleva a la solución y que aparece en la parte superior de la imagen.
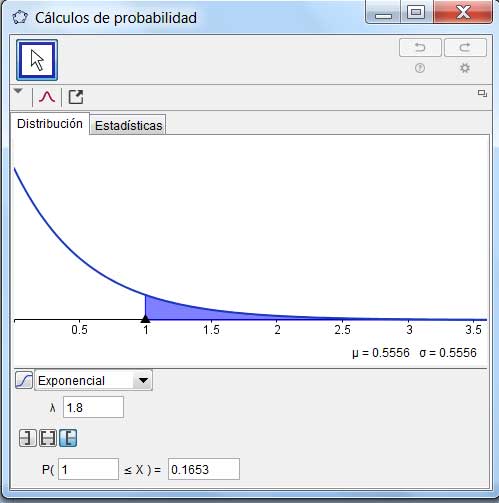
Verificación del resultado obtenido mediante el GeoGebra.
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México, pp. 195 a 200.
El tiempo de espera para que un cliente sea atendido en la línea de cajas de un determinado banco se distribuye exponencialmente con una media de 10 minutos. Teniendo en cuenta la relación entre la media y el parámetro \(\lambda\), se pide calcular la probabilidad de que una persona sea atendida en menos de 5 minutos.
El promedio de partículas detectadas por un contador Geiger ante un determinado material esde dos por minuto.
- ¿Cuál es la probabilidad de que no sea detectada ninguna partícula durante un intervalo de tiempo de 30 segundos?
- ¿Cuál es la probabilidad de que la primera de las partículas sea detectada en menos de 10 segundos?

