Estimación de parámetros
Objetivos
Que el alumno:
- Adquiera la noción de estimación de un parámetro y la importancia de dicha operatoria a la hora de trabajar con muestras de una población.
- Aprenda a calcular dichos estimadores.
8.1. Introducción
Al tomar muestras de una población nos interesa estimar sus propiedades, las que dependerán, en principio, de la distribución de frecuencia de dicha población. Así, por ejemplo, si inspeccionásemos la calidad de un producto en una línea de fabricación, nuestro “experimento” tendría dos resultados posibles: rechazar aquellos artículos que no cumpliesen con las especificaciones y aceptar los restantes. Puesto que estamos hablando de “éxito” o “fracaso”, en función de encontrar un producto disconforme o no, se tratará de un experimento Bernoulli, y la distribución de probabilidades a emplearse habrá de ser la binomial.
En ese caso, sabemos que los parámetros habrán de ser el número de artículos inspeccionados n (que puede asimilarse al número de “experimentos” que se han llevado a cabo) y la probabilidad de que alguno de ellos sea rechazado, p. Recordemos que estos dos valores reciben el nombre de parámetros de la distribución.
Puesto que la cantidad de artículos que componen la muestra suele ser fijado de antemano, nuestro problema habrá de limitarse a estimar el valor de la probabilidad de encontrar artículos disconformes en la población a partir de lo observado en nuestra muestra.
Si nuestra inspección no se basara en un conjunto de especificaciones sino que el criterio de aceptación o rechazo estuviese vinculado, por ejemplo, con una determinada característica (como, por ejemplo, el peso de la bolsa que contiene al producto), la base estadística del procedimiento sería diferente a la descripta en el ejemplo anterior. La característica que decide si el artículo se rechaza o no habrá de distribuirse normalmente.
En ese caso, los parámetros que la caracterizan serán la media μ y la desviación estándar \(\sigma\). Hemos, entonces, de estimar dichos valores a partir de nuestro muestreo.
8.1.1. Estimación puntual
Existen dos tipos de estimaciones. La primera es la puntual, que se aplica frecuentemente. Supongamos que la resistencia de un determinado material hubiese sido medida en una muestra de tamaño 20. Los valores obtenidos aparecen en la tabla que se reproduce en la imagen 8.1.
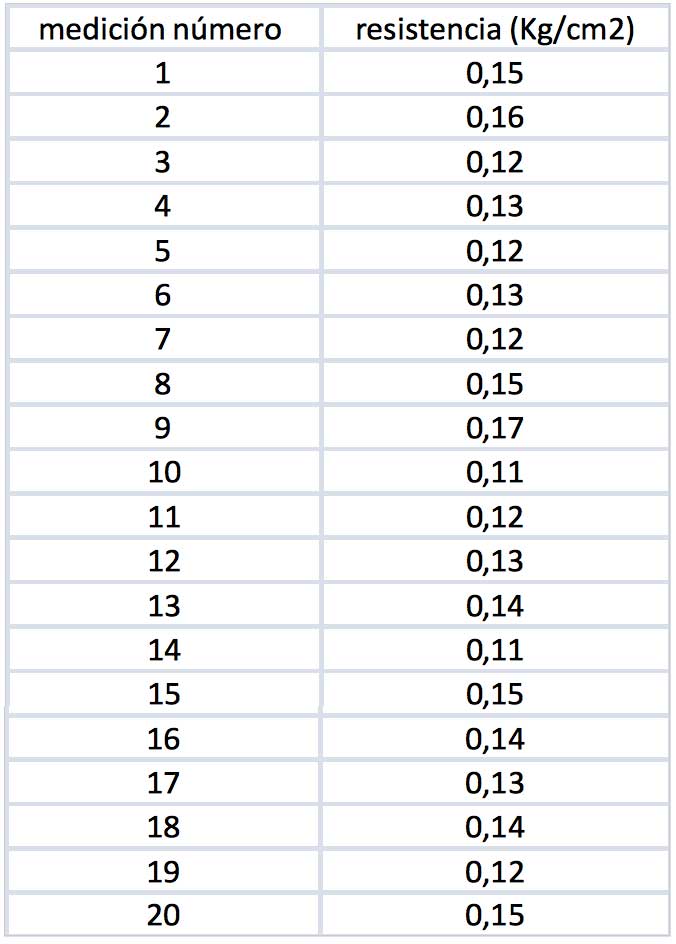
Resistencia obtenida en cada ensayo dentro de la muestra
Dado que la resistencia puede considerarse como una variable aleatoria que se distribuye normalmente, la media de la muestra \(\overline{X}\) puede considerarse como un estimador puntual de la media poblacional \(\mu\).
Puesto que el valor de dicha media es 0,1345 kg/cm2, este valor resulta entonces ser una estimación de \(\mu\).
Además, resulta que la desviación estándar de la muestra S vale 0,0167 kg/cm2. Ese será entonces el valor de la desviación estándar poblacional \(\sigma\).
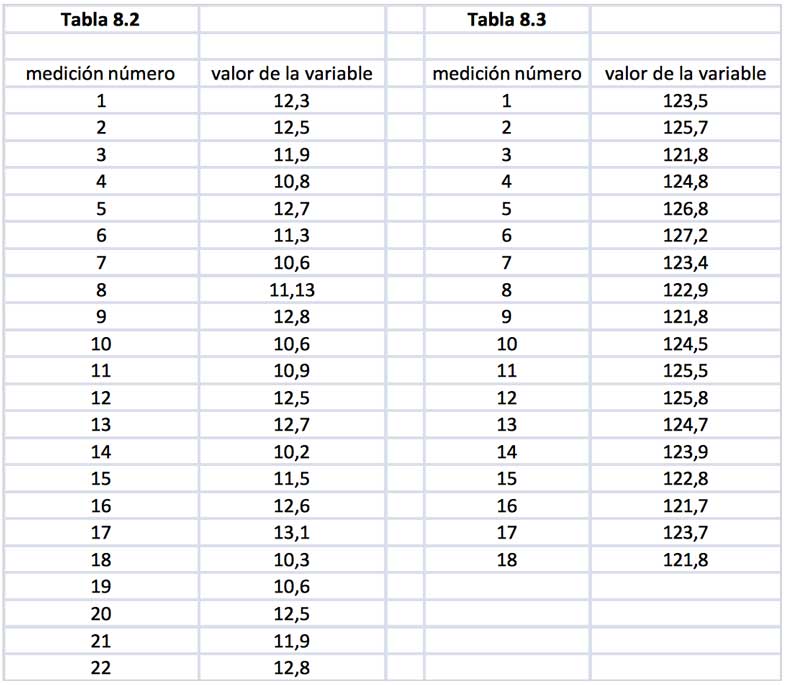
Las tablas 8.2 y 8.3 de la imagen 8.2 reproducen las lecturas correspondientes a dos muestras de distintos tamaños y diferentes variables. Para cada una de ellas, se pide estimar en forma puntual \(\mu\) y \(\sigma\).
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México. pp. 283 a 292.
Devore, J. (2005), Probabilidad y Estadística para Ingeniería y Ciencias, International Thomson Editores, México, pp. 253 a 265.
8.1.2. Estimadores puntuales para distribuciones Poisson
Supongamos que la cantidad de impurezas detectadas por unidad de volumen en un determinado producto resulta ser la variable de calidad que nos interesa estimar a partir de una muestra. A dicha variable le corresponde una distribución de probabilidades de tipo Poisson. En ese caso, el estimador adecuado para el parámetro λ será el siguiente:
\[\large{ \hat{\lambda}= \frac{1}{n}\sum^n_{i=1}x_i=\overline{X} }\]
Así, si por ejemplo, la tabla que se reproduce en la imagen 8.3 nos ofrece la cantidad de impurezas detectadas por unidad de volumen en una muestra compuesta por 21 mediciones.
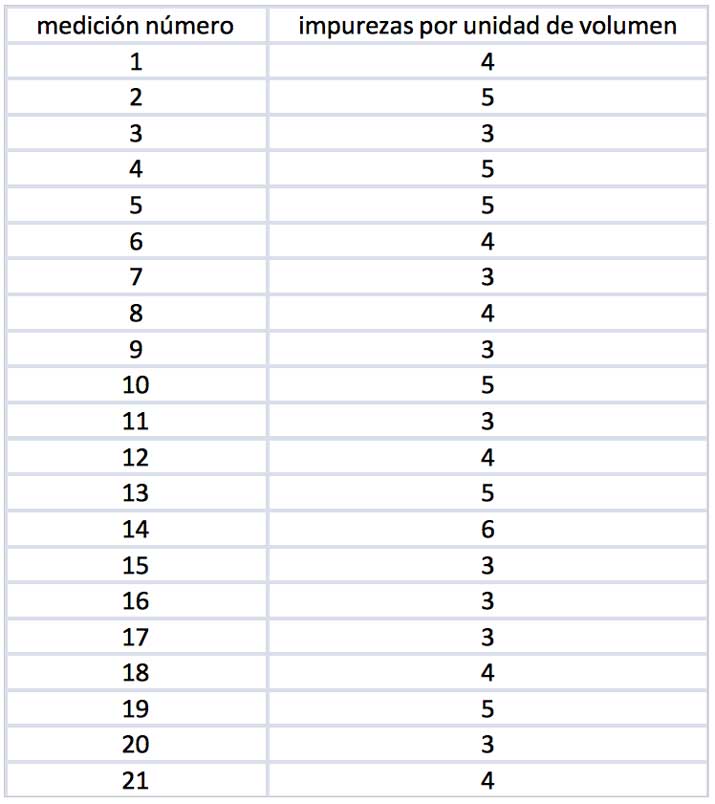
Efectuando el cálculo correspondiente, obtenemos como estimador del parámetro de la distribución el valor \( \hat{\lambda}= 4 \).
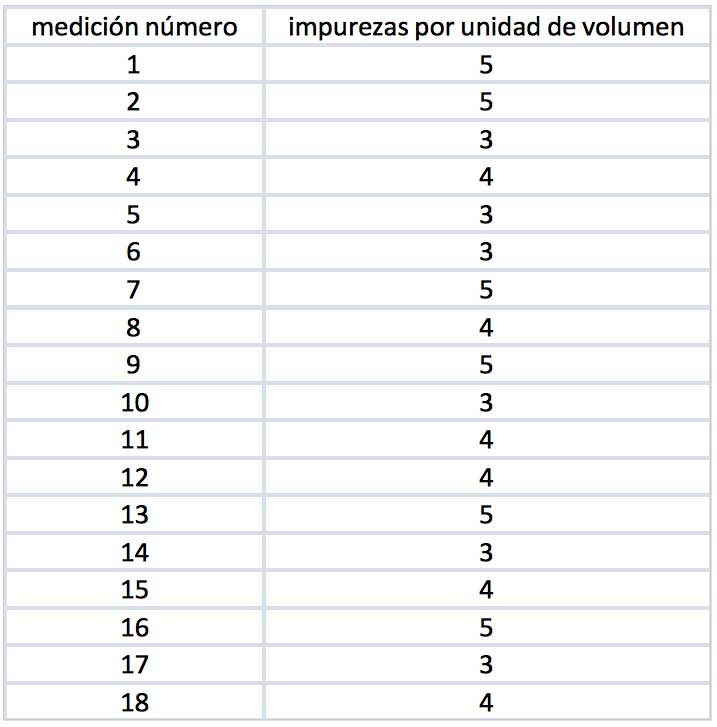
La tabla de la imagen 8.4 reproduce los valores de cantidad de impurezas por unidad de volumen correspondientes a una segunda muestra correspondiente a la misma población. Calcular el valor estimado del parámetro \( \lambda \) y compararlo con el obtenido anteriormente. ¿Qué conclusión puede obtener?
8.1.3. Estimador puntual para distribución binomial
Para una distribución binomial, un buen estimador del parámetro p será:
\[\large{ \hat{p}= \frac{1}{n}\sum^n_{1=1}x_i=\overline{X} }\]
El número de “experimentos” deberá ser constante y la variable x solo podrá adoptar valores 0 o 1 (correspondientes a “fracaso” o “éxito”, respectivamente).
8.2. Estimación por intervalo
Se denomina de este modo a un intervalo aleatorio que incluye al valor real del parámetro, de tal modo que la probabilidad de que dicho intervalo contenga al parámetro pueda especificarse. Estos intervalos reciben el nombre de intervalos de confianza.
Suponiendo que, por ejemplo, deseáramos calcular el intervalo de confianza para la media μ, podemos entonces decir que nuestro objetivo es buscar dos valores, a los que denominaremos límite inferior (LI) y límite superior (LS), tales que:
\[\large{ P(LI \le \mu \le LS)=1-\alpha }\]
Tal intervalo recibe el nombre de intervalo de confianza al \(100(1-\alpha)\%\).
La diferencia entre los límites superior e inferior del intervalo de confianza (valor al que algunos autores denominan longitud del intervalo de confianza) nos da una idea de la precisión de nuestra estimación. Por eso, resulta conveniente que dicha diferencia sea pequeña y, simultáneamente, el nivel de confianza sea alto. En general, el tamaño del intervalo aumenta a medida que lo hagan la varianza de la población y el nivel de confianza. Se observa, además, que la diferencia entre los límites superior e inferior de la muestra se reduce a medida que el tamaño de la muestra aumenta.
8.2.1. Intervalo de Confianza para la media con varianza conocida
Dada una variable aleatoria con media μ desconocida, pero de la que sí se conoce su varianza \(\sigma^2\), el procedimiento para obtener el intervalo de confianza al 100(1-\(\alpha\))% será el siguiente: se toma una muestra aleatoria de tamaño n, de la que se calculmusigma^2\) será entonces: será entonces:
\[\large{ \overline{X}-Z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \le \mu \le \overline{X}+Z_{\alpha/2} \frac{\sigma}{\sqrt{n}} }\]
A modo de ejemplo, supongamos que una máquina dosificadora empleada en la industria alimentaria estuviese programada para que la harina que dejara caer en cada bolsa fuese una variable aleatoria que tiene distribución normal con \(\sigma\) =0,01 kg. Se selecciona una muestra de 30 bolsas, que arrojan un peso promedio de 995 gramos; se nos pide estimar el peso promedio poblacional, con un 95 % de confianza.
Ante todo, necesitamos conocer \(Z_{\alpha/2}=Z_{0,025}\) . Dicho valor puede obtenerse de tablas, pero nosotros lo obtendremos empleando una planilla de cálculo. En la imagen 8.5 mostramos de qué modo se puede obtener dicho valor.
Así, el límite inferior del intervalo de confianza será:
\[\large{ LI=0,995 - 1,96.\frac{0,01}{\sqrt{30}}=0,991kg }\]
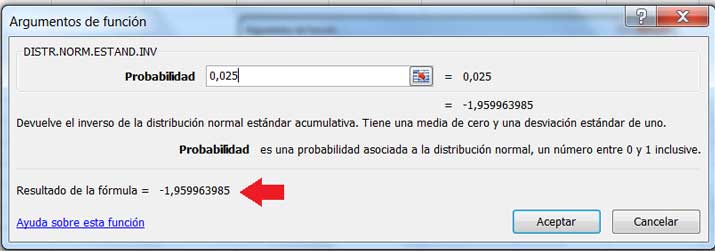
Obtención de Z0,025 empleando una planilla de cálculo
Seguidamente, calculamos el límite superior de dicho intervalo:
\[\large{ LS=0,995 - 1,96.\frac{0,01}{\sqrt{30}}=0,998kg }\]
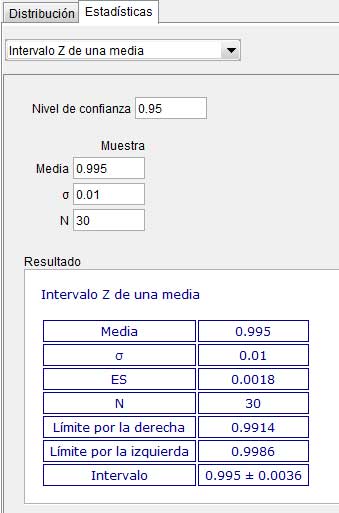
Los valores que acabamos de calcular pueden verificarse empleando el GeoGebra, tal como se observa en la imagen 8.6.
Es necesario interpretar correctamente el resultado obtenido: si tomáramos cien muestras de tamaño treinta de la misma población, el peso promedio de noventa y cinco de las bolsas habría de encontrarse entre los 0,991 kg y los 0,998 kg.
- ¿Cuál sería el intervalo de confianza del 99 % para la máquina llenadora del ejemplo anterior?
- ¿Qué conclusión puede obtener comparando los resultados obtenidos en cada caso?
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México. pp. 323 a 327.
8.2.2. Intervalo de confianza para una media de una distribución normal con varianza desconocida
En el caso de que la variable aleatoria con la que estuviésemos trabajando fuese normal, pero ignorásemos tanto su media como su varianza, hemos de partir de una muestra aleatoria de tamaño n, calculando su media \(\overline{X}\) y su varianza \(S^2\). El intervalo de confianza para la media de dicha variable al \(100\ (1-\alpha)\%\) habrá de obtenerse a partir de la siguiente expresión:
\[\large{ \overline{X}-t_{\alpha/2},n-1\frac{S}{\sqrt{n}}\le \mu \le \overline{X}+ t_{\alpha/2},n-1\frac{S}{\sqrt{n}} }\]
En dicha expresión, \(t_{\alpha/2},n-1\) representa el punto porcentual de la distribución \(t\) con \(n-1\) grados de libertad.
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México,pp. 335 a 338.
Supongamos que nos proponemos estimar la media de la vida útil de cierto tipo de lámpara. Para ello tomamos una muestra de tamaño siete, obteniéndose los valores que se reproducen en la tabla de la imagen 8.7.
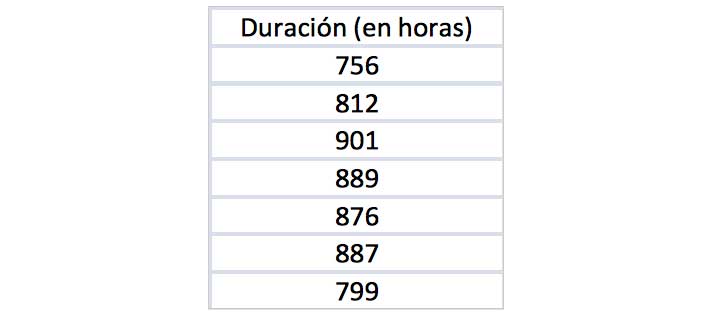
Obtenemos entonces su media y su desviación estándar, empleando para ello nuestra planilla de cálculo, tal como puede observarse en las imágenes 8.8 y 8.9, respectivamente.
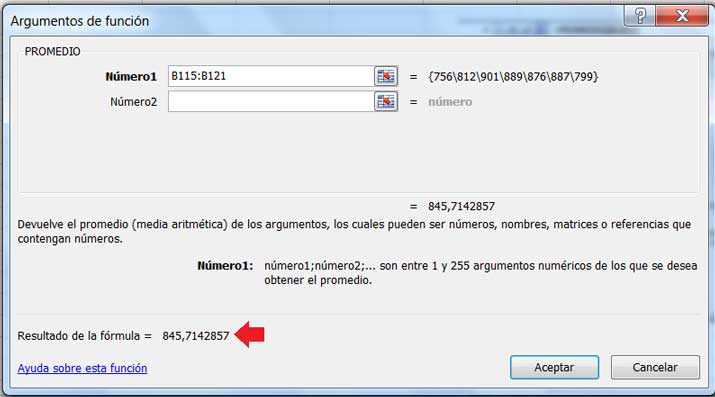
Se observa que la media de la muestra vale 845,71 horas.
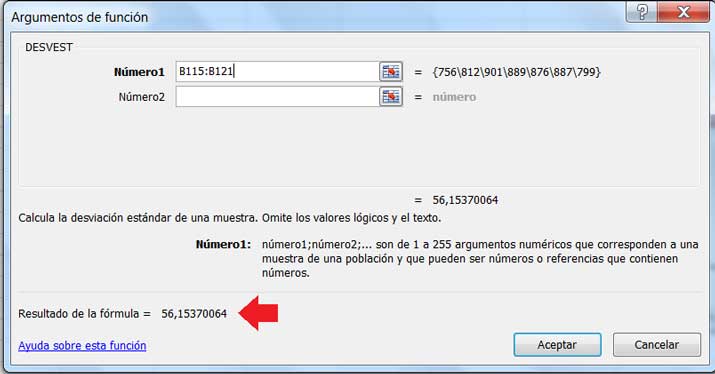
La desviación estándar de la muestra vale 56,13 horas
En lo que respecta a \(t_{0,025;6}\), lo obtendremos igualmente gracias a la planilla de cálculo, como se observa en la imagen 8.10.
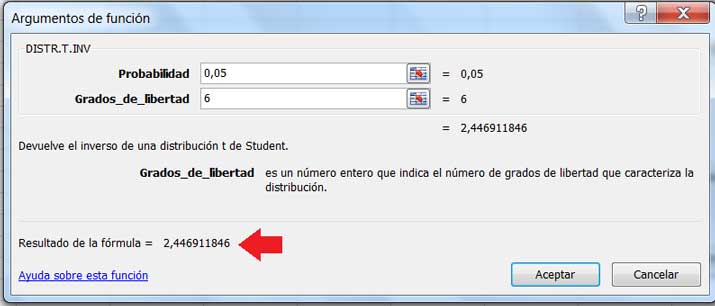
Debemos ingresar el valor 0,05 para la probabilidad por tratarse de una estimación a dos colas.
El límite inferior del intervalo se calculará entonces de la siguiente manera:
\[\large{ LI=845,71-2,45.\frac{56,17}{\sqrt{7}}=793,71 }\]
En cuanto al límite superior:
\[\large{ LS=845,71-2,45.\frac{56,17}{\sqrt{7}}=897,71 }\]
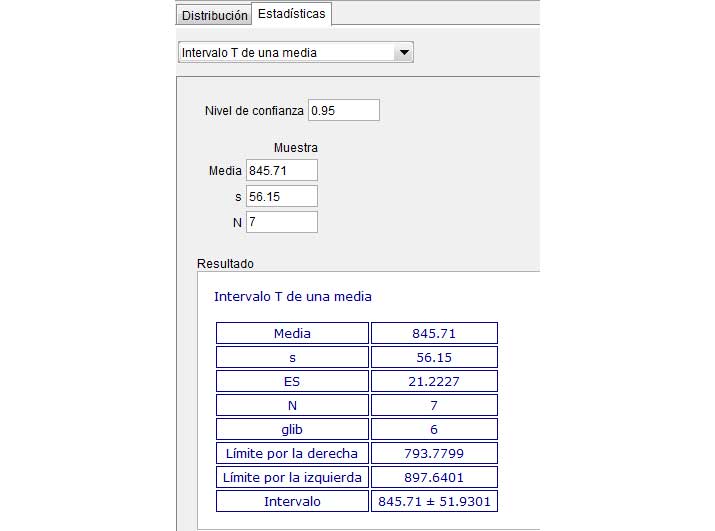
En la imagen 8.11 verificamos los valores obtenidos utilizando el GeoGebra.
En la presentación de la imagen 8.10 hablamos de “estimación a dos colas”. El concepto puede interpretarse a partir del resultado que acabamos de obtener: de cada cien muestras de tamaño siete que podamos tomar, en noventa y cinco de ellas la vida útil promedio de las lámparas adoptará valores entre 793,78 y 897,64 horas. Quedan así definidos dos conjuntos de valores (aquellas lámparas que dejan de funcionar antes de las 793,78 horas y aquellas que lo hacen después de las 897,64 horas) que se excluyen de nuestro resultado, conformando las dos “colas” a las que nos referíamos al principio. En el apartado 8.4 veremos otro tipo de problema, donde solo se excluye un grupo de valores (ya sea a la derecha o la izquierda del conjunto de valores de nuestro interés), en cuyo caso hablaremos de “ estimación a una cola”.
Una empresa desea estimar el diámetro de las arandelas de presión que produce cierta máquina que acaba de adquirir, para compararlo con el que, de acuerdo con las especificaciones del fabricante de la máquina, habrían de tener. Para ello, toman una muestra de quince arandelas, obteniéndose los valores que se reproducen en la tabla de la imagen 8.12. Se pide entonces, calcular el intervalo de confianza al 95 % para el diámetro. Verificar dicho resultado empleando el GeoGebra.

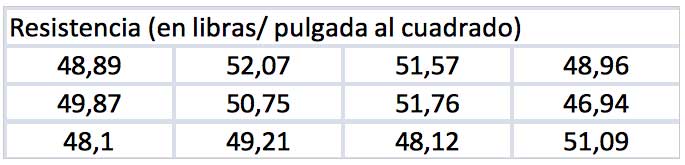
Un fabricante desea obtener el intervalo de confianza al 98 % para la resistencia media a la tracción de una determinada fibra sintética con la que elabora su producto. Para ello lleva a cabo doce ensayos destructivos, obteniendo los valores que se reproducen en la tabla de la imagen 8.13.
Se pide entonces obtener dicho intervalo de confianza empleando la planilla de cálculo.
Verificar los resultados obtenidos utilizando el GeoGebra.
8.3. Intervalo de confianza para la varianza de una distribución normal
En muchas ocasiones nos encontraremos ante poblaciones normales de las que hemos de ignorar tanto su media como su varianza. Y puede ser que sea este valor el que necesitemos estimar con un grado de confianza dado.
Para ello hemos de emplear la distribución chi-cuadrado. La curva de esta distribución no es simétrica.
El intervalo de confianza al 100(1-\(\alpha\))% para la varianza se calculará de la siguiente manera:
\[\Large{ \frac{(n-1)S^2}{X^2_{\alpha/2},n-1}\le\sigma^2\le \frac{(n-1)S^2}{X^2_{\alpha/2},n-1} }\]
Volvamos al problema propuesto en 8.2.2, en el que habíamos calculado la vida útil de cierto tipo de lámparas. Puesto que ignorábamos la media y la varianza poblacionales, podría interesarnos también estimar este segundo parámetro.
En la imagen 8.14 vemos de qué modo empleamos la planilla de cálculo para obtener la desviación estándar de la muestra. En las imágenes 8.15 y 8.16, en cambio, vemos de qué modo emplear la planilla de cálculo para obtener los valores de \(X^2_{\alpha/2}, n-1\) y \(X^2_{1-\alpha/2}, n-1\), respectivamente.
Montgomery, D.; Runger, G. (2000), Probabilidad y Estadística aplicadas a la Ingeniería, Mc Graw Hill, México. pp. 349 y 350.
Walpole, R.; Myers, R; Myers, S.; Keying Ye (2007), Probabilidad y Estadística para Ingeniería y Ciencias, Pearson Education, México, pp. 306 y 307.
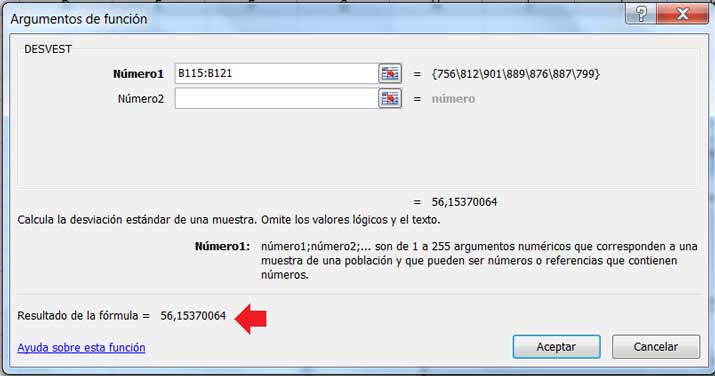
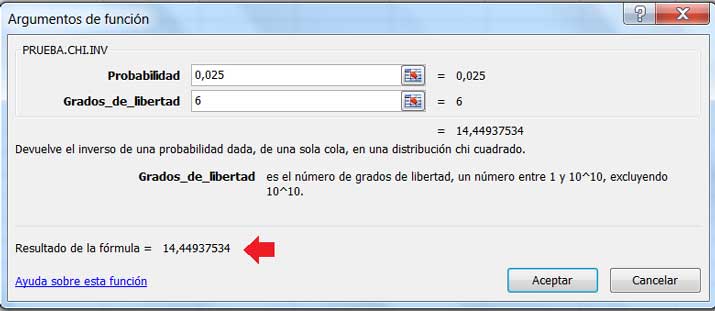
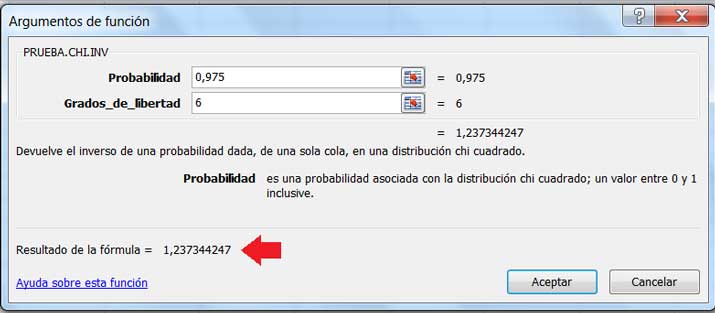
En la imagen 8.17 verificamos que los valores anteriormente obtenidos corresponden al intervalo buscado.
Seguidamente, calculamos el límite inferior del intervalo de confianza para el cálculo de la varianza:
\[\large{ LI=\frac{6.(56,1537)^2}{14,4493}=1309,3664 }\]
El límite superior del intervalo de confianza, por otro lado, será:
\[\large{ LS=\frac{6.(56,1537)^2}{1,2373}=15290,8980 }\]
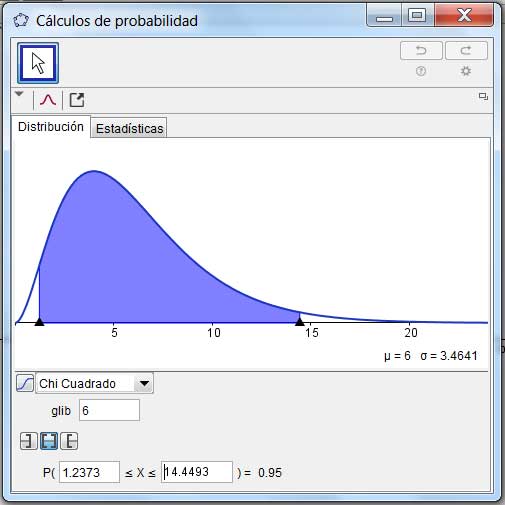
Operando adecuadamente, llegamos entonces a la conclusión de que, si tomamos otras cien muestras de tamaño siete, su desviación estándar habrá de encontrarse entre las 36,18 horas y las 123,65 horas. Estos dos valores se obtienen simplemente calculando las raíces cuadradas de los dos límites que acabamos de calcular (que se corresponden con los límites inferior y superior del intervalo de confianza de la varianza).
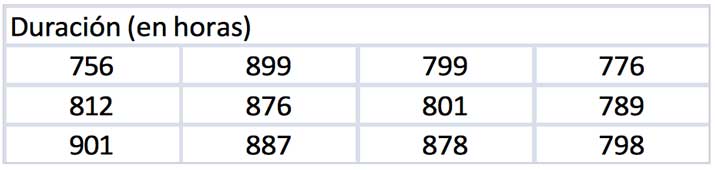
Volviendo al problema de la vida útil de las lámparas, supongamos ahora que la cantidad de lámparas testeadas hubiese sido mayor. Es decir, a las doce mediciones originales habrían de sumársele otras cinco, alcanzando así un total de doce. Los datos obtenidos se consignan en la tabla de la imagen 8.18. Se pide entonces:
- Obtener el intervalo de confianza al 95 % para la vida útil media de las lámparas.
- Obtener el intervalo de confianza al 95 % para la varianza de la vida útil de las lámparas. Calcular los valores de la desviación estándar correspondientes a los límites de dicho intervalo y compararlos con los obtenidos para un tamaño menor de la muestra.
- Comparar el valor de la media obtenido para la muestra inicial de tamaño siete con el obtenido para la muestra de tamaño doce. ¿Puede extraer alguna conclusión a partir de dicha comparación?
8.4. Estimación de parámetros a una sola cola
La estimación de parámetros es igualmente aplicable al caso de que solo nos interese estimar un parámetro superior o inferiormente. Por ejemplo, supongamos que la resistencia del material de las bolsas que un industrial emplea para la comercialización de su producto fuese la variable de interés en nuestro problema. En este ejemplo, podría suceder que al industrial no le interesase el límite superior, sino que su preocupación se centrara en estimar el valor mínimo de dicha resistencia. Si la varianza poblacional fuese conocida, el intervalo de confianza inferior al 100(1-\(\alpha\))% para la media se obtendría entonces como:
\[\large{ \overline{X}-Z_{\alpha}\frac{\sigma}{\sqrt{n}}\le \mu }\]
Si, en cambio, la varianza de la población fuese desconocida, el cálculo sería el siguiente:
\[\large{ \overline{X}-t_{\alpha,n-1}\frac{S}{\sqrt{n}}\le \mu }\]
Análogamente, si en nuestro problema nos interesara estimar la media de la variable de interés solo superiormentey la varianza de la población fuese conocida, entonces:
\[\large{ \mu \le \overline{x}+Z_{\alpha}\frac{\sigma}{\sqrt{n}} }\]
Si la varianza de la población no fuese conocida, entonces:
\[\large{ \mu \le \overline{x}+t_{\alpha,n-1}\frac{S}{\sqrt{n}} }\]
Emplear los datos de la tabla que aparece en la imagen 8.17 para estimar con un 95 % el mínimo valor de la media para la vida media de las lámparas.
8.5. Otros casos de interés
Para finalizar la presente unidad, ofrecemos al estudiante las expresiones que nos permiten obtener los límites inferior y superior del intervalo de confianza para la diferencia entre dos medias y para el cociente entre dos varianzas.
En el primero de los casos, tenemos que:
\[\Large{ (\overline{X_1}-\overline{X_2})-t_{\alpha/2,n_1+n_2-2}S_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}} < \mu_1 - \mu_2 }\]
\[\Large{ \mu_1 - \mu_2 < (\overline{X_1}-\overline{X_2})-t_{\alpha/2,n_1+n_2-2}S_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}} }\]
En dichas expresiones, \[\Large{ S_p=\sqrt{\frac{(n_1-1)S^2_1+(n_2-1)S^2_2}{n_1+n_2-2}} }\]
Los límites inferior y superior del intervalo de confianza para el cociente de dos varianzas se obtendrán utilizando la distribución F. Expresamos entonces:
\[\Large{ \frac{S^2_1}{S^2_2}F_{1-\alpha/2,n_2-1.n_1-1}\le \frac{\sigma^2_1}{\sigma^2_2} \le \frac{S^2_1}{S^2_2}F_{\alpha/2,n_2-1.n_1-1} }\]

