Conceptos básicos de Estadística
Objetivos
Que el alumno:
- conozca los alcances de la Estadística y de los primeros pasos de su aprendizaje.
- comprenda las diferencias entre dos conceptos esenciales de la disciplina: población y muestra.
- se familiarice con el empleo de las planillas de cálculo para la resolución de los problemas.
1.1. La Estadística como ciencia
A través de la web, la radio o la televisión, podemos enterarnos que un estudio científico determinó que jóvenes que realizaban al menos sesenta minutos diarios de actividad física por día presentaron un menor riesgo de contraer enfermedades, reduciéndose asimismo en ellos los niveles de estrés y ansiedad; o que, de acuerdo con otra investigación, se determinó que las frutas secas, el té y el chocolate, en cantidades discretas, benefician al sistema inmunológico.
Las conclusiones de dichos estudios, que en muchos casos pueden ser de nuestro interés, son el resultado de experimentos diseñados ad hoc, en los que tomaron parte un gran número de personas.
Y la ciencia que brinda las herramientas necesarias para llevarlos a cabo recibe el nombre de Estadística.
En los siguientes enlaces se encuentran los estudios mencionados en el párrafo anterior:
<http://www.efdeportes.com/efd214/actividad-fisica-y-rendimiento-academico.htm>
[Consulta: 17 noviembre 2017]
Quienes llevan a cabo ese tipo de estudios desarrollan su actividad profesional en el campo de la ciencia y la tecnología y se dedican a la resolución de problemas de interés para la sociedad, aplicando eficientemente principios científicos. La tarea exige, en primer lugar, una descripción clara del problema a resolver, en la que se identifiquen aquellos factores o variables que influyen en el fenómeno o proceso bajo estudio.
Es probable que algunos de dichos factores sean finalmente menos decisivos de lo que se suponía; o que existan factores que no hayan sido tenidos en cuenta inicialmente y que, a la larga, deban ser considerados a la hora de proponer una forma de resolver el problema. Por ello, con todo el conocimiento disponible sobre el tema, se debe construir un modelo apropiado, a partir del cual habrán de diseñarse una serie de experimentos que permitan evaluarlo. En esta etapa, la recolección de datos resulta ser de vital importancia: la información permitirá validar o perfeccionar el modelo adoptado.
Como vemos, se trata de un proceso cíclico, no lineal, en el cual el o los profesionales involucrados deberán estar dispuestos a perfeccionar o corregir su modelo original, con el fin de resolver el problema eficientemente.
La metodología que acabamos de describir someramente muestra la fuerte relación entre el problema, los factores que pueden influir sobre su solución, el modelo que se aplique y la experimentación que permita decidir la validez o no del modelo propuesto para la resolución de ese problema. Vemos, entonces, que la recolección, presentación y análisis de los datos obtenidos en la experimentación resulta ser una actividad clave en el proceso y la ciencia que se ocupa de aquellas tres acciones no es otra que la Estadística.
Definimos la Estadística como la ciencia que se ocupa de recolectar, presentar y analizar los datos obtenidos para tomar decisiones, resolver problemas o diseñar productos o procesos industriales.
Montgomery, D.; Runger, G. (2003), AppliedStatistics and Probability for Engineers, John Wiley & Sons Inc., New York, pp. 2-5.
1.2. La variabilidad
Aun en nuestra vida cotidiana se observa un fenómeno tan imprevisible como (en muchas ocasiones) indeseable. Si, por ejemplo, acostumbramos tardar una hora para ir desde nuestro hogar hasta el trabajo, no nos causa ninguna gracia que, por alguna razón, el tiempo de nuestro viaje se extienda significativamente. Sin embargo, sabemos que, aun tomando el mismo colectivo o tren de todos los días a la hora de costumbre, existe la posibilidad de que eso suceda.
El fenómeno al que nos estamos refiriendo recibe el nombre de variabilidad: sucesivas observaciones de un sistema o de un fenómeno, por causas atribuibles o factores fortuitos, no producen siempre exactamente el mismo resultado.
Como veremos en el presente material didáctico, los métodos estadísticos nos ayudan a comprender y describir el fenómeno de la variabilidad.
1.3. Muestra y población
Poco antes de un acto electoral, diversas consultoras llevan a cabo estudios que presentan un panorama de los resultados que podrían obtenerse en las urnas. La imagen 1.1 muestra, a modo de ejemplo, los resultados de una de las tantas encuestas que se llevaron a cabo antes de las Primarias Abiertas, Simultáneas y Obligatorias llevadas a cabo en agosto de 2017.
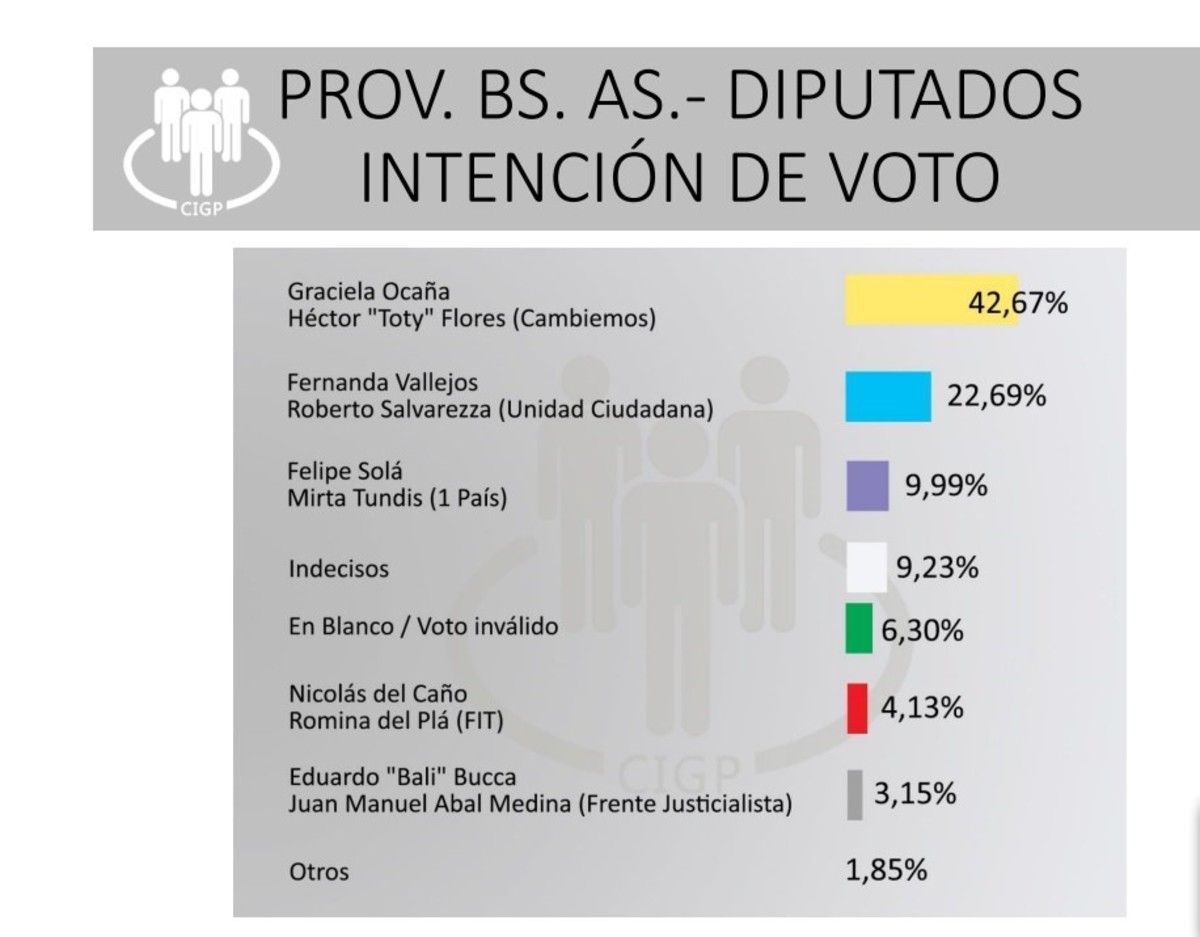
Resultados de la encuesta llevada a cabo por la Consultora de Imagen y Gestión Política (CIyGP) sobre 1700 datos telefónicos.
Diario Clarín, Política, 16 de julio de 2017. [EN LÍNEA] Disponible en: <https://www.clarin.com/politica/guerra-encuestas-ultimas-mediciones-provincia-fuertes-diferencias_0_SyP0m4KBZ.html> [Consulta: 11 septiembre 2017].
Sin embargo, estas encuestas solo brindan un pronóstico previo a la elección definitiva, en la que todos los ciudadanos habilitados a votar deberán emitir su voto. El acto electoral habrá de brindarnos la respuesta definitiva, porque nos ofrece la opinión de la población, a diferencia de los resultados de las encuestas, obtenidos a partir de muestras de tamaño reducido.
Definimos como población al total de la información o de los objetos de interés para una característica numérica dada en una investigación particular; en cambio, definimos como muestra a cualquier subconjunto de dicha población.
Es decir, todos los ciudadanos habilitados para votar representan la población, mientras que aquellos que tomaron parte de alguna de las encuestas previas a la votación representan una muestra de aquella.
1.4. Media de una muestra
Supongamos que nos interesa estudiar el nivel de nitratos en el agua potable de una fábrica. Tomamos entonces una muestra, consistente en dieciocho mediciones representativas. Los resultados obtenidos se reproducen en la tabla que aparece en la imagen 1.2.

Muestra del nivel de nitratos en agua potable, medidos en partes por millón (ppm).
Definiremos como media de la muestra al promedio de los valores de esta. Si efectuamos n observaciones en una muestra y las expresamos x1, x2, …, xn, definimos entonces mediante la siguiente expresión a la media muestral:
\[{\large\overline {x} = \frac {x_1 + x_2 + \dots + x_n}{n} = \frac {\sum^n_{i = 1} x_i} {n}}\]
Para la obtención de dicho valor medio, recomendamos utilizar una planilla de cálculo. Después de seleccionar los valores que figuran en la tabla, habrá de seleccionarse entre las funciones disponibles la categoría Matemáticas y trigonométricas, tal como se indica en la imagen 1.3. Seguidamente, dentro de dicha categoría, habrá que buscar la función PROMEDIO, tal como se observa en la imagen 1.4.
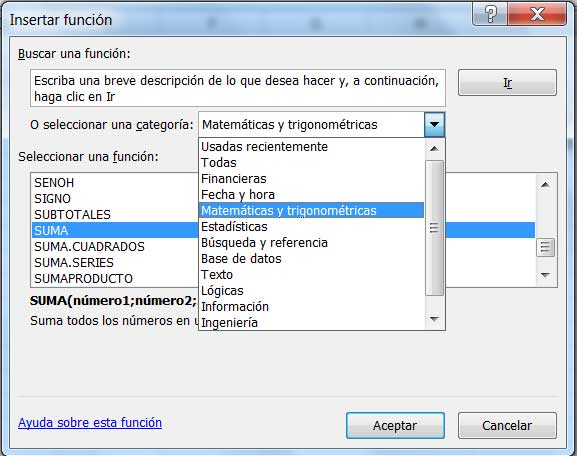
Captura de pantalla en la que se observa cómo seleccionar entre las funciones disponibles la categoría Matemáticas y trigonométricas.
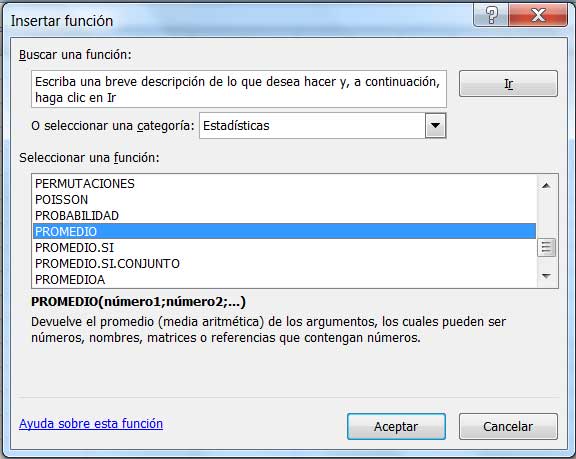
Dentro de la categoría de funciones estadísticas, se selecciona la función PROMEDIO:
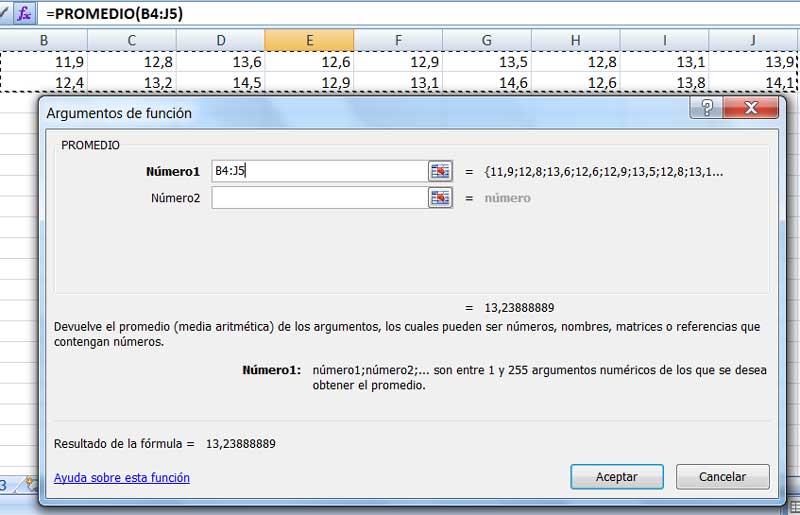
Captura de pantalla en la que observamos de qué modo se ingresan los datos para el cálculo de la media de la muestra.
Se abrirá una tercera ventana; tendremos que seleccionar los valores de la tabla, como se observa en la imagen 1.5., y hacer clic en “Aceptar” para obtener finalmente el valor de la media muestral buscada, que se señala en la imagen con una flecha roja.
Para que el cálculo de la media de una muestra no se limite al empleo de una instrucción, podríamos habernos detenido en lo que propone la expresión matemática que nos permite calcularla. Así, tal como se observa en las imágenes 1.6. y 1.7., el valor medio de la muestra cuyos datos se reprodujeron en la imagen 1.2. puedeconseguirse aplicando la función SUMA y dividiendo el resultado obtenido por el tamaño de la muestra para obtener la media buscada.
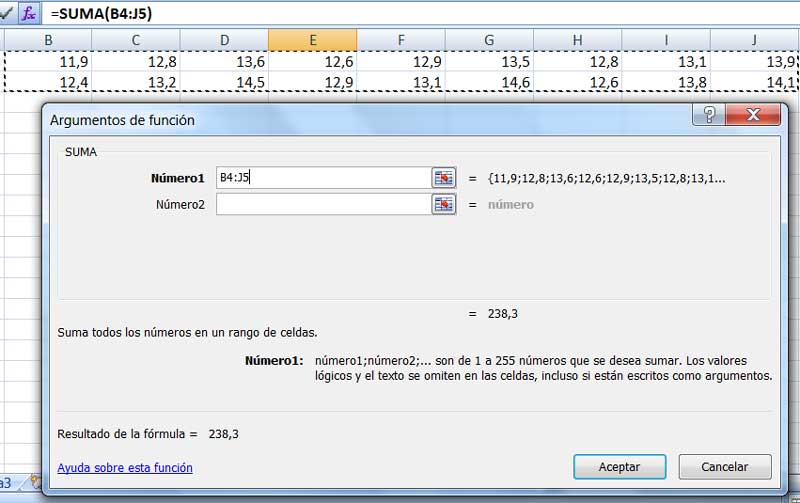
Captura de pantalla donde se observa la ventana correspondiente a la función SUMA, con la que podemos calcular la media de la muestra a partir de la definición.
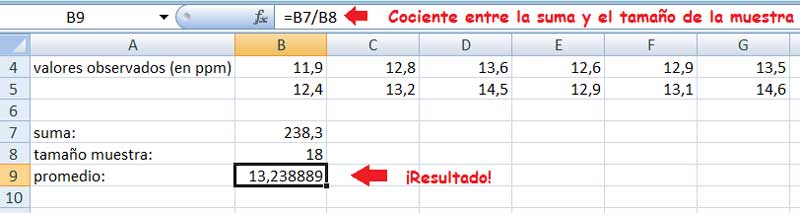
En la ventana de la parte superior se observa el cálculo que habrá de realizarse para la obtención de la media a partir de la definición.
1.5. Desviación estándar de una muestra
Supongamos ahora que tomamos dos muestras correspondientes a una característica de un producto dado. Los valores de la primera son 13, 9, 8, 14, 7 y 9. En cuanto a la segunda, los valores obtenidos son 11, 9, 8, 11, 10 y 11.
Verificar que los valores medios de cada una de las dos muestras de tamaño seis, que describimos en el párrafo precedente, son iguales y valen diez.
Aun cuando ambas muestras tengan la misma media, la diferencia entre cada uno de los valores de ambas muestras y la media debe estudiarse detenidamente. En la imagen 1.8. se reproduce una tabla en la que aparecen los datos recogidos en las columnas X y AC de la planilla de cálculo empleada. En las columnas Y y AD se calcularon las diferencias entre cada uno de los valores observados y la media de la muestra respectiva. Se observa que las sumas de dichas diferencias valen cero en ambos casos.
Sin embargo, en las columnas Z y AE procedimos a calcular los cuadrados de los valores de dichas diferencias. En este caso, se observa que la suma de dichos cuadrados es mucho mayor en el caso de la muestra 1 que en el de la muestra 2. No debería sorprendernos este hecho si tenemos en cuenta que los valores de la primera de las muestras están mucho más alejados de la media que los de la otra muestra.
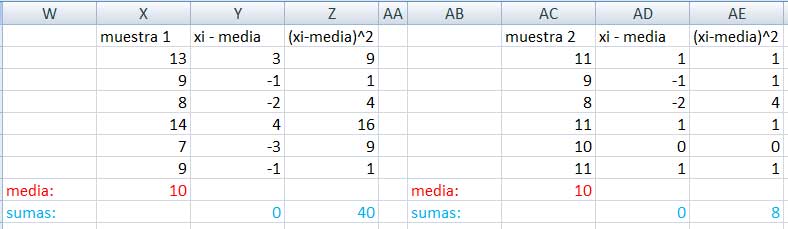
Captura de pantalla de la tabla en la que se pone en evidencia la diferencia entre las variabilidades de ambas muestras.
Podemos decir, entonces, que la variabilidad de la primera muestra es mucho mayor que la de la segunda; para que esa característica quede reflejada, definiremos seguidamente la varianza y la desviación estándar de una muestra.
La varianza de cualquier muestra se expresa como S2 y se calcula del siguiente modo:
\[{\large S^2 = \frac {\sum^n_{i=1} (x_i - \overline {x})^2} {n - 1}}\]
En cuanto a la desviación estándar de la muestra, a la que se expresa como S, se calcula como la raíz cuadrada positiva de la varianza, es decir:
\[{\large S = \sqrt{\frac {\sum^n_{i=1} (x_i - \overline {x})^2} {n - 1}}}\]
Limitémonos a decir, por el momento, que la varianza es una medida descriptiva de la dispersión. Sin embargo, su interpretación puede resultar confusa, teniendo en cuenta que sus unidades resultan ser el cuadrado de las unidades de medida de la variable que estemos analizando.
Calcularemos, entonces, la varianza y la desviación estándar correspondientes a la muestra 1. Volvemos a seleccionar la categoría “estadísticas”, pero empleamos ahora la función VAR, como se observa en la imagen 1.9. Seguidamente, utilizamos la función DESVEST (correspondiente a la misma categoría que la anterior) para obtener la desviación estándar de la muestra. El resultado se puede ver en la imagen 1.10.
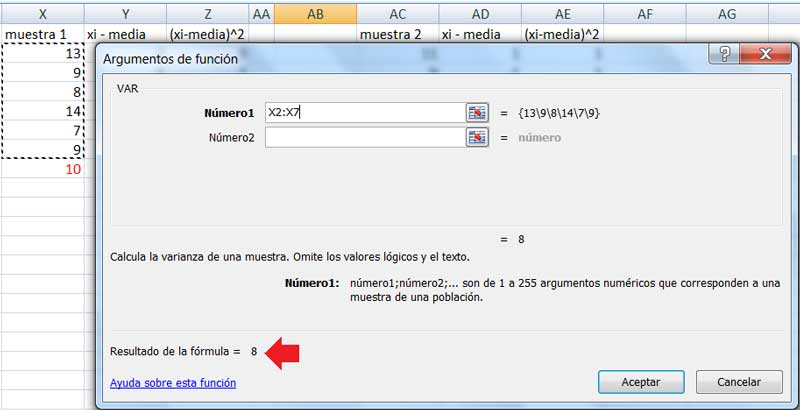
Captura de pantalla del cálculo de la varianza de la muestra 1. El resultado aparece señalado con una flecha roja.
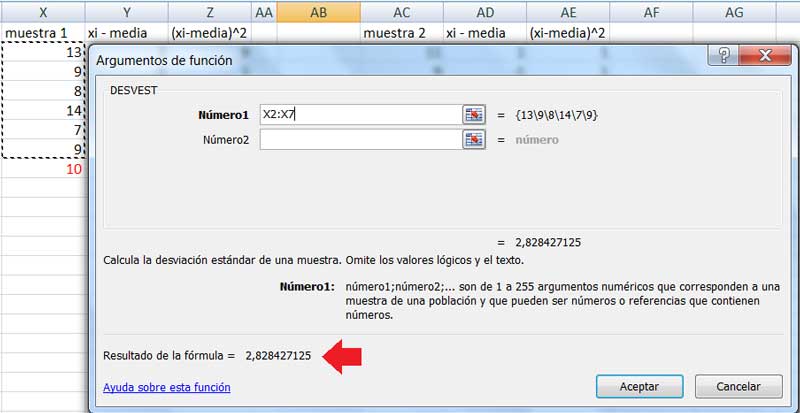
Captura de pantalla del cálculo de la desviación estándar de la muestra 1. El resultado aparece señalado con una flecha roja.
Obtener la varianza y la desviación estándar de la muestra 2 utilizando la planilla de cálculo.
Comparar los valores de las varianzas y desviaciones estándar de ambas muestras. ¿Puede interpretar los resultados obtenidos?
Calcular la varianza y la desviación estándar de la muestra del nivel de nitratos en el agua potable de una fábrica cuyos valores se reprodujeron oportunamente en la tabla que aparece en la imagen 1.2.
Con el mismo criterio empleado para el caso del cálculo de la media de una muestra, proponemos verificar el resultado obtenido en la actividad anterior a partir de la aplicación de las expresiones matemáticas de la varianza y la desviación estándar ofrecidas oportunamente.
El primer paso será escribir los datos en forma de columna, tal como se puede observar en la imagen 1.11. En una segunda columna, a la derecha de la que contiene los datos, copiamos el valor de la media de la muestra, obtenida en su momento.
Seguidamente, como se observa en la imagen 1.12., procedemos a calcular la diferencia entre cada uno de los valores medidos y la media. Basta con llevar a cabo la operación con el primer valor de la tabla, para luego apoyarnos en el extremo inferior derecho de la casilla y arrastrar el mouse para que el cálculo se repita automáticamente con los restantes valores.
El paso siguiente consiste en elevar al cuadrado cada una de las diferencias calculadas en el paso anterior. La operación se reproduce en la imagen 1.13. Como lo indicamos en el párrafo anterior, bastará con calcular el primero de los valores, para luego operar con el mouse para que la operación se repita en forma automática para los restantes.
Sumamos los valores de la columna K, tal como lo muestra la imagen 1.14., empleando para ello la instrucción SUMA. Seguidamente, dividimos el resultado de dicha operación por el tamaño de la muestra disminuido en uno (imagen 1.15.), para, finalmente, utilizar la función RAIZ, con la que se obtiene la desviación estándar de la muestra, como puede observarse en la imagen 1.16.
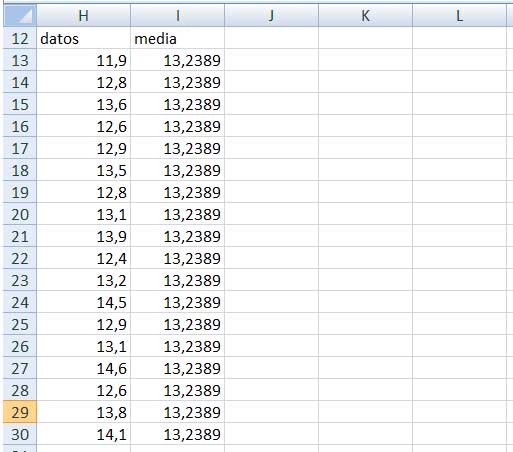
Captura de pantalla de los primeros pasos para la construcción de la tabla con la que calcularemos la varianza y la desviación estándar de la muestra a partir de las expresiones matemáticas que las definen.
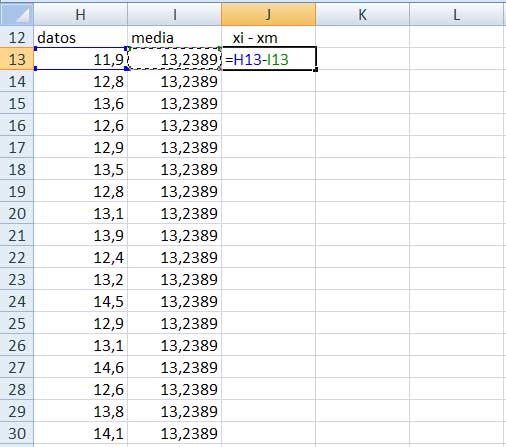
En el paso siguiente, calculamos la diferencia entre cada uno de los valores de la muestra y la media.
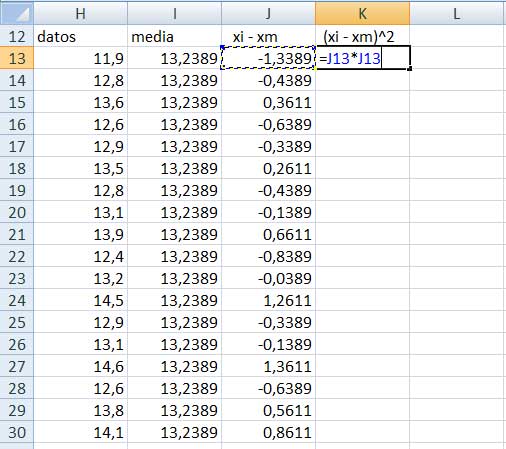
Elevamos al cuadrado los valores calculados en el paso anterior. Recordemos que, de ese modo eliminamos el efecto de compensación que impedía observar la variabilidad de la muestra.
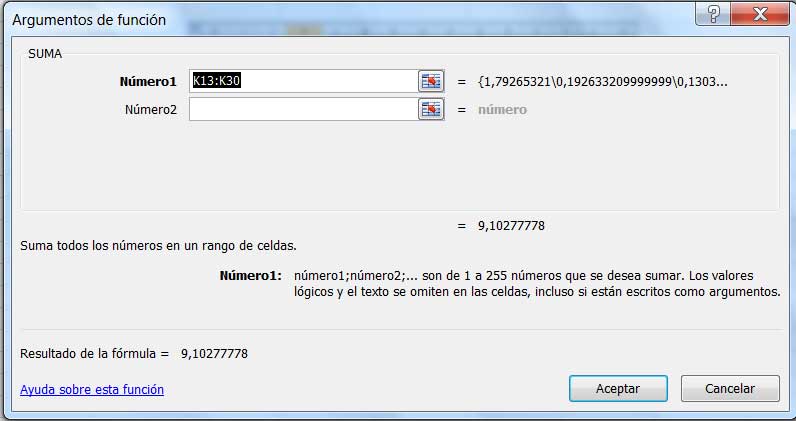
A partir de utilizar la instrucción SUMA, obtenemos la sumatoria de las diferencias entre cada una de las mediciones y la media, elevadas al cuadrado.
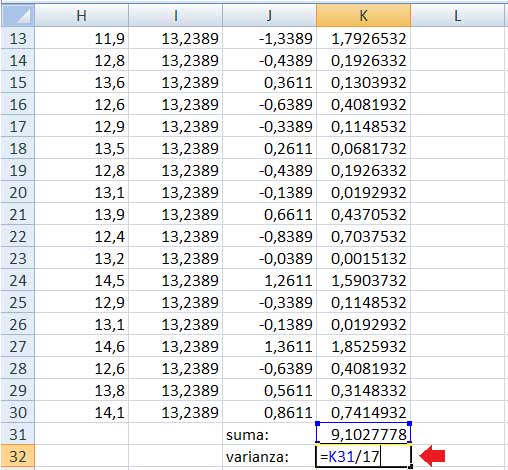
Basta con dividir al valor de la suma calculada en el paso anterior por el tamaño de la muestra disminuido en uno para obtener el valor de la varianza. El cálculo se señala con una flecha roja.
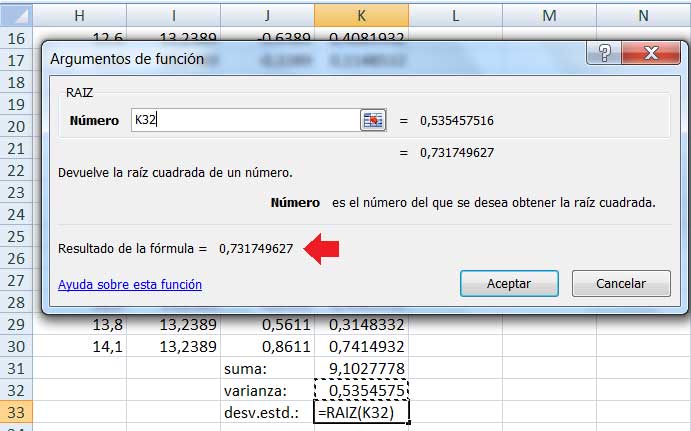
Finalmente, calculamos la desviación estándar de la muestra utilizando la función RAIZ. El resultado, que aparece en la ventana correspondiente, ha sido señalado con una flecha roja en la imagen.
1.6. Estadística descriptiva e inferencial
Supongamos que un profesor dicta la misma materia en dos cursos y, al finalizar el cuatrimestre, decide comparar el rendimiento académico de ambos. Observa entonces que en uno de los cursos (curso 1) 7 alumnos consiguieron promocionar, 15 están en condiciones de rendir final y 4 han quedado libres. En el otro grupo de estudiantes (curso 2), 6 alumnos promocionaron, 8 quedaron en condiciones de rendir final y 13 quedaron libres. La imagen 1.17 reproduce los diagramas de pastel que permiten representar gráficamente la información.
La comparación de ambos gráficos parece indicar que el rendimiento del curso 1 es bastante bueno, en tanto que el del curso 2 deja mucho que desear. El profesor podrá analizar entonces los motivos por los cuales el desempeño del segundo grupo de estudiantes no fue el esperable: el sencillo estudio puso en evidencia que algo no funcionó bien con ellos.
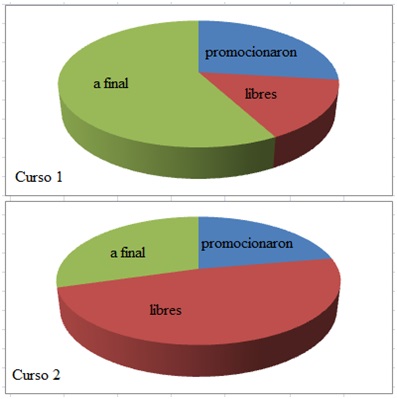
Diagramas de pastel en los que se volcó la información correspondiente al rendimiento académico de los alumnos de los cursos 1 y 2.
Definiremos como estadística descriptiva a la rama de la estadística que permite interpretar la información obtenida una vez que esta fue expresada mediante algún tipo de gráfico.
Supongamos ahora que una empresa alimenticia envasa su producto utilizando bolsas plásticas que compra periódicamente a un determinado proveedor. La resistencia a la tracción de dichas bolsas es una de las características de calidad que el personal de compras de la empresa controla cada vez que recibe un envío de su proveedor.
El fabricante asegura que la resistencia a la tracción de las bolsas, es decir, la resistencia a la rotura,es de 0,002 kPa(kilopascales). Sin embargo, el ensayo de rutina de uno de los lotes recibidos indica que la resistencia promedio de una muestra de cuatro bolsas es de solo 0,0018 kPa.
Surgen entonces las siguientes inquietudes: ¿es posible que, a pesar de que la media de la muestra sea 0,0018 kPa, corresponda a un lote cuya resistencia sea 0,002 kPa? ¿O, efectivamente, la resistencia del lote recibido es inferior a la que garantizaba el proveedor del insumo?
No se trata de preguntas triviales: de la respuesta dependerá que el lote sea aceptado o rechazado. Por eso, habrá de emplearse algún procedimiento estadístico (el test de hipótesis que habremos de tratar en la unidad 9) que nos brinde evidencia estadística que nos ayude a tomar una decisión respecto del lote de bolsas.
Definimos la estadística inferencial como el conjunto de métodos y técnicas que permiten hacer generalizaciones, predicciones o estimaciones sobre una población a partir de una muestra de esta.
El método estadístico aplicado en la muestra nos debería permitir estimar si la resistencia a la tracción del lote recibido (que representa en este caso a la población) es o no la que garantiza el proveedor.
La estadística inferencial es una herramienta de enorme valor. Rara vez contamos con toda la información deseable para tomar una decisión y los métodos de la estadística inferencial nos brindarán, con un determinado grado de certeza, un panorama de la situación bajo estudio. La confiabilidad de una inferencia es un aspecto fundamental de la estadística inferencial y diremos que una inferencia es confiable cuando podemos depender de ella con un alto grado de seguridad. La determinación acerca de la confiabilidad de una inferencia se basa en la teoría de las probabilidades, que habremos de tratar en una de las próximas unidades.
1.7. Inferencias y deducciones
Supongamos ahora que un fabricante de equipos rociadores contra incendios garantiza a sus clientes que la temperatura media de activación de sus productos es de 130ºC (ciento treinta grados centígrados). Aun cuando no haya probado todos los rociadores que salieron de su planta, a lo largo del tiempo ha podido verificar el dato con un gran número de equipos que fueron sometidos a un control de calidad.
Por otro lado, una empresa de ingeniería necesita comprar un gran número de rociadores contra incendios para un edificio de oficinas que está construyendo. Las condiciones del contrato aclaran que la temperatura media de activación de estos deberá ser, casualmente, de 130ºC, razón por la cual los ingenieros se ponen en contacto con el fabricante. Ponen a prueba a un cierto número de rociadores y, aplicando alguno de los métodos estadísticos que estudiaremos a lo largo del curso, concluyen que, con un cierto nivel de certeza, pueden confiar en la palabra del fabricante.
El fabricante de equipos rociadores contra incendios deduce que los equipos que habrá de venderle a la empresa constructora tendrán la misma temperatura media de activación que el resto de los que produce su planta. Y los ingenieros que construyen el edificio de oficinas infieren, a partir de los ensayos llevados a cabo con una muestra, que la temperatura de activación de todos los equipos que compren sea la que garantiza el fabricante.
Diremos, entonces, que la inducción o inferencia consiste en llevar a cabo un razonamiento partiendo de ejemplos, llegando a una generalización. En cambio, la deducción consiste en obtener una opinión sobre algo particular, partiendo de un conocimiento general.
Weimer, R. (2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 10-14.
1.8. Recolección de datos
A lo largo de la unidad, el estudiante habrá observado que los datos con los que trabajamos en cada estudio corresponden a una muestra obtenida a partir de una población.
Uno de los procedimientos que exige la recolección de información y el empleo de la herramienta estadística es el diseño experimental, metodología de amplio empleo en la investigación aplicada y en la industria. Partiendo de la definición de experimento como una determinada acción dirigida a responder una o más preguntas cuidadosamente formuladas, el diseño experimental consiste en provocar pequeños cambios controlados en algunas de las variables del proceso previamente seleccionadas, para observar los efectos que provoquen en otra variable de interés que dependa de dichas variables.
Por ejemplo, se desea determinar el rendimiento de una reacción orgánica a partir de dos variables de interés, la temperatura a la que se lleva a cabo el proceso y la duración de este. Se generan ciclos de ensayos como el que se representa gráficamente en la imagen 1.18 para combinaciones de valores de las variables independientes del proceso. Estas (en nuestro caso, la temperatura y el tiempo) pueden controlarse y del valor que se les asigne dependerá el rendimiento (que recibe entonces el nombre de variable dependiente).
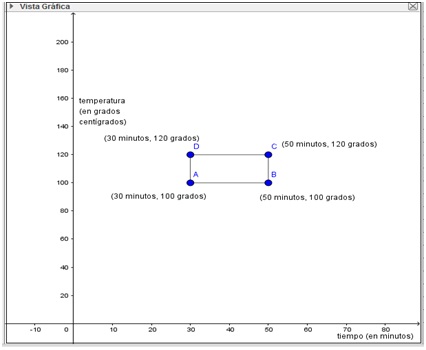
El proceso se lleva a cabo cuatro veces por ciclo, combinando en cada caso las dos temperaturas y los dos tiempos de proceso entre los cuales se lleva a cabo el experimento. El ciclo comienza para las condiciones correspondientes a las coordenadas del punto A (30 minutos a 100 grados centígrados), siguiendo por el punto B y pasando luego por las condiciones representadas por los puntos C y D. En cada uno de los cuatro ensayos se mide el valor del rendimiento del proceso.
Es entonces cuando la importancia del estudio estadístico habrá de ponerse en evidencia, ya que, al comparar la información obtenida en cada ciclo con la obtenida en los demás, se observará que los valores del rendimiento no habrán de repetirse exactamente. El hecho de que, bajo las mismas condiciones, el proceso no responda del mismo modo es consecuencia de su propia variabilidad. Es allí donde el procedimiento estadístico aplicado permitirá determinar hasta qué punto y en qué proporción cada una de las variables consideradas afecta dicho rendimiento.
Como lo anticipamos en esta misma sección, el diseño experimental se aplica tanto en la investigación como en el entorno de la producción. En este último caso, se logra que el propio proceso industrial nos brinde información sobre sí mismo, mientras se elaboran productos que cumplen con las especificaciones. El experimento nos brinda así estimaciones confiables para mejorar el proceso objeto de nuestro estudio.
En algunas industrias, como por ejemplo la de la construcción, los datos que se recolectan a lo largo del tiempo permiten obtener los tiempos estándar de las tareas u operaciones necesarias para la fabricación de un producto. Estos tiempos serán esenciales en la determinación del camino crítico en el empleo de diagramas PERTN para optimizar recursos y cumplir con los tiempos de producción preestablecidos.
La sigla PERT proviene de ProgramEvaluation and ReviewTechnique, es decir, Técnica de Revisión y Evaluación de Programas. El diagrama PERT está compuesto por un conjunto de nodos que habrán de indicar el final de una tarea y el principio de la siguiente. Todas esas tareas son las que habrán de llevarse adelante para la fabricación de un producto de alta complejidad (¡desde un edificio de varios pisos hasta un submarino nuclear!). El segmento que une a un par de nodos consecutivos representa alguna de las tareas que habrán de llevarse a cabo y, generalmente, son varias las que se estarán ejecutando al mismo tiempo.
Los nodos representan entonces posiciones en el tiempo y, una vez que el diagrama está terminado, se procede a obtener el camino crítico, que representa el tiempo mínimo para fabricar el producto en cuestión. Dicho camino coincide con la trayectoria de mayor extensión entre el primero y el último de los nodos del diagrama.
Walpole, R.; Myers, R; Myers, S.; Keying Ye (2007), Probabilidad y Estadística para Ingeniería y Ciencias, Pearson Education, México, pp. 1 a 11.
Montgomery, D.; Runger, G. (2003), Applied Statistics and Probability for Engineers, John Wiley & Sons Inc., New York, pp. 5-11.

