Estadística descriptiva
Objetivos
Que el alumno:
- Comience a familiarizarse con los procedimientos de organización de la información estadística y aprenda a manejarla.
- Aprenda a construir diagramas de frecuencias, histogramas y diagramas de pastel, empleando el softwaremás apropiado para cada caso.
- Aprenda a calcular las medidas de tendencia central y sea capaz de determinar la existencia o no de sesgo de una muestra.
2.1. Datos cualitativos y cuantitativos
Los datosrecogidos al efectuar un estudio de tipo estadístico pueden clasificarse en dos grandes categorías: datos cuantitativosy datoscualitativos.
Los cuantitativos se relacionan con información numérica y se miden en una escala numérica. El peso de una persona en kilos, su edad en años, la longitud de una pieza metálica en centímetros o el volumen de un recipiente en centímetros cúbicos son ejemplos de este tipo de datos.
En cambio, los cualitativos representan categorías o atributos que pueden clasificarse según un criterio o una cualidad. El género de una persona, su religión o nacionalidad; la marca de automóvil seleccionada por un potencial comprador o la carrera universitaria seguida por un estudiante pueden tomarse como ejemplos de este segundo tipo de datos.
2.2. Datos continuos y discretos
Los datos cuantitativos, a su vez, pueden clasificarse como discretos o continuos.
Aquellos datos que se obtienen a partir de un proceso de conteo entran en la categoría de discretos. Cuando, por ejemplo, arrojamos un dado al aire varias veces y registramos el número que se observa en su cara superior, la cantidad de veces que se obtenga un as representa un dato discreto.
En cambio, los datos obtenidos a partir de un proceso de medición, donde la característica que se mide puede tomar cualquier valor numérico dentro de un intervalo dado, entran en la categoría de datos continuos. El peso de una persona en kilogramos, el tiempo que dura un proceso de fabricación dado en minutos o la longitud de una pieza producida en milímetros son solo algunos ejemplos de este tipo de información.
Todo proceso de medición que proporcione datos continuos queda limitado por la precisión del instrumento de medición que se utilice. Si para medir la altura de un individuo utilizamos un instrumento cuya mínima unidad sea el centímetro, habrá de redondearse la estatura a dicha unidad.
Comprendemos entonces que la medición no deja de ser una aproximación de la medida real. Nuestras mediciones, entonces, resultarán ser valores aproximados y por lo tanto discretos, desde el momento que han de existir un número finito (aunque pueda ser muy grande) de valores posibles.
Toda medida física resulta ser discreta debido a la restricción que nos produce el empleo de un determinado instrumento de medición. Sin embargo, aun cuando debamos redondear los valores debido a la precisión del instrumento de medición empleado, debemos recordar que la naturaleza de los datos es continua.
Walpole, R.; Myers, R; Myers, S.; KeyingYe (2007), Probabilidad y Estadística para Ingeniería y Ciencias, PearsonEducation, México, pp. 17 y 18.
2.3. Organización de datos mediante tablas
En general, los datos obtenidos resultan ser un conjunto de valores que, en principio, no parece presentar orden alguno. Como veremos seguidamente, será muy conveniente organizarlos para simplificar la tarea de análisis que sigue a la etapa de recolección de la información.
Decimos que un conjunto de datos no está agrupado cuandolos valores no presenten orden aparente entre sí.El procedimiento habitual para organizar la información consiste en ordenarlos valores numéricos en forma descendente o ascendente. Este arreglo puede no ser fácilmente manejable cuando el número de datos sea muy grande, razón por la cual se suelen emplear tablas para organizar de algún modo los datos no agrupados.
El hecho de que la mayoría de los valores que conformen nuestra muestra se repita una cierta cantidad de veces resulta ser una característica particularmente útil en el momento de organizar la información y nos lleva a definir lo que recibe el nombre de frecuencia de una medida o una categoría (es decir, un conjunto de valores que se encuentren dentro de un cierto rango).
Se define como frecuencia de una medida o de una categoría al número de veces que esta aparece en un conjunto de datos. El uso de frecuencias es muy conveniente cuando se trabaja con datos cualitativos o discretos, y la letra f es la que se suele emplear para indicar la frecuencia de una medida dada.
Supongamos que los datos consignados en la tabla de la imagen 2.1 correspondieran al número de inasistencias a clases de los alumnos de un curso de Estadística Aplicada. Nos proponemos construir la tabla de frecuencias, empleando para ello una planilla de cálculo.
La simple observación de la tabla que contiene los datos nos indica que la cantidad de faltas posibles va de un máximo de nueve a la asistencia perfecta (es decir, con cero faltas). Calculamos las frecuencias en forma directa aplicando la función FRECUENCIA, que se selecciona de la categoría de funciones estadísticas, como se observa en la imagen 2.2.
En el extremo derecho de la imagen 2.3 aparece una tabla auxiliar de dos columnas; la primera contiene el número de faltas consignadas, mientras que en la segunda habrá de indicarse la frecuencia acumulada.
La función empleada nos ofrece el número de veces que en la matriz aparecen los números que definen al grupo. Por ejemplo, el valor 31 que aparece en la casilla J28de la imagen 2.4 indica que en la matriz de datos hay 31 valores menores o iguales a 6, siendo este el número que define al grupo.
Finalmente, en la imagen 2.5 puede observarse que agregamos una tercera columna a la tabla auxiliar, que contiene las frecuencias de cada grupo o clase (que, como veremos más adelante, también suelen expresarse como frecuencias absolutas). Bastará con restarle a cada una de las frecuencias acumuladas de una clase la frecuencia acumulada de la que la precede, operación que en la imagen 2.5 aparece señalada con una flecha roja, en correspondencia con el cálculo correspondiente a la casilla K31 de la planilla de cálculo empleada en el presente ejemplo.
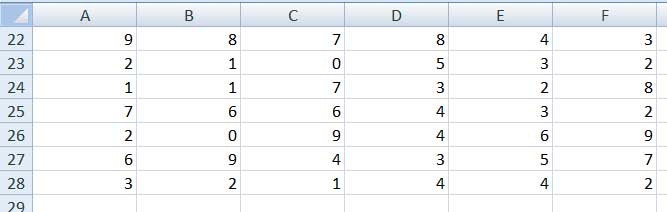
Tabla de valores correspondiente al ejemplo
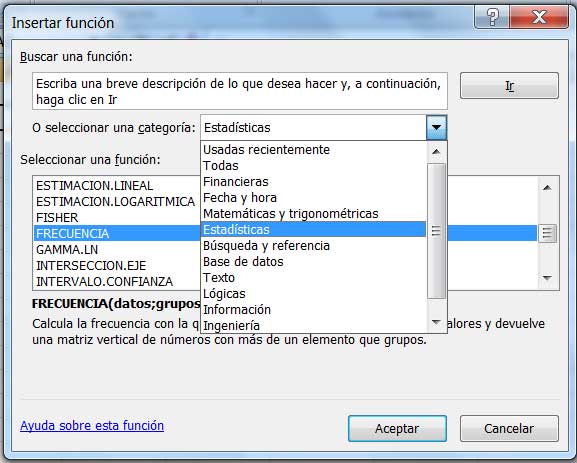
En la categoría de funciones estadísticas encontramos la función FRECUENCIA.
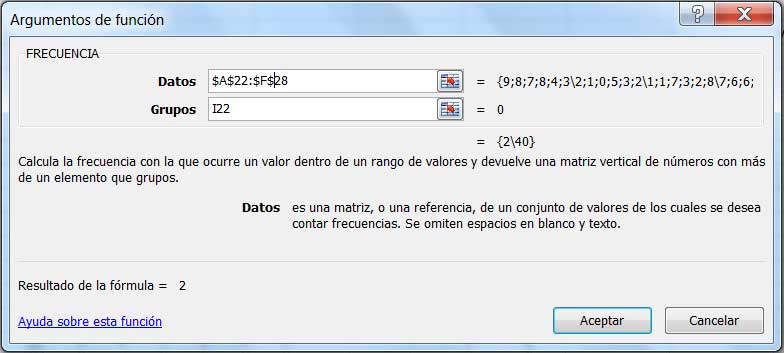
Obsérvese que deben ingresarse en primer lugar los datos contenidos en la matriz, para agregar seguidamente el valor que define al grupo.
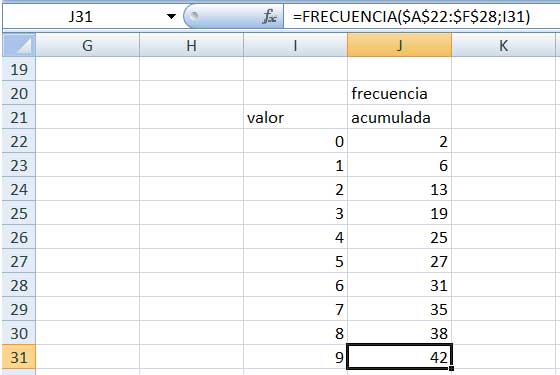
Cuando deslizamos hacia abajo el cursor, obtenemos las frecuencias acumuladas. Por ejemplo, en la celda J31 aparece la cantidad de valores de la tabla que son menores o iguales a nueve.
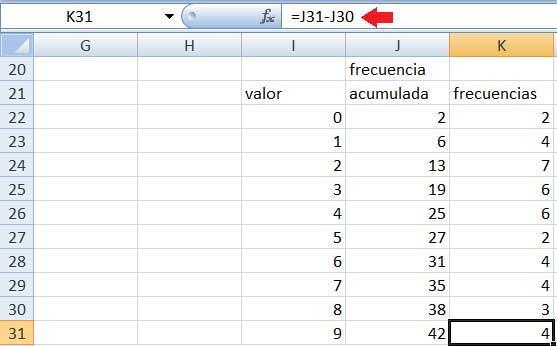
La flecha roja señala la operación que llevamos a cabo para calcular la cantidad de alumnos que faltaron a clase nueve veces, cuyo resultado aparece en la casilla K31.
2.3.1. Polígono de frecuencias
Se trata de una gráfica compuesta por una serie de segmentos que unen puntos de coordenadas (X,f). En general, muchos se limitan a representar la correspondiente a frecuencias acumuladas, pero puede resultar conveniente en la misma gráfica superponer estas con las correspondientes a cada valor en particular, que es lo que haremos en las siguientes secciones.
Weimer, R.(2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 58 a 62.
2.3.2. Empleo de la planilla de cálculo para construir los diagramas de frecuencias
Vemos en la imagen 2.6 de qué modo seleccionar el tipo de gráfico con el que construiremos los diagramas de frecuencias. Seleccionando las tres columnas de la tabla auxiliar construida al desarrollar el ejemplo y haciendo clic en el ícono correspondiente a dispersión con líneas rectas y marcadores, se obtienen en forma inmediata los diagramas de frecuencia absolutas y acumuladas que se reproducen en la imagen 2.7.
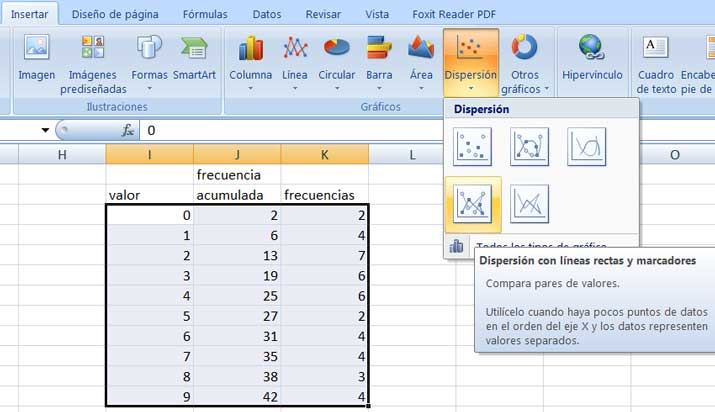
Una vez que seleccionamos todos los valores de la tabla de la derecha, buscamos la categoría diagrama de dispersión en el menú de la parte superior, como se observa en la imagen. Dentro de la ventana que se abre, recomendamos seleccionar dispersión solo con marcadores.
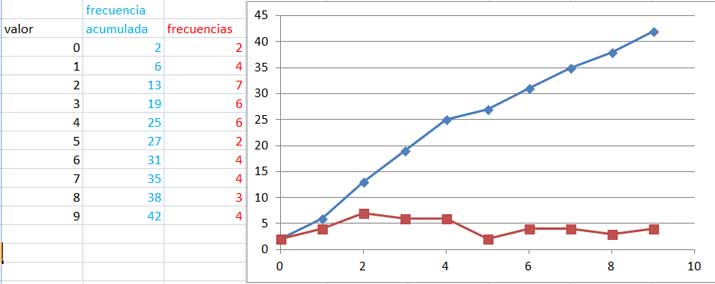
Diagramas de frecuencias por grupo (en color rojo) y de frecuencias acumuladas (en color azul).
Supongamos que se arroja un dado un gran número de veces, registrando cuál es el número que queda en la cara superior de este después de cada lanzamiento. Los valores obtenidos son los que aparecen en la tabla que reproduce la imagen 2.8.
Construir los diagramas de frecuencias por grupo y acumuladas. ¿Puede sacar alguna conclusión a partir de los resultados obtenidos?
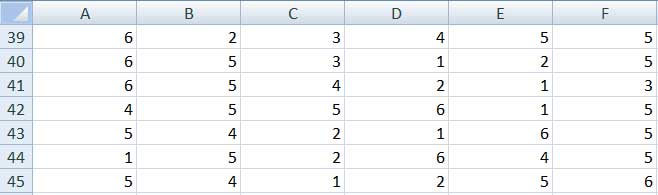
Tabla de valores donde se indica el número que se observó en la cara superior del dado en cada uno de los tiros.
2.3.3. Tabla de frecuencias agrupadas
Cuando la cantidad de datos continuos recopilados es muy grande, se suelen presentar en grupos o clases de medidas, en tablas que reciben el nombre de tablas de frecuencias agrupadas.
Estas facilitan tanto la ejecución de ciertos cálculos estadístico como la construcción de presentaciones gráficas que hemos de estudiar seguidamente.
Una ART decide estudiar la cantidad de días en el año que los empleados de una determinada empresa no concurrieron a trabajar como consecuencia de accidentes sufridos en ella. En la imagen 2.9 se reproduce la tabla en la que se registra dicha información.
Veremos en la siguiente sección qué nuevas herramientas nos permitirán construir la tabla de frecuencias agrupadas para situaciones como la del presente ejemplo.
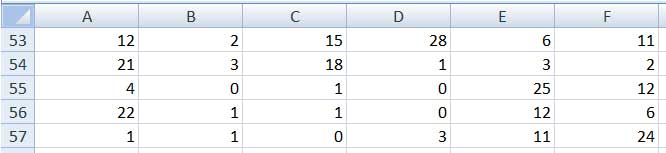
Cantidad de días al año que no asistieron al trabajo los empleados de una empresa como consecuencia de los accidentes sufridos en ella.
2.3.4. Regla de Sturges
Si comparamos la tabla de la imagen 2.1 con la de la imagen 2.9, notaremos que en esta última el rango de valores presentes es mucho más amplio. Además, algunos valores numéricos se repiten varias veces, mientras que muchos de los que incluye el rango no figuran (si miramos detenidamente la tabla, notaremos que, por ejemplo, ninguno de los empleados faltó 7 días, mientras que hay varios que no faltaron ni un solo día).
Debemos entonces definir un cierto número de clases dentro de las cuales habremos de agrupar los datos obtenidos. Al hacerlo, debemos tener en cuenta que si todos los datos se agruparan en un número pequeño de clases, las características del conjunto de los datos originales podrían ocultarse, perdiéndose entonces información relevante. Por otro lado, si se adoptase un número grande de clases, se perdería el propósito original del agrupamiento: condensar los datos en forma significativa y facilitar su interpretación. Además, un gran número de clases podría dar lugar a muchas clases vacías, lo que le quita sentido al agrupamiento de los datos.
No existe un acuerdo general entre los estadísticos acerca del número de clases que deban usarse. Ello depende, por ejemplo, del número total de datos recogidos.Dada la cantidad de datos que aparecerán en los ejemplos de nuestra Carpeta de trabajo, será conveniente definir entre cinco y quince clases.
Una de las reglas que podemos aplicar es la de Sturges, que establece que el número de clases necesario puede obtenerse en forma aproximada aplicando la expresión:
\[{\large c = 3,3 \ast log(n) + 1}\]
Aquí, c representa la cantidad de clases, n corresponde a la cantidad de datos de que se dispone, y log es el logaritmo en base 10.
En nuestro problema, el valor de c obtenido es 5,87, razón por la cual emplearemos seis clases paraconstruir la tabla de frecuencias por clase.
Teniendo en cuenta que la amplitud de todos los grupos ha de ser la misma y que los valores máximo y mínimo registrados en nuestra tabla son 28 y 0, definimos entonces para dichas clases los intervalos que se observan en la columna de la derecha de la captura de pantalla de la imagen 2.10. Dado que a partir de la naturaleza de los datos no tenía sentido tomar valores negativos, el extremo inferior del primer grupo ha sido, naturalmente, el cero.
Restaría entonces determinar manualmente por conteo la cantidad de elementos incluidos en cada una de las clases. Sin embargo, y a partir de lo visto anteriormente, proponemos utilizar nuevamente la función FRECUENCIA; ello no solo reducirá la posibilidad de cometer errores sino que, además, nos permitirá llegar al resultado en menor tiempo.
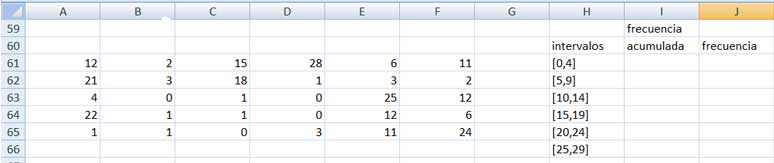
En el extremo derecho de la imagen se observan los intervalos definidos para nuestro problema.
En las imágenes 2.11 y 2.12 hemos obtenido la cantidad de elementos de cada clase en forma acumulada, aplicando el procedimiento aplicado con anterioridad. En la imagen 2.13, finalmente, operamos con los valores de las frecuencias acumuladas para obtener la tabla de frecuencias agrupadas.
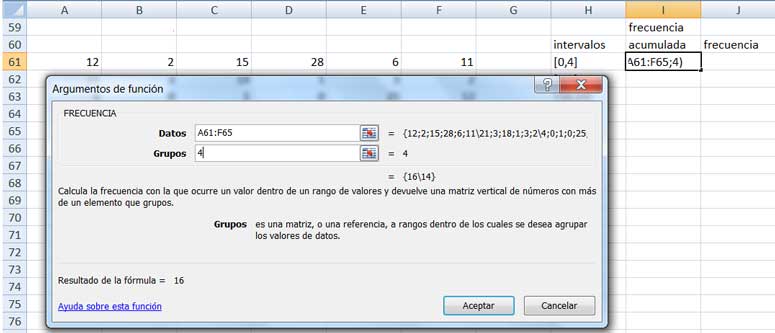
En la casilla I61 obtenemos el número de empleados que como máximo faltó cuatro veces en el año utilizando la función FRECUENCIA. Para cada una de las clases, hemos de escribir en la ventana “grupos” el número correspondiente al extremo superior de aquella.
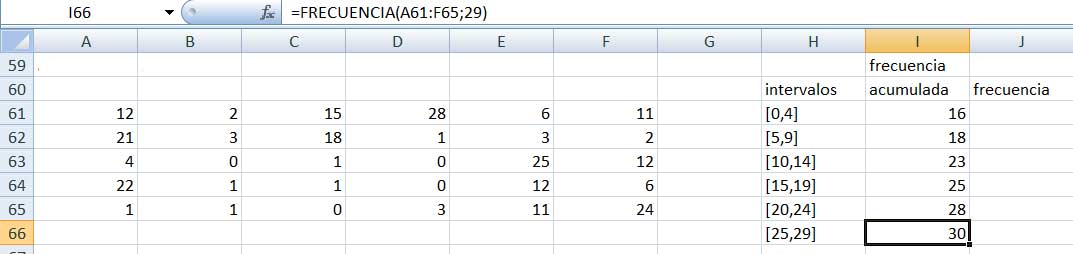
Apoyando el cursor sobre la cruz sobre el extremo inferior derecho de la casilla I61 y moviéndonos hacia abajo, obtenemos las frecuencias acumuladas para todas las clases.
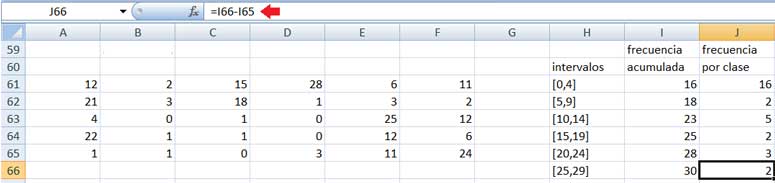
Finalmente, en color azul mostramos las dos columnas que nos permiten definir la tabla de frecuencias agrupadas que buscábamos. Obsérvese detenidamente la operación llevada a cabo para obtener el valor de la celda J66, que aparece señalado con una flecha roja en la parte superior de la imagen.
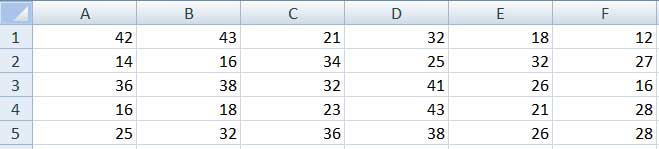
Obtener la tabla de frecuencias agrupadas a partir de los datos de la siguiente tabla:
2.4. Gráficas de pastel
Este tipo de gráfica, que ya hemos empleado en la unidad 1, es de uso muy frecuente y permite interpretar la información obtenida de un modo muy claro y accesible. Su construcción puede partir, en algunos casos, de una tabla de datos agrupados, como la del ejemplo estudiado en la sección anterior.
En las imágenes 2.14, 2.15 y 2.16 se describen sucintamente los pasos que habrán de seguirse para obtener la gráfica de pastel correspondiente al problema que estamos estudiando.
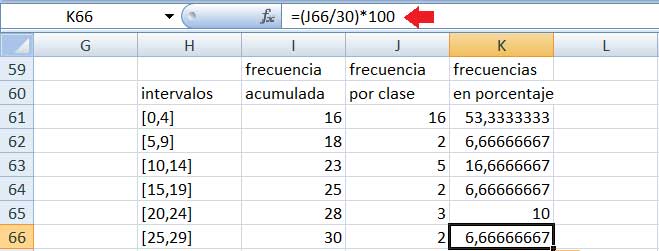
A la tabla que aparece en la imagen 2.13 le agregamos la columna K, donde expresamos las frecuencias por clase en porcentaje. En la ventana señalada con una flecha roja se observa cuál fue el cálculo llevado a cabo para obtener el valor que figura en la celda K66.
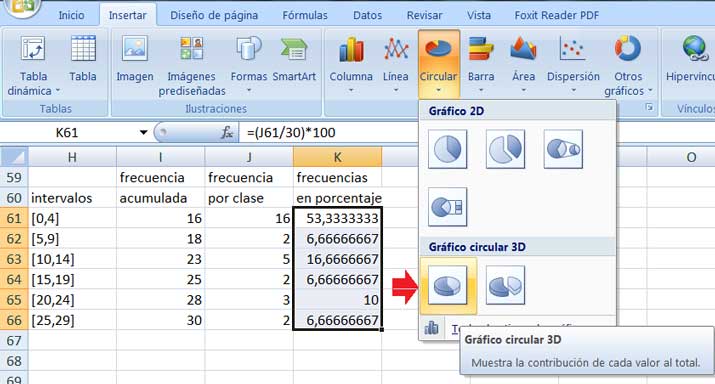
Una vez seleccionada la columna de frecuencias en porcentaje, debemos “Insertar imagen”, eligiendo el gráfico que se señala con la flecha roja.
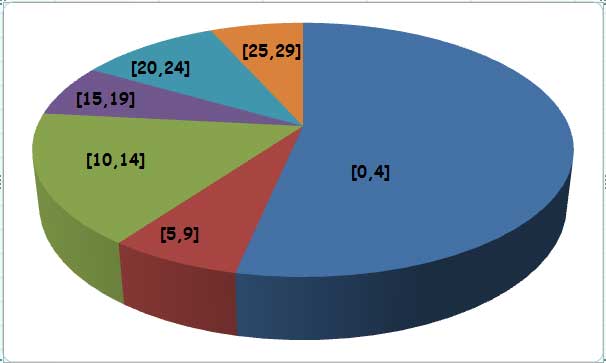
Finalmente, haciendo clic en el ícono señalado en la figura anterior, obtenemos la gráfica de pastel buscada. El área azul nos indica de un modo inmediato que es muy grande el porcentaje de empleados que han faltado cuatro días o menos en el año debido a accidentes de trabajo.
Vale aclarar que en la gráfica de pastel de la imagen 2.16 el sector azul (a la derecha) corresponde a la clase que comprende a los empleados que, a los sumo, han dejado de asistir cuatro días por accidentes de trabajo. A partir de allí y moviéndonos en sentido horario, nos encontramos seguidamente con un sector rojo (empleados que faltaron entre cinco y nueve días).Por otro lado, el sector verde corresponde a los empleados que no han podido asistir entre diez y catorce días; el sector violeta representa a los empleados que no han asistido entre quince y diecinueve días; el sector celeste a los que faltaron entre veinte y veinticuatro días;y, finalmente, el sector en color anaranjado, a los empleados que, por accidentes de trabajo, no pudieron asistir entre veinticinco y veintinueve días.
Construir la gráfica de pastel correspondiente a la tabla de frecuencias agrupadas correspondiente a la siguiente muestra:

Weimer, R. (2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 46-47.
2.5. Histogramas
Los histogramas son un tipo de representación gráfica muy conveniente para los datos consignados en las tablas de frecuencias agrupadas. Se los conoce también como gráficos de barras y su construcción es muy sencilla.
Básicamente, se indican sobre el eje de abscisas los extremos de las clases definidas para las tablas de frecuencias mencionadas en el párrafo anterior, trazándose luego en sentido vertical columnas proporcionales a las frecuencias de cada clase.
Si bien es cierto que no es compleja su construcción en forma manual, volvemos a proponer al alumno el empleo de un software adecuado para la tarea.
En esta oportunidad, la planilla de cálculo que hemos empleado hasta el momento no resulta ser la mejor herramienta, razón por la cual emplearemos el R, un programa ampliamente utilizado para estadística.
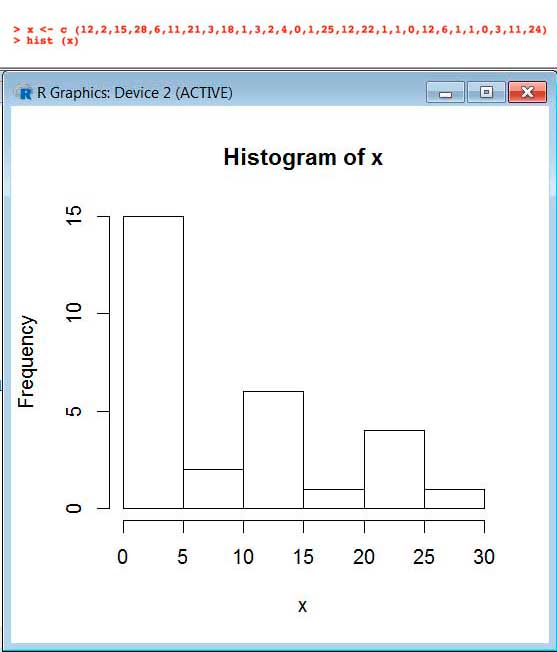
En la imagen 2.17 se observa el histograma correspondiente a los datos de la tabla que se reprodujo en la imagen 2.10.
En la parte superior de la imagen, en color rojo, las dos únicas instrucciones requeridas: en primer lugar, la definición de un vector (x), que contiene todos los datos que se nos entregaron inicialmente. Cada vez que en este programa se deseen asignar valores a un vector, deberá escribirse después de su nombre “<─ c” y detrás de esta última letra (y entre paréntesis) los datos que habrá de contener el vector, separados entre sí por comas.
En la segunda línea, la instrucción “hist(x)”basta para que el histograma aparezca en una ventana gráfica (que generalmente se presenta a la derecha de la ventana de comandos y no debajo de estos, como se observa en la imagen 2.17).
Obsérvese que la cantidad de clases coincide con la que previamente obtuvimos aplicando la regla de Sturges. Sin embargo, ello no necesariamente habrá de suceder en todos los casos.
Histograma obtenido con el R
Devore, J.(2005), Probabilidad y Estadística para Ingeniería y Ciencias, International Thomson Editores, México, pp. 15 a 21
Walpole, R.; Myers, R; Myers, S.; Keying Ye (2007), Probabilidad y Estadística para Ingeniería y Ciencias, Pearson Education, México, pp. 20 a 24.
Weimer, R. (2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 53 a 56.
2.6. Media de una muestra
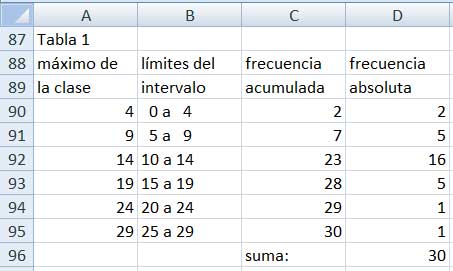
Volvamos al caso de la ART; supongamos que se lleva a cabo un segundo estudio, siendo los datos obtenidos en este caso son los que se registran en la tabla de la imagen 2.18.
Con esta información y utilizando la instrucción FRECUENCIA (imagen 2.19), armamos la tabla 1 (imagen 2.20), a partir de la cual (operando como lo hemos hecho en anteriores oportunidades) construimos los diagramas de frecuencias absolutas y acumuladas (imagen 2.21) y el correspondiente histograma (imagen 2.22).
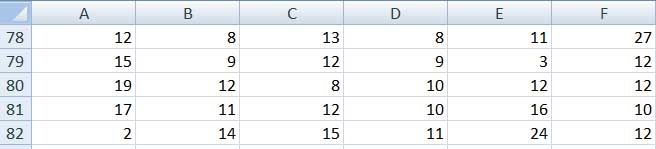
Tabla de valores
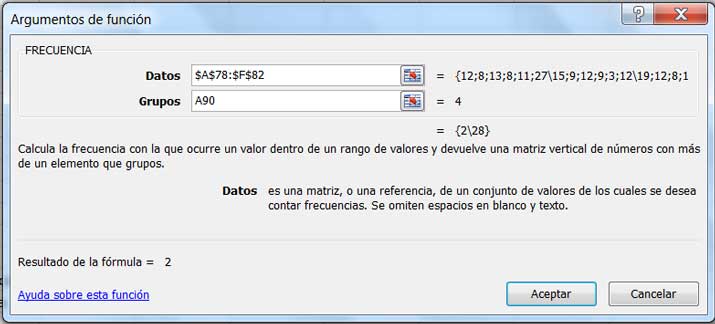
Aplicamos la función FRECUENCIA
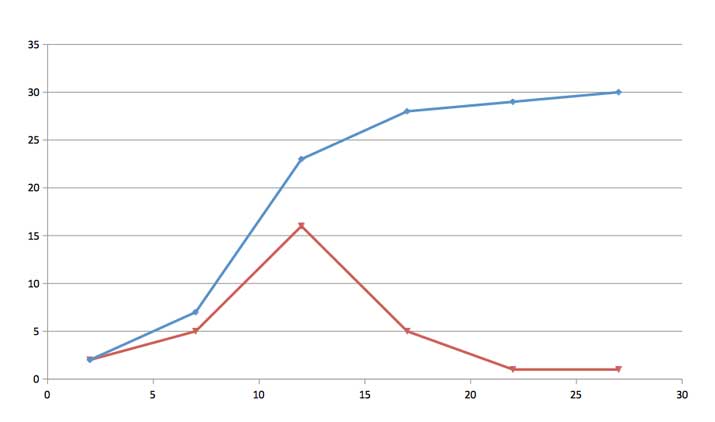
Diagramas de frecuencias absolutas y acumuladas
La tabla 2 (imagen 2.23) permite calcular la media utilizando la expresión:
(2.1) \[{\large\overline{x} = \frac {\sum f \cdot x}{\sum f}}\]
La primera columna de dicha tabla contiene el valor medio correspondiente a cada uno de los intervalos. Así, por ejemplo, 2 es el valor medio del intervalo que contiene a los valores desde el cero hasta el cuatro.
Compárense los valores de la media calculados, en primer lugar, empleando la expresión en la que se trabaja con las clases y sus frecuencias (en azul) y, en segundo lugar,el que se obtiene directamente con la expresión
(2.2)\[{\large\overline{x} = \frac {\sum^n_i =_1 x_i}{n}}\]
que en la tabla 2 (imagen 2.23) aparece en color rojo. ¿Considera que la diferencia entre ambos valores sea significativa?
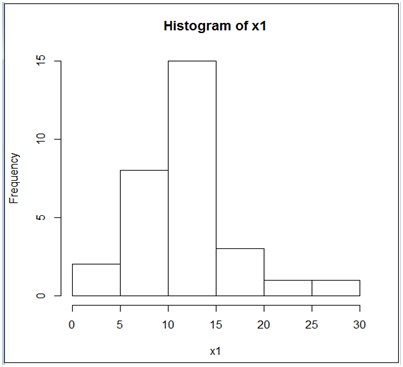
Histograma construido a partir de los datos de la tabla que aparece en la imagen 2.20.
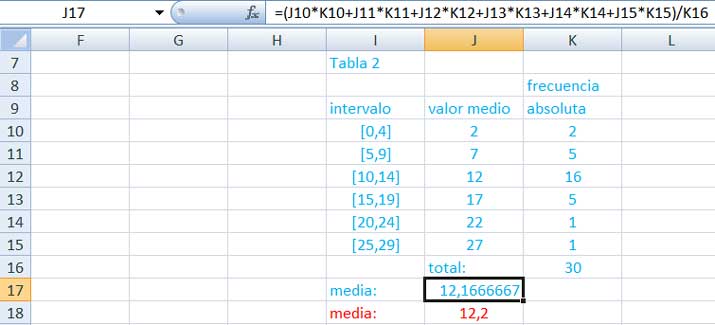
En la ventana de la parte superior se observa de qué modo se aplica la expresión (2.1) para el cálculo de la media. El valor de dicha media es el que aparece en la casilla J17 (en color azul). Debajo de este, en color rojo, el valor de la media calculado a partir de la expresión (2.2).
Supongamos que al año siguiente, la empresa define un plan de premios por asistencia, a la vez que pone mayor énfasis en la aplicación de las normas de seguridad vigentes. La ART vuelve a registrar la cantidad de días en el año en los que cada uno de los treinta empleados de la empresa no concurrió a trabajar como consecuencia de accidentes sufridos en ella. Los datos obtenidos en esta oportunidad se consignan en la tabla de la imagen 2.24.
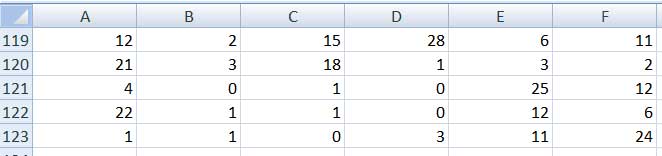
Datos obtenidos por la ART después de que la empresa aplicara un plan de premios por asistencias.
La tabla de frecuencias absolutas y acumuladas, junto con lo gráfica correspondiente, se reproducen en la imagen 2.25.
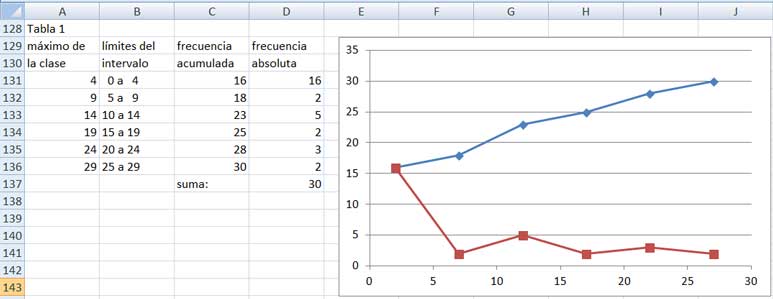
Frecuencias absolutas y acumuladas para la muestra obtenida después de ser implantado el plan de premio por asistencia.
Nuevamente, los valores de la tabla 2 (imagen 2.26) permiten calcular la media utilizando la expresión (2.1).
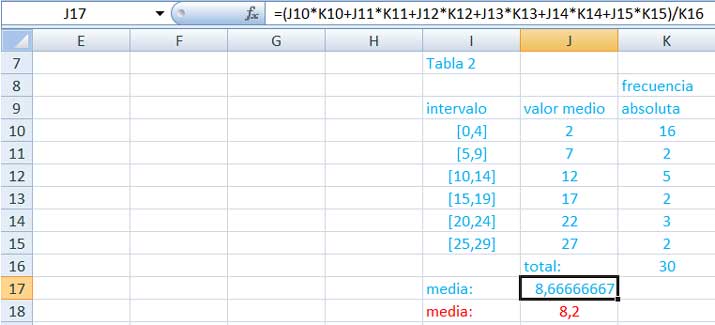
Tabla 2 correspondiente a la nueva muestra de la ART. Dado que la planilla de cálculo quedó programada, nos limitamos a reemplazar los valores de la columna K (obtenidos en la tabla 1de la imagen 2.25) para obtener la media correspondiente a la nueva situación.
Dichos valores permiten calcular la media que aparece en color azul en la parte inferior de la tabla de la imagen 2.26, en tanto que en rojo aparece el valor calculado mediante la expresión (2.2).Este último puede obtenerse directamente aplicando la función PROMEDIO.
El histograma correspondiente a este nuevo estudio puede observarse en la imagen 2.27.
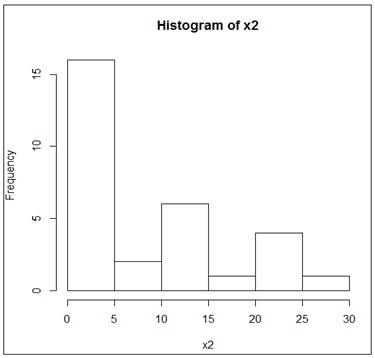
Histograma correspondiente al nuevo estudio
¿Qué diferencia observa entre ambos histogramas? Cree que exista una relación entre esta y la que,en la segunda de las muestras, se observa entre los valores de las medias calculados de formas distintas?¿Por qué dicha diferencia no se hace tan notable en la primera de las muestras?
Walpole, R.; Myers, R; Myers, S.; Keying Ye (2007), Probabilidad y Estadística para Ingeniería y Ciencias, Pearson Education, México, pp. 11 y12.
Weimer, R.(2003), Estadística, Compañía Editorial Continental CECSA, México, pp. 72 a 75.
2.7. Mediana y moda de una muestra
Supongamos ahora que una empresa de viajes que organiza excursiones para centros de jubilados, a pedido de una compañía aseguradora, estudia las edades de un grupo de personas que tomaron parte de un tour por el noroeste argentino. Las edades de los asistentes al viaje se reproducen en la imagen 2.28.
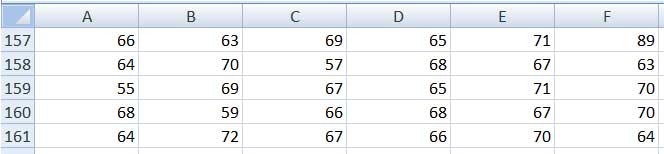
Tabla de valores donde aparecen las edades de las personas que tomaron parte en el tour.
Nos resultará muy útil contar con el histograma de modo que empleamos el R.La imagen 2.29 reproduce dicho histograma. Puesto que en nuestro ejemplo el rango no es muy grande, consideramos apropiado adoptar solo cuatro clases y no seis, como indicaba que lo hiciéramos la regla de Sturges.
Aplicando la función FRECUENCIA, como lo hemos hecho anteriormente, obtenemos la cantidad de valores que habrán de ser incluidos en cada una de las clases (imagen 2.30).
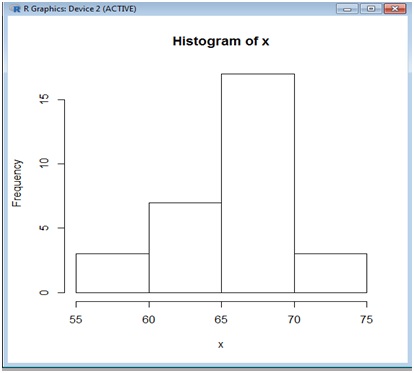
Histograma correspondiente al conjunto de datos de la muestra obtenido mediante el R.
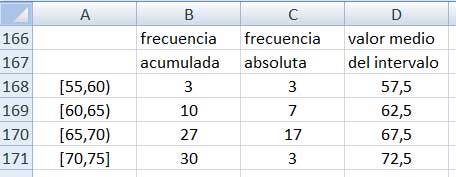
Empleando la planilla de cálculo y la función FRECUENCIA, obtenemos la cantidad total de valores que incluye cada una de las clases. Los correspondientes valores aparecen en la columna del extremo derecho.
Calculamos entonces la media de nuestra muestra:
\[{\large\overline {x} = \frac {3 \ast 57,5 + 7 \ast 62,5 + 17 \ast 67,5 + 3 \ast 72,5 }{3 + 7 + 17 + 3} = 65,83}\]
En muchos casos la media puede verse afectada por los valores extremos de la distribución. Por ejemplo, un estudiante cuyas calificaciones a lo largo de un curso hubiesen sido 10,9,10,10 y 1 vería seriamente afectado su promedio (¡y perdería sin duda el régimen de promoción!) debido a su aplazo final. Por ese motivo, suele definirse la mediana, otra medida de la tendencia central.
Podemos definir la mediana como el valor central de un conjunto de datos ordenados (cuando la cantidad de datos sea un número impar) o como el promedio de los dos valores centrales del conjunto (en el caso de que la cantidad de datos recogidos sea un número par). En general, se puede definir a la mediana como el puntaje ordenado medio.
En un caso como el de nuestro ejemplo, donde el tamaño de la muestra hace recomendable la organización de los datos en grupos o clases, la mediana habrá de obtenerse a partir del diagrama de frecuencias acumuladas.
Cada punto de dicho diagrama tendrá como abscisa al valor medio de la clase (xn) y como ordenada la frecuencia acumulada correspondiente a esta (fn). Con los datos que figuran en la tabla que se observa en la imagen 2.30 construimos el diagrama de frecuencias acumuladas de la imagen 2.31 Utilizamos para ello el softwareGeoGebra.
Obtenemos la mediana gráficamente, trazando una horizontal cuya ordenada se corresponda con el valor central de la muestra (15, en nuestro ejemplo) que interseque al diagrama de frecuencias acumuladas. La abscisa de dicho punto será entonces la mediana de nuestra muestra, como puede observarse en la imagen 2.32.
En la imagen 2.33 reproducimos la captura de pantalla correspondiente al protocolo de construcción con el que obtuvimos la mediana, a los fines de que el estudiante pueda utilizar este mismo software para problemas similares.
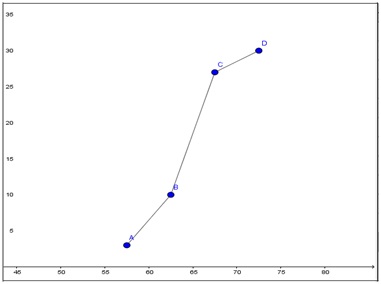
Diagrama de frecuencias acumuladas construido con el GeoGebra.
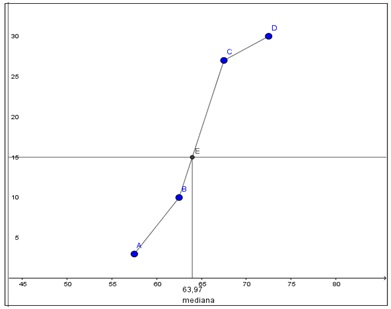
Obtención gráfica de la mediana, que en nuestro caso, vale 63,97.
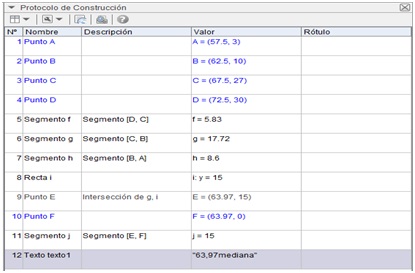
Captura de pantalla del protocolo de construcción del diagrama de frecuencias acumuladas.
Existe aún una tercera medida de la tendencia central de la muestra que recibe el nombre de moda.Para muestras pequeñas, puede definirse sencillamente como el valor que, dentro de una muestra, se repita la mayor cantidad de veces. Así, por ejemplo, si tuviésemos una muestra compuesta por los valores 12, 13, 14, 14, 15, 15, 15, 16, 17,17, 18, 21, la moda sería el valor 15.
La obtención de la moda no es tan sencilla en casos como el que nos compete. Primeramente, hemos de construir el histograma y observar cuál de las clases tiene la mayor frecuencia. En la imagen 2.34 se observa claramente el procedimiento a seguir: dentro de dicho grupo se trazan dos segmentos. La abscisa del punto intersección entre ambos será la moda correspondiente a nuestro conjunto de datos.
Nuevamente hemos empleado el GeoGebra. En la imagen 2.35 reproducimos el protocolo de Construcción, en el que se indican las instrucciones para obtener el histograma y la moda en nuestro ejemplo. Invitamos al estudiante a revisarlo para aplicarlo en la resolución de otros problemas similares.
Los valores de la media (65,83), la mediana (63,97) y la moda (67,08) obtenidos en nuestro problema difieren significativamente entre sí. Veremos seguidamente que ello refleja una característica importante presente en muchas muestras: el sesgo.
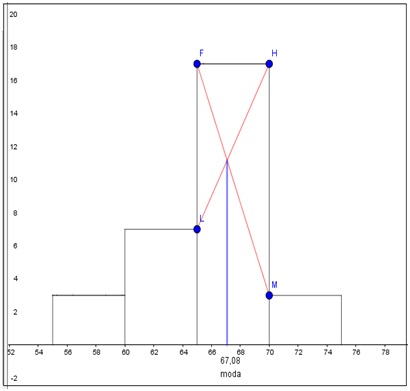
Obtención de la moda para el problema de las edades. Como puede observarse, a partir de la clase cuya frecuencia es la mayor, se trazan dos segmentos, en rojo, que unen los puntos F y M, por un lado, y los puntos H y L, por el otro. La abscisa del punto intersección entre ambos segmentos representa la moda de nuestra media.
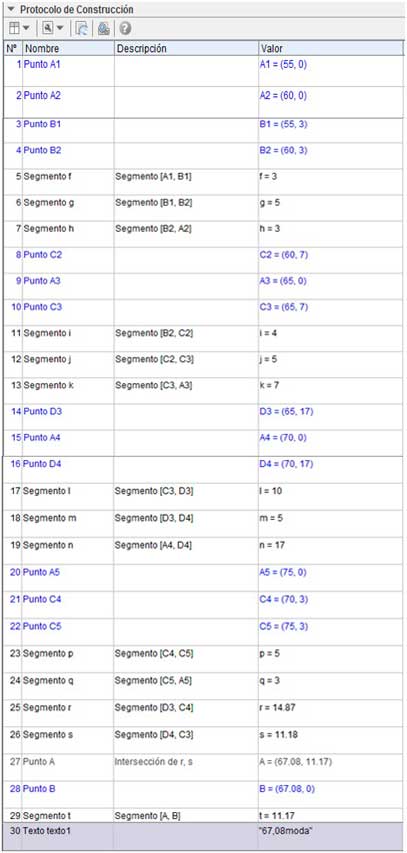
Protocolo de construcción para obtener la moda de nuestro problema.
2.8. Sesgo
La forma de un histograma estará relacionada con la posición relativa de la media, la mediana y la moda. A medida que los valores de estas tres medidas se vayan diferenciando claramente, la simetría de aquel irá desapareciendo y diremos que la muestra presenta sesgo.
Por ejemplo, dada la muestra cuyos valores fueron volcados a la tabla de la imagen 2.36, su histograma (ver imagen 2.37) presenta una notable simetría: por ese motivo se lo clasifica como histograma simétrico. A simple vista se observa que ambos lados, determinados por la media, son idénticos. Pero, además, la media, la mediana y la moda de la muestra coinciden (adoptando el valor 3,5).

Tabla conteniendo los valores de una muestra dada.
Calcular la media, la mediana y la moda de la muestra para confirmar que los tres valores coinciden, tal como lo que asevera el texto.
En cambio, dada la muestra cuya tabla de valores se reproduce en la imagen 2.38, su histograma, que se observa en la imagen 2.39, nos indica que aquella carece de la simetría que mostró el caso anterior. Decimos entonces que se trata de un histograma sesgado hacia la izquierda.
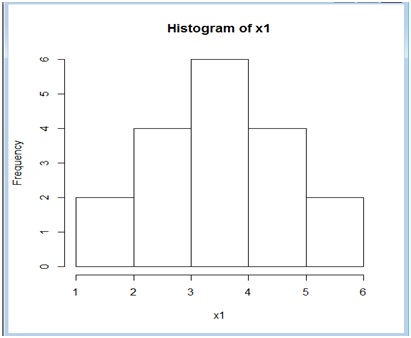
Histograma correspondiente a la muestra presentada en la imagen 2.36.
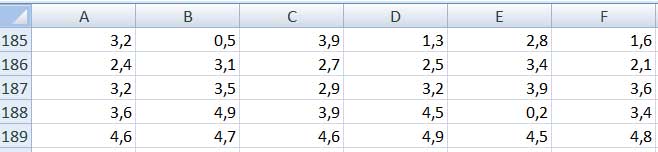
Tabla de valores correspondiente al segundo ejemplo propuesto en esta sección.
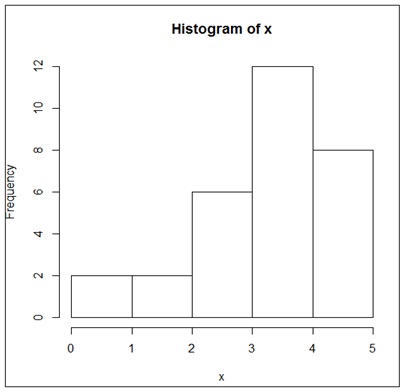
Histograma sesgado hacia la izquierda.
Calcular la media, la mediana y la moda para la muestra cuyos datos se reproducen en la tabla de la imagen 2.38. ¿Puede relacionar dichos valores con el sesgo que se observa en el histograma de la imagen 2.39?
En un puesto de trabajo de mecanizado de piezas se mide el ruido empleando dos metodologías distintas, la A y la B.
Los datos obtenidos empleando la metodología A, medidos en decibeles A, se volcaron en la siguiente tabla:

En cambio, los datos obtenidos aplicando la metodología B fueron los que se consignan a continuación:

Determinar si alguna de las metodologías aplicadas presenta sesgo.
2.9. Percentiles y cuartiles
Se define como enésimo percentil (y se lo escribe como Pn) al valor para el cual al menos el n % de la muestra cae en o por debajo de él. En general, es más común trabajar con los cuartiles, que son números que dividen en cuatro partes a un conjunto de medidas, extendiéndose desde la mínima hasta la máxima, razón por la cual cada una cuenta con aproximadamente el 25 % de las medidas.
Hay tres puntos cuartiles, a los que se suele expresar como Q1, Q2 y Q3. Al primero de ellos se lo conoce como primer cuartil, y coincide con el vigésimo quinto percentil (es decir, Q1 = P25). El segundo cuartil es el percentil cincuenta (es decir, la mediana), en tanto que el tercer cuartil coincide con el percentil setenta y cinco (o sea,Q3 = P75).
Para calcularlo puede volver a utilizarse la planilla de cálculo. En la imagen 2.40 se muestra la obtención del primer cuartil de una muestra dada.
Devore, J. (2005), Probabilidad y Estadística para Ingeniería y Ciencias, International Thomson Editores, México, pp. 28 a 33.
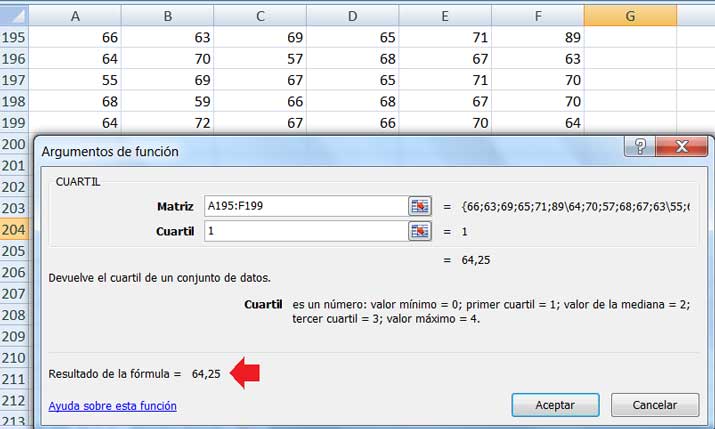
Obtención del primer cuartil de una muestra dada empleando la planilla de cálculo.

