9. Ecuaciones diferenciales
Objetivos
Que el alumno:
- Comprenda el concepto de modelo matemático y su valor en el estudio de fenómenos de la realidad.
- Aprenda a resolver ecuaciones diferenciales en variables separables.
- Descubra el amplio campo de aplicación de las ecuaciones diferenciales en general.
- Amplíe su manejo del software, aplicándolo también a la verificación de las soluciones generales y particulares de una ecuación diferencial.
9.1. Ecuaciones diferenciales
En la unidad 6 del presente MDM resolvimos una serie de problemas a partir de expresiones matemáticas que el propio enunciado nos ofrecía. Por ejemplo, en la sección 6.1.2, se describía un proceso en el cual se introducía en un autoclave una muestra que poseía inicialmente unas 800 bacterias por mililitro. Se nos informaba, además, que al cabo de media hora solo quedaba en la muestra un promedio de unas 6 bacterias por mililitro. Finalmente, se interpretaba matemáticamente el caso bajo estudio a partir de la expresión:
[9.1] \[ N(t)=800e^{-0,547t} \]
En la misma, N(t) representaba el número de bacterias presentes por mililitro en función del tiempo, medido a partir del instante en que la muestra se había introducido en el autoclave.
¿Qué sucedería si, por ejemplo, la muestra poseyese inicialmente otra cantidad de bacterias por mililitro, se tratase de otro tipo de bacteria, o se expusiese a una temperatura diferente? Aun cuando podemos suponer que la expresión que describiese a la situación fuera similar, necesitaríamos profundizar en el tema para obtener la fórmula que describiese nuestro nuevo experimento.
Es entonces cuando debemos tener en cuenta la siguiente ley empírica: la tasa de decrecimiento en un instante dado es directamente proporcional a la cantidad de microorganismos presentes en dicho instante. Matemáticamente, podemos expresar dicha ley como:
[9.2] \[ \frac {dN(t)}{dt}=kN(t) \]
Nos encontramos entonces ante una ecuación que se caracteriza por:
- contener la derivada de una función y
- tener por incógnita a dicha función.
Las ecuaciones que presenten dichas características reciben el nombre de ecuaciones diferenciales y resultan ser sumamente importantes por sus aplicaciones en el campo de ciencias tan disímiles como la Física, la Biología o la Economía.
9.2. Concepto de modelo matemático
La palabra modelo tiene diversas acepciones. Podríamos comenzar diciendo que un modelo es el diseño de un objeto o máquina que habrá de construirse, o que se trata de una analogía empleada para ayudarnos a comprender de qué modo funciona o cómo se comporta un objeto que no puede ser observado en forma directa, como, por ejemplo, un átomo.
Pero también podemos definir como modelo a un conjunto de postulados, datos e inferencias que nos permiten obtener una descripción matemática de una entidad o de un estado de cosas.
Modelar sería entonces (Dym, 2004) una actividad cognitiva que nos permite construir modelos mediante los cuales habremos de describir de qué modo se producen determinados fenómenos o cómo funcionan mecanismos u objetos de nuestro interés.
Para describir diversos aparatos o comportamientos pueden emplearse distintos elementos: palabras, dibujos o bosquejos, fórmulas matemáticas o programas de computadora. La actividad de modelado, entonces, podrá llevarse a cabo en diversos lenguajes. En muchos casos, estos habrán de ser empleados en forma simultánea o habrán de complementarse.
DYM, C. (2004). “What is Mathematical Modeling?” En B. HOLLAND (Ed.), Principles of Mathematical Modeling, pp. 3-12. Elseiver Academic Press, New York.
A partir de lo dicho hasta este punto, podríamos entonces definir un modelo matemático como una representación en términos matemáticos del comportamiento real de artefactos o de fenómenos del mundo físico.
El proceso de modelización no debe ser entendido como un proceso lineal sino como uno de tipo cíclico, donde las reflexiones sobre el modelo y la intención de uso de este pueden conducir a su redefinición. Blomhøjy Højgaard Jensen (2003) proponen los siguientes seis pasos para el proceso de establecer una relación entre alguna idea matemática y una situación real:
- Formulación del problema.
- Sistematización: seleccionar los objetos y relaciones relevantes del dominio de investigación y posterior idealización de estos para hacer posible una representación matemática.
- Traducción de dichos objetos y relaciones al lenguaje matemático.
- Empleo de métodos matemáticos para obtener resultados matemáticos y arribar a conclusiones.
- Interpretación de los resultados y conclusiones a partir del dominio de investigación inicial.
- Evaluación de la validez del modelo por comparación con datos observados o predichos, con el conocimiento teórico, la experiencia personal o la compartida.
BLOMHØJ, M.; HØJGAARD JENSEN, T. (2003). “Developing mathematical modeling competence: Conceptual clarification and educational planning”. Teaching mathematics and its applications 22 (3), pp. 123-139.
El problema al que hicimos alusión en la sección anterior fue oportunamente preparado a partir de la situación experimental que describe el siguiente ejemplo. Su análisis nos servirá como aproximación al proceso de modelado matemático.
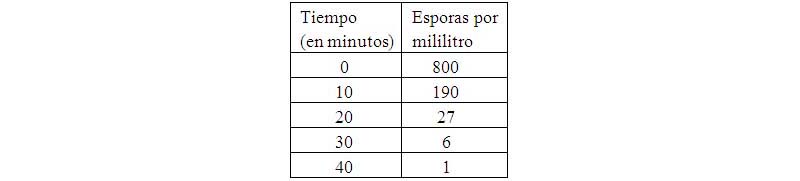
Un cultivo que contiene 800 esporas por mililitro se divide entre cuatro recipientes que se someten a una temperatura de 245 ºC por distintos períodos de tiempo. La cantidad de esporas supervivientes para cada uno de los distintos períodos de tiempo se reproduce en la tabla que aparece en la imagen 9.1.
Si se sabe que la velocidad de decrecimiento del número de esporas en un instante dado es proporcional a la cantidad de esporas presentes en ese instante, se pide obtener una expresión matemática aproximada que nos permita conocer la cantidad de esporas supervivientes en función del tiempo.
Tabla de valores experimentales que contiene la cantidad de esporas por mililitro presentes en una muestra en función del tiempo
Observemos que en el enunciado (en el que se nos formula el problema) se habla de velocidad de decrecimiento, que no es otra cosa que la tasa de decrecimiento a la que habíamos hecho referencia oportunamente.
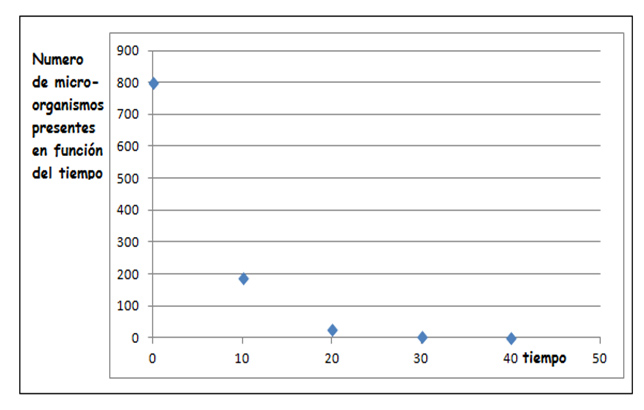
Empleamos una de las aplicaciones de la planilla de cálculo para construir el diagrama de dispersión que se reproduce en la imagen 9.2. Sobre el eje de abscisas se representa al tiempo transcurrido y sobre el de ordenadas, el número de microorganismos por mililitro (que representan dos de los factores relevantes dentro de nuestra investigación). Cada punto, entonces, representa a alguno de los pares de valores experimentales que aparecen en la tabla de la imagen 9.1.
En la sección 9.2.1 veremos cómo, a partir de la expresión [9.2] se llega a la fórmula:
\[ N(t)=N_0 e^{-kt} \]
En ella, N(t) representa al número de microorganismos presentes en un instante t dado, \( N_0 \)el número de microorganismos presentes en el instante inicial y k una constante positiva, que dependerá de diversos factores del experimento, como la temperatura a la que se lleva a cabo, el tipo de bacteria de que se trate, etc. Desde el punto de vista matemático, nos encontramos con dos incógnitas \( (N_0 \ \text{y} \ k ) \), de modo que bastaría con conocer la cantidad de bacterias presentes en dos instantes determinados para generar (y resolver)el sistema no lineal de dos ecuaciones con dos incógnitas que nos permita llegar a la expresión que solicita el enunciado del problema.
El párrafo anterior hace entonces referencia a dos de las etapas propuestas por Blomhøj y Højgaard Jensen, la traducción de los objetos de interés al lenguaje matemático y el empleo de métodos matemáticos para obtener resultados matemáticos y arribar a conclusiones.
Volcamos los datos que aparecían en la tabla en un par de ejes cartesianos.
Hemos dicho que la obtención de la expresión matemática que interprete el fenómeno bajo estudio resulta aparentemente sencilla, pues se limita a resolver un sistema de dos ecuaciones con dos incógnitas. Sin embargo, contamos con cinco puntos experimentales. Podríamos entonces preguntarnos con cuáles de ellos quedarnos (¡o cuáles descartar!) para cumplir con nuestro objetivo. Pero es entonces cuando debemos avanzar en el campo de las herramientas a emplear y, partiendo de que todos los datos obtenidos son relevantes, buscar un método mejor que el originalmente propuesto.
El método de los cuadrados mínimos se encuentra fuera de los alcances de nuestro curso, pero resulta ser el más apropiado para cumplir con nuestro objetivo. Nos limitaremos a decir que dicho método trabaja con todos los puntos obtenidos experimentalmente, buscando la curva que mejor se ajuste a los mismos. Por fortuna, la propia planilla de cálculo nos brinda la expresión matemática de dicha curva, como se observa en la imagen 9.3.
El propio software nos ofrece la curva de tipo exponencial que mejor se ajusta a los datos experimentales.
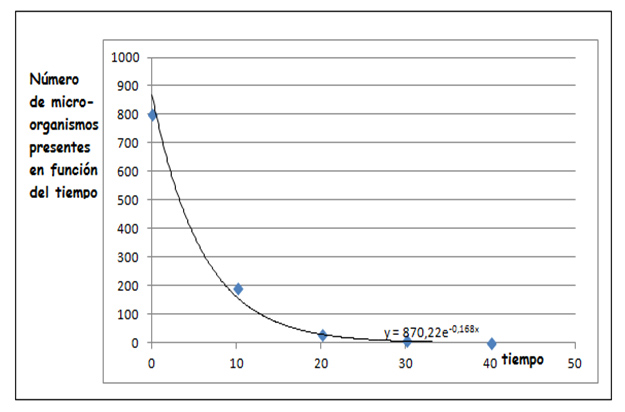
Si comparamos la expresión [9.1] con la que figura en la imagen 9.3, observaremos que no son exactamente iguales. Dado que aquella fue obtenida solo a partir de dos de los puntos, consideramos que la que mejor representa el fenómeno bajo estudio es la que nos brindó el software.
El valor de los modelos matemáticos es enorme y solo nos hemos limitado a brindar al alumno una aproximación. En las siguientes secciones volveremos a concentrarnos en la resolución de ecuaciones diferenciales que, no por casualidad, estarán vinculadas con modelos matemáticos de interés para el estudiante.
9.3. Ecuaciones diferenciales en variables separables
Existe un gran número de procedimientos diferentes para resolver ecuaciones diferenciales, basados generalmente en distintas sustituciones. Su aplicación no es arbitraria y, salvo escasas excepciones, existirá un único procedimiento para resolver tal o cual ecuación diferencial.
El procedimiento más sencillo (y habitual) es el que hemos de aplicar en la mayoría de los casos que estudiaremos a continuación, el de resolución por variables separables. Como veremos, la disposición de las variables nos permitirá alcanzar el resultado simplemente resolviendo dos simples integrales, ya que cada uno de los miembros habrá de contener solo una de las dos variables involucradas.
9.3.1. Crecimiento de una población
El tiempo que tardan en formarse dos células a partir de una común recibe el nombre de tiempo de duplicación. Supongamos que dentro de un recipiente mal esterilizado se encontrase una determinada bacteria, con un peso aproximado de \( 10^{-12} \) gramos. Teniendo en cuenta que su tiempo de duplicación es de veinte minutos y suponiendo que las condiciones fuesen ideales para su crecimiento, calcular el valor del peso de su descendencia al cabo de cuarenta y ocho horas.
Resolución:
Podemos adaptar la [9.2] a nuestro problema, expresando
[9.3] \[ \frac{dM(t)}{dt}=kM(t) \]
M(t) representa la masa en un momento determinado, en tanto que k es una constante positiva cuyo valor habremos de obtener. Partiendo de la 9.3, escribimos:
\[ \frac{dM(t)}{M(t)}=kdt \to \displaystyle\int \frac{dM}{M} =\displaystyle\int k.dt \to ln(M(t))=kt+C \]
El primer paso del cálculo precedente es el que justifica el nombre del presente procedimiento: obsérvese que en el miembro de la izquierda quedó solamente la variable dependiente M, mientras que en el miembro de la derecha la única variable presente es la independiente, el tiempo.
A partir de la definición del logaritmo podemos escribir:
[9.4]\[ M(t)=e^{kt+C} \to M(t)=e^{kt} e^C \to M(t)=K_2 e^{kt} \]
En la \( [9.4], K_2=e^C \)
Como de acuerdo con el enunciado la población se duplica en veinte minutos, suponemos una masa inicial a la que expresamos como \( M_0 \) que habrá de duplicarse en un tiempo \( t= \frac{1}{3} h \) de modo que:
\[ 2M_0=M_0 e^{k \frac13} \to \frac{2M_0}{M_0} =e^{\frac{1k}{3}} \to e^{\frac{k}{3}} =2 \to \]
\[ \to ln \left(e^{\frac{k}{3}} \right)=ln(2) \to \frac{k}{3} ln(e)=ln(2) \to k=3.ln(2)\cong 2,079 \]
Como en el instante inicial, de acuerdo con el enunciado, solo había una bacteria presente, podemos entonces escribir:
\[ M(t)=10 ^{-12} gr.e^{2,079t} \]
Entonces, transcurridas 48 horas, la masa de la descendencia ascenderá a:
\[ M(48)=10^{-12} gr.e^{2,079 \times 48}=2,18.10^{31} gr \]
¡valor que resulta ser muy superior al peso de la Tierra!
El resultado del problema anterior resulta inquietante. Sin embargo, las poblaciones microbianas raramente mantienen el crecimiento exponencial durante largos períodos de tiempo, razón por la cual la situación que propone el ejemplo no se condice con una situación del mundo real.
Edwards, H.; Penney, D.; Calvis, C. (2009), Ecuaciones diferenciales y problemas con valores en la frontera, Cómputo y Modelado, Pearson Educación, México, pp. 37 a 42.
Un modelo matemático más comúnmente empleado para describir el crecimiento de una población se basa en lo que se conoce como ecuación logística, que habrá de aplicarse en el siguiente ejemplo.
Cuando una enfermedad contagiosa se disemina en una población de tamaño n, la velocidad con la que se propaga no solo es proporcional a la cantidad de personas que después de transcurrido un tiempo t la han contraído (valor que indicamos como N(t)) sino también a la cantidad de personas que aún no se han contagiado, que indicamos como M(t)
Es decir:
[9.5] \[ \frac{dN(t)}{dt}=kN(t)M(t) \]
Supongamos que en t=0 una persona que ya contrajo la enfermedad se pone en contacto con una población sana de tamaño constante n. Podemos escribir entonces:
[9.6] \[ N(t)+M(t)=n+1 \to M(t)=n+1-N(t) \]
Sustituyendo [9.6] en [9.5] se obtiene la siguiente ecuación diferencial:
[9.7] \[ \frac{dN(t)}{dt}=kN(t)(n+1-N(t)) \]
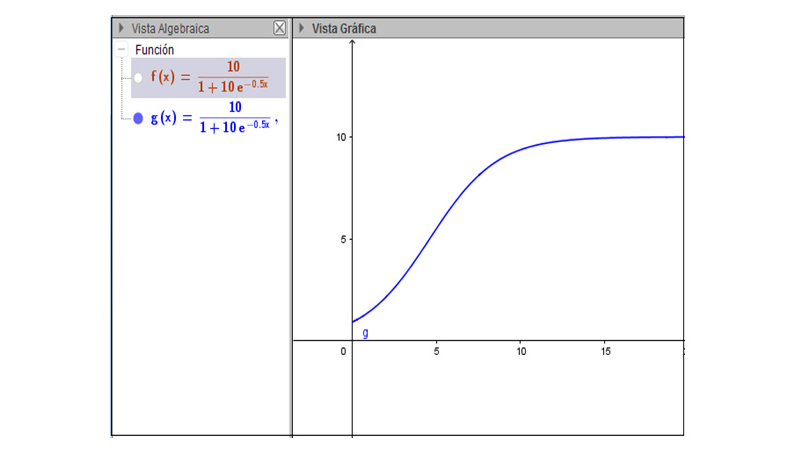
La representación gráfica aproximada de N(t) es la que puede observarse en la imagen 9.4.
Edwards, H.; Penney, D.; Calvis, C. (2009), Ecuaciones diferenciales y problemas con valores en la frontera, Cómputo y Modelado, Pearson Educación, México, pp. 46 y 47.
Resolver la ecuación diferencial [9.7] dejándola expresada en función del tamaño original de la población, n. Tener en cuenta que, para t=0, N(0)=1
Los coeficientes de la función logística que se observa en la imagen 9.4 fueron adoptados para que sus características quedasen claramente expuestas. Nótese que inicialmente crece rápidamente, hasta alcanzar un punto de inflexión, a partir del cual el crecimiento se va frenando hasta adquirir un comportamiento asintótico.
Aun cuando el dominio de la función resulta ser todo el campo real, para que represente mejor el fenómeno bajo estudio, la hemos representado gráficamente solo para los valores positivos de la variable independiente.
Representación gráfica aproximada de la función logística.
9.3.2. Ley de enfriamiento de Newton
En la sección 6.2.2 del presente MDM dijimos que la ley de enfriamiento de Newton expresa que un cuerpo que se encuentra a una temperatura superior a la del ambiente que lo rodea habrá de enfriarse según la siguiente expresión matemática:
[9.8] \[ T(t)-T_{ambiente} = C.e^{kt} \]
Sin embargo, vale aclarar que la [9.8] en realidad se obtiene a partir de un hecho experimental que podría resultarnos curiosamente familiar: la tasa de disminución de la temperatura de un cuerpo en función del tiempo es directamente proporcional a la diferencia entre la temperatura del cuerpo en cada instante y la temperatura del ambiente. Es decir:
[9.9] \[ \frac{dT}{dt}=k(T-T_{ambiente} ) \]
Invitamos al estudiante a que compare la [9.10] con la [9.3]. Dejando de lado el hecho de que en la primera se le reste una constante a la variable dependiente (nos referimos a la temperatura ambiente), es evidente que dos fenómenos totalmente distintos pueden modelizarse matemáticamente a partir de dos expresiones muy similares.
Partimos de la [9.10] con el objeto de obtener la expresión que nos brinde el valor de la temperatura del cuerpo en función del tiempo.
\[ \frac{dT}{dt}=k(T-T_{ambiente} ) \to \frac{dT}{(T-T_{ambiente})} )=k.dt \to \]
\[ \to \displaystyle\int \frac{dT}{(T-T_{ambiente} )} = \displaystyle\int k.dt \to ln (T-T_{ambiente} )=k.t+C \to \]
\[ \to (T-T_{ambiente} )=e^{k.t+C} \to (T-T_{ambiente} )=e^C e^{k.t} \to \]
[9.11] \[ \to (T-T_{ambiente} )=C^* e^{k.t} \]
Lo que en la [9.11] expresamos como C* no es otra cosa que el \( e^C \) que apareció en el paso previo, despues de aplicar propiedades de la potenciación.
Recordemos que la solución de una integral indefinida no era única, sino que se obtenían infinitas curvas que diferían entre sí en una constante de integración, representada en nuestro caso por C*. Diremos entonces que la [9.11] es la solución general de la ecuación diferencial (a la que, generalmente, se indica como S.G.).
Ahora bien: dentro de esa familia de infinitas curvas existe una sola que se corresponde con el caso particular que nos interesa y que habrá de obtenerse a partir de un punto conocido de esta. Como, en general, el dato corresponde al valor nulo de la variable independiente, se dice que dicho punto representa las condiciones iniciales del problema.
En nuestro caso, digamos que la temperatura inicial del cuerpo era \( T_0 \) Reemplazamos entonces en la [9.11] a t por cero y a T por \( T_0 \) y despejamos entonces el valor de C*.
[9.12] \[ (T_0-T_{ambiente} )=C^* e^0 \to C^*=(T_0-T_{ambiente} ) \]
Sustituyendo finalmente [9.12] en la [9.11], obtenemos:
\[ (T-T_{ambiente} )=(T_0-T_{ambiente} ) e^{k.t} \to \]
[9.13] \[ \to T(t)=T_{ambiente}+(T_0-T_{ambiente} ) e^{k.t} \]
Conocidos entonces \( T_{ambiente}, T_0 \ \text{y} \ k \) la [9.13] se convertirá, entonces, en la solución particular de nuestro problema (que suele expresarse como S.P.).
9.3.3. Decaimiento radioactivo
El fenómeno del decaimiento radioactivo se comentó en la sección 6.2.2, al utilizar como ejemplo la desintegración del carbono 14.
El modelo matemático del que se partía tenía la forma:
[9.14] \[ N(t)=N_0 e^{-kt} \]En dicha expresión, \( N_0 \) representaba la masa inicial, N(t) masa del isótopo presente al cabo de un tiempo t y k era una constante positiva, que habíamos obtenido y cuyo valor era -0,00012.
Lo que queremos dejar en claro en este momento es que, para llegar a la [9.14], se partía del hecho de que la velocidad de desintegración resulta ser directamente proporcional a la masa de la sustancia radioactiva presente en un instante dado, lo que matemáticamente se expresa como:
[9.15] \[ \frac{dN}{dt}=kN \]
¡Matemáticamente, la [9.15] no presenta diferencia alguna respecto de la [9.3], a pesar de que cada una de ellas represente a un fenómeno físico de naturaleza totalmente distinta!
Haciendo las consideraciones del caso y teniendo en cuenta que k=-0,00012, partir de la [9.15]y operar convenientemente para obtener la [9.14].
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 413 a 417.
9.3.4. Velocidad límite
Un fenómeno interesante vinculado con el tema de dinámica de fluidos es el de la fuerza resistente que se manifiesta en todo cuerpo que se desplaza dentro de un fluido de densidad \( \delta_F \) y viscosidad \( \eta_F \). Estudiemos, entonces, el siguiente ejemplo:
Una burbuja de gas \( \left(\delta_{gas}=0,0014 g⁄ cm ^3 \right) \) comienza a ascender desde el fondo de un vaso de gaseosa \( \left(\delta_{gaseosa}=1 g⁄ cm^3 \right)\) Si el radio de la burbuja es de 0,05 cm y la viscosidad del agua vale 0,0103 g⁄(cm.seg), escribir y resolver la ecuación diferencial que permite obtener la velocidad de la burbuja en función del tiempo y graficarla. Interpretar qué es lo que representa la asíntota horizontal de dicha función.
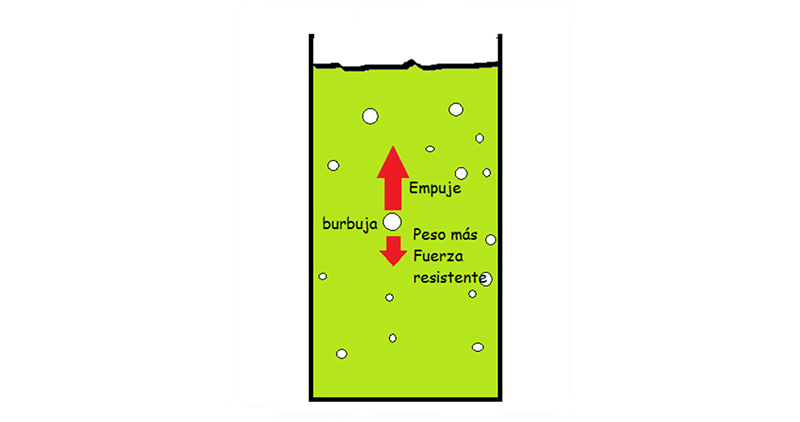
En la imagen 9.5 representamos esquemáticamente la situación. La experiencia cotidiana confirma el hecho de que las burbujas de gas, de muy baja densidad, ascienden en el seno de un líquido (en nuestro caso, dentro del vaso de gaseosa). Sin embargo, solo cuando estudiamos detenidamente el fenómeno en Física comprendemos el motivo: todo cuerpo sumergido en un fluido sufre una fuerza ascendente, denominada empuje.
El siguiente dibujo intenta representar la situación: el vaso contiene una determinada gaseosa y vemos cómo van subiendo las burbujas en el seno del líquido. Más allá de una serie de factores fortuitos que definen de algún modo en qué momento cada burbuja comienza a moverse, la experiencia habitual nos indica que no todas las burbujas lo hacen con la misma aceleración. En teoría, ninguna de ellas debería alcanzar la velocidad límite.
Dicha fuerza se calcula como el producto entre el peso específico del fluido y el volumen del cuerpo. En nuestro caso:
[9.16] \[ E=\rho_L \frac43 \pi r^3 \]
La letra E representa al empuje, \( \rho_L \) es el peso específico del fluido (en nuestro caso, la gaseosa), y \( \frac43 \pi r^3 \) corresponde al volumen de una esfera de radio r , es decir, la burbuja.
Como en el caso de cualquier otro cuerpo, debemos tener en cuenta al peso de la burbuja, que habremos de expresar como:
[9.17] \[ P= \rho_G \frac43 \pi r^3 \]
La [9.17] se dedujo a partir de la definición de peso específico, que el alumno ha estudiado en Química; en ella \( \rho_G \) representa el peso específico del gas contenido en la burbuja.
Al analizar en detalle el fenómeno, debemos tener en cuenta que hay una tercera fuerza, que habrá de oponerse al movimiento y que es proporcional a la velocidad de la burbuja en cada instante. De acuerdo con la ley de Stokes, para un cuerpo esférico, dicha fuerza habrá de calcularse como:
[9.18] \[ F_R=6 \pi \eta_L rv \]
Nuevamente expresamos con r al radio de la esfera, v es su velocidad en el instante considerado, y \( \eta_L \) representa la viscosidad del fluido.
La segunda ley de Newton de la Dinámica nos dice que la resultante de las fuerzas actuantes sobre un cuerpo es igual al producto de su masa por su aceleración (es decir, la derivada de su velocidad respecto del tiempo), de modo que en muestro caso podemos escribir:
[9.19] \[ E-P-F_R=m \frac{dv}{dt} \]
Resnik, R.; Hallyday, D. (1981), Física Parte I, Compañía Editorial Continental, México, pp. 85 a 92.
Finalmente y a partir de la definición de densidad, la masa de la burbuja podrá expresarse como:
[9.20] \[ m=\frac43 \pi r^3 \frac{\rho_G}{g} \]
Recordando que g representa la aceleración de la gravedad, reemplazamos [9.16],[9.17], [9.18] y [9.20] en [9.20], obteniendo así:
[9.21] \[ \rho_L \frac43 \pi r^3- \rho_G \frac43 \pi r^3-6 \pi \eta_L rv= \frac43 \pi r^3 \frac{\rho_G}{g} \frac{dv}{dt} \]
Dividiendo ambos miembros de la [9.21] por \( \frac43 \pi r^3 \frac {\rho_G}{g} \) y operando convnientemente, obtenemos la ecuación:
[9.22] \[ g \left( \frac {\rho_L-\rho_G} {\rho_G} \right) -\frac92 \frac{\eta_L g}{\rho_G r^2} v= \frac{dv}{dt} \]
Para que la resolución de la ecuación diferencial sea más sencilla, definimos:
[9.23] \[ A=g\left( \frac {\rho_L-\rho_G} {\rho_G} \right) \]
y
[9.24] \[ B=\frac92 \frac{\eta_L g}{\rho_G r^2} \]
Si reemplazamos [9.23] y [9.24] en [9.22] , obtenemos:
\[ A-Bv= \frac{dv}{dt} \to \frac{dv}{(v-\frac{A}{B})} =-Bdt \to \]
\[ \to \displaystyle\int \frac{dv}{(v-\frac{A}{B})} =-B \displaystyle\int dt \to ln \left(v-\frac{A}{B}\right) =-Bt+K \to \]
[9.25] \[ \to v(t)=\frac{A}{B}+Ke^{-Bt} \]
La [9.25] es la solución general de la ecuación diferncial en variables separables. Suponiendo que la velocidad inicial de la burbuja es cero, despejamos la constante de integración k y podemos escribir:
[9.26] \[ v(t)=\frac{A}{B}(1-e^{-Bt}) \]
Para que la expresión recobre su sentido físico, sustituimos en la [9.26] los valores de A y B por las expresiones [9.23] y [9.24] , obteniendo:
[9.27] \[ v(t)=\frac29 \frac{r^2}{\eta_L} (\rho_L-\rho_G ) \left(1-e^{-\frac92 \frac{\eta_L g}{\rho_G r^2} t} \right) \]
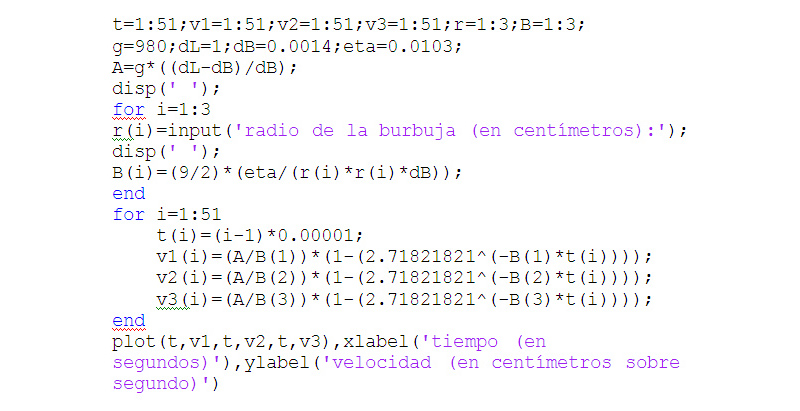
Antes de continuar con las consignas del problema, nos detenemos en el siguiente detalle: ¿el alumno ha observado que no todas las burbujas en un vaso de gaseosa ascienden con la misma velocidad? Hemos avanzado lo suficiente en el tema como para tratar de encontrar la causa de dicho fenómeno. En la imagen 9.6 el alumno puede observar un programa de computadora que nos permite responder aquella pregunta.
Invitamos al estudiante a detenerse en el programa para observar que algunas instrucciones prácticamente repiten algunas de las operaciones matemáticas que llevamos a cabo oportunamente.
Es muy importante que el alumno advierta las inesperadas posibilidades que brinda el empleo de computadoras personales.
La [9.27] nos lleva a pensar que, en un vaso de gaseosa, lo único que realmente diferencia entre sí a las burbujas es su radio. Por ese motivo, el programa que desarrollamos nos permite comparar las curvas de velocidad de la burbuja en función del tiempo para tres burbujas de distintos radios. Hemos corrido el programa y la imagen 9.7 reproduce las curvas obtenidas para 0,01, 0,03 y 0,05 centímetros de radio, respectivamente. Todas las curvas comienzan creciendo rápidamente, para luego hacerse asintóticas a un valor que, como veremos, corresponde a la velocidad límite de la burbuja.
Si calculamos:
[9.28] \[ \displaystyle\lim_{t \to \infty} v(t)= \displaystyle\lim_{t \to \infty} \frac29 \frac{r^2}{\eta_L} (\rho_L-\rho_G )\left(1-e^{-\frac92 \frac{\eta_L g}{\rho_G r^2} t} \right) =\frac29 \frac{r^2}{\eta_L} (\rho_L-\rho_G )\]
Cuando la resultante de las fuerzas que actúan sobre la burbuja se anula (por el aumento de la velocidad y, por ende, de la fuerza resistente), la burbuja no se detiene sino que sigue subiendo con velocidad constante. Dicha velocidad es la que denominamos velocidad límite.
Programa de computadora que nos permite comparar las curvas de velocidad en función del tiempo para burbujas de distinto radio.
9.7. Gráficas obtenidas utilizando el programa de computadora presentado en la imagen 9.6.
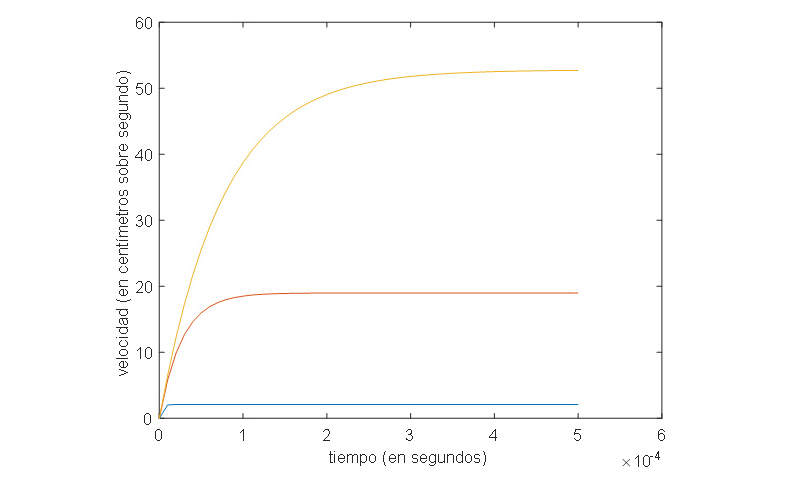
Es evidente que dicha velocidad no es otra cosa que el valor de la ordenada de la asíntota horizontal de cada una de las distintas curvas obtenidas. El hecho de que para obtener dicho valor hayamos calculado el límite tendiendo a infinito, debe interpretarse dentro del marco correspondiente al modelo matemático: no debemos pensar que la velocidad límite habrá de alcanzarse en un tiempo infinitamente grande, sino que una vez transcurrido un tiempo "lo suficientemente largo" (expresión aparentemente ambigua que debe interpretarse dentro del contexto propio del fenómeno bajo estudio), la burbuja deja de acelerar y sigue moviéndose a dicha velocidad.
El estudiante habrá comprobado que la descripción de un fenómeno aparentemente trivial puede obligarnos a profundizar en una serie de conceptos teóricos y manejar adecuadamente buena parte de lo visto hasta el momento en nuestra MDM.
¡Y hasta aquí solo hemos trabajado con ecuaciones diferenciales en variables separables!
Finalizaremos el presente MDM avanzando apenas un poco más en el campo de las ecuaciones diferenciales. Para ello, retomaremos uno de los ejemplos vistos en la unidad 6: el estudio de la vibración de un resorte ideal.
9.4. Otros tipos de ecuaciones diferenciales
En la presente unidad nos hemos limitado a resolver problemas que pueden resolverse aplicando el método de resolución por variables separables. Sin embargo, anticipamos que, según las características de la ecuación que hayamos de resolver, nos veremos en la necesidad de aplicar diversos tipos de sustituciones. Por ejemplo, las ecuaciones diferenciales lineales.
Las ecuaciones diferenciales de la forma
\[ \frac{dy}{dx}+y.P(x)=Q(x) \]
reciben el nombre de ecuaciones diferenciales lineales de primer orden. P(x) y Q(x) representan a dos funciones conocidas y el objetivo es el de hallar y=f(x) . Para resolverlas en forma expeditiva, recomendamos aplicar la sustitución y=u(x).v(x))
u(x) y v(x) son dos funciones auxiliares que dependen exclusivamente de la variable independiente que habremos de despejar para obtener la solución general de la ecuación.
Edwards, H.; Penney, D.; Calvis, C. (2009), Ecuaciones diferenciales y problemas con valores en la frontera, Cómputo y Modelado, Pearson Educación, México, pp. 48 a 55.
De acuerdo con las leyes de Kirchhoff, la ecuación diferencial correspondiente a un circuito en serie RL (es decir, conformado por una resistencia de valor R y una bobina de autoinductancia conectadas a una fuente de corriente alterna) tiene la forma:
\[ L \frac{di}{dt}+Ri(t)=E(t) \]
Tanto la corriente eléctrica i como la tensión de la fuente E son en este caso función de la variable independiente, el tiempo t . La solución de la ecuación diferencial nos brinda la función que describe a la corriente que circula por el circuito en función del tiempo, es decir, , i=f(t).
Leyes de Kirchhoff
<https://circuitoelectricosite.wordpress.com/ley-de-kirchoff/>
Circuitos RL:
<https://www.sc.ehu.es/sbweb/fisica/elecmagnet/induccion/autoinduccion/autoinduccion.htm>
En general, denominamos ecuaciones diferenciales de primer orden a aquellas en las que aparece solamente la derivada primera de la función incógnita. Además de las del tipo variables separables o las lineales, entran dentro de esta categoría las ecuaciones de tipo Bernoulli, las homogéneas, las de tipo Riccati o las de tipo Clairaut. Pero no nos detendremos en ellas y terminaremos la presente unidad introduciéndonos en el estudio de las ecuaciones diferenciales lineales a coeficientes constantes de segundo orden.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 437 y 438.
Denominamos ecuaciones diferenciales homogéneas a coeficientes constantes de segundo orden a las que tienen la forma:
[9.29] \[ a_2 y^{''}+a_1 y^{'}+a_0 y=0 \ con \ a_2 \ne 0 \]
Para resolver este tipo de ecuación se aplica la sustitución
[9.30] \[ y=e^{rx} \]
con r constante. Si calculamos las dos primeras derivadas de la [9.30] obtendremos:
[9.31] \[ y{'}=re^{rx} \]
e
[9.32] \[ y{''}=r^2 e^{rx} \]
Sustituimos [9.30],[9.31] y [9.32] en la [9.29] y escribimos:
\[ a_2 r^2 e^{rx}+a_1 re^{rx}+a_0 e^{rx}=0 \]
Sacamos factor común:
[9.33] \[ ( a_2 r^2+a_1 r+a_0)e^{rx}=0 \]
Puesto que la función exponencial nunca vale cero, la [9.33] solo se anulará cuando \( a_2 r^2+a_1 r+a_0=0. \) . Entonces, basta con resolver una ecuación de segundo grado para obtener los valores de r .
La solución de la [9.29] tendrá entonces la forma:
- \( y(t)=C_1 e^{r_1 x}+C_2 e^{r_2 x} \)cuando las dos raíces de la cuadrática \( r_1 \text{y} r_2 \) sean reales e iguales.
- \( y(t)=C_1 e^{rx}+C_2 xe^{rx} \) cuando \( r_1=r_2=r, \) es decir, la cuadrática tenga una raíz real doble.
- \( y(t)=e^{αx} (C_1 cos(\beta t)+C_2 sin(\beta t)) \) cuando las soluciones de la cuadrática sean complejos conjugados, es decir, tengan la forma
\[ r_{1,2}=\alpha \pm \beta i \]
Resolver \( y'' - 4y' + 3y = 0 \)
Solución:
Si reemplazamos nuestra incógnita y sus dos primeras derivadas, obtenemos:
\[ r^2 e^{rx}-4re^{rx}+3e^{rx}=0 \to e^{rx} (r^2-4r+3)=0 \to \]
\[ \to (r^2-4r+3)=0 \]
Las raíces de la ecuación de segundo grado son \( r_1=1 \text{ y } r_2=3 \), de modo que la solución general de la ecuación diferencial tendrá la forma:
\[ y(t)=C_1 e^x+C_2 e^{3x} \]
Para hallar la solución particular de una ecuación diferencial homogénea de segundo orden necesitamos sus condiciones iniciales, que nos permitirán definir un sistema de dos ecuaciones con dos incógnitas, las constantes \( C_1 \) y \( C_2 \).
Dada \( y^{''}-4y^{'}+3y=0 \) hallar su solución particular para las condiciones iniciales \( y(0)=1 \ e \ y' (0)=-1 \)
Solución:
Acabamos de obtener la solución general de la ecuación, a saber:
[9.34] \[ y(t)=C_1 e^x+C_2 e^{3x} \]
Teniendo en cuenta que y(0)=1 podemos escribir:
[9.35] \[ y(0)=C_1+C_2=1 \]
Si derivamos la [9.34] y aplicamos la condición \( y^{'} (0)=-1: \)
\[ y^{'} (t)=C_1 e^x+3C_2 e^{3x} \to \]
[9.36] \[ \to y^{'} (0)=C_1+3C_2=-1 \]
El sistema de dos ecuaciones con dos incógnitas determinado por [9.35] y [9.36] tiene por soluciones a \( C_1=2 \text{ y } C_2=-1\) , de modo que la solución particular que pide el enunciado es:
\[ y(t)=2e^x-e^{3x} \]
Obtener la solución particular de cada una de las siguientes ecuaciones diferenciales para las condiciones iniciales indicadas en cada caso:
- \( y''+4y'-5y=0 \ con \ y(0)=y'(0)=0 \)
- \( y''-4y'+4y=0 \ con \ y(0)=-1 \ e \ y' (0)=2 \)
- \( y''+9y=0 \ con \ y(0)=0 \ e \ y' (0)=1 \)
En muchas aplicaciones, la ecuación diferencial está igualada a una función de la variable independiente. En esos casos, dejará de ser homogénea.
En la próxima sección veremos de qué modo poder resolver algunas de dichas ecuaciones.
9.4.1. Aplicación de ecuaciones diferenciales de segundo orden con coeficientes constantes a fenómenos de la realidad
En la sección 6.3.2 hablamos sobre el movimiento de un péndulo elástico ideal como el que se observa en la imagen 9.8 y dijimos que la ecuación que describía dicho movimiento podía tener la forma:
[9.37] \[ y=f(t)=a.sen(wt\pm\varphi)\pm b \]
o
[9.38] \[ y=f(t)=a.cos(wt\pm \varphi)\pm b \]
Analizaremos el comportamiento de un péndulo elástico, compuesto por un resorte del que cuelga un cuerpo de pequeñas dimensiones. El punto S representa el centro de masa del cuerpo.
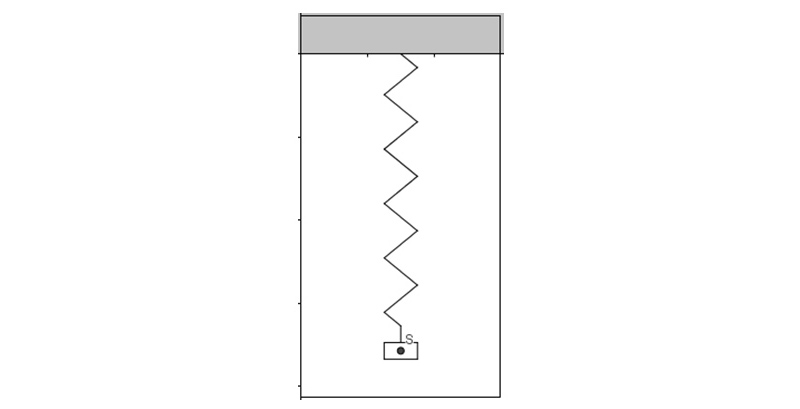
En la unidad 6 nos limitamos a describir el movimiento oscilatorio armónico, pero, avanzando un poco sobre lo visto en la presente unidad, podríamos demostrar porqué las [9.37] y [9.38] representan dicho movimiento.
Nuevamente, hemos de aplicar algunos conceptos estudiados en Física para lograr nuestro objetivo.
Para comenzar, observemos detenidamente la imagen 9.19. En (a) se muestra el resorte, inicialmente descargado, sobre el cual no actúan fuerzas exteriores. Si se cuelga de él con cuidado un peso de valor mg (donde m representa su masa y g la aceleración de la gravedad), la posición de equilibrio se alcanzará una vez que el resorte se haya estirado una longitud s , como se muestra en (b). Para dar comienzo a la oscilación, debemos alejar el peso una distancia x respecto de la posición de equilibrio alcanzada, como se observa en (c), para luego liberar el peso.
En (a) el resorte cuelga del punto de suspensión, siendo su longitud la conocida como longitud natural. Cuando se cuelga un cuerpo de su extremo, como se observa en (b), el resorte habrá deestirarse, hasta que la fuerzaelástica equilibre su peso (para evitar oscilaciones, se recomienda en este paso acompañar el descenso del cuerpo y no simplemente liberarlo). Finamente, en (c) el cuerpo es arrancado de su posición de equilibrio: se lo aleja una distancia x de esta, para luego liberárselo, dando así comienzo el movimiento que describimos como oscilatorio armónico.
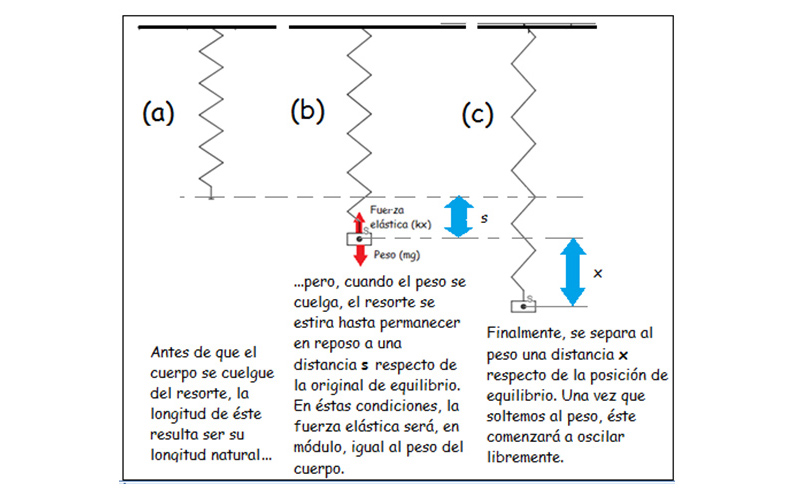
Recordando que la fuerza elástica se calculaba como el producto de la constante elástica del resorte k por la elongación de este, encontramos que en (b), donde la fuerza que hace el resorte equilibra al peso del cuerpo que se ha colgado, se cumplirá la condición:
[9.39] \[ mg-ks=0 \]
Aplicando la segunda ley de Newton en el momento de liberar al cuerpo después de alejarlo una distancia x de la posición de equilibrio, obtenemos la ecuación:
\[ m \frac{d^2 x}{dt^2}=-k(s+x)+mg \to \]
\[ \to m \frac{d^2 x}{dt^2}=-ks-kx+mg \to \]
[9.40] \[ \to m \frac{d^2 x}{dt^2}=-kx+(mg-ks) \]
Teniendo en cuenta la [9.39], la [9.40] podrá escribirse como:
\[ m \frac {d^2 x}{dt^2}=-kx \to m \frac{d^2 x}{dt^2}+kx=0 \to \]
[9.41] \[ \to \frac{d^2 x}{dt^2}+\frac{k}{m} x=0 \]
Finalmente, obtuvimos la ecuación diferencial que describe el movimiento del resorte.
Si, como vimos en la sección 9.3, aplicamos la sustitución
[9.42] \[ x=e^{rt} \]
bastará entonces con calcular sus dos primeras derivadas:
[9.43] \[ x'=\frac{dx}{dt} =re^{rt} \]
y
[9.44] \[ x''= \frac{d^2 x}{dt^2}=r^2 e^{rt} \]
Sustituimos [9.42] y [9.44] en [9.41]:
\[ r^2 e^{rt}+\frac{k}{m} e^{rt}=0 \to e^{rt} \left(r^2+ \frac{k}{m} \right)=0 \to \]
[9.45] \[ \to r^2+\frac{k}{m}=0 \]
Las raíces de la [9.45] se encuentran fuera del campo real (no hay número real que elevado al cuadrado dé resultado positivo) y tendrán la forma
\[ \alpha \pm \beta i= \pm \sqrt{\frac{k}{m}} \ i \]
Entonces, de acuerdo con lo visto en la sección 9.3, podemos escribir:
[9.46] \[ x(t)=C_1 cos \left( \sqrt{\frac{k}{m}} \times t\right) +C_2 sin \left( \sqrt{\frac{k}{m}} \times t \right) \]
Llamando A al valor de la máxima elongación (que, como vimos en la unidad 6 recibía el nombre de amplitud de la oscilación) y teniendo en cuenta que en el momento de liberar al cuerpo, este habrá de partir del reposo, podemos escribir:
\[ x(0)=A \ \ \ y \ \ \ x'(0)=0 \]
Entonces:
[9.47] \[ x(0)=C_1 \ cos(0)+C_2 \ sin(0)=A \to C_1=A \]
Además:
\[ x' (t)=- \sqrt{\frac{k}{m}} C_1 sin \left(\sqrt{\frac{k}{m}} t \right) +\sqrt{\frac{k}{m}} C_2 cos \left(\sqrt{\frac{k}{m}} t \right) \to \]
\[ \to x' (0)=-\sqrt{\frac{k}{m}} C_1 sin(0)+\sqrt{\frac{k}{m}} C_2 cos(0)=0 \to \]
[9.48] \[ \to \sqrt{\frac{k}{m}} C_2 =0 \to C_2 =0 \]
Finalmente, sustituyendo [9.47] y [9.48] en la [9.46], obtenemos la ecuación del movimiento del cuerpo colgado del resorte:
[9.49] \[ x(t)=Acos \left(\sqrt{\frac{k}{m}}t \right) \]
La [9.49] resulta equivalente a la [9.38], teniendo en cuenta que \( A=a,w= \sqrt{\frac{k}{m}}\) y \( \varphi=b=0\)
Edwards, H.; Penney, D.; Calvis, C. (2009), Ecuaciones diferenciales y problemas con valores en la frontera, Cómputo y Modelado, Pearson Educación, México, pp. 147 a 195.
9.4.2. Empleo del software para resolución de ecuaciones diferenciales ordinarias
En esta última sección le ofreceremos al alumno una herramienta que esperamos le sea útil para el estudio del presente tema. El wxMaxima nos permite también resolver ecuaciones diferenciales, de modo que se pueden verificar los resultados obtenidos manualmente empleando dicho software.
Veamos cómo aplicar entonces el software para resolver un ejemplo similar a los planteados en la presente unidad.
Un cultivo contiene inicialmente \( N_0 \) bacterias, y se introduce la cápsula de Petri que lo contiene dentro de un autoclave a 37℃. Al cabo de dos horas se determina que el número de bacterias presentes se ha triplicado.
Teniendo en cuenta que la velocidad de crecimiento es directamente proporcional a la cantidad de bacterias presentes en un instante determinado, obtener la expresión que permita calcular el número de bacterias presentes en función del tiempo.
De acuerdo con el enunciado, la ecuación diferencial correspondiente al proceso es la siguiente:
[9.50] \[ \frac{dN}{dt}=kN \]
Nos propusimos resolver dicha ecuación empleando el wxMaxima, de modo que lo primero que hacemos es buscar en el menú que el programa ofrece en la parte superior de la pantalla la opción “Ecuaciones” (imagen 9.10).
El primer paso consiste en seleccionar “Ecuaciones”en la barra de menú de la parte superior de la pantalla.
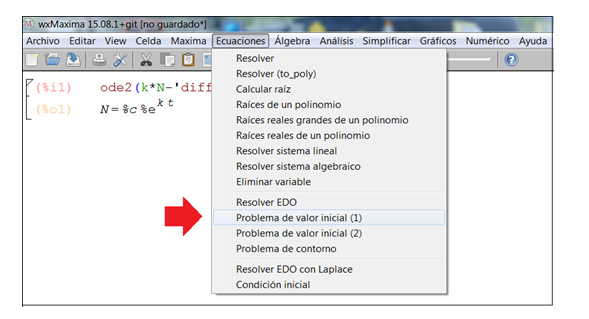
Se abre una ventana que nos brinda un gran número de posibilidades. Debemos seleccionar “Resolver ODE” (que traducido del inglés significa Ecuaciones Diferenciales Ordinarias), opción que señalamos en la imagen 9.11 con una flecha de color rojo.
Una vez que se despliega la ventana, debemos seleccionar “ ” (es decir, ecuación diferencial ordinaria).
” (es decir, ecuación diferencial ordinaria).
La ventana que se abre a continuación nos permite introducir la ecuación diferencial, seleccionando además cuáles son la variable dependiente (en nuestro caso N , cantidad de bacterias presentes) y la variable independiente (el tiempo t ). En la imagen 9.12 se observa de qué modo habrá que ingresar dicha información. A partir de la [9.50] podemos escribir:
[9.51] \[ kN- \frac{dN}{dt}=0 \]
Para ingresar la derivada debemos escribir:
\[ ´diff(N,t) \]
Dentro del paréntesis debe escribirse en primer lugar la variable dependiente, seguida por la independiente.
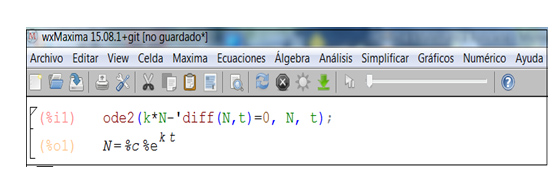
Una vez que se hace clic sobre “Aceptar”, aparecerá en pantalla el resultado de la ecuación, como se observa en la imagen 9.13. Se trata de la solución general de la ecuación, puesto que %c representa a la constante de integración que debemos calcular para escribir la solución particular.
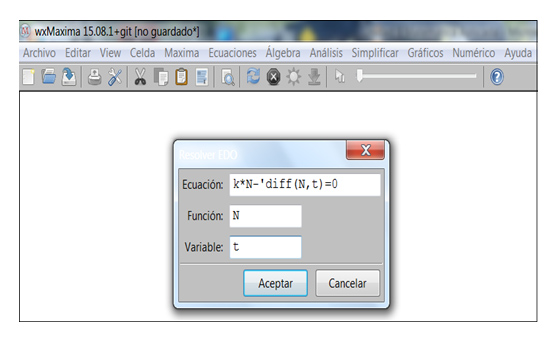
Para despejarla, volvemos al menú original y seleccionamos “Problema de valor inicial (1)”, como se indica en la imagen 9.14.
Se abre una ventana en la que debemos ingresar la ecuación diferencial, la variable dependiente (es decir, la que se corresponde con la función que debemos obtener) y la variable independiente.
La solución general de la ecuación diferencial podría también obtenerse si, en lugar de utilizar el Menú, escribimos la instrucción “ode2”, tal como se observa en la captura de pantalla.
Para ingresar las condiciones iniciales que nos permitan llegar a la solución particular, debemos seleccionar “Problema de valor inicial (1)”.
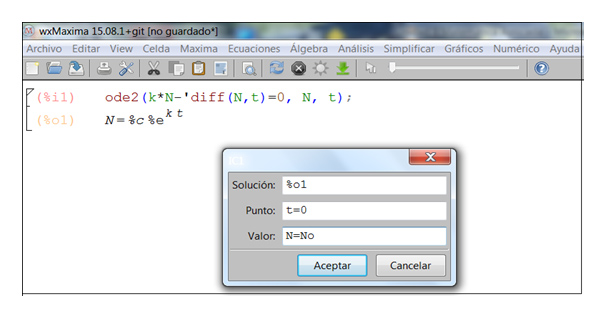
En la ventana que se abre a continuación (imagen 9.15) debemos introducir la solución general de la ecuación diferencial y los valores de las variables para las condiciones iniciales. No es necesario escribir la solución, pues basta con indicar %o1, que es el nombre con el que el propio programa reconoce a la solución ofrecida.
El programa nos pide la solución general obtenida (bastará para ello que escribamos las letras y números que aparecen a la izquierda de la expresión). Donde dice “Punto” debemos introducir la variable independiente, en tanto que la variable dependiente debe introducirse donde dice “Valor”.
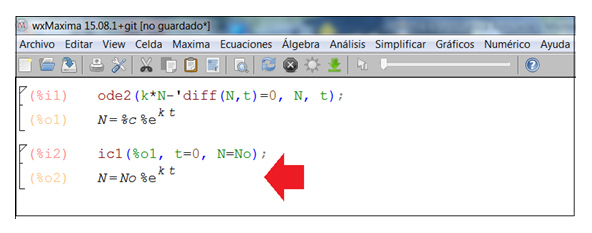
Haciendo clic en acepta, el programa nos ofrece la solución particular de la ecuación diferencial (imagen 9.16).
La flecha de color rojo señala la solución particular de la ecuación.
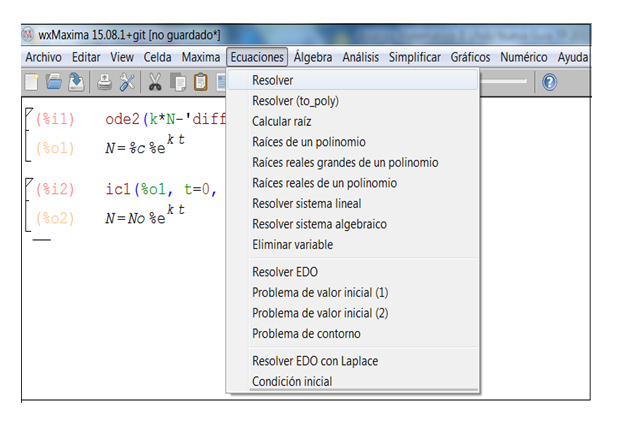
Nos resta despejar el valor de la constante k , para lo cual tendremos en cuenta que, de acuerdo con el enunciado, el número de bacterias se ha triplicado a las dos horas. Para obtener dicha constante regresamos al menú y seleccionamos “Resolver”, que, como puede observarse en la imagen 9.17, es la primera de las opciones que se nos ofrece.
Como en el presente problema también necesitamos calcular la constante presente en la expresión original, volvemos al menú y seleccionamos “Resolver”.
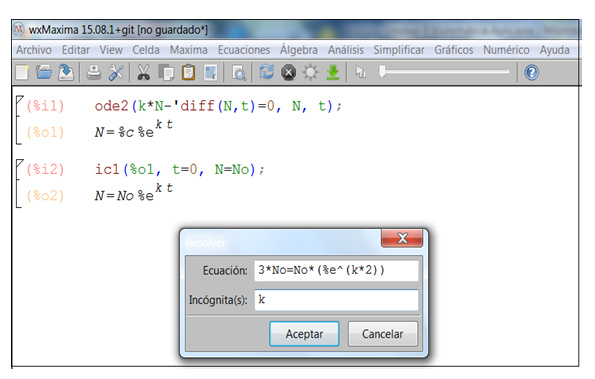
Dentro de la ventana ingresamos la ecuación exponencial. Para ello, reemplazamos N por 3*No (la población se ha triplicado), y t por 2 (pues el dato se obtuvo dos horas después de que la cápsula de Petri fuera introducida en el autoclave), como puede observarse en la imagen 9.18.
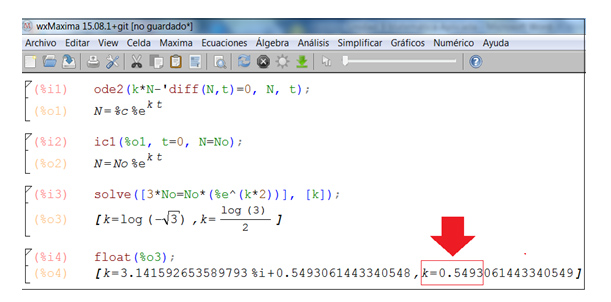
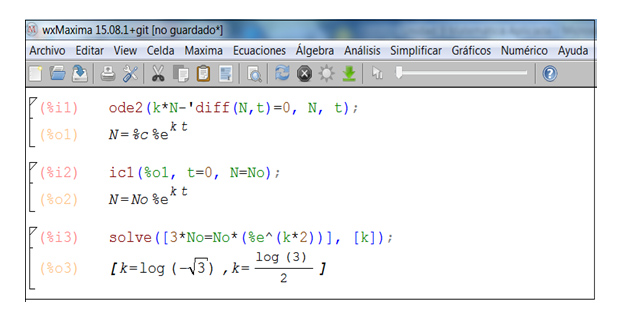
Al hacer clic en “Aceptar” el programa aplica automáticamente la instrucción solve y nos devuelve el resultado exacto de la variable k, tal como puede verse en la imagen 9.19.
En la ventana que se abre ingresamos la ecuación y la incógnita.
El programa nos brinda dos soluciones, de modo que debemos aplicar nuestro criterio para seleccionar la adecuada. En este caso, es evidente que es el segundo valor el que hemos de considerar.
Puesto que a los fines prácticos necesitamos un valor aproximado, utilizamos la instrucción float. El valor de la constante que corresponde a nuestro problema es el que aparece en la imagen 9.20 señalado con una flecha roja. Evidentemente, bastará con tomar solo tres o cuatro decimales para utilizar la expresión matemática obtenida.
Necesitamos el valor aproximado de la constante, que obtenemos aplicando la instrucción float.