3. Vectores
Objetivos
Que el alumno:
- Comprenda que la matemática no solo maneja los números como tales, sino que requiere elementos que almacenan mayor cantidad de información, como los vectores.
- Aprenda a reconocer los elementos característicos de todo vector.
- Aprenda a representar vectores en el plano y en el espacio empleando el software adecuado.
- Aprenda las operaciones elementales de los vectores y descubra cómo se aplican en la resolución de situaciones problemáticas concretas.
- Descubra que nuevos elementos matemáticos, como el vector, permiten definir nuevas operaciones, como el producto escalar.
3.1. Concepto de vector y elementos característicos
Dados dos puntos A y B, contenidos en una recta (imagen 3.1), sabemos que puede definirse un segmento que los una (imagen 3.2).
Los infinitos puntos alineados con A y B determinan una recta en el espacio.
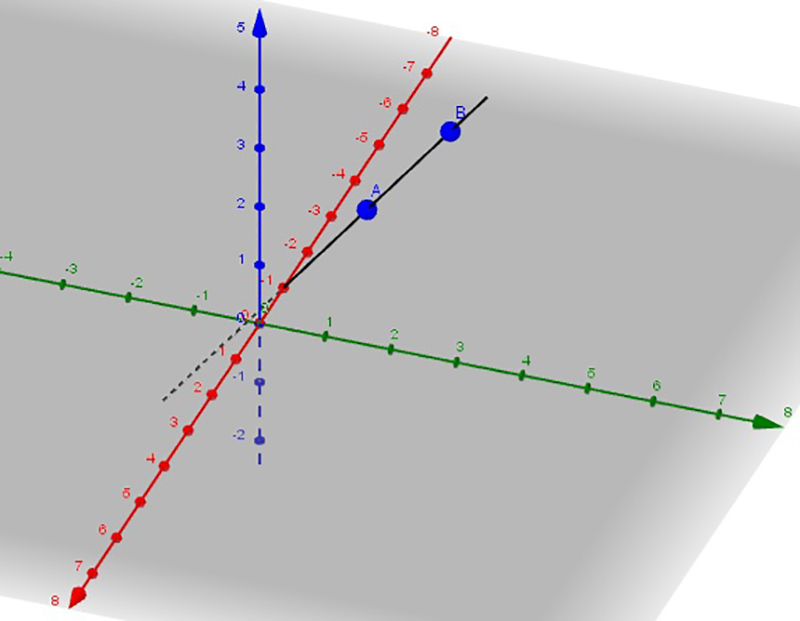
El segmento habrá de contener exclusivamente los puntos de la recta que se encuentran entre A y B.
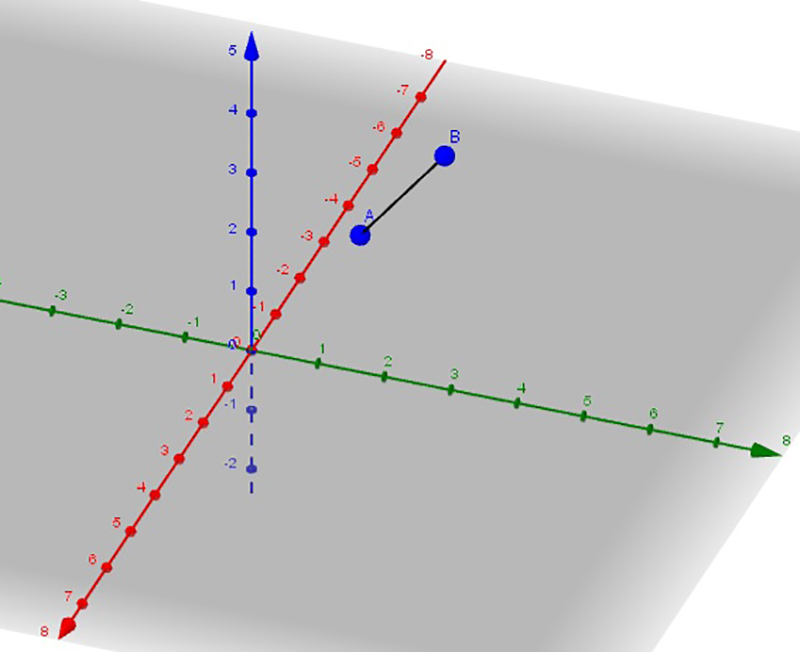
Diremos entonces que el segmento \( \overrightarrow{AB} \) posee una dirección, que queda definida a partir de la recta que une ambos puntos.
Sin embargo, algunas aplicaciones nos llevan a asignarle otra característica al segmento: el sentido. Este brinda un significado más específico a los puntos A y B. Por ejemplo, en lugar de hablar del lugar geométrico de los puntos de la recta entre A y B (es decir, del segmento en cuestión), podríamos especificar que se trata de los puntos de la recta que van desde A hacia B. Así, aquel punto recibiría el nombre de origen, en tanto que el segundo de los puntos representaría el extremo de dicho segmento orientado.
Podemos definir entonces como vector a cualquier segmento orientado.
La imagen 3.3 nos muestra el vector \( \overrightarrow{AB} \). Obsérvese la forma en que lo expresamos: en primer lugar, el punto origen; en segundo lugar, su extremo y, sobre ambas letras, una flecha.
El alumno podrá comprobar que no es esa la única forma en que los vectores aparecen expresados. Es muy común que se los indique simplemente mediante una letra minúscula en negrita. En la imagen 3.4, en la vista algebraica de la captura de pantalla, se observa que el vector \( \overrightarrow{AB} \) aparece simplemente como u.
La flecha indica el sentido que va desde el origen (punto A) hasta el extremo (punto B).
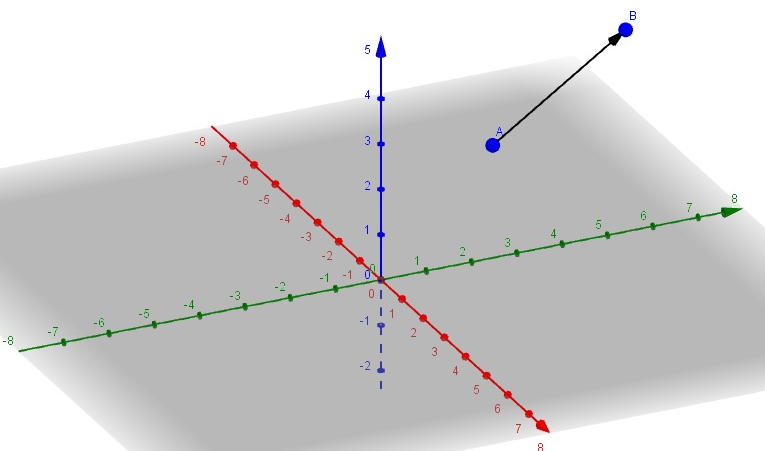
La flecha en la ventana correspondiente a la vista algebraica señala el nombre con que el propio software reconoce al vector.
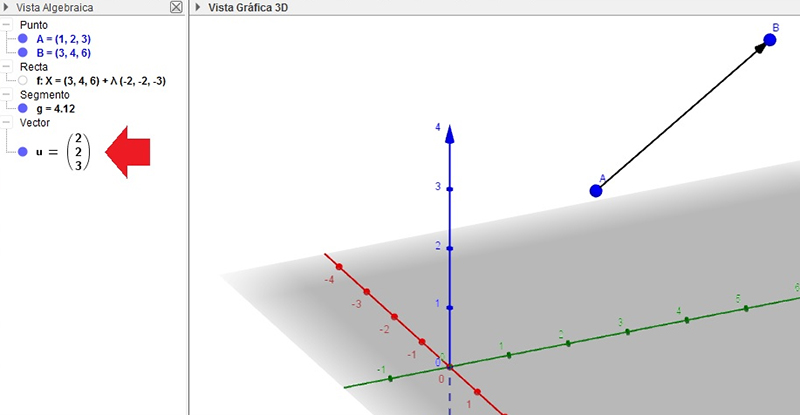
Volviendo a la imagen 3.4, vale aclarar que las coordenadas del vector se obtienen restando a las del punto extremo las del punto origen. Es decir,
\[ \overrightarrow{AB} = B - A = (3,4,6) - (1,2,3) = (3 - 1,4 - 2,6 - 3) = (2,2,3) \]
Los elementos que caracterizan, entonces, un vector son:
- Su dirección o recta de acción.
- Su sentido.
- Su punto de aplicación (que coincide con su origen).
- Su intensidad, módulo o norma.
La intensidad o módulo del vector no es otra cosa que su longitud. Para un vector genérico del plano cuyo origen fuera el punto \( A = (x_A , y_A) \) y su extremo el punto \( B = (x_B , y_B) \), la intensidad habrá de calcularse a partir de la aplicación del Teorema de Pitágoras, empleando la siguiente expresión:
\[ \left | \overrightarrow{AB} \right | = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} \]
En cambio, en el caso de que se tratara de un vector en el espacio, cuyo origen fuera \( A = (x_A , y_A, z_A) \) y su extremo \( B = (x_B , y_B, z_B) \), entonces:
\[ \left | \overrightarrow{AB} \right | = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2 + (z_B - z_A)^2} \]
3.2. Representación de vectores en el plano y el espacio empleando software
El software nos permite representar con exactitud los vectores y operar con ellos rápidamente. Proponemos seguidamente varias formas sencillas de hacerlo.
Vamos a representar en el plano al vector cuyo origen es el punto A = (2,1) y su extremo el punto B = (6,3).
Para comenzar, escribimos en la ventana de entrada las coordenadas del punto A. Tengamos en cuenta que el GeoGebra reconoce los puntos cuando los expresamos con una letra mayúscula (imagen 3.5).
La flecha roja señala la ventana de entrada donde se ingresa la información. Ya antes de oprimir la tecla “Enter”, el punto aparece representado en al plano.
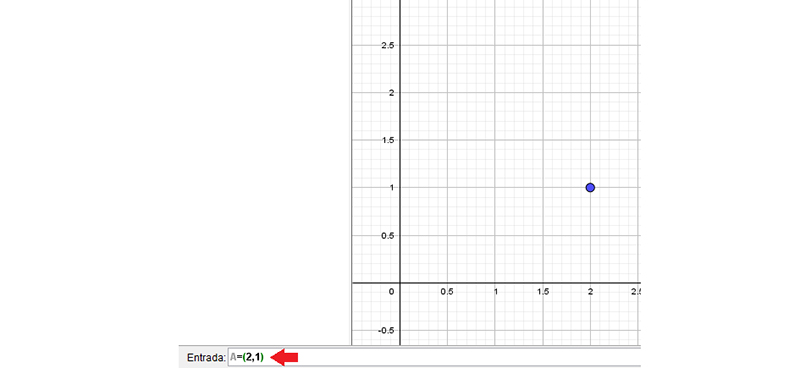
Después de ingresar las coordenadas del punto B, bastará con escribir “vec” en la ventana de entrada para que aparezca un menú, como se observa al pie de la imagen 3.6.
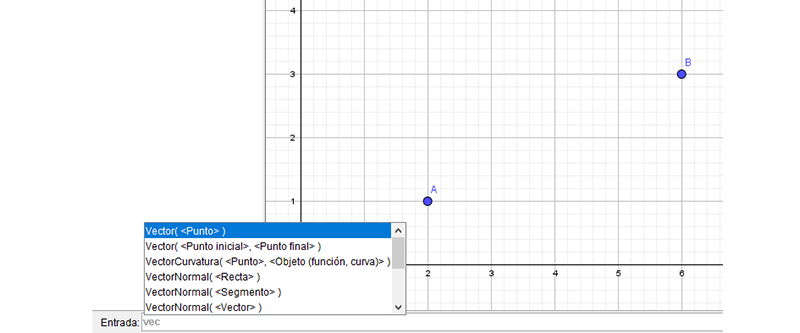
Debemos entonces seleccionar “Vector (Punto Inicial, Punto Final)”, reemplazando cada uno de ellos por los datos ingresados anteriormente, es decir, las letras con las que reconocemos el origen y el extremo de nuestro punto (imagen 3.7).
Aun antes de oprimir la tecla “Enter”, el vector aparece representado en la vista gráfica.
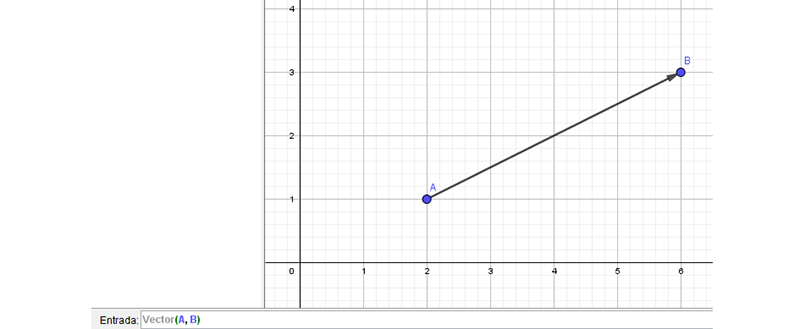
De este modo, hemos graficado el vector \( \overrightarrow{AB} \).
Veamos a continuación otra forma de poder representar un vector empleando nuestro software.
Vamos a representar ahora en el espacio al vector cuyo origen es el punto A = (1,1,2) y cuyo extremo es el punto B = (3,4,3). Nuevamente, ingresamos en la ventana que aparece en la parte inferior de la pantalla a ambos puntos. Pero seguidamente, buscamos en el menú que aparece en la parte superior, seleccionando el ícono que aparece en tercer lugar (contando desde la izquierda). Se abre así una ventana que nos ofrece un segundo menú, del que hemos de seleccionar, justamente, la opción “Vector” (imagen 3.8).
El menú que aparece en la parte superior de la pantalla nos permite abrir una ventana. De las seis opciones presentes, la quinta corresponde al elemento que queremos obtener, un vector.
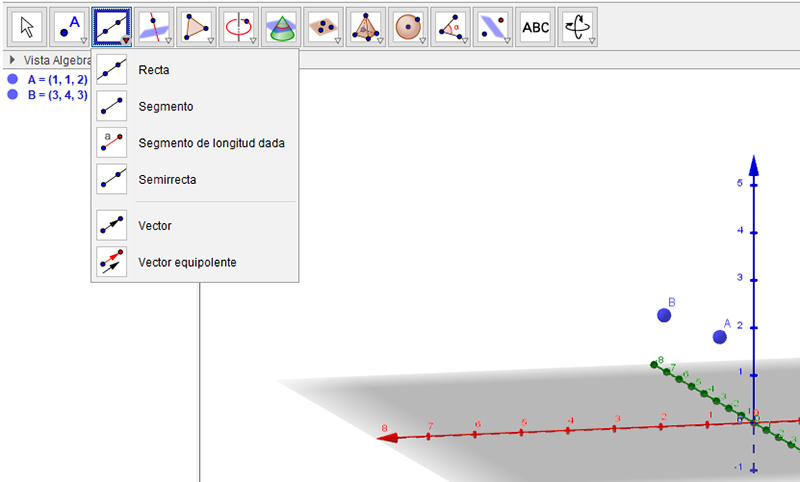
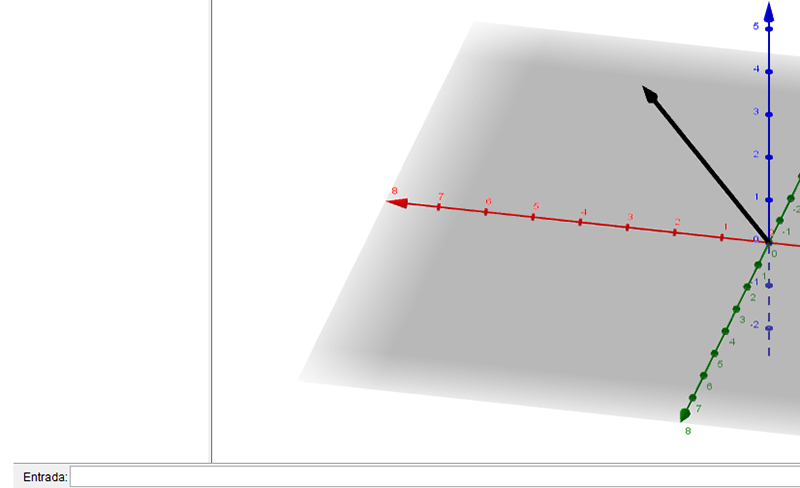
Con el cursor nos apoyamos primeramente en el punto A, para luego desplazarnos hasta el punto B. El vector aparecerá automáticamente en pantalla, como se observa en la imagen 3.9.
En la imagen hemos borrado a los puntos A y B para que se observe con claridad la flecha que indica el sentido del vector.
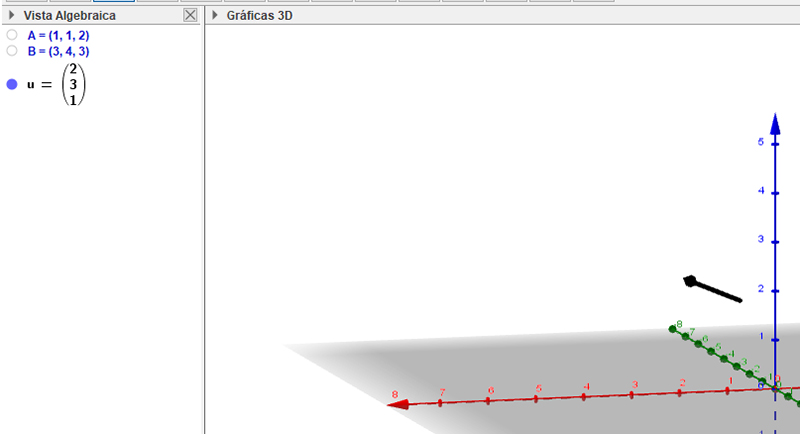
Representemos en el gráfico al vector libre u = (2, 3, 5). Llamaremos vectores libres a aquellos en los que no nos interese definir el punto de aplicación, que representaremos generalmente como vectores cuyo origen es el origen de coordenadas. Tal como puede observarse en la imagen 3.10, bastará en este caso con expresar el vector mediante una letra minúscula y aparecerá de inmediato en la pantalla.
En la parte inferior de la pantalla se encuentra la ventana de entrada. Es allí donde ingresamos al nombre del vector, seguido por sus coordenadas.
En los dos últimos ejemplos pudimos observar que tanto los puntos como los vectores pueden ingresarse empleando ternas ordenadas. Es por ello que debemos tener en cuenta que, para que el software los distinga, los primeros habrán de ingresarse mediante letras mayúsculas, mientras que los segundos directamente con una letra minúscula.
3.3. Operaciones con vectores
3.3.1. Suma y resta
La suma y la resta de vectores resultan ser dos operaciones prácticamente intuitivas, al menos cuando dichos vectores se definen en una sola dimensión, a la que representamos gráficamente como una recta. Para interpretar mejor lo que acabamos de decir, proponemos el siguiente ejemplo.
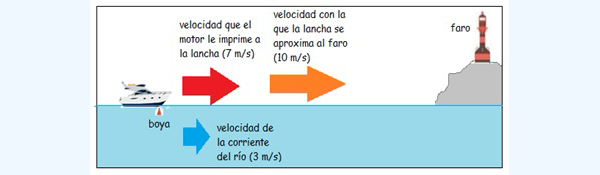
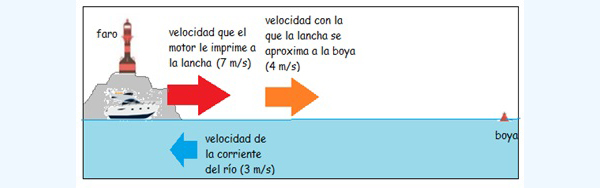
Una lancha navega aguas abajo por un río que desemboca en el mar. Se dirige hacia un faro, que marca de algún modo el límite entre ambos. La velocidad que el motor le imprime a la lancha es de unos siete metros sobre segundo, mientras que la velocidad de la corriente es de tres metros sobre segundo. Entonces, si un observador ubicado cerca del faro pudiese medir de algún modo la velocidad con la que la lancha se acerca, determinaría que es de diez metros sobre segundo. La situación aparece esquematizada en la imagen 3.11.
La embarcación se aproxima al faro moviéndose en el mismo sentido que la corriente del río.
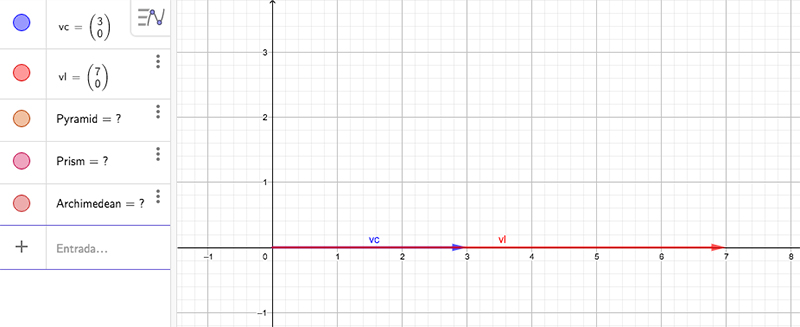
En la imagen 3.12 representamos los vectores empleando el Geogebra. Nuevamente utilizamos el color rojo para el vector que representa a la velocidad que el motor le imprime a la lancha, mientras que usamos el color azul para indicar la velocidad de la corriente.
En la imagen 3.13 mostramos de qué modo se obtiene la velocidad resultante, que no es otra cosa que la suma de ambos vectores.
Velocidades de la corriente y de la lancha, representadas como vectores.
Obsérvese la simple instrucción que hemos de dar al software para que nos brinde el vector resultante en la ventana de entrada que aparece en el extremo inferior de la imagen.
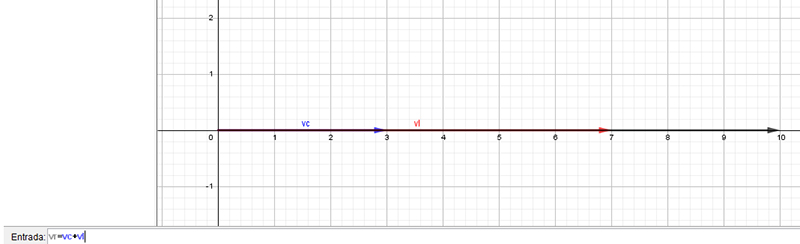
Cabe aclarar que tuvimos que colocar cero como segunda componente de cada uno de los vectores para que estos aparecieran representados sobre el eje de abscisas de la vista 2D de nuestro software.
Desde el punto de vista del cálculo, observemos detenidamente la vista algebraica de la imagen 3.14. La primera componente del vector resultante vr no es otra cosa que la suma algebraica de la primera componente de los dos sumandos.
Una vez que oprimimos la barra de entrada, el vector queda registrado en la vista algebraica de la pantalla.
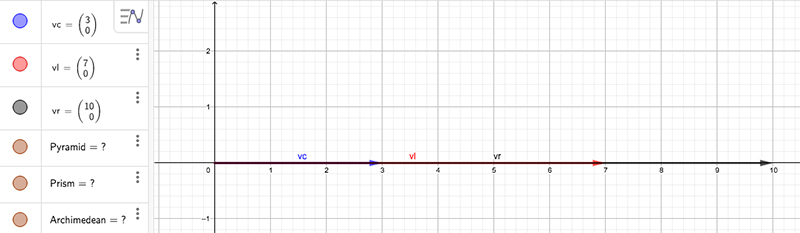
Podemos decir entonces que, dados dos vectores \( u = (u_x, u_y) \) y \( v = (v_x, v_y) \), la suma de ambos vectores habrá de calcularse como \( u + v = (u_x + v_x, u_y + v_y) \)
Como veremos a continuación, la resta entre vectores tampoco habrá de presentar mayores dificultades.
Supongamos ahora que la lancha alcanzó el faro y debe regresar a su punto de origen, navegando entonces aguas arriba. Tanto la velocidad que el motor le imprime a la embarcación como la de la corriente del río mantienen los valores que se indicaron en el ejemplo anterior. Sin embargo, si un observador ubicado cerca del faro pudiese medir la velocidad con la que la embarcación se aleja, notaría que lo hace a solo cuatro metros sobre segundo, tal como lo grafica la imagen 3.15.
La boya representa al punto de partida (ver imagen 3.11).
A partir de la gráfica, y empleando la nomenclatura que nos brinda el software (donde los vectores se presentan como columnas), podemos calcular:
\[ v_1 - v_c = \left( \begin{array}{cc} 7 \\ 0 \end{array} \right) - \left( \begin{array}{cc} 3 \\ 0 \end{array} \right) = \left( \begin{array}{cc} 4 \\ 0 \end{array} \right) \]
En la última expresión, el cuatro corresponde a la velocidad resultante de cuatro metros sobre segundo.
Podemos decir entonces que, dados dos vectores \( u = (u_x, u_y) \) y \( v = (v_x, v_y) \), la resta de ambos vectores habrá de calcularse como \( u - v = (u_x - v_x, u_y - v_y) \)
A continuación, avancemos en el tema con un ejemplo en el que tendremos que operar con vectores en el plano.
Un avión despega para dirigirse a un aeródromo ubicado a trescientos veinte kilómetros al norte de su punto de partida. Dado que su velocidad es de trescientos veinte kilómetros por hora, se espera que llegue a destino en exactamente sesenta minutos.
Sin embargo, antes de partir, se le indica al piloto que durante el vuelo la aeronave se verá afectada por un viento cruzado, de dirección oeste-este, de cien kilómetros por hora. Interesa entonces cuál habrá de ser la corrección que el piloto habrá de hacer en su rumbo para llegar a destino y con cuánta demora habrá de hacerlo.
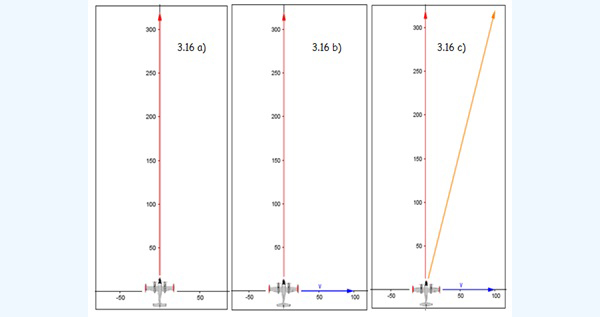
La imagen 3.16 resume en cierto modo la situación que acabamos de describir. En la imagen 3.16.a) representamos exclusivamente (en color rojo) el vector que representa la velocidad que tendría el avión si no hubiese viento. En la imagen 3.16.c), en color naranja, se observa el vector velocidad resultante: el avión se mueve en un fluido, el aire, que a su vez está en movimiento. Le sucede lo mismo que a la embarcación de los ejemplos 3.4 y 3.5, es decir, la velocidad con la que efectivamente se mueve (y con la que lo ven moverse desde la torre de control) es la suma vectorial de la que le imprimen sus propios motores y la del medio en el cual se produce el movimiento.
El vector en color rojo representa la velocidad del avión en ausencia del viento. El vector en color azul representa la velocidad del viento; finalmente, el vector en color naranja representa la suma de los dos anteriores, que refleja, en definitiva, la dirección y el sentido en los cuales verán moverse al avión desde la torre de control si el piloto no efectúa una maniobra para corregir el rumbo.
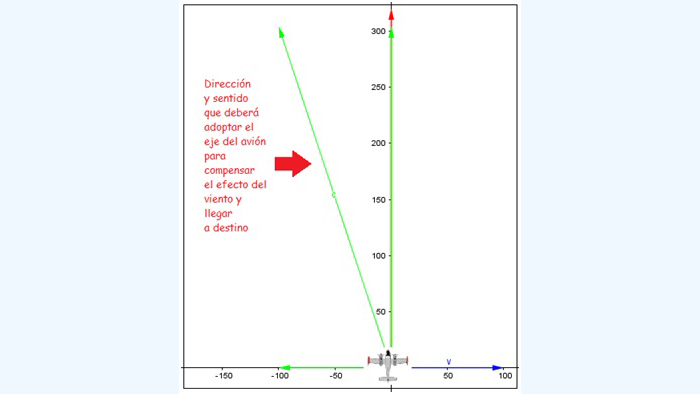
Para compensar el efecto del viento, el piloto deberá alterar su rumbo, de tal modo que el eje de la aeronave deje de tener dirección sur-norte. En la imagen 3.17 se observa que dicho eje deberá desplazarse hacia la izquierda respecto de la dirección prevista para el vuelo, de modo de compensar el efecto del viento.
Con una flecha roja señalamos la dirección y el sentido que habrá de adoptar el eje de la aeronave, de modo tal de compensar el efecto del viento.
No olvidemos que el objetivo es que, una vez compensado el efecto del viento, el avión se siga moviendo con dirección sur-norte. Así, la suma vectorial entre el “nuevo” vector velocidad del avión —que seguirá teniendo un módulo de 320 km/h, pero otra dirección y otro sentido— y el vector velocidad del viento deberá ser un vector que mantenga la dirección original de la aeronave.
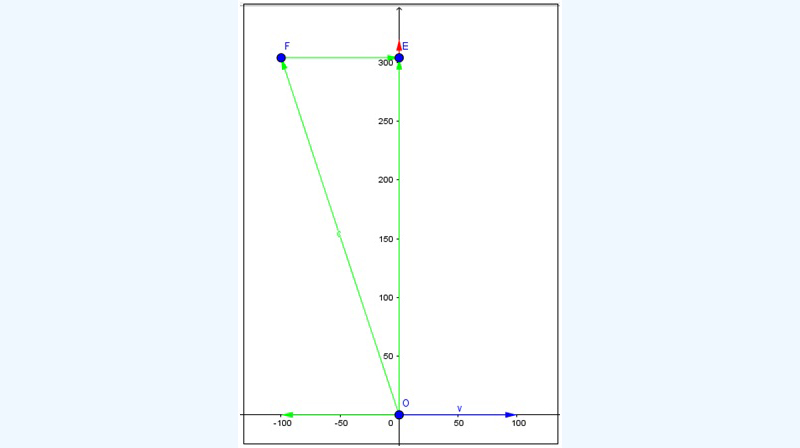
Desde el punto de vista gráfico, dicha suma puede efectuarse aplicando un procedimiento que recibe el nombre de método de la poligonal. Este consiste en trasladar sobre el plano al segundo de los vectores que han de sumarse, de modo que su origen coincida con el extremo del primero de los vectores. El resultante partirá del origen del primero de los vectores a sumarse, y su extremo será el extremo del segundo. En la imagen 3.18, el vector con origen en el punto O y extremo en el punto F representa el rumbo del avión corregido por el piloto. Obsérvese que este último punto representa el origen del vector cuyo extremo es el punto E y que no es otra cosa que el vector v (velocidad del viento). El vector resultante, con origen en O y extremo en F, corresponde a la velocidad con la que el avión se desplaza, de acuerdo con lo que se observa en la torre de control.
Aplicando el método de la poligonal podemos verificar que el rumbo de la aeronave, una vez compensado el efecto del viento, sigue siendo efectivamente sur-norte.
Otro procedimiento gráfico para obtener la suma entre dos vectores recibe el nombre de regla del paralelogramo. Teniendo en cuenta que este último es el nombre que recibe un cuadrilátero que tiene sus dos pares de lados opuestos paralelos entre sí, habrán de emplearse dos rectas auxiliares, como se observa en la imagen 3.19.
También podemos resolver el problema empleando la regla del paralelogramo.
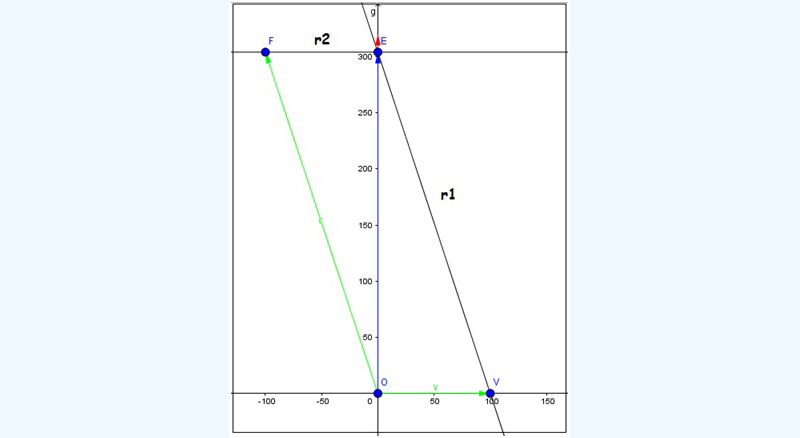
Así, a partir del punto V trazamos una recta r1 paralela al vector que representa la velocidad del avión una vez corregido el rumbo. Seguidamente, trazamos una recta r2, paralela al vector velocidad del viento, pero que pasa por el punto F. ambas rectas se intersecan en el punto E, que representa el extremo del vector resultante (cuyo origen es, como vimos anteriormente, el punto O).
Al efectuar la corrección del rumbo, el módulo de la velocidad resultante podrá calcularse simplemente aplicando el Teorema de Pitágoras. En la imagen 3.19 se observa claramente que el OFE es un triángulo rectángulo; su hipotenusa es el segmento que va desde O hasta F (cuyo módulo es de 320 km/h) y uno de sus catetos es el segmento de origen en F y extremo en O, de módulo 100 km/h.
Entonces, el cateto que va desde O hasta E (¡cuyo módulo corresponde al de la velocidad con la que la torre de control ve moverse a la aeronave!) se obtendrá a partir del siguiente cálculo:
\[ 100^2 + \overline{OE}^2 = 320^2 \to \]
\[ \to \overline{OE}^2 = 320^2 - 100^2 \to \]
\[ \to \overline{OE} = \sqrt{320^2 - 100^2} \]
El resultado de dicha raíz es 303,97 km/h y corresponde a la velocidad con la que el avión se mueve, según el radar.
Si dividimos la distancia que el avión debe recorrer (320 km) por su velocidad en la dirección sur-norte (303,97 km/h), el resultado será 1,0527 horas, es decir, aproximadamente una hora y tres minutos.
Podemos entonces responder que el avión llegará a destino con tres minutos de demora.
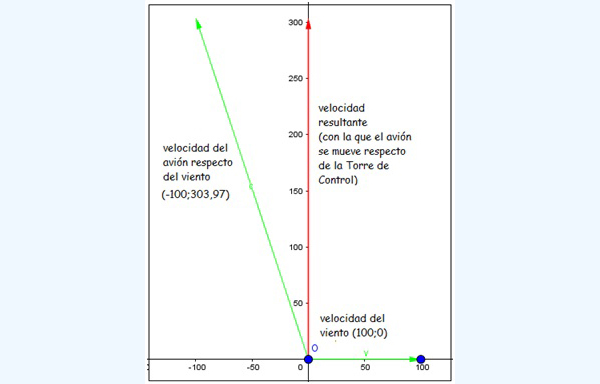
Desde el punto de vista analítico, vamos a confirmar el resultado obtenido en forma gráfica. En la imagen 3.20 observamos los dos vectores que hemos de sumar: el que representa la velocidad del viento —que habrá de expresarse como (100 km/h; 0)— y el que nos indica cuál es la velocidad con la que el avión se mueve respecto del viento, (-100 km/h; 303,97 km/h).
El vector resultante será entonces:
\[ v_{\text{avión según Torre}} = \left( -100 \frac{km}{h}; 303,97 \frac{km}{h} \right) + \left( 100 \frac{km}{h}; 0 \right) \]
\[ v_{\text{avión según Torre}} = \left( 0; 303,97 \frac{km}{h} \right) \]
Como era de esperar, la velocidad resultante (con la que el avión se mueve respecto de la torre de control) tiene dirección sur-norte, garantizando que la aeronave llegue a destino.
El avión deberá desviarse respecto del rumbo original para compensar el efecto del viento y llegar finalmente a destino.
3.3.2. Producto de un escalar por un vector
Desde el punto de vista algebraico, se trata de una operaciónentre elementos de dos conjuntos distintos: los escalares, por un lado, y los vectores, por el otro. La operación se clasifica como una ley de composición externa, porque su resultado es un elemento que pertenece a uno de esos dos conjunto (en este caso, un vector).
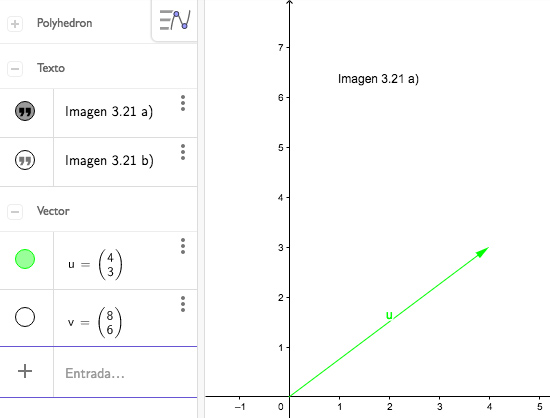
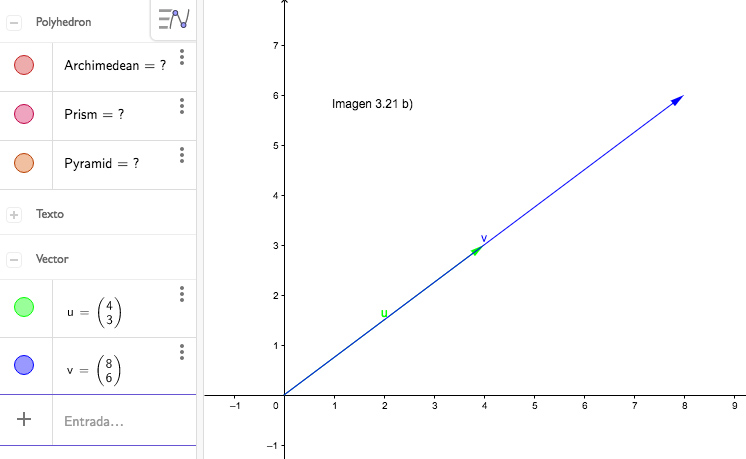
Cuando multiplicamos a un vector por un escalar (es decir, un número), el vector resultante tendrá la dirección del vector original. Por ejemplo, en la imagen 3.21 a) se observa el vector u, de coordenadas (4,3). A dicho vector lo multiplicamos por 2, obteniéndose así el vector v, representado en la imagen 3.21 b).
Desde el punto de vista analítico, habrá de operarse del siguiente modo:
\[ 2 . (4,3) = (2 \times 4,2 \times 3) = (8.6) \]
Es decir: se multiplica cada una de las componentes por el escalar, obteniéndose de ese modo las coordenadas del vector resultante.
En este primer ejemplo hemos multiplicado al vector por un escalar positivo y mayor que la unidad; por esa razón, el vector resultante conserva el sentido del original, mientras aumenta el valor de su módulo.
Al vector u se lo multiplica por un escalar, de modo que se obtiene otro vector, con distinto módulo.
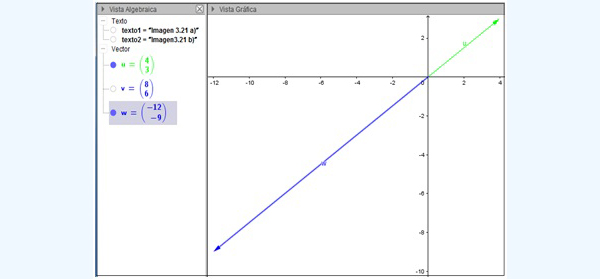
Si, en cambio, multiplicásemos al vector u por un número negativo, como por ejemplo -3, el vector resultante será:
\[ -3 . (4,3) = (-3 \times 4,-3 \times 3) = (-12,-9) \]
Ambos vectores aparecen representados gráficamente en la imagen 3.20. En este caso, como el escalar, en valor absoluto, es mayor que la unidad, el módulo del vector resultante aumenta. Pero, puesto que el escalar es negativo, aun cuando la dirección de ambos vectores siga siendo la misma, el sentido del vector resultante es opuesto al del vector u.
Al multiplicar a un vector por un número negativo, el vector resultante tiene sentido opuesto al del primero.
El producto de un vector \( v = (v_1, v_2) \) por un escalar a se calcula como:
\[ a . v = a . (v_1, v_2) = (a . v_1 , a . v_2) \]
Cuando el escalar a por el que se multiplica al vector original es positivo, el sentido del vector resultante es el mismo que el que tenía aquel.
Si, en cambio, el escalar a resulta ser negativo, ambos vectores tendrán sentidos opuestos.
Finalmente, si el escalar fuese cero, el vector resultante sería el vector nulo, que tiene módulo cero y suele representarse como un punto.
Cuando el módulo del escalar a por el cual multiplicamos al vector sea mayor que la unidad, el vector resultante tendrá un módulo superior al del vector original.
Si, en cambio, el módulo del escalar resulta ser menor que la unidad, el módulo o intensidad del vector resultante será inferior al del vector original.
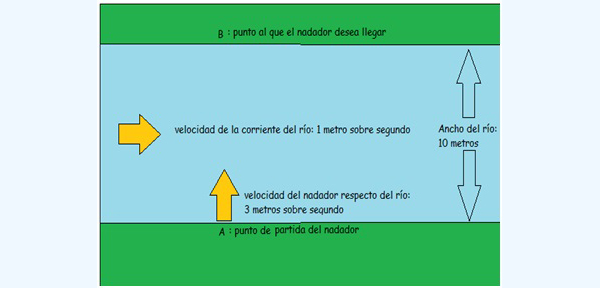
Un nadador parte de un punto A y desea alcanzar la costa opuesta del río en un punto B, exactamente frente a su punto de partida (imagen 3.23). El hombre puede nadar con una velocidad de tres metros sobre segundo, pero sabe que la velocidad del río es de un metro sobre segundo.
Sabiendo que el ancho del río en esa zona es de diez metros, se pide calcular cuánto tardará el nadador en alcanzar el punto B, indicando igualmente de qué modo habrá de desplazarse para compensar el efecto de la corriente del río.
El nadador parte del punto A, pero debe tener en cuenta la corriente del río para alcanzar la costa opuesta exactamente en el punto B.
Dados los vectores u = (2, -3); v = (-4, 2) y w = (-3, -4) se pide calcular:
- u + v
- u + 2.w
- 2.u – 3.w
En todos los casos, utilizar el GeoGebra para verificar los resultados obtenidos analíticamente.
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 655 a 669.
3.3.3. Producto escalar entre dos vectores
El resultado obtenido en las operaciones estudiadas hasta el momento es siempre un vector. En esta oportunidad y tal como lo expresa el nombre de la operación, el resultado habrá de ser un escalar.
Dados dos vectores del plano como \( u = (u_1, u_2) \) y \( v = (v_1, v_2) \), se define como producto escalar entre ellos al número que se obtiene como se indica a continuación:
\[ u.v = (u_1, u_2).(v_1, v_2) = u_1.v_1 + u_2.v_2 \]
Esta operación puede generalizarse para vectores en el espacio de tres o más dimensiones de la siguiente forma:
\[ u.v = (u_1, u_2, ... , u_n).(v_1, v_2, ... , v_n) \]
\[ u.v = u_1 . v_1 + u_2 . v_2 + ... + u_n . v_n \]
Calcular el producto escalar entre los vectores \( u = (2, -2.3) \) y \( v = (-3,5.1) \)
De acuerdo con lo indicado previamente, operamos como sigue:
\[ u . v = 2 . (-3) + (-2) . 5 + 3.1 = -13 \]
Acabamos de ver que es el cálculo del producto escalar de dos vectores resulta ser muy sencillo. Sin embargo, vale preguntarse qué representa el número resultante, cuál es su utilidad.
Para responder a esas preguntas será conveniente emplear otra expresión equivalente a la que ya dimos para el cálculo del producto escalar.
Dados dos vectores u y vtales que el ángulo entre las semirrectas que los contienen tenga valor \( \alpha \), el producto escalar entre ellos podrá calcularse como el producto entre los módulos de dichos vectores y el coseno de dicho ángulo. En símbolos:
\[ u . v = |u| . |V| . cos (\alpha) \]
Esta segunda forma de definir al producto escalar nos ofrece una interpretación geométrica de gran utilidad. En la imagen 3.24 representamos a los vectores u =(4,3) y v = (7,0). El ángulo entre ambos aparece en la misma imagen.
Puesto que tanto los módulos de los vectores como el coseno del ángulo son escalares y entre estos vale la propiedad conmutativa, podemos escribir:
\[ u . v = |u| . |v| . cos (\alpha) \to u . v = |v| . |u| . cos (\alpha) \]
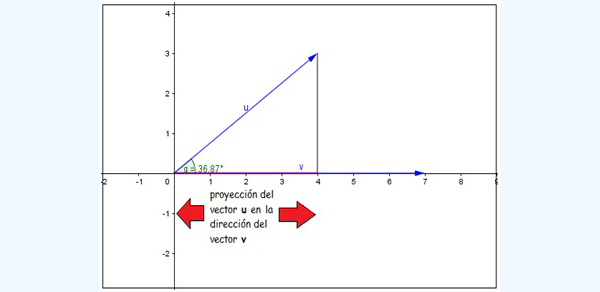
Ahora bien: tal como se indica en la imagen 3.25, el producto \( |u| . cos (\alpha) \) no es otra cosa que la proyección del vector u sobre la dirección del vector v. Es decir: el producto escalar sería entonces el producto entre el módulo de uno de los vectores y el de la proyección del otro vector sobre su recta de acción.
En la próxima sección ofreceremos un ejemplo que nos permitirá brindar un sentido físico al producto escalar.
Dados dos vectores u y v…
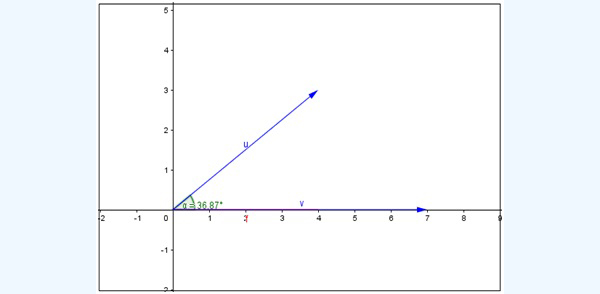
…el producto escalar entre ambos representa numéricamente la proyección de uno de ellos en la dirección del otro.
3.4. Aplicación física del producto escalar: trabajo mecánico de una fuerza
Uno de los conceptos básicos de la Mecánica es el de trabajo de una fuerza. Su importancia radica en que este habrá de vincularse con el concepto de energía mecánica, que los alumnos estudiarán en su curso de Física. Por el momento, nos limitaremos a dar su definición que, como se podrá observar, está íntimamente relacionada con el tema que estamos desarrollando.
Dada una fuerza \( \overline{F} \) que se aplica sobre un cuerpo, provocándole un desplazamiento que queda definido por un vector \( \overline{d} \), y siendo \( \alpha \) el ángulo que queda determinado entre las semirrectas que contienen a los mencionados vectores, definiremos al trabajo de la fuerza \( \overline{F} \) de la siguiente manera:
\[ \text{Trabajo de } \overline{F} = \overline{F} . \overline{d} \]
O lo que es lo mismo:
\[ \text{Trabajo de } \overline{F} = |\overline{F}| . |\overline{d}| . cos(\alpha) \]
Vale observar que, mientras la fuerza y el desplazamiento son magnitudes vectoriales, el trabajo resulta ser una magnitud de tipo escalar.
Para aclarar el concepto, proponemos el siguiente ejemplo:
Un niño arrastra una locomotora de juguete mientras camina por el patio de su casa, empleando para ello una cuerda que determina con la horizontal un ángulo de unos 53 grados aproximadamente, como se muestra en la imagen 3.26. De ese modo, el juguete recorre una distancia de un metro (diez decímetros, de acuerdo con lo que se observa en la imagen).
Si la fuerza con la que tira de la cuerda es de unos 0,5 Newtons (unidad de fuerza en el Sistema Internacional, SI), el trabajo de dicha fuerza será de unos 0,3 Joules (unidad de trabajo y de energía en el SI).
Este valor habrá de obtenerse, de acuerdo con lo expresado anteriormente, aplicando la expresión:
\[ \text{Trabajo de } \overline{F} = |\overline{F}| . |\overline{d}| . cos(\alpha) \]
\[ \text{Trabajo de } \overline{F} = 0,5 \ Newton . 1 . metro . cos(\alpha) \]
\[ \text{Trabajo de } \overline{F} = 0,3 \ Joules \]
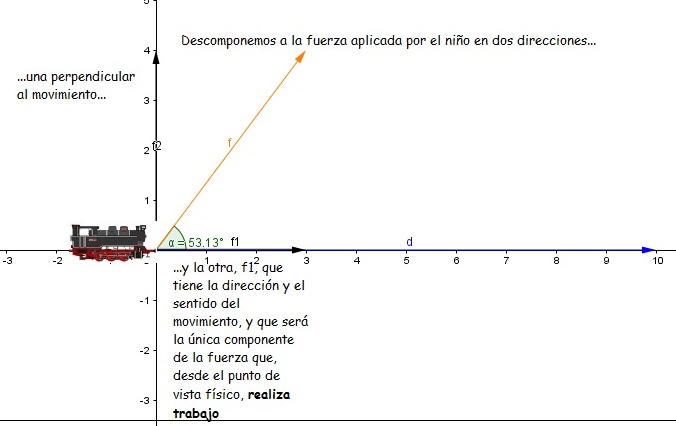
Tal como lo anticipamos, solo una de las componentes de la fuerza aplicada habrá de realizar trabajo: la que se obtiene proyectándola sobre la dirección del movimiento (ver imagen 3.27).
Se aplica una fuerza sobre la locomotora de juguete…
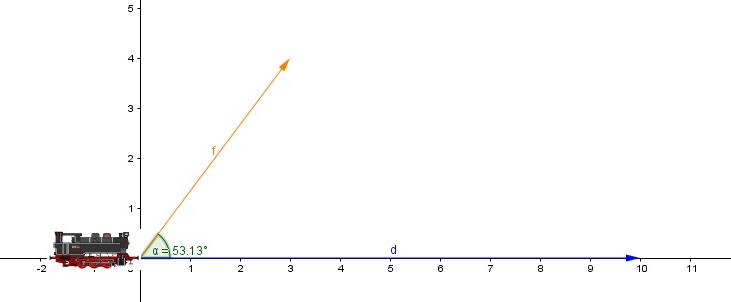
…pero solo la componente de dicha fuerza en la dirección del movimiento será la que “trabaje”…
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 669 a 676.
Tipler, P.; Mosca, G. (2003), Física para la Ciencia y la Tecnología, Volumen 1a, Editorial Reverté S. A., Barcelona, pp. 141 a 143.
Es interesante analizar de qué modo nuestra experiencia cotidiana no necesariamente habrá de coincidir con los conceptos tal como los manejamos desde el punto de vista de las ciencias naturales. Para demostrarlo, basta con analizar el siguiente ejemplo.
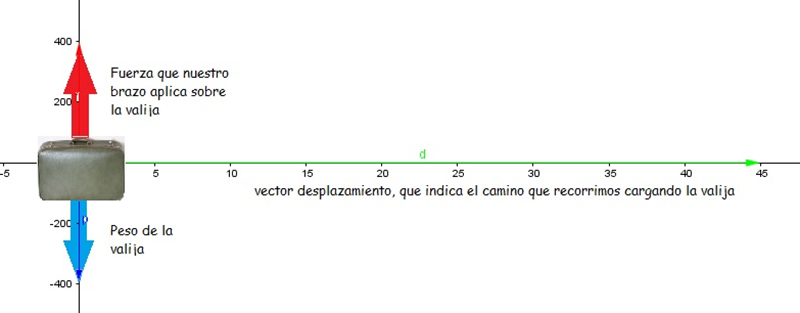
Supongamos que cargamos una valija de unos 40 kilogramos (es decir, aproximadamente unos 400 Newtons de peso), transportándola sobre un pasillo horizontal durante una distancia de 45 metros. La situación aparece representada en la imagen 3.28.
En la imagen representamos en color azul a la fuerza peso y en color rojo a la fuerza que debe hacer nuestro brazo para mantener la valija a una cierta distancia del suelo, permitiéndonos así cargarla. El módulo de la fuerza aplicada será igual al del peso, tendrá la misma dirección pero sentido opuesto, de modo que la resultante de ambas valga cero (la valija no habrá de moverse en sentido vertical).
Seguramente, para cuando hayamos recorrido los 45 metros, consideraremos que llevamos a cabo un gran trabajo… ¡pero dicho trabajo (de tipo muscular) no es el que hemos de tener en cuenta desde el punto de vista de la Mecánica!
El motivo es muy sencillo: dado que en el cálculo debemos multiplicar los módulos de los vectores (en este caso, la fuerza que hace nuestro brazo y el desplazamiento) por el coseno del ángulo que queda determinado por ellos, puesto que dicho ángulo vale en nuestro caso, noventa grados (¡cuyo coseno vale cero!), entonces concluimos que el trabajo mecánico es este caso vale cero.
La fuerza necesaria para trasladar la valija “no trabaja”, porque su dirección es perpendicular a la del movimiento.
3.5. Magnitudes escalares y vectoriales
Antes de finalizar la presente unidad consideramos oportuno detenernos en un ejemplo que nos permita diferenciar claramente las magnitudes escalares de las vectoriales. Nos referimos específicamente al caso del peso y la masa de un cuerpo.
La masa es un ejemplo típico de lo que denominamos una magnitud escalar, pues basta con un número (expresado en la correspondiente unidad de medida) para que quede perfectamente definida.
El peso, en cambio, es una magnitud vectorial, de la que no solo necesitamos conocer su valor numérico (su intensidad o módulo) sino, además, su dirección y sentido.
La masa de un cuerpo podría definirse como la cantidad de materia que lo constituye. En cambio, el peso del cuerpo es la manifestación de la fuerza de atracción que la Tierra ejerce sobre todo cuerpo que se encuentre dentro de su campo gravitatorio.
No corresponde a los alcances del presente MDM profundizar en temas de Física. Sin embargo, recordemos que la fuerza gravitatoria, junto con las electromagnéticas, la fuerte y la débil, es una de las cuatro elementales que dicha ciencia reconoce en la actualidad.
Como el módulo de la fuerza de atracción gravitatoria es proporcional al producto de las masas de los dos cuerpos involucrados, solo se manifiesta de un modo evidente cuando al menos uno de los dos cuerpos tiene gran masa (como es el caso de los cuerpos celestes). Por ejemplo, entre la Tierra y la Luna (imagen 3.29) o nuestro planeta y cualquier cuerpo que se encuentre sobre su superficie(por ejemplo, el propio lector en este instante). En cambio, dicha fuerza es prácticamente insignificante cuando el orden de magnitud de las masas de los cuerpos involucrados sea pequeño (el alumno no puede percibir en este instante la fuerza de atracción que ejerce sobre cualquiera de los objetos que se encuentren sobre su mesa de trabajo).
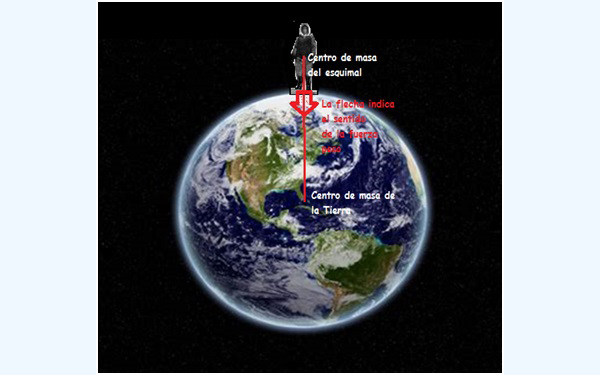
Así, cuando hablamos del peso de un cuerpo nos estamos refiriendo a la fuerza de atracción que dicho cuerpo manifiesta por encontrarse sobre la superficie de la Tierra. Desde el punto de vista matemático, el peso resulta ser un vector cuya dirección resulta ser una recta que une al objeto con el centro de la Tierra. En lo que respecta a su sentido, digamos que su origen se encuentra en el cuerpo en cuestión, en tanto que su extremo apunta justamente hacia el centro del planeta, como se representa en la imagen 3.30.
Las flechas de color rojo definen la dirección de la fuerza de atracción gravitatoria entre ambos cuerpos celestes.

Una línea roja indica la dirección del peso de un esquimal. La flecha señala el sentido de dicha fuerza, apuntando hacia el centro de la Tierra.
El módulo del peso de un cuerpo en la superficie de la Tierra se calcula multiplicando a la masa por el valor de la aceleración de la gravedad… que no vale lo mismo que la aceleración de la gravedad en la superficie de la Luna. Si, por ejemplo, tomásemos un cuerpo cuya masa fuese de 600 gramos y lo pesáramos en nuestro planeta, su peso sería de aproximadamente seis Newtons (unidad con el que se miden las fuerzas en el Sistema Internacional, SI). Sin embargo, si ese mismo cuerpo fuese llevado a la Luna, su peso en el satélite sería de solamente un Newton (imagen 3.31).
En un laboratorio en la Tierra (izquierda) la balanza registraría un peso para el cuerpo de 6 N. Sin embargo, la misma balanza en la Luna registraría, para el mismo cuerpo, un peso seis veces menor.

El valor del peso de un cuerpo dependerá entonces de dónde sea registrado (de hecho, como la Tierra no es una esfera perfecta, el peso de un cuerpo en los polos es levemente mayor que el que se registra en el ecuador terrestre). En cambio, la masa del cuerpo es una característica inherente a él y su valor será independiente del lugar donde se la mida.
Es probable que la confusión entre ambos conceptos esté relacionada justamente con los sistemas de unidades que se emplean para medir ambas magnitudes. El SI define como unidad de masa al kilogramo y como unidad de fuerza al Newton. Sin embargo, es aún común que se siga utilizando para el peso una unidad que en el antiguo Sistema Técnico recibía el nombre de kilogramo fuerza.
El valor numérico de la masa de un cuerpo en kilogramos (SI) es igual al del peso de un cuerpo en kilogramos fuerza (Sistema Técnico); además, la adopción del SI no parece haber alcanzado los usos y costumbres de la mayoría de las personas, que aún acostumbran a expresar el peso de un cuerpo en kilogramos (¡sin aclarar que se trata de kilogramos fuerza!). Los productos que consumimos habitualmente e incluso algunos instrumentos de uso hogareño, como las balanzas, tampoco han adoptado aún el SI. Todo ello influye, sin duda, para que el peso y la masa, dos magnitudes de naturalezas distintas, suelan confundirse.

