2. Nociones de trigonometría plana y relaciones trigonométricas
Objetivos
Que el alumno:
- Comprenda que las relaciones trigonométricas se basan en el concepto de proporcionalidad.
- Descubra de qué modo se obtienen las gráficas del seno y el coseno.
- Reconozca las características representativas de las funciones trigonométricas, su período y amplitud y aprenda de qué modo afectan a las gráficas correspondientes.
- Aprenda a desplazar horizontal y verticalmente cualquier gráfica a partir del modo en que dichos movimientos se llevan a cabo con las funciones seno y coseno.
- Descubra que el empleo del software facilita su proceso de aprendizaje, al aplicarlo al estudio de las transformaciones de las gráficas de las funciones trigonométricas.
- Aprenda las relaciones entre las funciones trigonométricas más empleadas.
- Descubra de qué modo resolver situaciones problemáticas en las que sea necesario aplicar relaciones trigonométricas.
- Aprenda a resolver triángulos oblicuángulos aplicando para ello los teoremas del seno y del coseno.
2.1. Nociones de trigonometría plana y relaciones trigonométricas
Las imágenes 2.1, 2.2 y 2.3 nos muestran tres triángulos rectángulos, el de vértices A1, B1 y C1; el de vértices A1, B2 y C2; y, finalmente, el que tiene como vértices a los puntos A1, B3 y C3, respectivamente.
Ahora bien: los tres tienen un vértice en común y podríamos representar todos ellos en un mismo gráfico, como se observa en la imagen 2.4.
Comenzamos dibujando un triángulo rectángulo de vértices A1, B1 y C1…
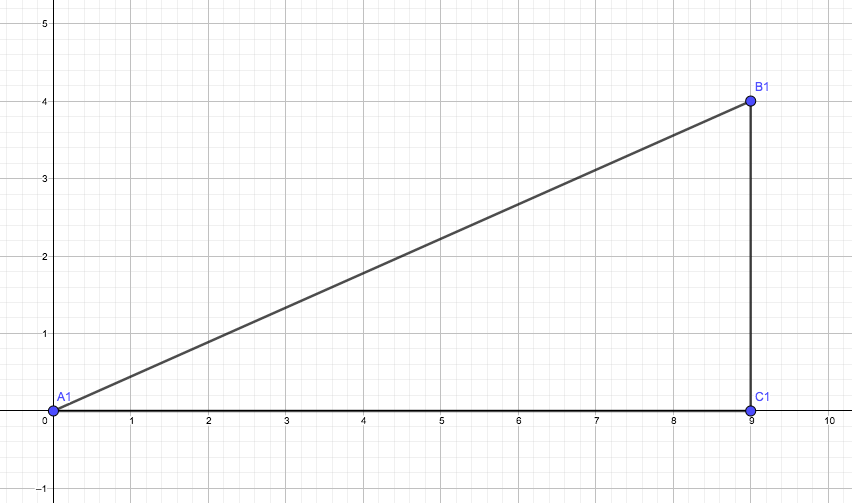
…para luego dibujar un segundo triángulo rectángulo de vértices A2, B2 y C2.
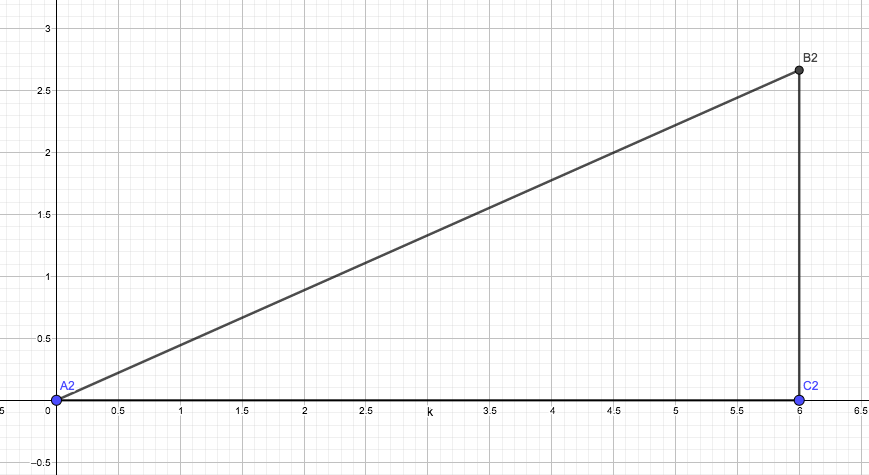
Finalmente, dibujamos un tercer triángulo rectángulo, con vértices A3, B3 y C3.
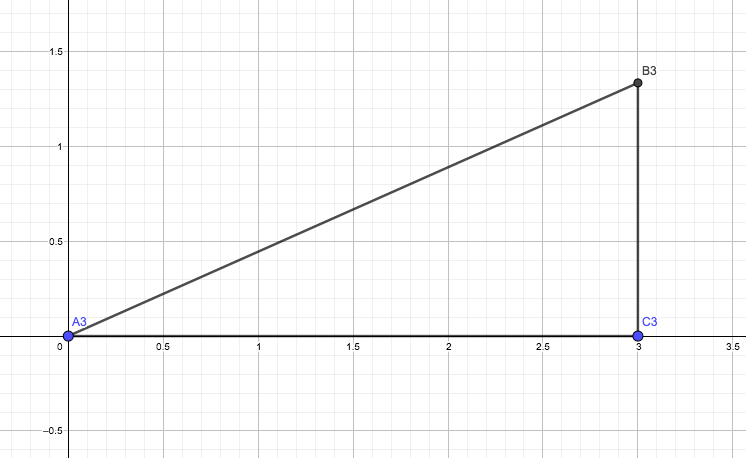
Como todos ellos tienen un vértice común coincidente con el origen de coordenadas y un lado sobre el eje de abscisas, los podemos representar como puede observarse a continuación
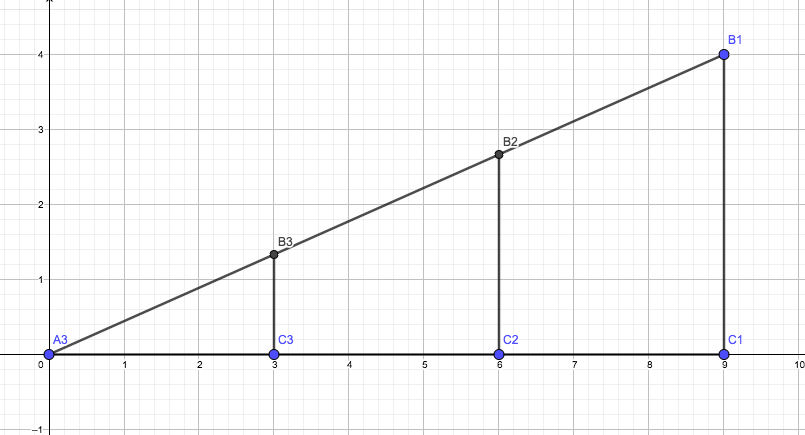
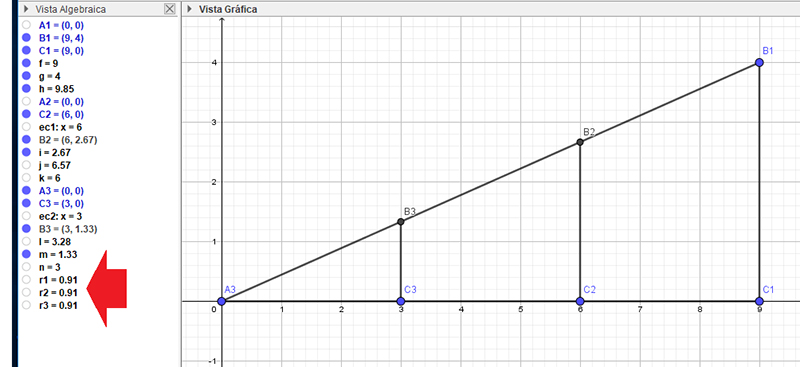
Siendo rectángulos y teniendo un vértice en común, nos encontraremos con que se cumplen ciertas relaciones entre las razones de los catetos con las hipotenusas. Así, en la imagen 2.5, hemos señalado, dentro de la vista algebraica y con una flecha roja, los cocientes r1, r2 y r3. Estos fueron obtenidos dividiendo como se indica a continuación:
\[ r1 = \frac{\overline{A_1C_1}} {\overline{A_1B_1}} = 0,91 \]
\[ r2 = \frac{\overline{A_1C_2}} {\overline{A_1B_2}} = 0,91 \]
\[ r3 = \frac{\overline{A_1C_3}} {\overline{A_1B_3}} = 0,91 \]
Teniendo en cuenta el ángulo \( \ \), común a los tres triángulos, las tres razones que acabamos de obtener se obtuvieron al dividir los catetos adyacentes de aquellos por sus respectivas hipotenusas.
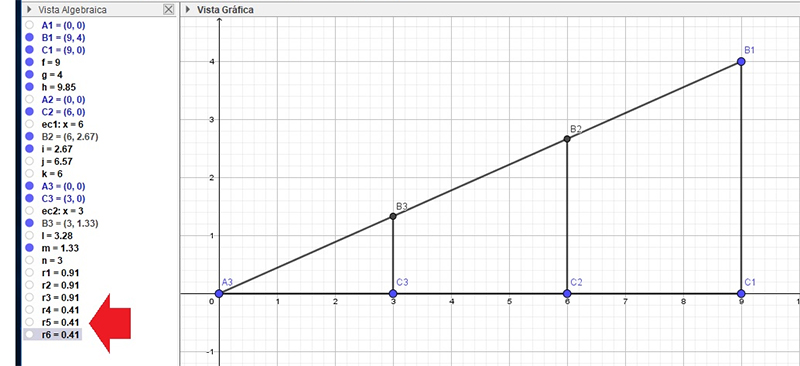
Del mismo modo, en la imagen 2.6 se observan otras tres razones, r4, r5 y r6:
\[ r4 = \frac{\overline{B_1C_1}} {\overline{A_1B_1}} = 0,41 \]
\[ r5 = \frac{\overline{B_2C_2}} {\overline{A_1B_2}} = 0,41 \]
\[ r6 = \frac{\overline{B_3C_3}} {\overline{A_1B_3}} = 0,41 \]
En este último caso, las tres razones calculadas se obtuvieron dividiendo los catetos opuestos adyacentes de los tres triángulos por sus respectivas hipotenusas.
Las razones entre los lados AiCi y los lados AiBi dan como resultado un mismo valor…
…y lo mismo sucede entre los lados BiCi y los lados AiBi
Se pone de manifiesto la proporcionalidad entre los tres triángulos a partir de un dato clave; en este caso, el ángulo \( \widehat{A_1} \).
Teniendo en cuenta lo que acabamos de ver, estamos entonces en condiciones de definir las siguientes relaciones entre los lados de un triángulo rectángulo.
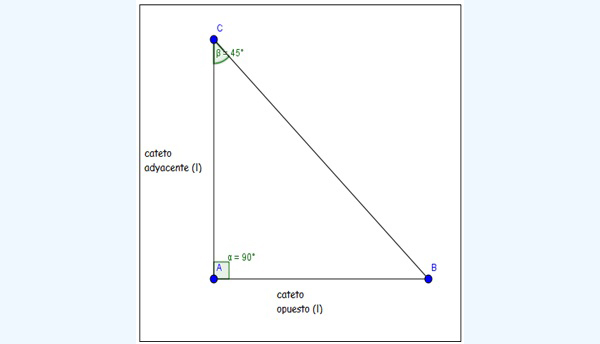
Dado un triángulo rectángulo de vértices A, B y C (imagen 2.7), y suponiendo que fuese rectángulo en \( \hat{B} \), podemos definir las siguientes relaciones entre suslados:
\[ seno (\hat{A}) = \frac{\text{cateto opuesto}}{hipotenusa} \]
\[ coseno (\hat{A}) = \frac{\text{cateto adyacente}}{hipotenusa} \]
\[ tangente (\hat{A}) = \frac{\text{cateto opuesto}}{\text{cateto adyacente}} \]
Definimos los distintos catetos y la hipotenusa, respecto de uno de los ángulos del triángulo.
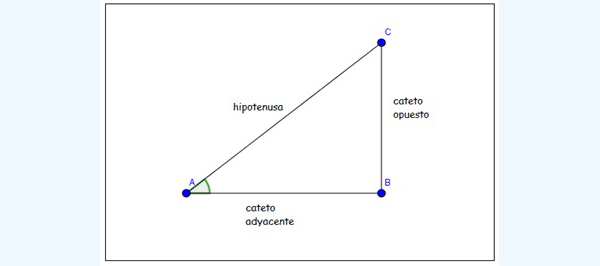
Existen otras tres relaciones que no se emplean con tanta frecuencia, pero que el alumno debe conocer.
Dado un triángulo rectángulo de vértices A, B y C (imagen 2.7) y suponiendo que fuese rectángulo en \( \hat{B} \), podemos definir las siguientes relaciones entre sus lados:
\[ cosecante (\hat{A}) = \frac{hipotenusa}{\text{cateto opuesto}} \]
\[ secante (\hat{A}) = \frac{hipotenusa}{\text{cateto adyacente}} \]
\[ cotangente (\hat{A}) = \frac{\text{cateto adyacente}}{\text{cateto opuesto}} \]
Para muchas aplicaciones prácticas será conveniente graficar los valores de las relaciones que acabamos de definir para distintos ángulos. Los fenómenos ondulatorios son muy frecuentes en la naturaleza y dichas gráficas resultan muy valiosas para su interpretación y análisis.
Stewart, J.; Redlin, L.; Watson, S. (2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 359-360.
Como veremos más adelante, las relaciones trigonométricas que hemos definido en esta sección nos permitirán definir las funciones trigonométricas, cuyas representaciones gráficas serán, justamente, las que hemos de construir en la próxima sección.
2.2. Circunferencia unitaria y representaciones gráficas
A partir de la definición de circunferencia (“el lugar geométrico de los puntos equidistantes respecto de uno dado llamado centro”), llamaremos circunferencia unitaria a aquella que tenga radio de valor igual a la unidad. Dicha circunferencia nos resultará sumamente útil para construir las representaciones gráficas del seno y el coseno de un ángulo dado.
Nos proponemos, en principio, construir una curva que representa a los posibles valores que pueda adoptar la razón a la que denominamos seno en función del ángulo que se escoja. Es necesario aclarar que dejaremos de lado el sistema sexagesimal (es decir, aquel donde un ángulo recto vale noventa grados; un ángulo llano, ciento ochenta grados; etc.) y mediremos los ángulos en otra unidad, denominada radián.
Cada vez que utilizamos distintas unidades para la medición de una misma magnitud, necesitamos una equivalencia entre ambas. En este caso, diremos que \( 360˚ = 2\pi \ radianes \).
El pasaje de una unidad a la otra se puede llevar a cabo empleando una regla de tres simple. Fácilmente puede determinarse entonces que \( 90˚ \) sexagesimales equivalen a \( \frac{\pi}{2} \) radianes; o que \( 45˚ \) se pueden expresar como \( \frac{\pi}{4} \) radianes.
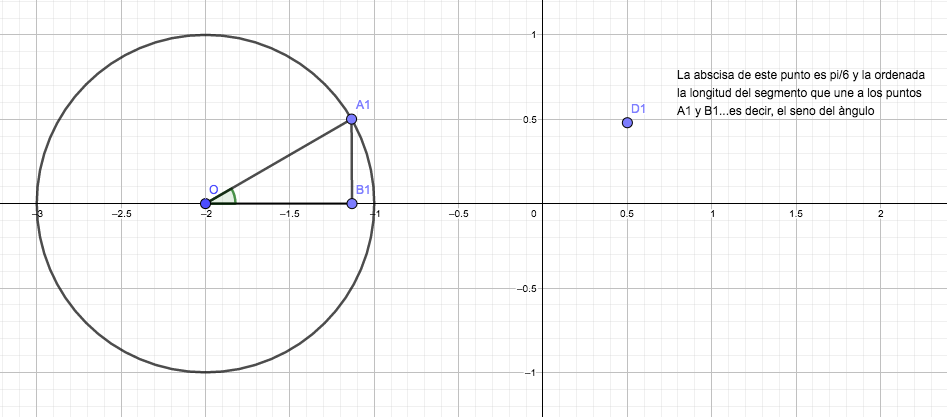
En la imagen 2.8 dibujamos una circunferencia unitaria, con centro en el punto (-2, 0). Dentro de ella, dibujamos un triángulo de vértices O, A1 y B1, que resulta ser rectángulo en este último vértice. El ángulo entre el segmento que une a los puntos O y A1 con la horizontal es de \( 30˚ \)(es decir, de \( \frac{\pi}{6} \) radianes).
El cociente entre el segmento que une a los puntos A1 y B1 y la hipotenusa del triángulo (que siendo uno de los radios de la circunferencia habrá de tener valor uno) resulta ser igual al seno de \( \frac{\pi}{6} \).
En la imagen 2.9 aparece un punto D1, cuya abscisa es \( \frac{\pi}{6} \) y su ordenada la longitud del segmento que une los puntos A1 y B1 (¡es decir, el seno del ángulo!).
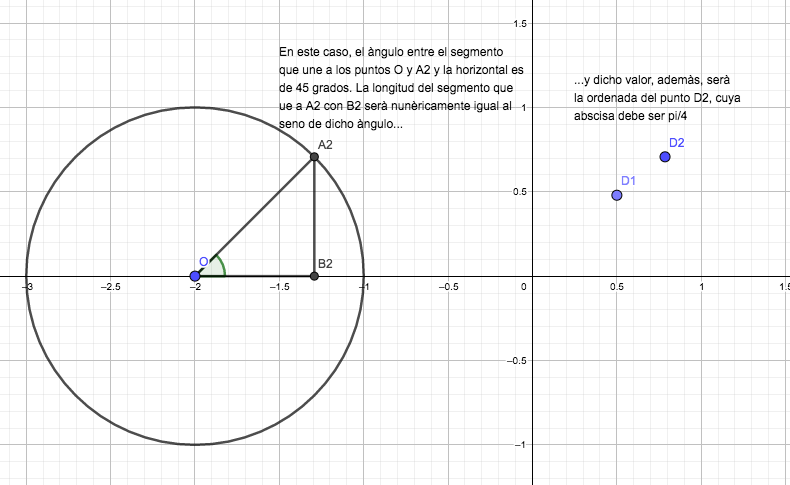
Seguidamente, dibujamos dentro de la circunferencia otro triángulo rectángulo, cuyos vértices son los puntos O, A2 y B2 (imagen 2.10). El ángulo que queda determinado entre el segmento que une a los puntos O y A2 y la horizontal es ahora de \( 45˚ \) (es decir, \( \frac{\pi}{4} \) radianes). Y el cociente entre la longitud del segmento que une a los puntos A2 y B2 y la hipotenusa (que no debemos olvidar, es igual a la unidad) es igual al valor del seno del ángulo.
Como la hipotenusa tiene valor uno, la longitud del segmento \( \overline{A_1B_1} \) resulta ser numéricamente igual al seno del ángulo.
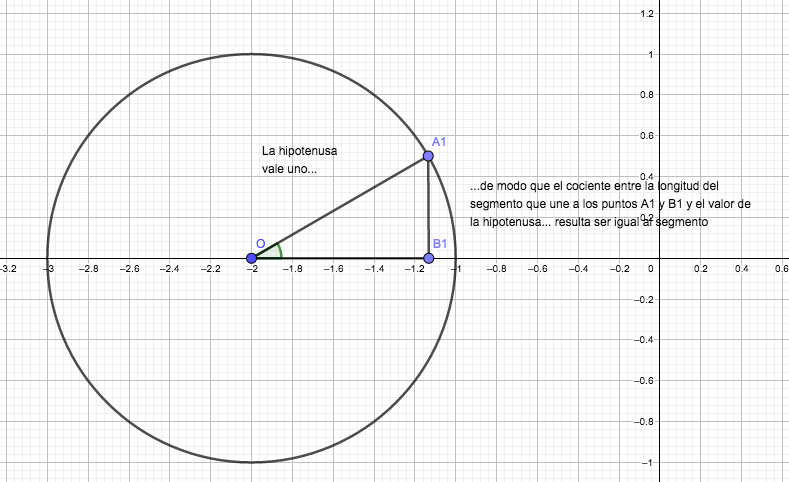
El valor numérico de la ordenada del punto D1 es igual al del seno del ángulo.
A la derecha de la imagen 2.10 se observa el punto D2, cuya abscisa vale \( \frac{\pi}{4} \) y su ordenada resulta igual a la longitud del segmento que une a los puntos A2 y B2 (que, reiteramos, no es otra cosa que el seno del ángulo).
La ordenada del punto de abscisa \( \frac{\pi}{4} \) es numéricamente igual al seno del ángulo de 45˚.
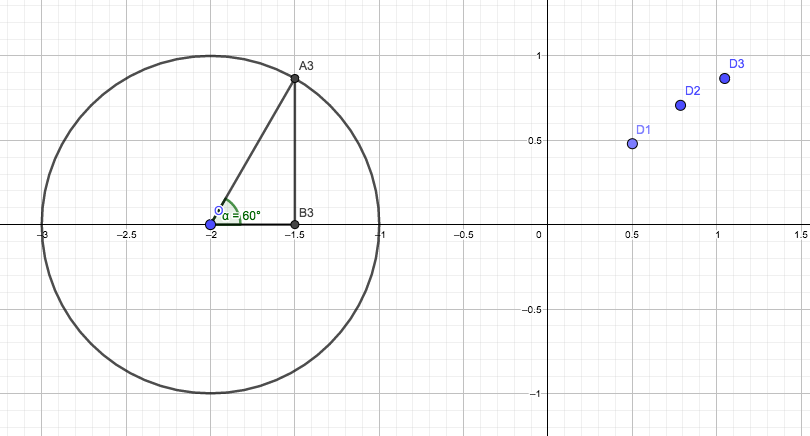
Repetimos el procedimiento aplicado en los dos casos anteriores. Dibujamos dentro de la circunferencia unitaria un triángulo cuyos vértices son los puntos O, A3 y B3, de tal modo que el ángulo entre la horizontal y el segmento que une a los puntos O y A3 sea en esta oportunidad de \( 60˚ \) (es decir, \( \frac{\pi}{3} \) radianes). Aplicando el criterio detallado previamente, concluimos que la longitud del segmento que une a los puntos A3 y B3 (imagen 2.11) es igual al seno del ángulo señalado en el dibujo. Dibujamos ahora un punto D3, cuya abscisa es igual al ángulo en cuestión y su ordenada, el seno de dicho ángulo.
El alumno comprenderá que, aplicando el procedimiento que nos permitió obtener a los puntos D1, D2 y D3, podríamos continuar indefinidamente. Pero, para que el razonamiento no se torne tedioso, nos limitaremos a comentar lo siguiente:
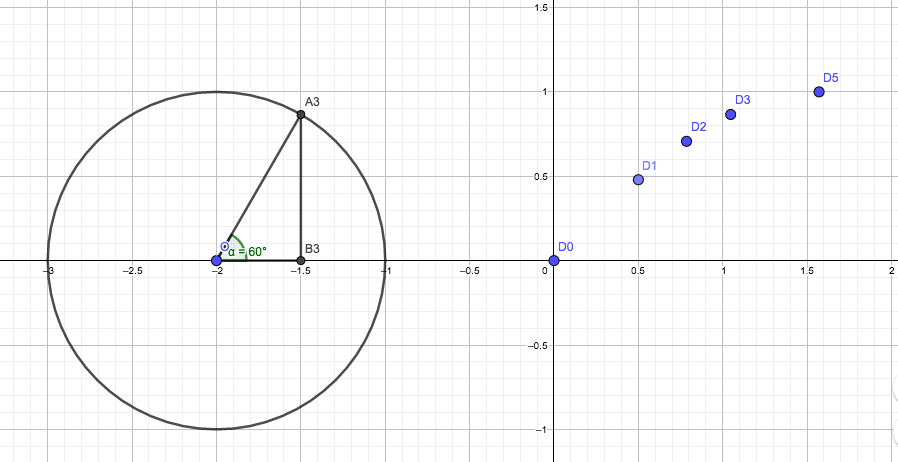
(i) Observemos que el segmento que une a los puntos A1 y B1 tiene una longitud menor que el que une a los puntos A2 y B2 y que este, a su vez, es más corto que el que une a los puntos A3 y B3. Es decir: a medida que el ángulo entre la horizontal y el segmento que va de O al punto Ai disminuye, el cateto opuesto también lo hace y, por lo tanto, lo mismo sucede con el valor del seno del ángulo. Así, cuando el ángulo sea muy pequeño, el valor del seno se aproximará a cero. El caso extremo se dará entonces cuando el ángulo sea efectivamente igual a cero; entonces, el cateto opuesto adoptará dicho valor y el seno también. Ello nos habilita a agregar en nuestra construcción un cuarto punto, el Do, cuyas coordenadas serán entonces (0,0) (en correspondencia con el ángulo y el valor del seno de este).
Aplicamos el mismo criterio que en los dos casos anteriores y representamos un punto cuya ordenada tiene el mismo valor que el seno de \( \frac{\pi}{3} \).
(ii) Siguiendo el mismo razonamiento, pero moviéndonos en sentido contrario, observamos que el cateto opuesto aumenta a medida que lo hace el ángulo. El caso extremo se presenta cuando el ángulo vale \( 90˚ \), porque entonces el valor del cateto opuesto y el de la hipotenusa coinciden. Así, el seno del ángulo recto será igual a la unidad. En la imagen 2.12 agregamos entonces los puntos Do y D5; este último tiene por abscisa \( \frac{\pi}{2} \), es decir, el valor del ángulo recto en radianes y por ordenada la unidad (que, como vimos, no es otra cosa que el valor del seno de dicho ángulo).
A los puntos obtenidos previamente le agregamos los que representan al seno de cero grados y del ángulo recto.
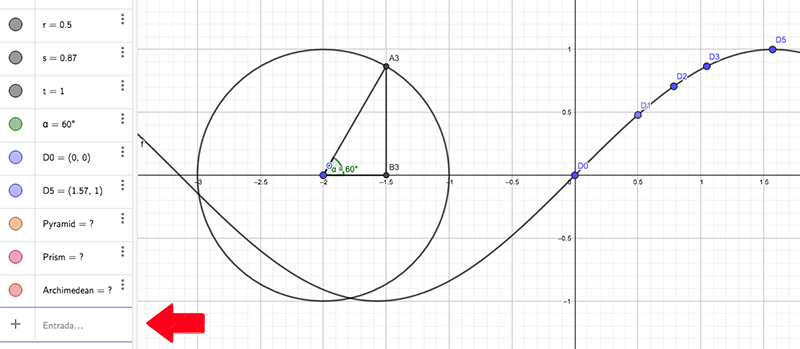
Ahora bien: aprovechando el software disponible, unimos los puntos obtenidos escribiendo en la ventana de entrada el nombre de la función (lo que se observa en la parte inferior de la imagen 2.13). Obsérvese que los puntos obtenidos se encuentran (¡como era de esperar!) sobre dicha curva.
En la parte inferior, una flecha roja señala la ventana dentro de la que habrá de escribirse “f(x)=sin(x)”, instrucción mediante la cual la curva aparece en pantalla. Obsérvese que los cinco puntos previamente obtenidos se encuentran exactamente sobre la curva.
Cuando los ángulos sean mayores que \( 90˚ \), una sencilla construcción nos permitirá calcular los valores del seno del ángulo (¡aun cuando previamente hayamos aclarado que estas relaciones solo se podían definir para triángulos rectángulos!).
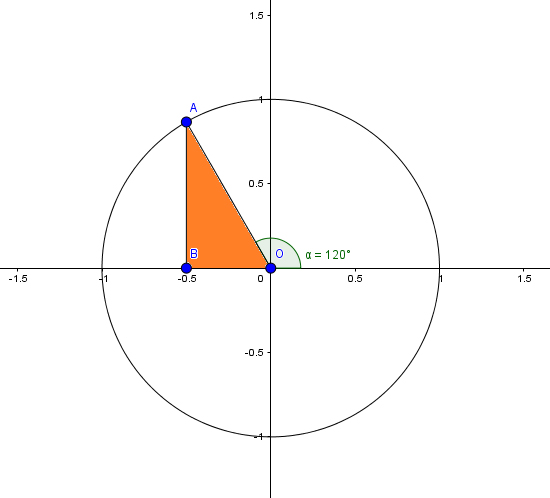
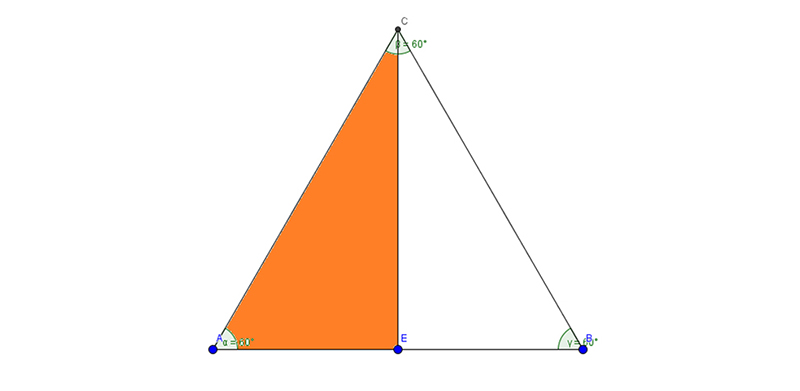
Supongamos que el ángulo en cuestión fuese de \( 120˚ \) (es decir, \( \frac{2}{3}\pi \ radianes \). En la imagen 2.14, el ángulo determinado entre el eje de abscisas y el segmento \( \overline{OA} \) adopta justamente dicho valor. Para calcular el seno o el coseno del ángulo, utilizaremos el triángulo rectángulo cuyos vértices son los puntos O, A y B (cuya área aparece pintada de color naranja en la imagen mencionada en el presente párrafo). Así:
\[ seno \left( \frac{2}{3} \pi \right) = \frac{\overline{AB}}{\overline{OA}} \]
\[ coseno \left( \frac{2}{3} \pi \right) = \frac{\overline{OB}}{\overline{OA}} \]
Cabe aclarar que el segmento \( \overline{OA} \), hipotenusa de nuestro triángulo rectángulo, tendrá siempre valor positivo. El cateto opuesto, cuya proyección sobre el eje de ordenadas queda sobre el semieje positivo de las ordenadas, será entonces positivo, de modo que el valor del seno también lo será. En cambio, la proyección del cateto adyacente sobre el eje de abscisas se encuentra sobre el semieje negativo, de tal modo que el coseno del ángulo también lo será.
Cuando el ángulo sea superior al recto, hemos de utilizar triángulos que se encuentren fuera del primer cuadrante para definir los valores de las funciones trigonométricas.
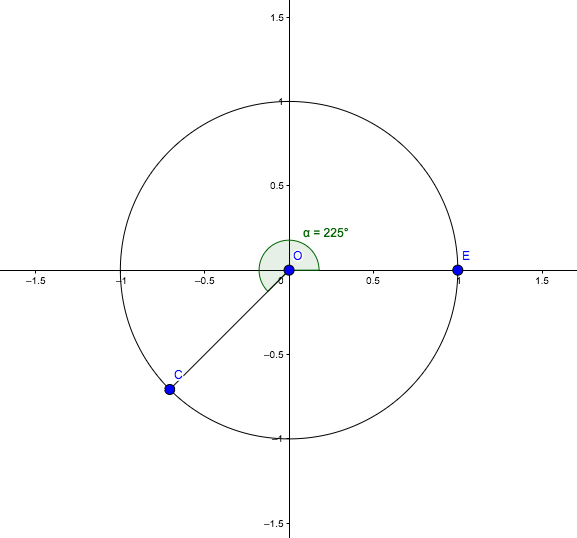
En la imagen 2.15, los segmentos \( \overline{OE} \) y \( \overline{OC} \) determinan un ángulo de \( 225˚ \) (es decir, \( \frac{5}{4} \pi \) radianes). En esta oportunidad, para el cálculo del seno y el coseno de dicho ángulo trabajaremos con el triángulo de vértices O, C y D (ver Imagen 2.16). Los valores del seno y coseno del ángulo se obtendrán a partir de las siguientes expresiones:
\[ seno \left( \frac{5}{4} \pi \right) = \frac {\overline{CD}}{\overline{OC}} \]
\[ coseno \left( \frac{5}{4} \pi \right) = \frac {\overline{OD}}{\overline{OC}} \]
Puesto que ahora las proyecciones de ambos catetos sobre los respectivos ejes cartesianos aparecerán sobre los semiejes negativos, tanto el seno como el coseno adoptarán valores negativos.
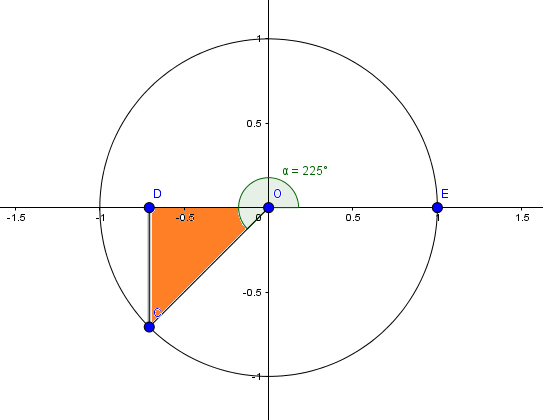
Pasamos ahora al tercer cuadrante, a partir del ángulo que queda determinado entre los segmentos \( \overline{OE} \) y \( \overline{OC} \).
En esta oportunidad, el triángulo a partir del cual definiremos los valores de las relaciones trigonométricas se encuentra dentro del tercer cuadrante.
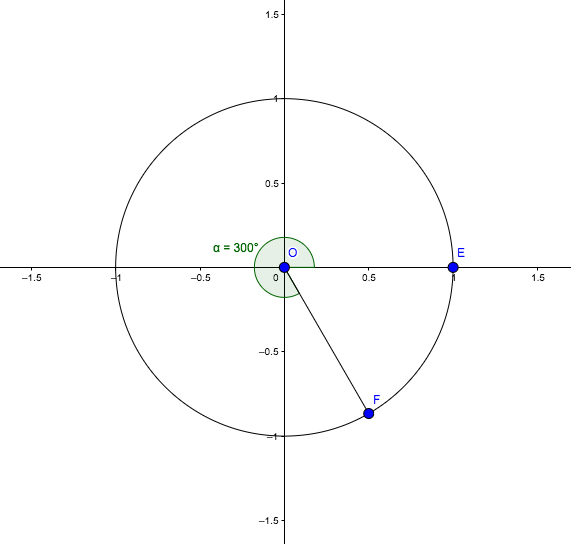
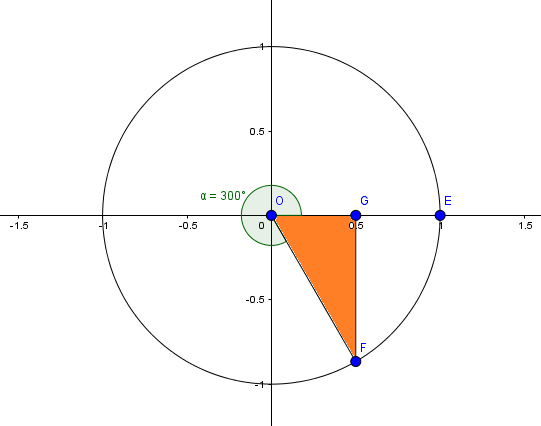
Finalmente, analicemos el caso de un ángulo que se encuentre en el cuarto cuadrante. En la imagen 2.17, los segmentos \( \overline{OE} \) y \( \overline{OF} \) limitan un ángulo de \( 300˚ \) (es decir, de \( \frac{5}{3} \pi \) radianes). El triángulo rectángulo que nos permitirá calcular el seno y el coseno será el de vértices O, F y G, que se observa en la imagen 2.18. Deberán emplearse para ello las siguientes expresiones:
\[ seno \left( \frac{5}{3} \pi \right) = \frac {\overline{OG}}{\overline{OF}} \]
\[ coseno \left( \frac{5}{3} \pi \right) = \frac {\overline{GF}}{\overline{OF}} \]
En este caso, la proyección del cateto adyacente sobre el eje de abscisas quedará sobre el semieje positivo, mientras que la proyección del cateto opuesto sobre el eje de ordenadas se apoyará en el semieje negativo; como consecuencia de ello, el coseno resultará ser positivo, mientras que el seno será negativo.
Moviéndonos siempre en sentido antihorario, definimos ahora un ángulo superior a \( \frac{3 \pi}{2} \)…
…y volvemos a definir un triángulo rectángulo dentro del cuadrante correspondiente; en este caso, el cuarto.
En general, podemos decir lo siguiente:
El seno de un ángulo será positivo si dicho ángulo es mayor que cero y menor que \( \pi \) radianes; en cambio, será negativo si el ángulo es mayor que \( \pi \) y menor que \( 2 \pi \).
El coseno, en cambio, será negativo si el ángulo es mayor que \( \frac{\pi}{2} \) y menor que \( \frac{3}{2} \pi \). Si se encuentra entre cero y \( \frac{\pi}{2} \) o es mayor que \( \frac{3}{2} \pi \) y menor que \( 2 \pi \), el coseno será positivo.
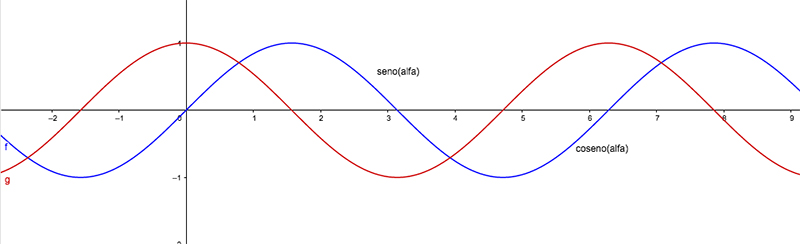
A partir de la circunferencia unitaria y siguiendo un razonamiento similar al que aplicamos en la primera parte de esta sección, podemos obtener la curva cuyos puntos tienen por abscisa el valor de un ángulo y por ordenada el coseno de dicho ángulo. En la imagen 2.19 se puede comparar esta curva con la que se vislumbra en la imagen 2.13. Obsérvese que ambas son iguales, aunque están desfasadas exactamente en \( \frac{\pi}{2} \) radianes. Los valores de sus imágenes están acotados entre -1 y 1.
En la siguiente sección comenzaremos a detenernos en el análisis de dichas curvas.
Ambas curvas fueron representadas en una misma gráfica. En color azul, la que corresponde al seno y en rojo, la del coseno.
Stewart, J.; Redlin, L.; Watson, S. (2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 351 a 357.
2.3. Noción elemental de función y funciones trigonométricas
En la sección anterior indicamos que existía una relación entre un ángulo y el valor de la razón definida con el nombre de seno al comenzar la presente unidad. Esa relación (a la que pudimos, incluso, representar gráficamente) cumple con ciertas condiciones y recibe el nombre de función.
Podemos aproximarnos al concepto de función (que estudiaremos con mayor detenimiento a partir de la unidad 5) diciendo que se trata de un tipo particular de relación entre elementos de dos conjuntos conformados por números, en la que a cada elemento del primero de ellos se le hace corresponder uno y solo un elemento del segundo.
Dicha correspondencia se expresa a partir de una expresión matemática perfectamente definida y, como vimos, puede representarse mediante una curva que se construye sobre un par de ejes cartesianos.
Así, por ejemplo, a cada ángulo propuesto le correspondía un único valor para el seno. Lo mismo habrá de suceder para el caso del coseno o la tangente.
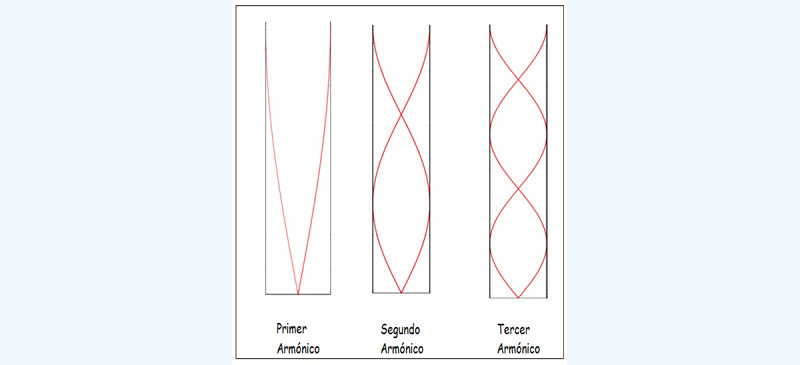
Las funciones seno y coseno resultan de gran interés, porque nos permiten interpretar, entre otros, los fenómenos ondulatorios. En la imagen 2.20 esquematizamos el modo en que se explican los tres primeros armónicos (las tres primeras frecuencias sonoras) que se obtienen al soplar sobre la boca de un tubo cerrado en su parte inferior. Las líneas en negro representan en forma esquemática las paredes y el techo del tubo cilíndrico, mientras que en color rojo se representa la onda sonora. Obsérvese que esta presenta un nodo (punto) en la parte inferior y un vientre (región de máxima amplitud) en coincidencia con la cara abierta del tubo.
Es probable que el alumno intuya que la curva que representa a la onda sonora habrá de expresarse matemáticamente mediante la función seno o la función coseno, de acuerdo con lo que más adelante definiremos como condiciones de contorno.
Toda función, como dijimos, vincula dos valores. Cada uno de ellos recibe el nombre de variable y, según su rol dentro de la relación, habrán de clasificarse como dependiente o independiente. Así, en el caso de la función seno, el ángulo representará la variable independiente (a la que le asignaremos un valor dado en cada caso particular); en cambio, el seno de ese ángulo será la variable dependiente (su valor depende o es función del ángulo seleccionado previamente).
Los fenómenos ondulatorios, como la obtención de los distintos armónicos en el interior de un tubo abierto en su parte superior, pueden comprenderse con mucha facilidad a partir del estudio de las funciones seno y coseno.
Por convención, en el momento de representar gráficamente las funciones, la variable independiente se indica sobre el eje de abscisas, en tanto que a la variable dependiente le corresponde el eje de ordenadas.
Las curvas que representan las funciones seno y coseno presentan dos características particulares: la amplitud y el período. Estas pueden ser afectadas por ciertos coeficientes que, como veremos en las siguientes secciones, deformarán las curvas respecto de su fisonomía original. Además, como sucederá con las curvas representativas de otros tipos de funciones, otros coeficientes podrán provocar desplazamientos horizontales o verticales de las gráficas, siempre referidas a las que presentamos en la sección anterior.
Apoyándonos en el empleo del software, estudiaremos en las siguientes secciones de qué modo las gráficas de las funciones seno y coseno pueden ser afectadas por dichos coeficientes.
Stewart, J.; Redlin, L.; Watson, S. (2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 360 a 364.
2.3.1. Desplazamientos horizontales
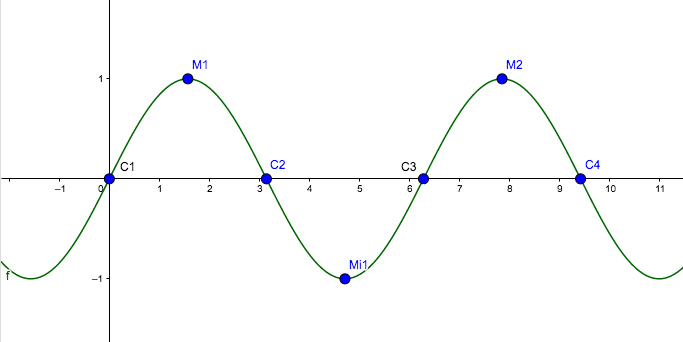
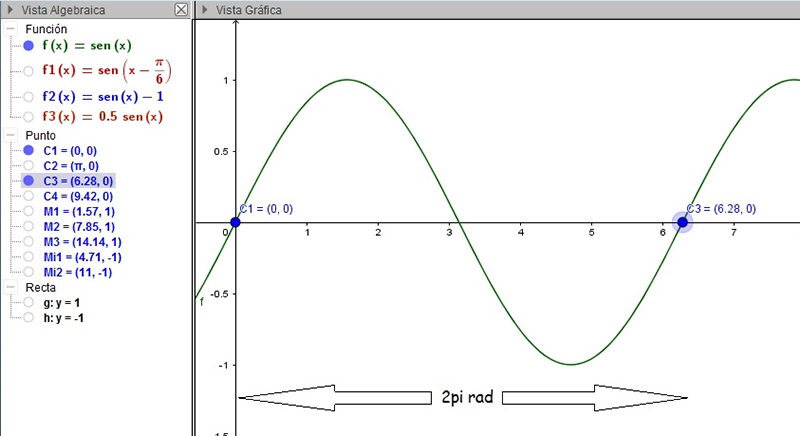
En la imagen 2.21 volvemos a representar a la función seno. Observamos que se trata de una función acotada (que adopta -1 como valor mínimo y 1 como valor máximo) y periódica, porque los valores de su imagen se repiten a medida que se incrementa el valor de la variable independiente. Así, el máximo M1 se presenta cuando el ángulo (la variable independiente) es de \( \frac{\pi}{2} \) radianes; el siguiente máximo, M2, tiene entonces por abscisa a \( \frac{\pi}{2} + 2 \pi \). Lo mismo habrá de suceder con los mínimos: el primero que figura en la imagen 2.21 tiene por abscisa al valor \( \frac{3}{2} \pi \) radianes, en tanto que el siguiente mínimo se presenta cuando la variable independiente adopta valor \( \frac{3}{2} \pi + 2 \pi \). En lo que respecta a los ceros de la función (es decir, las intersecciones de esta con el eje de abscisas), la distancia que separa a dos consecutivos será de \( \pi \) radianes. Dichos ceros o raíces aparecen en la imagen como C1, C2, C3 y C4.
Representación gráfica de la función seno.
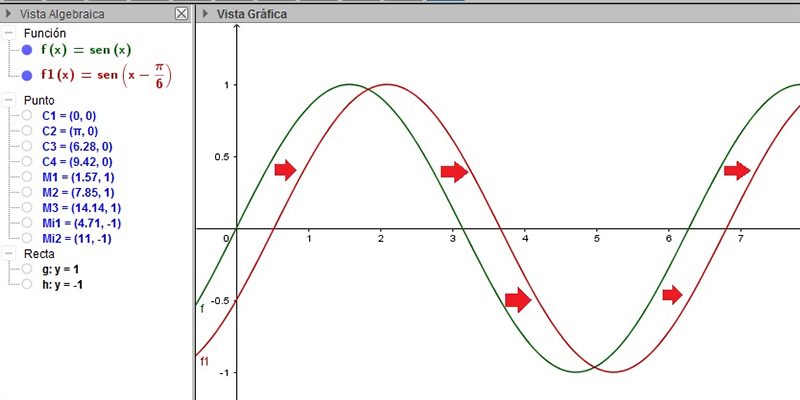
En la imagen 2.22 dibujamos a la función f(x) = seno(x) (donde x, la variable independiente, representa al ángulo) acompañada de la función \( f1(x) = seno \left( x + \frac{\pi}{6} \right) \). La primera aparece en color verde, y la segunda se dibujó en color rojo. Las pequeñas flechas rojas señalan el sentido en el que la segunda función se desplazó respecto de la primera.
Las flechas indican el sentido del desplazamiento horizontal de \( f1(x) = seno \left( x + \frac{\pi}{6} \right) \) respecto de \( f(x) = seno (x) \).
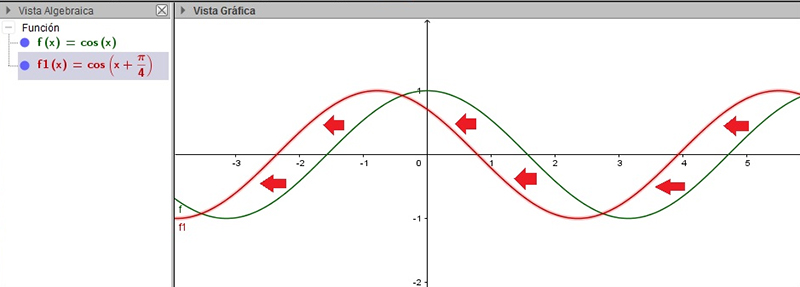
En la imagen 2.23 representamos las funciones \( f(x) = coseno (x) \) (en color verde) y \( f1(x) = coseno \left( x + \frac{\pi}{4} \right) \) (en color rojo). Nuevamente utilizamos flechas rojas para señalar el desplazamiento de la segunda de las curvas respecto de la primera. A diferencia de lo que sucedía en el caso anterior, en esta oportunidad la curva se desplaza hacia la izquierda.
Aquí también se observa el desplazamiento horizontal de una función trigonométrica. En este caso, \( f1(x) = coseno \left( x + \frac{\pi}{4} \right) \) se mueve hacia la izquierda respecto de la función coseno. Es sencillo reconocer el sentido del desplazamiento a partir del signo del ángulo que afecte a la variable independiente: cuando se resta, el desplazamiento es hacia la derecha, mientras que, cuando se suma, el desplazamiento será hacia la izquierda.
Lo dicho para las funciones trigonométricas es válido para todo tipo de función.
Podemos concluir que, cuando a la variable independiente se le suma o resta un coeficiente —que en el caso de las funciones trigonométricas habrá de ser un ángulo medido en radianes—, se obtiene una segunda curva que está desplazada hacia la izquierda o derecha (respectivamente).
Dicho desplazamiento será igual al del ángulo que se sumó o restó a la variable.
2.3.2. Desplazamientos verticales
Cuando a la propia función se le suma o resta un escalar, se observará un desplazamiento de aquella hacia arriba o hacia abajo.
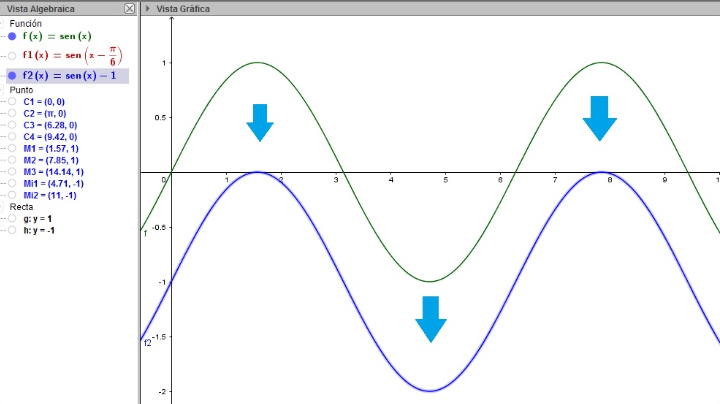
En la imagen 2.24 volvemos a representar a la función f(x) = seno(x), pero esta vez junto a la función f2(x) = seno(x) - 1 (la primera de ellas en color verde y la segunda, en color azul). En este caso, hemos señalado con flechas de color azul el sentido en el que se produjo el desplazamiento.
Cuando a la función (y no a la variable independiente, como vimos en la sección anterior) se le suma o resta un valor, la función obtenida se desplazará verticalmente respecto de la original (que en el presente ejemplo es la función seno).
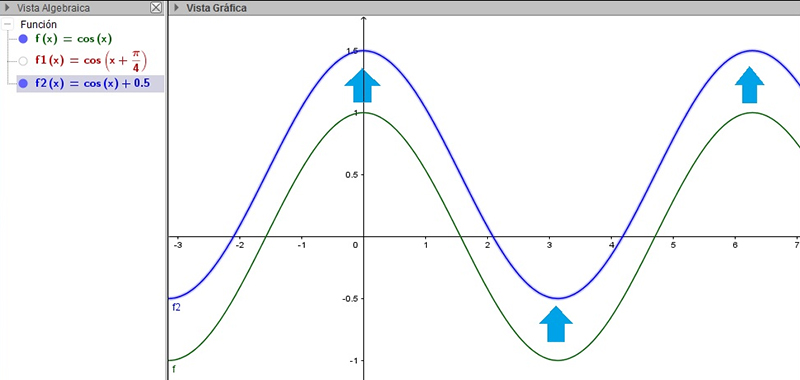
En la imagen 2.25 representamos la función f(x) = coseno (x), pero esta vez junto a la función f2(x) = coseno (x) + 1/2 (la primera de ellas en color verde y la segunda, en color azul). Nuevamente, señalamos con flechas de color azul el sentido en el que se produjo el desplazamiento.
Al sumarle a la función coseno(x) el valor \( \frac{1}{2} \), observamos el desplazamiento vertical ascendente de aquella.
Cuando a la función le sumamos o restamos un escalar “a”, la función toda se desplaza hacia arriba o abajo en “a” unidades.
2.3.3. Cambio de amplitud
La amplitud es una característica notable para las funciones seno y coseno. Podemos definirla sencillamente como la distancia (medida en sentido vertical) desde el eje de abscisas y el máximo (o mínimo) de dicha función (resulta indistinto si hablamos de máximo o mínimo, pues tratándose de una distancia, lo que nos interesa es el módulo o valor absoluto).
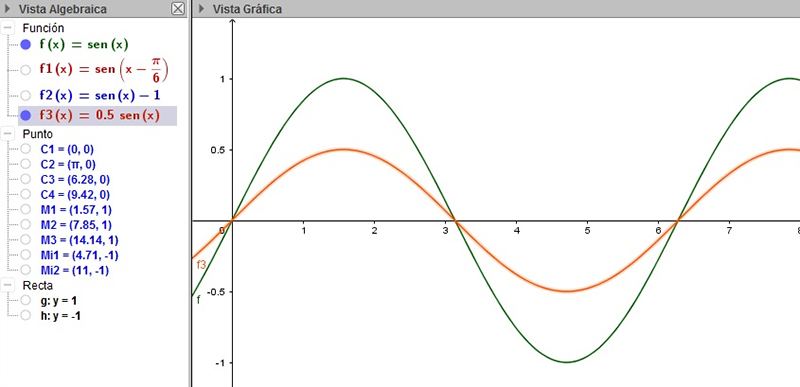
En la imagen 2.26 se observan las funciones \( f (x) = seno(x) \) (en color verde) y \( f3(x) = 0.5 \ast seno(x) \) (en color naranja). El escalar que multiplica a la función define el cambio de la amplitud. Nótese que esta última se ha reducido a la mitad respecto de la que correspondía a la función original (la amplitud de las funciones seno y coseno es igual a la unidad). Además, es importante reconocer el hecho de que, a diferencia de lo que sucedía en los desplazamientos verticales y horizontales, en esta oportunidad los ceros de la función siguen siendo los mismos que los de la función original.
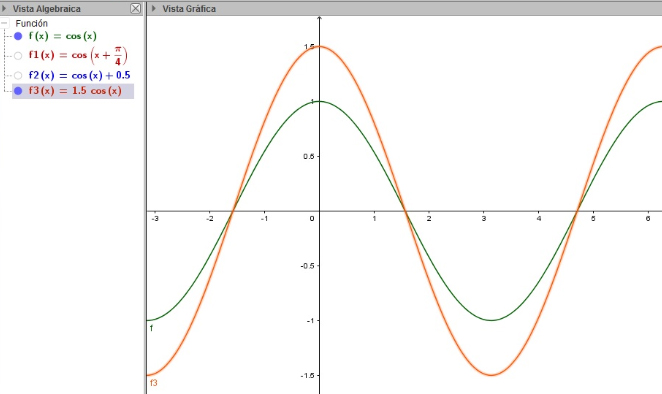
En la imagen 2.27 se comparan las funciones \( f (x) = coseno(x) \) con \( f3(x) = 1.5 \ast coseno(x) \). En este caso, siendo el escalar que multiplica a la función mayor que la unidad, la amplitud aumenta.
Al multiplicar a la función por un escalar se obtiene un cambio de amplitud.
La amplitud aumenta o disminuye respecto de la de la función original a partir del hecho de que el número por el cual se multiplique sea en módulo mayor o menor que la unidad.
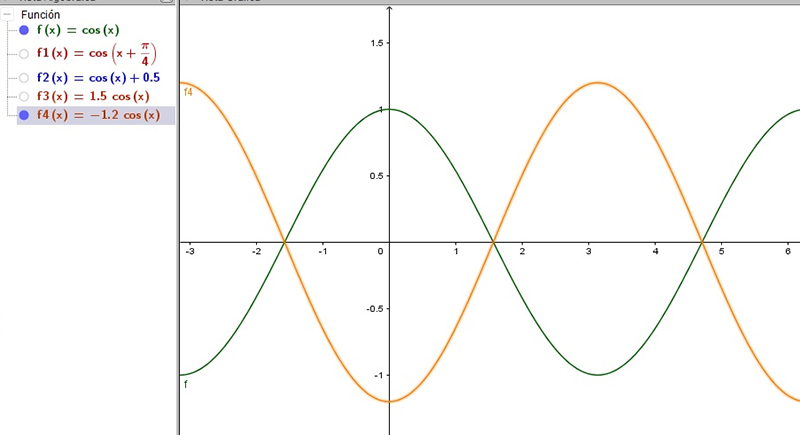
Cabe aclarar que el número que multiplica a la función no solo afecta su amplitud, sino que también puede alterar su comportamiento desde otra perspectiva: invertir los ciclos de crecimiento y decrecimiento. Esto puede observarse en la imagen 2.28, donde se comparan las funciones \( f (x) = coseno(x) \) con \( f4(x) = -1.2 \ast coseno(x) \); nótese que las abscisas de los máximos de la primera se corresponden con los de los mínimos de la segunda y viceversa.
En este caso, siendo el escalar que multiplica a la función mayor que la unidad, la amplitud aumenta.
Cuando el número por el cual se multiplica a la función original es negativo, no solo cambia la amplitud, sino que también se altera totalmente su comportamiento: en aquel intervalo donde la función original crecía, la nueva función será decreciente (y viceversa).
Cuando a la función seno o coseno se la multiplica por un número no nulo “a”, la amplitud de la función cambia.
Si, además, “a” resulta ser negativo, se invierten los ciclos de crecimiento y decrecimiento, convirtiéndose los máximos en mínimos y viceversa.
2.3.4. Cambio de período
Ante todo, definiremos como período al ángulo (medido en radianes) que la curva requiere para describir una oscilación completa. Tanto en el caso de las funciones seno como coseno, dicho período es de \( 2 \pi \) radianes.
Aclaremos que un cambio de escala apropiado puede convertir al período en un simple número. En el caso de las ondas sonoras o las electromagnéticas (dentro de las cuales se encuentra la luz visible), ese número habrá de medirse en metros y se le dará el nombre de longitud de onda. En cambio, en el caso de estudiar la oscilación de un péndulo, por ejemplo, el período suele definirse como el tiempo para que se describa una oscilación completa; en este caso, dicho período se medirá en unidades de tiempo (generalmente, en segundos).
En la imagen 2.29, el período de la función queda determinado entre C1 y C3.
El período de las funciones seno(x) y coseno(x) vale \( 2 \pi \) radianes.
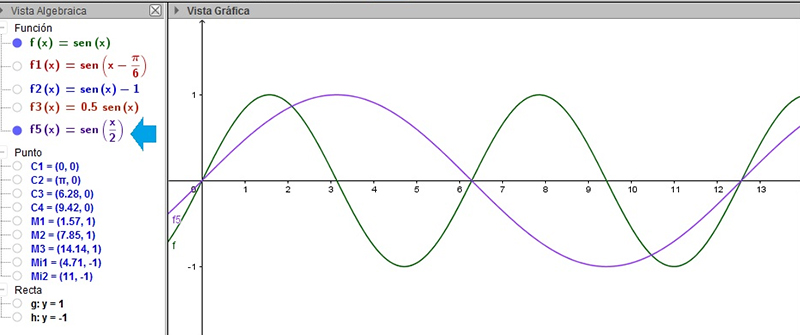
El cambio de período se produce cuando la variable independiente es multiplicada por un coeficiente dado. En la imagen 2.30, representamos conjuntamente las funciones \( f (x) = seno(x) \) y \( f5(x) = seno \left( \frac{x}{2} \right) \).
El \( \frac{1}{2} \) que multiplica a la variable independiente duplica el período respecto del de la función original. Nótese que para cuando la curva azul (que representa a f5(x)) describe una oscilación completa, la función original (siempre representada en color verde) ya produjo dos oscilaciones.
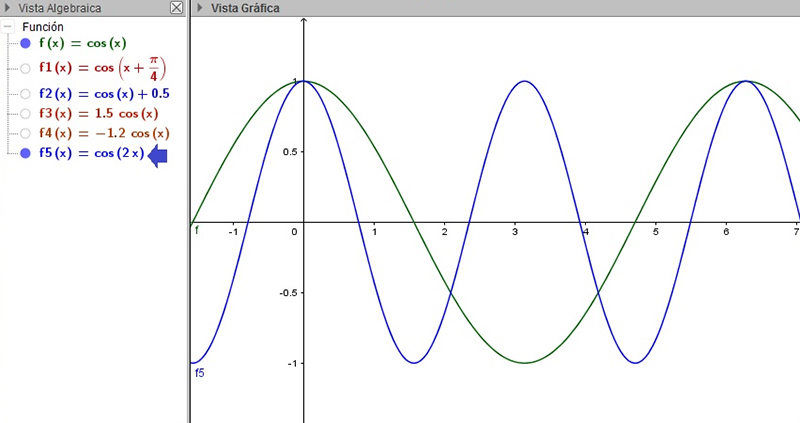
La imagen 2.31, en cambio, representa a las funciones \( f (x) = coseno(x) \) y \( f5(x) = coseno ( 2 \ast x) \). En este caso se observa que el período de la segunda resulta ser la mitad del de la función original.
El período de f(x) =seno (a.x) o g(x) =coseno (a.x) podrá calcularse fácilmente dividiendo a \( 2 \pi \) por a.
Representamos en la misma gráfica las funciones \( f (x) = seno(x) \) junto con \( f5(x) = seno \left( \frac{x}{2} \right) \).
Representamos en el mismo gráfico las funciones \( f (x) = coseno(x) \) y \( f5(x) = coseno ( 2 \ast x) \)
Utilizando el software, representar en un mismo gráfico las funciones trigonométricas que se detallan en cada caso (es decir, obtener tres gráficos, en cada uno de los cuales figuren las tres curvas que se detallan en cada ítem). Comparar las gráficas y extraer conclusiones.
- \( f1(x) = seno (x); f2(x) = seno (2x); f3 (x) = 2seno (x) \)
- \( g1(x) = coseno(x); g2(x) = coseno (x - \pi /2 ); g3(x) = seno(x) \)
- \( h1(x) = coseno (x); h2 (x) = coseno(x) + 2; h3(x) = 2coseno (x) \)
Stewart, J.; Redlin, L.; Watson, S. (2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 368 a 376.
2.4. Relaciones trigonométricas: seno, coseno, tangente, cotangente, secante y cosecante
En la sección 2 definimos las seis relaciones posibles a partir de las razones de los lados de los triángulos rectángulos. Sin embargo, es conveniente conocer algunas de las relaciones que existen entre dichas razones, especialmente, aquellas que las vinculen con el seno o el coseno.
(Cuando, por ejemplo, se calculen las derivadas de la mayoría de estas razones, será conveniente hacerlo a partir de las expresiones que hemos de brindar seguidamente).
Para comenzar, teniendo en cuenta que:
\[ seno(\hat{A}) = \frac{cateto \ opuesto}{hipotenusa} \]
y que:
\[ cosecante(\hat{A}) = \frac{ hipotenusa}{cateto \ opuesto} \]
podremos entonces decir que:
\[ cosecante(\hat{A}) = \frac{1}{seno(\hat{A})} \]
Análogamente, si recordamos que:
\[ coseno(\hat{A}) = \frac{cateto \ adyacente}{hipotenusa} \]
y que:
\[ secante(\hat{A}) = \frac{ hipotenusa}{cateto \ adyacente} \]
se deduce que:
\[ secante(\hat{A}) = \frac{1}{coseno(\hat{A})} \]
Por otro lado, teniendo en cuenta que:
\[ tangente(\hat{A}) = \frac{cateto \ opuesto}{cateto \ adyacente} \]
y que:
\[ catangente(\hat{A}) = \frac{cateto \ adyacente}{cateto \ opuesto} \]
se deduce fácilmente que:
\[ catangente(\hat{A}) = \frac{1}{tangente(\hat{A})} \]
Otra relación de suma utilidad es la siguiente:
\[ tangente(\hat{A}) = \frac{seno(\hat{A})}{coseno(\hat{A})} \]
A partir de las definiciones del seno y el coseno, demostrar la validez de esta última igualdad.
Existen otras relaciones un tanto más complejas, de suma utilidad. Tal vez la más importante de todas ellas recibe el nombre de identidad pitagórica y expresa lo siguiente:
\[ (seno(\hat{A}))^2 + (coseno(\hat{A}))^2 = 1 \]
Las identidades que permiten calcular el seno o coseno de la suma o resta de ángulos también pueden ser de interés en el caso de algunos desarrollos matemáticos. Por ese motivo, las reproducimos seguidamente:
\[ seno(\hat{A} + \hat{B}) = seno(\hat{A}) coseno (\hat{B}) + seno(\hat{B}) coseno (\hat{A}) \]
\[ seno(\hat{A} - \hat{B}) = seno(\hat{A}) coseno (\hat{B}) - seno(\hat{B}) coseno (\hat{A}) \]
\[ coseno(\hat{A} + \hat{B}) = coseno(\hat{A}) coseno (\hat{B}) - seno(\hat{B}) seno (\hat{A}) \]
\[ coseno(\hat{A} - \hat{B}) = coseno(\hat{A}) coseno (\hat{B}) + seno(\hat{B}) seno (\hat{A}) \]
A partir de las expresiones anteriores, demostrar que:
\[ seno(2 \hat{A}) = 2seno(\hat{A}) coseno (\hat{A}) \]
\[ coseno(2 \hat{A}) = (coseno(\hat{A}))^2 - (seno (\hat{A}))^2 \]
2.4.1. Tabla de valores usuales para el seno, el coseno y la tangente
En muchas aplicaciones es conveniente conocerel valor del seno o el coseno de algunos ángulos significativos, como \( \pi /6 \), \( \pi /4 \) o \( \pi /3 \). Veremos seguidamente de qué modo obtenerlos y confeccionaremos una pequeña tabla que habrá de resultarnos de suma utilidad: la tabla de valores usuales, dentro de la cual se vuelcan dichos valores.
En la imagen 2.32 se representa un triángulo equilátero, es decir, un triángulo que tiene todos sus lados iguales. Ello implica, por otro lado, que sus ángulos interiores también lo serán y cada uno de ellos será de \( \pi / 3 \) radianes.
Todo triángulo equilátero tiene sus tres lados y sus tres ángulos interiores iguales.
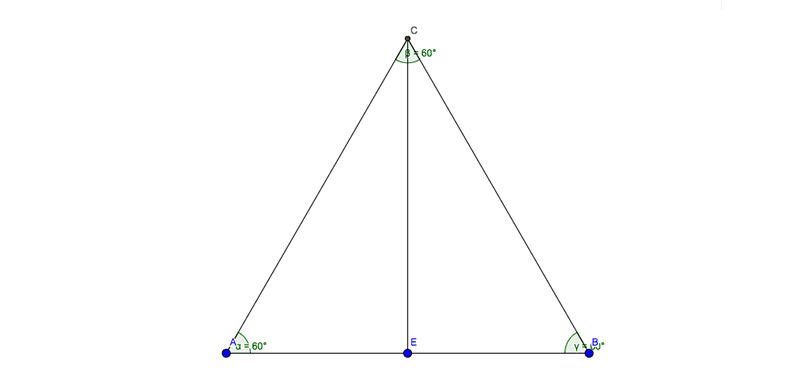
Trazamos un segmento perpendicular a la base que pase por su punto medio, de modo que el triángulo equilátero quede dividido en dos triángulos rectángulos. Vamos a trabajar con el triángulo de vértices A, E y C, que aparece coloreado en la imagen 2.33. Calcularemos el seno y el coseno del ángulo \( \hat{A} \), suponiendo que cada uno de los lados del triángulo original valía l. Este será entonces el valor de la hipotenusa del triángulo rectángulo, en tanto que su cateto adyacente tendrá una longitud de valor l/2 (dado que la distancia entre A y E resulta ser la mitad de uno de los lados del triángulo equilátero).
Dividimos al triángulo equilátero en dos, a partir de una vertical trazada desde el punto medio de su base.
Para el cálculo del cateto opuesto aplicaremos el Teorema de Pitágoras. De acuerdo con su enunciado, sabemos que:
\[ hipotenusa^2 = cateto \ opuesto^2 + cateto \ adyacente^2 \]
Reemplazando entonces para nuestro caso:
\[ l^2 = \left( \frac{l}{2} \right) ^2 + \overline{EC}^2 \]
Operamos a partir de dicha expresión:
\[ l^2 - \left( \frac{l}{2} \right) ^2 = \overline{EC}^2 \to \frac{3}{4} l^2 = \overline{EC}^2 \to \overline{EC} = \frac{\sqrt{3}}{2} l \]
Una vez calculado el valor del cateto opuesto, podemos escribir:
\[ seno (\pi / 3) = \frac{cateto \ opuesto}{hipotenusa} = \frac{\frac{\sqrt{3}}{2}l}{l} = \frac{\sqrt{3}}{2} \]
\[ coseno (\pi / 3) = \frac{cateto \ adyacente}{hipotenusa} = \frac{\frac{l}{2}}{l} = \frac{1}{2} \]
Obtuvimos de ese modo el seno y el coseno de \( \pi / 3 \)
Si volvemos a trabajar con el triángulo rectángulo coloreado de la imagen 2.33, pero estudiamos las razones entre los lados vistas desde el ángulo \( \hat{C} / 2 \), cuyo valor es de \( \pi / 6 \) radianes, lo que cambiará será la posición relativa de los catetos (el opuesto para el ángulo \( \hat{A} \) resulta ser el adyacente para el \( \hat{C} / 2 \) y viceversa). Entonces, podemos calcular:
\[ seno (\pi / 6) = \frac{cateto \ opuesto}{hipotenusa} = \frac{\frac{1}{2}}{l} = \frac{1}{2} \]
\[ coseno (\pi / 6) = \frac{cateto \ adyacente}{hipotenusa} = \frac{\frac{\sqrt{3l}}{2}}{l} = \frac{\sqrt{3}}{2} \]
Para obtener los valores del seno y el coseno de \( \pi / 4 \) radianes vamos a trabajar con un triángulo rectángulo isósceles. Es decir, un triángulo tal que sus dos catetos habrán de medir lo mismo (imagen 2.34).
Todo triángulo rectángulo isósceles tiene sus dos catetos iguales. Además, como la suma de sus tres ángulos interiores debe valer 180 grados y uno de ellos es recto, los otros dos deberán ser iguales entre sí. El valor de estos últimos, entonces, será de 45 grados.
En esta oportunidad, diremos que l es el valor de la longitud de cada uno de los catetos y tendremos que obtener la longitud de la hipotenusa. Aplicando otra vez el Teorema de Pitágoras, podemos escribir:
\[ \overline{BC}^2 = l^2 + l^2 = 2l^2 \to \]
\[ \to \overline{BC} = \sqrt{2l^2} \to \overline{BC} = \sqrt{2} l \]
Teniendo en cuenta que ambos catetos tienen la misma longitud, podemos entonces escribir:
\[ seno ( \pi / 4) = \frac{cateto \ opuesto}{hipotenusa} = \frac{l}{\sqrt{2}l} = \frac{1}{\sqrt{2}} \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
\[ coseno ( \pi / 4) = \frac{cateto \ adyacente}{hipotenusa} = \frac{l}{\sqrt{2}l} = \frac{1}{\sqrt{2}} \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
Es decir:
\[ seno ( \pi / 4) = coseno ( \pi / 4) = \frac{\sqrt{2}}{2} \]
A partir de lo expresado en la sección 2.1, en la que se obtuvieron los valores del seno y el coseno para los ángulos de cero y de \( \pi /2 \) radianes, volcamos todos los datos en la siguiente tabla, que recibe el nombre de tabla de valores usuales:

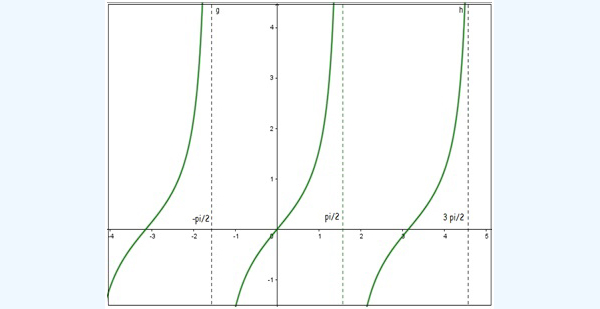
La última fila corresponde a los valores de la función tangente, que, de acuerdo con lo que anticipamos en la sección 2.3, no es otra cosa que el cociente entre el seno y el coseno de un determinado ángulo. En la imagen 2.35 representamos gráficamente la función tangente. Podrá interpretarse entonces el valor que aparece dentro de la tabla en último término: cuando el ángulo adopta valores próximos a los noventa grados, el valor de la tangente se hace infinitamente grande.
Gráfica de la función tangente. Se observa que al aproximarnos a los noventa grados, la función adopta valores que tienden a infinito (si nos aproximamos por la derecha) o a menos infinito (si lo hacemos por la izquierda).
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 47 a 55.
2.4.2. Resolución de situaciones problemáticas
Todo lo planteado hasta el momento ha de servirnos para la resolución de situaciones problemáticas. A continuación proponemos un par de problemas básicos y los resolveremos.
Un turista se detiene una noche frente al Cabildo. A su izquierda, a cinco metros de distancia, hay un farol, cuya luminaria se encuentra a cuatro metros de altura. El hombre mide 1,70 metros (imagen 2.36). En estas condiciones, ¿cuál será la longitud de la sombra que proyecte el hombre, medida sobre el suelo de la Plaza de Mayo?
Existen varias formas de resolver el problema. Nosotros proponemos hacerlo a partir de la proporcionalidad entre los lados de triángulos rectángulos. Partiendo de un razonamiento similar al empleado al principio de la presente unidad, vamos a definir tres triángulos rectángulos (imagen 2.37): para comenzar, el que tiene como vértices a los puntos A, C y E; luego tenemos al triángulo rectángulo de vértices A, B y F; y finalmente, el triángulo rectángulo que tiene por vértices a los puntos D, F y E. Es evidente que entre estos dos últimos debe existir proporcionalidad, dado que son rectángulos y comparten un ángulo, el \( \ \).
Por otro lado, si consideramos a la recta que contiene los puntos B y F y a la que contiene a los puntos C y E, ambas serán paralelas. Ambas son cortadas por la recta que contiene los puntos A y E, de modo que los ángulos \( \hat{F} \) y \( \hat{E} \) serán iguales por ser correspondientes entre paralelas. Por esa razón, también podremos definir las relaciones de proporcionalidad entre este último triángulo y los dos anteriores.
El objetivo es determinar la longitud de la sombra proyectada por el turista detenido frente al Cabildo y debida a la luz del farol que aparece a la izquierda de la imagen.

Los puntos A, B, C, D, E y F nos permiten definir una serie de triángulos mediante los cuales resolveremos el problema.

Entonces, dado que \( \hat{F} = \hat{E} \), entonces:
\[ tan(\hat{F}) = tan(\hat{E}) \to \frac{\overline{AB}}{\overline{BF}} = \frac{\overline{FD}}{\overline{DE}} \to\]
\[ \to \overline{DE} = \frac{\overline{BF} \cdot \overline{FD}}{\overline{AB}} = \frac{5 m \cdot 1,70 m}{4 m - 1,70 m} \cong 3,21 m \]
Respondemos entonces que la longitud de la sombra del turista debida a la luz del farol mide poco más de tres metros veinte de longitud.
Veremos a continuación un segundo ejemplo en el que se hace alusión a un concepto elemental de Óptica, el de profundidad aparente. La refracción es un fenómeno que se produce cuando la luz pasa de un medio que presenta cierta densidad a otro que tiene una densidad distinta. En el enunciado del siguiente ejemplo incluimos el enunciado de la Ley de Snell, o Segunda Ley de la Refracción. El alumno no necesita conocerla previamente, sino tan solo aplicarla correctamente para la resolución del problema.
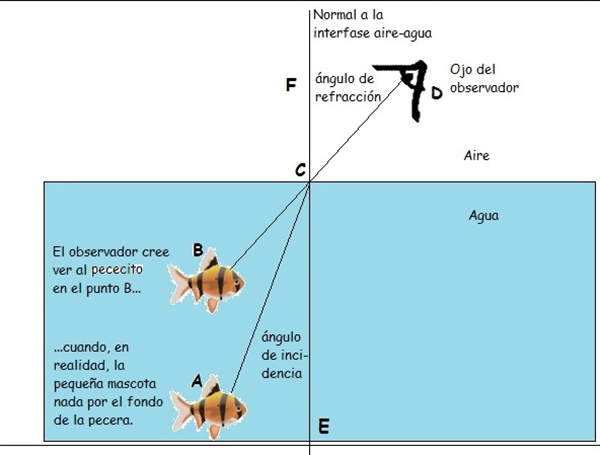
Un pequeño pez nada por el fondo de una pecera de 30 centímetros de profundidad pero, por efecto de la refracción, un observador cree verlo nadando relativamente cerca de la superficie, tal como se muestra en la imagen 2.38.
La expresión matemática del fenómeno recibe el nombre de Ley de Snell y dice lo siguiente:
\[ \frac{\text{seno del ángulo de incidencia}}{\text{seno del ángulo de refracción}} = \text{índice de refracción relativo} \]
Sabiendo que dicho índice de refracción es en este caso igual a 2/3, y que el pequeño pez se encuentra a unos diez centímetros de la normal a la interfase aire-agua (una recta imaginaria que pasa por el punto C donde la luz reflejada por el pez “se desvía” al pasar de un medio más denso, el agua, a otro menos denso, que es el aire), se pide calcular a qué distancia de la superficie del agua cree el observador que se encuentra la pequeña mascota.
Para resolver el problema utilizaremos como figura de análisis la que aparece en la imagen 2.39.
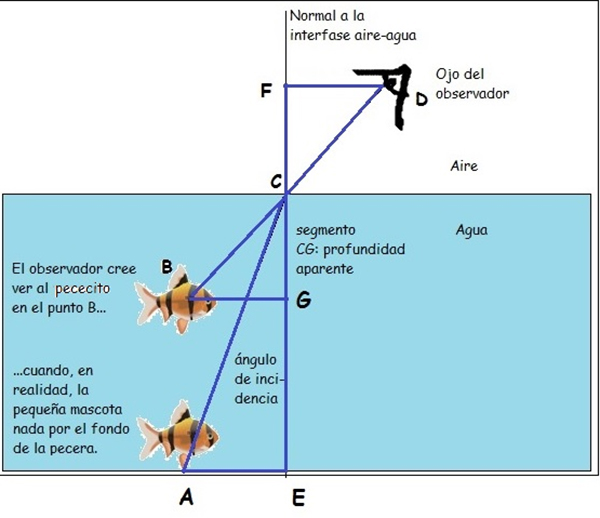
En dicha imagen, el ángulo de incidencia es el \( \widehat{ACE} \), en tanto que el ángulo de refracción es el \( \widehat{FCD} \). Este último resulta ser igual al ángulo \( \widehat{BCG} \), por ser ángulos opuestos por el vértice.
Sabiendo que el segmento \( \overline{AE} \) mide 10 centímetros y que el segmento \( \overline{CE} \) mide 30 centímetros, podemos calcular la hipotenusa del triángulo rectángulo de vértices en A, C y E, aplicando nuevamente el Teorema de Pitágoras. Tenemos entonces:
\[ \overline{AC}^2 = (10 cm)^2 + (30 cm)^2 \to \]
\[ \to \overline{AC} = \sqrt{100 + 900} = \sqrt{1000} cm \]
El seno del ángulo de incidencia se obtendrá haciendo:
\[ \text{seno del ángulo de incidencia} = \frac{\overline{AE}}{\overline{AC}} \to \]
\[ \to \text{seno del ángulo de incidencia} = \frac{10}{\sqrt{1000}} \to \]
\[ \to \text{seno del ángulo de incidencia} = \frac{1}{\sqrt{10}} = \frac{\sqrt{10}}{10} \]
Por otro lado, teniendo en cuenta que
\[ \frac{\text{seno del ángulo de incidencia}}{\text{seno del ángulo de refracción}} = \frac{2}{3} \to \]
\[ \text{seno del ángulo de refracción} = \frac{3}{2} \text{seno del ángulo de incidencia} \to \]
\[ \text{seno del ángulo de refracción} = \frac{3}{2} \times \frac{\sqrt{10}}{10} \]
Necesitamos conocer la tangente del ángulo de refracción para poder calcular la profundidad aparente. Sabiendo que la tangente de un ángulo es igual al cociente entre el seno y el coseno del este y habiendo obtenido el seno del ángulo de refracción, calcularemos el coseno teniendo en cuenta la relación pitagórica:
\[ \left( \text{seno del ángulo de refracción} \right)^2 + \left( \text{coseno del ángulo de refracción} \right)^2 = 1 \to \]
\[ \to \left( \text{coseno del ángulo de refracción} \right)^2 = 1 - \left( \text{seno del ángulo de refracción} \right)^2 \to \]
\[ \to \left( \text{coseno del ángulo de refracción} \right)^2 = 1 - \frac{90}{400} = \frac{400 - 90}{400} \to \]
\[ \to \left( \text{coseno del ángulo de refracción} \right)^2 = \frac{31}{40} \to \text{coseno del ángulo de refracción} = \frac{\sqrt{31}}{2 \sqrt{10}} \]
Tenemos así:
\[ \text{tangente del ángulo de refracción} = \frac{\text{seno del ángulo de refracción}}{\text{coseno del ángulo de refracción}} = \frac{\frac{3}{2} \frac{\sqrt{10}}{10}}{\frac{\sqrt{31}}{2\sqrt{10}}} \]
\[ \text{tangente del ángulo de refracción} = \frac{3}{\sqrt{31}} \cong 0,538816 \]
Ya anticipamos que el ángulo \( \widehat{BCG} \) era igual al ángulo de refracción, de modo que podemos escribir:
\[ \text{tangente del ángulo de refracción} = \text{tangente del } \widehat{BCG} = \frac{\text{10 centímetros}}{\text{profundidad aparente}} \]
Así:
\[ \frac{\text{10 centímetros}}{\text{profundidad aparente}} = 0,538816 \to \text{profundidad aparente} = \frac{\text{10 centímetros}}{\text{0,538816}} \]
Finalmente:
\[ \text{profundidad aparente} = 18,56 \ centímetros \]
Respondemos entonces que la profundidad aparente para el observador es de 18,56 centímetros.
Sears, F.; Zemansky, M; Young, H.; Freedman, R., (2009), Física Universitaria con Física Moderna, Volumen 2, Pearson Educación de México, México, pp. 1121 a 1130.
Múltiples problemas prácticos pueden resolverse aplicando los conocimientos de trigonometría que brindamos en la presente unidad. Proponemos al alumno la siguiente actividad para que pueda ejercitarse.
Una embarcación se aproxima a la costa. Desde el puente de la nave, la visual que llega hasta el punto más alto de un faro determina un ángulo de 37˚ con la horizontal (imagen 2.40, parte superior). La nave avanza 200 metros; en estas nuevas condiciones, la visual forma entonces un ángulo de 45˚ respecto de la horizontal (imagen 2.40, parte inferior).
Calcular la altura del faro y la distancia a la que se encontraba la embarcación respecto del primero en el momento en que se llevó a cabo la primera observación (es decir, aquella en la que la visual era de solo 37˚).
En la parte superior de la imagen observamos la primera medición. La horizontal une el puente de la embarcación con la base del faro. En la parte inferior, la nave redujo su distancia al faro en 200 metros, aumentando entonces el ángulo de la visual.
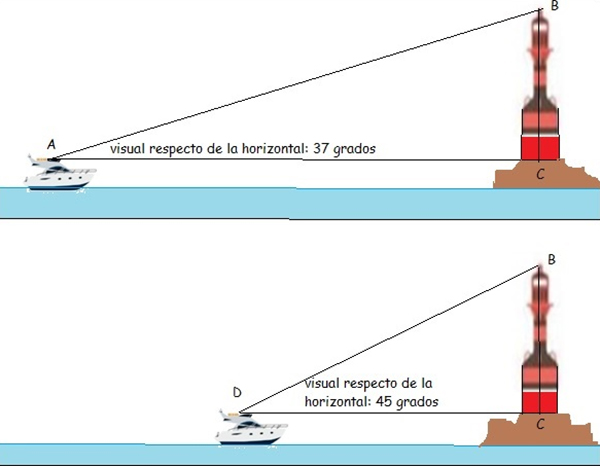
Stewart, J.; Redlin, L.; Watson, S. (2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 393 a 405 y 418 a 421.
2.5. Teoremas del seno y el coseno
Muchos problemas prácticos nos obligan a trabajar con triángulos que no tienen ningún ángulo interior recto. Para esos casos, existen dos teoremas que resultan muy útiles: el del seno y el del coseno.
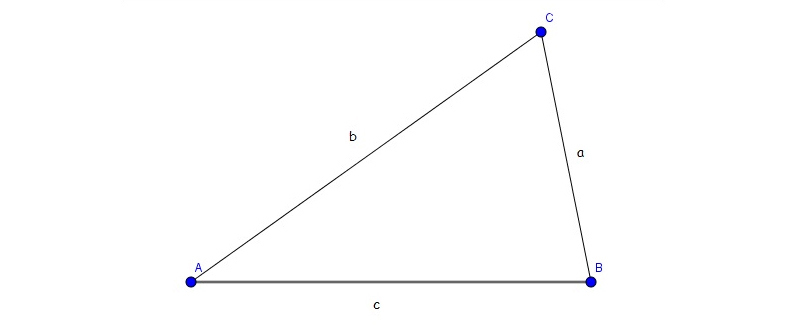
Dado un triángulo cualquiera, como el de vértices A, B y C de la imagen 2.41, donde identificamos como a, b y c la longitud de los lados opuestos a cada uno de dichos vértices, habrá de verificarse la siguiente identidad:
\[ \frac{seno(\hat{A})}{a} = \frac{seno(\hat{B})}{b} = \frac{seno(\hat{C})}{c} \]
Triángulo de vértices A, B y C
En el momento en que un pequeño aeroplano sobrevuela el pueblo A es captado por un radar militar ubicado en B y por el radar del aeródromo de la ciudad C.
Sabiendo que la distancia entre los puntos B y C es de 381 kilómetros y conocidos los ángulos \( \hat{B} \) y \( \hat{C} \), tal como se observa en la imagen 2.42, se pide calcular a qué distancia se encuentra en ese momento el avión respecto de la ciudad C.
El proceso de triangulación se utiliza desde hace muchísimos años para la navegación.
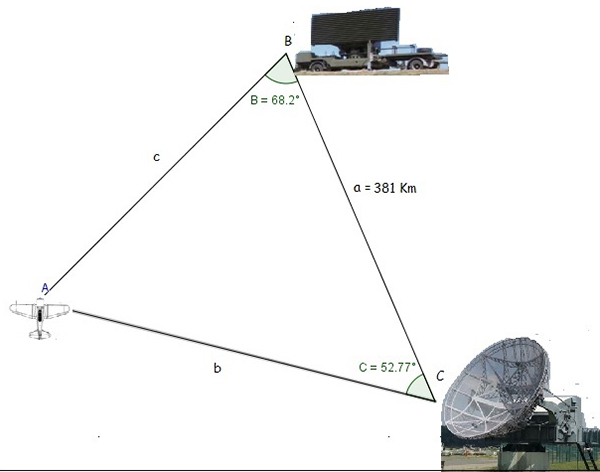
En la resolución del problema aplicaremos el teorema del seno y expresaremos:
\[ \frac{sen(\hat{B})}{b} = \frac{sen(\hat{A})}{a} \]
Nuestra incógnita es b, distancia entre el lugar donde se encuentra el aeroplano y la ciudad C. Necesitamos conocer el ángulo \( \hat{A} \), que podemos calcular teniendo en cuenta que la suma de los ángulos interiores de todo triángulo vale 180°:
\[ 180° - (68,2° + 52,77°)\cong 59° \]
Podemos entonces escribir:
\[ \frac{sen(\hat{B})}{b} = \frac{sen(\hat{A})}{a} \to \frac{sen(68,2°)}{b} = \frac{sen(59°)}{381 km} \to \]
\[ \to b = 381 km \frac{sen(68,2°)}{sen(59°)} = 412,66 km \]
Respondemos entonces que, en el momento en que el aeroplano sobrevuela el pueblo A, se encuentra a 412,66 kilómetros de la ciudad C.
El teorema del seno suele utilizarse en aquellos problemas en los que se conocen dos de los ángulos interiores del triángulo y uno de los lados. En cambio, cuando se conocen dos de los lados y el ángulo que queda determinado entre ellos, se suele utilizar el teorema del coseno.
Volviéndonos a referir al triángulo de la imagen 2.41, se verifican las siguientes tres igualdades:
\[ a^2 = b^2 + c^2 - 2bc \cdot cos (\hat{A}) \]
\[ b^2 = a^2 + c^2 - 2ac \cdot cos (\hat{B}) \]
\[ c^2 = b^2 + a^2 - 2ba \cdot cos (\hat{C}) \]
Una embarcación atraviesa un lago, desde un muelle ubicado en el punto B hacia el embarcadero representado por el punto A (imagen 2.43).
Un topógrafo ubicado en un punto C (que se encuentra a 5,39 km del embarcadero A y a 7,07 km de muelle B) determina que el ángulo entre las direcciones CA y CB es de 66,8°.
¿Cuál será la distancia total a recorrer por la embarcación, suponiendo que lo hace en línea recta entre los puntos de partida y de llegada?
La embarcación parte de B y navega hacia A y deseamos calcular la distancia que separa esos dos puntos
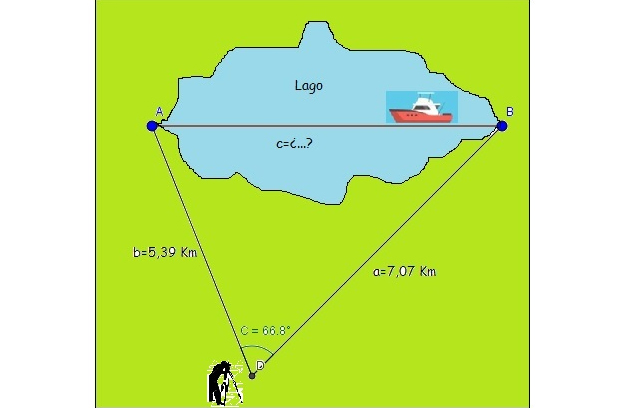
Siendo la longitud c nuestra incógnita, escribiremos:
\[ c^2 = b^2 + a^2 - 2ba \cdot cos (\hat{C}) \to \]
\[ \to c^2 = (5,39 km)^2 + (7,07 km)^2 - \]
\[ - 25,38 km \cdot 7,07 km \cdot cos (\widehat{66,8°}) = 49 km^2 \]
Respondemos entonces que la distancia que habrá de recorrer en línea recta la embarcación es de 7 km.
Stewart, J; Redlin, L; Watson, S. (2001) Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 435 a 444.

