8. Primitivas e integrales
Objetivos
Que el alumno:
- Comprenda la relación entre derivadas e integrales, lo que le facilitará el cálculo de las primitivas.
- Aprenda los distintos métodos de integración y desarrolle algunos criterios básicos para aplicar en cada caso el procedimiento adecuado.
- Descubra las aplicaciones de las integrales definidas.
- Aprenda a resolver ecuaciones diferenciales elementales.
- Aprenda a calcular integrales aplicando desarrollos de Taylor.
8.1. Primitivas e integrales
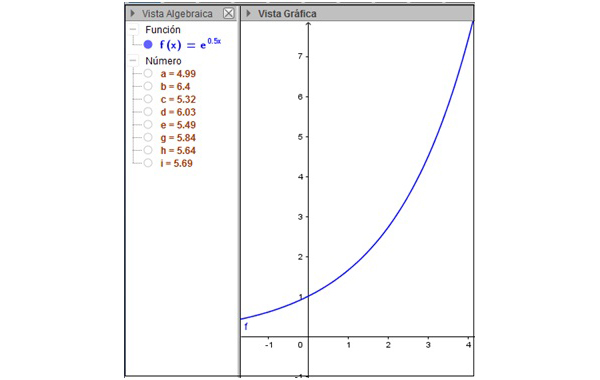
La imagen 8.1 representa a la función \( f(x)=e^{0,5x} \). Supongamos que nos interesara calcular el área encerrada entre la curva representativa de la función y el eje de abscisas, en el intervalo [1,3].
Como el alumno aún no dispone de una herramienta mejor, proponemos aproximar el valor de dicha área a través de rectángulos cuya base se encuentre sobre el eje de abscisas y que tengan uno de sus vértices superiores sobre la curva. Todos esos rectángulos tendrán bases de la misma longitud.
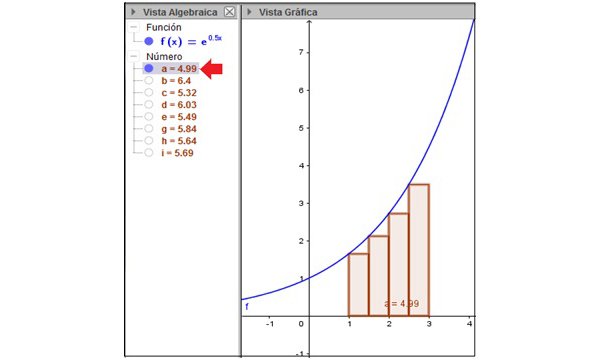
El software del que disponemos posee un par de aplicaciones que nos resultan muy valiosas (suma inferior y suma superior), que dibujan dichos rectángulos y calculan la suma de sus áreas. En las imágenes 8.2 y 8.3 se observan las capturas de pantalla correspondientes a la aproximación del área mediante cuatro rectángulos; en el primer caso, el vértice superior izquierdo de cada uno de los rectángulos es un punto perteneciente a la curva, mientras que, en el segundo, es el vértice superior derecho del rectángulo el que toca a la curva. Puesto que la función es creciente, la suma de las áreas de los rectángulos que se observan en la imagen 8.2 resulta ser menor que la de los rectángulos de la imagen 8.3.
El número \( a \ \)que aparece señalado con una flecha en la vista algebraica de la imagen 8.2 representa la suma de las áreas de los cuatro rectángulos definidos en ese caso.
Nos proponemos calcular el área encerrada entre la curva y el eje de abscisas, en el intervalo [1,3]
En principio, definimos cuatro rectángulos de igual base, de tal modo que el vértice ubicado en el extremo superior izquierdo de cada uno de ellos se encuentre sobre la curva. La suma de las áreas de los cuatro rectángulos será inferior al área buscada, pero nos brindará una primera aproximación al valor que nos propusimos obtener.
Nuevamente definimos cuatro rectángulos que nos permitan obtener un valor aproximado del área buscada. Pero en esta oportunidad es su vértice superior derecho el que se encuentra sobre la curva representativa de la función.
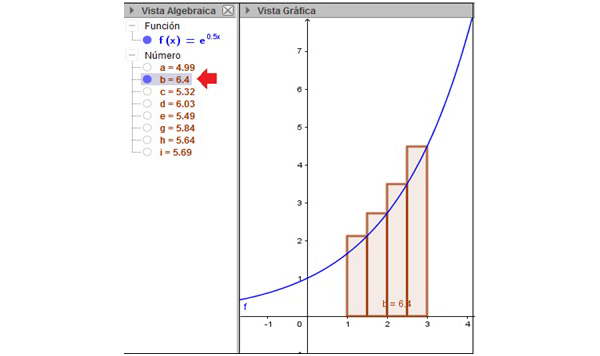
Análogamente, el número b que aparece señalado en la vista algebraica de la imagen 8.3 representa la suma de las áreas de los cuatro rectángulos definidos en ese caso. Observando detenidamente ambas imágenes, se hace evidente que b es menor al verdadero valor del área entre la curva representativa de la función y el eje de abscisas, en tanto que b habrá de ser superior. Es decir, el verdadero valor del área buscada quedará acotado entre los valores de a y b. A los fines prácticos, digamos que:
\[ a \cong 4,99 {<} \mbox{área bajo la curva} {<}b \cong 6,4 \]
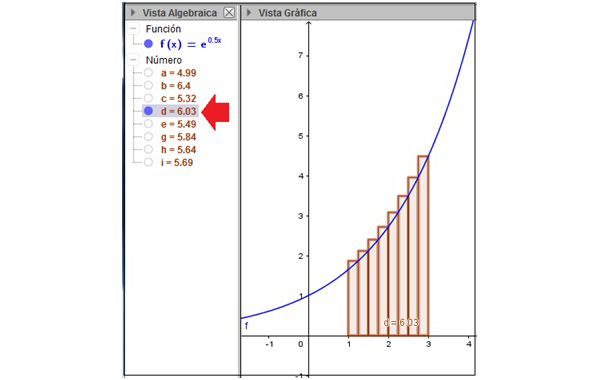
Aprovechamos la aplicación para repetir la experiencia. Pero esta vez utilizamos ocho rectángulos en lugar de cuatro. En la imagen 8.4 se observan los rectángulos cuyo vértice izquierdo se encuentra sobre la curva, en tanto que en la imagen 8.5 podemos ver los ocho rectángulos cuyo vértice derecho se apoya sobre f(x). En la vista algebraica de la imagen 8.4 señalamos el valor de la suma de las áreas de los ocho pequeños rectángulos, \( c \cong 5,32 \), mientras que el área de los ocho rectángulos de la imagen 8.5 viene representado por el número \( d \cong 6,3 \).
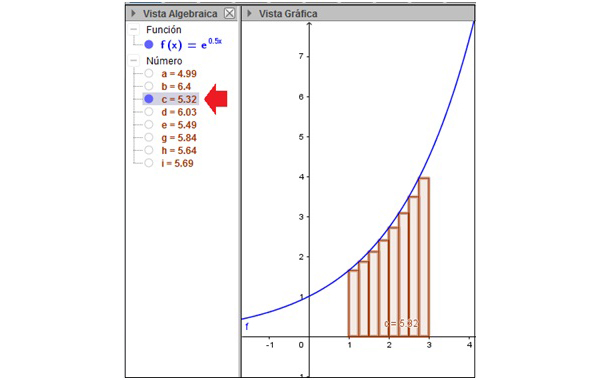
Seguimos el procedimiento descrito en la imagen 8.2, pero en este caso duplicamos el número de rectángulos empleados. El error por defecto disminuye respecto del cometido anteriormente.
Aproximamos el valor del área buscado utilizando ocho rectángulos tales que su vértice superior derecho se encuentre sobre la gráfica de la función.
Podríamos entonces escribir:
\[ a \cong 4,99 \ {<} \ c \cong 5,32 \ {<} \mbox{ área bajo la curva } {<} \ d \cong 6,3 \ {<} \ b \cong 6,4 \]
Esto significa que, a medida que el número de intervalos considerados para la aproximación aumenta, los valores de la suma inferior y superior se van aproximando entre sí.
El fenómeno se va haciendo cada vez más notable. Pedimos al alumno que se detenga en los valores e y g y en los valores h e i de la imagen 8.5. Los dos primeros representan las sumas inferior y superior, respectivamente, para el caso en que el intervalo fue dividido en 16 partes. Los últimos dos valores, prácticamente coincidentes, corresponden al caso en que el intervalo llegó a dividirse en 100 partes (la captura de pantalla de la imagen 8.6 hace prácticamente imposible diferenciar los rectángulos del área buscada).
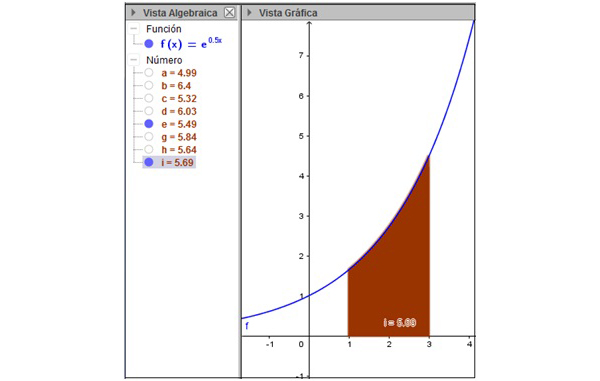
Cuando la cantidad de rectángulos aumenta dramáticamente (en la imagen se han utilizado cien rectángulos), el error que se comete con la aproximación es prácticamente despreciable.
Entonces, dada una función f(x) positiva para todo valor de la variable independiente dentro de un intervalo genérico \( [x_0,x_n ] \) al que dividimos enn segmentos iguales, podríamos escribir:
\[ \displaystyle\sum_{i=0}^{n-1} f(x_i ) (x_{i+1}-x_i ) \le \mbox {área bajo la curva} \]Y, simultáneamente:
\[ \mbox {área bajo la curva} \le \displaystyle\sum_{i=1}^{n} f(x_i ) (x_{i}-x_{i-1} ) \]
Como todos los intervalos deben ser iguales, podríamos simplificar las dos expresiones anteriores, escribiendo:
\[ \displaystyle\sum_{i=0}^{n-1} f(x_i ) \ \Delta x \le \ \mbox {área bajo la curva} \le \displaystyle\sum_{i=1}^{n} f(x_i ) \ \Delta x \]
Vimos además que, a medida que \( \Delta x \) se hacía menor (y el número de rectángulos considerados aumentaba), los valores de ambas sumatorias tendían a aproximarse. Si llevamos esta situación al extremo, podríamos decir que:
\[ \displaystyle\lim_{ \Delta x \to 0} \displaystyle\sum_{i=0}^{n-1} f(x_i ) \ \Delta x \ \le \mbox {área bajo la curva} \le \displaystyle\lim_{ \ \Delta x \to 0} \displaystyle\sum_{i=1}^{n} f(x_i ) \ \Delta x \]
La diferencia entre los límites de ambas sumatorias sería prácticamente nula, y podríamos entonces escribir:
\[ \displaystyle\lim_{ \ \Delta x \to 0} \displaystyle\sum_{i=0}^{n-1} f(x_i ) \ \Delta x \ \cong \displaystyle\int_{x_0}^{x_n} f(x)dx \ = \mbox{área bajo la curva} \]
El límite de la sumatoria sería reemplazado por \( \int_{x_0}^{x_n} f(x)dx \), que habrá de leerse como integral de la función f(x) entre x0 y xn.
Podemos entonces decir que la integral definida de una función que sea positiva dentro de un determinado intervalo representa numéricamente el área encerrada entre dicha curva y el eje de abscisas.
La pregunta que podemos hacernos ahora es: ¿cómo se calcula una integral definida? Como veremos en la sección 8.3, existe una regla debida a Isaac Barrow (1630-1677) que nos permitirá obtener el valor numérico, pero que nos obliga a manejar previamente lo que recibe el nombre de primitiva o integral indefinida.
Dada una función f(x), diremos que la función F(X) es la primitiva de f(x) si se cumple que:
\[ F(x)= \displaystyle\int f(x)dx \]
O, lo que es lo mismo, cuando F'(x) = f(x)
Antiguamente la primitiva también recibía el nombre de antiderivada. El dato sería irrelevante si no fuera porque, como veremos en la siguiente sección, la relación entre derivadas e integrales es fundamental en el campo del Análisis Matemático.
8.2. Cálculo de primitivas utilizando tablas y reglas
Así como para el cálculo de las derivadas empleamos una pequeña tabla, en la que figuraban las derivadas de ciertas funciones elementales, comenzamos la presente sección ofreciendo al alumno una tabla de integrales elemental.
Tener presente que:
- \( \displaystyle\int 1.dx=x+C \)
- \( \displaystyle\int x^n dx= \frac {x^{n+1}}{n+1}+C \ \ \ \ si \ n \not= -1 \)
- \( \displaystyle\int e^x dx=e^x+C \)
- \( \displaystyle\int a^x dx= \frac {a^x}{ln(a)}+C \)
- \( \displaystyle\int cos(x)dx=sin(x)+C \)
- \( \displaystyle\int sin(x)dx=-cos(x)+C \)
- \( \displaystyle\int \frac 1x dx=ln|x|+C \)
Obsérvese que en todos los casos se suma una constante C, que recibe el nombre de constante de integración. Esta nos indica que una integral definida no tiene una solución única, sino infinitas soluciones que difieren entre sí de acuerdo con el valor que pueda adoptar dicha constante.
Paralelamente existen un par de sencillas reglas que nos permitirán comenzar a obtener el valor de ciertas integrales elementales.
Primera regla:
\[ \displaystyle\int k.f(x)dx=k \displaystyle\int f(x)dx \]
Es decir, si dentro de una integral hay una constante, esta puede sacarse fuera de la integral, de modo que terminará multiplicando el resultado de aquella.
Calcular \( \displaystyle\int 5x^3 dx \)
Resolución:
Podemos escribir: \( \displaystyle\int 5x^3 dx=5 \displaystyle\int x^3 dx=5 \frac {x^4}{4} +C=\frac 54 x^4+C \)
Calcular \( \displaystyle\int 3.2^x dx \)
Resolución:
Podemos escribir: \( \displaystyle\int 3.2^x dx =3 \displaystyle\int 2^x dx=3 \frac {2^x}{ln(2)} +C \)
Segunda regla:
\( \displaystyle\int f(x) \pm g(x)dx= \displaystyle\int f(x)dx \pm \displaystyle\int g(x)dx \)
Es decir, la integral de la suma o resta de dos o más funciones es igual a la suma o resta de las integrales de cada una de dichas funciones.
Calcular \( \displaystyle\int (2^x+x^2)dx \)
Resolución:
Podemos escribir: \( \displaystyle\int (2^x+x^2)dx = \displaystyle\int 2^x dx+ \displaystyle\int x^2 dx= \frac {2^x}{ln(2)} + \frac {x^3}{3}+C \)
Ambas reglas pueden aplicarse simultáneamente, tal como veremos en el siguiente ejemplo.
Calcular \( \displaystyle\int \left(2x^3-3 sin(x)+\frac 5x \right) dx \)
Resolución:
Podemos escribir: \( \displaystyle\int \left(2x^3-3 sin(x)+\frac 5x \right) dx \) \( = \displaystyle\int 2x^3 dx- \displaystyle\int 3 sin(x)dx+ \displaystyle\int \frac 5x dx= \) \( =2 \displaystyle\int x^3 dx-3 \displaystyle\int sin(x)dx+5 \displaystyle\int \frac 1x dx= \) \( =2 \frac {x^4} {4 }+3 cos(x)+5ln|x|+C \)
Obsérvese en estos dos últimos ejemplos que no se escribe una constante de integración por cada una de las integrales que se resuelven, sino que solo se adopta una única constante, supuesta para la integral inicial.
Aquellas integrales que pueden resolverse aplicando exclusivamente la tabla y las reglas reciben el nombre de integrales inmediatas.
Resolver las siguientes integrales inmediatas:
- \( \displaystyle\int (x^3-5+cos(x)) dx \)
- \( \displaystyle\int \left(3x- \frac5x +x^5 \right) dx \)
- \( \displaystyle\int \left(\frac2x+2cos(x)-9 \right)dx \)
- \( \displaystyle\int \left(3e^x+6/x-4x^3 \right)dx \)
- \( \displaystyle\int \left(5x^4-3x^2+\frac 2x-cos(x)\right)dx \)
Recomendamos al alumno verificar los resultados obtenidos empleando el wxMaxima. En la sección 8.5 encontrará las instrucciones necesarias para poder hacerlo.
Como veremos seguidamente, no todas las integrales podrán ser calculadas en forma inmediata. Es por eso que, en las próximas secciones, nos detendremos en los diversos métodos de integración.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 247 a 267.
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 243 a 248.
8.3. Métodos de integración
La presencia de una función compuesta dentro de una integral, del producto de dos funciones o del cociente de funciones polinómicas nos llevarán a aplicar distintos procedimientos para la obtención de una primitiva, como veremos a continuación.
8.3.1. Método de resolución por sustitución
Cuando por simple observación nos demos cuenta de que nuestra integral no es inmediata, debemos buscar alguna alternativa para su resolución. Por ejemplo, si nos encontramos ante una función compuesta (es decir, una función en la que la variable independiente es reemplazada por otra función), nos veremos en la necesidad de efectuar lo que se denomina un cambio de variable o,más simplemente, una sustitución.
Sabiendo que \( F(x)= \displaystyle\int x.sin(x^2 ) dx \) , hallar F(x)
Resolución:
Dentro de la integral encontramos el producto de dos funciones. Pero una de ellas es una función compuesta: no se trata de la función sin(x) con la que acostumbramos trabajar, sino que la función seno se aplica en este caso a una cuadrática, x2.
Definimos entonces una variable auxiliar:
[8.1] \[ t=x^2 \]
Si derivamos ambos miembros, obtendremos:
[8.2] \[ dt=2x.dx \to \frac {dt} {2}=xdx \]
Ahora bien, la conmutatividad del producto nos permite hacer lo siguiente:
[8.3] \[ \displaystyle\int x.sin(x^2 ) dx=\displaystyle\int sin(x^2 ) .xdx \]
Sustituyendo [8.1] y [8.2] en la [8.3], podríamos escribir:
\[ \displaystyle\int sin(x^2 ) .xdx \to \displaystyle\int sin(t) dt/2 =1/2 \displaystyle\int sin(t) dt \]
Esta última integral es inmediata, de modo que:
\[ \frac12 \displaystyle\int sin(t) dt=\frac12 (-cos(t))+C \]
Si ahora recordamos la sustitución definida en [8.1], podríamos escribir:
\[ \frac12 (-cos(t))+C=- \frac12 cos(x^2 )+C \]
De modo que, en definitiva:
\[ F(x)= \displaystyle\int x.sin(x^2 ) dx=- \frac12 cos(x^2 )+C \]
Sabiendo que \( F(x)= \displaystyle\int e^{x{^3}} x^2 dx \) , hallar F(x)
Resolución:
Es evidente que \( e^{x{^3}} \) es una función compuesta, de modo que proponemos la siguiente sustitución:
[8.4] \[ t=x^3 \]
Si, como hicimos en el ejemplo anterior, derivamos ambos miembros de la expresión, nos encontraremos ante la siguiente igualdad:
[8.5] \[ dt=3x^2 dx \to \frac{dt}3=x^2 dx \]
Si ahora sustituimos [8.4] y [8.5] en el enunciado original, obtenemos:
[8.6] \[ \displaystyle\int {e^{x^3}} x^2 dx \to \displaystyle\int e^t \frac {dt}3=\frac13 \displaystyle\int e^t dt=\frac13 e^t+C \]
A partir de la [8.4] la [8.6] podría escribirse como:
\[ \frac13 e^t+C =\frac13 {e^{x^3}}+C \]
De modo que, en definitiva:
\[ F(x)= \displaystyle\int {e^{x^3}} x^2 dx= \frac13 {e^{x^3}}+C \]
Sabiendo que \( F(x)= \displaystyle\int \frac {x}{\sqrt{x^2+5}} dx \), hallar F(x)
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 8.5 encontrará las instrucciones necesarias para poder hacerlo.
Algunas integrales que no presentan funciones compuestas en su interior también se resuelven por este método, como veremos a continuación.
Sabiendo que \( F(x)= \displaystyle\int \frac {ln(x)}{x} dx \), hallar F(x)
Resolución:
Aplicando propiedades del producto, escribimos:
[8.7] \[ \displaystyle\int \frac{ln(x)}{x} dx=\displaystyle\int ln(x) \frac1x dx \]
Si definimos:
[8.8] \[ t=ln(x) \to dt=\frac1x dx \]
Sustituyendo en [8.7] las expresiones obtenidas en [8.8], nos queda:
\[ \displaystyle\int ln(x) \frac1x dx = \displaystyle\int t.dt= \frac{t^2}2 +C \]
Considerando la sustitución aplicada:
\[ \displaystyle\int ln(x) \frac1x dx =\frac{(ln(x))^2}{2} +C \]
Pero, entonces, se obtiene:
\[ F(x)= \displaystyle\int \frac{(ln(x))}{x} dx=\frac{(ln(x))^2}{2} +C \]
En general, cuando en el numerador aparezca el logaritmo natural y en el denominador se encuentre la variable independiente, será conveniente llevar a cabo la sustitución presentada en el ejemplo anterior.
Sabiendo que \( f (x) \displaystyle\int \frac{(ln(x))^2+3 ln(x)}x dx \) , hallar F(x)
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 8.5 encontrará las instrucciones necesarias para poder hacerlo.
El siguiente ejemplo corresponde a una integral aparentemente sencilla, pero para cuya resolución debemos recordar las relaciones entre las relaciones trigonométricas estudiadas en la unidad 2.
Sabiendo que \( f (x) \displaystyle\int tg(x) dx \) , hallar F(x)
Resolución:
Recordemos que \( tg(x)= \frac {sin(x)}{cos(x)} \), de modo que podemos escribir:
[8.9] \[ \displaystyle\int tg(x) dx \displaystyle\int \frac {sin(x)}{cos(x)} \]
En esta oportunidad, resulta conveniente adoptar como variable auxiliar la función que aparece en el denominador, es decir:
[8.10] \[ t=cos(x) \to dt= -sin(x)dx \to -dt=sin(x)dx \]
Sustituyendo [8.10] en [8.9], obtenemos:
[8.11] \[ \displaystyle\int \frac {sin(x)} {cos(x)} dx = \displaystyle\int \frac{-dt}{t} =- \displaystyle\int \frac{dt}t =-ln|t|+C \]
Considerando entonces la sustitución aplicada, podemos escribir finalmente:
\[ F(x)= \displaystyle\int tg(x) dx=-ln|cos(x)|+C \]
Para finalizar la presente sección, proponemos un ejemplo en el que la función que aparece dentro de la integral resulta ser racional, siendo el grado del polinomio del denominador inferior al del denominador en una unidad. En estos casos, como veremos en el siguiente ejemplo, lo recomendable es definir la variable auxiliar a partir del denominador.
Sabiendo que \( F(x)= \displaystyle\int \frac {5x}{x^2+1} dx \) , hallar F(x)
Resolución:
Tal como lo anticipamos, escribimos:
[8.12] \[ t=x^2+1→dt=2xdx \to \frac {dt}2=x.dx \]
A partir de lo expresado en [8.12] nos queda:
\[ \displaystyle\int \frac{5x}{x^2+1} dx=5 \displaystyle\int \frac {x}{x^2+1} dx=5 \displaystyle\int \frac {dt⁄2}{t}= \frac52 \displaystyle\int \frac{dt}t =\frac52 ln|t|+C \]
Considerando entonces la sustitución aplicada, obtenemos:
\[ F(x)=\displaystyle\int \frac{5x}{x^2+1} dx= \frac52 ln|x^2+1|+C \]
Sabiendo que \( F(x)= \displaystyle\int (sin(x) )^3 cos(x) dx \) , hallar F(x)
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 8.5 encontrará las instrucciones necesarias para poder hacerlo.
Sabiendo que \( F(x)= \displaystyle\int x\sqrt{x^2-1} dx \) , hallar F(x)
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 8.5 encontrará las instrucciones necesarias para poder hacerlo.
Sabiendo que \( F(x)=\displaystyle\int x.cos(6-x^2 ) dx \) , hallar F(x)
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 8.5 encontrará las instrucciones necesarias para poder hacerlo.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 295 a 303.
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 249 a 256.
8.3.2. Método de resolución por partes
Este método suele aplicarse en el caso de que dentro de la integral aparezca el producto de dos funciones de distinta naturaleza (por ejemplo, una función polinómica por una trigonométrica). El procedimiento aplicado consiste en asignar a una de dichas funciones el nombre de u(x), mientras que la otra función (junto con el diferencial) habrán de expresarse como el diferencial de una segunda función, dv(x). Escribiremos entonces:
[8.13] \[ \displaystyle\int u(x).dv=u(x).v(x)- \displaystyle\int v(x).du \]
Los siguientes ejemplos le permitirán al alumno comprender de qué modo aplicar dicha expresión.
Sabiendo que \( F(x)=\displaystyle\int x.sin(x) dx \) , hallar F(x)
Resolución:
Si definimos
[8.14] \[ u(x) = x \ , \]entonces
[8.15] \[ du = dx \]
Por otro lado, siendo:
[8.16] \[ dv=sin(x)dx \to \displaystyle\int dv= \displaystyle\int sin(x)dx \to v(x)=-cos(x) \]
Reemplazando [8.14], [8.15] y [8.16] en la [8.13] nos queda:
\[ \displaystyle\int x.sin(x) dx=x.(-cos(x) )- \displaystyle\int -cos(x).dx \to \]
\[ \to \displaystyle\int x.sin(x) dx = -x.cos(x)+ \displaystyle\int cos(x).dx \to \]
\[ \to \displaystyle\int x.sin(x) dx=-x.cos(x)+sin(x)+C \]
Así, finalmente:
\[ F(x)= \displaystyle\int x.sin(x) dx=-x.cos(x)+sin(x)+C \]
Obsérvese que en la [8.16] no se sumó constante de integración alguna, a pesar de tratarse de la resolución de una integral indefinida. Se trata de una práctica habitual, que evita el hecho de ir arrastrando a lo largo de un desarrollo una constante que, finalmente, habrá de sumarse con la que se obtenga en el último paso del desarrollo.
Sabiendo que \( F(x)=\displaystyle\int ln(x).x^5 dx \) , hallar F(x)
Resolución:
Si definimos [8.17] \( u(x)=ln(x) \) ,
entonces [8.18] \( du= \frac1x dx \)
Por otro lado, siendo:
[8.19] \[ dv=x^5 dx \to \displaystyle\int dv= \displaystyle\int x^5 dx \to v(x)= \frac{x^6}6 \]
Reemplazando [8.17], [8.18] y [8.19] en la [8.13] nos queda:
\[ \displaystyle\int ln(x).x^5 dx=ln(x). \frac{x^6}6- \displaystyle\int \frac {x^6}6. \frac1x dx \to \]
\[ \to \displaystyle\int ln(x).x^5 dx=ln(x). \frac{x^6}6- \frac16 \displaystyle\int x^5dx \to \]
\[ \to \displaystyle\int ln(x).x^5 dx=ln(x). \frac{x^6}6- \frac16 \frac{x^6}6 + c \]
Así, finalmente:
\[ F(x)= \displaystyle\int ln(x).x^5 dx=ln(x). \frac{x^6}6- \frac16 \frac{x^6}6 + c \]
Sabiendo que \( F(x)= \displaystyle\int ln(x) dx \) , hallar F(x)
Consejo: Adoptar u(x)=ln(x) y dv=dx
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 8.5 encontrará las instrucciones necesarias para poder hacerlo.
Sabiendo que \( F(x)= \displaystyle\int x.ln(x^{-1}) dx \) , hallar F(x)
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 8.5 encontrará las instrucciones necesarias para poder hacerlo.
Sabiendo que \( F(x)= \displaystyle\int e^x sin(x) dx \) , hallar F(x)
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 8.5 encontrará las instrucciones necesarias para poder hacerlo.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 525 a 530.
8.3.3. Método de resolución por descomposición en fracciones simples
Cuando debamos integrar una función racional, seguiremos una serie de pasos que detallaremos a continuación, de modo tal de transformarla en la suma (o resta, según corresponda) de una serie de integrales más elementales.
Sabiendo que \( F(x)= \displaystyle\int \frac {(x+1)}{(x-1)(x+2)} dx \) , hallar F(x)
Resolución:
Vamos a descomponer a la función en la suma de dos funciones racionales, cuyos denominadores sean de grado uno. Para ello, escribimos:
[8.20] \[ \frac{(x+1)}{(x-1)(x+2)} = \frac{A}{(x-1)} + \frac{B}{(x+2)} \]
El primer paso consiste en determinar cuánto valen los números A y B que aparecen como numeradores en la [8.20].
[8.21] \[ \frac{A}{(x-1)} + \frac{B}{(x+2)} =\frac{A(x+2)+B(x-1)}{(x-1)(x+2)} \]
Igualamos el primer miembro de la [8.20] con el segundo de la [8.21] y operamos:
[8.22] \[ \frac{(x+1)}{(x-1)(x+2)} =\frac{A(x+2)+B(x-1)}{(x-1)(x+2)} \to (x+1)=A(x+2)+B(x-1) \]
Si en la [8.22] reemplazamos a la variable independiente por el número uno, obtenemos:
[8.23] \[ (1+1)=A(1+2)+B(1-1) \to 3A=2 \to A=\frac23 \]
Del mismo modo, reemplazando en la [8.22] a la variable x por menos dos, podremos despejar el valor de B:
[8.23] \[ (-2+1)=A(-2+2)+B(-2-1) \to -3B=-1 \to B=\frac13 \]
Sustituimos los valores de A y B expresados en las [8.22] y [8.23] en la [8.20]
[8.24] \[ \frac{(x+1)}{(x-1)(x+2)} =\frac{\frac32}{(x-1)} + \frac{\frac13}{(x+2)} \]
Si, aplicando la propiedad uniforme, integramos a ambos miembros, reemplazaremos el cálculo de una única integral por el de dos integrales inmediatas:
\[ \displaystyle\int \frac{(x+1)}{(x-1)(x+2)}dx = \displaystyle\int \left( \frac{\frac32}{(x-1)} + \frac{\frac13}{(x+2)} \right) dx \]
\[ \displaystyle\int \frac{\frac23 dx}{(x-1)}dx \displaystyle\int \frac{\frac13 dx}{(x+2)}dx =\frac23 \displaystyle\int \frac {dx}{(x-1)} + \frac13 \displaystyle\int \frac {dx}{(x+2)} = \]
\[ =\frac23 ln|x-1|+\frac13 ln|x+2|+C \]
Así, finalmente:
\[ F(x)= \displaystyle\int \frac{(x+1)}{(x-1)(x+2)} dx= \frac23 ln \ |x-1|+\frac13 ln|x+2|+C \]
A las integrales de la tabla de la sección 8.1 podríamos agregar las siguientes:
- \( \displaystyle\int \frac{1}{x+a} dx =ln|x+a|+C \)
- \( \displaystyle\int \frac{1}{x-a} dx =ln|x-a|+C \)
- \( \displaystyle\int e^{ax} dx=\frac1a e^{ax}+C \)
- \( \displaystyle\int sin(ax) dx=-\frac1a cos(ax)+C \)
- \( \displaystyle\int cos(ax)dx=\frac1a sin(ax)+C \)
Sabiendo que \( F(x)= \displaystyle\int \frac{(x+2)} {(x-1) (x+1)^2} dx \) , hallar F(x)
Resolución:
El hecho de que uno de los factores del denominador se encuentre elevado al cuadrado nos obliga a cambiar en parte la estrategia de resolución. Por eso, escribiremos:
[8.25] \[ \frac {(x+2)}{(x-1) (x+1)^2} =\frac{A}{(x-1)} +\frac{B}{(x+1)} +\frac{C}{(x+1)^2} \]
Sacamos común denominador en el segundo miembro de la [8.25]
\[ \frac {(x+2)}{(x-1) (x+1)^2} =\frac{A (x+1)^2+B(x-1)(x+1)+C(x-1)}{(x-1) (x+1)^2} \]
Nuevamente, igualamos los numeradores:
[8.26] \[ x+2=A(x+1)^2+B(x-1)(x+1)+C(x-1) \]
Seguidamente, sustituimos la variable independiente por el valor de una de las raíces de la expresión original, es decir, por uno:
[8.27] \[ 1+2=A(1+1)^2+B(1-1)(1+1)+C(1-1) \to \]
\[ \to 3=4A \to A=\frac34 \]
Volvemos a la [8.26], pero ahora sustituimos la variable independiente por menos uno, que es la otra raíz del denominador del polinomio original:
[8.28] \[ -1+2=A(-1+1)^2+B(-1-1)(-1+1)+C(-1-1) \to \]
\[ \to 1=-2C \to C=-\frac12 \]
Aplicando el procedimiento visto en el ejemplo anterior solo hemos podido despejar dos de las tres incógnitas. Entonces, asignaremos un valor conveniente a la variable independiente y losustituiremos en la [8.26], además de reemplazar A y C, de acuerdo con los valores que obtuvimos en las [8.27] y [8.28]. Así, para x=0:
[8.29] \[ 2=\frac34 (1)^2+B(-1)(+1)-\frac12 (-1) \to \]
\[ \to 2=\frac34-B+\frac12 \to B=-\frac34 \]
Sustituimos [8.27], [8.28] y [8.29] en la [8.25], para luego integrar ambos miembros, tal como lo hicimos en el ejemplo anterior:
\[ \frac{(x+2)}{(x-1) (x+1)^2} =\frac{\frac34}{(x-1)} +\frac{- \frac34}{(x+1)} +\frac{\frac12}/{(x+1)^2} \to \]
\[ \to \displaystyle\int \frac{(x+2)}{(x-1) (x+1)^2} dx =\frac34 \displaystyle\int \frac{1}{(x-1)} dx-\frac34 \displaystyle\int \frac{1}{(x+1)} dx \]
\[ +\frac12 \displaystyle\int \frac{1}{(x+1)^2} dx \]
Resolviendo cada una de las tres integrales obtenidas, llegaremos al valor de F(x) pedido. Dejamos en manos del alumno la resolución de dichas integrales.
En el tercer ejemplo nos encontraremos con una dificultad adicional: las raíces de uno de los factores del denominador no pertenecerán al campo de los números reales. Veamos entonces de qué modo resolver ese tipo de integral.
Sabiendo que \( F(x)=\displaystyle\int \frac{(x+2)}{(x-1)(x^2+1)} dx \) , hallar F(x)
Resolución:
En esta oportunidad, escribiremos:
[8.30] \[ \frac{(x+2)}{(x-1)(x^2+1)} =\frac{A}{(x-1)} +\frac {(Bx+C)}{(x^2+1)} \]
Obsérvese que, al no poder factorizar en el campo real x2 + 1, sobre él colocamos un polinomio de grado uno, Bx + C.
Sacamos común denominador y operamos:
[8.31] \[ \frac{A} {(x-1)} +\frac {(Bx+C)}{(x^2+1)} =\frac{A(x^2+1)+(Bx+C)(x-1)}{(x-1)(x^2+1)} \]
Igualamos el primer miembro de la [8.30] con el segundo de la [8.31]
\[ \frac{(x+2)}{(x-1)(x^2+1)} =\frac{A(x^2+1)+(Bx+C)(x-1)}{(x-1)(x^2+1)} \] [8.32] \[ \to (x+2)=A(x^2+1)+(Bx+C)(x-1) \]
Seguidamente, sustituimos la variable independiente por la única raíz real de la expresión original, el número uno:
[8.33] \[ (1+2)=A(1^2+1)+(B.1+C)(1-1) \to A=\frac32 \]
Para despejar los valores de B y C asignamos dos valores convenientes a la variable independiente y sustituimos A por el valor que acabamos de despejar. Si en la [8.32], por ejemplo, asignamos a x el valor cero:
\[ (0+2)=\frac32 (0+1)+(B.0+C)(0-1) \to \] [8.34] \[ \to 2=\frac32-C \to C=-\frac12 \]
Seguidamente, sustituimos A y C en la [8.32] y damos a la variable independiente otro valor conveniente, por ejemplo, menos uno:
\[ (-1+2)=\frac32 ((-1)^2+1)+\left(B(-1)-\frac12\right)(-1-1) \to \] [8.35] \[ \to B=-\frac32 \]
Reemplazamos los valores de A, B y C en la [8.30] e integramos ambos miembros de la expresión obtenida, como lo hicimos en ejemplos anteriores:
\[ \frac{(x+2)}{(x-1)(x^2+1)} = \frac{\frac32}{(x-1)} + \frac{-\frac32 x -\frac12}{(x^2+1)} \to \] \[ \to F(x)= \displaystyle\int \frac{(x+2)}{(x-1)(x^2+1)} dx=\frac32 \displaystyle\int \frac{1}{(x-1)} dx- \] \[ -\frac32 \displaystyle\int \frac{x}{(x^2+1)} dx-\frac12 \displaystyle\int \frac{1}{(x^2+1)} dx \]
Dejamos nuevamente en manos del alumno la resolución de dichas integrales.Para ello, le aclaramos que
\[ \displaystyle\int \frac{1}{(x^2+1)} dx=arctg(x)+C \]
Sabiendo que \( F(x)= \displaystyle\int \frac {(x+3)}{(x-2)(x+4)} dx \) , hallar F(x)
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 8.5 encontrará las instrucciones necesarias para poder hacerlo.
Ahora que hemos visto de qué modo calcular integrales indefinidas, estamos en condiciones de avanzar sobre el cálculo de integrales definidas.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 552 a 558.
8.4. Integrales definidas: regla de Barrow
A partir del concepto de primitiva, la aplicación de la regla de Barrow nos permitirá evaluar la integral, dentro de un intervalo perteneciente al dominio de nuestra función.
Dada f(x), integrable en un intervalo (a, b), entonces:
[8.36] \[ \displaystyle\int_a^b f(x)dx=F(b)-F(a) \]
Donde F(x) es la primitiva de f(x)
La expresión [8.36] se conoce comúnmente como regla de Barrow
Evaluar \( \displaystyle\int _2^3 x^2 dx \)
Resolución:
Hemos visto que si \( F(x)=\displaystyle\int x^2 dx \) , entonces \( F(x)=\frac{x^3}{3}+C. \) .
Entonces:
\[ \displaystyle\int _2^3 x^2 dx =F(3)-F(2)=\frac{3^3}{3}-\frac{2^3}{3}=9-\frac83=\frac{19}{3} \]
En la imagen 8.7 representamos la función con el software. Utilizamos una de las aplicaciones del programa para verificar el resultado que acabamos de obtener analíticamente. El valor que señalamos en la vista algebraica corresponde, en forma aproximada, al de la integral que acabamos de calcular.
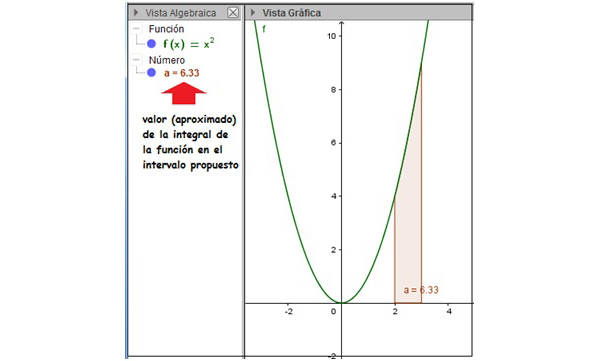
Empleando el software podemos obtener, en forma aproximada, el valor del área encerrada entre el eje de abscisas y la curva en el intervalo [2,3].
En la imagen se observa una región sombreada, la que queda acotada entre la curva representativa de la función y el eje de abscisas. Podríamos entonces suponer que la integral definida siempre representa un área. Pero el siguiente ejemplo nos mostrará que dicha circunstancia no siempre habrá de verificarse.
Evaluar \( \displaystyle\int _2^{3\pi/2} cos(x)dx \)
Resolución:
Hemos visto que si \( F(x)= \displaystyle\int cos(x)dx \) , entonces \( F(x)=sin(x)+C \) .
Entonces:
\[ \displaystyle\int _0^{3\pi/2} cos(x)dx =sin(3\pi/2)-sin(0)=-1 \]
Es evidente que, en este caso, el resultado no representa un área (¡que nunca puede ser negativa!). En la imagen 8.8 representamos la función y calculamos el valor de la integral de la función en el intervalo definido por los límites de integración que propone el enunciado del ejemplo.
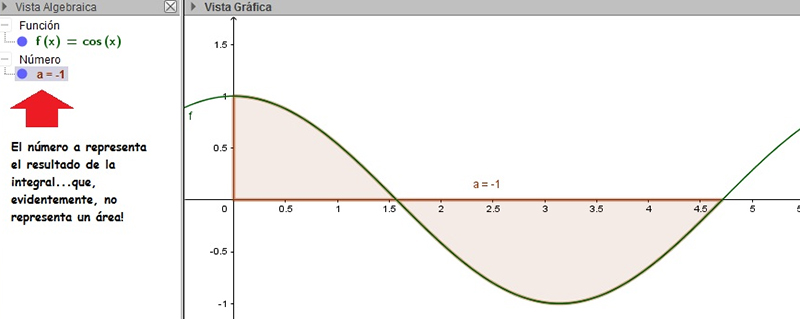
El cálculo de la integral no representa en todos los casos un área, como sucede en este caso con la función coseno, en el intervalo \( [ 0 , 3 \pi / 2 ] \)
Para interpretar el resultado del ejemplo anterior nos detendremos un momento en una de las propiedades de las integrales definidas.
Dados a, b y c, valores pertenecientes al dominio de la función f(x) tales que a < b < c, se verifica la siguiente propiedad:
\[ \displaystyle\int_a^c f(x)dx=\displaystyle\int_a^b f(x)dx+\displaystyle\int_b^c f(x)dx \]
Si aplicamos dicha propiedad a la integral del último ejemplo, podemos escribir:
\[ \displaystyle\int_0^{3\pi/2} cos(x)dx =\displaystyle\int_0^\frac{\pi}{2} cos(x)dx+\displaystyle\int_\frac{\pi}{2}^\frac{3\pi}{2} cos(x)dx= \]
\[ =\left[ sin(x)|_{0}^{\pi/2} \right] + \left[ sin(x)|_{\pi/2}^{3\pi/2} \right] = \]
\[ =\left[sin (\frac{\pi}{2})-sin(0)\right]+ \left[sin \left(\frac{3\pi}{2}\right)-sin \left(\frac{\pi}{2}\right)\right]= \]
\[ =[1-0]+[-1-1] \]
El resultado del primer corchete corresponde al área encerrada entre la función coseno y el eje de abscisas, en el intervalo que va desde 0 hasta \( \frac{\pi}{2} \). El resultado del segundo corchete, en cambio, resulta ser numéricamente igual al área entre la función y el eje de las x multiplicado por menos uno.
Debemos entonces tener en cuenta que, en la medida que dentro de un determinado intervalo la función sea positiva, su integral representará el área entre dicha función y el eje de abscisas. Sin embargo, dado que dicho eje puede considerarse como una función, el concepto podría ampliarse, llevándonos a una aplicación de enorme utilidad que estudiaremos en la siguiente sección.
8.4.1. La integral definida como área bajo una curva
Al comenzar la presente unidad comentamos que la integral nos permitía calcular el área bajo una curva. Pero en la sección anterior anticipamos que deben cumplirse algunas condiciones para que ello sea factible.
Seguidamente, definiremos el concepto de área entre curvas, que nos permitirá interpretar mejor todo lo dicho al respecto hasta el momento.
Dadas dos funciones f(x) y g(x), derivables en un intervalo (a, b) y tales que \( f(x)\ge g(x) \forall x \in (a,b) \), entonces
[8.37] \[ \displaystyle\int_a^b (f(x)-g(x)) dx \]
representa al área encerrada entre ambas funciones en dicho intervalo.
Cuando al comienzo de la sección 8.3 se nos pidió evaluar la \( \displaystyle\int_2^3 x^2 dx \), observamos que el resultado no era otra cosa que el área encerrada entre la curva representativa de la función \( f(x)=x^2 ) \)y el eje de abscisas. A partir de lo que expresa la [8.37] podemos interpretar el resultado obtenido considerando al eje de abscisas como otra función, g(x) = 0.
De modo que, siempre que calculemos
\[ \displaystyle\int_a^b f(x)dx \]
tal que \( f(x) \ge 0 \ \forall \ x \in (a,b) \), estaremos en realidad calculando el área entre la curva representativa de dicha función y la función g(x) = 0; es por esa razón que el resultado de dicho cálculo representará numéricamente al área encerrada entre dicha curvas.
En los siguientes ejemplos mostraremos de qué modo aplicar la regla de Barrow.
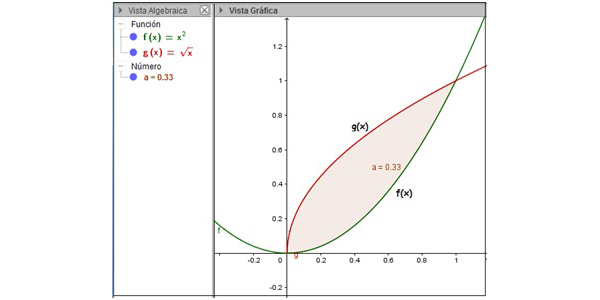
Hallar el área encerrada entre las funciones \( f(x)= x^2 \) y \( g(x)= \sqrt{x} \).
Resolución:
En primer lugar, deberíamos determinar las abscisas de los puntos donde ambas funciones se intersecan. Para ello, basta con igualar las ecuaciones de las dos funciones:
\[ x^2=\sqrt{x}\to(x^2 )^2=(\sqrt{x})^2 \to x^4=x\to x^4-x=0\to \]
\[ \to x(x^3-1)=0 \]
Las soluciones reales de dicha ecuación son x = 0 y x = 1. Es necesario entonces determinar cuál de las dos funciones se encuentra por encima de la otra dentro del intervalo (es decir, cuál será la función techo). Para ello, basta con evaluar ambas funciones para un mismo valor de la variable independiente perteneciente al intervalo definido por las dos raíces. Por ejemplo, \( g(\frac12)>f(\frac12) \), lo que significa que la función g(x) será el techo que nos permitirá calcular la integral.
Escribimos entonces:
\[ área=\displaystyle\int_0^1 (g(x)-f(x)) dx=\]
\[ = \displaystyle\int_0^1 (\sqrt{x}-x^2 ) dx= \frac23 x^{3⁄2}- \frac{x^4}{4} \Big|^1_0 \]
\[ =\frac23-\frac14=\frac{5}{12} \]
En la imagen 8.9 pueden observarse ambas funciones. El valor del área aparece en la vista algebraica y nos permite verificar el resultado que acabamos de obtener analíticamente.
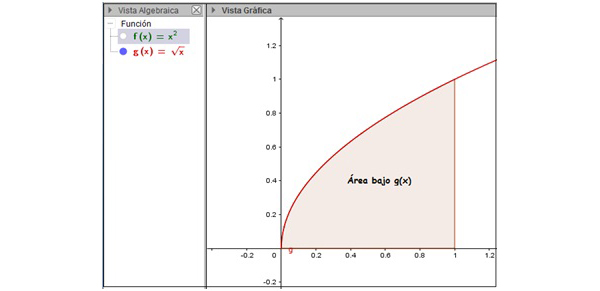
Vamos a utilizar el ejemplo anterior para comprender mejor la expresión presentada al comienzo de la presente sección, que puede interpretarse como la integral de la diferencia entre las funciones “techo” y “piso”. En la imagen 8.10 se observa el área encerrada entre la función g(x) y el eje de abscisas en el intervalo (0,1).
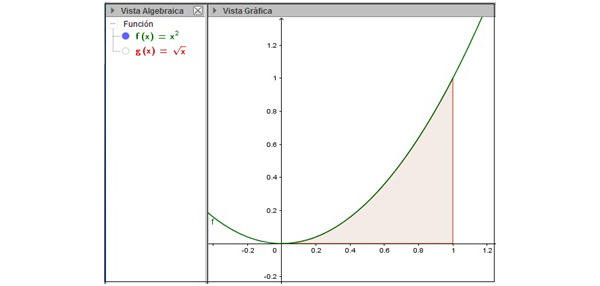
En cambio, la imagen 8.11 representa al área encerrada entre la función f(x) y el eje de las x en el mismo intervalo. Desde el punto de vista geométrico, se interpreta fácilmente que la diferencia entre las áreas (representadas por las integrales) no es otra cosa que el área encerrada entre ellas. Así:
\[ área= \displaystyle\int_0^1 \sqrt{x} dx-\displaystyle\int_0^1x^2 \ dx=\displaystyle\int_0^1(\sqrt{x}-x^2 ) dx \]
Esa fue, justamente, la integral que nos permitió calcular el área encerrada entre ambas curvas.
Área encerrada entre dos curvas
Al área encerrada entre la función g(x) y el eje de abscisas…
…le restamos el área entre f(x) y el eje de abscisas, de modo de obtener el área entre las curvas.
Las funciones en cuestión podrían intersecarse en más de dos puntos, lo que podrían obligarnos a resolver más de una integral, como veremos en el próximo ejemplo.
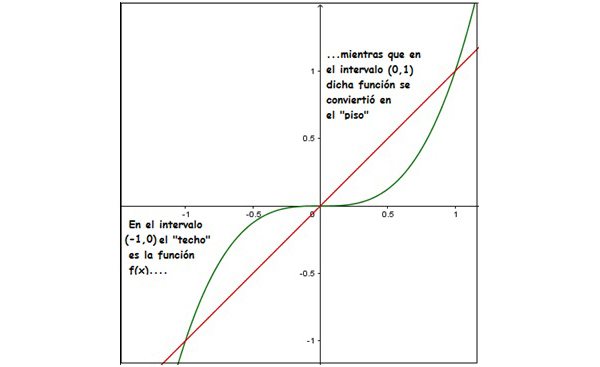
Hallar el área encerrada entre las funciones \( f(x)=x^3 \)y \( g(x)=x \)
Resolución:
Nuevamente igualamos las expresiones de las curvas para obtener los límites de integración:
\[ x^3=x \to x^3-x=0 \to x(x^2-1)=0 \to \]
\[ \to x(x-1)(x+1)=0 \]
En este caso, la ecuación es de tercer grado y sus raíces son menos uno, cero y uno; ello significa que tendremos dos intervalos de integración, el (-1,0) y el (0,1). La imagen 8.12 nos permite observar, además, que las funciones techo y piso no son las mismas en cada uno de dichos intervalos.
Teniendo en cuenta lo que acabamos de decir, escribimos:
\[ área= \displaystyle\int_{-1}^0 (x^3-x)dx \ + \displaystyle\int_0^1(x-x^3 ) dx\]
\[ = \frac{x^4}{4}-\frac{x^2}{2} \Big|_{-1}^0 + \frac{x^2}{2}-\frac{x^4}{4}\Big|_0^1= \]
\[ =-\left(\frac{(-1)^4}{4}-\frac{(-1)^2}{2}\right)+\left(\frac{1^2}{2}-\frac{1^4}{4}\right)= \]
\[ =-(\frac14-\frac12)+\frac12-\frac14=\frac12 \]
Cuando ambas curvas se cortan en más de dos puntos, determinan un número mayor de intervalos de integración. En cada uno de ellos tendremos que determinar cuál es la función “techo” y cuál la función “piso”.
Calcular el área encerrada entre las funciones f(x) = -x2 + 7 y g(x) = 6x
Calcular el área encerrada entre las funciones f(x) = 5 - x2 y \( g(x)=2- \frac{1}{4} x^2 \)
Calcular el área encerrada entre las funciones \( f(x)=\frac1x \)y \( g(x)=-x+\frac{26}{5} \)
En la siguiente sección veremos una de las tantas aplicaciones de la integral definida.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 271 a 278.
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 263 a 280.
8.4.2. Una aplicación importante: la integral definida como trabajo de una fuerza
En la sección 3.4, como ejemplo de aplicación del producto escalar, definimos el trabajo de una fuerza desde un punto de vista vectorial.
Sin embargo, si los vectores que representan la fuerza y el desplazamiento del cuerpo tuviesen la misma dirección y sentido, el trabajo producido por dicha fuerza al mover a un cuerpo desde un punto ubicado en x = a hasta otro en x = b podrá calcularse como:
[8.38] \[ W=\displaystyle\int_a^b F(x)dx \]
Si fuese constante (es decir, no variase con la posición del móvil), la [8.38] podría escribirse como:
\[ W=\displaystyle\int_a^b Fdx =F\displaystyle\int_a^b dx =F(x|_a^b ) =F(b-a) \]
Sin embargo, es frecuente que nos encontremos con fuerzas que varíen con la distancia. Un ejemplo es el de la fuerza elástica, que se observa cuando un resorte es comprimido o estirado respecto de lo que se conoce como su longitud natural (es decir, la longitud que tiene cuando no existen fuerzas externas aplicadas sobre él).
La fuerza elástica también se conoce como fuerza de restitución, porque se opone siempre a la causa que la provoca. En la imagen 8.13 mostramos lo que sucede con una bola que se acerca con velocidad constante a un resorte. En el momento en que se pone en contacto con él, comienza a comprimirlo. Cuando ello sucede, se manifiesta una fuerza que se opone a dicha compresión y que aumenta (en módulo) a medida que dicha compresión lo hace. Esa fuerza se expresa matemáticamente como:
[8.39] \[ F_e (x)=-kx \]
El signo negativo indica que la fuerza es opuesta a la causa que la provoca y no necesariamente habrá de aparecer en la expresión que hayamos de emplear en los cálculos. En cuanto a k, se trata de la constante elástica del resorte, valor empírico que caracteriza al elemento con el que trabajemos en cada caso.
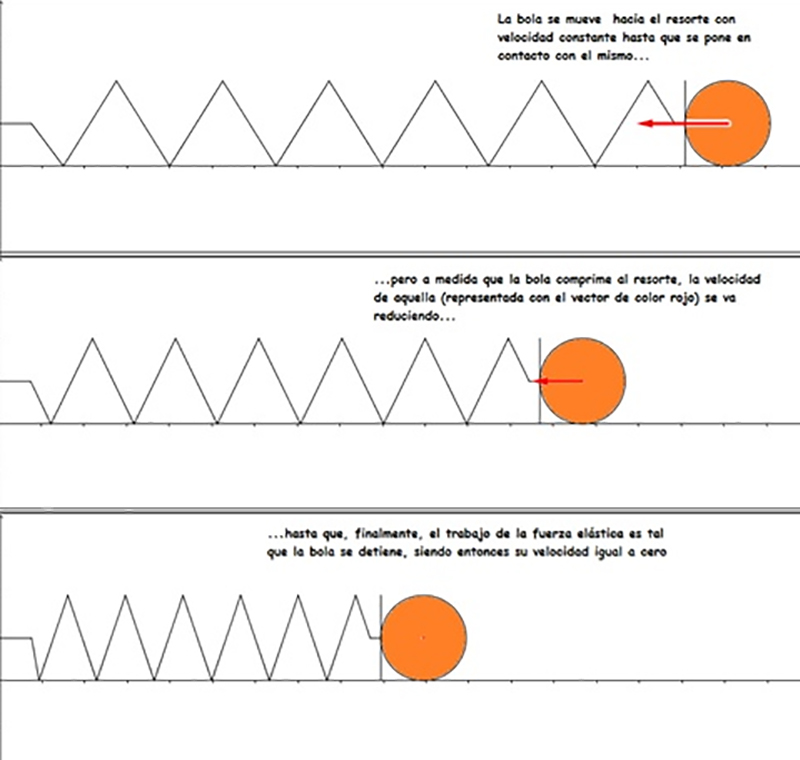
El cuerpo tiene una determinada velocidad en el momento de ponerse en contacto con el resorte. A medida que lo va comprimiendo, la fuerza de restitución aumenta. Como consecuencia de ello, la aceleración de frenado aumenta y la velocidad se va reduciendo, hasta que el cuerpo se detiene. Nosotros suspendemos en este punto el análisis del problema, pero debemos tener en cuenta que la fuerza de restitución obligará seguidamente al resorte a recobrar su longitud natural (la que tenía antes de que el cuerpo comenzara a comprimirlo).
Supongamos que la bola que aparece en la parte superior de la imagen 8.13 se pone en contacto con el resorte a una determinada velocidad. Digamos que, en ese momento, la longitud (natural) del resorte resulta ser x = 1 metro.
En las dos viñetas siguientes de la imagen 8.13 se observa cómo va disminuyendo la velocidad de la bola, hasta detenerse totalmente. Digamos que, en esas condiciones, el valor de la variable independiente resulta ser x = 0,6 metros.
Si la constante elástica del resorte valiese en este caso \( 100 Newton⁄m \), entonces, el trabajo que la fuerza elástica hace sobre la bola hasta detenerla se calcula sustituyendo la [8.35] en la [8.34], para luego reemplazar las variables con los datos del problema. Así:
\[ W=\displaystyle\int_a^b F(x)dx =\displaystyle\int_a^b k.x.dx \to \]
\[ → W=\displaystyle\int_{1m}^{0,6m} 100 N/m.x.dx = \]
\[ =100 N/m \left( \frac{x^2}{2}\Big|_{1m}^{0,6m} \right)=100 \frac{N}{m} (0,18m^2-0,5m^2 ) \to \]
\[ \to W=-32Nm=-32Joule \]
El signo negativo se condice con la convención que se aplica en Física (el trabajo que el resorte hace sobre la bola reduciendo a cero su energía cinética se contempla desde el punto de vista de esta), de modo que no nos detendremos en su sentido físico. Lo que nos interesa que el alumno tenga en cuenta es que los temas que desarrollamos en el presente MDM tienen importantes aplicaciones en otros campos.
Tipler, P.; Mosca, G. (2003), Física para la ciencia y la tecnología, Volumen 1a, Editorial Reverté S. A., Barcelona, pp. 146 a 148.
8.5. Resolución de integrales definidas en forma aproximada aplicando el polinomio de Taylor
Para finalizar la presente unidad, consideramos apropiado comentar una valiosa aplicación del polinomio de Taylor (ver sección 7.2.3). Existen integrales cuya resolución por los métodos que hemos estudiado se hace sumamente laboriosa. Un caso bastante frecuente es el de integrales que contienen el producto de una función polinómica de grado n con otra función de distinta naturaleza (ya sea trigonométrica, exponencial, etcétera).
Dada una integral de la forma \( \displaystyle\int P_n (x).f(x)dx \), donde \( P_n (x) \) resulta ser una función polinómica de grado n y f(x) una función de otra naturaleza (que no sea de tipo logarítmica), para resolver dicha integral hemos de aplicar el método de resolución por partes n veces, adoptando en el primer paso como u(x) a Pn(x).
En el siguiente ejemplo veremos de qué modo evaluar en forma aproximada una integral, evitando un largo procedimiento, aplicando el polinomio de Taylor de la función f(x).
Evaluar en forma aproximada \( \displaystyle\int_0^1 x^5 sin(x)dx \) utilizando un Polinomio de Taylor apropiado.
Resolución:
Tal como lo comentamos anteriormente, resolver esta integral por partes nos llevaría a adoptar inicialmente:
\[ u(x)=x^5 \to du=5x^4 dx. \]
En ese caso, \( dv=sin(x)dx \to \displaystyle\int dv=\displaystyle\int sin(x)dx \)
Así, \( v=-cos(x) \) y, aplicando la [8.13], escribiríamos:
\[ \displaystyle\int x^5 sin(x)dx=x^5 (-cos(x)) — \displaystyle\int -cos(x).5x^4 dx \]La última integral de la expresión anterior debería a su vez resolverse por partes, haciendo \( u(x)=x^4 \). Pero, si siguiéramos ese camino, y tal como lo anticipamos, llegaríamos a otra expresión que, a su vez, debería resolverse por partes… ¡Debiendo repetirse el procedimiento otras cuatro veces!
Dejemos de lado dicho procedimiento y busquemos el polinomio de Taylor de la función seno en el entorno de \( x_0 = 0 \). En primer lugar, calcularemos las primeras cinco derivadas de la función y las evaluaremos en cero:
\[ f(x) = sin(x) \to f(0) = sin(0) = 0 \]
\[ f'(x) = cos(x) \to f'(0) = cos(0) = 1 \]
\[ f^{''}(x) = -sin(x) \to f^{''}(0) = -sin(0) = 0 \]
\[ f^{'''} (x)=-cos(x) \to f^{'''} (0)=-cos(0)=-1 \]
\[ f^{iv} (x)=sin(x) \to f^{iv} (0)=sin(0)=0 \]
\[ f^v (x)=cos(x) \to f^v (0)=cos(0)=1 \]
De este modo, el polinomio de grado cinco de la función seno de x en el entorno del origen será:
\[ P_5 (x)=f(0)+ \frac{f^{'}(0)}{1!} x+\frac{f^{''}(0)}{2!} x^2+\frac{f^{'''}(0)}{3!} x^3+ \]
\[ +\frac{f^{iv} (0)}{4!} x^4+\frac{f^v (0)}{5!} \to \]
[8.40] \[ \to P_5 (x)=x-\frac{x^3}{3!}+\frac{x^5}{5!} \]
Si reemplazamos a la función seno por la [8.40] podemos escribir:
\[ \displaystyle\int_0^1 x^5 sin \ (x)dx \cong \displaystyle\int_0^1 x^5 \left(x-\frac{x^3}{3!}+\frac{x^5}{5!}\right)dx= \]
\[ =\displaystyle\int_0^1 \left(x^6-\frac{x^8}{6}+\frac{x^{10}}{120}\right) dx= \frac{x^7}{7}-\frac{x^9}{54}+\frac{x^{11}}{1320}\Big|_0^1 \]
\[=\frac17-\frac{1}{54}+\frac{1}{1320} \]
En la imagen 8.14 reproducimos la captura de pantalla correspondiente a la obtención del resultado de nuestro cálculo empleando el wxMaxima. En primer lugar, hemos señalado el resultado obtenido por nuestro procedimiento aproximado expresado como fracción. Seguidamente, y gracias a la instrucción “float”, escribimos el resultado mediante decimales. Obsérvese que el valor obtenido difiere muy poco del obtenido por el propio software al calcular directamente la integral, valor que aparece al pie de la imagen.

Resultado aproximado obtenido empleando el wxMaxima.
El adecuado empleo de polinomios de Taylor sirve, además, para el cálculo de ciertas integrales (como, por ejemplo, \( \displaystyle\int_0^1 e^{-x^2} dx \)) que no pueden resolverse por ninguno de los métodos mencionados en la presente unidad.
Evaluar en forma aproximada \( \displaystyle\int_0^1 x^5 cos \ (x)dx \) utilizando un polinomio de Taylor apropiado.
Evaluar en forma aproximada \( \displaystyle\int_0^1 x^5 e^x dx \) utilizando un polinomio de Taylor apropiado.
8.6. Empleo del software para autocorrección
Nuevamente proponemos al estudiante que haga uso del software para acelerar su proceso de aprendizaje, verificando los resultados obtenidos durante la práctica. Como lo hemos hecho en unidades anteriores, seguiremos empleando el wxMaxima.
Evaluar \( \displaystyle\int \frac{x.dx}{\sqrt{x^2+6}} \)
Resolución empleando el software:
En este caso, seleccionamos “Integrar” en el menú, como se muestra en la imagen 8.15.
Seleccionamos “Integrar” dentro del menú
Como se observa en la imagen 8.16, se abre una ventana que nos permite introducir la expresión de la función que deseamos integrar. Bastará entonces con hacer clic en Aceptar para que el programa nos devuelva el resultado de la integral, que aparece en la imagen 8.17.
Obsérvese que, a pesar de que se trata de la solución de una integral indefinida, el programa no agrega la constante de integración.
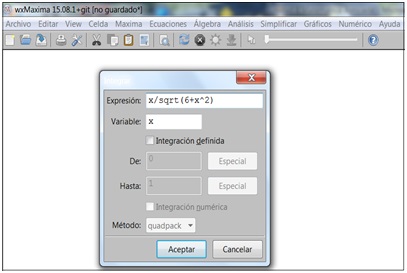
Ingresamos la expresión correspondiente a la función.
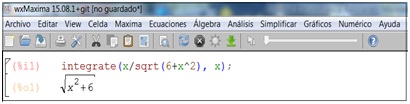
El software calcula la primitiva.
Como veremos en el siguiente ejemplo, el software también nos permite calcular integrales definidas.
Evaluar \( \displaystyle\int_{-1}^2 xe^{x^2} \ dx \)
Resolución empleando el software:
Nuevamente, seleccionaremos “Integrar” en el menú. Sin embargo, como en este caso tenemos que resolver una integral definida, tendremos que tildar la opción correspondiente en la ventana que se abre para ingresar la información, indicando seguidamente cuáles son los límites inferior y superior de integración, como se muestra en la imagen 8.18. Bastará luego con hacer clic en “Aceptar” para que el programa nos brinde el resultado pedido (imagen 8.19).
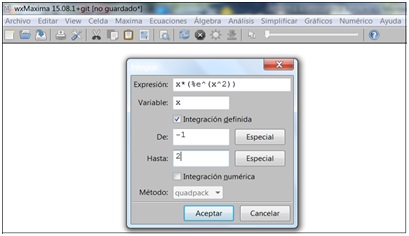
Tratándose de una integral definida, tenemos que indicar los límites de integración.
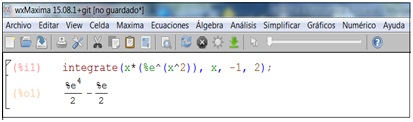
El programa nos devuelve el resultado exacto de la integral definida.
En la siguiente unidad nos concentraremos en otra aplicación de las integrales de sumo interés, la resolución de ecuaciones diferenciales.

