5. Funciones reales de una variable independiente
Objetivos
Que el alumno:
- Comprenda que una función es mucho más que una relación abstracta entre dos variables, a partir de sus múltiples aplicaciones.
- Aprenda a distinguir los elementos característicos de las funciones elementales y reconozca rápidamente las representaciones gráficas de cada una de ellas.
- Descubra la necesidad de obtener el dominio de cualquier función.
- Adquiera el concepto de límite de una función en un punto.
- Aprenda a obtener las asíntotas de una función.
- Aprenda a representar en forma aproximada las funciones racionales.
- Aprenda a utilizar los nuevos recursos para representar en forma aproximada las funciones racionales.
5.1. La función real como relación entre dos variables
Supongamos que, durante un partido de fútbol, el jugador A, ubicado a 80 metros del arco rival, patea la pelota para convertir un tanto. Si la velocidad con la que efectúa el disparo fuese de 28,28 metros sobre segundoy el ángulo que la pelota determina con la horizontal en el instante de hacerlo fuese de 45 las ecuaciones que describen su movimiento serían las siguientes:
[5.1] \[ x = 80m - 20 \frac{m}{s} . t \]
[5.2] \[ y = 20 \frac{m}{s} . t \ –5\frac{m}{s^{2}}. t^{2}\]
La situación aparece esquematizada en la imagen 5.1. Utilizamos un par de ejes cartesianos cuyo origen se encuentra en el punto adonde la pelota debería llegar (si el arquero, jugador B, no hace nada para detenerla). Sobre el eje de abscisas y a 80 metros del arco, se encuentra el punto desde el cual se efectuó el disparo.
Las ecuaciones [5.1] y [5.2] describen desde el punto de vista físico lo que sucede con la pelota. Lo que a nosotros nos interesa desde el punto de vista matemático es lo que cada una de ellas nos permite calcular: la primera de ellas indica a qué distancia del arco, medida sobre el suelo, habrá de encontrarse la pelota en función del tiempo; la segunda, en cambio, nos permite saber a qué altura del suelo se encuentra la pelota, también en función del tiempo transcurrido desde el instante en que se efectuó el disparo.
Entonces, si el jugador B quisiera saber cuánto tiempo tardará la pelota en alcanzar el arco o donde deberá ubicarse antes de que el balón alcance su valla (¡y suponiendo que supiese algo de Física y fuese muy bueno con los cálculos mentales!), bastaría con que el arquero aplicase esas expresiones.
El movimiento de la pelota en el plano puede describirse con un par de ecuaciones donde las coordenadas horizontal y vertical quedan expresadas en función del tiempo.
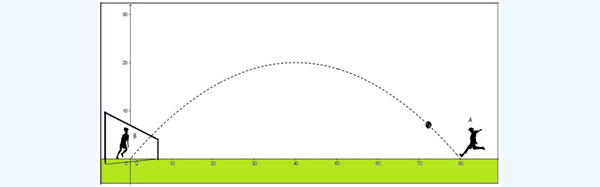
Así, si el arquero decidiera atajar la pelota 3,5 segundos después de que fuera pateada por su oponente, debería alejarse unos 10 metros del arco… y dar un salto de más de ocho metros de altura (¡no solo tendría que ser un prodigio en el campo de las Matemáticas!). Si, en cambio, se limitara a ubicarse en el origen de coordenadas a los 4 segundos del disparo, simplemente podría detener la pelota entre sus pies.
En definitiva, cada una de las expresiones vincula a una magnitud (distancia del arco y altura, para la [5.1] y la [5.2], respectivamente) con otra (en ambos casos, el tiempo). Estas relaciones, como veremos en la presente unidad, reciben el nombre de funciones.
Detengámonos un instante en la expresión [5.1]. Relacionamos dos magnitudes que recibirán el nombre de variables (porque, según el caso, podrán adoptar distintos valores); una de ellas (la distancia respecto del arco) depende del instante de tiempo que se considere. Por ello diremos en este caso que la distancia representa la variable dependiente, en tanto que el tiempo será la variable independiente.
Podemos decir que una función es una relación entre dos variables que puede expresarse mediante una identidad matemática. El valor que adoptará una de ellas (a la que denominaremos variable dependiente) podrá obtenerse utilizando dicha expresión, una vez que se adopte un valor conveniente para la otra variable, que recibirá el nombre de variable independiente.
Cabe aclarar que, para que una relación pueda considerarse función, a cada valor de la variable independiente habrá de corresponderle uno y solo un valor de la variable dependiente.
Si bien es cierto que, en nuestro ejemplo, el tiempo transcurrido desde el momento del disparo hasta que la pelota vuelve a tocar el suelo es de tan solo cuatro segundos (valor que verificaremos en la sección 5.3), nuestra variable independiente podría adoptar cualquier valor real entre cero y cuatro, según el instante seleccionado. Como consecuencia de ello, la distancia a la que la pelota habría de encontrarse en dicho instante habría de ser otro número real, que se obtendría reemplazando el valor del tiempo en la [5.1]. Es por eso que diremos que estamos en presencia de una función escalar de variable real.
Como veremos en la próxima sección, las funciones escalares de variable real podrán representarse gráficamente en un par de ejes cartesianos. Los valores de la variable independiente aparecerán sobre el eje de abscisas y los de la variable independiente, sobre el de ordenadas. Por eso, mientras no nos veamos obligados a cambiar de nomenclatura por razones propias del problema, indicaremos con la letra x a la variable independiente y con la letra y a la dependiente. Por esa razón, la mayoría de las funciones se expresan de la siguiente manera:
\[ y = f(x) \]
La igualdad debe leerse, entonces, como “y es función del valor que adopte x”.
En la sección siguiente nos dedicaremos a una de las funciones elementales más utilizadas: la función lineal.
5.2. Funciones lineales
Volviendo a la expresión [5.1], observemos que posee tan solo dos términos y que la variable independiente t aparece solo una vez, elevada a la uno. Si asignásemos algunos valores a la variable independiente, podríamos construir una tabla de valores que nos indicara a qué distancia del arco se encuentra el balón para cada uno de los instantes representado por aquella. Por ejemplo:
|
Tiempo, t |
Distancia del arco, x |
|
0 segundos |
80 metros |
|
1 segundo |
60 metros |
|
2 segundos |
40 metros |
|
3 segundos |
20 metros |
|
4 segundos |
0 metros |
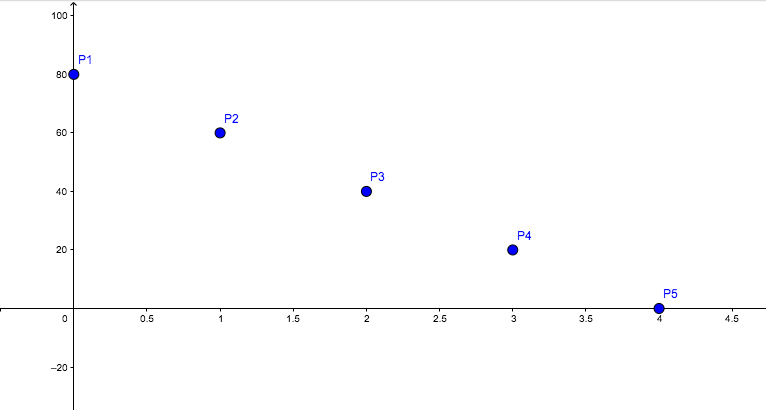
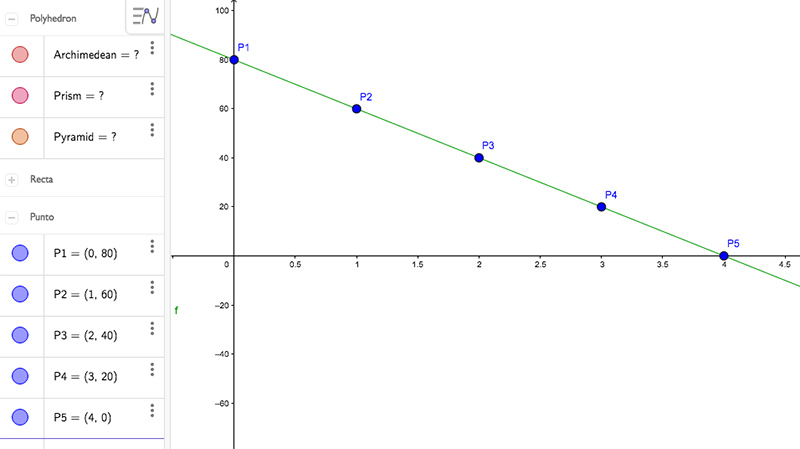
Representamos dichos puntos en un sistema de ejes coordenados (imagen 5.2) y observamos que parecen encontrarse alineados. Ello se verifica rápidamente con el software disponible (imagen 5.3), lo que significa que la representación gráfica de esta función es una recta.
Cuando esto sucede, decimos que nos encontramos en presencia de una función lineal.
Sobre el eje de abscisas representamos el tiempo, mientras que sobre el eje de las ordenadas, la distancia a la que se encuentra la pelota respecto del arco en función del tiempo…
Se observa que todos los puntos se encuentran sobre una recta. En la vista gráfica aparece explícitamente la expresión de la función. Vale aclarar que el GeoGebra asigna siempre la x a la variable independiente y la y a la dependiente.
Toda función lineal tendrá una expresión de la forma:
\[ y = f(x) = a · x + b \]
Los coeficientes a y b podrán adoptar cualquier valor real (siempre y cuando \( a \not= 0 \)), de modo que la representación gráfica de dicha función será una recta.
Si a fuese igual a cero, nos encontraríamos ante un caso particular al que definimos como función constante: como el coeficiente que acompaña a la variable independiente es nulo, la variable independiente adoptará siempre el mismo valor y la representación gráfica será una recta horizontal.
Acabamos de ver que la representación gráfica de cualquier función lineal es una recta. Sin embargo, no toda recta representa a una función lineal, como veremos a continuación.
Ninguna recta de ecuación x = a podrá ser la representación gráfica de una función lineal.
Justificar lo que acabamos de decir resulta sencillo, si tenemos en cuenta que, para que una relación pueda considerarse función, a cada valor de la variable independiente habrá de corresponderle uno y solo un valor de la variable dependiente. Ninguna recta vertical de ecuación x = a podrá entonces ser función, porque dicho valor de la variable independiente se relacionará con más de un valor(¡de hecho, lo hará con infinitos!) de la variable dependiente y.
En el siguiente ejemplo aplicaremos lo visto en la unidad anterior para obtener la expresión de una función lineal.
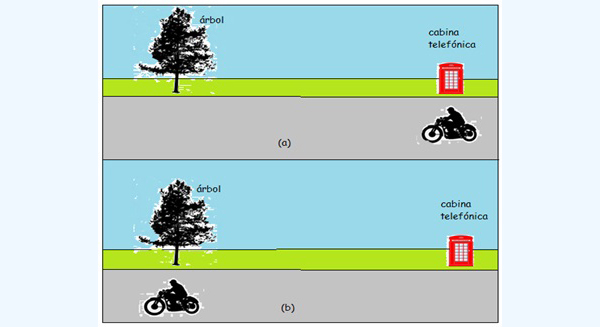
Un motociclista viaja por un camino rural con velocidad constante. En un momento dado, pasa frente a una cabina telefónica y 10 segundos después, frente a un árbol que se encuentra a 250 metros de aquella (imagen 5.4).
Sabiendo que la función que nos permita calcular a qué distancia del árbol se encuentra el motociclista en un instante dado es lineal, obtener su expresión y graficarla.
Como el enunciado nos dice que la función buscada es lineal, podemos escribirla como:
[5.3] \[ x(t) = a · t + b \]
El tiempo t representa a la variable independiente y la posición del motociclista respecto del árbol, x, será la variable dependiente.
Puesto que en el instante inicial (es decir, cuando comenzamos a analizar el movimiento del motociclista), este se encuentra a 250 metros del árbol, podemos escribir:
\[ 250 = a · 0 + b \]
En la imagen de la parte superior, el motociclista pasa frente a una cabina telefónica. Diez segundos después, viajando a velocidad constante, el mismo motociclista pasa frente al árbol que está ubicado a doscientos cincuenta metros de la cabina.
En forma inmediata, se despeja el valor de la ordenada al origen
\[ b = 250 m \]
Por otro lado, teniendo en cuenta que 10 segundos después pasa frente al árbol, podemos escribir:
\[0=a.10+b→0=a.10+250→\]
\[→–250=a.10→-\frac{250}{10}=a→a=–25\]
Así, la función buscada se puede escribir como:
[5.4] \[x(t)=–25.t+250\]
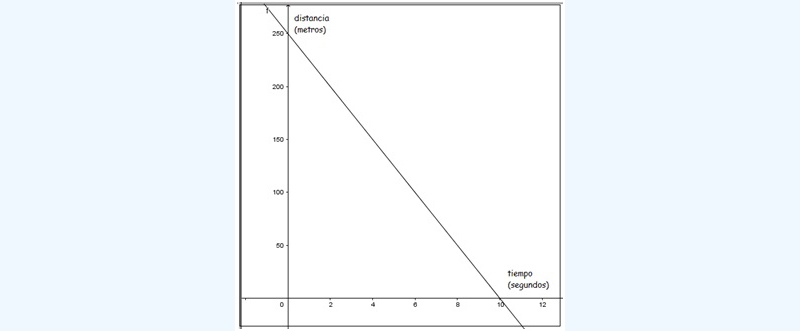
La representación gráfica puede observarse en la imagen 5.5.
La gráfica representa a qué distancia del árbol se encuentra el motociclista en función del tiempo.
Lo interesante de las funciones es que pueden representar un fenómeno dado, permitiéndonos obtener información de una circunstancia particular a partir de una expresión general. Si, por ejemplo, quisiéramos saber a qué distancia del árbol se encontrará el motociclista 3 segundos después de haber pasado frente a la cabina telefónica, bastará con asignar valor 3 a la variable independiente en la expresión [5.4]. Así:
\[ x(3)=-25.3+250=175metros \]
Al consultar material técnico extranjero, podríamos encontrarnos con el inconveniente de que las temperaturas aparecieran en grados Fahrenheit. Sabiendo que la temperatura de fusión del hielo a presión atmosférica vale 32 grados Fahrenheit y que la temperatura de ebullición del agua en las mismas condiciones de presión es de 212 grado Fahrenheit, obtener la función lineal que nos permita, conocida una temperatura en grados Fahrenheit, obtener su valor en grados centígrados. Tener en cuenta que el hielo se derrite a cero grados centígrados, en tanto que la temperatura de ebullición del agua es de 100 grados centígrados.
Stewart, J.; Redlin, L.; Watson, S.(2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 102 a 112.
5.3. Función cuadrática
Volviendo al ejemplo propuesto en la sección 5.1, si analizamos la altura de la pelota en función del tiempo, puede completarse la siguiente tabla utilizando la expresión [5.2]:
|
Tiempo, t |
Altura de la pelota, y |
|
0 segundos |
0 metros |
|
1 segundo |
15 metros |
|
2 segundos |
20 metros |
|
3 segundos |
15 metros |
|
4 segundos |
0 metros |
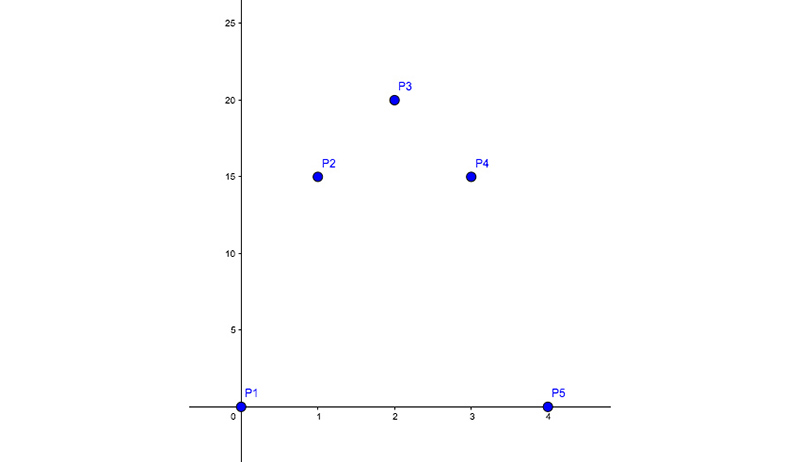
Si convertimos en puntos del plano cada uno de los pares ordenados que figuran en la tabla y los ubicamos en un par de ejes cartesianos, obtenemos la gráfica que reproducimos en la imagen 5.6.
En este caso representamos la altura a la que se encuentra la pelota en función del tiempo. A diferencia de lo que sucedía al estudiar el movimiento del objeto en sentido horizontal, la gravedad afecta el movimiento del cuerpo, que ya no puede describirse mediante una recta.
Es evidente que, a diferencia de lo visto al comenzar la sección anterior, nos encontramos en este caso con un conjunto de puntos que no están alineados. Sin embargo, basta con escribir la expresión [5.2] en la ventana de entrada del software para comprobar de inmediato que los puntos se encuentran sobre una parábola (imagen 5.7).
Al unir los puntos encontramos que estos se encuentran sobre una parábola.
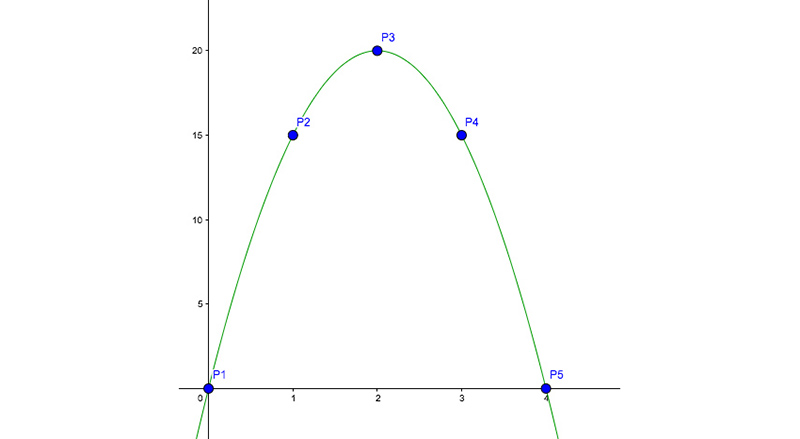
Nos encontramos, entonces, frente a una función cuadrática.
Toda función cuadrática tendrá una expresión de la forma:
\[ y = f(x) = a · x^2 + b · x + c \]
Independientemente de los valores que tomen b y c, deberá cumplirse la condición de que \(a \not= 0\)
Aun cuando toda función cuadrática tenga como representación gráfica una parábola, no toda parábola habrá de ser la representación gráfica de una función cuadrática.
En la imagen 5.8 se observa una parábola de eje focal horizontal. Por ejemplo, al valor x =6 le corresponden dos valores de la variable dependiente y (representados por los puntos A1 y B1). Como sabemos que en toda función a cada valor de la variable independiente debe corresponderle un único valor de la variable dependiente, la parábola representada no puede ser la gráfica de función alguna.
Solo aquellas parábolas cuyo eje focal sea vertical habrán de representar gráficamente funciones cuadráticas. El caso de las parábolas de eje focal horizontal nos permite justificar tal aseveración. Dado que en toda función a cada valor de la variable independiente debe corresponderle un único valor de la variable dependiente, como eso no sucede en parábolas como la que aparece a continuación, es obvio que esta no podrá representar ningún tipo de función.
Solo aquellas parábolas cuyo eje focal sea vertical habrán de representar gráficamente funciones cuadráticas. El caso de las parábolas de eje focal horizontal nos permite justificar tal aseveración. Dado que en toda función a cada valor de la variable independiente debe corresponderle un único valor de la variable dependiente, como eso no sucede en parábolas como la que aparece a continuación, es obvio que esta no podrá representar ningún tipo de función.
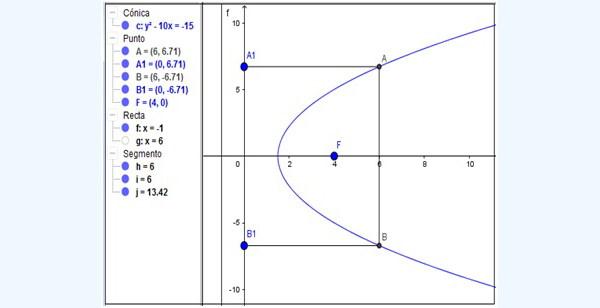
Digamos entonces que solamente aquellas parábolas cuyo eje focal sea vertical podrán ser la representación gráfica de alguna función.
Acabamos de ver que la curva que nos permite graficar toda función cuadrática es una parábola. En la siguiente sección, repasaremos brevemente algunos de sus elementos característicos.
5.3.1. Características de la parábola, curva que representa la función cuadrática
De acuerdo con lo planteado en la sección anterior, nos interesan solamente aquellas parábolas cuyo eje focal o eje de simetría sea vertical.
Se define como parábola al lugar geométrico de los puntos equidistantes respecto de una recta llamada directriz y de un punto llamado foco.
En las imágenes 5.9 y 5.10 se observa una parábola cuyo eje focal es vertical. Fue representada en color azul. En color rojo se indicaron la directriz, que en este caso es la recta horizontal de ecuación y = 2, y el foco F. Los números d y e (señalados con una flecha roja) indican las distancias de un punto genérico P al foco y a la directriz, respectivamente.
La flecha roja en la vista algebraica señala el valor de la distancia desde un punto P cualquiera de la parábola a su foco y a su directriz. Se observa que ambas distancias son iguales entre sí.
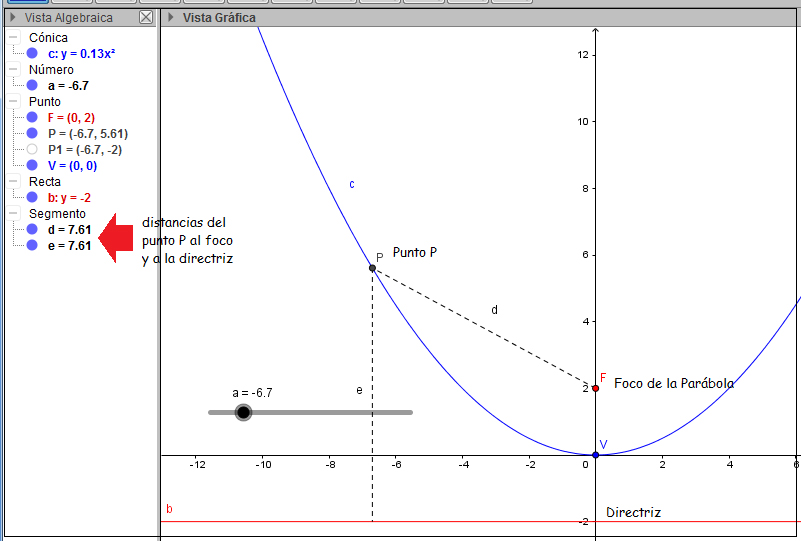
El “deslizador” nos permite cambiar de posición el punto P. Sin embargo, las distancias de esteal foco y a la directriz siguen siendo iguales entre sí.
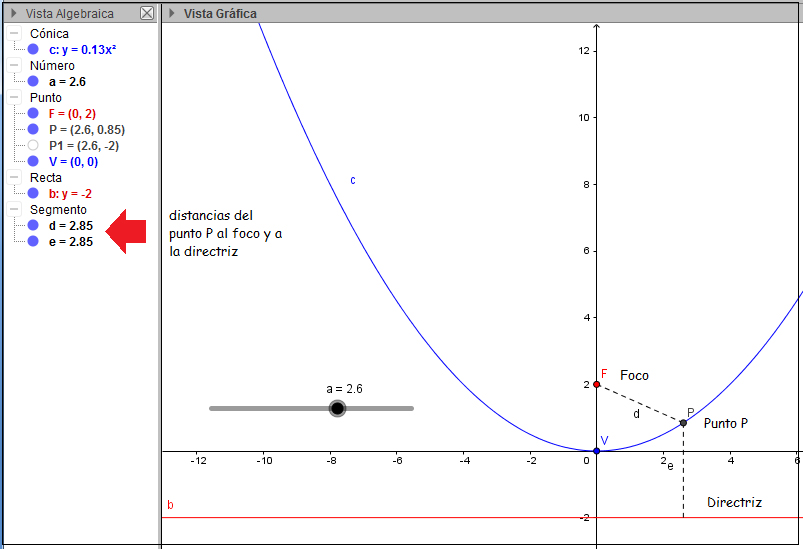
Obsérvese que, independientemente de dónde se encuentre el punto, esas dos distancias adoptan siempre el mismo valor.
A partir de la definición, se deduce que la ecuación de la parábola tiene la forma:
[5.5] \[ y-y_v=\frac{1}{4p} \ (x-x_v )^2 \]
En dicha expresión, \((x_v,y_v ) \) representan las coordenadas del vértice (punto que resulta de intersecar a la curva con el eje focal), en tanto que p es la distancia entre el vértice y el foco (que, de acuerdo con la definición, será también la distancia entre el vértice y la directriz).
Desarrollando la expresión [5.5] y efectuando convenientes sustituciones, obtenemos la siguiente ecuación:
[5.6] \[ y=ax^2+bx+c\]
En este caso, a recibe el nombre de coeficiente principal, b el de coeficiente lineal y c el de término independiente.
El término principal de la parábola nos permite determinar de inmediato una de las características más representativas de la curva, que es su concavidad. Así, si a es positivo, diremos que la curva presenta concavidad positiva o que es cóncava hacia arriba. En cambio, si a es negativo, la parábola será convexa o cóncava hacia abajo (imagen 5.11).
En azul, a la izquierda, la función f(x) cuya representación gráfica es una parábola de concavidad positiva; en rojo, a la derecha, la función g(x), cuya curva es una parábola de concavidad negativa.
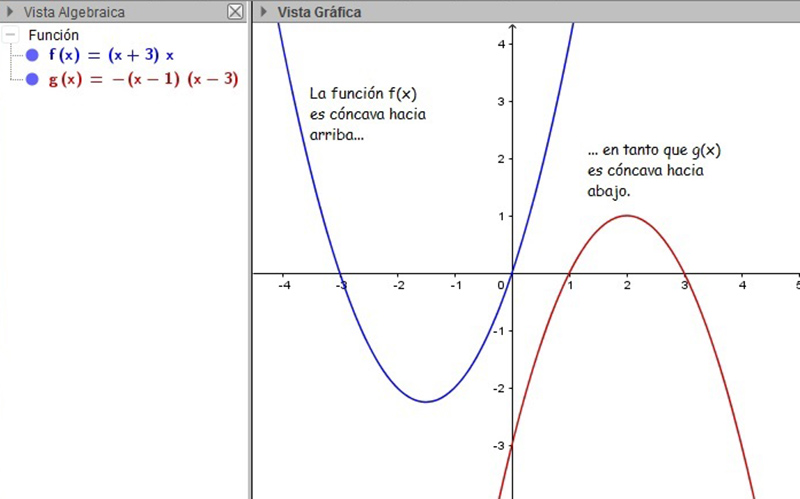
El vértice de la parábola resulta ser un punto de gran interés en el momento de trabajar con problemas concretos en los que deben emplearse funciones cuadráticas, puesto que, según cuál sea la concavidad de la curva, dicho vértice representará un extremo (ya sea máximo o mínimo) de la función.
Diremos que el punto de coordenadas \( ( x_M,f(x_M ) \) es un máximo absoluto de la función cuando, para cualquier valor de la variable independiente x perteneciente a su dominio se verifique la condición:
\[ f(x){<}f(x_M ) \]
Análogamente, podemos decir que el punto de coordenadas \( (x_m,f(x_m )) \) es un mínimo absoluto de la función cuando, para cualquier valor de la variable independiente x perteneciente a su dominio se verifique la condición:
\[ f(x)>f(x_m ) \]
Para obtener la abscisa correspondiente al vértice de una parábola, cuando esta se expresa tal como lo muestra la ecuación [5.6], utilizamos la siguiente expresión:
[5.7] \[ x_v=- \frac{b}{2a} \]
De modo que las coordenadas del vértice podrán expresarse, en forma genérica, de la siguiente manera:
\[ V= (x_v , y_v) = \left( - \frac{b}{2a}, f \left( - \frac{b}{2a} \right) \right) \]
Ahora que sabemos cómo obtener el vértice y teniendo en cuenta lo dicho respecto de la concavidad de una parábola, podemos concluir lo siguiente:
Dada una función cuadrática de concavidad positiva, su vértice representará el mínimo absoluto de dicha función. Si, en cambio, la función cuadrática resulta ser cóncava hacia abajo, su vértice representará al máximo absoluto.
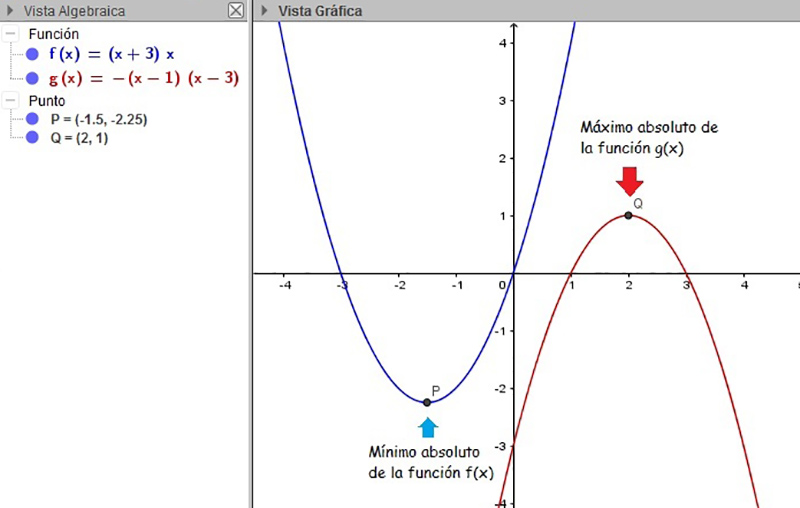
En la imagen 5.12, se observa claramente que el punto P —vértice de la función f(x)— resulta ser el mínimo de dicha función; en cambio, el punto Q (vértice de la función g(x)) es claramente un máximo absoluto.
De acuerdo con la concavidad de la función, su vértice habrá de representar su máximo o su mínimo absoluto.
Para las siguientes funciones cuadráticas, se pide indicar cuál es su concavidad y obtener las coordenadas del vértice de cada una de ellas. Indicar si este representa un máximo o un mínimo de la función.
- \( f_1 (x)=x^2+x-6 \)
- \( f_2 (x)=-x^2+x+6 \)
- \( f_3 (x)=2x^2-6x-20 \)
En toda función definiremos como ceros o raíces a los valores de la variable independiente para los cuales la curva corta al eje de abscisas. En el caso particular de la función cuadrática, cuando ella aparezca expresada como lo muestra la [5.6], disponemos de la fórmula resolvente, debida al matemático hindú Bhaskara (1114-1185).
Las raíces de una ecuación de segundo grado de la forma
\[ ax^2+bx+c=0 \]
se obtienen aplicando la siguiente ecuación:
\[ x_{1,2}=\frac{-b±\sqrt{b^2-4ac}}{2a} \]
Dicha ecuación también se conoce como ecuación de Bhaskara, en honor a su autor.
Para las funciones cuadráticas propuestas en la actividad anterior, obtener las raíces aplicando la fórmula de Bhaskara.
Acabamos de ver que una de las raíces de nuestra función podría obtenerse resolviendo la expresión:
[5.8] \[ x_1=\frac{-b+\sqrt{b^2-4ac}}{2a} \]
La otra de las raíces, en cambio, se obtendría a partir de la expresión:
[5.9] \[ x_2=\frac{-b-\sqrt{b^2-4ac}}{2a} \]
Veamos qué sucede al sumar [5.8] y [5.9]:
\[ x_1+x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}+\frac{-b-\sqrt{b^2-4ac}}{2a} \]
\[ x_1+x_2=\frac{-b+\sqrt{b^2-4ac}-b-\sqrt{b^2-4ac}}{2a} \]
Al sacar común denominador, se cancelan los dos términos que presentan raíces cuadradas y nos queda:
\[ x_1+x_2=\frac{-b-b}{2a}=-\frac{2b}{2a}=-\frac{b}{a} \]
Si, finalmente, dividimos los dos miembros de la expresión que acabamos de obtener por dos, nos queda:
\[ \frac{x_1+x_2}{2}=-\frac{b}{2a} \]
Compárese el miembro de la izquierda con la expresión [5.7] : acabamos de obtener otra forma de calcular la abscisa del vértice de la parábola. No olvidemos que dicho valor puede resultarnos muy valioso, dado que habrá de corresponder al máximo o mínimo de la función.
Dada una función cuadrática de la forma \( f(x)=ax^2+bx+c \), cuyas raíces sean \( x_1 \) y \( x_2 \), la abscisa del máximo o mínimo de dicha función podrá calcularse resolviendo la igualdad:
[5.10] \[ x_{extremo}=\frac{x_1+x_2}{2} \]
Dicha abscisa deberá coincidir con la del vértice de la parábola que representa gráficamente la función.
Finalizaremos la presente sección presentando otra forma de escribir a la función cuadrática, la forma factorizada.
Dada una función cuadrática de la forma \( f(x)=ax^2+bx+c \), cuyas raíces sean \( x_1, \) y \( x_2, \)podrá también escribirse como:
[5.11] \[ f(x)=a(x-x_1 )(x-x_2 ) \]
Esta recibe el nombre de forma factorizada de la función.
En la siguiente sección proponemos una aplicación de todo lo repasado en la presente.
Stewart, J.; Redlin, L.; Watson, S. (2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 130 a 145 y 162 a 172.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 2 a 23.
5.3.2. Ejemplo de optimización a partir de una función cuadrática
Según un estudio, se determinó que en cierta región, cuando la cantidad de manzanos por hectárea ascendía a 60, cada uno de ellos producía en promedio unos 900 frutos por año. El mismo estudio agregaba que, por cada árbol más que se plantara por hectárea, el promedio de frutos recogidos disminuía en 10 unidades.
Se desea saber entonces cuál es la cantidad de árboles que deberá plantarse por hectárea para que el número de manzanas obtenidas sea el mayor posible. Se pide, además, calcular cuál será entonces la máxima producción por hectárea posible.
A partir de los datos que nos ofrece el enunciado, debemos obtener una función que relacione la cantidad de manzanas obtenidas por hectárea con el número de árboles frutales plantados en ella. Como conocemos la cantidad promedio de frutos por árbol cuando hay 60 árboles por hectárea, proponemos como variable independiente x al número de árboles por sobre los 60 que hayan sido plantados en dicha hectárea.
Así, el número de árboles por hectárea será igual a 60 + x, en tanto que el número promedio de manzanas producidas por cada árbol se podrá calcular como 900 – 10.x, teniendo en cuenta que por cada árbol más que se hubiera plantado, cada árbol produciría diez manzanas menos.
Llamando N(x) al número de manzanas producidas por hectárea en función del número de árboles (por sobre los sesenta) que hubiesen sido plantados en dicha hectárea, entonces la expresión para el cálculo de dicho valor será:
\[ N(x)=(60+x).(900-10x)\]
Si extraemos convenientemente factor común, la expresión anterior puede escribirse como:
\[ N(x)=-10(x-90)(x+60) \]
La forma factorizada nos permite obtener en forma inmediata las raíces, que serán los valores de la variable independiente que anulan cada uno de los factores; en nuestro caso serán x = 90 y x = -60.
Utilizando la expresión [5.10], y teniendo en cuenta que el término principal es negativo (lo que significa que la parábola tiene concavidad negativa y que su vértice representa el máximo de la función), calculamos:
\[ x_{máximo}=\frac{90+(-60)}{2}=15 \]
Como este valor corresponde al número de árboles por sobre los sesenta que hubiera plantados por hectárea, concluimos que las parcelas en las que se obtendrá la mayor producción posible serán aquellas en las que haya 75 árboles por hectárea.
En cuanto a la máxima producción, bastará con utilizar la expresión obtenida inicialmente:
\[ N(15)=(60+15).(900-10.15)=56250 \]
Ese será el mayor número de manzanas obtenidas por hectárea, teniendo en cuenta las conclusiones del estudio al que hace referencia el enunciado del problema.
Un objeto se dispara verticalmente hacia arriba, con una velocidad inicial de 30 metros sobre segundo. Si se desprecia el rozamiento y solo se tiene en cuenta la acción de la gravedad sobre el objeto, la función que nos permite conocer su altura en función del tiempo será:
\[ h(t)=30t-5t^2 \]
Calcular entonces en qué instante alcanzará la máxima altura y cuál será el valor de esta.
5.4. Funciones racionales
Reciben este nombre aquellas funciones de la forma
\[ f(x)=\frac{P(x)}{Q(x)} \]
Es decir, son funciones que se obtienen como razón o cociente entre dos funciones polinómicas.
Recordemos que un polinomio de grado n habrá de escribirse como
\[ P(x)=a_0+a_1 x+a_2 x^2+⋯+a_n x^n \]
donde \( a_n \not= 0 \)
Las imágenes 5.13, 5.14 y 5.15 nos muestran las gráficas de tres funciones racionales distintas.
La expresión de cada una de las funciones aparece en la vista algebraica correspondiente (señalada en todas las imágenes con una flecha de color rojo). La función representada en la imagen 5.13 no presenta, a primera vista, elementos que puedan llamarnos la atención. En cambio, las funciones cuyas gráficas se observan en las imágenes 5.14 y 5.15 presentan, entre otras “novedades”, saltos infinitos.
El estudio de este tipo de funciones nos obligará a introducir uno de los conceptos característicos del Análisis Matemático: el del límite de una función en un punto.
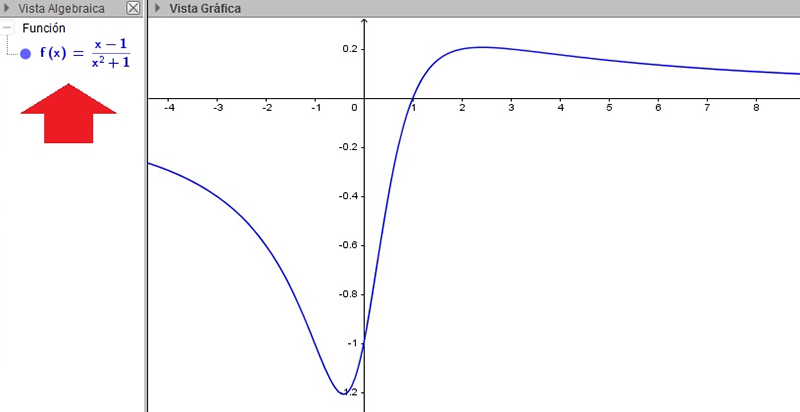
Gráfica de la función \( f(x)=\frac{x-1}{x^2+1} \)
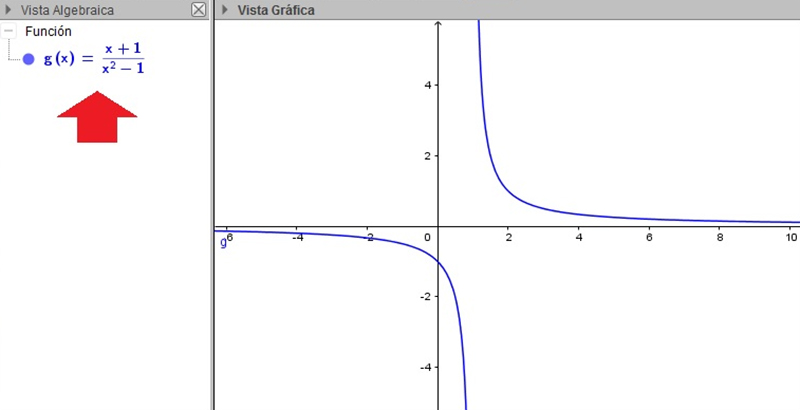
Gráfica de la función \( f(x)=\frac{x+1}{x^2-1} \)
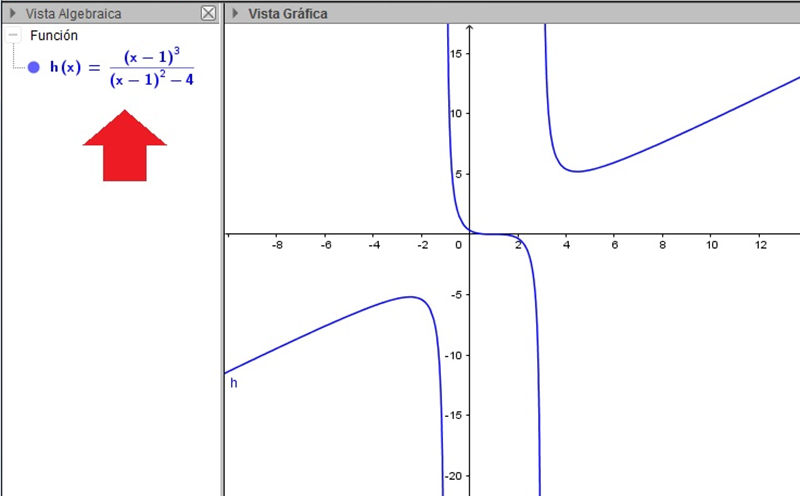
Gráfica de la función \( f(x)=\frac{(x-1)^3}{(x-1)^2-4} \)
5.4.1. Obtención del dominio de una función racional: condiciones
Dentro de esta unidad hemos mencionado en varias oportunidades al dominio de una función, definiéndolo como el conjunto conformado por todos aquellos números reales para los cuales la función puede definirse. No nos hemos detenido mayormente en ese concepto hasta el momento, porque las funciones lineales y las cuadráticas tienen por dominio todo el campo real.
Sin embargo, al trabajar con las funciones racionales debemos tener en cuenta que no existe la división por cero. La definición del dominio de este tipo de funciones nos obligará entonces a buscar las raíces del denominador, valores que tendremos que restar del conjunto de los reales en el momento de definir el dominio de estas funciones.
Por ejemplo, comencemos por la función \( f(x)=(x-1)⁄(x^2+1) \), cuya representación gráfica aparece en la imagen 5.13. Su denominador no se anula para ningún valor de la variable independiente x, razón por la cual diremos que está definida para todos los reales. En símbolos:
\[ D_f= \mathbb{R} \]
Si observamos, en cambio a \( g(x)=(x+1)⁄(x^2-1) \), cuya representación gráfica vemos en la imagen 5.14, veremos que existen dos valores de la variable independiente (x = 1 y x = -1) para los cuales el denominador se anula. Recordando que no existe la división por cero, escribiremos entonces:
\[ D_g=\mathbb{R}-\{-1,1\} \]
Es decir, esta función quedará definida para todo número real exceptuando al uno y al menos uno.
Finalmente, en el caso de la función representada en la imagen 5.15, \( h(x)=\frac{(x-1)^3}{(x-1)^2-4} \) , nos encontramos ante una situación similar a la de la función g(x): existen valores reales para los cuales el denominador se anula. En este caso, hacemos:
\[ (x-1)^2-4=0 \to (x-1)^2=4 \to \]
\[ \to \sqrt{(x-1)^2 }=\sqrt{4} \to |x-1|=2 \]
Para comprender lo que hicimos en los dos últimos pasos de cálculo, recordar que la raíz cuadrada de un número real elevado al cuadrado es igual al módulo de dicho número.
Teniendo eso en cuenta, podemos continuar el cálculo de la siguiente manera:
\[ |x-1|=2 \left \{ \begin{matrix} x-1=2→x=3 \\ x-1=-2→x=-1\end{matrix}\right. \]
Podemos entonces escribir el dominio de esta función:
\[ D_h= \mathbb{R}- \{-1,3\}\]
El dominio de toda función racional quedará definido restando al conjunto de los reales todos aquellos valores reales que anulen al polinomio que aparece en el denominador de nuestra función.
Obtener el dominio de las siguientes funciones:
- \( f_1 (x)=\frac{x+2}{x^3-3x^2+2x} \)
- \( f_2 (x)=\frac{x^5+2}{x^3-8} \)
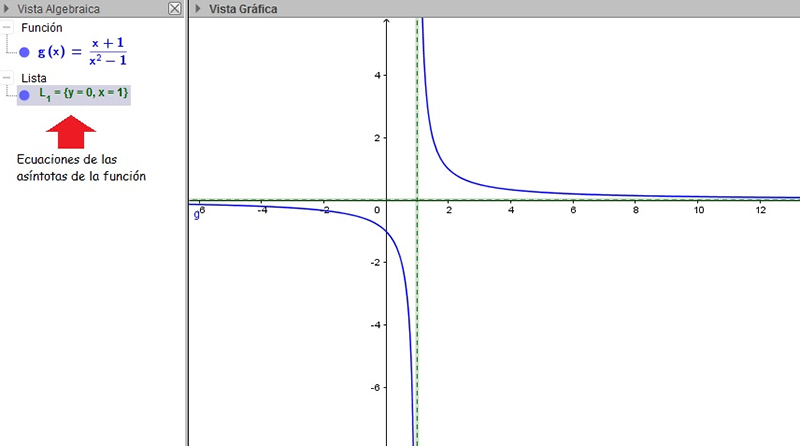
El comportamiento de las funciones g(x) y h(x), reflejado en sus gráficas, resulta bastante particular. En la imagen 5.16 volvemos a dibujar la primera de ellas, pero agregamos en línea punteada un par de rectas (x =1 e y =0) a las cuales la función se hace prácticamente paralela. Dichas rectas reciben el nombre de asíntotas de la función.
La función \(f(x)=\frac{x+1}{x^2-1} \) no está definida para todos los reales. Además, se observa que a medida que la variable independiente adopta valores muy grandes (o muy pequeños), la curva se hace prácticamente paralela al eje de abscisas. El propio programa nos ofrece las dos asíntotas de la curva, que se señalan en la vista algebraica con una flecha de color rojo.
Para la obtención de dichas rectas necesitamos definir el límite de una función en un punto, cosa que haremos en la siguiente sección.
5.4.2. Obtención de las asíntotas de una función racional: aplicación del límite de una función en un punto
Volviendo entonces a la función g(x), nos interesa saber qué sucede a medida que nos acercamos tanto como queramos a los valores para los cuales la función no está definida. La expresión que aparece en negrita no parece muy rigurosa desde el punto de vista matemático, pero conceptualmente nos ayudará a comprender qué significa hablar de límite de una función para un valor dado de la variable x.
Llamaremos límite de una función cuando la variable independiente tiende a un valor \( x_0 \) al valor que la función toma o debería tomar a medida que nos aproximemos tanto como lo deseemos a dicho valor.
En símbolos, \( L=\displaystyle\lim_{x \to x_0}f(x) \)
Si bien es cierto que el límite puede calcularse para cualquier valor de la variable independiente, nos interesará hacerlo en particular allí donde la función no esté definida.
En el caso de g(x), comencemos estudiando qué sucede si la variable se aproxima a x = -1 (uno de los valores que se encuentra fuera del dominio), “tanto como queramos”. Escribimos entonces:
\[ \displaystyle\lim_{x \to -1}\frac{x+1}{x^2-1} \]
En principio, podríamos pensar en reemplazar a la x por el valor al cual tiende la variable, es decir, menos uno. Pero si lo hacemos, veremos que se anulan tanto el numerador como el denominador. Nos encontraremos entonces ante lo que denominamos una indeterminación del tipo cero sobre cero, a la que debemos “salvar” aplicando algún procedimiento matemáticamente válido.
Notemos que el denominador de la función podría factorizarse, por tratarse de una diferencia de cuadrados. Entonces, podríamos escribir:
\[ \displaystyle\lim_{x \to -1}\frac{x+1}{x^2-1}= \displaystyle\lim_{x \to -1}\frac{x+1}{(x+1)(x-1)}= \displaystyle\lim_{x \to -1}\frac{1}{(x-1)}=- \frac{1}{2} \]
En el segundo paso simplificamos el factor (x + 1) que aparecía tanto en el numerador como en el denominador, de modo que el valor menos uno puede reemplazarse en la expresión resultante, dándonos por resultado menos un medio.
Desde el punto de vista estrictamente matemático esto significa que, si bien la función no está definida para x = -1, podemos asignarle a la variable independiente valores muy cercanos a ese y la función adoptará entonces valores muy próximos a menos un medio.
Cuando algo así sucede (es decir, la función no está definida pero su límite existe, y tiene por resultado un valor finito) decimos que la función presenta una discontinuidad evitable. Desde el punto de vista gráfico, la curva debería presentar un “agujero” en el punto —en nuestro ejemplo, en (-1,-1/2)—, cosa que el software, debido al modo en que construye las curvas, no muestra en la imagen.
Continuando con la función g(x), veamos ahora qué sucede a medida que nos acercamos a x = 1.
\[ \displaystyle\lim_{x \to 1}\frac{x+1}{x^2-1} \]
En este caso, el numerador valdría dos y el denominador cero. Esto ya no es una indeterminación: la división por cero no existe, pero cuando se divide un número finito no nulo por otro que tiende a cero, diremos que el resultado tiende a infinito. En símbolos:
\[ \displaystyle\lim_{x \to 1}\frac{x+1}{x^2-1}= \infty \]
En la imagen 5.16 se observa que, a medida que la variable x toma valores cada vez más próximos a uno, la función adopta valores muy grandes (o muy chicos), haciéndose prácticamente paralela a la recta vertical de ecuación x= 1. Esta recta recibe entonces el nombre de asíntota vertical de la función.
Dada una función f(x), x = a será asíntota vertical de dicha función si se cumplen las siguientes condiciones:
- x = a no pertenece al dominio de la función
- \( \displaystyle\lim_{x \to a} f (x)= \infty \)
Volviendo a la imagen 5.16, se observa que, a medida que la variable independiente adopta valores muy grandes (o muy chicos), la curva se hace prácticamente paralela al eje de abscisas (de ecuación y = 0). Al hablar de valores muy grandes (o muy chicos) de x podemos llegar al extremo de decir más o menos infinito.
Puesto que no podemos reemplazar en la expresión de g(x) la variable independiente por algo que no es un número sino un concepto (como lo es el infinito), volveremos a aplicar el límite, del modo que mostramos a continuación:
\[ \displaystyle\lim_{x→∞}\frac{x+1}{x^2-1} \]
En este caso, reemplazando a la variable independiente por un número tan grande como pudiésemos imaginar, nos encontraríamos ante otro tipo de indeterminación, que se conoce con el nombre de infinito sobre infinito. Para “salvarla” podemos sacar factor común x tanto en el numerador como en el denominador:
\[ \displaystyle\lim_{x \to \infty}\frac{x+1}{x^2-1}= \displaystyle\lim_{x \to \infty }\frac{x \left({1+\displaystyle\frac{1}{x}}\right)}{x \left({x+\displaystyle\frac{1}{x}}\right)} = \displaystyle\lim_{x \to \infty}\frac{ \left({1+\displaystyle\frac{1}{x}}\right)}{ \left({x+\displaystyle\frac{1}{x}}\right)} = 0 \]
Cuando un número finito no nulo se divide por un número muy grande (digamos, que tiende a infinito), el cociente tiende a cero. Por eso, el segundo miembro del numerador y del denominador de la última expresión se anulan. Pero entonces el numerador tenderá a uno y el denominador tenderá a infinito, razón por la cual el cociente tiende a cero. Entonces, y=0 representará la asíntota horizontal de la función, pues a medida que la variable independiente adopta valores muy grandes, la curva se va haciendo prácticamente paralela a aquella recta horizontal.
Cuando \( lim_{x \to \infty} \ f(x)=k \), siendo k un número real finito, entonces, y = k será asíntota horizontal de dicha función.
Cuando nos proponemos representar gráficamente en forma aproximada una función, particularmente en el caso de las racionales, resulta de suma utilidad comenzar por el trazado de sus asíntotas. El hecho de que la curva se haga prácticamente paralela a ellas resulta un dato muy útil en el momento de graficar.
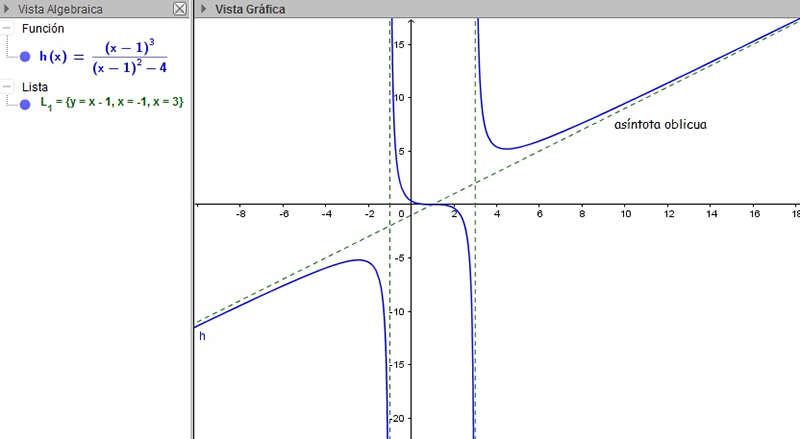
Por eso, debemos aclarar que, además de las horizontales y verticales, existen otro tipo de asíntotas, que reciben el nombre de asíntotas oblicuas. Se trata de rectas cuya pendiente puede ser positiva o negativa, pero nunca cero ni infinita (que es el caso de las asíntotas verticales). En la imagen 5.17 volvemos a representar la función h(x); pero en esta oportunidad, hemos agregado a la gráfica de la curva (que ya habíamos visto en la imagen 5.15) tres rectas: dos verticales y una tercera que tiene pendiente positiva.
Dicha recta es la asíntota oblicua de nuestra función.
Calcular las ecuaciones de las asíntotas verticales de la función \( h(x)= \frac{(x-1)^3}{(x-1)^2-4} \)
La función \( f(x)= \frac{(x-1)^3}{(x-1)^2-4} \) presenta dos asíntotas verticales y una asíntota oblicua. Es frecuente que esto último suceda cuando el grado del polinomio que aparece en el numerador de la función racional supera en una unidad al grado del polinomio que aparece en el denominador.
Para la obtención de la asíntota oblicua de h(x), debemos tener en cuenta lo siguiente:
Cuando en una función racional el grado del polinomio que aparece en el numerador supera en una unidad al polinomio presente en su denominador, es frecuente que aquella tenga una asíntota oblicua.
Esta, como toda recta, habrá de tener una ecuación de la forma
\[ y=mx+b \]
\[ \text{donde } \ m=\displaystyle\lim_{x \to \infty}\frac{f(x)}{x} \]
\[ \text{y } \ b=\displaystyle\lim_{x \to \infty}f(x)-mx \]
Calculamos seguidamente la asíntota oblicua de h(x). Comenzamos por su pendiente:
\[ m=\displaystyle\lim_{x \to \infty}\frac{h(x)}{x} = \displaystyle\lim_{x \to \infty}\frac{(x-1)^3}{x((x-1)^2-4)} = \displaystyle\lim_{x \to \infty}\frac{ x^3-3x^2+3x-1}{ x^3-2x^2-3x} \]
\[ =\displaystyle\lim_{x \to \infty} \frac {x^3 \left( 1- \displaystyle\frac{3}{x} + \displaystyle\frac{3}{x^2} - \displaystyle\frac{1}{x^3} \right)} {x^3 \left( 1- \displaystyle\frac{2}{x} - \displaystyle\frac{3}{x^2} \right)} =1 \]
En el último paso, para salvar la indeterminación del tipo infinito sobre infinito, procedimos a sacar factor común x3.
Conocido el valor de la pendiente, calculamos ahora la ordenada al origen:
\[ b=\displaystyle\lim_{x \to \infty}{h(x)} - mx= \displaystyle\lim_{x \to \infty}\frac{ x^3-3x^2+3x-1}{ x^2-2x-3} -x= \]
\[ =\displaystyle\lim_{x \to \infty} \left( \frac {-x^2+6x-1}{x^2-2x-3} \right) =\displaystyle\lim_{x→∞} \frac {x^2\left( -1+ \frac{6}{x}-\frac{1}{x^2} \right) } {x^2\left( 1+ \frac{2}{x}-\frac{3}{x^2} \right) } = - 1 \]
Así, y = x -1 resulta ser la asíntota oblicua de la función h(x), tal como se observa en la vista algebraica de la imagen 5.17.
Hallar todas las asíntotas de las siguientes funciones:
- \( f_1 (x)=\frac{x^2+2x-3} {x-1}\)
- \( f_1 (x)=\frac{x^2+2x-3} {x^2-1} \)
- \( f_3 (x)=\frac{x^3+2x-3} {x^2-1} \)
Recomendamos al alumno verificar los resultados obtenidos empleando el wxMaxima. En la siguiente sección encontrará las instrucciones necesarias para poder hacerlo.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 41 a 76.
Stewart, J.; Redlin, L.; Watson, S. (2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 221 a 243 y 262 a 273.
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 60 a 90.
5.5. Empleo del software para el cálculo de límites
Con el fin de que el alumno pueda verificar los resultados obtenidos en forma manual, proponemos seguidamente algunos ejemplos que habrán de ser resueltos empleando el wxMaxima.
Evaluar
\[ \displaystyle\lim_{x \to 1}\frac {x^2-1}{x^3+5x-6} \]
Resolución empleando el software:
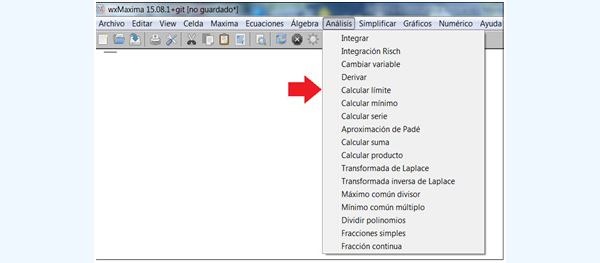
Nos movemos sobre la barra superior de Menú hasta “Análisis”, y allí seleccionamos “Calcular límite” (imagen 5.18).
El primer paso para el cálculo de un límite consiste en seleccionar en el Menú la opción “Calcular límite”.
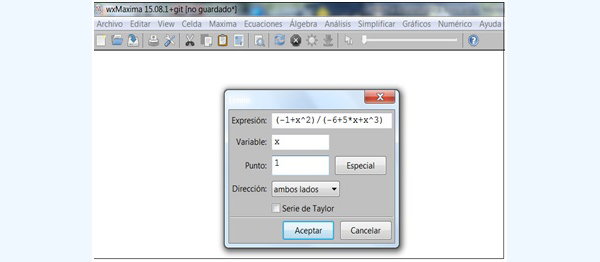
En la ventana que se abre debemos ingresar la función y el valor de x al que hacemos tender a la variable independiente (imagen 5.19). Una vez que hacemos clic en “Aceptar”, el programa nos devuelve en pantalla el resultado del cálculo (imagen 5.20).
Una vez que se abre la primera ventana debemos introducir con cuidado la función, la variable independiente y el valor de esta última al cual hacemos tender la función.
Basta con hacer clic en “Aceptar”para queel programa nos devuelva el resultado en forma inmediata.

La interpretación del resultado obtenido nos permitirá, por ejemplo, confirmar la presencia de asíntotas verticales, como veremos en el siguiente ejemplo.
Evaluar
\[ \displaystyle\lim_{x \to 1}\frac {x+2}{x^3+5x-6} \]
Resolución empleando el software:
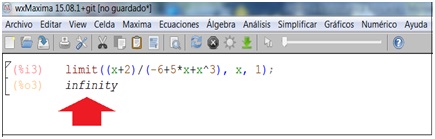
Siguiendo los mismos pasos que en el caso anterior, obtenemos como resultado “infinity”, como se observa en la imagen 5.21. Ese resultado nos indica que x = 1 resulta ser asíntota vertical de la función.
Debemos interpretar el resultado obtenido: cuando el límite de una función tendiendo a un valor finito da como resultado infinito, significa que dicho valor se corresponde con la abscisa de todo punto de la asíntota vertical de la función.
Teniendo en cuenta que el límite infinito nos permite determinar la existencia de asíntotas horizontales, veremos, para finalizar la presente unidad, de qué modo calcular ese tipo de límite.
Evaluar
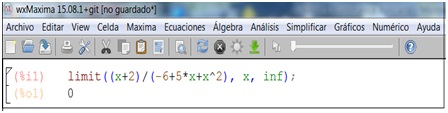
\[ \displaystyle\lim_{x \to \infty}\frac {x+2}{x^3+5x-6} \]
Resolución empleando el software:
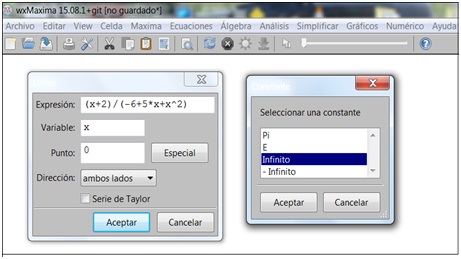
En esta oportunidad, dentro de la ventana que nos permite ingresar los datos, tendremos que hacer clic en “Especial”. Se abrirá entonces una segunda ventana, dentro de la cual, en nuestro caso, hemos de seleccionar “Infinito”.
En la imagen 5.22 figuran ambas ventanas, una al lado de la otra.
Pero advertimos al estudiante que la de la izquierda aparecerá en primer lugar, y que, al hacer clic en “Especial”, se abrirá la ventana menor.
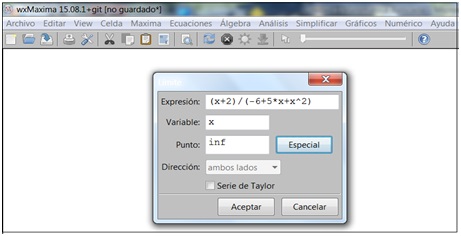
Una vez que hagamos clic en “Aceptar”, pero en la ventana menor, esta desaparecerá y nos encontraremos nuevamente con la ventana mayor. Pero en esta oportunidad, en la casilla donde dice “Punto” (es decir, el valor hacia el cual tendía el límite) vemos que aparece el cartel “inf” (imagen 5.23).
Una vez que nos apoyamos en “Aceptar”, el programa nos devuelve el resultado (imagen 5.24), que en este caso representa la ordenada de la asíntota horizontal de nuestra función.
Existen valores a los que el programa señala como especiales. Siel límite tiende a alguno de ellos, tendremos que hacer clic sobre la tecla virtual de la ventana que aparece a la izquierda para que aparezca la pequeña ventana que se observa a la derecha.
Una vez que se hace clic sobre el valor seleccionado (en nuestro caso, “Infinito”), desaparece la ventana menor y en la original aparece como “Punto” el valor seleccionado.
El programa nos brinda finalmente el resultado del límite.