6. Funciones trascendentes
Objetivos
Que el alumno:
- Aprenda algunas de las principales aplicaciones de las funciones exponenciales.
- Recuerde en qué consiste el logaritmo y cuáles son sus propiedades.
- Descubra la relación entre funciones logarítmicas y exponenciales.
- Comprenda la importancia de las funciones trascendentes al aplicarlas a procesos físicos muy diversos o a la determinación del pH de una solución.
- Descubra cómo los modelos matemáticos se van aproximando a la realidad al estudiar cómo se pasa del movimiento oscilatorio armónico ideal al movimiento oscilatorio amortiguado.
6.1. Función exponencial
Microorganismos como las bacterias, hongos y algas se emplean cada vez más para la obtención de productos químicos como la insulina o los antibióticos. También se emplean para la producción de alcohol por fermentación y en la fabricación de productos alimenticios como los quesos y el yogur. Las bacterias, además, se utilizan para el tratamiento de residuos y afluentes. Aquellas se reproducen en forma asexuada, a través de un proceso denominado fisión binaria.
Al respecto, recomendamos visitar las siguientes páginas:
Fisión binaria:
< https://10celula.com/fision-binaria/>
Las bacterias ácido-lácticas en la industria alimenticia:
<https://www.argenbio.org/index.php?action=novedades¬e=190>
Escherichia coli:
La fisión binaria consiste en la duplicación del ADN, a la que le sigue la división del citoplasma. Como consecuencia de dicho proceso, al cabo de unos minutos, una célula se divide en dos idénticas. La bacteria Escherichia coli, por ejemplo, puede dividirse cada veinte minutos bajo ciertas condiciones. El proceso aparece esquematizado en la imagen 6.1.
Observando el esquema (que, de acuerdo con lo indicado en el párrafo anterior, representaría lo que podría suceder a partir de una sola bacteria al cabo de unos sesenta minutos) notamos que se puede definir una ley de crecimiento, que nos permitiría calcular en forma aproximada el número de bacterias presentes en función del tiempo.
En el esquema se grafica, de izquierda a derecha, lo que va sucediendo a medida que pasa el tiempo: a partir de una única bacteria, el proceso de fisión binaria da lugar a la creación de un gran número de bacterias.
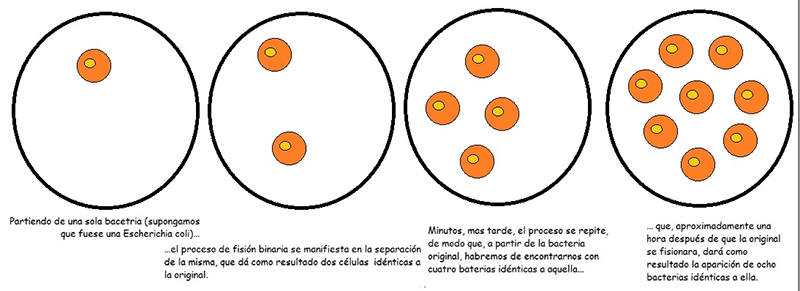
Suponiendo entonces que se trata de la Escherichia coli, podemos suponer que:
- En el instante \( t=0 \) solo hay una bacteria presente…
- pero, para \( t=20 \) minutos, ya hay dos bacterias…
- que se han fisionado 20 minutos más tarde (es decir, para \( t=40 \) minutos), de modo de que el número de bacterias presentes es entonces de cuatro…
- para que, 60 minutos después de que la primera bacteria se fisionara, ya se observe un total de 8 bacterias…
¡Es decir, el número de bacterias presentes se duplica cada veinte minutos!
Si indicamos con la variable x la unidad de tiempo necesario para que se produzca la fisión binaria (que en el ejemplo visto era de veinte minutos) y con la variable y expresamos el número de bacterias presentes a partir de la original, podemos escribir:
\[y = 2^x \]
He aquí entonces un nuevo tipo de función, que se caracteriza porque la variable independiente aparece como potencia de un número dado (al que, generalmente, llamamos base). Este tipo de funciones reciben el nombre de funciones exponenciales.
6.1.1. Representación gráfica
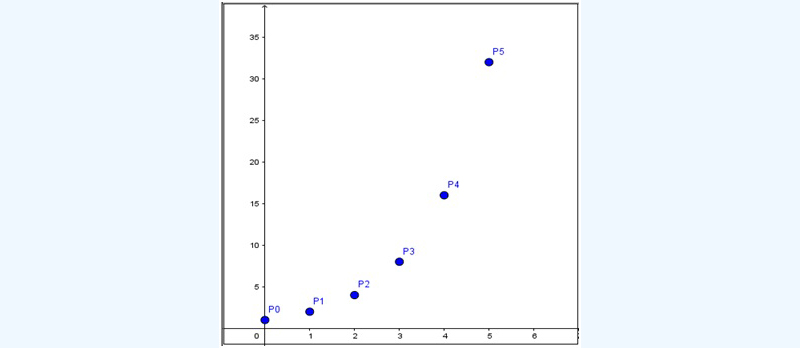
Siguiendo con el ejemplo presentado en la sección anterior, procedemos a graficar en un par de ejes cartesianos algunos de los puntos que reflejan el proceso que estamos analizando. La abscisa de cada uno de esos puntos representa el tiempo (cuya unidad, para la bacteria del ejemplo, se corresponde con veinte minutos), mientras que su ordenada indica el número de bacterias presentes. En la imagen 6.2 vemos entonces como el punto P1 representa el instante inicial (en el que solo había una bacteria presente), mientras P6 corresponde al número de bacterias transcurridos cien minutos desde que el proceso de fusión binaria diera comienzo en la primera bacteria.
La abscisa de cada uno de los puntos representa al tiempo, en tanto que la ordenada indica la cantidad de microorganismos presentes. Partiendo de solamente uno en el instante inicial, se observa que, al cabo de cien minutos, ya hay treinta y dos bacterias. Cada unidad en el eje de abscisas corresponde a veinte minutos.
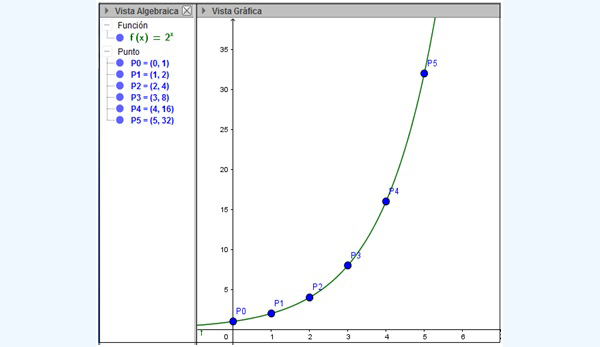
En la imagen 6.3 unimos dichos puntos para obtener la gráfica correspondiente a la función
\[y = 2^x \]
Obsérvese que el crecimiento es “explosivo”, ya que se hace cada vez más acentuado
Al unir los puntos representados en la imagen 6.2 se observa que estos se encuentran sobre una curva del tipo \(y = 2^x \)
Dejando de lado el ejemplo y concentrándonos exclusivamente en la función, existe una serie de características que vale la pena tener en cuenta:
- La función es estrictamente creciente; es decir, a medida que aumenta el valor de la variable independiente, también se incrementa el valor de la variable dependiente.
Diremos que una función \(f(x) \) es estrictamente creciente cuando, para cualquier par de valores de la variable independiente a y b se verifique que, siendo a < b, entonces \(f(a) < f(b)\) .
La función se hace asintótica al eje de abscisas cuando la variable independiente se hace infinitamente pequeña, lo que matemáticamente podemos expresar como
\[\displaystyle\lim_{x\to-\infty} 2^x=0\]
La función adopta valores cada vez mayores a medida que aumenta la variable independiente, es decir
\[\displaystyle\lim_{x\to\infty} 2^x=+\infty\]
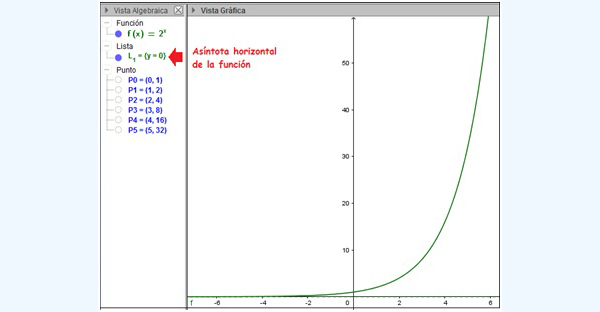
En la imagen 6.4 volvemos a dibujar la función. En la vista algebraica se observa la ecuación de su asíntota horizontal, obtenida por el propio software.
El software nos ofrece la ecuación correspondiente a la asíntota horizontal de la función.
¿Las características que acabamos de observar serán las mismas para toda función exponencial? En la siguiente sección analizaremos otro ejemplo muy vinculado con el que acabamos de estudiar, para tener una visión más amplia al respecto.
Por una serie de factores que no corresponde detallar en el presente trabajo, el proceso de crecimiento bacteriano que acabamos de describir no suele mantenerse en forma exponencial durante períodos de tiempo muy largos. Más allá de lo que pueda estudiarse desde el punto de la Microbiología, el sentido común confirma lo que acabamos de expresar. ¡Una sola bacteria cuyo tiempo de generación fuese de veinte minutos (es decir, el mismo que el de la Escherichia coli) produciría al cabo de cuarenta y ocho horas una descendencia cuya masa sería cuatro mil veces la del planeta Tierra!
6.1.2. Modelo de decrecimiento poblacional
Otro fenómeno que puede modelizarse matemáticamente a partir de la función exponencial es el del decrecimiento bacteriano.
Instrumentos quirúrgicos o alimentos deben soportar el proceso de esterilización, que destruye todos los organismos patógenos y formadores de toxinas que estos pudiesen presentar. Por ejemplo, el C botulinum es una bacteria que ha de eliminarse en el caso de los alimentos enlatados, llevándose a cabo la operación en el interior de equipos denominados autoclaves, en los que las latas se ven sometidas a altas temperaturas (superiores a los ciento veinte grados centígrados) durante un determinado período de tiempo (alrededor de dos horas).
Supongamos entonces que una determinada muestra posee inicialmente unas 800 bacterias por mililitro. Dicha muestra se introduce en un autoclave, observándose que, al cabo de 30 minutos, solo queda un promedio de unas 6 bacterias por mililitro.
La expresión matemática que permite conocer el número de bacterias por mililitro (\(N\)) en función del tiempo, para el proceso que acabamos de describir, es la siguiente:
\[ N(t)=800e^{-0,547t} \]
El tiempo debe expresarse en minutos y e es un número irracional (es decir, que tiene infinita cantidad de decimales no periódicos) cuyo valor aproximado es 2,71828. En la imagen 6.5 representamos gráficamente dicha función.
Si comparamos a esa curva con la de la imagen 6.4, observamos que:
- La función es estrictamente decreciente, es decir que, a medida que aumenta el valor de la variable independiente, disminuye el valor de la variable dependiente.
Diremos que una función f(x) es estrictamente decreciente cuando, para cualquier par de valores de la variable independiente a y b se verifique que, siendo a < b, entonces
\[ f(a)>f(b) \]
Representación gráfica de la función \( f(x)=800e^{-0,547x} \)
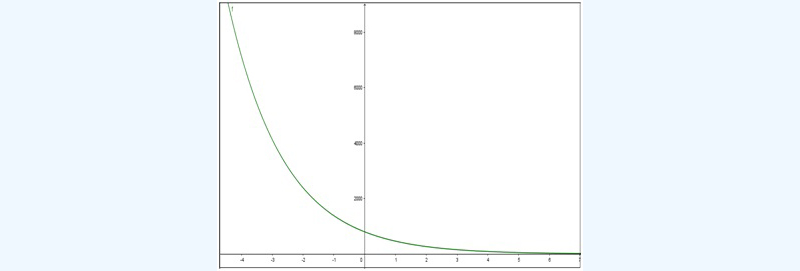
La función se hace asintótica al eje de abscisas cuando la variable independiente se hace infinitamente grande, lo que matemáticamente podemos expresar como
\[ \displaystyle\lim_{t\to+\infty }=800e^{-0,547t}=0 \]
La función adopta valores cada vez mayores a medida que disminuye la variable independiente, es decir
\[ \displaystyle\lim_{t\to-\infty }=800e^{-0,547t}=+\infty \]
¿Qué hace que el comportamiento de ambas funciones sea tan distinto? La respuesta es muy sencilla: en el caso estudiado en la sección anterior, el número que acompañaba a la variable independiente era positivo (uno), en tanto que en el ejemplo que acabamos de analizar, dicho coeficiente es negativo (-0,547).
Toda función exponencial de la forma \( f(x)=ka^{bx} \), con \( k>0 \), \( a>1 \ y \ b> \) y \( b>0 \) presentará las siguientes características:
- Será estrictamente creciente
- Tendrá asíntota horizontal para \( x\to -\infty \)
- Tenderá a infinito cuando \( x\to +\infty \)
Toda función exponencial de la forma \( f(x)=ka^{bx} \), con \( k>0 \), y \( a>1 \ y\ b<0 \) presentará las siguientes características:
- Será estrictamente decreciente
- Tendrá asíntota horizontal para \( x\to + \infty \)
- Tenderá a infinito cuando \( x\to - \infty \)
En las dos situaciones que acabamos de generalizar aclaramos que la base debía ser un número mayor que la unidad. Como veremos en la sección siguiente, la función exponencial y la logarítmica están íntimamente relacionadas, razón por la cual la base no podrá ser menor que cero ni tampoco uno.
De todos modos, vale aclarar que, cuando la base es positiva pero menor que la unidad, habrá de observarse lo siguiente:
Toda función exponencial de la forma \( f(x)=ka^{bx} \), con \( k>0 \), y \( 0{<}a <1 \ y\ b>0 \) presentará las siguientes características:
- Será estrictamente decreciente
- Tendrá asíntota horizontal para \( x\to +\infty \)
- Tenderá a infinito cuando \( x\to -\infty \)
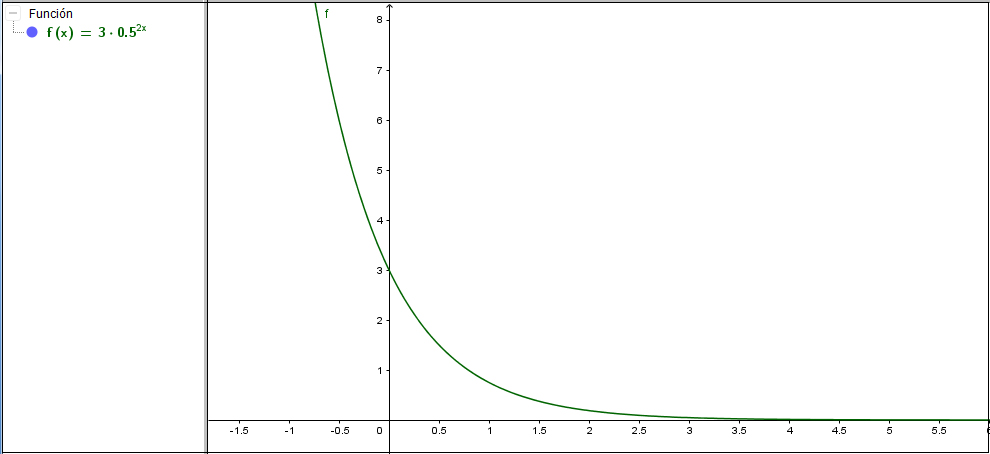
En la imagen 6.6 representamos una función que cumple con las condiciones del apartado anterior, es decir, tiene la forma \( f(x)=ka^{bx} \), con \( k>0 \), y \( a < 1 \ y\ b > 0 \) . Obsérvese que es decreciente a pesar de que el coeficiente que acompaña a la variable independiente sea positivo.
La función exponencial puede ser decreciente aun cuando la constante que multiplique a la variable independiente sea positiva. Ello dependerá, en este caso, del valor de la base.
Toda función exponencial de la forma \( f(x)=ka^{bx} \), con \( k>0 \), \( 0 < a < 1 \) y \( b<0 \) presentará las siguientes características:
- Será estrictamente creciente
- Tendrá asíntota horizontal para \( x \to -\infty \)
- Tenderá a infinito cuando \( x \to +\infty \)
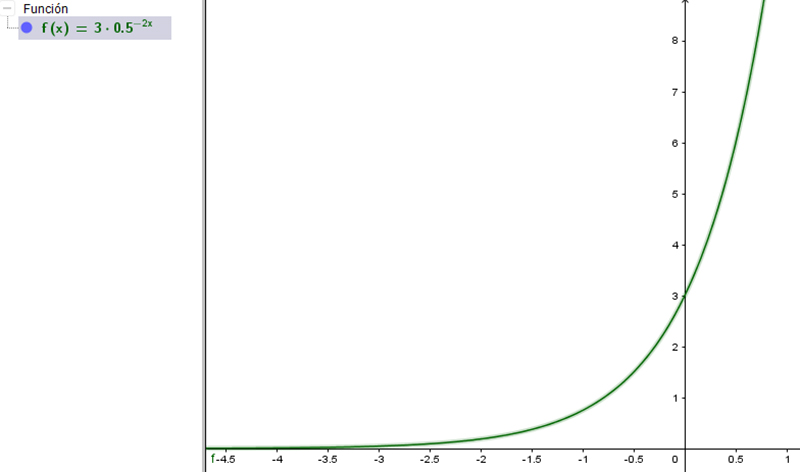
En la imagen 6.7 representamos una función que cumple con las condiciones del apartado anterior, es decir, tiene la forma \( f(x)=ka^{bx} \), con \( k>0 \)>, \( 0{<}a <1 \) y \( b{<}0 \). Obsérvese que es creciente a pesar de que el coeficiente que acompaña a la variable independiente sea negativo.
En esta oportunidad, la función resulta ser creciente a pesar de que el coeficiente que acompaña a la variable independiente sea negativo. Nuevamente es el valor de la base el que define el tipo de curva obtenida.
La función exponencial tiene un sinnúmero de aplicaciones. Pero muchas de ellas habrán de descubrirse a partir de una herramienta creada hacia el año 1600 por el matemático escocés John Napier (1550-1617): el logaritmo.
Stewart, J.; Redlin, L.; Watson, S. (2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 286 a 300.
6.2. Definición de logaritmo y función logarítmica
Definimos como logaritmo de un número b en la base a al número c, de tal modo que se verifique la siguiente igualdad: \[{log}_a b=c \leftrightarrow a^c=b \]
La base a será cualquier número positivo excepto uno, y el número b será un real positivo y no nulo.
A partir de esa definición, podemos escribir, por ejemplo:
\[ log_2 32=5 \] pues \[ 2^5=32 \]
o
\[ log_3 81=4 \] pues \[ 3^4=81 \]
o
\[ log_4 64=3 \] pues \[ 4^3=64 \]
Como veremos en la sección 6.2.2, la relación entre el logaritmo y las expresiones de tipo exponencial será de enorme aplicación en la resolución de problemas concretos.
De acuerdo con lo que dijimos al definir el logaritmo, este no puede definirse ni para cero ni para valores negativos. Si pensamos entonces en el logaritmo como función, debemos tener muy en cuenta lo que acabamos de decir.
Dada \( f(x)=log_a x \)(con a número real positivo distinto de la unidad), su dominio será \( D(f)=\mathbb{R}_{>0} \), es decir, los números reales positivos.
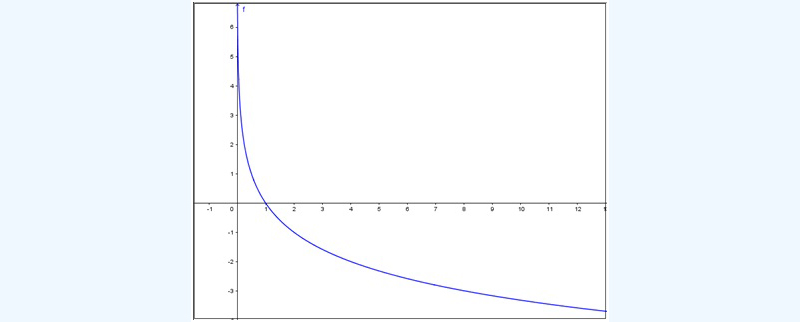
La representación gráfica de la función logaritmo presenta algunas características que el alumno debe tener muy presentes. En la imagen 6.8 reproducimos la gráfica de la función logaritmo con base e (número irracional cuyo valor aproximado es de 2,7182818).
La función \( f(x)=log_e x \) (que se conoce como logaritmo natural de x y se expresa como \( f(x)=ln (x) \)) presenta las siguientes características:
- \( \displaystyle\lim_{x \to0^+} ln(x)=-\infty \)
- \( \displaystyle\lim_{x \to\infty} ln(x)=\infty \)
- Es estrictamente creciente.
La primera de las condiciones nos indica que la función se hace asintótica al eje de ordenadas.
El crecimiento o decrecimiento de la función dependerá del valor de la base. En la imagen 6.9 representamos la función \( g(x)=log_{1⁄2}x \) . Obsérvese que la función es decreciente.
Gráfica de la función \( f(x)=ln(x) \) . Siendo la base del logaritmo un número mayor que la unidad, la curva resulta creciente.
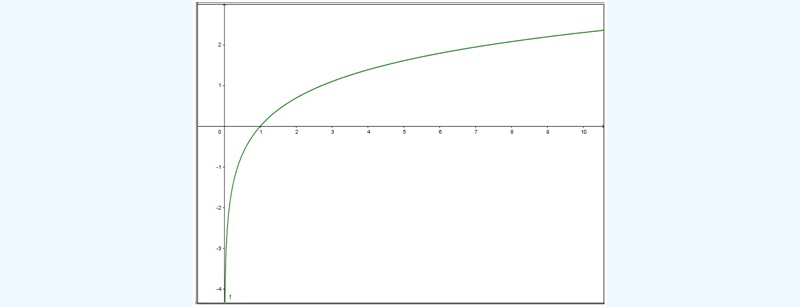
Cuando la base del logaritmo resulta ser un número positivo menor que la unidad, la función es decreciente. Ello se observa claramente en la gráfica que presentamos a continuación.
La función \( f(x)=log_a x \) (con \( 0 < a < 1 \)) presenta las siguientes características:
- \( \displaystyle\lim_{x \to0^+} ln(x)=+\infty \)
- \( \displaystyle\lim_{x \to \infty} ln(x)=-\infty \)
- Es estrictamente decreciente
La primera de las condiciones nos indica que la función se hace asintótica al eje de ordenadas.
Dejemos por el momento a la función logaritmo para detenernos en las propiedades de la herramienta en sí. En la sección 6.22 veremos algunas de sus aplicaciones.
6.2.1. Propiedades del logaritmo
El logaritmo tiene una serie de propiedades que, desde el momento de su creación, lo convirtieron en una herramienta de enorme utilidad. Hasta antes de que las calculadoras manuales se convirtieran para el estudiante en una herramienta de uso habitual, las dos primeras propiedades que habremos de enunciar eran ampliamente utilizadas por quienes tuviesen que hacer gran número de cálculos en forma manual. Dichas propiedades permitían reemplazar productos por sumas y cocientes por restas y siguen siendo claves en la demostración de teoremas y propiedades.
Veremos en la sección siguiente que la tercera y la cuarta de las propiedades enunciadas resultan fundamentales para resolver un tipo de problema muy común, el de las ecuaciones exponenciales.
Enunciaremos a continuación cinco propiedades del logaritmo que el alumno no puede ignorar:
El logaritmo del producto entre dos números b y c es igual a la suma de los logaritmos de cada uno de esos números.
En símbolos: \( log_a(b.c)=log_a b+log_ac \)
El logaritmo del cociente entre dos números b y c es igual a la diferencia de los logaritmos de esos números.
En símbolos: \( log_a(b/c)=log_a b-log_ac \)
El logaritmo de un número b elevado a la c es igual al producto entre c y el logaritmo del número b.
En símbolos: \( log_ab^c=c.log_a b \)
El logaritmo en base a del número a es igual a la unidad.
En símbolos: \( log_aa=1 \)
El logaritmo en cualquier base posible de la unidad vale cero.
En símbolos: \( log_a1=0 \)
Existe, además, una expresión que consideramos oportuno agregar en esta sección. Se trata de la fórmula del cambio de base, de gran utilidad en muchos cálculos. Es frecuente que necesitemos calcular el logaritmo de un número en una base que no sea diez ni el número e (que son, respectivamente, las bases de los logaritmos decimal y neperiano o natural, los que podemos obtener usando calculadora); en tal circunstancia, la fórmula que daremos a continuación nos permitirá acceder al resultado buscado.
En símbolos, la fórmula del cambio de base expresa lo siguiente:
\[ log_ab=log_cb ⁄ log_ca \]
Supongamos que necesitamos conocer el logaritmo en base 5 del número 12, es decir \( log_512 \) . Aplicando la fórmula del cambio de base, podemos escribir:
\[ log_512=ln(12)⁄ln(5) \cong 1,54395 \]
El resultado se obtuvo con el wxMaxima, como puede observarse en la imagen 6.10. Recordar, además, que la expresión ln corresponde al logaritmo natural o neperiano, cuya base es el número e (número irracional cuyo valor aproximado es 2,7182818).
Cálculo del logaritmo en base cinco del número doce con el wxMaxima. La instrucción “float”nos permite obtener un valor aproximado del resultado.

Stewart, J.; Redlin, L.; Watson, S. (2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 304 a 310 y 313 a 321
6.2.2. Empleo del logaritmo para la resolución de ecuaciones exponenciales
Desintegración del carbono 14
La desintegración radioactiva, fenómeno por el cual una determinada masa de un isótopo se convierte en energía a lo largo del tiempo (y que, por ejemplo, representa el fundamento teórico del conocido método del carbono 14, ampliamente utilizado en datación de restos arqueológicos) sigue un modelo exponencial.
Digamos, además, que se define como semivida al tiempo que ha de transcurrir para que la mitad de una determinada masa del isótopo en cuestión se desintegre. Por ejemplo, la semivida del carbono 14 es de aproximadamente 5370 años.
El decaimiento radioactivo del carbono-14:
<https://www.uv.es/gidprl/c14/el_decaimiento_radioactivo_del_carbono14.html>
Estamos interesados en obtener la expresión matemática que nos permita calcular la cantidad de carbono 14 que habrá de presentar una muestra dada en función del tiempo, suponiendo conocida la masa de este presente inicialmente.
El modelo exponencial al que se hizo alusión tiene la forma:
\[ N(t)=N_0 e^{-kt} \]
En dicha expresión, \( N_0 \) es la masa inicial, \( N (t) \)la masa del isótopo presente al cabo de un tiempo t y k una constante positiva, que obtendremos seguidamente.
Para despejar dicha constante, tengamos en cuenta la información de que disponemos; si suponemos que 5370 años atrás la cantidad del isótopo presente en la muestra valía \( N_0 \), en la actualidad solo quedará la mitad, lo que en símbolos puede escribirse de la siguiente manera:
\[ N(t=5730)= \frac {N_0}{2}=N_0 e^{-5730.k} \]
Las ecuaciones que, como la anterior, poseen una incógnita como potencia, reciben el nombre de ecuaciones exponenciales. Como veremos a continuación, el empleo de algunas de las propiedades del logaritmo nos permitirá despejar dicha incógnita:
\[ \frac {N_0}{2}=N_0 e^{-5730.k} \to \frac {N_0}{2} \frac {1}{N_0}= e^{-5730.k} \to e^{-5730.k}= \frac {1}{2} \]
Obsérvese que el valor de la constante no depende de la masa del isótopo inicialmente presente en la muestra.
Aplicamos logaritmo neperiano a ambos miembros de la última igualdad obtenida:
\[ lne^{-5730.k}=ln(1/2) \to -5730.k.lne =ln(1/2) \]
Teniendo en cuenta que el logaritmo neperiano del número e es igual a uno (de acuerdo con la cuarta propiedad de los logaritmos enunciada en la sección 6.2.1), escribimos:
\[ -5730.k =ln(1/2) \to k = - \frac {ln \left( 1/2 \right)}{5370} \to k \cong 0,00012 \]
Así, si en un momento dado la cantidad de carbono 14 presente en una muestra era \( N_0 \), entonces taños más tarde la masa remanente se podrá calcular a partir de la expresión:
\[ N(t)=N_0 e^{-0,00012t} \]
Tipler, P.; Mosca, G. (2003), Física para la Ciencia y la Tecnología, Volumen 2, Editorial Reverté S. A., Barcelona, pp. 1219 a1224.
El decrecimiento del número de bacterias presentes en una muestra introducida en autoclave a 130ºC puede expresarse matemáticamente mediante la fórmula:
\[ N(t)=500e^{-kt} \]
En dicha expresión, N(t) indica el número de bacterias t horas después de iniciado el proceso de esterilización, mientras que k es una constante positiva que depende de las condiciones del proceso. Se sabe que dos horas después de iniciado el procedimiento, el número de bacterias presentes es de tan solo diez. Se pide calcular cuánto tiempo transcurrió desde que la muestra fue introducida en el autoclave hasta que el número de bacterias presentes en ella resultó ser la quinta parte de las presentes originalmente.
Un arqueólogo encuentra un conjunto de tejidos en los que se ha desintegrado el setenta por ciento del carbono 14 que tenían en el momento de quedar depositados en el yacimiento que está explorando. ¿Cuál será, entonces, la antigüedad de dichos restos?
Ley de Newton del enfriamiento de los cuerpos
La ley de enfriamiento de Newton expresa que un cuerpo que se encuentra a una temperatura superior a la del ambiente que lo rodea habrá de enfriarse según la siguiente expresión matemática:
\[ T(t)-T_{ambiente=C.e^{kt} } \]
En ella, T(t) corresponde a la temperatura del cuerpo, siendo C y k dos constantes que habremos de despejar con los datos disponibles. Supongamos entonces que en un momento dado, se saca un pastel del horno, siendo en ese instante la temperatura de aquel de 150ºC. La temperatura ambiente en ese momento es de 20ºC y, tres minutos más tarde, se determina que la temperatura del pastel ha descendido hasta los 95ºC. Proponemos obtener la expresión matemática que nos permita conocer la temperatura del pastel en función del tiempo transcurrido desde que se lo saca del horno, suponiendo constante la temperatura ambiente.
De acuerdo con lo que propone el ejemplo, podemos escribir:
\[ T(t)-20=Ce^{kt} \]
Si en dicha igualdad reemplazamos algunos de los factores presentes por los datos que brinda el enunciado, obtenemos un sistema de ecuaciones. Así, para el instante inicial, en el que el pastel tenía una temperatura de ciento cincuenta grados centígrados:
\[ 150-20=Ce^{k0} \to C=130 \]
Sabemos, además, que tres minutos más tarde la temperatura del pastel había descendido hasta los noventa y cinco grados, lo que puede escribirse como sigue:
\[ 95-20=130e^{3k} \]
Nos encontramos nuevamente ante una ecuación exponencial, que resolveremos bajo estas líneas:
\[ 75=130e^{3k} \to e^{3k}=\frac{75}{130}\to ln(e^{3k} )=ln \left(\frac{75}{130}\right) \to \]
\[ \to3k.ln(e)=ln\left(\frac{75}{130}\right) \to k=\frac13 ln\left(\frac{75}{130}\right) \to k \cong-0,1833 \]
Escribimos entonces:
\[ T(t)-20=130e^{-0,1833t} \]
O, más correctamente:
\[ T(t)=20+130e^{-0,1833t} \]
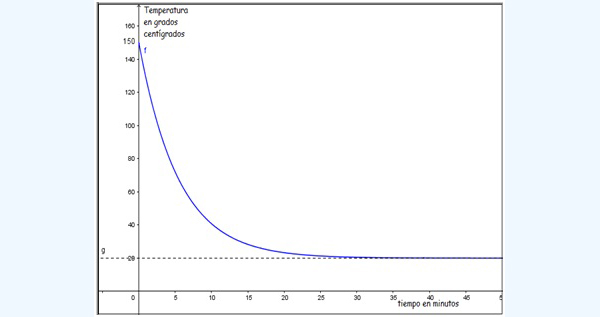
Es interesante graficar la función y observar que presenta una asíntota horizontal (imagen 6.11). En efecto:
\[ \displaystyle\lim_{x\to\infty} T(t)= \displaystyle\lim_{x\to\infty} T(t)=20+130e^{-0,1833t}=20 \]
La interpretación física del resultado es muy sencilla: cuando el tiempo sea lo suficientemente grande (en nuestro caso, de acuerdo con lo que muestra la imagen 6.11, de unos treinta minutos), el objeto (en este caso la torta) deberá alcanzar el equilibrio térmico con el medio.
Gráfica de la función que representa el enfriamiento de un cuerpo a partir de la correspondiente ley de Newton.
Una masa de agua que fue calentada en un horno de microondas hasta una temperatura de 90ºC se deja enfriar, lejos de eventuales corrientes de aire, en un ambiente que se encuentra a 25ºC. Veinte minutos después de que se la comenzó a dejar enfriar, se determina que la temperatura del agua alcanzó los 50ºC
¿En qué instante la temperatura del agua fue de 75 grados?
6.2.3. Representación gráfica de la función logaritmo
Dijimos anteriormente que la base de un logaritmo podía ser cualquier número real positivo distinto de la unidad. Seguidamente veremos que el dato es significativo, pues las características de la función (y, por ende, de su gráfica) dependerán del valor de la base.
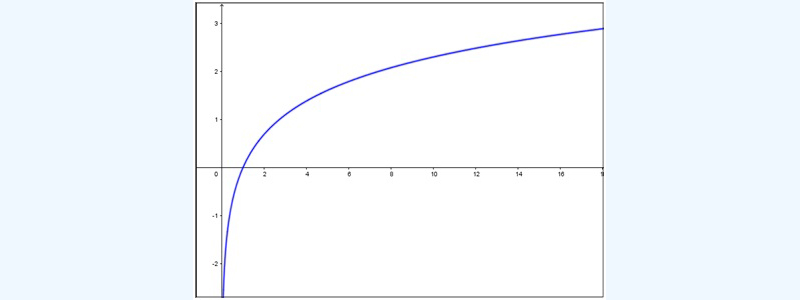
Cuando la base de un logaritmo sea un número real positivo mayor que la unidad, la representación gráfica de su correspondiente función tendrá las siguientes características:
- Presentará asíntota vertical de ecuación x = 0.
- A medida que la variable independiente tienda a cero, la función tenderá a menos infinito.
- \( \displaystyle\lim_{x\to 0^+} log_ax =-\infty \)
- La función será creciente y deberá cumplirse la condición \( \displaystyle\lim_{x\to \infty} log_ax =+\infty \)
Todas estas características pueden observarse claramente en la curva representada en la imagen 6.12.
Función logaritmo, cuando la base sea un número positivo mayor que la unidad.
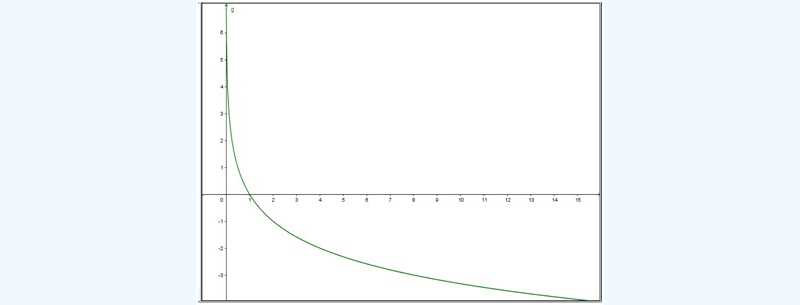
Cuando la base de un logaritmo sea un número real positivo menor que la unidad, la representación gráfica de su correspondiente función tendrá las siguientes características:
- Presentará asíntota vertical de ecuación x = 0.
A medida que la variable independiente tienda a cero, la función tenderá a más infinito.
En símbolos: \( \displaystyle\lim_{x\to 0^+} log_ax =+\infty \)
- La función será decreciente y deberá cumplirse la condición \( \displaystyle\lim_{x\to \infty} log_ax =-\infty \)
Todas estas características pueden observarse claramente en la curva representada en la imagen 6.13.
Función logaritmo, cuando la base sea un número positivo menor que la unidad.
6.2.4. Una aplicación importante: acidez de una sustancia a partir de su pH
En 1923, el químico danés Johannes Brønsted propuso definir como ácido a toda aquella sustancia dadora de protones y como base a la que acepta dichos protones. Al hablar de protones, Brønsted se refería a iones hidrógeno, que se expresan generalmente como \( H^+ \).
En las disoluciones acuosas, las concentraciones de iones \( H^+ \)y \( OH^-\) resultan ser números muy pequeños. Por ese motivo, ya en 1909 otro danés, el bioquímico Søren Sørensen, propuso una medida más adecuada para operar, a la que denominó pH y que resulta ser el logaritmo negativo de la concentración del ion hidrógeno medido en moles sobre litro.
En símbolos:
[6.1] \[ pH=-log[H_3 O^+ ] \ \ o \ \ pH=-log[H^+] \]
(Los corchetes expresan “concentración de”.)
Como las concentraciones de los iones hidróxido e hidrógeno son números positivos pero menores a la unidad, los resultados se multiplican por menos uno (no olvidemos que el logaritmo en base diez de un número positivo inferior a la unidad resulta ser negativo).
En las [6.1] solo se toma el valor numérico de la concentración, sin incluir las unidades correspondientes (es decir, mol/litro). El pH resulta ser entonces un valor adimensional que ha de interpretarse de la siguiente manera:
- Si \( [H^+]>1.10^{-7} M \to pH<7 \) y decimos que la disolución es ácida.
- Si \( [H^+]{<}1.10^{-7} M \to pH{>}7 \) y decimos que la disolución es básica.
- Si \( [H^+]=1.10^{-7} M \to pH=7 \) y decimos que la disolución es neutra.
Es común que conozcamos el pH de una disolución y se pida obtener la concentración de ion hidrógeno. Entonces es necesario tener en cuenta que, a partir de la [6.1] puede escribirse:
[6.2] \[ [H^+]=10^{-pH} \]
Nos encontramos nuevamente frente a una ecuación exponencial que, como vimos anteriormente, habrá de resolverse aplicando adecuadamente las propiedades del logaritmo.
La concentración de iones \( H^+ \) de cierto producto hogareño de limpieza vale \( [H^+]=4.10^{-12} M \)
Se pide calcular el pH del producto.
De acuerdo con [6.2]:
\[ [H^+]=10^{-pH} \]
Reemplazamos la concentración de ion hidrógeno por la correspondiente al producto de limpieza, aplicamos logaritmo en base diez a ambos miembros, y operamos:
\[4.10^{-12}=10^{-pH} \to log(4.10^{-12} )=log(10^{-pH} ) \to \]
\[ \to log(4)log(10^{-12} )=-pH.log(10) \to \]
\[ \to log(4).(-12.log(10))=-pH.log(10) \to \]
Teniendo en cuenta que log(10), se llega finalmente a:
\[ \to pH=12.log(4)=7,22 \]
Concluimos entonces que el producto en cuestión es débilmente básico.
Se recoge agua de lluvia en una localidad próxima a una planta industrial, siendo la concentración de ion hidrógeno media medida del orden de \( 1,5.10^{-5} M \).
¿Existe alguna evidencia de peligro de lluvia ácida en dicha localidad?
Lluvia ácida:
<https://www.nationalgeographic.es/medio-ambiente/lluvia-acida>
6.2.5. Otra aplicación valiosa: medición del nivel de intensidad sonora
La ley de Weber Fechner propone una relación numérica entre la magnitud de un estímulo físico y la forma en que este es percibido por el ser humano. Dicha ley psicofísica se refiere a estímulos sensoriales como la luz o el ruido. Nos detendremos brevemente en este último caso, definiendo para ello el nivel de intensidad sonora \( (\boldsymbol{\beta}) \) a partir de la siguiente expresión:
\[ \beta=10.log \left(\frac {I}{I_0} \right) \]
La intensidad sonora de la fuente I se mide en Watt sobre metro cuadrado, y se divide por \( I_0 \), que representa a la intensidad sonora del umbral de audición, correspondiente a un sonido prácticamente inaudible, de valor \( 10^{-12} W⁄m^2 \) .
La unidad en la que se mide la intensidad sonora recibe el nombre de decibel (dB) y el umbral de dolor es de aproximadamente 120 dB.
Prevención de la intensidad sonora en los ámbitos de trabajo:
<https://www.srt.gob.ar/index.php/prevencion-de-la-intensidad-sonora-en-los-ambitos-de-trabajos/>
Ley de Weber-Fechner:
<https://www.psicologia-online.com/las-leyes-psicofisicas-ley-de-weber-2070.html>
¿Cuál será el nivel de intensidad sonora correspondiente al tráfico de camiones en la bajada de la autopista, si la intensidad sonora medida es de \( 1.10^{-3} W⁄m^2 \)?
Para responder a la pregunta, bastará con emplear la fórmula, aplicando seguidamente las propiedades de los logaritmos enumeradas oportunamente:
\[ \beta=10.log\left( \frac {1.10^{-3 } W ⁄ m^2} {10^{-12} W⁄m^2} \right)=10.log(10^{-3-(-12)} ) \]
\[ \beta=10.log (10^9 )=10.9.log(10) \to \beta=90dB \]
El valor puede considerarse molesto, pero se encontraría por debajo del umbral de dolor. Sin embargo, hay que tener en cuenta que, cuando N fuentes sonoras son percibidas simultáneamente, sus intensidades sonoras deben sumarse. El nivel de intensidad sonora habrá de obtenerse entonces a partir de la expresión:
\[ \beta=10.log \left( \frac {I_1+I_2+⋯+I_N} {I_0} \right) \]
Supongamos que se mide la intensidad sonora a la bajada de la autopista en un instante en el cual hay muchos camiones transitando \( (I_1=1.10^{-3 } W⁄m^2 ), \), una cuadrilla trabajando en obras de mantenimiento \( (I_2=1.10^{-1 } W⁄m^2 ) \) y, además, un avión comercial sobrevuela el lugar \( (I_3=1.10^2 W⁄m^2 ). \). ¿Cuál será en ese instante el nivel de intensidad sonora? ¿Superará el umbral de dolor?
6.3. Funciones trigonométricas
En la sección 2.2 ya habíamos presentado las funciones seno y coseno de un ángulo. Recordemos que son funciones periódicas, que presentan infinidad de aplicaciones prácticas.
Diremos que una función f(x) es periódica cuando exista un número positivo p tal que, para todo x perteneciente al dominio de la función, se verifique la condición f(x+p)=f(x) .
En la próxima sección nos detendremos en elementos particularmente significativos de las funciones seno y coseno, como son sus raíces, máximos y mínimos.
6.3.1. Representaciones gráficas
La imagen 6.14 muestra la gráfica de la función seno. En ella, señalamos particularmente las raíces de la función, es decir, las intersecciones de la curva con el eje de abscisas.
Gráfica de la función \( f(x)=sin(x) \)
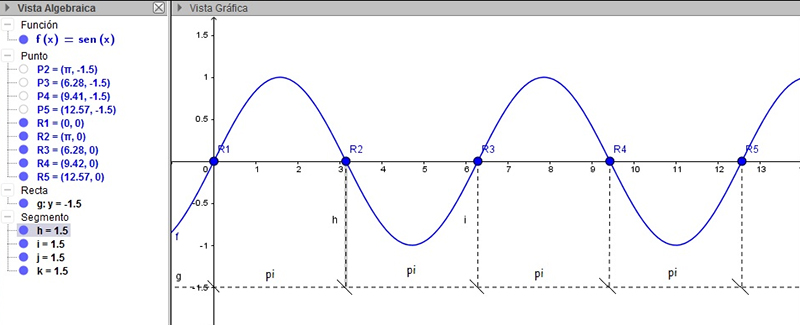
Obsérvese que la distancia entre dos raíces consecutivas es de \( \pi \) radianes. Podemos expresar en forma genérica la situación escribiendo:
\( x \in \mathbb{R} \) es raíz de \(f(x)=sen(x) \leftrightarrow x=k \pi, \ con \ k \ \in \mathbb{Z} \)
Es decir, si multiplicamos a \( \pi \) por cualquier número entero, obtendremos la abscisa de alguna de las raíces de la función.
En la imagen 6.15, en cambio, marcamos dos máximos (MA1 y MA2) y dos mínimos sucesivos (MI1 y MI2). La distancia entre ellos es en cada caso de un período completo, es decir:
\( x \in \mathbb{R} \) es máximo de \(f(x)=sen(x) \leftrightarrow x= \frac {\pi} {2} +k2 \pi \ con \ k \in \mathbb{Z} \)
\( x \in \mathbb{R} \) es mínimo de \(f(x)=sen(x) \leftrightarrow x= \frac {3 \pi}{2} +k2 \pi \ con \ k \in \mathbb{Z} \)
Se observa claramente que dos máximos o dos mínimos sucesivos se encuentran separados entre sí exactamente por un período, es decir, 2π radianes.
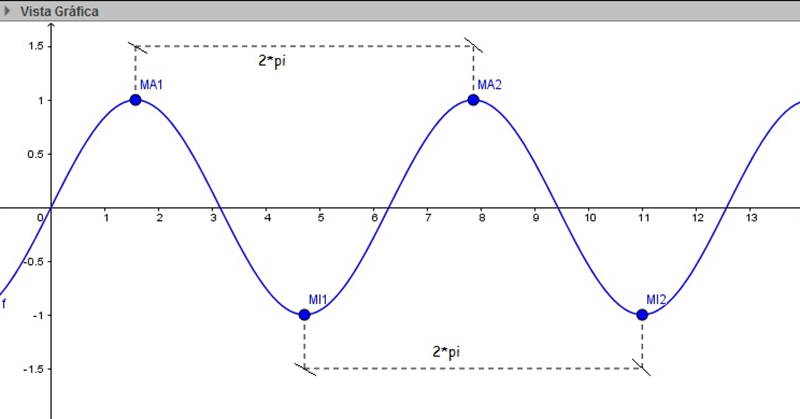
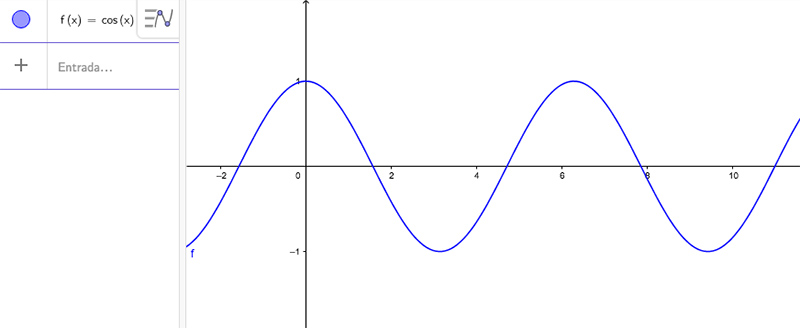
En la imagen 6.16 puede observarse la función coseno. Razonando en forma análoga a la aplicada para el caso de la función seno, verificar que:
\( x \in \mathbb{R} \) es raíz de \(f(x)=cos(x) \leftrightarrow x= \frac π2 +k\pi \ con \ k \in \mathbb{Z} \)
\( x \in \mathbb{R} \) es máximo de \(f(x)=cos(x) \leftrightarrow x= k2\pi \ con \ k \in \mathbb{Z} \)
\( x \in \mathbb{R} \) es mínimo de \(f(x)=cos(x) \leftrightarrow x= π +k2\pi \ con \ k \in \mathbb{Z} \)
Representación gráfica de la función \( f(x)=cos(x) \)
En la imagen 2.35 representamos gráficamente la función \( f(x)=tg(x) \) . Estudiando detenidamente la gráfica, verificar que:
\( x \in \mathbb{R} \) es raíz de \(f(x)=tg(x) \leftrightarrow x= k\pi \ con \ k \in \mathbb{Z} \)
\( x =a \) es asíntota vertical de \(f(x)=tg(x) \leftrightarrow a= \frac {\pi}{2} +k\pi \ con \ k \in \mathbb{Z} \)
6.3.2. Una aplicación importante: vibración de un resorte ideal
La imagen 6.17 corresponde a una simulación que permite estudiar el movimiento de un resorte ideal. Este aparece representado dentro de un sistema de ejes cartesianos; sobre el eje de abscisas se mide el tiempo (en segundos) y sobre el eje de ordenadas la distancia del pequeño peso que cuelga del resorte al punto de suspensión. En la situación representada por la imagen, dicha distancia es de 17,53 unidades y aparece señalada con una flecha roja en la vista algebraica.
En la imagen 6.18 se observan distintas disposiciones del resorte en función del tiempo y en la 6.19, empleando uno de los recursos que nos brinda el software, observamos las distancias a las que se encuentra la pesa respecto del punto de suspensión del resorte en distintos instantes de tiempo.
En la simulación, el eje de abscisas representa el tiempo. Mediante un deslizador, podemos observar cómo se estira o se comprime el resorte respecto de su posición de equilibrio a medida que pasa el tiempo.
El valor señalado con una flecha roja en la vista algebraica representa la ordenada del punto que, en teoría, representa el centro de masa del cuerpo que cuelga del extremo del resorte. El valor t corresponde a la variable tiempo.
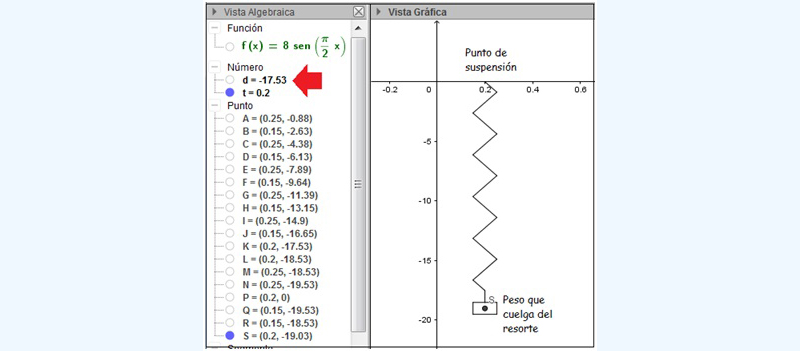
Empleando el deslizador se observan las distintas posiciones que el centro de masa del cuerpo colgado del extremo del resorte fue tomando, a medida que transcurrió el tiempo.
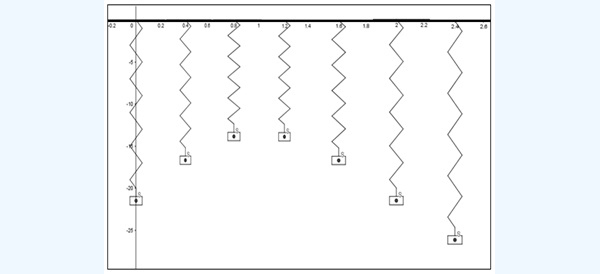
Uno de los recursos de que disponemos con el GeoGebra es el Rastro, que registra las distintas posiciones que adopta un punto a medida que se lo desplaza por la pantalla mediante un deslizador. En la imagen pueden observarse así las posiciones del centro de masa del cuerpo (medidas sobre el eje de ordenadas) en función del tiempo (que, como ya dijimos, ha de medirse sobre el eje de abscisas). En el extremo superior derecho puede observarse el deslizador.
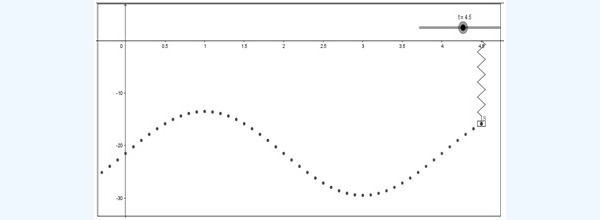
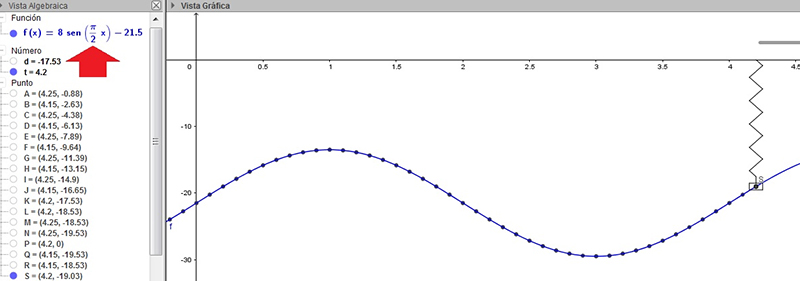
Finalmente, si unimos dichos puntos, nos encontramos que estos se encuentran sobre la curva de ecuación:
\[ f(x)=8sen \left(\frac {\pi} {2} x \right)-21,5 \]
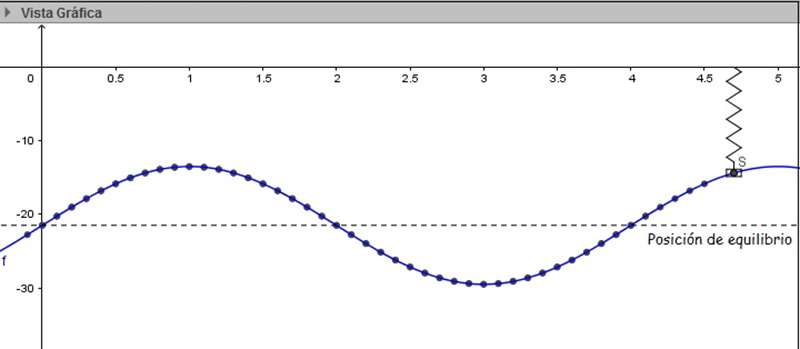
El hecho no debe sorprendernos: los fenómenos oscilatorios se ajustan perfectamente a funciones como el seno y el coseno. El cuerpo que cuelga del resorte pasa por la posición de equilibrio (representada en nuestro caso por la recta y = -21,5, como se observa en la imagen 6.21) una y otra vez y después de pasar por dicha posición tres veces consecutivas, diremos que el cuerpo describe un ciclo.
Todos los puntos obtenidos empleando el Rastro se encuentran sobre una curva, la correspondiente a la función:
\[ f(x)=8sin \left( \pi x/2 \right)-21,5 \]
Dibujamos una línea horizontal, que corresponde a la posición de equilibrio.
Cuando la ecuación que describa el movimiento de un cuerpo sea de la forma:
\[ y=f(t)=a.sen(wt \pm \phi) \pm b \]
o de la forma
\[ y=f(t)=a.cos(wt \pm \phi) \pm b \]diremos que dicho objeto está sujeto a un movimiento oscilatorio armónico simple.
Las características de dicho movimiento son:
Su amplitud, desplazamiento máximo del objeto respecto de su posición de equilibrio, cuyo valor es el módulo de a.
Su período, tiempo necesario para completar un ciclo, que suele expresarse como T y que se calcula como \( T=\frac{2\pi}{w} \)
Su frecuencia, número de ciclos por unidad de tiempo, que suele expresarse como \( \vartheta \) y que se calcula como \( \vartheta =\frac{w}{2\pi} \).
En cuanto a \( \varphi \), se trata de un ángulo que recibe el nombre de ángulo de fase, en tanto que b corresponde al desplazamiento vertical de la curva.
El movimiento armónico simple es ideal. Cuando observamos la onda que se propaga al caer una piedra a un estanque, notamosque su amplitud se va reduciendo a medida que la onda se aleja del punto en el que cayó la piedra. Efectos como el del rozamiento son los causantes de tal fenómeno, que será el objeto de la siguiente sección.
6.3.3. Otra aplicación importante: movimiento armónico amortiguado
El efecto de la fuerza de rozamiento que normalmente actúa sobre un resorte se verá reflejado en la paulatina disminución en la amplitud de la oscilación. La imagen 6.22 es comparable con la 6.19, con la diferencia que, en aquella, los puntos representan las distancias del peso que cuelga del resorte al punto de suspensión en función del tiempo para un resorte real, en el que actúa el rozamiento.
El movimiento amortiguado representa lo que sucede en el mundo real, donde el rozamiento transforma la energía mecánica original. Como consecuencia de ello, la amplitud de la oscilación se va reduciendo con el tiempo, hasta que el centro de masa del cuerpo queda detenido en la posición de equilibrio.
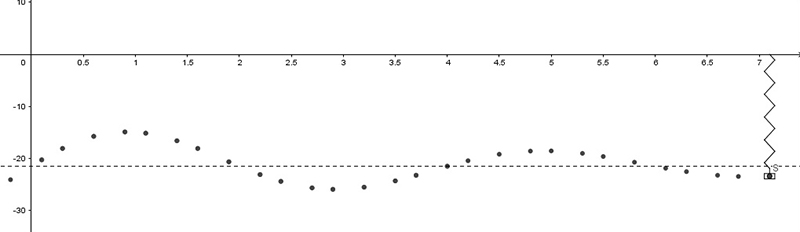
En la imagen 6.23 se observa que dichos puntos se ajustan perfectamente a la curva de ecuación:
\[ y=f(t)=8e^{-0,2t} sen \left( \frac \pi 2 t \right)-21,5 \]
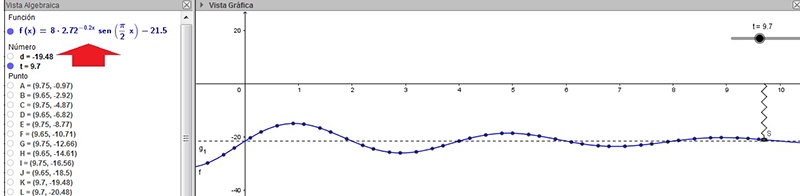
Llegará un momento en que el resorte deje de oscilar, permaneciendo en su posición de equilibrio. En la imagen 6.24 puede observarse claramente dicho fenómeno.
Cuando un movimiento oscilatorio reduzca paulatinamente su amplitud hasta alcanzar el estado de reposo, diremos que se trata de un movimiento oscilatorio armónico amortiguado.
Cuando la ecuación que describa el movimiento de un cuerpo sea de la forma:
\[ y=f(t)=a.e^{-ct} sen(wt \pm \varphi) \pm b \]o de la forma
\[ y=f(t)=a.e^{-ct} cos(wt \pm \varphi)\pm b \]diremos que dicho objeto está sujeto a un movimiento oscilatorio armónico amortiguado. La constante positiva crecibe el nombre de constante de amortiguamiento.
Del valor de la constante de amortiguamiento dependerá el tiempo que tarde el resorte en alcanzar la posición de equilibrio. A medida que dicha constante aumente, el tiempo necesario para que el movimiento desaparezca habrá de reducirse.
Los puntos obtenidos mediante el empleo del Rastro se encuentran sobre la curva de ecuación:
\[ y=f(t)=8e^{-0,2t} sen \left(\frac {\pi} {2} t \right)-21,5 \]
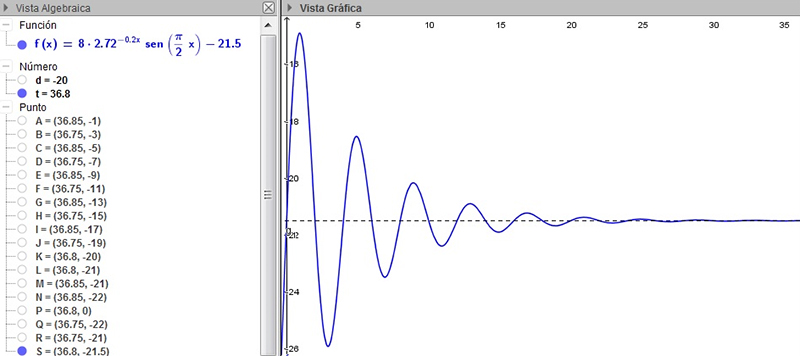
Nuevamente representamos la función correspondiente a una oscilación amortiguada. En esta oportunidad, un conveniente cambio de escala permite ver con mayor claridad cómo disminuye la amplitud de la oscilación con el transcurso del tiempo.
Stewart, J.; Redlin, L.; Watson, S. (2001), Precálculo, Matemáticas para el cálculo, International Thomson Editores, México, pp. 393 a 405.

