7. Derivada y diferencial
Objetivos
Que el alumno:
- Adquiera el concepto de derivada de una función en un punto y sea capaz de obtenerla, manualmente o aplicando reglas y propiedades.
- Aprenda a resolver problemas de optimización y descubra la importancia de la derivada como herramienta a partir de una de sus múltiples aplicaciones.
- Comprenda el concepto de diferencial de una función en un punto y, a partir de este, sea capaz de aproximar el valor de funciones.
- Descubra que una función puede reemplazarse, en el entorno de un punto, por otra de tipo polinómico, gracias al polinomio de Taylor asociado a la función. El valor de dicho reemplazo habrá de comprenderse en la próxima unidad, una vez que el alumno haya aprendido a resolver integrales definidas.
7.1. Definición de derivada de una función en un punto y su interpretación geométrica
Dada una función f(x) como la que aparece en la imagen 7.1 (en color azul), unimos dos de sus puntos, P y Q con una recta (que en la misma imagen aparece en color rojo). Dicha recta es secante a la curva porque la corta en dos puntos.
Recordemos que las posiciones relativas de una recta respecto de una curva son las siguientes:
- una recta será secante a la curva cuando la interseque en dos puntos;
- una recta será tangente a la curva cuando solo tenga un punto en común con ella; y
- una recta será exterior a la curva cuando no tenga ningún punto en común con ella.
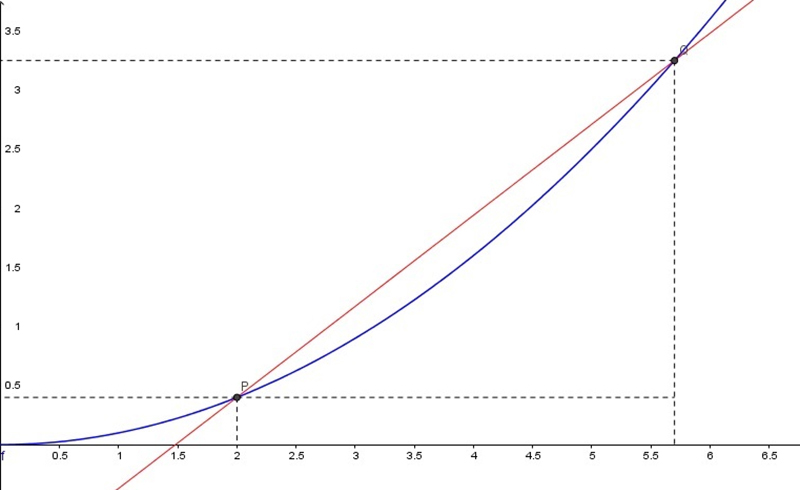
Dada una función (en color azul), se traza una recta (en color rojo) que pasa por un punto P de aquella.
La pendiente de dicha recta secante no es otra cosa que la tangente del ángulo que dicha recta determina con la horizontal, que puede expresarse como:
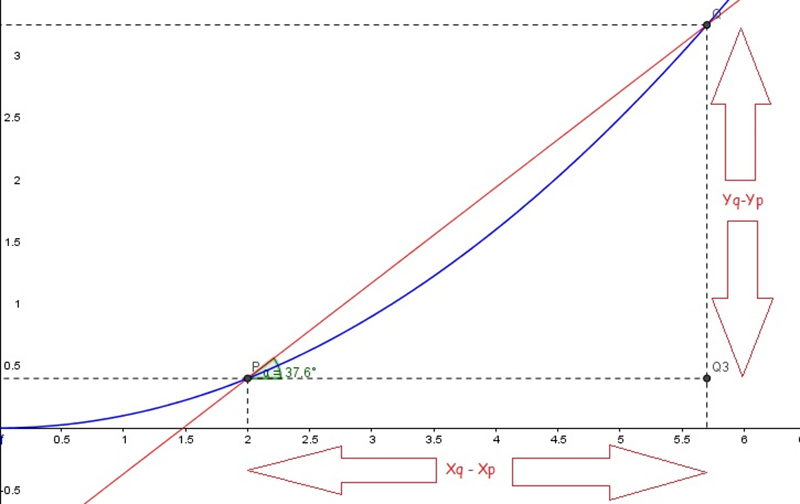
\[ \text {pendiente de la recta secante} = \frac{y_Q - y_P}{x_Q - x_P} = \frac{\Delta y}{\Delta x} \]
Cabe aclarar que la letra griega \( \Delta \) (delta) se emplea tanto en Física como en Matemática para indicar la variación de una variable.
El último cociente se conoce generalmente como cociente incremental. En la imagen 7.2 se indican claramente su numerador y su denominador.
Ahora bien, ¿qué sucede si el incremento de la variable independiente se va reduciendo?
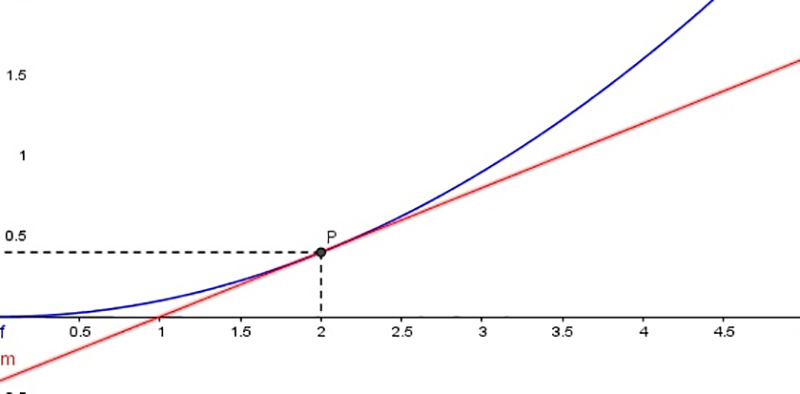
En la imagen 7.3 observamos que, cuando el incremento se hace infinitesimalmente pequeño, los puntos P y Q prácticamente coinciden, de modo que la recta dejaría de ser secante a la curva en el punto para ser tangente en él. Esta forma de expresarnos no es del todo propia desde el punto de vista matemático, de modo que escribiremos:
\[ \text {pendiente de la recta tangente} = \displaystyle\lim_{\Delta x \to 0} \frac{y_Q - y_P}{x_Q - x_P} = \displaystyle\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \]
El límite del cociente incremental que acabamos de definir es lo que denominamos derivada de la función en el punto y podemos decir entonces que, desde el punto de vista geométrico, representa a la pendiente de la recta tangente a una función en un punto dado.
El segmento de la recta secante definido por los puntos P y Q se convierte en la hipotenusa de un triángulo rectángulo, cuyos catetos valen \( (y_Q - y_P) \)) y \( (x_Q - x_P) \).
Cuando el incremento de la variable independiente tiende a cero, los puntos P y Q terminan coincidiendo y la recta deja de ser secante para ser tangente a la curva.
¿Qué tan valioso puede ser conocer la pendiente de la recta tangente a una curva en un punto? La respuesta a tan inocente pregunta se relaciona con las aplicaciones de la herramienta de cálculo que acabamos de definir. Bástenos con tener en cuenta que uno de los padres del cálculo infinitesimal, Sir Isaac Newton (1643-1727) la empleó, por ejemplo, para perfeccionar el estudio de la Mecánica, una de las principales ramas de la Física. El siguiente ejemplo nos brindará una aplicación elemental de la derivada.
Un motociclista parte del reposo con una aceleración constante de \( 4\frac{m}{s^2} \). La expresión matemática que permite calcular a qué distancia se encuentra respecto del punto de partida en función del tiempo es la siguiente:
\[ x(t) = \frac{1}{2}4\frac{m}{s^2}t^2 \]
¿Cuál será la velocidad del motociclista un segundo después de haber comenzado a moverse?
En la imagen 7.4 representamos gráficamente la distancia recorrida en función del tiempo. Obsérvese que, para intervalos iguales de tiempo, las distancias recorridas resultan ser cada vez mayores, a medida que nos alejamos del instante en el que el motociclista se puso en marcha.
Newton definió la velocidad como el cociente entre la distancia recorrida y el tiempo empleado. Entonces, la velocidad en un instante dado puede calcularse como:
[7.1] \[ \displaystyle\lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} = \displaystyle\lim_{\Delta t \to 0} \frac{x(t_0 + \Delta t) - x(t_0)}{\Delta t} \]
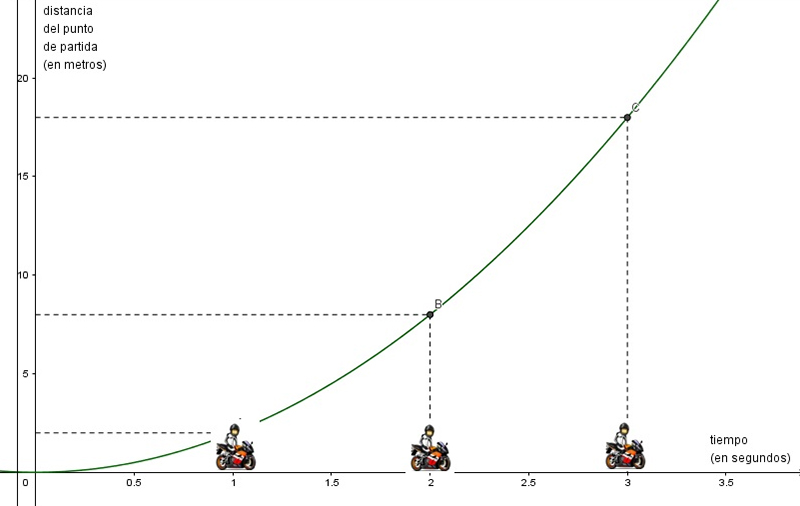
En iguales períodos de tiempo, el motociclista va recorriendo trayectos cada vez mayores.
Entonces, la velocidad del motociclista un segundo después de comenzar a moverse podrá calcularse como:
\[ v (t = 1 seg) = \displaystyle\lim_{\Delta t \to 0} \frac{x(1+\Delta t) - x (1)}{\Delta t} = \]
\[ = \displaystyle\lim_{\Delta t \to 0} \frac{ \frac{1}{2} 4(1+\Delta t)^2 - 2}{\Delta t} = \displaystyle\lim_{\Delta t \to 0} \frac{ \frac{1}{2} 4(1+ 2\Delta t + \Delta t^2) - 2}{\Delta t} = \]
\[ = \displaystyle\lim_{\Delta t \to 0} \frac{ (2+ 4\Delta t + 2\Delta t^2) - 2}{\Delta t} = \displaystyle\lim_{\Delta t \to 0} \frac{ 4\Delta t + 2\Delta t^2 }{\Delta t} = \]
\[ \displaystyle\lim_{\Delta t \to 0} \frac{ \Delta t (4 + 2\Delta t)}{\Delta t} = \displaystyle\lim_{\Delta t \to 0} (4 + 2\Delta t) = 4 \frac{m}{s} \]
Observamos entonces que la velocidad en un instante dado no es otra cosa que la pendiente de la curva que representa a la posición del móvil en función del tiempo, o sea, la derivada de dicha función.
Aplicando el mismo procedimiento, calcular la velocidad del motociclista tres segundos después de haber iniciado el movimiento.
Como acabamos de ver, el cálculo de la derivada de una función aplicando la definición, puede ser trabajoso. Sin embargo, nos detuvimos en dicha operación ya que, en ciertos casos, no podremos obtenerla si no es por este camino. Afortunadamente, contaremos con un procedimiento de cálculo más expeditivo, que será desarrollado en las próximas secciones. Pero antes, consideramos oportuno definir otro elemento fundamental del cálculo: el diferencial.
7.2. Derivada y diferencial
En la imagen 7.5 observamos a la función \( f(x) = \frac{1}{4} x^2 \). En el gráfico vemos al punto P y a la recta tangente a la curva en dicho punto.
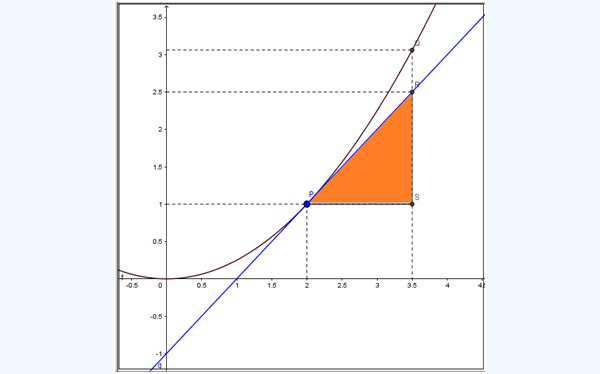
En la imagen 7.6 volvemos a graficar la misma función; pero ahora no solo mostramos el punto \( P \), sino también el punto \( Q \). Teniendo en cuenta que \( P = (2, f(2)) \) y que \( Q = ( 2 + \Delta x, f (2+ \Delta x)) \), obtendremos el incremento en el valor de la función al pasar de \( P \) a \( Q \) como
\[ \Delta y = f(2 + \Delta x) - f(2) \]
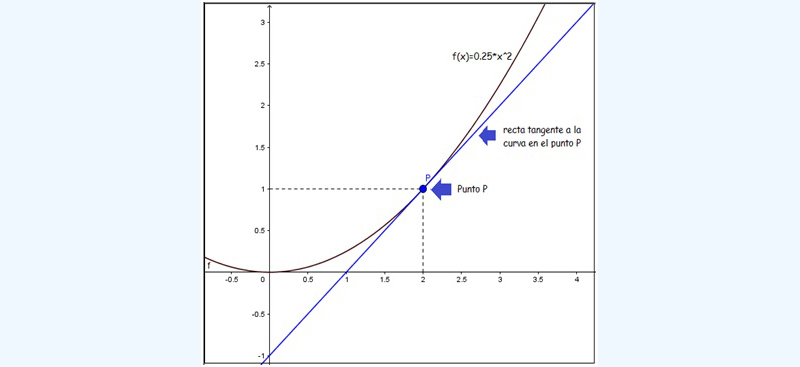
La función \( f (x) = 0,25 x ^2 \) y su recta tangente en el punto P.
Sin embargo, vale la pena detenernos un momento en el punto \( R \) que se obtiene como intersección de una recta vertical que pasa por \( Q \) y la recta tangente a la función en \( P \). En la imagen 7.6 hemos coloreado el triángulo de vértices en \( P, R \ y \ S \), siendo rectángulo en este último punto.
La pendiente de la recta tangente a la curva en el punto \( P \) podría entonces calcularse como:
\[ m = tgt \left( \widehat{RPS} \right) = \frac{\overline{RS}}{\overline{PS}} \]
Si recordamos que la derivada de la función en el punto no es otra cosa que la pendiente de la recta tangente a la curva en aquel, podemos escribir:
\[ f´(P) = \frac{\overline{RS}}{\overline{PS}} = \lim_{\Delta x \to 0} \frac{y_Q - y_P}{x_Q - x_P} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \]
Al límite del cociente incremental podemos finalmente escribirlo de la siguiente manera:
\[ f´(P) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \frac{d y}{d x} \]
El último cociente se lee como “diferencial y sobre diferencial x”.
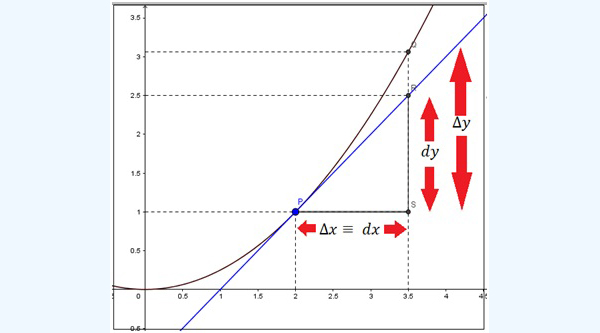
El segmento que va de S a R no es exactamente igual al que va de S a Q. De ahí el error que se comete al emplear el diferencial. Dicho error habrá de reducirse a medida que el incremento de la variable independiente lo haga.
Las flechas verticales de color rojo indican claramente la diferencia entre \( d y \) y \( \Delta y \). En cambio, se observa que \( d x \) y \( \Delta x \) coinciden.
En la imagen 7.7 indicamos claramente cuál es la diferencia entre el incremento del valor de la función, \( \Delta y \) y el diferencial, \( d y \).
En la siguiente sección veremos cómo calcular la derivada de una función sin necesidad de aplicar la definición; pero más adelante estudiaremos algunas de las aplicaciones del diferencial.
7.3. Cálculo de derivadas aplicando reglas y tabla
Volviendo a la función aplicada en la sección anterior, nos proponemos calcular, aplicando la definición, su derivada en x=2. Escribimos entonces:
\[ f´(2) = \lim_{\Delta x \to 0} \frac{f ( 2 + \Delta x) - f(2)}{\Delta x} = \lim_{\Delta x \to 0} \frac{\frac{1}{4} (2 + \Delta x)^2 - \frac{1}{4} (2)^2}{\Delta x} = \]
\[ \lim_{\Delta x \to 0} \frac{\frac{1}{4} (4 + 4 \Delta x + \Delta x^2) - 1}{\Delta x} = \lim_{\Delta x \to 0} \frac{1 + \Delta x + \frac{1}{4} \Delta x^2 - 1}{\Delta x} = \]
\[ \lim_{\Delta x \to 0} \frac{\Delta x + \frac{1}{4} \Delta x^2}{\Delta x} = \lim_{\Delta x \to 0} \frac{\Delta x \left( 1 + \frac{1}{4} \Delta x^2 \right) }{\Delta x} = \lim_{\Delta x \to 0} \left( 1 + \frac{1}{4} \Delta x^2 \right) = 1 \]
En el segundo paso del cálculo, al reemplazar a \( \Delta x \) por 0, nos encontramos con una indeterminación del tipo \( 0/0 \), que tuvo que ser salvada, sacando factor común \( \Delta x \) en el numerador.
Es evidente que el cálculo de la derivada de una función en un punto aplicando la definición puede no resultar muy práctico. Si, por ejemplo, nos pidiesen ahora calcular la derivada de la misma función en x=4 nos veríamos obligados a repetir todos los cálculos anteriores, pero reemplazando el valor de la variable independiente.
En ese sentido, la derivada resulta ser también una función y podemos calcularla en forma genérica.
Calcular la derivada de \( f(x) = \sqrt{x} \).
Resolución:
Aplicando la definición, podemos escribir
\[ f´(x) = \lim_{\Delta x \to 0} \frac{\sqrt{x + \Delta x}- \sqrt{x}}{\Delta x} \]
La presente indeterminación podrá salvarse aplicando el siguiente artificio:
\[ f´(x) = \lim_{\Delta x \to 0} \frac{(\sqrt{x + \Delta x} - \sqrt{x})} {\Delta x} \frac{(\sqrt{x + \Delta x}+ \sqrt{x})} {(\sqrt{x + \Delta x} + \sqrt{x})} = \]
\[ = \lim_{\Delta x \to 0} \frac{(\sqrt{x + \Delta x})^2 - (\sqrt{x})^2} {\Delta x (\sqrt{x + \Delta x}+ \sqrt{x}) } = \lim_{\Delta x \to 0} \frac{x + \Delta x - x} {\Delta x (\sqrt{x + \Delta x}+ \sqrt{x}) } = \]
\[ = \lim_{\Delta x \to 0} \frac{ \Delta x } {\Delta x (\sqrt{x + \Delta x}+ \sqrt{x}) } = \lim_{\Delta x \to 0} \frac{ 1 } {(\sqrt{x + \Delta x}+ \sqrt{x}) } = \frac{1}{2 \sqrt{x}} \]
Es decir, si \( f(x) = \sqrt{x} \) entonces \( f´(x) = \frac{1}{2 \ \sqrt{x}} \).
Si quisiéramos ahora calcular la derivada de \( f(x) = \sqrt{x} \) para x=9 bastará entonces con escribir \( f´(9) = \frac{1}{2 \sqrt{9}} = \frac{1}{6} \)
Sin embargo, aun el cálculo a partir de la expresión genérica puede resultar poco práctico cuando se trate de una pequeña parte de un cálculo mucho más extenso.
Por ese motivo, se confecciona una tabla de derivadas, en la que aparecen los resultados de derivar una serie de funciones elementales.
Proponemos al alumno la siguiente tabla de derivadas, que incluye las utilizadas más comúnmente:
- Si \( f(x) = x \to f´(x) = 1 \)
- Si \( f(x) = x^n \to f´(x) = nx^{n-1} \)
- Si \( f(x) = e^x \to f´(x) = e^x \)
- Si \( f(x) = a^x \to f´(x) = a^xln(a) \)
- Si \( f(x) = ln(x) \to f´(x) = \frac{1}{x} \)
- Si \( f(x) = \sqrt{x} \to f´(x) = \frac{1}{2 \ \sqrt{x}} \)
- Si \( f(x) = sin(x) \to f´(x) = cos(x) \)
- Si \( f(x) = cos(x) \to f´{(x)} = -sin(x) \)
- Si \( f(x) = k \to f´{(x)} = 0 \)
Recomendamos al alumno verificar los resultados obtenidos empleando el wxMaxima. En la sección 7.6 encontrará las instrucciones necesarias para poder hacerlo.
Para obtener la derivada de la gran mayoría de las funciones hay que emplear una serie de reglas, que vamos a enumerar a continuación.
Primera regla:
Dada \( f(x) = k . g(x) \), donde k es una constante, entonces:
\[ f'(x) = k . g'(x) \]
Aplicando la tabla y la regla que acabamos de enunciar, calcular la derivada de \( f(x)= 3x^2 \)
Resolución:
Si \( f(x) = 3x^2 \to f´(x) = 3.2x = 6x \)
Segunda regla:
Dada \( f(x) = g(x) \pm h(x) \), entonces:
\[ f´(x) = g´(x) \pm h´(x) \]Esta última propiedad podría generalizarse diciendo que la derivada de la suma o resta de dos o más funciones es igual a la suma o resta de las derivadas de las respectivas funciones.
Aplicando la tabla y la regla que acabamos de enunciar, calcular la derivada de \( f(x) = x^2 + ln(x) - sin(x) \)
Resolución:
Si \( f(x) = x^2 + ln(x) - sin(x) \to f´{(x)} = 2x + \frac{1}{x} - cos (x) \)
Tercera regla:
Dada \( f(x) = g(x) . h(x) \), entonces:
\[ f´{(x)}= g´{(x)} . h(x) + g (x) . h´(x)\ \]
Aplicando la tabla y la regla que acabamos de enunciar, calcular la derivada de \( f(x) = x^2 . sin(x) \)
Resolución:
Si \( f(x) = x^2 . sin(x) \to f´{(x)} = 2x . sin(x) + x^2 . cos(x) \)
Cuarta regla:
Dada \( f(x) = \frac{g(x)}{h(x)} \), entonces:
\[ f´(x) = \frac{g´(x)h(x) - g(x)h´(x)}{(h(x))^2} \]
Aplicando la tabla y la regla que acabamos de enunciar, calcular la derivada de \( f(x) = \frac{3^x}{sin(x)} \)
Resolución:
Si \( f(x) = \frac{3^x}{sin(x)} \to f´(x) = \frac{3^x ln(3) . sin (x) - 3^x cos (x)}{(sin(x))^2} \)
Las cuatro reglas que acabamos de enunciar pueden combinarse para resolver ejemplos más complejos, como veremos seguidamente.
Dada \( f(x) = \frac{x^2 - 2}{x^3 - x} \) , calcular su derivada.
Resolución:
Comenzamos aplicando la cuarta regla, correspondiente a la derivada del cociente entre dos funciones.
\[ f(x) = \frac{x^2 - 2}{x^3 - x} \to f´(x) = \frac{(x^2 - 2)´(x^3-x)-(x^2 - 2)(x^3-x)´}{(x^3 - x)^2} \]
La notación aplicada corresponde a un paso intermedio de cálculo. Las funciones que aparecen dentro de los paréntesis con comillas deberán derivarse aplicando la segunda regla (derivada de una suma o resta de funciones).
\[ \to f´(x) = \frac{2x(x^3 - x)-(x^2 - 2)(3x^2-1)}{(x^3 - x)^2} \]
Por el momento, dejaremos expresado de ese modo el resultado. Restaría aplicar la propiedad distributiva en los dos términos del numerador, para luego reducirlo convenientemente. Llevar a la mínima expresión posible a la derivada puede ser muy útil en problemas más complejos, como los que estudiaremos al finalizar la presente unidad.
Dada \( f(x) = tg(x) \), calcular su derivada.
Resolución:
Teniendo en cuenta que \( tg(x) = \frac{sin(x)}{cos(x)} \) , la derivada de la función se obtendrá simplemente aplicando la cuarta regla de la derivación:
\[ f(x) = \frac{sin(x)}{cos(x)} \to f´(x) = \frac{cos(x). cos (x) - sin(x). (-sin(x)) }{(cos(x))^2 } \to \]
\[ \to f´(x) = \frac{(cos(x))^2 + (sin(x))^2 }{(cos(x))^2 } = \frac{1}{(cos(x))^2} \]
Para llegar al último paso, basta con recordar la identidad pitagórica, \( (sin(a))^2 + (cos(a))^2 = 1 \).
Calcular, aplicando las reglas de derivación y la tabla, las derivadas de las siguientes funciones:
- \( f_1(x) = x^5 cos(x) \)
- \( f_2(x) = 4^xsin(x) \)
- \( f_3(x) = x^3ln(x) \)
- \( f_4(x) = 5^xx^5 \)
- \( f_5(x) = \frac{x^5 -4}{x^3 + 3^x} \)
- \( f_6(x) = \frac{x^2}{ln(x)} \)
- \( f_7(x) = 2^x ln(x) \)
Recomendamos al alumno verificar los resultados obtenidos empleando el wxMaxima. En la sección 7.6 encontrará las instrucciones necesarias para poder hacerlo.
Existe un gran número de funciones como \( f(x) = \sqrt{x^2 - 5x} \) (en la que se aplica la función raíz cuadrada a una función polinómica) o \( g(x) = ln(x^3 + x) \) (en la que tenemos el logaritmo de un polinomio) que reciben el nombre de funciones compuestas y no pueden resolverse simplemente a partir de las reglas enunciadas hasta el momento. En la siguiente sección veremos cuál es el procedimiento práctico para el cálculo de sus derivadas.
7.3.1. Funciones compuestas: regla de la cadena
Dadas tres funciones \( f(x), g(x) \ y \ h(x) \), llamamos función compuesta a una función de la forma \( f(x) = g(h(x)) \).
Si volvemos al caso de \( f(x) = \sqrt{x^2-5x} \), mencionado al final de la sección anterior, tenemos que \( h(x) = x^2 - 5x\ \) y que \( g(x) = \sqrt{x} \). Teniendo en cuenta que \( f(x) = g(h(x)) \), podemos escribir \( f(x) = g(x^2- 5x) \), lo que en forma inmediata nos lleva a la expresión de la función f presentado al comenzar el párrafo.
Ahora bien: ¿cómo hacemos para calcular la derivada de esta función?
Dada una función de la forma \( f(x) = g(h(x))\), su derivada se obtendrá a partir de la expresión \( f´{(x)} = g´(h(x)).h´(x) \).
Cuando operemos de ese modo diremos que estamos aplicando la regla de la cadena.
Entonces, dada \( f(x) = \sqrt{x^2 - 5x} \), podemos calcular:
\[ f´(x) = \frac{1}{2 \sqrt{x^2 - 5x}} (2x-5) \]
Es decir, multiplicamos la derivada de la raíz del polinomio \( \left( \frac{1}{2 \sqrt{x^2 - 5x}} \right) \) por la derivada de dicho polinomio, 2x - 5.
La regla de la cadena puede extenderse a funciones donde la composición involucre más de dos funciones.
Calcular la derivada de la función \( f(x) = ln \sqrt{x^4 + x^2} \)
Resolución:
La función f(x) debe pensarse como el logaritmo de la raíz de un polinomio. Entonces, multiplicaremos la derivada del logaritmo de la raíz del polinomio \( \left( \frac{1}{\sqrt {x^4 + x^2}} \right) \) por la derivada de la raíz del polinomio \( \left( \frac{1}{2 \sqrt{x^4 + x^2}} \right) \), que a su vez deberá ser multiplicada por la derivada del polinomio (4x3 + 2x).
Es decir:
\[ f´(x) = \frac{1}{\sqrt {x^4 + x^2}} \frac{1}{2 \sqrt{x^4 + x^2}} (4x^3 + 2x) \]
Dijimos anteriormente que es recomendable reducir en la medida de lo posible la expresión de la derivada obtenida, teniendo en cuenta que esta habrá de emplearse para futuras operaciones. En el caso de la derivada del ejemplo anterior, podemos escribir:
\[ f´(x) = \frac{1}{2 ( \sqrt {x^4 + x^2})^2} (4x^3 + 2x) \to \]
\[ \to f´(x) = \frac{1}{2 ( \sqrt {x^4 + x^2})^2} 2(2x^3 + x) \to \]
\[ \to f´(x) = \frac{(2x^3 + x)}{( \sqrt {x^4 + x^2})} \]
Aplicando la regla de la cadena, calcular la derivada de las siguientes funciones:
\( f_1(x) = \sqrt{ln(x)} \)
\( f_2(x) = sin^2 (x^3 - 5x) \)
\( f_3(x) = ln(cos(x)) \)
\( f_4(x) = sin(ln(x^4+2x^2)) \)
\( f_5(x) = ln(sin(x^4+1)) \)
Recomendamos al alumno verificar los resultados obtenidos empleando el wxMaxima. En la sección 7.6 encontrará las instrucciones necesarias para poder hacerlo.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 95 a 103, 107 a 114, 119 a 125.
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 103 a 154.
7.3.2. Empleo del diferencial para la aproximación de funciones
El diferencial nos permite aproximar el valor de una función en un punto. Siempre a partir de la función \( f(x) = \frac{1}{4} x^2 \), supongamos que conocemos su valor en P y que deseamos obtener, aunque más no sea en forma aproximada, su valor en \( Q = (x_P + \Delta x, f (x_P + \Delta x)) \). En ese caso, podríamos escribir:
[7.1] \[ f(Q) \cong f(P) + dy \]
Como, además:
([7.2] \[ f´(P) = \frac{dy}{dx} \to dy = f´(P). dx \]
Reemplazando [7.2] en [7.1], podemos entonces decir que:
[7.3] \[ f(Q) \cong f(P) + f´(P) . dx \]
La expresión [7.3] pone en evidencia que se comete un error al aplicar este tipo de aproximación. Sin embargo, dicho error se reduce a medida que el incremento de la variable independiente lo hace.
A la izquierda de la imagen 7.8 se observa claramente el error (representado en este caso por el segmento \( \overline{QR} \)), cuando el incremento de la variable independiente es igual a la unidad. Dicho error se reduce notablemente cuando el incremento de la variable independiente se reduce a la mitad, tal como aparece a la derecha de la imagen 7.8.
Se observa cómo, a medida que el incremento de la variable independiente se reduce, el error (representado gráficamente por el segmento que va del punto Q al punto R) también se reduce.
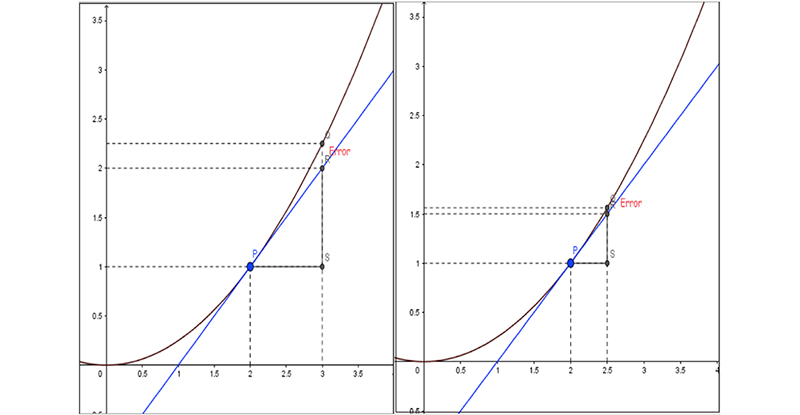
Seguidamente, proponemos un ejemplo que nos permita ver cómo aplicar el diferencial para efectuar cálculos en forma aproximada.
Empleando diferenciales, obtener el valor aproximado de \( \sqrt{3,98} \)
Para resolver el problema planteado debemos, ante todo, buscar una función conveniente y definir en el entorno de qué valor de la variable independiente vamos a trabajar. Adoptamos entonces \( f(x) = \sqrt{x} \) y \( x = 4 \) como valor de la variable independiente. El valor de \( \Delta x \) será entonces -0,02.
Alguien podría proponer trabajar en el entorno de x = 3, con \( \Delta x = 0,98 \). Sin embargo, la elección que propusimos originalmente es la más apropiada, teniendo en cuenta que el error cometido en el cálculo se reduce a medida que lo hace \( \Delta x \).
Podemos escribir entonces:
\[ \sqrt{3,98} = f (4 + (-0,02)) \]
Y, de acuerdo con lo que indica la expresión [7.3], escribimos:
[7.5] \[ \sqrt{3,98} = f (4 + (-0,02)) \cong f(4)+ f´(4) . (-0,02) \]
Calculamos seguidamente la derivada de la función y la evaluamos en x = 4.
\[ f(x) = \sqrt{x} \to f´(x) = \frac{1}{2 \sqrt{x}} \to f´(4) = \frac{1}{2 \sqrt{4}} = \frac{1}{4} \]
Teniendo en cuenta que \( \ \), estamos en condiciones de escribir:
\[ \sqrt{3,98} \cong f(4)+ f´(4) . (-0,02) = 2 + \frac{1}{4} \left( - \frac{2}{100} \right) \]
Obsérvese que hemos reemplazado al número decimal por la fracción correspondiente. El operar con fracciones evita que cometamos errores de cálculo.
Finalmente, obtenemos:
\[ \sqrt{3,98} \cong 2 + \frac{1}{4} \left( - \frac{2}{100} \right) = 2 - \frac{1}{200} = \frac{399}{200} \]
Empleando diferenciales, obtener el valor aproximado de \( \sqrt[3]{8,03} \)
Empleando diferenciales, obtener el valor aproximado de ln (0,97)
7.3.3. Polinomio de Taylor
En la próxima unidad veremos cómo calcular las primitivas (antiguamente denominadas antiderivadas) de diversas funciones. Dichos cálculos se llevaran a cabo aplicando diversos métodos, pero muchas funciones deberán convertirse en polinomios para poder ser integradas, aunque más no sea, en forma aproximada.
El procedimiento a aplicar nos exige previamente definir el concepto de derivadas sucesivas.
Dado que \( f'(x) \) derivada de la función \( f(x) \) es a su vez otra función, podemos derivarla, obteniendo \( f''(x) \). Diremos entonces que esta última es la derivada segunda de \( f(x) \).
Si, a su vez, dicha derivada segunda fuese derivable, podríamos calcular \( f '''(x) \), que recibirá el nombre de derivada tercera de la función original.
En la medida que cada una de las derivadas obtenidas siga siendo una función derivable, podríamos operar del mismo modo, obteniéndose de ese modo lo que recibe el nombre de derivadas sucesivas de la función.
Dada \( f(x) = x^3 - 3x^2 + 6 \) , calcular todas sus derivadas sucesivas.
Resolución:
Como veremos, las funciones polinómicas se caracterizan por poseer un número finito de derivadas, razón por la cual la consigna puede pedirnos todas las derivadas.
Entonces:
\[ f'(x) = 3x^2 - 3.2.x = 3x^2 - 6x \] \[ f''(x) = 3.2.x - 6 = 6x - 6 \] \[ f'''(x) = 6 \]Como la derivada de una constante vale cero, no tiene sentido seguir derivando a la función (¡sus restantes derivadas serán idénticamente nulas!).
Vamos a tomar ahora una función f(x) que admita derivada en el entorno de x0 un valor cualquiera perteneciente al dominio de la función. Expresaremos entonces dicha función como:
\[ f(x) = a_0 + a_1 (x - x_0) + a_2 (x- x_0)^2 + a_3 (x - x_0)^3 + ... \]
[7.4] \[ ... + a_n (x - x_0)^n + ... \]
Seguidamente, reemplazamos en la [7.4], x por x0
\[ f(x_0) = a_0 + a_1 (x_0 - x_0) + a_2 (x_0 - x_0)^2 + a_3 (x_0 - x_0)^3 + ... \]
\[ ... + a_n (x_0 - x_0)^n + ... \]
Con excepción del primer término del segundo miembro, todos los demás habrán de anularse, de modo que podemos escribir:
[7.5] \[ a_0 = f(x_0) \]
A continuación, derivamos la [7.4]:
\[ f'(x) = a_1 + a_2 2(x - x_0) + a_3 3(x - x_0)^2 + ...\]
[7.6] \[ ... + a_n n(x - x_0)^{n-1} + ... \]
Si en la [7.6] reemplazamos x por x0
\[ f'(x_0) = a_1 + a_2 2(x_0 - x_0) + a_3 3(x_0 - x_0)^2 + ...\]
\[... + a_n n(x - x_0)^{n-1} + ... \]
Nuevamente, el único término del segundo miembro que no se anula es el independiente, y podemos escribir:
[7.7] \[ a_1 = f'(x_0)\]
Calculamos la derivada segunda de la función a partir de la [7.6]:
\[ f''(x) = 2a_2 + a_3 3.2.(x - x_0) + ... \]
[7.8] \[... + a_n n(n - 1) (x - x_0)^{n - 2} + ...\]
En la [7.8] repetimos el procedimiento aplicado anteriormente, es decir, el de reemplazar a x por x0
\[ f''(x_0) = 2a_2 + a_3 3.2.(x_0 - x_0) + ... \]
\[... + a_n n(n - 1) (x_0 - x_0)^{n - 2} + ...\]
De este modo, obtenemos:
[7.9] \[ a_2 = \frac{1}{2} f''(x_0) \]
A partir de la [7.8] calculamos la derivada tercera de la función:
\[ f'''(x) = a_3 3.2 + ... \]
[7.10] \[ ... + a_n n(n - 1) (n - 2) (x - x_0)^{n - 3} + ... \]
Como el lector imaginará, si volvemos a reemplazar a x por x0, solo el primer término del segundo miembro de la [7.10] será distinto de cero, y podremos escribir:
[7.11] \[ a_3 = \frac{f'''(x_0)}{3.2} \]
Podríamos repetir el procedimiento y llegaríamos entonces a una expresión genérica para los coeficientes de la [7.4]
[7.12] \[ a_n = \frac{f^{(n)}(x_0)}{n (n - 1) (n-2)... 3.2.1} \]
El producto que aparece en el denominador del segundo término podrá expresarse de un modo más reducido, a partir del concepto de factorial, que presentamos a continuación.
Dado un número natural n, definimos como factorial de n a la productoria de todos los números naturales desde uno hasta n.
El factorial de n se expresa como n!
Calcular el factorial de 4.
Resolución:
Al hablar de la productoria nos referimos al producto de todos los naturales desde 1 hasta n, de modo que en nuestro caso tenemos:
\[ 4! = 1.2.3.4 = 24 \]
Existen dos casos particulares de factorial que debemos tener en cuenta:
- 0! = 1
- 1! = 1
Si reemplazamos [7.7], [7.9], [7.11] y [7.12] en [7.4], nos queda:
\[ f(x) = f(x_0) + f´{(x_0)(x-x_0)} + \frac{f''(x_0)}{2!} (x-x_0)^2 + \]
[7.13] \[ + \frac{f'''(x_0)} {3!} (x - x_0)^3 + ... + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + ... \]
Como a los fines prácticos solo habremos de calcular un número finito de derivadas (en este caso, digamos que nos extenderemos solamente hasta la derivada enésima), la [7.13] podrá escribirse como:
\[ f(x) \cong P_n(x_0) = f´(x_0)(x-x_0) + \frac{1}{2!} f''(x_0)(x-x_0)^2 + \]
[7.14] \[ + \frac{f'''(x_0)} {3!} (x - x_0)^3 + ... + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + ... \]
La [7.14] define entonces al polinomio de Taylor de grado n de la función f(x) en el entorno de x = x0, al que expresamos como Pn(x0)
Dada f(x) = ln(x + 1), calcular el polinomio de Taylor de grado 3 de dicha funciónen el entorno de x0 = 1.
Resolución:
En primer lugar, tengamos en cuenta que debemos obtener
\[ f(x) \cong P_3(1) = f(1) + f´(1)(x-1) + \frac{1}{2!} f''(1)(x-1)^2 + \]
[7.15] \[ + \frac{f'''(1)} {3!} (x - 1)^3 \]
Procedemos entonces a calcular las tres primeras derivadas de la función:
\[ f'(x) = \frac{1}{x+1} = (x+1)^{-1} \]
\[ f''(x) = -1 (x+1)^{-2} \]
\[ f'''(x) = 2 (x+1)^{-3} \]
Seguidamente, evaluamos la función y sus tres primeras derivadas en x0 = 1:
[7.16] \[ f(1) = ln(2) \]
[7.17] \[ f'(1) = \frac{1}{1+1} = \frac{1}{2} \]
[7.18] \[ f''(1) = -1 (1+1)^{-2} = -\frac{1}{4} \]
[7.19] \[ f'''(1) = 2(1+1)^{-3} = \frac{2}{8} = \frac{1}{4} \]
Si sustituimos [7.16], [7.17], [7.18] y [7.19] en [7.15], obtenemos finalmente el polinomio que se pide en la consigna:
\[ P_3(1) = ln(2) + \frac{1}{2}(x-1)- \frac{1}{4} f''(1)(x-1)^2 + \frac{1}{4} (x-1)^3 \]
Dada \( f(x) = \sqrt{x+2} \), obtener el polinomio de Taylor de grado dos de la función en el entorno de X0 = 2.
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 7.6 encontrará las instrucciones necesarias para poder hacerlo.
Dada f(x) = sin(x), obtener el polinomio de Taylor de grado cinco de la función en el entorno de x0 = 0.
Recomendamos al alumno verificar el resultado obtenido empleando el wxMaxima. En la sección 7.6 encontrará las instrucciones necesarias para poder hacerlo.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 648 a 655.
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 580 a 586.
7.3.4. El diferencial como un caso particular de Taylor
La expresión [7.3] de la sección 7.2.2 indicaba lo siguiente:
\[ f (Q) \cong f(P) + f'(P).dx \]
Si tenemos en cuenta que \( x = x_0 + \Delta x \), entonces:
[7.20] \[ f (x) \cong f(x_0) + f'(x_0) . (x-x_0) \]
Paralelamente, recordemos que la [7.14] expresaba:
\[ f(x) \cong P_n (x_0) = f(x_o) + f'(x_o)(x-x_0)+ \frac{1}{2!}f''(x_0)(x-x_0)^2 + \]
\[ + \frac{f'''(x_0)}{3!}(x-x_0)^3 + ... + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \]
Si comparamos a la [7.14] con la [7.20] , comprobamos que esta última representaría entonces al polinomio de Taylor de grado uno de la función.
Ello nos da la pauta de que el polinomio de Taylor podrá emplearse, como el diferencial, para aproximar el valor de una función. Pero, además, veremos a continuación que el error que se comete aplicando Taylor puede reducirse tanto como deseemos, con tal de emplear un polinomio de un grado lo suficientemente alto.
Dada f(x) = sin(x), obtener los polinomios de Taylor de la función de grados uno, tres y cinco en el entorno del origen. Utilizando el software, graficar en un mismo par de ejes cartesianos la función y los tres polinomios obtenidos.
Resolución:
Como dijimos anteriormente, el primer paso consiste en calcular las derivadas sucesivas de la función. Así:
- \( f'(x) = cos(x)\)
- \( f''(x) = -sin(x)\)
- \( f'''(x) = -cos(x)\)
- \( f^{iv}(x) = sin(x)\)
- \( f^{v}(x) = cos(x)\)
Seguidamente, evaluamos dichas derivadas en x = 0:
- \( f'(0) = cos(0) = 1\)
- \( f''(0) = -sin(0) = 0\)
- \( f'''(0) = -cos(0) = -1\)
- \( f^{iv}(0) = sin(0) = 0\)
- \( f^v(0) = cos(0) = 1\)
Los polinomios que debemos obtener son:
\[ P_1(x) = f(0) + f'(0)x \]
\[ P_3(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 \]
\[ P_5(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + \]
\[ + \frac{f^{iv}(0)}{4!}x^4 + \frac{f^v(0)}{5!}x^5 \]
Reemplazando en cada una de las tres expresiones anteriores por los valores de las derivadas evaluadas en el origen, nos quedan:
\[ P_1(x) = x \]
\[ P_3(x) = x -\frac{1}{3!}x^3 \]
\[ P_5(x) = x -\frac{1}{3!}x^3 + \frac{1}{5!}x^5 \]
En la imagen 7.9 pueden observarse las cuatro funciones obtenidas. Es evidente que la aproximación a partir del polinomio de grado uno (representado por la recta roja de la imagen) se aleja rápidamente de la curva representativa de la función, en tanto que el polinomio de grado cinco (curva verde del gráfico) recién parece alejarse cuando el ángulo supera los noventa grados sexagesimales.
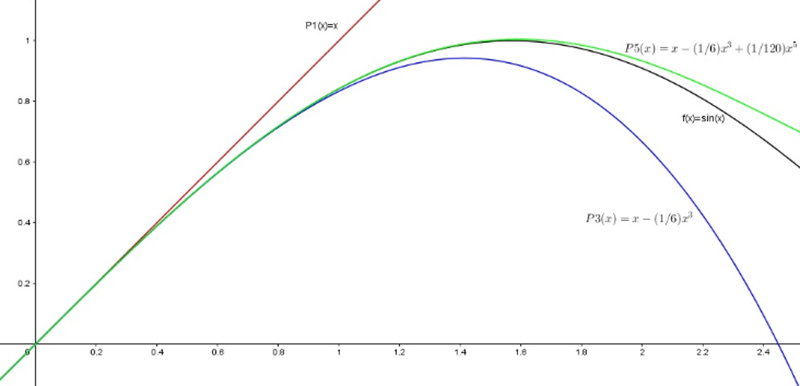
La aproximación a partir del polinomio de grado uno (representado por la recta roja de la imagen) se aleja rápidamente de la curva representativa de la función (que en la figura aparece en negro). En cambio, el polinomio de grado cinco (curva verde del gráfico) recién parece alejarse cuando el ángulo supera los noventa grados sexagesimales. Se hace evidente entonces que la aproximación aumentará a medida que lo haga el grado del polinomio adoptado.
7.4. Crecimiento y decrecimiento de una función
Teniendo en cuenta que la derivada de una función en un punto es numéricamente igual a la pendiente de la recta en dicho punto, podremos analizar otra característica valiosa de las funciones: sus intervalos de crecimiento y de decrecimiento.
Si una función \( f(x) \) es derivable para todo \( x \in (a, b) \), y, además, \( f'(x) > 0 \) para todo \( x \in (a, b) \), diremos entonces que (a,b) es un intervalo de crecimiento de la función.
Análogamente, si f(x) es derivable para todo \( x \in (a, b) \), y, además, \( f'(x) < 0 \) para todo \( x \in (a, b) \), diremos entonces que (a,b) es un intervalo de decrecimiento de la función.
Hallar los intervalos de crecimiento y de decrecimiento de la función f(x) = x3 - 12x.
Resolución:
Dijimos anteriormente que el crecimiento o decrecimiento de la función dependía del signo que adoptara la derivada primera, de modo que, como primera medida, hemos de derivar la función:
\[ f'(x) = 3x^2 - 12 \]Seguidamente, buscamos los valores de la variable independiente para los cuales se anule la función. Dichos valores serán los extremos de los intervalos de crecimiento y de decrecimiento.
\[ f'(x) = 3x^2 - 12 = 0 \to 3 (x^2 - 4) = 0 \to \]
\[ (x^2 - 4) = 0 \to x^2 = 4 \to \sqrt {x^2} = \sqrt{4} \to |x| = 2\]
Repasando rápidamente los pasos de cálculo que acabamos de presentar, al igualar a cero la derivada primera se obtuvo una ecuación de segundo grado que carecía de término lineal; por eso, bastó con pasar al otro miembro de la igualdad al término independiente, para luego aplicar raíz cuadrada a ambos miembros y obtener las dos soluciones buscadas, a saber:
\[ x_1 = -2 \ y \ x_2 = 2 \]
Los intervalos de crecimiento y de decrecimiento de la función serán entonces \( (-\infty, -2),(-2,2) \) y \( ( 2, + \infty ) \). El procedimiento habitual consiste en evaluar el signo de la derivada primera para un punto cualquiera de cada uno de dichos intervalos, para determinar el signo que esta habrá de tener en cada uno de ellos.
En la siguiente tabla, volcamos los resultados obtenidos:
|
|
Signo de \( f'(x) \) |
Clasificación |
|
\( ( - \infty , -2) \) |
+ |
Intervalo de crecimiento |
|
\( (-2,2) \) |
- |
Intervalo de decrecimiento |
|
\( ( 2, + \infty ) \) |
+ |
Intervalo de crecimiento |
Dichos intervalos se observan perfectamente en la representación gráfica de la función original, que puede observarse en la imagen 7.10.
7.5. Extremos relativos de una función
A partir del ejemplo anterior, y estudiando detenidamente la curva que aparece en la imagen 7.10, vemos que hay dos puntos particularmente significativos, el P1 y el P2. A la izquierda del primero la función crece, para decrecer a su derecha. Dicho punto recibe el nombre de máximo relativo de la función.
Análogamente, se observa que la función decrece a la izquierda de P2 para luego comenzar a crecer a su derecha. Cuando esto sucede, decimos que se trata de un mínimo relativo de la función.
Las abscisas de los puntos P1 y P2 resultaron ser valores de la variable independiente para los cuales la derivada primera se anulaba, lo que resulta significativo.
Sin embargo, veamos qué es lo que sucede con la función g(x) = x3: su derivada es g'(x) = 3x2, que se anula para x = 0. Sin embargo, al observar la representación gráfica de dicha función (imagen 7.11), nos damos cuenta que el punto (0,0) no es ni máximo ni mínimo de g(x)
La explicación es sencilla: si estudiamos el signo de la derivada primera de la función, veremos que adopta valor positivo a izquierda y derecha de x = 0 (único valor de la variable independiente para el cual la función no crece).
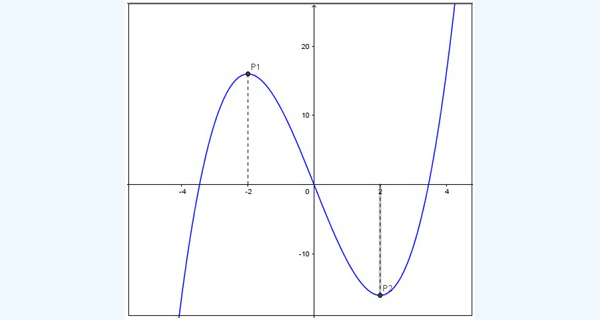
Los puntos P1 y P2 son extremos relativos de la función, como se observa claramente en la imagen.
Los valores de la variable independiente para los cuales la derivada primera de la función se hace cero o no existe definen a los que llamaremos puntos críticos de una función.
Dichos puntos no necesariamente representan máximos o mínimos de dicha función.
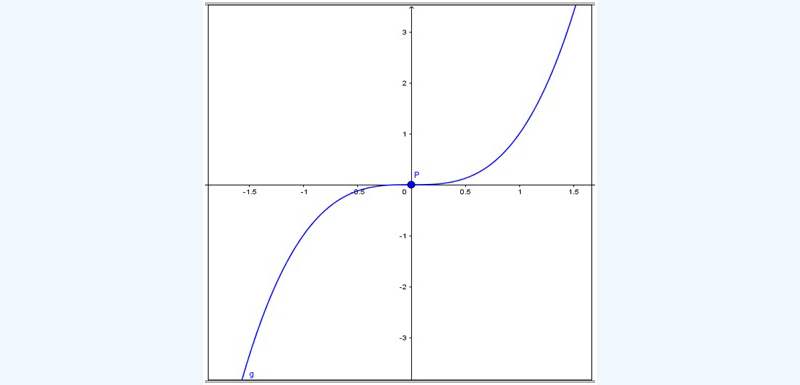
La derivada primera de la función en el punto P (que coincide con el origen de coordenadas) se anula, lo que significa que la recta tangente a la curva en ese punto resulta ser horizontal. Sin embargo, no puede ser extremo de la función, puesto que la derivada crece a izquierda y derecha de P.
Acabamos de ver que igualar a cero la derivada de una función no garantiza la obtención de un extremo relativo. Por eso, el análisis de los resultados deberá ser un poco más amplio, como veremos a continuación.
Condición necesaria para la existencia de un extremo relativo: La función f(x) podría presenta extremo relativo en x = x0 si dicho valor correspondiese a la abscisa de un punto crítico.
Condición suficiente para la existencia de un extremo relativo: Si el signo de la derivada primera a izquierda y derecha del punto crítico cambia para valores muy próximos a x = x0, la función efectivamente presentará allí un máximo o un mínimo relativo.
En este sentido:
- Si f(x) crece a la izquierda y decrece a la derecha de x = x0, nos encontraremos en presencia de un máximo relativo.
- Si, en cambio, la función decrece a la izquierda y crece a la derecha de x = x0' estaremos en presencia de un mínimo relativo.
Decimos que el extremo es relativo porque solo consideramos el entorno que rodea a x = x0. Si observamos nuevamente la función representada en la imagen 7.10, notaremos que la función sigue creciendo, de modo que, a medida que el valor de la variable independiente aumenta, también lo hace el de la variable dependiente (¡tendiendo a infinito!). Si, en cambio, la variable independiente tiende a menos infinito, también lo hará la función. Eso significa que los extremos representados por P1 y P2 solo lo son para valores de la variable independiente que se encuentren en entornos reducidos de dichos puntos (es decir, entornos que no los contengan).
Se define como entorno reducido con centro en x = x0 y radio r (y se lo expresa como \( E^*(x_0,r) \)) al conjunto de todos los números que sean simultáneamente mayores que x0 - r y menores que x0 + r , exceptuando al propio x0.
En algunos casos, sin embargo, un extremo relativo puede ser, a su vez, extremo absoluto de la función. En la sección 5.3.1, al hablar sobre máximos y mínimos de funciones cuadráticas, dijimos que:
El punto de coordenadas \( ( x_M, f (x_M)) \) es un máximo absoluto de la función cuando, para cualquier valor de la variable independiente x perteneciente al dominio de dicha función se verifique la condición:
\[ f(x) < f(x_M) \]
Análogamente, el punto de coordenadas \( \ \) es un mínimo absoluto de la función cuando, para cualquier valor de la variable independiente x perteneciente al dominio de dicha funciónse verifique la condición:
\[ f(x) > f(x_M) \]
En el caso de las funciones cuadráticas, se cumple que la recta tangente a las curvas resulta ser horizontal en los vértices, con lo que las pendientes de dichas rectas (y, por ende, sus derivadas) habrán de anularse. Pero como además de cumplirse en dichos vértices las condiciones necesaria y suficiente para la existencia de extremos relativos también se cumple la definición de extremo absoluto, nos encontramos en una situación muy particular.
Dadas las funciones:
\( f_1 (x) = \frac{x}{x^2 + 1} \);
\( f_2 (x) = \sqrt{x^2 + 2x + 4} \);
\( f_3 (x) = ln (x^2 + 4x + 8) \);
y \( f_4 (x) = ln \sqrt{x^2 + 4} \)
Se pide:
- Determinar el dominio.
- Hallar los puntos críticos y definir los intervalos de crecimiento y de decrecimiento.
- A partir de los resultados del punto (ii) indicar cuáles de los puntos críticos obtenidos resultan ser máximos o mínimos.
Larson, R.; Hostetler, R.; Edwards, B. (2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 179 a 194.
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 206 a 223.
7.6. Problemas de optimización
Uno de los objetivos de modelizar procesos y fenómenos de la realidad es el de optimizar resultados. Por ejemplo, el fabricante de un determinado producto estará interesado en gastar la menor cantidad posible de material para el envase en el que lo comercializa; si necesitamos viajar a una ciudad lejana por motivos de trabajo, estaremos interesados en hacerlo en el menor tiempo posible; o si una empresa diseña un motor para su último modelo de automóvil, podrá estar interesada en que su rendimiento sea el mayor posible.
Dado que la cantidad de material para fabricar un determinado tipo de envase, el tiempo para trasladarse de una ciudad a otra o el rendimiento de un motor pueden expresarse como funciones, la cuestión será obtener dichas funciones para luego obtener sus máximos o mínimos.
Seguidamente, desarrollaremos algunos ejemplos sencillos para que el alumno interprete lo que acabamos de plantear.
Demostrar que la lata cilíndrica de volumen dado de menor superficie total es aquella para la cual el diámetro es igual a la altura.
Para poder resolver el problema es necesario interpretarlo correctamente. Lo que se nos pide es que la superficie total de la lata sea mínima, con lo que la función a minimizar es la que permite calcular dicha superficie. Aun cuando no se exprese explícitamente su valor, se supone que el volumen de dicha lata es conocido, de modo que, de aquí en más, lo expresaremos como V.
Por otro lado, hay dos variables presentes: el radio de la lata (al que expresaremos en adelante como r) y su altura (que indicaremos con la letra h). El enunciado dice que el volumen de la lata es dado (es decir, lo interpretaremos como un dato), de manera que podemos escribir:
\[ V= \pi r^2h \]
El volumen de la lata se calcula como el producto de su base (que es la superficie de un círculo) por su altura.
Dicha ecuación representa una condición que habrá de cumplirse, y nos ofrece una relación entre las dos variables con las que tenemos que trabajar. Por ejemplo, podríamos escribir a la altura en función del radio, y nos quedaría:
\[ h = \frac{V}{\pi r^2} \]
Volviendo entonces a la función a optimizar, en la parte superior de la imagen 7.12 representamos una lata cilíndrica, indicando cuáles son las dos variables que habrán de definir sus características geométricas, a saber, su altura y su diámetro. En la parte inferior de la imagen, en cambio, hemos descompuesto a la superficie total en sus tres componentes elementales: la base, la tapa y la cara lateral. Las dos primeras son dos círculos iguales, en tanto que la última es un rectángulo, cuya base es igual al perímetro de aquellos.
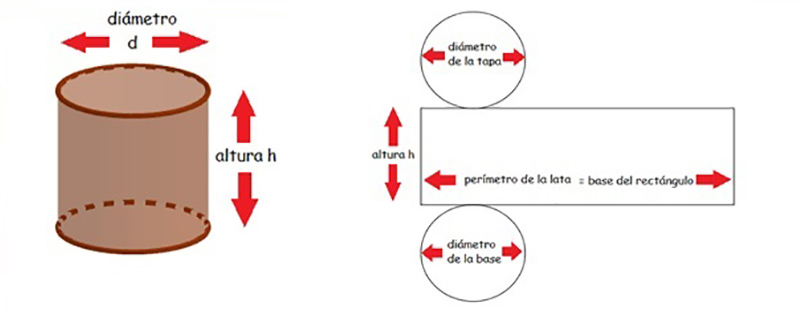
Las dos variables que nos interesan son la altura y el diámetro (o, en su defecto, el radio) de la lata. Para obtener la función a optimizar debemos pensar cuáles son las piezas que conforman la lata: su base, su tapa y su cara lateral.
Las superficies de la base y de la tapa se calculan mediante la expresión:
\[ \text{área de cálculo} = \pi r^2 \]
En cuanto a la superficie lateral, observamos que se trata de un rectángulo, cuya altura es igual a h, en tanto que su base debe coincidir con los perímetros de la base y la tapa (es decir, perímetro circunferencia =2πr).
De este modo, la superficie total de la lata puede expresarse como:
\[ S_T (h,r) = 2 \pi r^2 + 2 \pi rh \]
El primer término representa las áreas de la base y la tapa, y el segundo la superficie lateral.
Para aplicar lo estudiado hasta el momento, necesitamos que la función a optimizar solo dependa de una variable. Como vimos anteriormente:
\[ h = \frac{V}{\pi r^2} \]
Escribimos entonces:
\[ S_T(r) = 2 \pi r^2 + 2 \pi r \frac{V}{\pi r^2} \]
Simplificando nos queda:
\[ S_T(r) = 2 \pi r^2 + 2 \frac{V}{r} \]
Esta será entonces la función a optimizar. Recordemos que en dicha expresión, la única variable presente es el radio r.
La condición necesaria para obtener extremos de una función era que su derivada primera se anulara. Por eso, calculamos dicha derivada, la igualamos a cero y despejamos el valor de la variable dependiente correspondiente a dicha circunstancia:
\[ S´_T(r) = 4 \pi r - \frac{2V}{r^2} = 0 \to 4 \pi r = \frac{2V}{r^2} \to r^3 = \frac{V}{2\pi} \to r = \sqrt[3]{\frac{V}{2 \pi}} \]
En la sección 7.4 dijimos que para verificar que un punto crítico era un extremo relativo debíamos analizar el signo de la derivada primera a derecha e izquierda del aquel. Sin embargo, en muchos casos es conveniente aplicar el siguiente criterio:
- Si \( f'(x_0) = 0 \) y \( f''(x_0) < 0 \), entonces \( (x_0, f(x_0)) \) resultará ser un máximo relativo de la función.
- Si, en cambio, \( f'(x_0) = 0 \) pero \( f''(x_0) > 0 \), \( (x_0, f(x_0)) \) resultará ser un mínimo relativo de la función.
Para asegurarnos de que se trata de un mínimo utilizaremos el criterio de la derivada segunda. Calculamos entonces la derivada segunda de la función superficie total, para luego evaluarla en \( r = \sqrt[3]{\frac{V}{2 \pi}} \):
\[ S''\ _T (r) = 4 \pi + \frac{4V}{r^3} \to S''\ _r \left( r = \sqrt[a]{\frac{V}{2 \pi}} \right) = 4 \pi + \frac{4V}{\frac{V}{2 \pi}} = 12 \pi > 0 \]
Como la derivada segunda evaluada para el valor crítico resultó ser positiva, confirmamos que dicho valor corresponde a un mínimo de la función.
Sin embargo, no olvidemos que la consigna era más ambiciosa: debemos probar que, en estas circunstancias, el diámetro y la altura de la lata cilíndrica habrán de ser iguales.
Recordemos la relación entre la altura y el radio que habíamos definido al comenzar el análisis del problema:
\[ h = \frac{V}{\pi r^2} \]
Proponemos multiplicar y dividir al segundo miembro por el radio, lo que (como veremos de inmediato) habrá de simplificarnos los cálculos:
\[ h = \frac{V \ r}{\pi r^2 r} = \frac{Vr}{\pi r^3} \]
Reemplazamos entonces el valor crítico obtenido en el denominador de dicha expresión:
\[ h = \frac{V \ r}{\pi \left( \sqrt[3]{\frac{V}{2 \pi}} \right) ^3} = \frac{Vr}{\pi \frac{V}{2 \pi} } = \frac{2\pi Vr}{\pi V} = 2 r \]
Es decir, para el valor crítico obtenido, la altura es igual a dos veces el radio, es decir, se demuestra que la lata tendrá superficie lateral mínima cuando su altura y su diámetro sean iguales.
Seguidamente proponemos otro ejemplo donde el objetivo será el de minimizar una distancia, una de las aplicaciones más frecuentes del tema que estamos desarrollando.
Determinar las coordenadas de los puntos de la curva \( y = \frac{1}{4} x^2 \), tales que sus distancias al punto (0,4) sean mínimas.
Para poder interpretar mejor la situación, utilizaremos el software habitual. En la imagen 7.13 se observan la parábola, el punto P y un punto A sobre ella. En color rojo hemos indicado al segmento que une estos dos puntos, cuya longitud será igual a la distancia entre ambos.
Debe quedar en claro que la función a optimizar no es la que aparece en la imagen, sino la que nos permite calcular la distancia de un punto cualquiera del plano al punto P. Teniendo en cuenta la definición de distancia entre dos puntos del plano, podemos escribir:
\[ d ((0,4),(x,y)) = \sqrt{(x-0)^2 + (y-4)^2} \]
En esta función hay dos variables, de modo que debemos buscar en el enunciado alguna condición para redefinirla, convirtiéndola en una función de una sola variable independiente.
El estudio de funciones con dos o más variables independientes excede los alcances del presente curso. Sin embargo, es necesario que el alumno sepa que existen procedimientos para poder optimizar tales funciones sin necesidad de introducir en ellas las condiciones, como haremos a continuación.
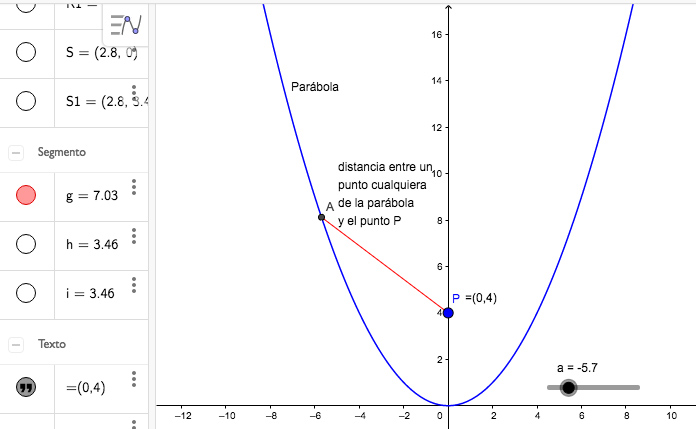
La longitud del segmento que une al punto P con un punto A cualquiera de la parábola representará la función a minimizar.
Como el punto en cuestión debe pertenecer a la parábola, la condición que habrá de cumplirse en todos los (x,y) de nuestro interés es \( \ \). Entonces, podemos escribir:
\[ d (x,y) = \sqrt{(x)^2 + (y-4)^2} \to d(x) = \sqrt{x^2 + \left( \frac{1}{4} x^2 - 4 \right)^2 } \to \]
\[ \to d(x) = \sqrt{x^2 + \left( \frac{x^2 - 16}{16} \right)^2 } \to d(x) = \sqrt{\frac{16x^2 + x^4 - 32x^2 + 256}{16}} \to \]
\[ \to d(x) = \frac{1}{4} \sqrt{x^4 - 16x^2 + 256} \]
Esta última representa entonces la función a optimizar.
Para hallar los puntos críticos derivamos la función y la igualamos a cero, siguiendo el procedimiento aplicado anteriormente:
\[ d'(x) = \frac{1}{4} \frac{4x^3 - 32x}{2 \sqrt{x^4 - 16x^2 + 256}} = 0 \to x^3 - 8x = 0 \to \]
\[ \to (x^2 - 8) = 0 \to \left\{ \begin{array}{c} x =-\sqrt{8} \\ x = 0 \\ x = \sqrt{8} \end{array} \right. \]
Obtuvimos tres resultados y debemos determinar cuál o cuáles de ellos corresponden al mínimo (o los mínimos) buscados.
En este caso, el criterio de clasificación de puntos críticos de acuerdo con el signo de la derivada segunda resulta poco conveniente, dada la complejidad de su cálculo. Proponemos entonces estudiar los intervalos de crecimiento y decrecimiento de la función.
Dado que las raíces de \( x^4 - 16x^2 + 256 \) están fuera del campo real, los intervalos de crecimiento y decrecimiento tendrán como extremos los puntos críticos obtenidos.
Puesto que el signo de la derivada primera determina de qué tipo de intervalo se trata y teniendo en cuenta que el denominador de aquella será positiva para cualquier valor real, bastará con evaluar el signo que adopte su numerador.
Se observa entonces que la función decrecerá en \( ( - \infty , - \sqrt{8} ) \) y \( ( 0 , \sqrt{8} ) \), mientras crecerá en los intervalos \( ( - \sqrt{8} , 0 ) \) y \( ( \sqrt{8} , + \infty ) \). Podemos asegurar entonces que los puntos de la parábola cuyas abscisas sean \( x = - \sqrt{8} \) y \( x = \sqrt{8} \) serán los más cercanos al punto P. Y dado que \( y = \frac{1}{4}x^2 \), respondemos finalmente a la consigna del problema diciendo que los puntos \( A = (- \sqrt{8} , 2) \) y \( B = (\sqrt{8} , 2 ) \) son los puntos de la parábola cuya distancia a P es mínima.
Es importante diferenciar la función a optimizar de la o las condiciones que aparezcan en el enunciado del problema.
En la vista algebraica de la imagen 7.13 aparece en último lugar el segmento g (en color rojo), cuyo valor no es otro que el de la distancia entre los puntos P y A.
La curva en color azul representa la parábola, que fija la condición que habrán de cumplir los puntos buscados (pertenecer a ella). Para poder representar la función objetivo en el mismo gráfico definimos un punto auxiliar Q, cuya abscisa coincide con la del punto A, en tanto que su ordenada resulta proporcional a la distancia entre A y P (eliminamos el 0,25 que precedía a la función distancia definida oportunamente, para que pudiese observarse con más claridad lo que deseamos mostrar a continuación). En la imagen 7.14 se observa el punto Q, tanto sobre la vista algebraica como sobre la gráfica, mediante una flecha de color azul. Se señala con una flecha roja la distancia entre los puntos A y P.
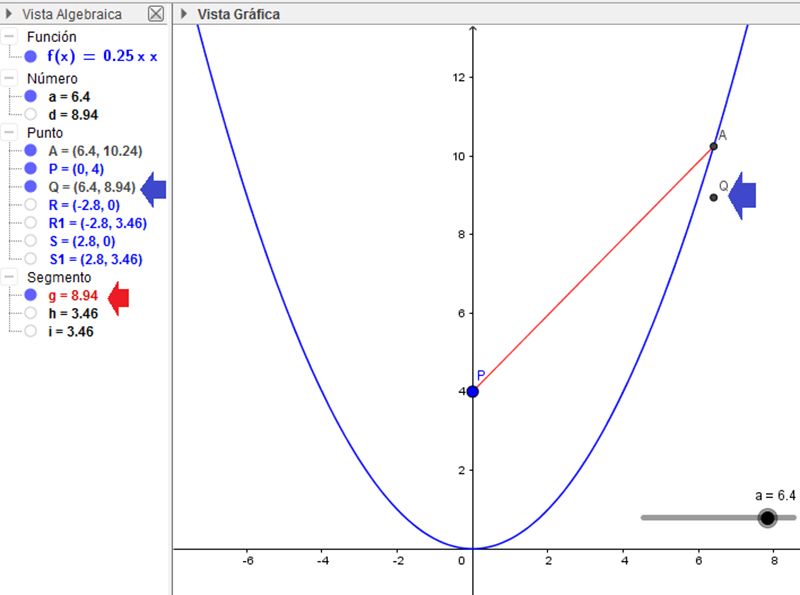
El punto Q nos permitirá, a partir del valor de su ordenada, definir la función que vincule la abscisa de un punto cualquiera de la parábola con su distancia al punto P.
El empleo del rastro (una de las aplicaciones de nuestro software) permite seguir el punto Q al desplazarlo mediante el deslizador. En la siguiente imagen se superponen los puntos que indican las posiciones de Q con la gráfica original. Esos puntos pertenecen a la función que utilizamos para representar la distancia de un punto de la parábola al punto P en función de su abscisa. En la imagen 7.15 mostramos cómo seleccionar la aplicación “rastro” en el GeoGebra,en tanto que en la imagen 7.16 mostramos, mediante una serie de puntos, la verdadera función objetivo. El cambio de escala adoptado permite ver con claridad que dicha funciónpresenta dos mínimos, cuyas abscisas se corresponden con las obtenidas analíticamente en el momento de obtener los mínimos de la función objetivo (imagen 7.17).
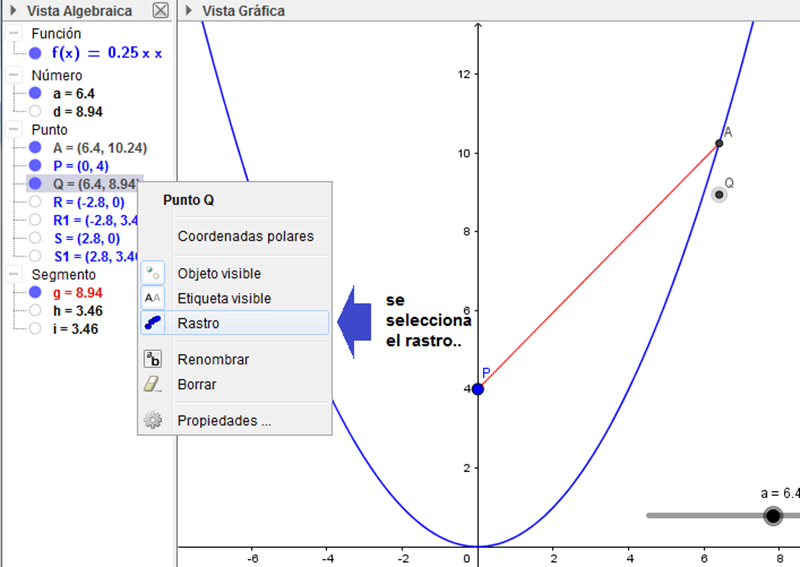
La flecha azul señala la función Rastro, que registra en el plano las distintas posiciones del punto seleccionado (en este caso, el punto Q).
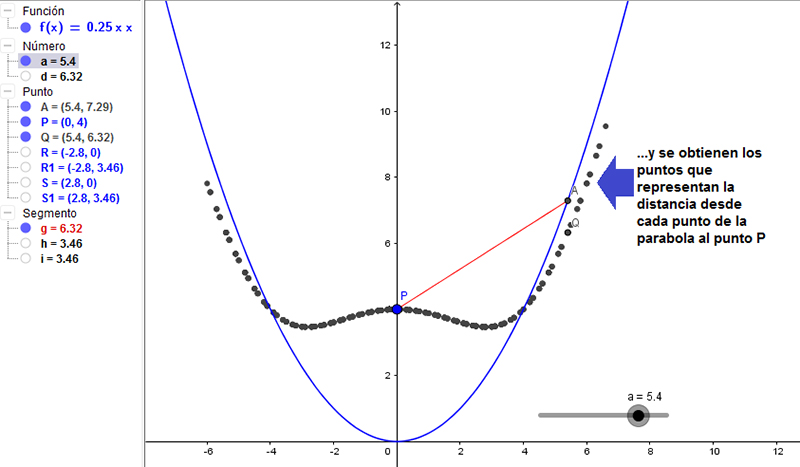
Empleando el deslizador, movemos el punto A a lo largo de la parábola. El punto Q va reflejando entonces de qué modo cambia la distancia del punto A al punto P, de modo que el rastro de Q define de algún modo la función objetivo de nuestro problema.
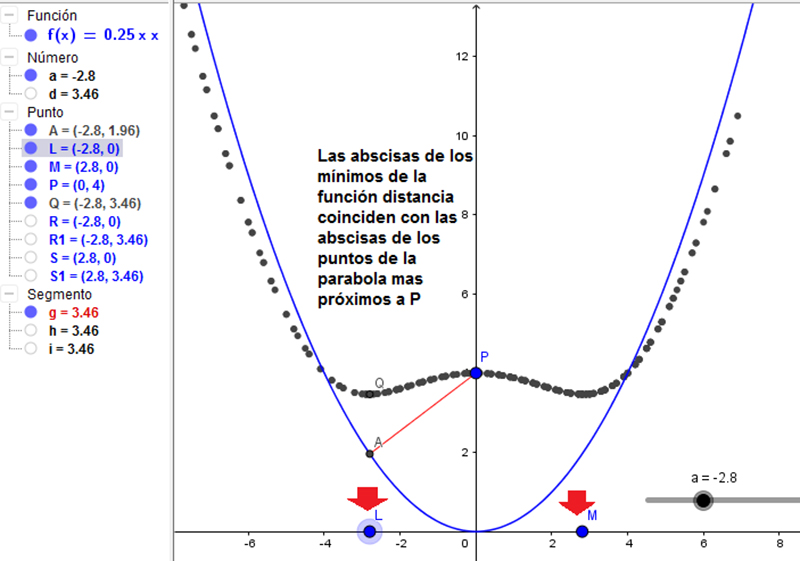
Las abscisas de los mínimos de la función objetivo coinciden con las de los puntos de la parábola cuya distancia al punto P resulta ser mínima.
Finalizaremos la presente sección con otro ejemplo de minimización. En este caso, utilizaremos una serie de imágenes armadas con el GeoGebra 3D para interpretar mejor el enunciado.
Una caja de base cuadrada debe tener una capacidad de 10 Ccm3. Calcular cuáles habrán de ser sus dimensiones para que su superficie total sea la mínima posible.
Nuevamente debemos interpretar adecuadamente el enunciado para diferenciar la función a optimizar de la condición que habrán de cumplir las variables involucradas (que en este caso son la altura de la caja, la que expresaremos con la letra h, y el lado de la base, al cual indicaremos con la letra a).
En la imagen 7.18 se observan cuatro “cajas” que cumplen con las condiciones del enunciado (es decir, su base es cuadrada y su volumen vale 10). De todas las cajas que cumplen con esas condiciones debemos hallar la que tiene superficie total mínima, de modo que es esa la función a optimizar.
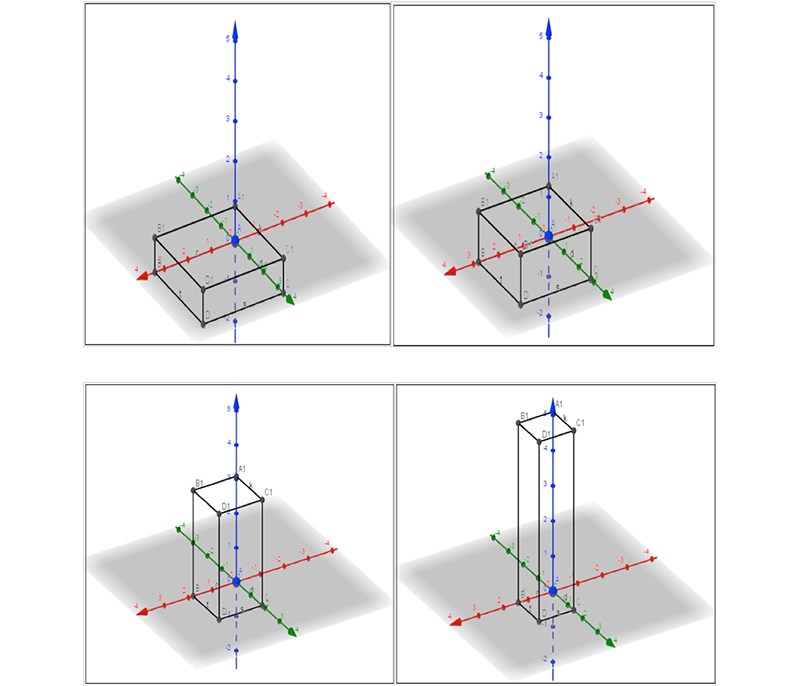
Las cuatro cajas parecen muy distintas… ¡pero todas ellas tienen el mismo volumen!
La caja está conformada por dos cuadrados de lado a más cuatro rectángulos de base a y altura h, tal como se observa en la imagen 7.19. Entonces, la función a minimizar será la suma de los dos cuadrados más los cuatro rectángulos:
\[ S_T (a,h) = 2a^2 + 4ah \]
Como el volumen es igual a la superficie de la base por la altura, tenemos:
\[ 10cm^3 = a^2 h \to h = \frac{10}{a^2} \]
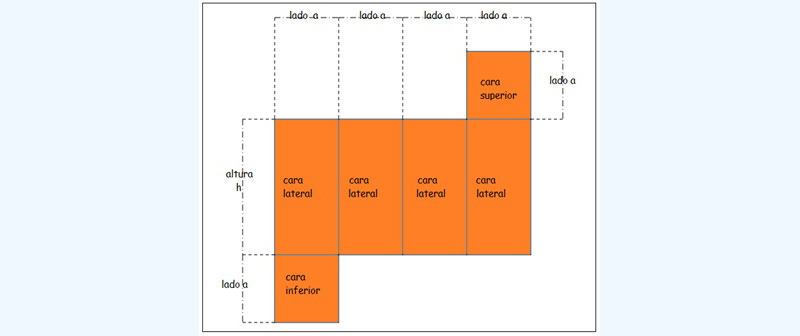
Para obtener la función a minimizar, imaginamos cómo habrá de verse antes de ser armada.
Si reemplazamos el valor de la altura h en función del lado de la base a en la expresión que nos permite calcular la altura total, obtenemos la función a optimizar:
\[ S_T (a,h) = 2a^2 + 4ah \to S_T(a) = 2a^2 + 4a \frac{10}{a^2} \to S_T(a) = 2a^2 + \frac{40}{a} \]
Derivamos dicha función y la igualamos a cero para obtener suspuntos críticos:
\[ S' \ _T(a) = 4a - \frac{40}{a^2} \to 4a = \frac{40}{a^2} \to a^3 = 10 \to a = \sqrt[3]{10} \cong 2,15 cms \]
Para asegurarnos de que dicho valor corresponde a un mínimo, utilizamos el criterio del signo de la derivada segunda. Calculamos entonces:
\[ S'' \ _T(a) = 4 - 40 (-2) a^{-3} \to S'' \ _T(a) = 4 + \frac{80}{a^3} \to \]
\[ \to S'' \ _T(a = \sqrt[3]{10} ) = 4 + \frac{80}{\sqrt[3]{10}^3} > 0 \]
Sabemos que si la derivada segunda en el punto crítico es positiva, la función presenta entonces un mínimo. Solo nos resta despejar el valor de la altura a partir de la expresión \( h = \frac{10cm^3}{a^2} \):
\[ h = \frac{10cm^3}{(\sqrt[3]{10cm})^2} \to h \cong 2,15 cms \]
Respondemos entonces que la caja de base de lado 2,15 centímetros y una altura de 2,15 centímetros será la de menor superficie total para una capacidad de 10 centímetros cúbicos (¡es decir, la caja resulta ser un cubo!).
El costo de alambrar un metro lineal de terreno es de $ 500. Para criar cerdos, un granjero decide cercar una superficie de 40.000 m2. ¿Cuáles deberán ser las dimensiones de un potrero rectangular de dicha superficie de modo tal que el costo para alambrarlo sea mínimo?
¿Cuáles deben ser las dimensiones de un rectángulo como el de la imagen 7.20, que tiene dos de sus lados sobre los semiejes cartesianos positivos y uno de sus vértices sobre la curva de ecuación y = 4 - x2, para que su área sea máxima?
Demostrar que el rectángulo inscripto dentro de una circunferencia de radio dado y superficie máxima es un cuadrado.
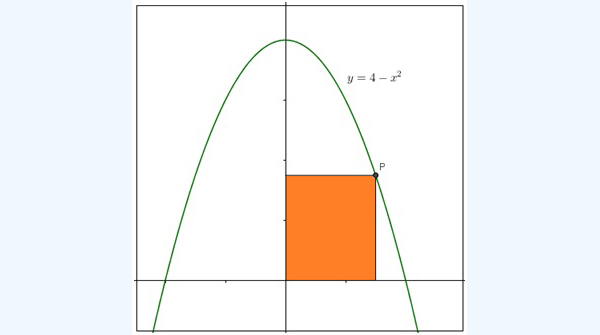
El rectángulo coloreado representa a uno de los que satisfacen las condiciones del enunciado: tiene dos de sus lados coincidentes con los semiejes cartesianos positivos y uno de sus vértices sobre la parábola.
Larson, R.; Hostetler, R.; Edwards, B.(2006), Cálculo con Geometría Analítica Volumen I, McGraw Hill Interamericana, México, pp. 218 a 222.
Zill, D. (1987), Cálculo con Geometría Analítica, Grupo editorial Iberoamérica, México, pp. 225 a 229.
7.7. Empleo del software para autocorrección
Aprender a derivar funciones aplicando reglas y tabla requiere de cierta práctica. Es una tarea mecánica y nos parece apropiado que el estudiante utilice el software disponible para verificar los resultados obtenidos durante la ejercitación. Es por esa razón que seguidamente le indicaremos cómo emplear el wxMaxima para dicho fin.
Calcular la derivada de f(x) = x5 . sin (x)
Resolución empleando software:
Para comenzar, seleccionamos en la parte superior de la pantalla “Análisis”. Aparece un Menú, dentro del que hemos de buscar la opción “Derivar”, como se observa en la imagen 7.21.
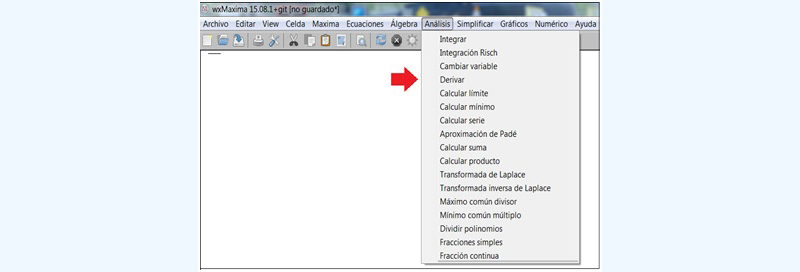
Dentro del Menú, comenzamos por buscar la opción “Derivar”.
Aparece luego una ventana, que nos permite ingresar a la función cuya derivada deseamos conocer (señalada en la imagen 7.22 con una flecha de color rojo).
Una vez que hacemos clic en “Aceptar”, el programa nos devuelve inmediatamente el resultado (imagen 7.23).
Dijimos que resulta conveniente expresar el resultado de un modo reducido, puesto que, en general, la derivada solo habrá de ser el primer paso en un cálculo más extenso. En este caso, entonces, volvemos al Menú y en “Simplificar” seleccionamos “Factorizar expresión”(imagen 7.24). Basta con hacer clic para obtener otra presentación del resultado (imagen 7.25).
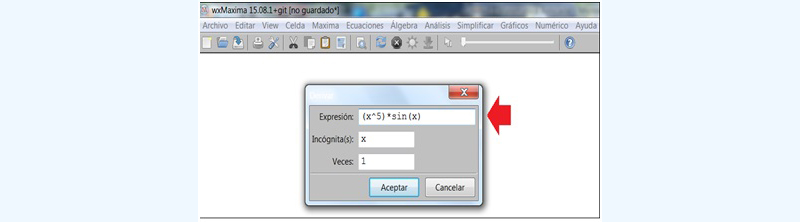
La flecha de color rojo señala el lugar dentro del cual hemos de ingresar a la función cuya derivada deseamos calcular.

Una vez que hacemos clic en “Aceptar”, el resultado aparece automáticamente en pantalla.
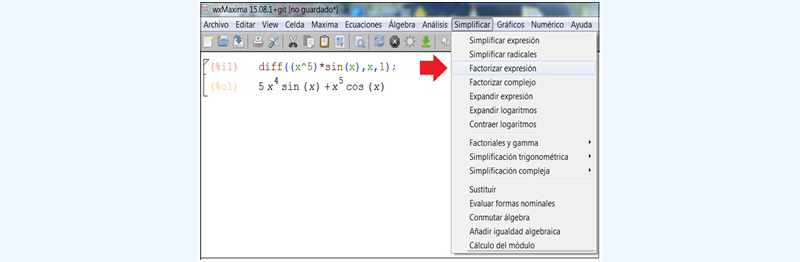
El propio Menú nos permite factorizar la expresión.
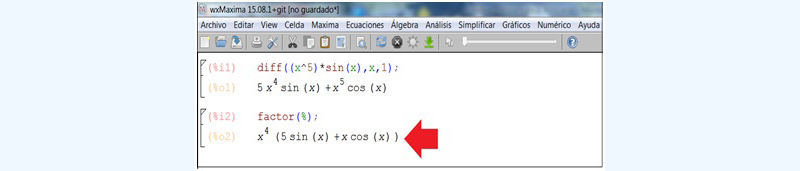
La flecha de color rojo indica el resultado de nuestra derivada, expresado de tal modo que nos facilite su aplicación a posteriores cálculos.
El siguiente ejemplo nos permitirá presentar algunas instrucciones útiles.
Calcular la derivada de \( f(x) = ln \left( \frac{x^2 + 1}{x^4 + 4} \right) \)
Resolución empleando software:
En lo que respecta al cálculo de la derivada, seguimos los pasos vistos en el ejemplo anterior, obteniendo así el resultado que se observa en la imagen 7.26. Obsérvese que el wxMaxima (como sucede con muchos otros programas) interpreta como log al logaritmo natural o neperiano.

El resultado que ofrece el programa puede sorprendernos cuando derivemos funciones compuestas.
Volvemos al menú y seleccionamos “Simplificar expresión” (imagen 7.27), obteniendo de inmediato el resultado que aparece señalado con una flecha de color rojo en la imagen 7.28.
Si volvemos a utilizar la instrucción “Factorizar expresión”, obtendremos como resultado final el que señalamos con una flecha roja en la imagen 7.29. Este, sin duda, resultará más cómodo para posteriores aplicaciones, como por ejemplo, obtención de extremos de la función original.
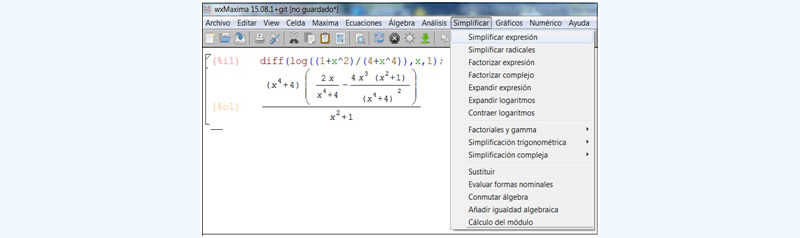
Volviendo al menú, tratamos de simplificar el resultado obtenido.
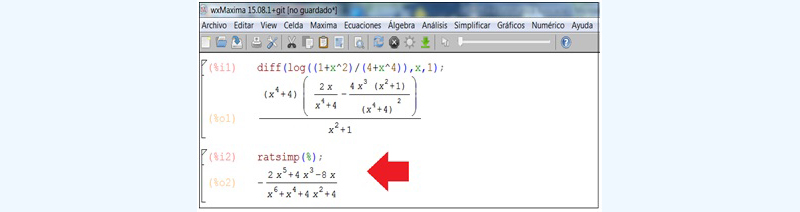
Evidentemente, la expresión que nos devuelve el programa resulta mucho más accesible que la que ofreció inicialmente.
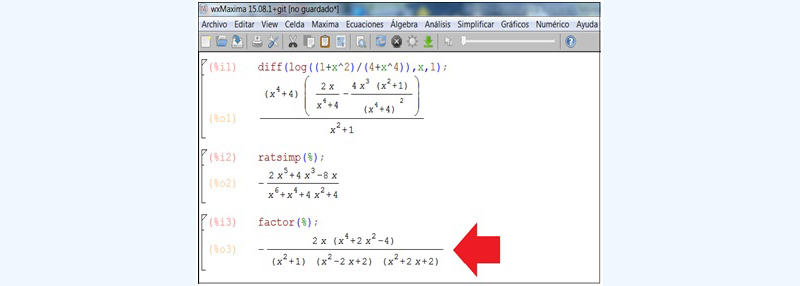
Volvemos a factorizar. Aun cuando a simple vista la última expresión parezca menos apropiada que la anterior, la experiencia nos indica que siempre es conveniente trabajar con el resultado descompuesto en producto de factores.
El software nos permitirá, además, verificar desarrollos de polinomios de Taylor, como veremos en el próximo ejemplo.
Obtener el polinomio de Taylor de grado cuatro de la función \( f(x) = \sqrt{x^2 + 5} \) en el entorno de \( x_0 = 2 \).
Resolución empleando el software: En este caso, debemos seleccionar “Calcular serie”, como se observa en la imagen 7.30.
Se abre una nueva ventana dentro de la cual hemos de ingresar la información pertinente al cálculo (imagen 7.31). Por empezar, donde dice "Expresión” tendremos que escribir la función. Debajo aparece otra ventana titulada "punto”, en la que tenemos que aclarar en el entorno de quien habrá de calcularse el desarrollo (en nuestro caso, \( x_0 = 2 \)). Finalmente, aparece otra ventana que lleva el título de "profundidad”. Allí debemos indicar el grado del polinomio buscado.
Una vez ingresados los datos, bastará con hacer clic sobre “Aceptar”, y el programa nos devolverá en pantalla el desarrollo pedido (imagen 7.32).
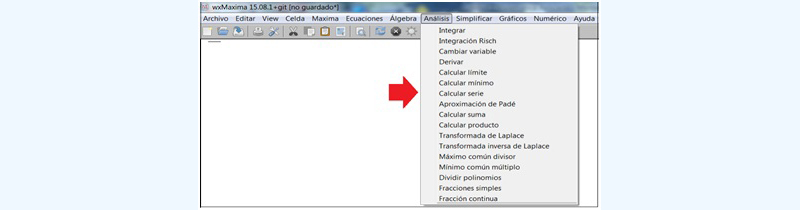
Volvemos al menú, pero seleccionamos “Calcular serie”.
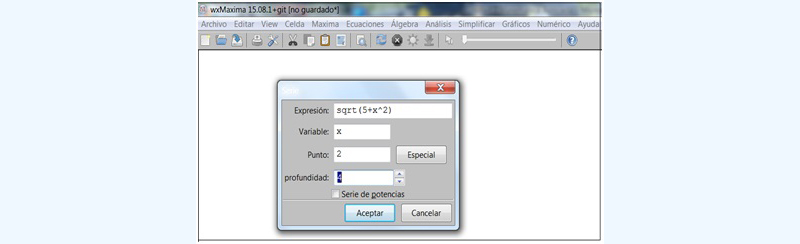
En la pequeña ventana debemos ingresar la función, la variable y el valor de la variable independiente alrededor del cual habremos de desarrollar al polinomio. El término profundidad debe ser interpretado como grado del polinomio buscado.

Los puntos suspensivos solo nos recuerdan que el desarrollo podría tener un número mayor de términos. De hecho, se habla de serie de Taylor (y no de polinomio) cuando se analizan los infinitos términos posibles de esta.

