1. Revisión de operaciones con números en el campo real
Objetivos
Que el alumno:
- Aprenda a diferenciar los distintos conjuntos numéricos.
- Recuerde las propiedades fundamentales de los números reales en general y de los números negativos en particular.
- Conozca las propiedades de las fracciones.
- Descubra la existencia de subconjuntos del campo real denominados intervalos y aprenda a reconocer las diferencias entre ellos, según si sus extremos están o no incluidos dentro del conjunto.
- Aprenda las propiedades del módulo de un número real.
- Recuerde las propiedades y leyes de la potenciación y la radicación.
1.1. Introducción
Los contenidos del presente MDM se corresponden, casi en su totalidad, con lo que tradicionalmente se conoce como Cálculo o Análisis Matemático en una variable independiente. Dicha variable se encontrará dentro del campo real, así como también el valor de su imagen o recorrido. Recién en la unidad 9, en oportunidad de resolver la ecuación diferencial que permite describir el movimiento oscilatorio armónico, nos veremos obligados a abandonar el conjunto de los números reales para asomarnos tímidamente al profundo campo de los números complejos.
Ahora bien: ¿a qué nos referimos al hablar de números reales? ¿Qué otros números existen? ¿Cuáles son esos otros números?
Sospechamos que en este momento el alumno no puede ofrecer una respuesta satisfactoria a las preguntas que acabamos de efectuar, en apariencia triviales. En la próxima sección, repasaremos rápidamente los distintos conjuntos numéricos, partiendo de los números naturales hasta llegar a los complejos.
1.2. Conjuntos numéricos: naturales, enteros, racionales, irracionales, reales y complejos
Nuestro primer contacto con los números llega a darse en muchos casos aun antes de que comencemos la escuela primaria. El niño se entusiasma contando una pequeña cantidad de caramelos u otros objetos de su interés, ayudándose muchas veces con los dedos de sus manos para conseguir su objetivo. Incluso es capaz de abstraer y agregar a los caramelos que tiene en la mano derecha los que lleva en la izquierda, descubriendo a su modo la primera de las operaciones elementales: la suma.
Esos primeros números pertenecen al conjunto de los naturales, que suelen expresarse con la letra ℕ. Podríamos escribir:
\[ \mathbb{N} = \{ 1,2,3,4,... \} \]
Aun cuando la notación no es del todo rigurosa desde el punto de vista de la Matemática (deberíamos interpretar que los puntos suspensivos nos indican los infinitos naturales que no estamos escribiendo explícitamente), nos permite, en todo caso, expresar al conjunto en cuestión.
En Álgebra se define como estructuras algebraicas a la combinación entre uno o dos conjuntos y una o dos operaciones que verifican una serie de propiedades. La más elemental de ellas recibe el nombre de grupo y está conformadapor un conjunto numérico y una operación que han de cumplir cuatro propiedades. La primera de ellas es la que nos interesa en este caso y recibe el nombre de ley de composición interna (LCI).
Dado un conjunto numérico A y una operación dada, llamémosla *, diremos que en (A,*) se cumple la ley de composición interna cuando:
\[ \forall a, b \in A \to a * b = c, con \ c \in A \]
(Lo anterior debe leerse como: “para todo par de elementos a y b pertenecientes al conjunto A, el resultado de aplicar la operación * entre ambos da como resultado un tercer número, c, que también pertenece al conjunto A”.)
Si, por ejemplo, el conjunto A fuese el de los números naturales y la operación * la suma,podríamos decir que “los naturales y la suma cumplen con la LCI, pues la suma de dos números naturales cualesquiera da como resultado otro número natural”.
Queremos dejar en claro que damos por sentado que lo que acabamos de decir es cierto, aun cuando no hemos demostrado que así sea. Lo hacemos porque sabemos que la proposición enunciada ha sido demostrada; lo que no podemos hacer es utilizar un ejemplo para demostrar que la proposición sea verdadera.
Una de las razones por las cuales la Matemática resulta ser la más exacta de las ciencias es que toda proposición (es decir, aseveración que habrá de tener un valor de verdad) debe ser demostrada en forma genérica. Es muy frecuente que el alumno crea que un ejemplo sirve para probar que algo es cierto, pero ese es un error conceptual gravísimo. Todo lo que podemos decir es que un contraejemplo nos sirve para probar que una proposición es falsa, como veremos en breve.
Insistimos en la idea de que, aun cuando los alcances de nuestro MDM no nos permiten demostrar que la suma de dos naturales cualesquiera dé siempre como resultado otro número natural, sabemos que se trata de una propiedad que ha sido demostrada.
Siguiendo con las operaciones elementales, podríamos preguntarnos qué sucede con la resta de naturales. Podríamos entonces plantear la siguiente proposición: “los naturales con la resta cumplen con la LCI”.
Dijimos anteriormente que se define como proposición a toda aseveración que posea valor de verdad, es decir, de la que se pueda decir que es verdadera o falsa.
También dijimos que para demostrar que una proposición es falsa basta con dar un contraejemplo, es decir, proponer un caso para el cual aquella no se verifique.
Llevando al lenguaje simbólico la proposición enunciada, escribimos:
\[ ( \mathbb{N},-) \text{ cumple con la LCI pues, } \forall a, b \in \mathbb{N}, a-b =c, \ con \ c \in \mathbb{N} \]
Tal proposición es falsa, lo que podemos demostrar con un simple contraejemplo:
\[ \text{Dados a } = 3, \ con \ a \in \mathbb{N}, \ y \ b = 8, con \ b \in \mathbb{N}, \ entonces: \]
\[ a - b = 3 - 8 = -5, \ con -5 \not\in \mathbb{N} \]
Basta entonces con haber presentado un ejemplo en el que no se cumple la proposición (de ahí lo de “contraejemplo”) para poder asegurar que la proposición es falsa.
Tratándose de una operación elemental, debemos encontrar un conjunto numérico dentro del cual la resta cumpla con la LCI. Definimos entonces al conjunto de los enteros, a los que expresamos mediante la letra \( \mathbb{Z} \). Escribimos entonces:
\[ \mathbb{Z} = \{ ..., -3,-2,-1,0,1,2,3,... \} \]
Es decir: este conjunto incluye tanto a números positivos como negativos; incluso, contiene un número muy especial, el cero.
Las particularidades del cero llevan a que muchos autores, antes de definir al conjunto de los enteros, definan al conjunto de los naturales con el cero, que puede expresarse de la siguiente manera:
\[ \mathbb{N}_0 = \{ 0,1,2,3,... \} \]
Siguiendo el curso de razonamiento propuesto anteriormente, resulta evidente que la proposición “los enteros con la división verifican la LCI” también es falsa. Si proponemos:
\[ \text{Dados a } = 3, \ con \ a \in \mathbb{Z}, \ y \ b = 8, con \ b \in \mathbb{Z}, \ entonces: \] \[ \frac{a}{b} = \frac{3}{8}, \ con \frac{3}{8} \not\in \mathbb{Z} \]
Nos vemos en la necesidad de definir otro conjunto más amplio, que incluya a los anteriores pero que, además, verifique con la división la LCI. Daremos el nombre de racionales a los números que conformen este nuevo conjunto y los indicaremos con el símbolo \( \mathbb{Q} \).
Escribimos entonces:
\[ \mathbb{Q} = \left\lbrace q = \frac{a}{b} , \ con \ a \in \mathbb{Z} \ y \ b \in \mathbb{Z} - \{0\} \right\rbrace \]
Es decir, se trata del conjunto de los números que se obtienen como resultado del cociente entre un número entero y otro número perteneciente al conjunto de los enteros menos el cero.
¡No olvidemos que no existe la división por cero!
Así, el conjunto de los racionales incluye a los naturales, al cero, a los enteros y a todos los números que puedan expresarse a partir de cocientes entre enteros, con la única condición de que el denominador sea distinto de cero. Como ejemplo de números racionales podemos pensar en el 4/8 (que podría expresarse también como 0,5) o en el 10/3, este último perteneciente al conjunto de los números periódicos.
Podríamos entonces decir que dentro del conjunto de los racionales encontramos:
(i) números que poseen una cantidad finita de números decimales y
(ii) números que contienen una cantidad infinita de decimales periódicos.
Es evidente que aún hay una gran cantidad de números que no estamos contemplando dentro de los racionales: aquellos que tienen una cantidad infinita de decimales no periódicos.
Dichos números, que no son racionales, se conocen con el nombre de irracionales.
En la imagen 1.1 utilizamos Diagramas de Venn para graficar de algún modo lo dicho hasta el momento. Obsérvese que los naturales están incluidos dentro de los enteros, mientras que estos, a su vez, están incluidos dentro del conjunto de los racionales. Los irracionales, en cambio, se representan aparte, dado que la intersección entre racionales e irracionales es vacía.
Además, cada número podría ubicarse sobre la denominada recta numérica. En la imagen 1.2 reproducimos una secuencia en la que vamos indicando las posiciones relativas de los puntos pertenecientes a cada uno de los conjuntos definidos hasta el momento. Aun cuando solo aparecen algunos números de cada uno de los conjuntos definidos, se hace evidente que, en definitiva, cada punto de la recta representará algún número, ya sea racional o irracional. Y, dado que toda recta contiene infinitos puntos, concluimos que existen infinitos números reales.
El razonamiento anterior nos permite inferir una característica muy interesante dentro del campo real. Recordemos que todo segmento es una porción de una recta limitado por dos puntos y que contiene infinitos puntos de esta. Entonces, entre dos números reales distintos (los extremos del segmento)habrá siempre infinitos números reales(en correspondencia con cada uno de los infinitos puntos interiores de dicho segmento).
Diremos entonces que:
\[ Racionales \ \cup \ Irracionales = Reales \]
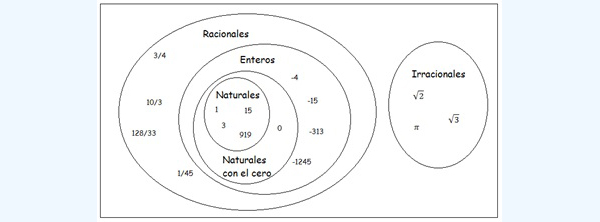
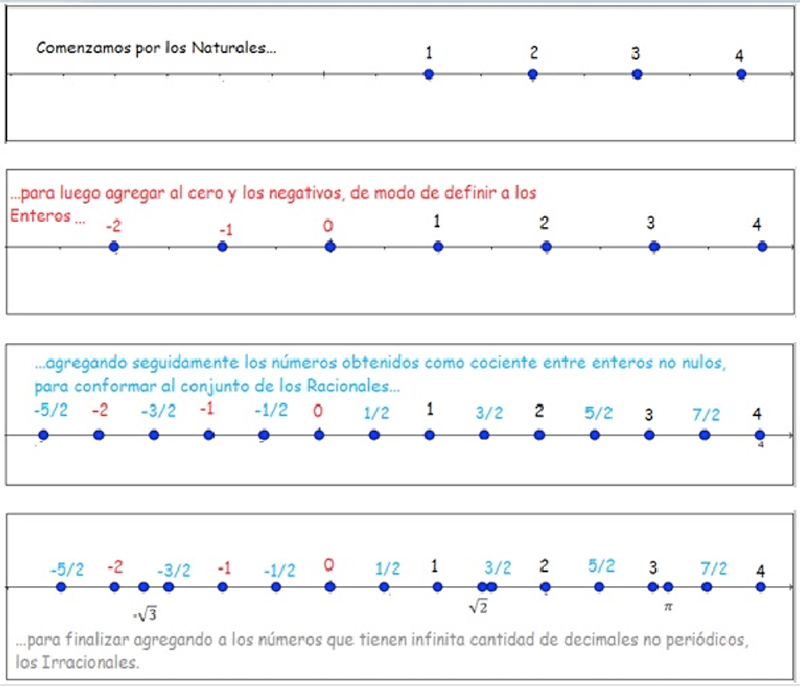
A medida que vamos ubicando a los elementos de los diversos conjuntos numéricos sobre la recta, observamos que cada uno de los puntos de esta representa uno de dichos elementos.
La unión entre todos los elementos de conjuntos de los racionales con todos los del conjunto de los irracionales da como resultado al conjunto de los números reales, que se representa con la letra \( \mathbb{R}\) y que podemos representar gráficamente mediante un diagrama de Venn como se observa en la imagen 1.3.
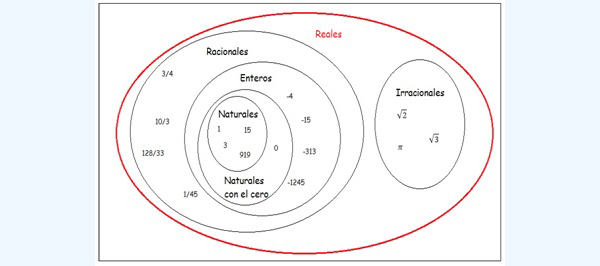
Tal como lo anticipamos al principio de la presente sección, será dentro del campo de los reales que habrá de desarrollarse prácticamente todo nuestro curso.
El alumno habrá observado que diversas limitaciones fueron obligándonos a definir conjuntos cada vez más amplios. En ese sentido, es muy probable que el estudiante haya escuchado muchísimas veces que “no existe la raíz cuadrada de números positivos”.
Lo que ignora es que tal proposición solo es verdadera… ¡en la medida que trabajemos en el campo real!
Creemos oportuno recordarle al estudiante la definición de raíz cuadrada para que pueda seguir mejor el razonamiento que haremos en breve:
La raíz cuadrada de un número \( a \) puede definirse en símbolos de la siguiente manera:
\[ \sqrt{a} = b \leftrightarrow b^2 = a, \ con \ b \ge 0 \]
Supongamos que necesitamos hallar las soluciones de la ecuación:
\[ x^2 + 4 = 0 \][1.1]
Efectuando un simple pasaje de términos, podríamos escribir:
\[ x^2 = -4 \]
Es decir, debemos hallar un número x que, elevado al cuadrado, de como resultado menos cuatro.
(¡Por no decir que necesitamos calcular la raíz cuadrada de menos cuatro!)
La [1.1] resulta ser una ecuacion en apariencia muy sencilla que, sin embargo, carece de solución en \( \mathbb{R} \). Durante siglos los matemáticos buscaron la forma de resolver ecuaciones como la que acabamos de plantear. Fue el suizo Leonhard Euler quien finalmente, encontró una forma de expresar la solución a dicho problema al definir un número, el número \( i \), que poseía una característica muy particular.
Se define como número imaginario \( i \) a aquel que, elevado al cuadrado, da como resultado menos uno.
En símbolos:
\[ i^2 = -1 \]
A partir de la definición de número imaginario, podemos responder que la [1.1] posee dos soluciones, \( 2i \) y \( -2i \), pues:
\[ (2i)^2 = 2^2i^2 = 4(-1) = -4 \]
y
\[ (-2i)^2 = (-2)^2i^2 = 4(-1) = -4 \]
¡Los números imaginarios nos permiten, entonces, calcular raíces cuadradas de números negativos!
Es conveniente que el alumno no se deje llevar por el lenguaje coloquial en el momento de internarse en el estudio de los números imaginarios. Dicha denominación trata exclusivamente de hacernos pensar en números totalmente distintos a los reales. Campos de la Física tan “reales” como el del electromagnetismo difícilmente podrían estudiarse en profundidad si careciésemos de los números imaginarios.
La existencia de los números imaginarios nos enfrenta a un dilema: ¿cómo podemos representarlos gráficamente?
Teniendo en cuenta que cada número real multiplicado por el número \( i \) se transforma en un número imaginario, y que cada número real puede representarse sobre una recta, bastará con trazar una segunda recta, perpendicular a la primera. Cada uno de los puntos de esta segunda recta representará, entonces, un número imaginario, tal como se observa en la imagen 1.4.
Se acostumbra, entonces, a representar sobre el eje horizontal a los números reales y en el vertical a los imaginarios. A pesar de que la imagen le resulte al alumno familiar, es importante que no olvide que los ejes cartesianos que está acostumbrado a manejar se corresponden con lo que denominamos \( \mathbb{R}^2 \), o plano real. En este caso, en cambio, insistimos que cada eje corresponde a un conjunto numérico diferente.
Ahora que sabemos a qué nos referimos al hablar de números imaginarios, estamos en condiciones de avanzar un paso más, llegando finalmente al conjunto de los números complejos:
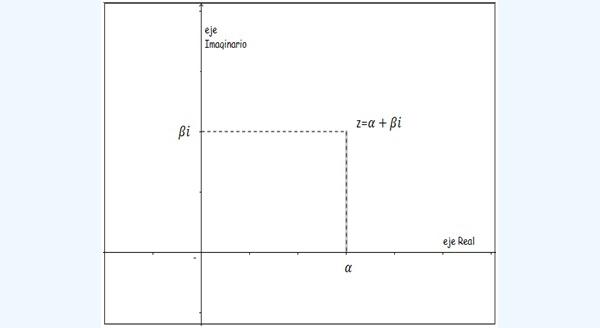
Definimos como número complejo a todo aquel que tenga la forma:
\[ z= \alpha + \beta i \]
donde \( \alpha \) recibe el nombre de parte real y \( \beta \) el de parte imaginaria de \( z \). Dicho número puede representarse gráficamente como se observa en la imagen 1.5.
Cabe aclarar que tanto \( \alpha \) como \( \beta \) son números reales.
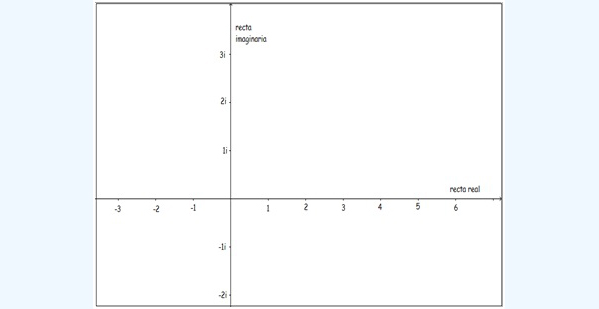
Los números imaginarios se ubican sobre un eje vertical, definiendo un plano…
Las operaciones y propiedades en \( \mathbb{C} \), el campo complejo, exceden ampliamente los alcances de la presente MDM. Sin embargo, opinamos que el estudiante no puede ignorar la existenciade ese conjunto numérico.
…y cada punto de dicho plano representará a un elemento de un conjunto numérico más amplio que el de los reales, el de los números complejos.
1.3. Propiedades de los números reales
La Matemática representa un poderoso lenguaje, que nos facilita generar modelos para interpretar la realidad que nos rodea. Resulta ser muy amplio y exige un firme conocimiento de ciertas reglas básicas. Es por esa razón que en las próximas secciones recordaremos un conjunto de propiedades que habremos de aplicar durante el resto del presente curso.
1.3.1. Propiedades de los reales
A continuación, enunciamos cinco propiedades fundamentales de los números reales.
Propiedad uno: conmutatividad de la suma
\( \forall a, b \in \mathbb{R} \) se verifica que \( a + b = b + a \)
Es decir: dados dos números reales cualesquiera, el resultado de la suma de ambos es independiente del orden en el que se los sume.
Propiedad dos: conmutatividad del producto
\( \forall a, b \in \mathbb{R} \) se verifica que \( a \cdot b = b \cdot a \)
Es decir, dados dos números reales cualesquiera, el resultado del producto de ambos es independiente del orden en el que se los multiplique.
Propiedad tres: asociativa de la suma
\( \forall a, b \ y \ c \in \mathbb{R} \) se verifica que \( (a + b) + c = a + (b+c) \)
Propiedad cuatro: asociatividad del producto
\( \forall a, b \ y \ c \in \mathbb{R} \) se verifica que \( (a \cdot b) \cdot c = a \cdot (b \cdot c) \)
Propiedad cinco: distributividad del producto respecto de la suma
\( \forall a, b \ y \ c \in \mathbb{R} \) se verifica que \( (i) a \cdot (b+ c) = a \cdot b + a \cdot c \)
\[ (ii) (b+c) \cdot a = b \cdot a + c \cdot a \]
Al hablar sobre los conjuntos numéricos, mencionamos las estructuras algebraicas y dijimos que la más elemental de todas ellas recibía el nombre de grupo.
Dados un conjunto A y una operación *, diremos que (A,*) es un grupo cuando cumpla las siguientes propiedades:
- \( \forall a, b \in A: a*b =b*a = c, \ con \ c \in A \) es decir, se verifique la LCI.
- \( \forall a, b, c \in A: a* (b*c) = (a*b) *c \), es decir, se cumpla la asociatividad.
- \( \forall a \in A \ \exists \ e \in A \text{ tal que } a * e = e * a = a \), donde \( e \) es único y recibe el nombre de elemento neutro de la operación*.
\( \forall a \in A \ \exists \ a^* \in A \text{ tal que } a * a^* = a^* * a = e \) es decir: para cada elemento del conjunto A, existe un elemento que recibe el nombre opuesto o inverso (según sea el caso), de modo tal que el resultado de la operación de como resultado al elemento neutro de la operación en el conjunto.
Si, además:
- \( \forall a, b \in A:a*b = b*a \), es decir, si se verifica la propiedad conmutativa, clasificaremos al grupo como abeliano.
Detengámonos un momento en \( (\mathbb{R}, +) \). Sabemos que la suma en reales verifica la LCI y la propiedad tres nos indica que, además, la suma resulta asociativa en \( \mathbb{R} \). Analicemos, entonces, la existencia del elemento neutro, para profundizar nuestro conocimiento sobre el conjunto de los números reales.
El número cero recibe el nombre de neutro de la adición, pues para todo número \( a \in \mathbb{R} \) se verifica que: \( a+0 = 0+a = a \)
Puesto que el cero pertenece al conjunto de los reales, entonces \( (\mathbb{R}, +) \) también posee elemento neutro y solo nos resta determinar si posee inverso aditivo para poder asegurar que posee la estructura de grupo.
En ese sentido, reescribamos la propiedad (iv) reemplazando al conjunto genérico A y a la operación * por \( \mathbb{R} \) y +, respectivamente:
\[ \forall a \in \mathbb{R} \ \exists \ a^* \in \mathbb{R} \text{ tal que } a + a^* = a^* + a = e = 0\]
Entonces, si \( a + a^* = 0 \to a^* = -a \), es decir, a cada número real \( a \) le corresponde otro número real \( -a \) tal que la suma de ambosdará como resultado cero, es decir, el elemento neutro de la suma.
Como la propiedad uno de los reales era la conmutatividad de la suma, podemos entonces asegurar que \( (\mathbb{R}, +) \) es un grupo abeliano.
El tema del inverso aditivo, al que también podemos denominar opuesto del número real a, resulta útilpara introducirnos en el estudio de los números negativos.
1.3.1. Propiedades de los reales
La experiencia nos indica que muchos estudiantes suelen pasar por alto algunas de las siguientes propiedades, en apariencia triviales, lo que les dificulta trabajar con gran número de desarrollos matemáticos. Por esa razón, le recomendamos al alumno que las tenga siempre presentes.
Primera propiedad: el producto de un número real \( a \) por menos uno es igual a su opuesto.
En símbolos: \( \forall a \in \mathbb{R}: (-1)a = -a \)
Segunda propiedad: el opuesto del opuesto de un número dado resulta ser el propio número.
En símbolos: \( \forall a \in \mathbb{R}: -(-a) = a \)
Tercera propiedad: \( \forall a, b \in \mathbb{R}: (-a)b = a(-b) = -(a\cdot b) \)
Cuarta propiedad: el producto de los opuestos de dos números reales \( a \ y \ b \) es igual al producto de \( \ a \text{ por } \ b \).
En símbolos: \( \forall a, b \in \mathbb{R}: (-a)(-b) = a \cdot b \)
Demostración: \( (-a)(-b) = (-1)a(-1)b = (-1)(-1)ab = ab \)
Quinta propiedad: el opuesto de la suma de dos reales cualesquiera es igual a la suma de sus opuestos.
En símbolos: \( \forall a, b \in \mathbb{R}: -(a+b) = - a - b \)
Demostración: \( -(a+b) = (-1)(a+b) = (-1)a + (-1)b =\)
\( = (-a) + (-b) = -a-b \)
Sexta propiedad: \( \forall a, b \in \mathbb{R}: -(a-b)= b-a \)
Demostración: \( -(a-b) = (-1)(a-b)= (-1)a - (-1)b = \)
\( = -a - (-b) = -a+b \)
Observar detenidamente las demostraciones de las propiedades de los negativos, señalando en cada caso cuáles de las propiedades de los números reales detalladas en la sección anterior se aplican en cada caso.
Al finalizar la sección anterior determinamos que los reales con la suma cumplían con todas las condiciones para ser un grupo abeliano. Ello nos introdujo en la discusión de las propiedades de los números negativos, a partir de la definición del inverso aditivo.
Comenzaremos la siguiente sección analizando si los reales con el producto también cumplen las condiciones para ser grupo abeliano. Así presentaremos las propiedades de las fracciones.
1.3.3. Operaciones con fracciones
Volviendo al tema de las estructuras algebraicas, los reales con el producto cumplen con las dos primeras condiciones para ser grupo: el producto de reales es LCI y, de acuerdo con la propiedad cuatro de los números reales, se verifica la asociatividad del producto.
En lo que respecta a la existencia del elemento neutro del producto, tengamos en cuenta que:
\[ \forall a \in \mathbb{R}:a \cdot 1 = 1 \cdot a = a \]
Es decir, el número uno resulta ser el elemento neutro para la multiplicación de los reales.
Para que \( (\mathbb{R},.) \) sea grupo, debe cumplirse aún una propiedad más: la existencia de inverso para todo número real.
En símbolos:
\[ \forall a \in \mathbb{R} \ \exists \ a^* \in \mathbb{R} \text{ tal que: } a \cdot a^* = a^* \cdot a = 1 \]
No resulta difícil determinar entonces que:
\[ a \cdot a^* = 1 \to a^* = \frac{1}{a} \]
Observamos que todo número real, exceptuando al cero, admite inverso multiplicativo. Pero basta con que un solo número real carezca de inverso para que podamos decir que la cuarta condición para la definición de grupo no se cumple en \( \mathbb{R} \).
La discusión de las restricciones al conjunto de los reales nos llevaría al estudio de estructuras algebraicas más complejas, que no son objeto de nuestro MDM, pero creemos que la definición del inverso multiplicativo (definido para todo número real no nulo) resulta oportuna para introducir las operaciones de las fracciones.
Producto de dos fracciones
\[ \forall \frac{a}{b}, \frac{c}{d}, \ con \ a \ y \ c \in \mathbb{R}, \ y \ b \ y \ d \in \mathbb{R} - \{ 0 \}, \frac{a}{b} \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \]
Cociente de dos fracciones
\[ \forall \frac{a}{b}, \frac{c}{d}, \ con \ a \in \mathbb{R}, \ y \ b, \ c \ y \ d \in \mathbb{R} - \{ 0 \}, \frac{a}{b} \div \frac{c}{d} = \frac{a \cdot d}{b \cdot c} \]
Suma o resta de fracciones con igual denominador
\[ \forall a, \ b, \ c, \ con \ a \ y \ b \in \mathbb{R} \ y \ c \in \mathbb{R} - \{ 0 \}, \frac{a}{c} \pm \frac{b}{c} = \frac{a \pm b}{c} \]
Suma o resta de fracciones con distinto denominador
\[ \forall a, \ b, \ c, \ d, \ con \ a \ y \ b \in \mathbb{R} \ y \ c \ y \ d \in \mathbb{R} - \{ 0 \}, \frac{a}{c} \pm \frac{b}{d} = \frac{a \cdot d \pm b \cdot c}{c \cdot d} \]
Demostrar la expresión para la suma o resta de fracciones con distinto denominador a partir de las restantes operaciones.
En la presente sección, el hecho de que la división por cero no esté definida nos llevó a restringir para ciertas aplicaciones el conjunto de los reales. A medida que avancemos, nos encontraremos con casos en que dichas restricciones pueden ser aún más estrictas, obligándonos a trabajar con conjuntos aún más reducidos.
Como veremos en la próxima sección, ello nos llevará a trabajar con conjuntos que geométricamente se podrán representar como segmentos sobre la recta real, que reciben el nombre de intervalos.
1.4. Intervalos
Recordemos que todo conjunto puede expresarse de dos formas distintas, por extensión y por comprensión. Tomemos, por ejemplo, al siguiente conjunto:
A = {1, 2, 3, 4, 5}
El conjunto queda explícitamente definido; dentro de las llaves aparecen todos y cada uno de los elementos que lo componen. Decimos entonces que dicho conjunto está expresado por extensión.
Sin embargo, dicho conjunto también podría escribirse de la siguiente manera:
\[ A = \{ x \in \mathbb{N} \text{ tales que } 1 \leq x \leq 5 \} \]
En este caso, solo dos de sus cinco elementos aparecen dentro de las llaves, pero la información que se nos brinda nos permite inferir exactamente cuáles son todos los elementos contenidos en dicho conjunto. Decimos entonces que el conjunto ha sido ahora expresado por comprensión.
Ahora bien, supongamos que tenemos al conjunto
\[ B = \{ x \in \mathbb{R} \text{ tales que } 1 \leq x \leq 5 \} \]
La diferencia a los conjuntos A y B no es en absoluto trivial. El primero de ellos cuenta con solo cinco elementos, por estar definido dentro del campo de los naturales. El conjunto B, en cambio, contiene infinitos elementos, por estar definido dentro del campo real.
El hecho de que nos hayamos detenido al principio de la presente unidad en el tema de los conjuntos numéricos está perfectamente justificado en la presente situación. El estudiante debe prestar mucha atención a la información que se le brinde en cada caso, a riesgo de cometer graves errores conceptuales que lo lleven a resultados incorrectos.
Resulta imposible escribir al conjunto B por extensión. Sin embargo, existe una notación muy extendida al trabajar en el campo real, el empleo de intervalos. Si escribimos 1,5, debemos interpretar:
\[ [1,5] = \{ x \in \mathbb{R} \text{ tales que } 1 \leq x \leq 5 \} \]
¡Que no era otra cosa que el conjunto B!
En este caso, tanto el extremo inferior como el superior del intervalo están incluidos en el intervalo, razón por la cual el intervalo se expresa entre corchetes. Cuando uno o ambos extremos no pertenezca al intervalo, el corchete deberá ser reemplazado por un paréntesis. Así:
\[ (1,5] = \{ x \in \mathbb{R} \text{ tales que } 1 < x \leq 5 \} \]
O:
\[ [1,5) = \{ x \in \mathbb{R} \text{ tales que } 1 \leq x < 5 \} \]
En muchos casos el intervalo solo está acotado superior o inferiormente; por ejemplo:
\[ [1, \infty ) = \{ x \in \mathbb{R} \text{ tales que } 1 \leq x \} \]
Cuando el infinito (o el menos infinito) se presentan como extremos superior (o inferior) del intervalo, debe colocarse el paréntesis en lugar del corchete.
Dados \(a \ y \ b \in \mathbb{R} \text{, con } a < b \), podemos interpretar cada uno de los intervalos como se indica en cada caso:
- \( (a, b) = \{ x \in \mathbb{R} \ / \ a < x < b \} \)
- \( [a, b] = \{ x \in \mathbb{R} \ / \ a \leq x \leq b \} \)
- \( [a, b) = \{ x \in \mathbb{R} \ / \ a \leq x < b \} \)
- \( (a, b] = \{ x \in \mathbb{R} \ / \ a < x \leq b \} \)
- \( [a, \infty ) = \{ x \in \mathbb{R} \ / \ a \leq x \} \)
- \( (a, \infty ) = \{ x \in \mathbb{R} \ / \ a < x \} \)
- \( ( - \infty , b ) = \{ x \in \mathbb{R} \ / \ x < b \} \)
- \( ( - \infty , b ] = \{ x \in \mathbb{R} \ / \ x \leq b \} \)
Proponemos las siguientes actividades para que el alumno practique todo lo expresado en la presente sección:
Escribir como intervalo cada uno de los conjuntos indicados a continuación:
- \( A = \{ x \in \mathbb{R} \ / \ 3 < x \leq 8 \} \)
- \( B = \{ x \in \mathbb{R} \ / \ x \leq 8 \} \)
- \( C = \{ x \in \mathbb{R} \ / \ 3 \leq x \} \)
- \( D = \{ x \in \mathbb{R} \ / \ 3 \leq x \leq 8 \} \)
Expresar por comprensión cada uno de los siguientes intervalos:
- \( [ 2, 5) \)
- \( ( 3, 9) \)
- \( ( 5, \infty ) \)
- \( [ 5, \infty ) \)
- \( ( - \infty , \infty) \)
1.5. Valor absoluto
Desde el punto de vista geométrico, podemos decir que el valor absoluto de un número real \( a \) es igual a la distancia (medida sobre la recta numérica) desde el número hasta el origen de coordenadas. Independientemente del signo que tenga \( a \), el valor absoluto deberá siempre ser positivo(¡una distancia nunca puede ser negativa!).
Con mayor rigor matemático, podemos definir al valor absoluto como:
\[ |a| = \begin{equation} \left\lbrace \begin{array}{ll} a, \ si \ a \geq 0 \\ -a, \ si \ a < 0 \end{array} \right. \end{equation} \]
Partiendo de dicha definición, pueden demostrarse las siguientes propiedades:
Primera propiedad del valor absoluto: el valor absoluto de un número y de su opuesto es el mismo.
En símbolos: \( \ |a| = |-a| \)
Segunda propiedad del valor absoluto: el valor absoluto del producto entre dos números reales es igual al producto de sus respectivos valores absolutos.
En símbolos: \( \ |a \cdot b| = |a||b| \)
Tercera propiedad del valor absoluto: el valor absoluto del cociente entre un real cualquiera y otro distinto de cero es igual al cociente entre sus valores absolutos.
En símbolos: \( \left| \frac{a}{b} \right| = \frac {|a|}{|b|} \) siempre que \( a \in \mathbb{R} \) y \( b \in \mathbb{R} - \{ 0 \} \)
Cuarta propiedad del valor absoluto: calcular el valor absoluto de un número real a previamente elevado a una potencia n es igual a elevar a la potencia n el valor absoluto del número real a.
En símbolos: \( \ |a^n| = |a|^n \)
En oportunidad de repasar los conceptos de potenciación y radicación volveremos sobre el tema del valor absoluto o módulo de un número real.
1.6. Potenciación
Recordemos que, más allá de las cuatro operaciones elementales (suma, resta, multiplicación y división) existen muchas otras que debemos dominar. Una de ellas es, justamente, la potenciación.
Dados un número real \( a \) y un número entero positivo \( n \) definiremos como potencia enésima de \( a \) al producto de \( a \) or sí mismo \( n \) veces.
En símbolos:
\[ a^n = \underbrace{a \cdot a \cdot a \ldots a}_{{n \ veces}} \]
Recordemos que al número \( a \) se lo denomina base, mientras que \( n \) recibe el nombre de exponente.
En la siguiente sección enunciaremos las propiedades más frecuentemente aplicadas de la potenciación. Recomendamos al alumno que les preste mucha atención, dado que habrán de ser aplicadas a lo largo de todo el presente MDM.
1.6.1. Propiedades y leyes de la potenciación
Comencemos por dos propiedades de frecuente aplicación:
Primera propiedad:
Si \( a \in \mathbb{R} - \{ 0 \} \), entonces: \( a^0 = 1 \)
Segunda propiedad:
Si \( a \in \mathbb{R} - \{ 0 \} \) y \( n \) es un entero positivo, entonces: \( a^{-n} = \frac{1}{a^n} \)
A continuación, enunciamos las leyes de la potenciación:
Primera ley: el producto de dos potencias de igual base es igual a la base elevada a la suma de las dos potencias.
En símbolos: \( a^m a^n = a^{m+n} \)
Segunda ley: el cociente entre dos potencias de igual base es igual a la base elevada a la potencia del numerador menos la potencia del denominador.
En símbolos: \( \frac{a^m}{a^n} = a^{m-n} \)
Tercera ley: el resultado de elevar an a una potencia m es igual al número a elevado al producto de m por n . Esta propiedad se conoce con el nombre de potencia de potencia.
En símbolos: \( (a^n)^m = a ^{n \cdot m} \)
Cuarta ley: la potenciación es distributiva respecto del producto.
En símbolos: \( (a \cdot b)^n = a^n b^n \)
Quinta ley: la potenciaciónes distributiva respecto del cociente.
En símbolos: \( \left( \frac{a}{b} \right)^n = \frac{a^n}{b^n} \)
Sexta ley: si una fracción es elevada a una potencia negativa, se invierte la fracción y se eleva a la misma potencia, pero cambiada de signo.
En símbolos: \( \left( \frac{a}{b} \right) ^{-n} = \left( \frac{b}{a} \right)^n \)
La potenciación resulta muy útil en aplicaciones científicas y técnicas, cuando tenemos que trabajar con números muy grandes o muy pequeños. Se aplica en esos casos la denominada notación científica.
1.6.2. Notación científica
La velocidad de la luz en el vacío es de trescientos mil kilómetros sobre segundo y puesto que las distancias en el Sistema Internacional de unidades (SI) se miden generalmente en metros, deberíamos decir, entonces, que aquella asciende a trescientos millones de metros en un segundo. Es decir, estamos hablando de un tres seguido por ocho ceros.
Por supuesto, mucho peor resulta expresar al Número de Avogadro, que expresa el número de partículas por mol, y debería escribirse como 6022… ¡seguido de veinte ceros!
En esos casos, aplicamos la notación científica, consistente en multiplicar la parte entera (o conteniendo un pequeño número de decimales) por diez elevado a la cantidad de ceros que sean necesarios. Por ejemplo, el Número de Avogadro que acabamos de mencionar se expresará como 6, 022 · 1023 partículas/mol.
Algo similar sucede cuando nos referimos a valores muy pequeños, como la masa de un electrón en reposo. Para expresarla en kilogramos, deberíamos escribir un cero, seguido de una coma…seguida de otros treinta ceros antes de que aparezca el primer número distinto de cero (en este caso, un nueve). Expresaremos entonces, 9,1086 · 10-31kg.
Ofrecemos a continuación algunos ejemplos de aplicación usuales en otras asignaturas:
- Masa del protón en reposo: 1,672 · 10-27kg
- Constante Universal de gravitación: \( 6,67 \cdot 10^{-11 \ N \cdot m^2 / kg^2} \)
- Masa de la Tierra: 5,9722 · 1024kg
1.7. Definición de la raíz enésima
En el presente MDM resolveremos distintos tipos de ecuaciones. Recordemos que una ecuación puede definirse como una igualdad que presenta (al menos) una incógnita.
Un ejemplo sencillo sería el siguiente:
x3 = 8
Es decir, buscamos un número x tal que, elevado al cubo, nos dé como resultado ocho.
El presente problema es muy sencillo, pues mentalmente podemos responder que x = 2, pues dos elevado al cubo es igual a ocho.
Pero, ¿qué herramienta nos permite resolver este y otros problemas similares de mayor complejidad?
Dados un número \( a \) y un número entero positivo \( n \), definiremos como raíz enésima de \( a \) (expresándola como \( \sqrt[n]{a} \)) a un número \( b \), tal que se verifique la siguiente condición:
\[ \sqrt[n]{a} = b \leftrightarrow b^n = a \]
Podemos entonces escribir:
\[ \sqrt[3]{8} = 2 \leftrightarrow 2^3 = 8 \]
Seguidamente, presentamos algunas de las propiedades de la radicación más empleadas.
1.7.1. Leyes de las raíces enésimas
Primera ley: para dos números \( a \) y \( b \) mayores o iguales a cero, se verifica la distributividad de la raíz enésima respecto del producto, tanto para \( n \) par como impar.
En símbolos: \( \forall a, b \in \mathbb{R} \geq 0 ; \sqrt[n]{a \cdot b} = \sqrt[n]{a} \sqrt[n]{b} \)
¿Por qué razón insistimos en que y deben ser mayores o iguales a cero?
Segunda ley: para dos números \( a \) y \( b \) cualesquiera, se verifica la distributividad de la raíz enésima respecto del producto para \( n \) impar.
En símbolos: \( \forall a, b, \sqrt[n]{a \cdot b} = \sqrt[n]{a} \sqrt[n]{b}, \text{ con n }= 2k + 1, \forall k \in \mathbb{Z} \)
Tercera ley: para dos números \( a \) y \( b \) mayores a cero, se verifica la distributividad de la raíz enésima respecto del cociente, tanto para \( n \) par como impar.
En símbolos: \( \forall a, b \in \mathbb{R} > 0, \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} \)
Cuarta ley: para dos números \( a \) y \( b \), con \( b \not= 0 \), se verifica la distributividad de la raíz enésima respecto del cociente para \( n \) impar.
En símbolos: \( \forall a, b, con \ b \not= 0, \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}, con \ n = 2k + 1, \forall k \in \mathbb{Z} \)
Quinta ley: para cualquier número \( a \) se verifica que \( \sqrt[n]{a^n} = a \), siempre y cuando \( n \) sea impar.
Sexta ley: para cualquier número \( a \) se verifica que \( \sqrt[n]{a^n} = |a| \), siempre y cuando \( n \) sea par.
Como el alumno habrá observado, puesto que estamos trabajando dentro del campo real, tenemos que cuidarnos de no escribir raíces pares de números negativos. En ese sentido, las últimas dos leyes son particularmente significativas, dada su aplicación en la resolución de ecuaciones.
Si, por ejemplo, se nos pide calcular \( \sqrt[3]{(-2)^3} \), lo primero que debemos hacer es elevar al menos dos al cubo, de modo de obtener \( \sqrt[3]{-8} \).
Finalmente, puesto que las raíces impares de números negativos tienen solución en los reales, concluimos que \( \sqrt[3]{-8} = -2 \). Es decir:
\[ \sqrt[3]{(-2)^3} = \sqrt[3]{-8} = -2 \to \sqrt[3]{(-2)^3} = -2 \]
En cambio, al resolver \( \sqrt[4]{(-2)^4} \), el valor negativo desaparece en cuanto elevamos menos dos a la cuarta, quedándonos \( \sqrt[4]{16} \).
El resultado será entonces un número positivo, es decir:
\[ \sqrt[4]{(-2)^4} = \sqrt[4]{16} = 2 \to \sqrt[4]{(-2)^4} = |-2| \]
Así, cuando por ejemplo nos pidan resolver la ecuación x2 - 9 = 0, podemos hacer lo siguiente:
\[ x^2 - 9 = 0 \to x^2 = 9 \to \sqrt{x^2} = \sqrt{9} \to |x| = 3 \to \begin{equation} \left\lbrace \begin{array}{ll} x = 3 \\ x = -3 \end{array} \right. \end{equation} \]
En el segundo paso calculamos la raíz cuadrada de ambos miembros, manteniéndose la igualdad. La presencia de módulo nos obliga a adoptar no una sino dos soluciones (la positiva y la negativa), lo que era esperable: la ecuación de segundo grado propuesta presenta dos soluciones.
En la siguiente sección, la última de la presente unidad, veremos una aplicación interesante de la radicación.
1.7.2. Racionalización de denominadores
Muchos resultados exactos presentan números irracionales y es costumbre el hecho de eliminar las raíces cuando estas se presentan en el denominador.
Para ello se suele emplear un procedimiento que recibe el nombre de racionalización, basado en la existencia del elemento neutro del producto —el número uno— y en el hecho que, como veremos a continuación, la unidad puede expresarse de infinitas formas distintas.
Racionalizar
\[ \frac{2}{\sqrt{3}} \]
Resolución:
Bastará con multiplicar y dividir a la expresión por \( \frac{2}{\sqrt{3}} = \frac{2}{\sqrt{3}} \frac{\sqrt{3}}{\sqrt{3}} = \frac{2 \sqrt{3}}{(\sqrt{3})^2} = \frac{2 \sqrt{3}}{3} \)
\[ \ \]
Como vemos, la clave fue multiplicar a la expresión original por uno… ¡expresado como \( \frac{\sqrt{3}}{\sqrt{3}} \)!
En algunos casos debemos combinar el mecanismo anterior con algún otro artificio, como veremos a continuación:
Racionalizar
\[ \frac{3}{2 - \sqrt{5}} \]
Resolución:
Cuando en el denominador la raíz aparezca acompañada por otro término, procederemos a multiplicar y dividir la expresión original por lo que denominaremos el conjugado del denominador:
\[ \frac{3}{2 - \sqrt{5}} = \frac{3}{ (2 - \sqrt{3})} \frac{(2 + \sqrt{3})}{ (2 + \sqrt{3})} \]
Obsérvese que dimos el nombre de conjugado a la expresión que se obtuvo al cambiar el signo del segundo término del denominador. Cuando apliquemos la propiedad distributiva en el denominador, nos encontraremos ante una diferencia de cuadrados, que hará desaparecer la raíz cuadrada del denominador:
\[ \frac{3}{2 - \sqrt{3}} \frac{(2 + \sqrt{3})}{ (2 + \sqrt{3})} = \frac{3 (2 + \sqrt{3})}{4 + 2 \sqrt{3} - 2 \sqrt{3} + (\sqrt{3})^2} = \]
\[ \frac{3 (2 + \sqrt{3})}{4 + (\sqrt{3})^2} = \frac{3 (2 + \sqrt{3})}{7} \]
En esta oportunidad, el neutro del producto se presentó en la forma del cociente \( \frac{(2+ \sqrt{3})}{(2 + \sqrt{3})} \).
Aconsejamos al alumno tener muy en cuenta todas las propiedades y leyes que se presentaron en la presente unidad. Como lo anticipamos, habrán de ser aplicadas a lo largo de todo el MDM.
Racionalizar:
- \( \frac{3}{\sqrt{6}} \)
- \( \frac{3 - \sqrt{2}}{\sqrt{3}} \)
- \( \frac{\sqrt{3}}{3 - \sqrt{2}} \)
- \( \frac{\sqrt{3}}{3 + \sqrt{2}} \)

