4. Ecuaciones lineales y sistemas de ecuaciones lineales
Objetivos
Que el alumno:
- Descubra que una ecuación es mucho más que un simple algoritmo: es una herramienta fundamental para la resolución de problemas del mundo real.
- Aprenda a interpretar el enunciado de una situación problemática y lo convierta en una expresión matemática que habrá de permitirle llegar a la solución.
- Conozca nuevas herramientas, como las matrices y los determinantes, y aprenda a utilizarlos para la resolución de sistemas de ecuaciones en los que la cantidad de incógnitas dificulte su resolución en forma manual.
- Aprenda a utilizar el software disponible para facilitar su proceso de aprendizaje a partir de la autocorrección, así como también para potenciar los conocimientos adquiridos en la unidad para la resolución de sistemas que tengan más de dos incógnitas.
4.1. Definición de ecuación
En principio, podríamos decir que una ecuación está conformada por dos expresiones matemáticas cuyo valor numérico resulta ser el mismo. Por ejemplo:
2 + 2 = 4
u
\[ \frac{8}{2} + 1 = 3 + 2 \]
En ambos casos, más allá de la validez de las expresiones, lo único que estamos haciendo es expresar una simple identidad algebraica.
Algunas ecuaciones contienen números y letras. Estas últimas representan, en realidad, otros números cuyo valor no está explicitado, pero que habrán de cumplir con la igualdad y reciben el nombre de variables. Por ejemplo:
(x + 1)2 = x2 + 2 · x + 1
Cualquiera sea el valor de la variable, la igualdad habrá de verificarse.
Cuando la igualdad se verifica para todo valor de la variable, diremos que nos encontramos ante una identidad.
Sin embargo, a los fines prácticos, nos interesaremos particularmente por expresiones como
5 · x - 3 = 12
Esta ecuación solamente habrá de ser verdadera para un valor de la variable \( x \). Dicho valor recibe el nombre de raíz o solución de la ecuación. Como veremos a continuación, la resolución de ecuaciones habrá de sernos muy útil cuando las apliquemos a problemas concretos.
4.1.1. La ecuación lineal como representación de un problema del mundo físico
Supongamos que un automóvil circula con una velocidad constante de veinte metros sobre segundo por una avenida. En un instante dado, pasa frente a un primer semáforo, tal como lo muestra la imagen 4.1. Cinco segundos después, el automóvil pasa frente a un segundo semáforo, tal como se observa en la misma imagen.
¿Qué distancia separa a ambos semáforos?
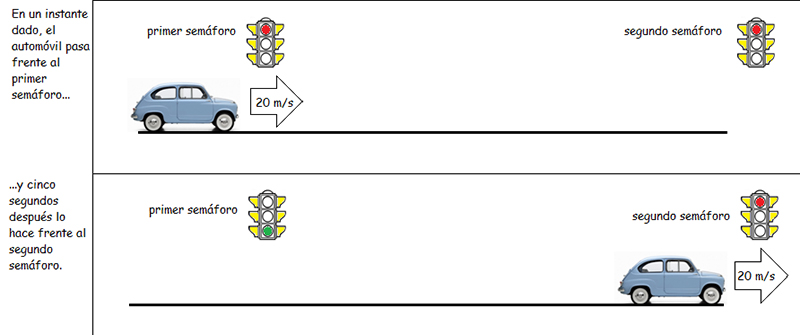
El problema nos pide calcular una distancia, conociendo el tiempo durante el cual se desplaza el vehículo y su velocidad. Aun cuando se trata de magnitudes que se estudian en Física, opinamos que la experiencia diaria del lector le facilitará la interpretación matemática de la situación.
El propio enunciado nos dice que la velocidad a la que se mueve el automóvil es de veinte metros sobre segundo; es decir, nos habla de la distancia que recorre dicho móvil en un tiempo determinado. Desde el punto de vista matemático, podemos escribir la siguiente identidad:
\[ velocidad = \frac{\text{distancia recorrida}}{\text{ tiempo empleado}} \]
Si en dicha identidad reemplazamos las magnitudes correspondientes por los datos que nos brinda el enunciado, podremos escribir:
\[ 20 m/seg = \frac{x}{5 seg} \]
He aquí una ecuación en la cual la incógnita , distancia recorrida, resulta ser igual a la distancia entre ambos semáforos (es decir, la incógnita de nuestro problema).
Como el tiempo aparece medido en segundos y la velocidad en metros sobre segundo, no necesitamos escribir las unidades, por lo que expresamos directamente:
\[ 20 = \frac{x}{5} \]
Cabe aclarar que:
- En Física siempre se dejan expresadas las unidades.
- Si, por ejemplo, la velocidad hubiese estado en kilómetros sobre hora y el tiempo en segundos, deberíamos haber pasado previamente la velocidad a metros sobre segundo (o el tiempo a horas; esto último no resulta conveniente para un caso como el que estamos planteando, como se verá al cursar Cinemática).
Para despejar la incógnita, debemos tener en cuenta lo siguiente:
Al multiplicar a ambos miembros de una igualdad por un número distinto de cero, dicha igualdad se mantiene.
En símbolos:
\[ Si \ A = B \text{, entonces } C . A = C . B \ con \ C \neq 0 \]
Entonces, si
\[ 20 = \frac{x}{5} \]
bastará con multiplicar ambos miembros por cinco y simplificar para despejar nuestra incógnita:
\[ 20 = \frac{x}{5} \to 5.20 = 5. \frac{x}{5} \to x = 100 \]
Recordando que las distancias debían medirse en metros, responderemos entonces que la distancia entre ambos semáforos es de cien metros.
Supongamos ahora que, en un momento dado, un automóvil viaja con una velocidad constante de treinta metros sobre segundo por el carril rápido de una autopista. Por el carril que se encuentra a la derecha de este automóvil, pero x metros por delante de él, viaja un segundo automóvil, a una velocidad constante de veinte metros sobre segundo. La situación aparece representada en la imagen 4.2.
El tramo de autopista es recto y, diez segundos después, el primero de los automóviles alcanza al segundo. Vamos a calcular a qué distancia se encontraban inicialmente ambos automóviles, incógnita a la que expresaremos con la letra x.
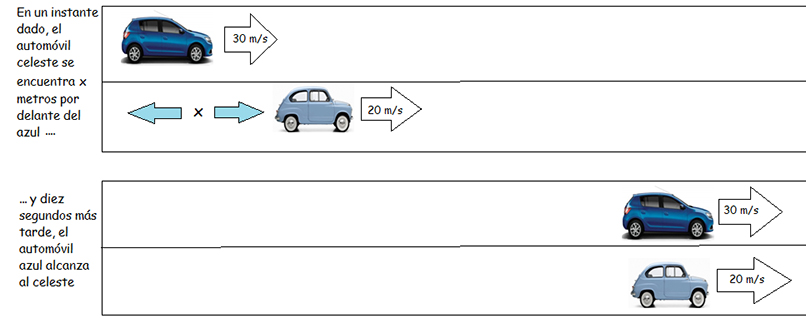
La ecuación que refleja la situación planteada es la siguiente:
\[ 30 \frac{m}{s}. 10s = x + 20 \frac{m}{s}. 10s \]
El miembro de la izquierda corresponde a la distancia recorrida durante los diez segundos que indica el enunciado, que es igual a la que recorrió el segundo móvil incrementada en x metros (que es lo que escribimos en el miembro de la derecha).
Si dejamos de lado las unidades y efectuamos los productos indicados, obtenemos la siguiente ecuación:
300 = x + 200
Para despejar la incógnita debemos tener en cuenta lo siguiente:
Al sumar (o restar) un mismo número a ambos lados de una igualdad, la ecuación que se obtiene es equivalente a la original, es decir, tiene la misma solución que esta.
En símbolos:
\[ A = B \leftrightarrow A + C = B + C \]
Entonces:
\[ 300 = x + 200 \leftrightarrow 300 \ {\color{red}{ - 200} } = x + 200 \ {\color{red}{ - 200} } \leftrightarrow 100 = x \]
Es decir, el primero de los automóviles se encontraba inicialmente cien metros por detrás del segundo.
Los dos casos planteados nos muestran que las ecuaciones pueden reflejar una situación concreta en el lenguaje de la matemática y que la solución de dicha ecuación habrá de representar, entonces, una magnitud correspondiente al mundo físico que nos rodea.
4.1.2. Resolución de problemas empleando ecuaciones lineales
Los dos problemas anteriores propuestos nos sirvieron para introducir el tema y hacerle recordar al alumno dos de las propiedades más útiles para la resolución de ecuaciones. Profundicemos el tema con una aplicación muy común en la industria alimenticia.
Para concentrar el jugo de naranja se parte de un extracto que contiene 12 % de sólidos. El jugo se pasa a los evaporadores que trabajan al vacío y parte se deriva, para luego diluir el jugo concentrado que sale del evaporador con 60 % de sólidos hasta la concentración final de 40 % de sólidos. La finalidad es mejorar el sabor del jugo, ya que durante la evaporación pierde ciertos saborizantes volátiles.
La situación aparece esquematizada en la imagen 4.3. Se pide calcular la cantidad de jugo obtenido por cada 100 kg de jugo diluido que entra al proceso.
En el esquema, L1 representa la cantidad de jugo que entra al proceso (en nuestro problema, 100 kg); L5, la cantidad de jugo concentrado y G6, la cantidad de vapor que sale del evaporador. El esquema corresponde al proceso completo, en el que se contemplan valores que no necesitamos en el presente problema: L4, cantidad de jugo que sale del evaporador con una concentración del 60 %; L2, cantidad de jugo que entra al evaporador, con una concentración inicial del 12 % y L3, cantidad de jugo que habrá de mezclarse con el que sale del evaporador para obtener el producto final, con un 40 % de sólidos.
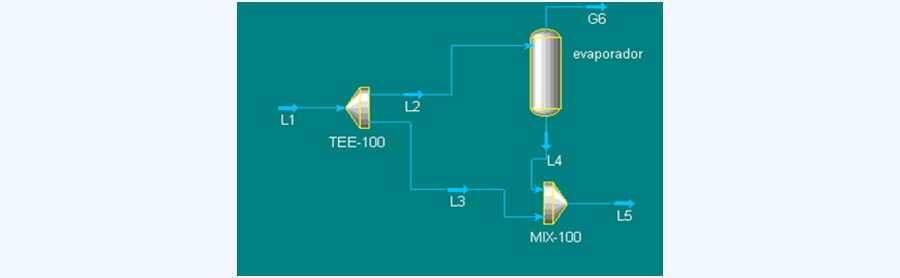
Tratándose de un problema técnico concreto, resulta muy importante reflexionar sobre el proceso descripto en el enunciado antes de comenzar a operar. Es fundamental dejar de lado la información que no nos interesa para responder a la pregunta planteada, para concentrarnos en lo que sí nos importa para responderla.
En nuestro caso, nos interesa el balance total de sólidos, es decir, la ecuación donde se contempla que la cantidad de sólidos no se evapora durante el proceso, permanece constante. Ello nos permite escribir:
\[ 100 kg . 0,12 = x . 0,40 \]
En el miembro de la izquierda, al multiplicar la cantidad de jugo diluido que entra al proceso por el porcentaje de sólidos, estamos calculando la masa de sólidos entrante. La incógnita representa la cantidad de jugo obtenida al final del proceso que, multiplicada por el porcentaje de sólidos que ha de tener, nos permite calcular la cantidad de sólidos a la salida.
Para resolver la ecuación, bastará con dividir a ambos miembros por 0,40, aplicando una de las reglas vistas en la sección anterior. Así:
\[ 100 kg . 0,12 = x . 0,40 \to \frac{1}{0,40} 100 kg . 0,12 = \frac{1}{0,40} x . 0,40 \to \]
\[ \to \frac{1}{0,4} 12 kg = x \to x = 30 kg \]
Es decir que, por cada 100 kg de jugo diluido que entran en el proceso, se obtienen 30 kg de jugo con la concentración del 40 % solicitada por las especificaciones del producto.
¡Como vemos, una ecuación no tiene por qué ser una expresión abstracta, sin vinculación alguna con la realidad!
A partir del ejemplo anterior, calcular el peso de agua evaporada en el proceso.
Ayuda: en este caso será conveniente plantear la ecuación de balance total, en la cual se tienen en cuenta las masas que entran y las que salen. Prestar mucha atención al texto que acompaña a la imagen 4.3, porque allí se nos indica claramente cuáles son las variables que no interesan a nuestro problema.
Un automóvil pasó frente a un puesto caminero a una velocidad de treinta y cinco metros sobre segundo, siendo la velocidad máxima en ese tramo de ruta de cien kilómetros por hora (es decir, poco menos de treinta metros sobre segundo). Cuando el vehículo se encontraba a sesenta metros del puesto, un patrullero parte en su persecución, alcanzándolo cuando ambos móviles se encuentran a cuatrocientos veinte metros del edificio (la imagen 4.4.A representa la situación que acabamos de describir). ¿Cuánto tiempo transcurrió desde el instante en que el patrullero comenzó la persecución hasta que alcanzó al automóvil?
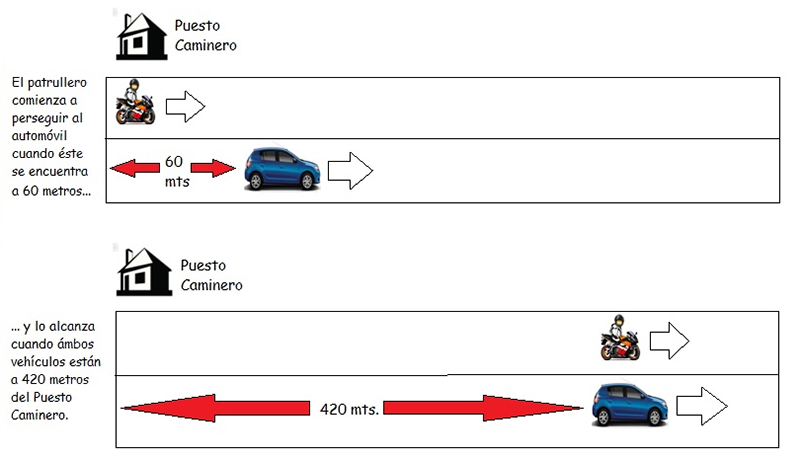
Para la resolución del problema, es necesario tener en cuenta que no debemos detenernos en el movimiento del patrullero, sino que basta con la información que tenemos acerca del automóvil para responder a la pregunta que hace el enunciado.
La ecuación que describe la situación es la siguiente:
\[ 420 m = 60 m + 35 m/s . t \]
El miembro de la izquierda indica la distancia total recorrida por el patrullero, mientras que t representa la incógnita del problema.
Aplicaremos las dos propiedades vistas en la sección anterior para resolver la ecuación. Para comenzar, restamos 60 a ambos miembros:
\[ 420 \ {\color{red}{ - 60} } = 60 + 35 . t \ {\color{red}{ - 60} } \to 360 = 35 . t \]
Multiplicamos ambos miembros por \(1/35 \):
\[ \frac{1}{35} . 360 = \frac{1}{35} . 35 . t \to 10,285 s = t \]
Es decir, el tiempo de la persecución fue de 10,285 segundos.
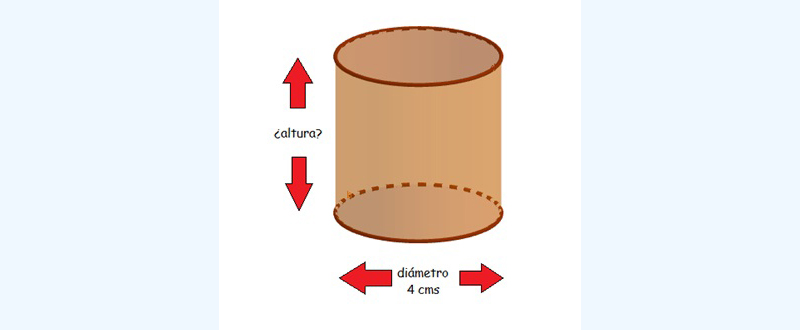
Una lata cilíndrica, como la que se observa en la imagen 4.4.B, tiene un radio de 2 centímetros y un volumen de aproximadamente 50,27 centímetros cúbicos.
Teniendo en cuenta que el volumen de un cilindro se calcula mediante la expresión \( \text{volumen cilindro } = \pi . r^2 . h \), donde r representa el radio y h la altura, se pide obtener el valor de la altura de la lata.
4.2. Sistemas de ecuaciones lineales
Detengámonos un instante en el ejemplo desarrollado en la sección anterior. Vimos que, por un lado, se pedía la cantidad de jugo que se obtenía en el proceso; y que, en una actividad posterior, había que calcular la cantidad de agua evaporada.
Es evidente que, en una situación problemática dada podríamos estar interesados en determinar más de una incógnita. Como veremos seguidamente, por cada incógnita necesitaremos de una ecuación. Cuando ello sucede, decimos que estamos en presencia de un sistema de ecuaciones.
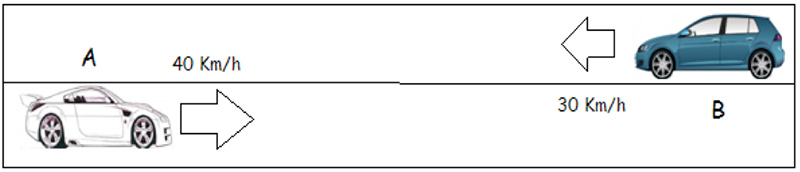
En un instante dado, un automóvil pasa por un punto A, dirigiéndose hacia otro punto B, distantes entre sí mil cuatrocientos metros. En ese mismo momento, un segundo automóvil pasa por el punto B, dirigiéndose hacia A.
El primero de los vehículos se mueve con una velocidad constante de cuarenta kilómetros por hora, mientras que el velocímetro del segundo indica todo el tiempo treinta metros sobre segundo. La imagen 4.5 grafica la situación descripta.
Se trata de un típico problema de encuentro, que suele resolverse en los cursos de física.
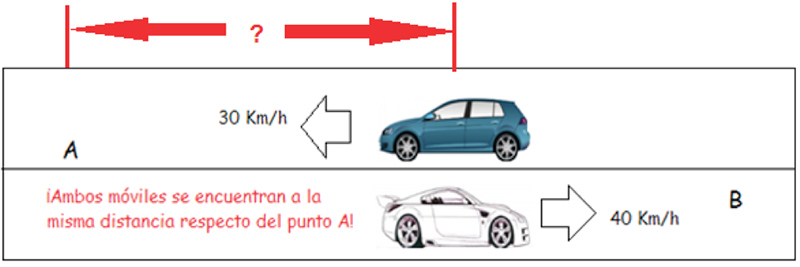
Nos preguntamos entonces a qué distancia del punto A los dos automóviles habrán de cruzarse y cuánto tiempo habrá de transcurrir para que ello suceda, circunstancia representada por la imagen 4.6.
Una de las preguntas que nos hacemos es cuál es la distancia que recorrerá uno de los móviles, el que inicialmente pasara por el punto A, antes de que ambos vehículos se crucen.
Para comenzar a resolver el presente problema, tengamos en cuenta que, al hablar de velocidad, nos estamos refiriendo a la distancia que recorre un vehículo en la unidad de tiempo.
Llamaremos dblanco a la distancia a la que ese móvil se encuentra respecto del punto A en un instante t… Y, con el mismo criterio, definiremos como dazul a la distancia a la que, en ese mismo instante t, el automóvil azul se encuentra respecto del mismo punto.
Escribimos entonces las expresiones que nos permitirán calcular a qué distancia se encontrará cada uno de los móviles respecto del punto A. Comencemos con la que representa al movimiento del automóvil blanco:
[4.1] \[ d_{blanco} = 40 m/s * t \]
Esta expresión es casi inmediata, pues resulta lógico pensar que, a medida que pasa el tiempo, el automóvil blanco se encontrará cada vez más lejos del punto A, es decir, su distancia respecto de A aumentará en forma proporcional al tiempo transcurrido… Pero, para obtener la expresión que nos permita conocer la distancia que separa al automóvil azul respecto del punto A, nos resultará útil detenernos en la imagen 4.7
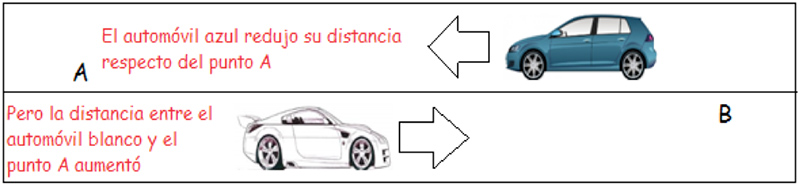
En dicha imagen se observa que, inicialmente, el automóvil azul se encontraba a mil cuatrocientos metros del punto A; pero esa distancia disminuye a medida que transcurren los segundos, razón por la cual debemos escribir:
[4.2] \[ d_{azul} = 1400m - 30 m/s * t \]
Ahora bien: nos encontramos con dos ecuaciones (las [4.1] y [4.2]) y, aparentemente, tres incógnitas. Sin embargo, esto último no es cierto. Debemos tener en cuenta que, en el momento en que los dos automóviles se crucen, \( d_{blanco} = d_{azul} = d_{encuentro} \). Es decir, las incógnitas son solamente el tiempo que tardan en cruzarse y la distancia a la que lo hacen respecto del punto A. Podemos reescribir a las dos ecuaciones mencionadas en el presente párrafo como:
[4.3] \[ d_{encuentro} = 40 m/s * t \]
[4.4] \[ d_{encuentro} = 1400m - 30 m/s * t \]
Obtuvimos así el sistema de ecuaciones que nos permitirá responder a las preguntas que nos plantea el enunciado.
Acabamos de obtener el sistema de ecuaciones lineales que nos permitirá resolver el problema planteado. En la siguiente sección veremos cómo hacerlo.
4.2.1. Método de igualación
Existen varios métodos para la resolución de sistemas de ecuaciones lineales. Aun cuando los resultados obtenidos deberán ser los mismos cualquiera sea el aplicado, con la práctica, el alumno podrá adoptar en cada caso aquel que le facilite la tarea.
Supongamos que el sistema de ecuaciones que hemos de resolver tiene la forma:
[4.5] \[ a · x + b · y = c \]
[4.6] \[ a · x + d · y = e \]
En dicho sistema, a, b , c, d y e son números conocidos. Se observa que la incógnita x está en ambas ecuaciones multiplicada por el mismo coeficiente no nulo (a), de modo que podríamos despejar dicha incógnita de cada una de las ecuaciones.
Así, de la [4.5]:
[4.7] \[ a · x + b · y = c \to a . x = c - b . y \to x = \frac{c-b.y}{a} \]
Y de la [4.6]:
[4.8] \[ a · x + d · y = e \to a . x = e - d . y \to x = \frac{e-d.y}{a} \]
Como los miembros de la izquierda en las ecuaciones [4.7] y [4.8] son iguales, los miembros de la derecha también deberán serlo. Entonces, pueden igualarse ambas expresiones, obteniéndose:
[4.9] \[ \frac{c-b.y}{a} = \frac{e-d.y}{a} \]
Se obtuvo así una ecuación que tiene una única incógnita (y), que habrá de resolverse utilizando los procedimientos aplicados en las secciones 4.1.1 y 4.1.2.
Una vez despejado el valor de y bastará con reemplazarlo en la [4.7] o en la [4.8] para obtener el valor de x.
Volvamos al ejemplo que desarrollamos en la sección anterior. Dado que \( d_{encuentro} \) aparece en el miembro de la izquierda de las expresiones [4.3] y [4.4], podríamos igualarlas para obtener:
[4.10] \[ 40 m/s * t = 1400m - 30 m/s * t \]
A continuación, los pasos de cálculo para despejar el tiempo de encuentro, t:
\[ 40 * t = 1400 - 30 * t \to 40 * t + 30 * t = 1400 \to \]
\[ \to 70 * t = 1400 \to = \frac{1400}{70} = 20 \]
Una vez obtenido el tiempo de encuentro (20 segundos), basta con reemplazar este valor en la [4.3] (o en la [4.4]) para obtener a qué distancia del punto A se produce el encuentro. Así:
\[ d_{encuentro} = d (t = 20s) = 40 m/s * 20 s = 800 \ metros \]
Análogamente, si nuestro sistema de ecuaciones hubiese tenido el siguiente formato:
[4.11] \[ a · x + b · y = c \]
[4.12] \[ d · x + b · y = e \]
hubiésemos podido operar de un modo similar, pero despejando la variable y, para luego operar de una forma equivalente a la expuesta en la primera parte de la sección.
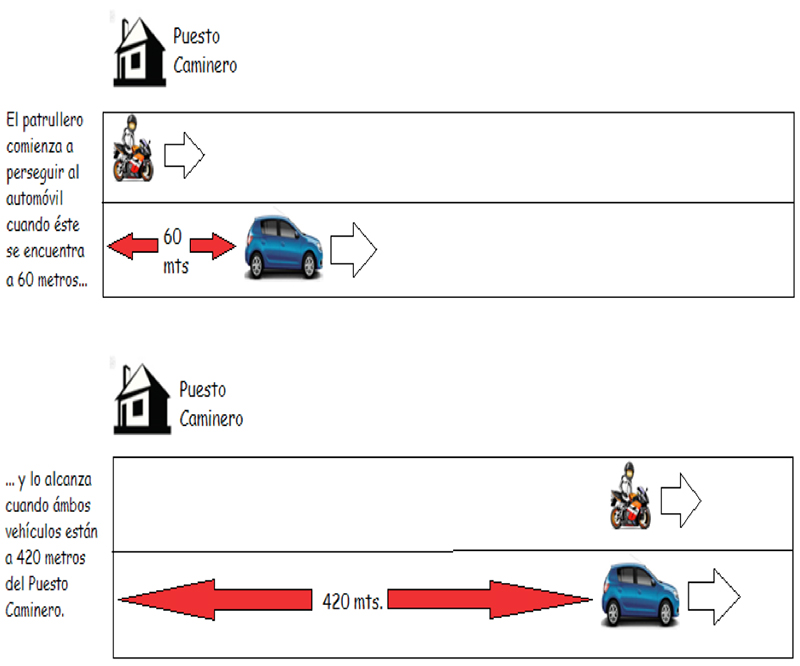
En el instante en que un automóvil que viaja con una velocidad constante de treinta metros sobre segundo se encuentra a cincuenta metros de un puesto caminero, un patrullero pasa frente a dicho puesto. El motociclista viaja con una velocidad constante de treinta y cinco metros sobre segundo, tal como lo grafica la imagen 4.8.
Calcular a qué distancia del puesto caminero el patrullero alcanza al automóvil. Obtener, además, cuánto tiempo transcurrió desde el momento en que el patrullero pasó frente al puesto hasta que alcanzó al vehículo infractor.
4.2.2. Método de sustitución
Veamos lo que sucede para un sistema de ecuaciones que tenga la forma:
[4.13] \[ a · x + b · y = c \]
[4.14] \[ d · x + e · y = f \]
En este caso, a, b, c, d, e y f son números. Un camino posible para la resolución del problema partiría de despejar una de las incógnitas de alguna de las dos ecuaciones. Por ejemplo, de la [4.13] y teniendo en cuenta que a deberá ser distinto de cero:
[4.15] \[ a . x + b . y = c \to a . x = c - b . y \to x = \frac{c-b.y}{a} \]
Seguidamente, sustituimos el valor de la incógnita obtenida en [4.15] en la ecuación [4.14]:
[4.16] \[ d . \frac{c-b.y}{a} + e.y = f \]
Aplicando propiedad distributiva y las reglas expresadas al principio de la presente unidad, operamos para despejar el valor de y:
\[ d . \frac{c-b.y}{a} + e.y = f \to \frac{d.c}{a} - \frac{d.b.y}{a} + e.y = f \to \]
\[ \to - \frac{d.b.y}{a} + e.y = f - \frac{d.c}{a} \to y \left( - \frac{d.b}{a} + e \right) = f - \frac{d.c}{a} \]
\[ \to y = \frac{f - \frac{d.c}{a}}{\left( - \frac{d.b}{a} + e \right)} \]
Una vez despejado el valor de y bastará reemplazar en la [4.15] para poder calcular el valor de la otra incógnita, x.
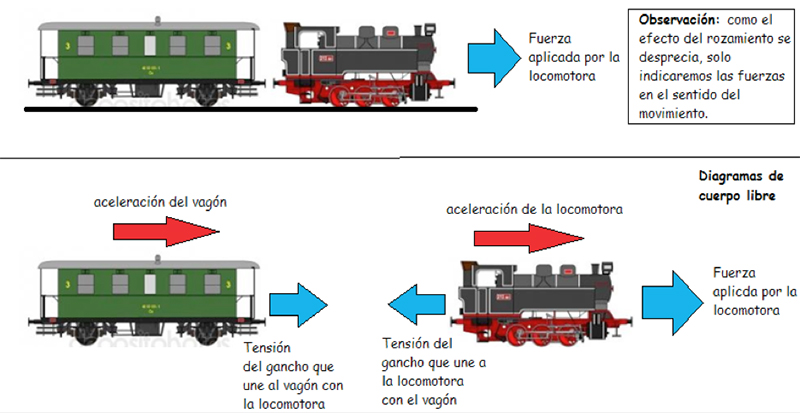
Una locomotora de juguete de masa 0,3 kilogramos se pone en marcha y arrastra a un pequeño vagón de plástico de 0,25 kilogramos. La fuerza motriz de la locomotora es de 1,5 Newtons y, tal como se indica en la parte superior de la imagen 4.9, se desprecia el rozamiento entre la locomotora, el vagón y los rieles.
A partir de diagrama de cuerpo libre (que se muestra para el vagón y la locomotora en la parte inferior de la imagen 4.9), se obtienen las ecuaciones de la dinámica que se aplican a la resolución del problema:
[4.17] \[ T = m_{vagón} . a \]
[4.18] \[ F- T = m_{locomotora} . a \]
En dichas ecuaciones, T representa la fuerza que se ejerce sobre el gancho que une a la locomotora y al vagón (a la que en física se le da el nombre de tensión); F es la fuerza tractora que hace la locomotora; a es la aceleración del conjunto; y, finalmente, \( m_{vagón} \) y \( m_{locomotora} \) representan a las masas del vagón y la locomotora, respectivamente.
Empleando entonces las ecuaciones que brinda el enunciado y los datos que figuran en él, se pide calcular, aplicando el método de sustitución, los valores de la tensión y de la aceleración de ambos móviles.
4.3. Concepto de matriz
Supongamos que, por motivos de trabajo, un técnico debe desplazarse varias veces por mes hasta tres localidades del interior de la provincia, en las que la empresa para la cual trabaja cuenta con plantas industriales. El hombre desea tener idea del costo de cada uno de sus viajes para el cálculo de sus viáticos y lo hace a partir de tres ítems básicos: kilómetros a recorrer, peajes y refrigerios. Gasta $250 por cada cien kilómetros a recorrer; cada peaje le sale (en promedio) unos $25; y cada vez que se detiene a comer algo en una estación de servicio, abona alrededor de $90.
Para llegar a una de las plantas debe recorrer unos trescientos veinte kilómetros, abonar cuatro peajes y hacer dos paradas para descansar. Entonces, sus viáticos se podrán calcular efectuando el siguiente cálculo:
[4.20] \[ 3,2*$250+4*$25+2*$90 = $1080 \]
En el primer término, 3,2 corresponde a los trescientos veinte kilómetros divididos por cien (nuestro hombre ha hecho su cálculo de costo del combustible por cada cien kilómetros recorridos).
El viaje a la segunda de las plantas industriales lo lleva a recorrer solo ciento cuarenta kilómetros. En este caso, debe abonar seis peajes, pero no se detiene a tomar refrigerio alguno. Sus viáticos se calcularán en este caso de la siguiente manera:
[4.21] \[ 1,4*$250+6*25+0*$90 = $500 \]
Finalmente, para alcanzar la tercera de las plantas, debe recorrer un total de cuatrocientos cuarenta kilómetros y atravesar cuatro peajes. En estos viajes, suele detenerse tres veces para tomar un refrigerio. Los viáticos correspondientes se obtienen, entonces, haciendo el siguiente cálculo:
[4.22] \[ 4,4*$250+4*$25+3*$90 = $1470 \]
Si observamos detenidamente las expresiones [4.20], [4.21] y [4.22] observaremos que, en cada una de ellas, hay una sumatoria de productos en la cual ciertos valores cambian (distancias, cantidad de peajes y de paradas en el camino), mientras que otros (costo de cada una de esas “variables”) permanece constante.
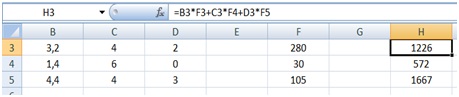
Nuestro técnico podría utilizar una planilla de cálculo como la que reproducimos en la imagen 4.10. La distancia, cantidad de peajes y número de paradas para cada uno de los tres destinos aparecen en las columnas B, C y D, respectivamente, en tanto que en las filas 3, 4 y 5 se registran los datos correspondientes a cada una de las tres plantas. En la misma imagen, pero en la columna F, podemos ver los costos “unitarios” de combustible, peaje y refrigerio. Pero, además, en la columna H aparecen los resultados de los cálculos llevados a cabo en [4.20], [4.21] y [4.22], que fueron obtenidos “programando” la planilla (en la ventana de la parte superior de la imagen 4.10 se observa el cálculo correspondiente a los viáticos para llegar a la primera de las tres plantas).
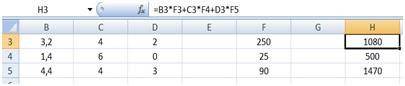
Como vemos, organizar la información en la planilla de cálculo facilitó la tarea de nuestro técnico. Sin embargo, este procedimiento puede ofrecernos aún más ventajas. Supongamos que los costos aumentasen, de modo que el costo por cada cien kilómetros recorridos pasase a costar $280, el valor promedio de los peajes $30 y el costo de cada refrigerio $105. En ese caso, bastaría con reemplazar los valores de la columna F, obteniéndose entonces en la columna H los nuevos costos, tal como se observa en la imagen 4.11.
Al cambiar los costos unitarios en la columna F, automáticamente aparecen en la columna H los nuevos valores de los viáticos a cada uno de los tres destinos.
El ejemplo nos muestra la utilidad de aplicar una planilla de cálculo en una situación que podría calificarse como cotidiana. Sin embargo, lo que realmente nos interesa es que el alumno comprenda que la información con la que hemos trabajado fue almacenada en forma ordenada dentro de dicha planilla. Desde el punto de vista matemático, diremos que el “arreglo” conformado por los números contenidos en las columnas B, C y D y las filas 3, 4 y 5 de nuestra planilla representa una matriz de tres filas y tres columnas.
Desde el punto de vista formal, esa matriz debería escribirse entre paréntesis, tal como lo indicamos a continuación:
\[ \left( \begin{array}{ccc} 3,2 & 4 & 2\\ 1,4 & 6 & 0\\ 4,4 & 4 & 3\\ \end{array} \right) \]
Las matrices suelen indicarse con letras mayúsculas (A, B, etc.) y no tienen por qué tener el mismo número de filas (o renglones) y de columnas. Volviendo a la imagen 4.11, podemos decir que las columnas F y H (que corresponden a los costos unitarios y viáticos a cada una de las plantas, respectivamente) son matrices que tienen tres filas y una columna, a las que podríamos escribir como:
\[ \left( \begin{array}{c} 280\\ 30\\ 105\\ \end{array} \right) \text{ y } \left( \begin{array}{c} 1226\\ 572\\ 1667\\ \end{array} \right) \]
El valor de las matrices y las propiedades de estas son tales que detenernos en ellos supera ampliamente las posibilidades de nuestro curso. Sin embargo, algunas propiedades se hacen evidentes: el simple ejemplo que propusimos para introducir esta sección nos muestra cómo la multiplicación de matrices (una de sus operaciones elementales) nos brinda una gran cantidad de información, con un notable grado de flexibilidad. Por ese motivo, el estudio de las matrices y sus características es uno de los pilares de todo curso de Álgebra de nivel universitario.
Nosotros nos limitaremos a utilizar las matrices para la resolución de sistemas de ecuaciones lineales, utilizando para ello un software apropiado, tal como se verá en la siguiente sección.
4.3.1. Aplicación de matrices para la resolución de sistemas de ecuaciones
Volvamos por un instante al problema propuesto en la actividad 4.4. Recordemos que se nos pedía calcular la aceleración de un sistema compuesto por una locomotora de juguete y un pequeño vagón que aquella arrastraría en un tramo recto de vías.
Vamos a verificar los resultados obtenidos matricialmente. Si en las ecuaciones [4.17] y [4.18] reemplazamos las variables conocidas, obtenemos el siguiente sistema de ecuaciones:
[4.23] \[ T = 0,25 * a \]
[4.24] \[ 1,5 - T = 0,3 * a \]
Reescribimos el sistema, dejando a la izquierda del signo igual los términos que contienen las incógnitas y a la derecha del signo los términos independientes. Operando adecuadamente, podemos escribir:
[4.25] \[ T - 0,25 * a = 0 \]
[4.26] \[ T + 0,3 * a = 1,5 \]
Teniendo en cuenta lo visto anteriormente en lo que respecta al producto de matrices, el sistema conformado por [4.25] y [4.26] podrá expresarse de la siguiente manera:
[4.27] \[ \left( \begin{array}{cc} 1 & -0,25\\ 1 & 0,3\\ \end{array} \right) \left( \begin{array}{cc} T\\ a\\ \end{array} \right) = \left( \begin{array}{cc} 0\\ 1,5\\ \end{array} \right) \]
En general, todo sistema de ecuaciones de la forma
\[ a * x + b * y = c \]
\[ d * x + e * y = f \]
Podrá expresarse matricialmente como:
[4.28] \[ \left( \begin{array}{cc} a & b\\ d & e\\ \end{array} \right) \left( \begin{array}{cc} x\\ y\\ \end{array} \right) = \left( \begin{array}{cc} c\\ f\\ \end{array} \right) \]
Ahora bien: toda matriz que tenga el mismo número de filas que de columnas recibe el nombre de matriz cuadrada. Y toda matriz cuadrada tiene un número asociado a ella que recibe el nombre de determinante.
Cuando una matriz cuadrada \( A \) tiene asociada a ella un determinante que sea distinto de cero (lo que se expresa como \( |A| \not= 0 \)), existirá una matriz \( A^{-1} \) (lo que se lee como inversa de la matriz A), tal que:
[4.29] \[ A * A^{-1} = A^{-1} * A = I \]
En la [4.29], I recibe el nombre de matriz identidad.
La matriz identidad no es única, pues depende del tamaño de la matriz cuadrada con la que se esté trabajando. Por ejemplo, en el problema que estamos resolviendo, la matriz de los coeficientes (es decir, la que contiene a los números que acompañan a las incógnitas en nuestras ecuaciones) tiene dos filas y dos columnas, de modo que:
\[ I = \left( \begin{array}{cc} 1 & 0\\ 0 & 1\\ \end{array} \right) \]
Si, en cambio, trabajásemos con matrices de 3x3 (es decir, tres filas por tres columnas), la matriz identidad sería:
\[ I = \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{array} \right) \]
En general, diremos que la matriz identidad tiene todos sus elementos nulos, con excepción de los ubicados dentro de la diagonal principal. Estos últimos tendrán valor uno.
La matriz identidad es el elemento neutro del producto de matrices.
La obtención de la inversa de una matriz dada puede obtenerse por distintos caminos.
Dada una matriz \( A \in R^{2x2} \) (es decir, una matriz cuadrada que tiene dos filas y dos columnas), a la que expresaremos en forma genérica como:
\[ A= \left( \begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{array} \right) \]
Entonces, \( A^{-1} \) (es decir, la inversa de dicha matriz) podrá calcularse a partir de la siguiente expresión:
\[ A^{-1} = \frac{1}{a_{11}. a_{22} - a_{12} . a_{21}} . \left( \begin{array}{cc} a_{22} & -a_{12}\\ -a_{21} & a_{11}\\ \end{array} \right) \]
La notación \( A_{ij} \) indica al número ubicado en la fila i y la columna j de la matriz.
Si nos detenemos un momento en la expresión [4.28], estapodría simplificarse escribiendo:
[4.30] \[ A · X = b \]
Como vimos anteriormente, A recibe el nombre de matriz de los coeficientes, mientras que X será la matriz de las incógnitas y b la de los términos independientes.
Si multiplicamos a la izquierda a ambos miembros de la [4.30] por A-1 y recordamos la condición definida por la [4.29], podemos escribir:
[4.31] \[ A · X = b \to A^{-1} . A . X = A^{-1}. b \to X = A^{-1} . b \]
Es decir que, para despejar las incógnitas de nuestro problema, bastará con multiplicar la inversa de la matriz de los coeficientes por la matriz de los términos independientes.
4.3.2. Resolución matricial de sistemas de ecuaciones empleando software
Ya estamos en condiciones de resolver el sistema de ecuaciones expresado matricialmente en [4.27]. Aplicando la nomenclatura empleada en la sección anterior, diremos que la matriz de los coeficientes es
\[ A = \left( \begin{array}{cc} 1 & -0,25\\ 1 & -0,3\\ \end{array} \right) \]
en tanto que \( x = \left( \begin{array}{c} T\\ a\\ \end{array} \right) \) será la matriz de las incógnitas y \( b = \left( \begin{array}{c} 0\\ 1,5\\ \end{array} \right) \) la matriz de los términos independientes.
Utilizaremos el programa wxMaxima. Buscamos en la barra horizontal de menú las aplicaciones de álgebra, como lo muestra la imagen 4.12.
La flecha roja señala la aplicación que hemos de abrir.

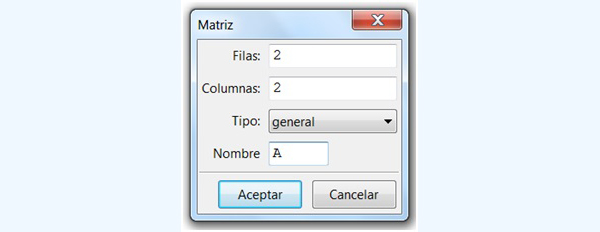
Ingresemos seguidamente la matriz de los coeficientes. Para ello, dentro del menú haremos clic sobre la opción “Introducir matriz”,tal como se observa en la imagen 4.13.
Aparece una primera ventana que nos permite dimensionar la matriz (ver imagen 4.14).
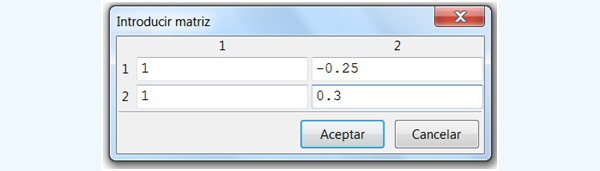
Haciendo clic en “Aceptar”, se abre otra ventana, dentro de la cual ingresamos los valores numéricos, tal como se observa en la captura de pantalla de la imagen 4.15.
Al hacer clic en “Aceptar”, en la pantalla aparecerá la matriz en cuestión (ver imagen 4.16).

Para obtener la inversa de esta matriz, volveremos al menú y seleccionaremos “Invertir matriz” (imagen 4.17). El resultado aparece en pantalla en forma inmediata (imagen 4.18).
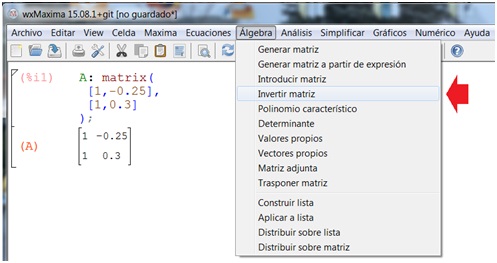

Operando del mismo modo, ingresamos la matriz de los términos independientes (imagen 4.19).

Finalmente, obtenemos los resultados del sistema, multiplicando la inversa de la matriz de los coeficientes por la matriz de los términos independientes, de acuerdo a lo que expresaba la fórmula [4.31] (ver imagen 4.20).
La tensión en el gancho que une a la locomotora con el vagón valdrá entonces 0,618 N, en tanto que la aceleración de los dos móviles será de 2,72 metros sobre segundo al cuadrado.

Acabamos de ver de qué modo verificar empleando el software la resolución de un sistema de ecuaciones de 2x2 que previamente había sido resuelto en forma manual. Ello puede hacer que nos preguntemos hasta qué punto el uso del wxMaxima pueda ser recomendable.
Sin embargo, cuando los sistemas son más complejos, es decir, están conformados por mayor cantidad de ecuaciones e incógnitas, la resolución manual se hace muy trabajosa. Como veremos en el problema propuesto para la siguiente actividad, el empleo del software puede resultar realmente ventajoso.
En la imagen 4.21 se representa un circuito de corriente continua, en el cual hay dos pilas o fuentes ( \( \varepsilon_1\), de 20 Volt; y \( \varepsilon_2\), de 5 Volt). Dicho circuito presenta tres resistencia en paralelo ( \( R_1\), de 10 \( \Omega \) (lease “ohm”); \( R_2\) de 20 \( \Omega \); y \( R_3 \), de 15 \( \Omega \).
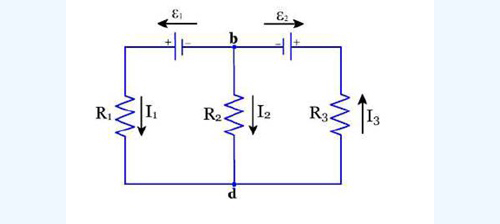
Las Leyes de Kirchoff aplicadas al circuito nos brindan el siguiente sistema de ecuaciones lineales:
[4.32] \[ I_3 = I_1 + I_2 \]
[4.33] \[ \varepsilon_1 - R_1 \cdot I_1 + R_2 \cdot I_2 = 0 \]
[4.34] \[ \varepsilon_2 - R_3 \cdot I_3 + R_2 \cdot I_2 = 0 \]
Resolver matricialmente el sistema de ecuaciones para obtener los valores de las corrientes eléctricas \( I_1, \ I_2 \) e \( I_3 \) que circulan por cada una de las resistencias.
Tener en cuenta que:
- Las corrientes se miden en amperes.
- Si alguno de los resultados obtenidos resultase negativo, ello significaría que el sentido de dicha corriente es opuesto al que aparece en la imagen 4.21 (los sentidos que se adoptan inicialmente para la resolución de este tipo de problemas suelen ser arbitrarios).
4.4. Clasificación de sistemas de ecuaciones: compatibles determinados, compatibles indeterminados e incompatibles
Los ejemplos con los que hemos estado trabajando hasta este momento se clasifican como sistemas compatibles determinados. Compatibles, porque tienen solución; determinados, porque dicha solución es única. Así, por ejemplo, en el problema de la locomotora y el vagón cuya solución se obtuvo a partir del sistema de ecuaciones [4.27], existían un único valor de T y un único valor de a que, reemplazados en las ecuaciones de dicho sistema, permitían que las igualdades se verificasen.
Sin embargo, existen muchos otros problemas de interés donde eso no sucede. Tomemos, por ejemplo, una ecuación química, en la que una cierta cantidad de moles de amoníaco reaccionan con otra cantidad de moles de oxígeno, para dar como resultado nitrógeno y agua. En símbolos:
[4.35] \[ n_1 NH_3 + n_2 O_2 \to n_3N_2 + n_4H_2O \]
Observemos que el signo “=” que utilizamos en Matemática se reemplaza por una flecha que indica el sentido en el cual la reacción se produce. Sin embargo, no deja de ser una ecuación de balance. En ella, \( n_1, \ n_2, \ n_3\) y \( n_4 \) representan el número de moles de amoníaco, oxígeno, nitrógeno y agua, respectivamente.
Una forma de resolver este tipo de problemas consiste en analizar lo que sucede con cada uno de los elementos que toman parte de la reacción. Escribiremos entonces:
Nitrógeno: \( n_1 = 2 \cdot n_3 \)
Hidrógeno: \( 3 \cdot n_1 = 2 \cdot n_4 \)
Oxígeno: \( 2 \cdot n_2 = n_4 \)
Nos encontramos ante un sistema de tres ecuaciones con cuatro incógnitas ( \( n_1, \ n_2 \ n_3 \) y \( n_4 \)). Cuando el número de ecuaciones y de incógnitas no coincide, es imposible su resolución en forma matricial.
El sistema puede resolverse manualmente con un poco de paciencia. Sin embargo, le proponemos al alumno volver a emplear el wxMaxima, a partir de otra de sus aplicaciones.
En la imagen 4.22 se observa cómo ha de seleccionarse, dentro del menú que aparece en la parte superior de la pantalla, la categoría “Ecuaciones”.
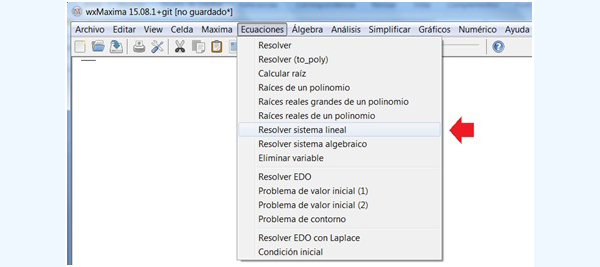
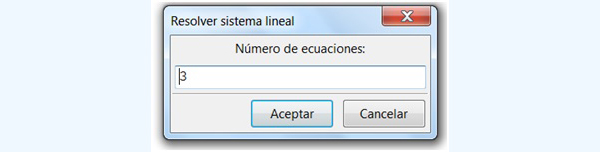
Dentro de dicha categoría, elegiremos “Resolver sistema lineal”, tal como aparece en la captura de pantalla de la imagen 4.23. Haciendo clic sobre la instrucción, veremos que aparece una pequeña ventana dentro de la cual debemos indicar cuál es el número de ecuaciones que habremos de ingresar (ver imagen 4.24). Haciendo clic en “Aceptar”, aparecerá una última ventana, dentro de la cual tendremos que ingresar las ecuaciones que conforman el sistema, aclarando, además, cuáles son las incógnitas (imagen 4.25). El resultado aparece en pantalla en cuanto hacemos clic en “Aceptar” para esta última ventana (imagen 4.26).
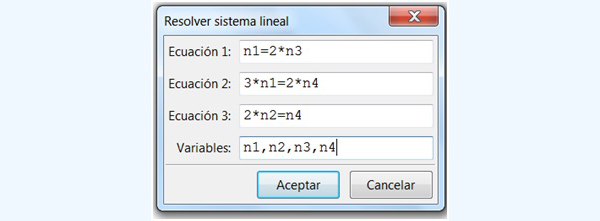

Entre corchetes, en la parte inferior, aparecen los resultados de las cuatro incógnitas, expresados en función de una variable, a la que en este caso el propio programa dio el nombre de %r1. Esto significa que el problema tiene solución, pero que no hay una sino infinitas soluciones posibles, que dependerán del valor que le asignemos a %r1. Por esa razón diremos que este sistema se clasifica como compatible indeterminado, puesto que tiene solución, aun cuando esta no sea única.
Desde el punto de vista químico, el criterio consiste en asignar a las incógnitas los menores valores enteros que la satisfagan. En este caso particular, estos habrán de obtenerse cuando %r1= 6, de manera que:
\[ n_1 = 2 * \frac{6}{3} = 4 \]
\[ n_2 = \frac{6}{2} = 3 \]
\[ n_3 = \frac{6}{3} = 2 \]
\[ n_4 = 6 \]
La ecuación equilibrada será finalmente:
\[ 4NH_3 + 3O_2 \to 2N_2 + 6H_2O \]
Dadas las siguientes ecuaciones químicas, equilibrarlas haciendo uso del software:
- \( n_1K + n_2H_2O \to n_3KOH + n_4H_2 \)
- \( n_1NaOH + n_2H_2SO_4 \to n_3Na_2SO_4 + n_4H_2O \)
- \( n_1NaHCO_3 \to n_2Na_2 CO_3 + N_3H_2O + n_4CO_2 \)
Para finalizar con la siguiente sección, debemos contemplar la posibilidad de que el sistema no tenga solución, en cuyo caso habrá de clasificarse como sistema incompatible.
Por ejemplo, analicemos el sistema:
\[ x + 2 * y + z = 3 \] \[ 2 * x - y + z = -2 \] \[ 3 * x + y + 2 * z = 6 \]Cada una de las ecuaciones puede representarse geométricamente como un plano en el espacio de tres dimensiones, de tal modo que la solución del sistema habrá de estar conformada por aquel o aquellos puntos que pertenezcan simultáneamente a los tres planos.
Para obtener la solución volvemos a aplicar el programa wxMaxima, obteniendo como resultado la respuesta que se observa en la parte inferior de la imagen 4.27.

Los corchetes que no contienen nada en su interior deben interpretarse como conjunto vacío, es decir, no existe en todo el espacio un solo punto que pertenezca simultáneamente a los tres planos.
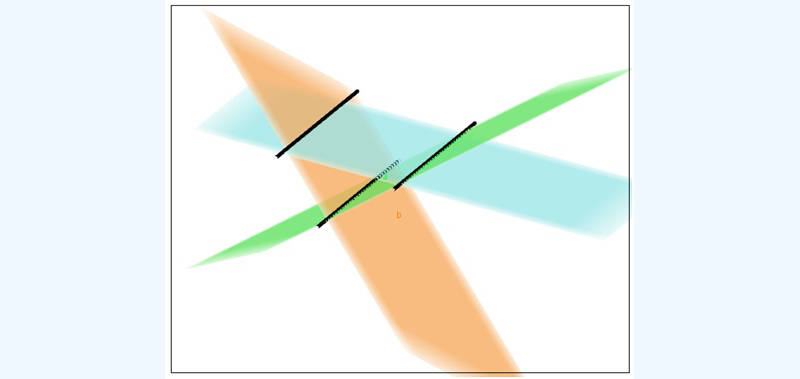
La imagen 4.28 fue confeccionada con el GeoGebra y nos permite interpretar la situación: en color negro aparecen las rectas intersección entre los planos tomados de a dos y se observa que dichas rectas son paralelas entre sí, confirmando el resultado que nos ofreció el wxMaxima.
Cada uno de los planos fue representado en un color distinto, pero las rectas intersección entre ambos aparecen todas en color negro. Se observa perfectamente que estas resultan ser paralelas entre sí, lo que implica que no existe ningún punto en el espacio que pertenezca simultáneamente a los tres planos.