3. Funciones de una variable
Objetivos
- Identificar relaciones y funciones matemáticas.
- Invertir y componer funciones.
- Representar en diagramas cartesianos funciones polinómicas, exponenciales y logarítmicas “a mano” y utilizando sistemas graficadores.
- Hallar intersecciones entre dos funciones.
Introducción
Una función expresa la idea de que una cantidad depende o está determinada por otra. Los ejemplos siguientes aclaran esta idea:
- el consumo de un hogar depende de sus ingresos. Si no hay cambios en otras circunstancias que podrían influir también, el nivel de ingresos de un hogar determina cuánto se consume en él.
- la cantidad demandada de cierto bien depende de su precio (nuevamente, si no hay cambios en otras circunstancias que podrían influir también). Entonces, para cada precio de ese bien, se espera cierta cantidad demandada.
- la cantidad de dinero que se debe pagar de Impuesto al Valor Agregado (IVA) por un producto, depende de su precio de costo. Por lo tanto, para cada precio de costo, habrá un cierto monto a pagar de IVA.
En esta unidad comienza el trabajo con funciones, que se extenderá hasta el final de este material didáctico. A lo largo de toda la unidad se presentan aplicaciones económicas.
3.1. Funciones
Una función es una relación entre dos conjuntos que expresa cómo a cada elemento del primer conjunto le corresponde uno y solo un elemento del segundo conjunto. Al primero de estos conjuntos se lo llama “conjunto de partida” y al segundo, “conjunto de llegada”. Gráficamente se puede representar de la siguiente manera:
Funciones

El precio de venta de un producto debe incluir un 21% de IVA. Entonces, el precio de venta se puede determinar en función del precio de costo, al que se le suma el impuesto:
\[\small{\begin{gather*} precio\ de\ venta=precio\ de\ costo\ +\ impuesto=precio\ de\ costo+\frac{21}{100}\cdot precio\ de\ costo \\ precio\ de\ venta=precio\ de\ costo\cdot\left(1+0,21\right)=precio\ de\ costo\cdot1,21 \\ precio\ de\ venta\ =1,21\cdot precio\ de\ costo \end{gather*} } \]
Esta última fórmula es la regla de asignación de la función. Cada precio de venta depende del precio de costo, y se puede obtener haciendo la cuenta indicada. El conjunto de partida es el de los números reales, igual que el de llegada. Sin embargo, como se trata de una relación económica, no tiene sentido pensar en precios negativos.
Por ese motivo se definen:
Dominio: es el subconjunto del conjunto de partida formado por todos los elementos para los cuales está definida la función.
Imagen: es el subconjunto del conjunto de llegada formado por todos los elementos que intervienen en la función.
Si se vuelve al ejemplo, se puede anotar que esta función está definida para números reales positivos (tanto el dominio como la imagen, porque se trata de precios):
\[f:\ \mathbb{R}^+ \rightarrow\ \mathbb{R}^+\]
Y la regla de asignación, es decir, la fórmula de la función es:
\[f\left(x\right)=y=1,21\cdot x\]
Esta fórmula permite calcular para cada precio de costo, simbolizado con la x, el precio de venta correspondiente, simbolizado con f(x) y también con y.
La variable x, que representa a los valores del conjunto de partida, se denomina variable independiente, y la variable y, que representa a los valores f(x) del conjunto de llegada, se denomina variable dependiente.
Para realizar el cálculo del precio de venta para varios precios de costo, conviene acomodar los valores en una tabla:
| \(\boldsymbol{x}\) | \(\boldsymbol{y=f(x)}\) |
| \(1\) | \(1,21\cdot 1=1,21\) |
| \(10\) | \(1,21\cdot 10=12,1\) |
| \(20\) | \(1,21\cdot 20=24,2\) |
| \(50\) | \(1,21\cdot 50=60,5\) |
En la tabla anterior se expresaron las cuentas que llevan a los valores de y. En general, sólo se pone el resultado, como en la tabla siguiente:
| \(\boldsymbol{x}\) | \(\boldsymbol{y=f(x)}\) |
| \(1\) | \(1,21\) |
| \(10\) | \(12,1\) |
| \(20\) | \(24,2\) |
| \(50\) | \(60,5\) |
Cada renglón de esta tabla se puede representar como un punto del plano en un diagrama cartesiano.
En el siguiente video, Alexánder Gómez, de Colombia, indica cómo representar puntos en un diagrama cartesiano:
En el siguiente diagrama, confeccionado con Geogebra (disponible en <https://www.geogebra.org/?lang=es>), aparecen ubicados los puntos de la tabla anterior. Cada uno de ellos es parte de la gráfica de la función:
Precio de venta (primera parte)
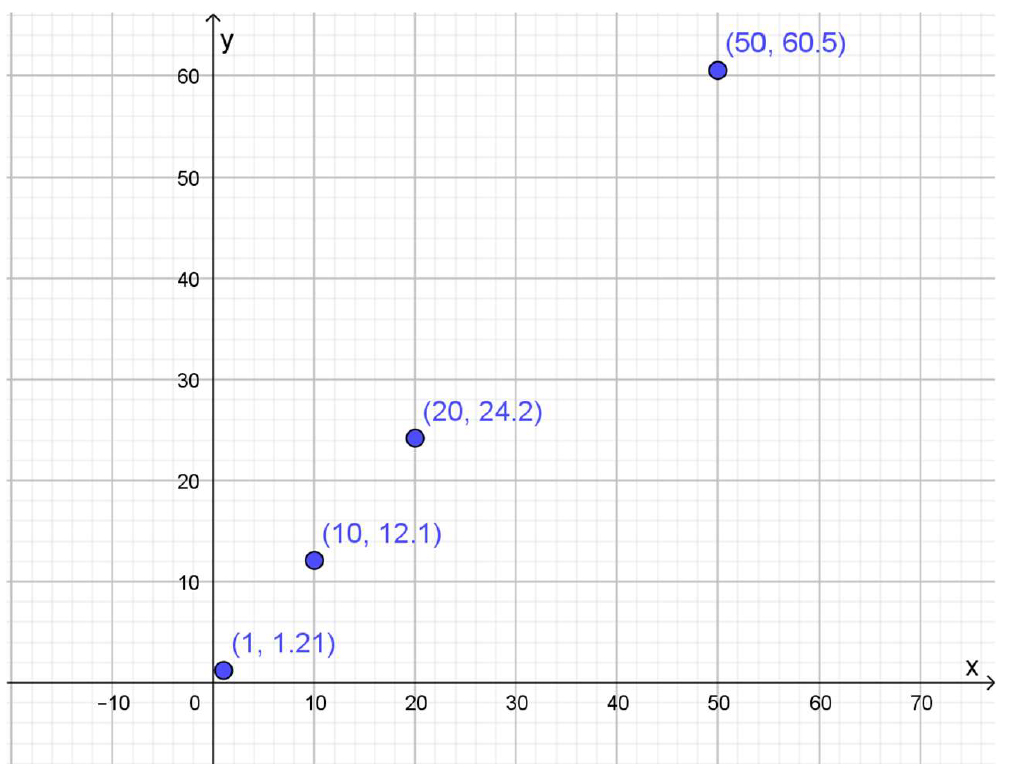
A partir de estos puntos se puede graficar la función. Como su dominio son todos los números positivos, la gráfica une los puntos del diagrama anterior, pero solo llega hasta el origen de coordenadas: no tienen sentido los precios negativos, por lo que la gráfica no es la recta completa, sino la semirrecta con origen en el par ordenado (0;0) a la que pertenecen los puntos del diagrama previo:
Precio de venta (segunda parte)
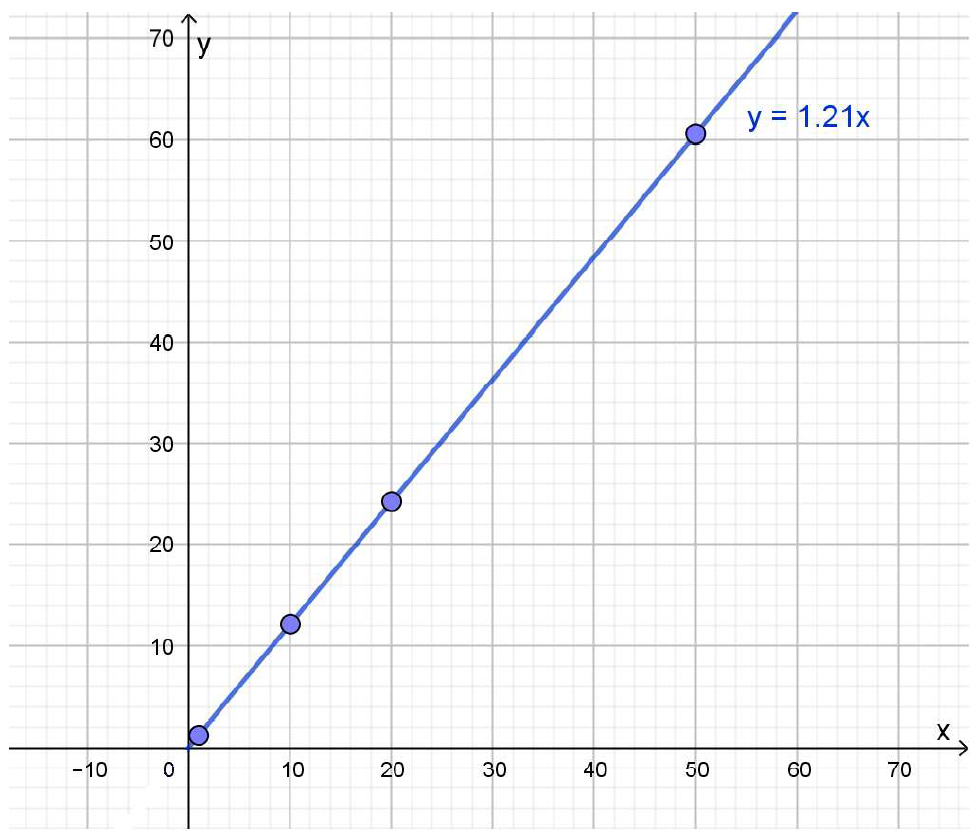
La tarifa de gas domiciliario se compone de un cargo fijo de $200 al que se suma el consumo, que cuesta $15 por cada metro cúbico. Con estos datos, se puede buscar una fórmula para hallar cuánto se pagará de gas por mes, en función del volumen consumido (antes de los impuestos, que también se cobran sobre las facturas de los servicios públicos).
Se llamará \(x\) al volumen, medido en metros cúbicos, del gas que se consumió durante un mes y \(y\) será el precio mensual a pagar (antes de los impuestos).
Esta función está definida para valores no negativos de \(x\). Por eso, es:
\[f:\ \ \left[0;\ \right.\left. \infty\right)\rightarrow\ \left[0;\ \right.\left. \infty\right)\]
Aquí, tanto el dominio como la imagen, es \(\left[0;\ \right.\left. \infty\right)\).
La fórmula de esta función es:
\[f\left(x\right)=200+15\cdot x\]
Su gráfica es:
Tarifa del gas

En el diagrama anterior, se modificó la escala del eje vertical para poder apreciar mejor la gráfica de la función.
Las sucesiones de números reales que se estudiaron en la Unidad 1 se pueden considerar como funciones cuyo dominio es N y su conjunto de llegada \(\mathbb{R}\).
Por ejemplo, la sucesión de Fibonacci se puede expresar con la tabla 3.3 y representar en un diagrama cartesiano como en la gráfica 3.5.:
| \(\boldsymbol{n}\) | \(\boldsymbol{f(n)}\) |
| \(1\) | \(1\) |
| \(2\) | \(1\) |
| \(3\) | \(2\) |
| \(4\) | \(3\) |
| \(5\) | \(5\) |
| \(6\) | \(8\) |
| \(7\) | \(13\) |
Sucesión de Fibonacci
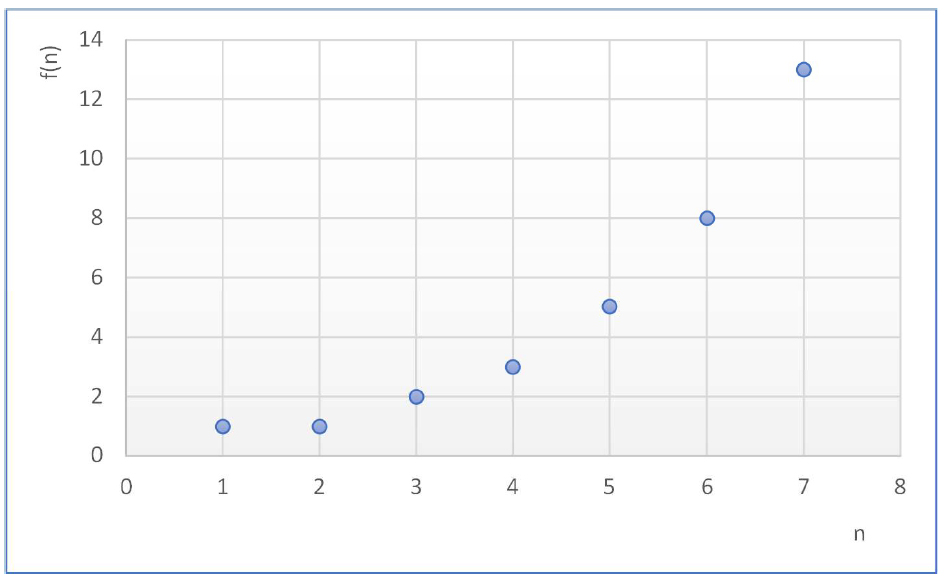
Es importante notar que la gráfica es un conjunto de puntos aislados, ya que el dominio es un conjunto discreto.
También en la unidad 1 se había ejemplificado con la sucesión \(\left\{\frac{n}{n+1}\right\}\), cuya tabla y gráfico se muestran a continuación.
| \(\boldsymbol{n}\) | \(\boldsymbol{f(n)}\) |
| \(1\) | \(0,50\) |
| \(2\) | \(0,6\) |
| \(3\) | \(0,75\) |
| \(4\) | \(0,80\) |
| \(5\) | \(0,83\) |
| \(6\) | \(0,86\) |
| \(7\) | \(0,88\) |
Otra sucesión

Se buscará el dominio y se graficarán las siguientes funciones:
- \(f\left(x\right)=\frac{x+5}{x-1}\)
- \(g\left(x\right)=x^2-3\)
- \(h(x)=\sqrt{5x+4}\)
- \(i(x)=2^x+3\)
- \(j(x)=ln\ (2x-3)\)
- \(k(x)=\left\{\begin{matrix} 2x-1 \ si\ x \leq 2 \\ 4-0,5 \cdot x\ si\ x > 2\end{matrix}\right.\)
En los siguientes apartados de esta misma unidad se verán estas funciones con mayor detalle. Pero con lo estudiado hasta aquí se pueden encontrar los dominios y las gráficas, utilizando Geogebra o buscando pares ordenados con una calculadora y ubicándolos en un diagrama cartesiano.
-
\(f\left(x\right)=\frac{x+5}{x-1}\)
Esta función es un cociente. Y en el denominador aparece la resta x-1. Como no está definida la división por cero, esta cuenta no puede tomar ese valor:
\[x-1\neq0\rightarrow x\neq1\]
Por ese motivo, el Dominio es: \(Dom= \mathbb{R}-\left\{1\right\}\)
Su gráfica es:
Gráfico 3.7.+Función ejemplo 3. a)
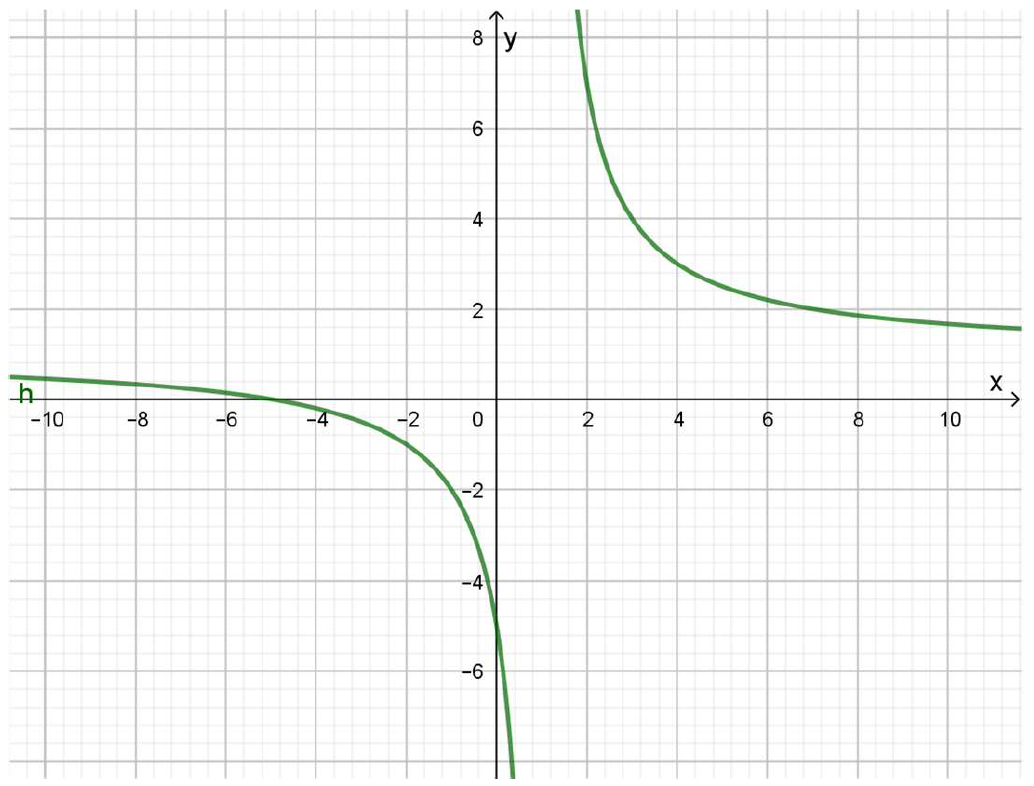
Como puede apreciarse no “corta” a la recta x=1, porque, para ese valor, la función no está definida.
En la Unidad 4 se retomará el estudio de este tipo de funciones.
-
\(g\left(x\right)=x^2-3\)
Esta función tiene una fórmula polinómica que no presenta inconvenientes con ningún valor de la incógnita. Por eso, su dominio son todos los números reales, es decir, \(Dom= \mathbb{R}\). Y su gráfica es la siguiente:
Gráfico 3.8.+Función ejemplo 3. b)

-
\(h(x)=\sqrt{5x+4}\)
Aquí, la fórmula contiene una raíz cuadrada cuyo radicando no puede ser negativo:
\[5x+4\geq0\ \ \rightarrow\ \ x\geq-\frac{4}{5}\]
Así es que el dominio es \(Dom=\left[-\frac{4}{5};\ \right.\left. \infty\right)\). Y la gráfica es:
Gráfico 3.9.+Función ejemplo 3. c)

-
\(i(x)=2^x+3\)
Este cálculo tampoco tiene restricciones para realizarse, de modo que es \(Dom= \mathbb{R}\). Y su gráfica es la siguiente:
Gráfio 3.10.+Función e ejemplo 3. d)
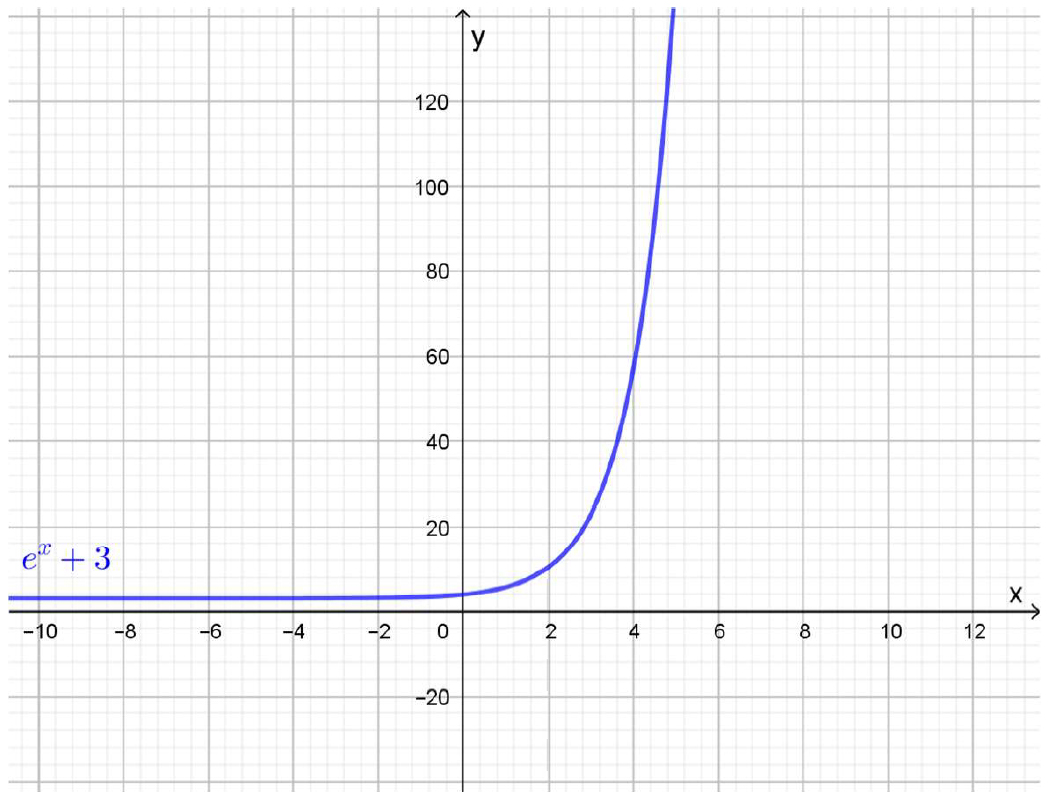
En este diagrama se modificó la escala del eje vertical para poder apreciar mejor la gráfica de la función.
-
\(j(x)=ln\ (2x-3)\)
Aquí hay un logaritmo natural. Solo admite valores positivos, por lo que deberá ser:
\[2x-3>0\ \ \ \rightarrow\ \ x>\frac{3}{2}\]
Por lo tanto, el \(Dom=\left(\frac{3}{2}\right.;\left. \infty\right)\). La gráfica es:
Gráfico 3.11.+Función ejemplo 3. e)

-
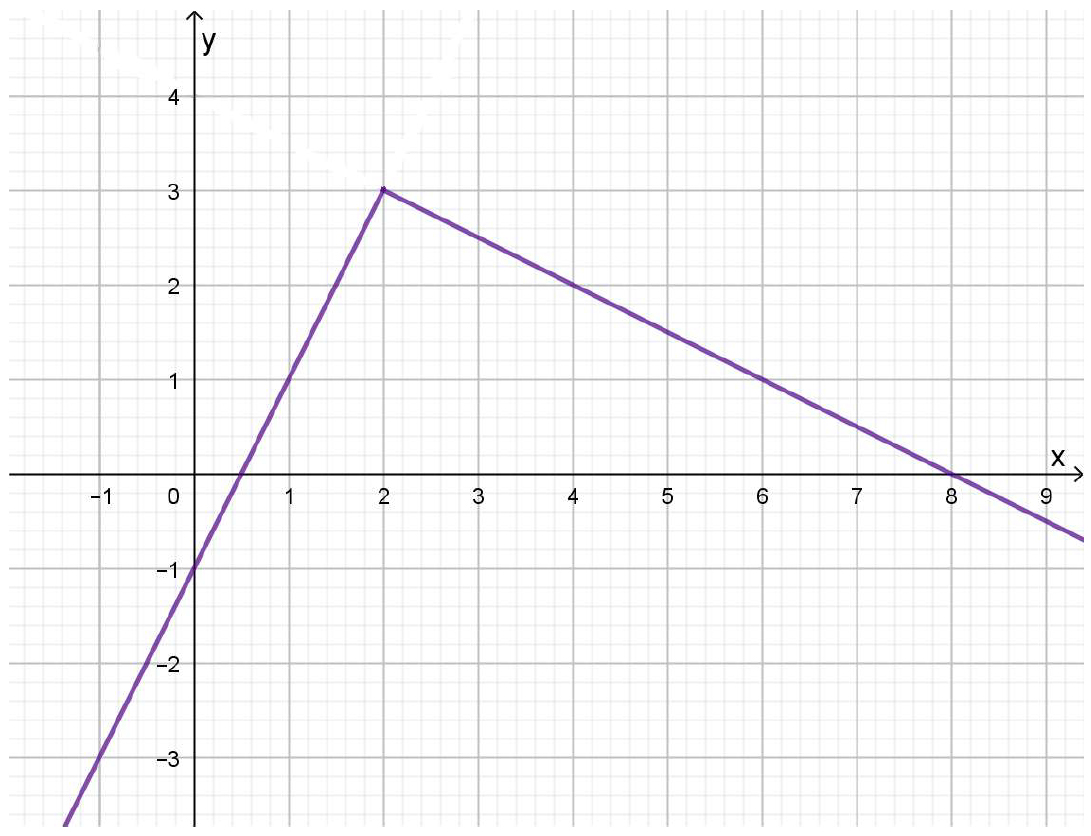
\(k(x)=\left\{\begin{matrix} 2x-1 \ si\ x \leq 2 \\ 4-0,5 \cdot x\ si\ x > 2\end{matrix}\right.\)
Esta es una función definida por tramos. Para determinar las imágenes del primer tramo, que es el intervalo \((-\infty;\ \left. 2\right]\), se utiliza la fórmula \(2x-1\). Para el resto de los números reales, es decir, para hallar las imágenes de valores pertenecientes al intervalo \((2;\ \infty)\), corresponde utilizar la fórmula \(4-0,5\cdot x\).
Como resulta posible calcular la imagen de todos los números reales, el \(Dom= \mathbb{R}\).
La gráfica es la siguiente:
Gráfico 3.12.+Función ejemplo 3. f)
3.1.1. Función inversa
A las funciones que a cada valor de \(y\) del conjunto imagen le corresponde un solo valor de \(x\) del conjunto de partida, se las llama funciones inyectivas.
Las funciones a, c, d y e del ejemplo 3.4. son inyectivas. En cambio, las funciones b y e no lo son.
Así, en la función del ejemplo 3.4.b., al valor 1 del conjunto imagen le corresponden dos valores de \(x\): \(x=2\) y \(x=-2\) y por eso no es inyectiva. Porque
\[f(-2)={(-2)}^2-3=1\ \text{ y también }\ f(2)=2^2-3=1\]
En la función del ejemplo 3.4.f., sucede lo mismo. Por ejemplo, al valor 0 del conjunto imagen le corresponden los valores de \(x=0,5\) y \(x=8\). Por eso, esta función tampoco es inyectiva.
Si una función \(f(x)\) es inyectiva existe una función inversa, \(f^{-1}\ (x)\), que es aquella que relaciona \(y\) con \(x\) en forma inversa a la función original \(f\) que relaciona \(x\) con \(y\). Es decir \(f^{-1}(y)=x\)
Para hallar la función inversa de una función inyectiva \(y = f(x)\), es preciso despejar \(x\) en función de \(y\) de la definición de la función. Así se obtienen las operaciones a realizar a \(y = f(x)\) para volver a obtener \(x\).
Se buscarán las funciones inversas de las siguientes funciones:
- \( f\left(x\right)=200+15x\)
- \(h(x)=\sqrt{5x+4}\)
Estas funciones son algunas de las que resultaron inyectivas de los ejemplos anteriores.
-
\( f\left(x\right)=200+15x\)
De esta expresión se despeja la \(x\):
\[y=200+15x\]
\[y-200=15x\]
\[\frac{y-200}{15}=x\]
\[\frac{y}{15}-\frac{200}{15}=x\]
\[\frac{y}{15}-\frac{40}{3}=x=f^{-1}(y)\]
Si se desea graficar esta expresión, se volverá a obtener el gráfico que ya se mostró en el Ejemplo 3.2. Para diferenciarlo, se “cambian las variables”:
\[\frac{x}{15}-\frac{40}{3}=y=f^{-1}(x)\]
Esta fórmula conviene escribirse ordenada de la siguiente manera:
\[f^{-1}(x)=y=\frac{x}{15}-\frac{40}{3}\]
Matemáticamente, esta función y su inversa pueden estar definidas con dominio e imagen en todos los números reales. En el Ejemplo 3.2., ambos conjuntos se habían restringido a \(\left[0;\ \right.\left. \infty\right)\), por cuestiones económicas.
En el siguiente gráfico se representan las dos funciones juntas. Es importante notar que aquí no se modificó la escala del eje vertical (como se había hecho en el Ejercicio 3.2.).
Gráfico 3.13.+Función tarifa del gas y su inversa
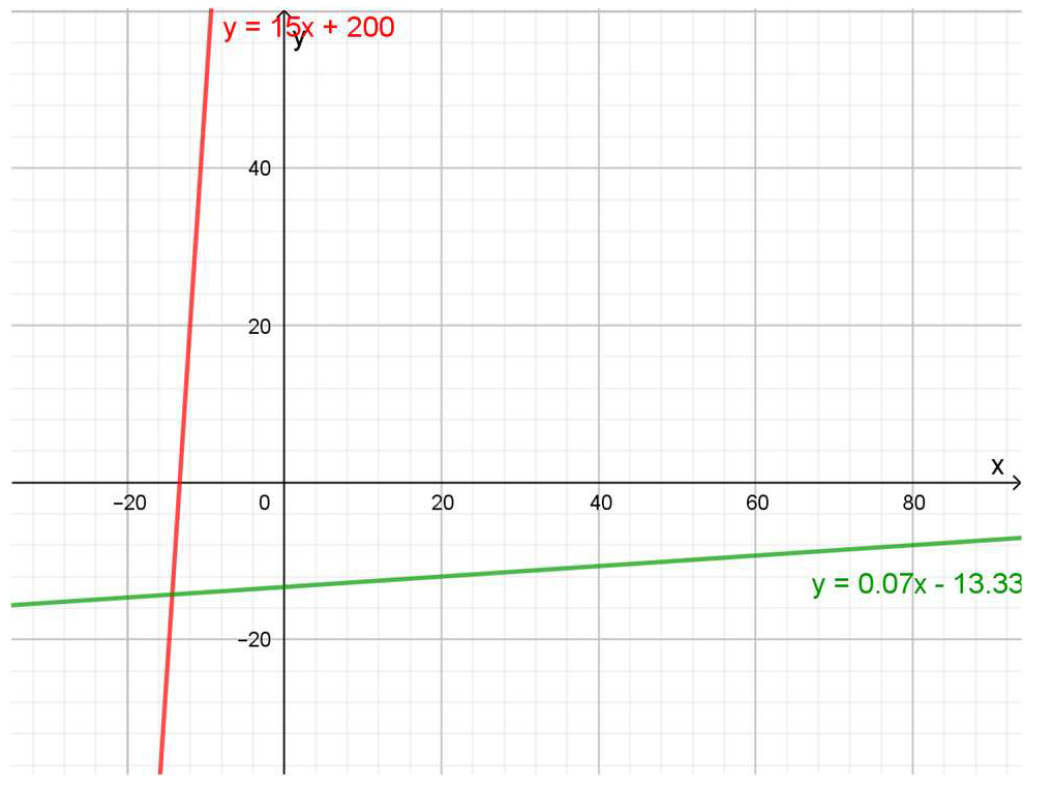
En aquel ejemplo, la función permitía calcular el monto a pagar en la factura mensual de gas, en función de la cantidad de metros cúbicos de gas consumidos.
La función inversa \(f^{-1}(x)\) permite calcular cuánto se abonó efectivamente por cada metro cúbico de gas, en función del monto pagado en la factura. Esta función es importante en el cálculo de costos de producción, que se abordará más adelante en esta misma unidad.
-
\(h(x)=\sqrt{5x+4}\)
Nuevamente, se despeja \(x\):
\[h(x)=y=\sqrt{5x+4}\]
\[y^2=5x+4\]
\[y^2-4=5x\]
\[\frac{y^2-4}{5}=x=h^{-1}(y)\]
Para graficar, se cambian las variables:
\[h^{-1}(x)=y=\frac{x^2-4}{5}\]
En este caso, es importante recordar cuál era el dominio de la función original: \(Dom=\left[-\frac{4}{5};\ \right.\left. \infty\right)\). Ahora, este conjunto será la Imagen de la función inversa. Y el conjunto Imagen de la función \(h(x)\), que era \(\left[0;\ \right.\left. \infty\right)\) ahora será el dominio. Es decir, \(h^{-1}: \left[ 0;\right. \left. \infty\right) \rightarrow \left[-\frac{4}{5}; \right.\left. \infty\right)\)
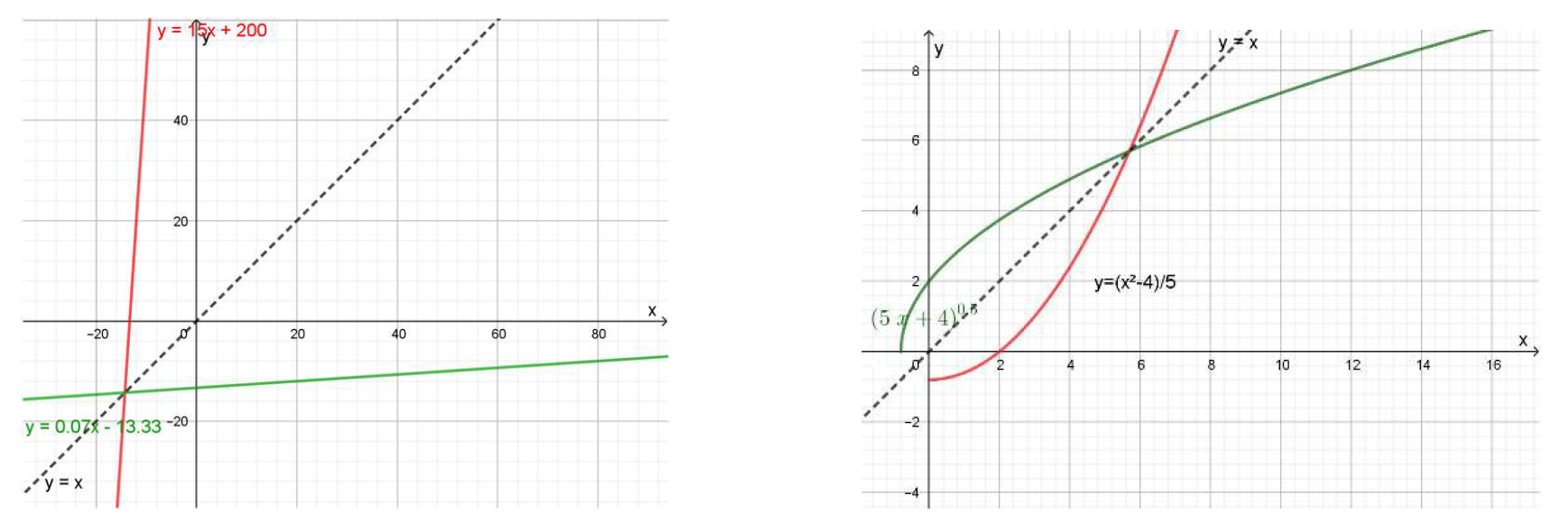
Al graficar ambas funciones en un mismo diagrama, se aprecia mejor la relación entre el dominio y la imagen de la función, en color verde y su inversa, representada en color rojo:
Gráfico 3.14.+Función ejemplo 3.4.c. y su inversa
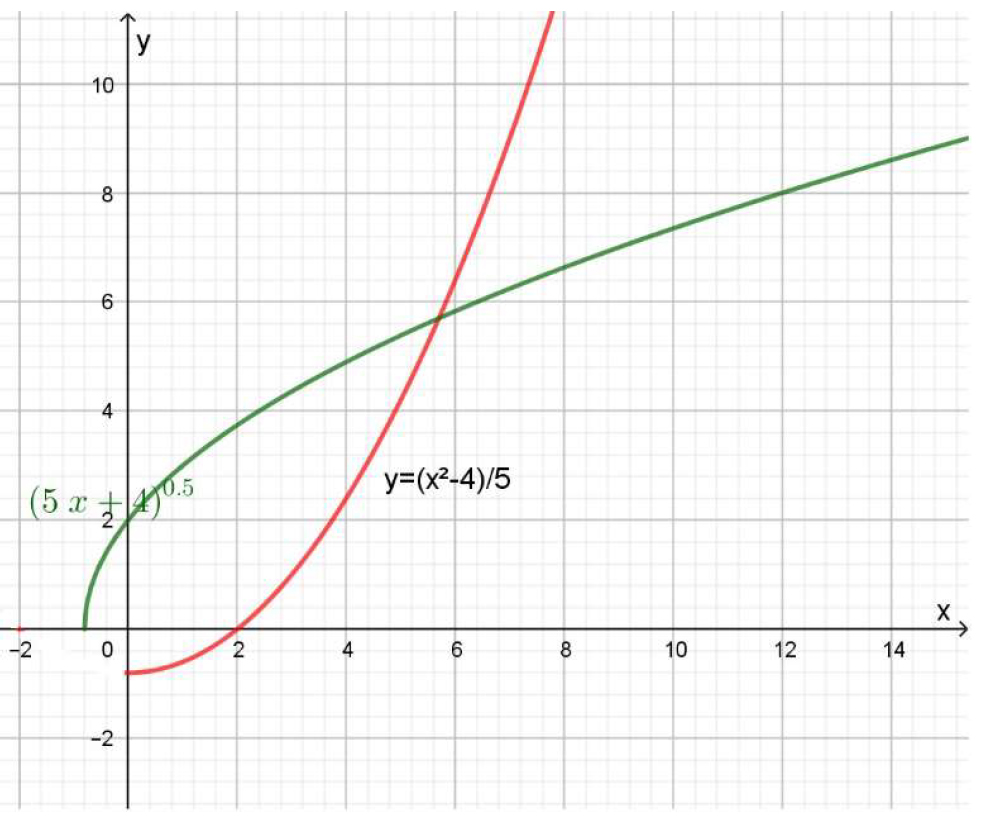
Es importante notar que las gráficas de las funciones inversas son simétricas respecto del eje \( y=x \) de las gráficas de las funciones originales:
Relación gráfica entre funciones inversas
La demanda de un mercado viene dada por \(D:q=\frac{100}{p}-10\). Se quiere representar gráficamente esta función.
En esta expresión se ve que la cantidad demandada depende del precio del producto. De modo que, en el eje horizontal deberían ubicarse los precios, que son la variable independiente. Sin embargo, en Economía se prefiere ubicar a los precios en el eje vertical.
Matemáticamente esto significa que hay que representar a la función inversa de la que aquí se tiene. Por eso, se buscará despejar los precios:
\[q=\frac{100}{p}-10\]
\[q+10=\frac{100}{p}\]
\[p\cdot\left(q+10\right)=100\]
\[p=\frac{100}{q+10}\]
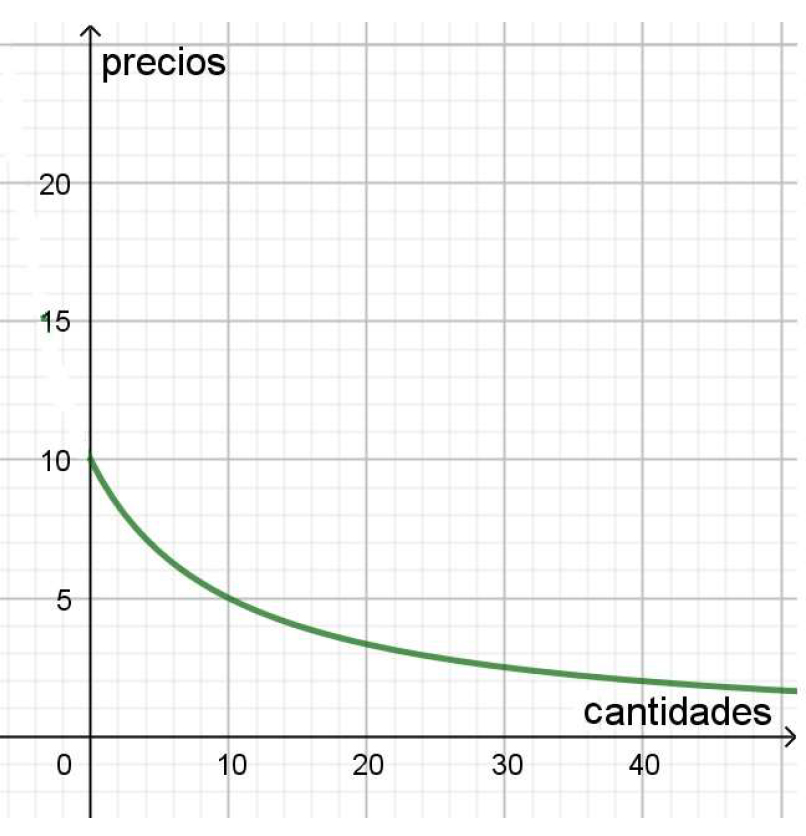
Esta es la expresión que se graficará, con los precios en el eje vertical y las cantidades en el horizontal:
Función de demanda
En <https://youtu.be/iS6IsnZ6Iqw> se puede acceder a un video, producido por la Universidad Nacional de Quilmes, en el que la profesora Gabriela Guerrero da una explicación detallada sobre las curvas de oferta y de demanda.
Busque las funciones inversas de las demás funciones inyectivas del Ejemplo 3.4.
3.1.2. Crecimiento y decrecimiento de una función
Una función es creciente en un intervalo de números reales si para todos los valores a y b de ese intervalo se cumple que \(si\ a< b\rightarrow f\left(a\right)\le f(b)\)
Por ejemplo, la función \(g\left(x\right)=x^2-3\) del ejemplo 3.4. es creciente en el intervalo \(\left[0;\ \right.\left. \infty\right)\).
Una función es decreciente en un intervalo de números reales si para todos los valores y de ese intervalo se cumple que \( si\ a< b\rightarrow f\left(a\right)\geq f(b) \)
La función \(g\left(x\right)=x^2-3\) del ejemplo 3.4. es decreciente en el intervalo \(\left(-\infty\right.;\ \left. 0\right]\).
Halle los intervalos de crecimiento y de decrecimiento de las demás funciones del Ejemplo 3.4.
3.1.3. Ceros o raíces de una función
Se denomina cero o raíz de una función a los valores de x en los cuales la gráfica de la función interseca al eje x. Es decir, si \(a\) pertenece al dominio de la función y \(f\left(a\right)=0\) se dice que \(a\) es una raíz o un cero de la función.
Por ejemplo, \(x=2\) es la única raíz de la función \(j(x)=ln\ (2x-3)\) del Ejemplo 3.4.
La función \(k(x)=\left\{\begin{matrix} 2x-1\ si\ x \leq 2 \\ 4-0,5 \cdot x\ si\ x>2\end{matrix}\right.\) de ese mismo ejemplo tiene dos raíces: \(x=\frac{1}{2}\) y \(x=8\).
3.2. Composición de funciones
En general, una función es una relación entre \(x\) e \(y\), y, a su vez, podemos relacionar el valor \(y\ =\ f(x)\), con otro número con una nueva relación o función \(g\) que relaciona dos valores, en este caso: el valor \(y\) con otro valor \(z\).
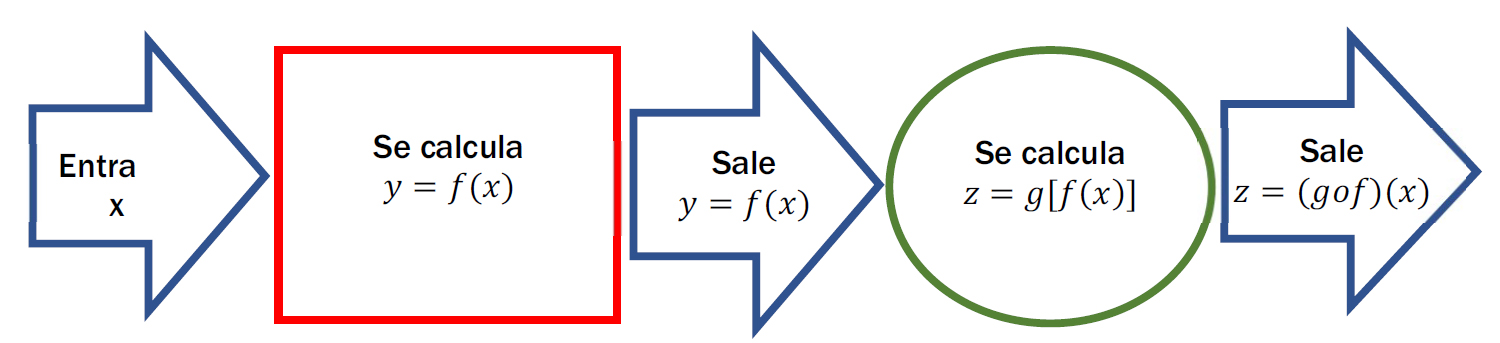
Al valor \(x\) se le asigna el valor \(y\)por medio de la función \(f\), luego a \(y\) se le asigna el valor \(z\) por medio de la función \(g\). A esta doble asignación se la llama composición. En este caso se dice que a la función \(g\) se la compone con la función \(f\) y se anota:
\[ (g\ o\ f\ )(x)\ =\ g\ \left[f(x)\right]\ \]
Composición de funciones
La dirección de cierta empresa calcula los costos totales mensuales de producción según la siguiente fórmula:
\[CT=CF+CV\]
Para cada mes, los costos fijos (\(CF\)) son de $30000, y los costos variables se calculan con base en el precio \(p\) efectivamente pagados por metro cúbico de gas, uno de sus principales insumos, así:
\[CV=\ 1,5\cdot p\]
De esta manera, la fórmula de los costos totales es:
(1)\[CT=30000+1,5\cdot p \]
Donde \(p\) es el precio efectivamente pagado por metro cúbico de gas.
Se pide que encuentre la fórmula de los costos totales de producción, en función del monto \( x\) de la factura mensual de gas.
En el Ejemplo 3.6.a. ya se había obtenido la relación entre el monto de factura y el precio abonado efectivamente por el gas:
\[y=\frac{x}{15}+\frac{40}{3}\]
En este nuevo ejemplo, al resultado de esta fórmula se lo llama \(p\) (por precio):
(2)\[p=\frac{x}{15}-\frac{40}{3}\]
Reemplazando (2) en (1), se obtiene:
\[CT=30000+1,5\cdot\left(\frac{x}{15}-\frac{40}{3}\right)\]
Al distribuir en el segundo término, se obtiene:
\[CT=30000+1,5\cdot\left(\frac{x}{15}-\frac{40}{3}\right)\]
\[CT=30000+\frac{x}{10}-20\]
\[CT=29980+\frac{x}{10}\]
Esta última es la fórmula de los costos totales de producción, en función del monto \( x\) de la factura mensual de gas.
En el ejemplo anterior se vio cómo una relación entre el monto de la factura y el precio del gas se vuelve a relacionar con los costos de producción de una empresa. Se "compusieron" la función monto de la factura de gas con la función de costos de producción.
Dadas las funciones \(f(x)=4x-2\) y \(g(x)=7x-x^2\) se pide que calcule \((gof)(x)\) y \((fog)(x)\).
\[(gof)(x)=g\left[f(x)\right]=g\left[4x-2\right]\]
Esta última expresión indica que hay que aplicar la función \(g\) a la expresión \(\left[4x-2\right]\). Es decir que, cada vez que en la fórmula de \(g\) aparezca una \(x\), hay que ubicar \(\left[4x-2\right]\):
\[(gof)(x)=g\left[f(x)\right]=g\left[4x-2\right]=7\cdot\left[4x-2\right]-\left[4x-2\right]^2\]
Solo falta resolver los cálculos indicados:
\[\begin{gather*} (gof)(x)=g\left[f\left(x\right)\right]=g\left[4x-2\right]=28\cdot x-14-\left({16\cdot x}^2-16\cdot x+4\right)=\\ =28x-14-16x^2+16x-4\\ (gof)(x)=-16x^2+44x-18 \end{gather*}\]
Entonces, \((gof)(x)=-16x^2+44x-18\)
Para calcular \((fog )(x)\) la composición es en orden inverso:
\[(fog )(x)=f\left[g(x)\right]=f\left[7x-x^2\right]\]
Aquí es necesario aplicar la función f a la expresión \(\left[7x-x^2\right]\):
\[\left(fog\right)\left(x\right)=f\left[g\left(x\right)\right]=f\left[7x-x^2\right]=4\cdot\left[7x-x^2\right]-2=28\cdot x-4\cdot x^2-2=\]
\[\left(fog\right)\left(x\right)=-4\cdot x^2+28\cdot x-2\]
Por lo tanto, \(\left(fog\right)\left(x\right)=-4\cdot x^2+28\cdot x-2\).
Como puede apreciarse, la composición de dos funciones no es conmutativa, ya que al cambiar el orden, se obtienen resultados diferentes.
-
Halle \((gof)\ (x)\ y\ \left(fog\right)\left(x\right)\) con las siguientes funciones:
- \(f(x)=3x+2\ g(x)=2x^2-3x\)
- \(f(x)=ln(x)+2\ g(x)=x^2-8\). En este caso, halle también el dominio de cada función y el dominio de las funciones compuestas. Compare ambos resultados.
- Las funciones del ejemplo 3.6. con sus inversas. Se comprobará que: \(\left(fof^{-1}\right)(x)=x\)
-
En una fábrica de zapatos, su dueño observó que el número de zapatos producido por día dependía de la cantidad de empleados que asistían a trabajar. Siendo x el número de empleados, la cantidad de zapatos producida estaba representada por la relación:
\[z\left(x\right)=\frac{30x-x^2}{3}\]
Por su parte, el dueño de la empresa obtiene por cada zapato que vende un beneficio de $80. El beneficio puede ser entonces representado por la función \(f(x) = 80 x\) si usamos \(x\) en este caso para representar el número de zapatos vendido. ¿Qué representa la composición de las funciones \(f\) y \(z, (f o z) (x)\)?
3.3. Funciones lineales
Se define como función lineal a una función de la forma \(f(x)=a\cdot x+b\) donde \(a\) y \(b\) son números reales cualesquiera. Al número que multiplica a la variable, \(a\), se lo llama pendiente y al término independiente, \(b\), ordenada al origen. El dominio y la imagen de esta función es todo el conjunto de números reales \(\mathbb{R}\) y su gráfico es una recta.
El precio de cada lata de 20 litros de pintura es de $4000. Además, se abonan $300 por gastos de envío. Calcule el monto de la factura a pagar en función de la cantidad x de latas de pintura que se adquieran. Identifique la pendiente y la ordenada al origen y confeccione un diagrama cartesiano de la situación.
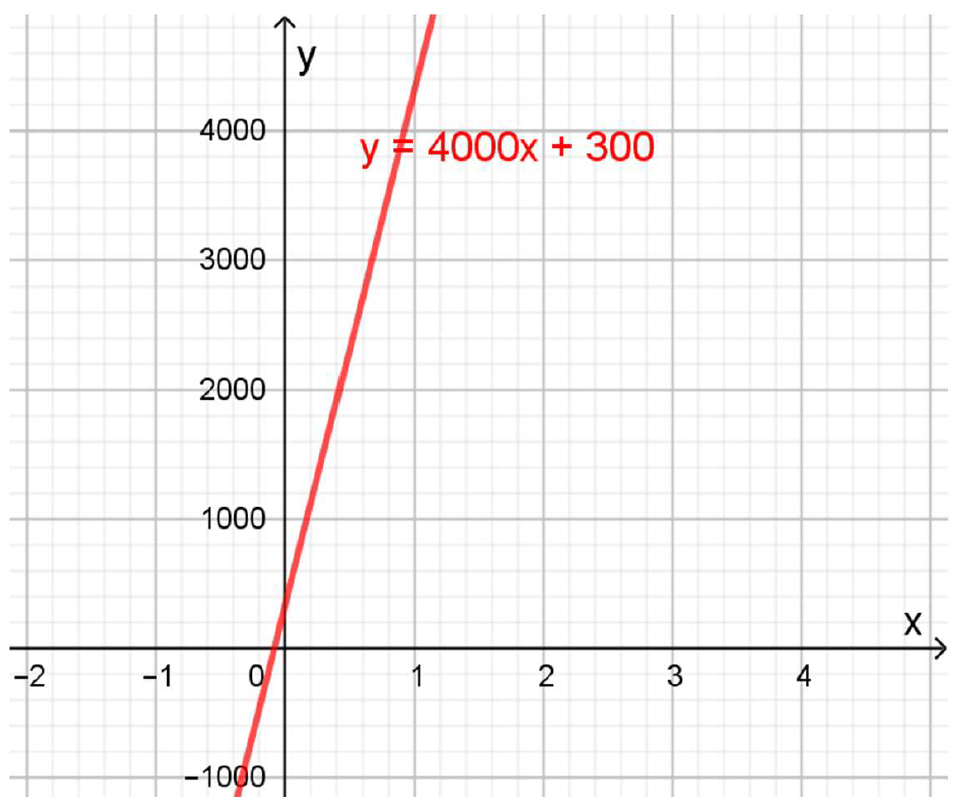
En este caso, \(f(x)=4000\cdot x+300\).
La pendiente es $4000 y $300 es la ordenada al origen.
Para hacer el diagrama es necesario modificar la escala del eje vertical y, así, poder apreciar la recta.
Función monto de la factura
Grafique en un mismo diagrama las siguientes funciones lineales:
\[\begin{align*} f_1\left(x\right)&=3x+1 & f_2\left(x\right)&=-1 & f_3\left(x\right)&=-2x+2 \\ f_4\left(x\right)&=-2x-1 & f_5\left(x\right)&=\frac{1}{2}x-1 & f_6\left(x\right)&=-\frac{1}{3}x \end{align*} \]
Funciones lineales

En el diagrama del Ejemplo 3.9. se pueden apreciar varias propiedades de las funciones lineales:
Crecimiento y decrecimiento
Las rectas cuyas fórmulas tienen una pendiente positiva (\(f_1\) y \(f_5\)), son funciones crecientes.
Las rectas en cuyas fórmulas el valor de a es negativo (\(f_3, f_4\) y \(f_6\)), son funciones decrecientes.
Si el valor de a es cero, la función es constante (\(f_2\)).
Ordenada al origen
La gráfica de cada recta interseca al eje vertical en el valor \(b\) de la fórmula.
Paralelismo
Las rectas paralelas tienen la misma pendiente
En el punto 1.4.1. del Material Didáctico Multimedia Guía de ejercicios resueltos hay un gráfico de Geogebra con un deslizador que permite observar diferentes funciones con sus gráficos en los que se advierten fácilmente estas propiedades.
En <https://miel.unlam.edu.ar/data/contenido/INGRESOMATE/POSICIONES-RELATIVAS-DE-DOS-RECTAS-EN-EL-PLANO-final1.pdf> hay un breve apunte en el que se menciona la relación entre las pendientes de las rectas paralelas y también la de las perpendiculares.
3.3.1. Ecuación de la recta que pasa por dos puntos
Cuando se conocen las coordenadas de dos puntos pertenecientes a una recta, se puede encontrar su fórmula.
Si se consideran conocidas las coordenadas de los puntos \(A=\left(x_1;\ y_1\right)\) y \(B=\left(x_2;\ y_2\right)\), ambos pertenecientes a una recta cuya función es \(f\left(x\right)=a\cdot x+b\), encontrar la fórmula significa hallar los valores de \(a\) (la pendiente) y de \(b\) (la ordenada al origen), de modo tal que se cumplan simultáneamente las siguientes ecuaciones:
(1)(2)\[\left\{\begin{matrix}y_1=a\cdot x_1+b \\ y_2=a\cdot x_2+b \end{matrix}\right.\]
Utilizando el método de sustitución, de la ecuación (1) se obtiene que:
(3)\[y_1-a\cdot x_1=b\]
Y, al reemplazar la ecuación (3) en la (2), queda:
\[y_2=a\cdot x_2+y_1-a\cdot x_1\]
\[y_2=y_1+a\cdot x_2-a\cdot x_1\]
\[y_2{-y}_1=a\cdot{(x}_2-x_1)\]
Finalmente al despejar la pendiente \(a\), se obtiene:
(4)\[a=\frac{y_2-y_1}{x_2-x_1}\]
La ecuación (4) también se anota como \(a=\frac{y_2-y_1}{x_2-x_1}=\frac{\Delta y}{\Delta x}\). El último miembro se lee “delta y sobre delta x” e indica que la pendiente es el “cociente incremental” entre dos puntos de la recta. En un gráfico cartesiano, estos incrementos “delta” se pueden apreciar de la siguiente manera:
Pendiente

Una vez obtenido el valor de la pendiente, el resultado de la ecuación (4) se reemplaza en la (3) y se calcula la ordenada al origen de la recta:
\[b=\ y_1-\frac{y_2-y_1}{x_2-x_1}\cdot x_1 \]
Encuentre la ecuación de la recta que une los puntos \(\left(-2;3\right)\) y \(\left(2;1\right)\).
Para encontrar la pendiente se utiliza la fórmula (4):
\[a=\frac{y_2-y_1}{x_2-x_1}\]
Es conveniente, para facilitar el uso de la fórmula, distinguir que en este ejercicio es:
\[x_1=-2\]
\[y_1=3\]
\[x_2=2\]
\[y_2=1\]
Por lo tanto:
\[a=\frac{1-3}{2-(-2)}=-\frac{2}{4}=-\frac{1}{2}\]
Entonces, la pendiente es:
\[b=\ 3-\frac{-1}{2}\cdot\left(-2\right)=3-1=2 \]
De este modo, la ecuación de la recta que une los puntos \(\left(-2;3\right)\) y \((2;1)\) es:
\[y=-\frac{1}{2}\cdot x+2\]
Si se realiza un gráfico con Geogebra se puede comprobar que, efectivamente, esta recta contiene a los puntos del enunciado.
3.3.2. Ceros o raíces de una función lineal
Las funciones lineales tienen a lo sumo una raíz. Es decir, intersecan al eje horizontal como máximo en un único punto.
Para hallarla, se resuelve la ecuación:
\[a\cdot x+b=0\]
Encuentre la raíz de la función del Ejemplo 3.9.:
\[f_1\left(x\right)=3x+1\]
Con este fin, se deberá resolver:
\[3x+1=0\]
\[3x=0-1=-1\]
\[x=-\frac{1}{3}\]
Por lo tanto, esta recta interseca al eje horizontal en el punto de coordenadas \(\left(-\frac{1}{3};0\right)\), como puede apreciarse en el Gráfico 3.19.
Busque las raíces de las otras funciones lineales del Ejercicio 3.11.
3.3.3. Rectas verticales
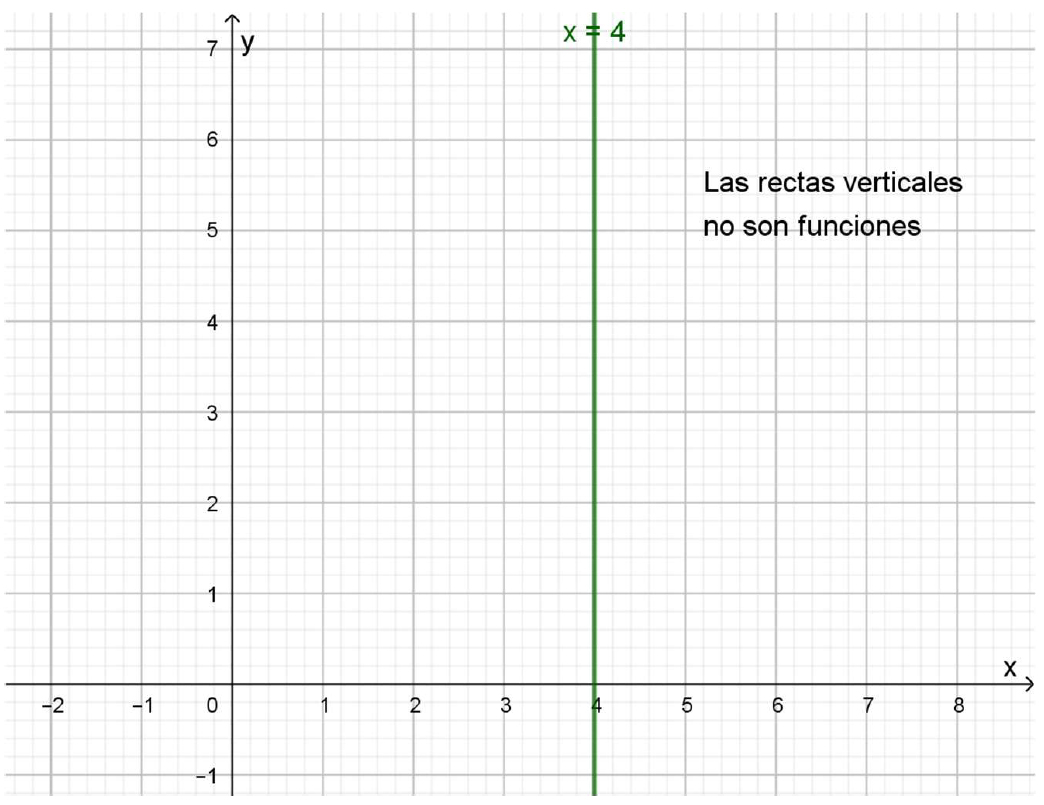
Si bien las rectas verticales no son funciones, es importante notar que sus fórmulas son del tipo \(x=c\) donde \(c\) es un número real cualquiera.
La recta \(x=4\), cuya gráfica es la del gráfico 3.21., no es una función porque el único número real que tiene imagen es el 4. Además, esa imagen no es única, ya que todos los pares ordenados de la forma \((4; y)\) cumplen con la ecuación de esta recta.
Recta vertical
3.4. Funciones cuadráticas
Se define como función cuadrática a una función de la forma
\[f(x) = a x^2 + b x + c\]
donde \(a\), \(b\) y \(c\) son números reales cualesquiera, debiendo ser \(a\ \neq\ 0\). El dominio de esta función es todo el conjunto de números reales \(\mathbb{R}\) y su gráfico es una parábola.
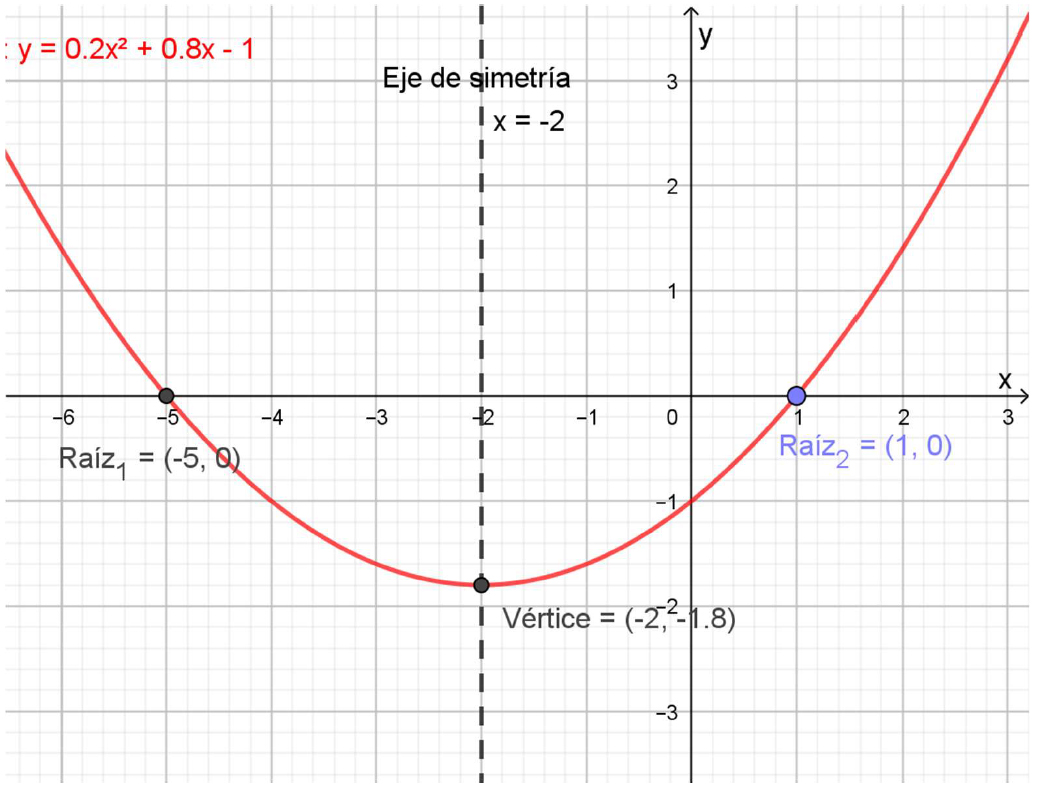
La función \(f\left(x\right)=\frac{1}{5}\cdot x^2+\frac{4}{5}\cdot x-1\) es cuadrática. En esta fórmula se puede reconocer que: \(a=\frac{1}{5},\ b=\frac{4}{5}\) y \(c=-1\).
Para graficarla manualmente, se puede armar una tabla de valores y representarlos en un diagrama cartesiano. Aquí se muestra el diagrama hecho con Geogebra. En él se destacaron los elementos de una parábola.
Parábola cóncava hacia arriba
3.4.1. Elementos de la parábola
Concavidad
La parábola del gráfico anterior es cóncava hacia arriba porque sus ramas o brazos se orientan hacia arriba. Las parábolas cóncavas hacia abajo abren sus ramas o brazos hacia abajo.
La diferencia en la orientación está definida por el signo del coeficiente \(a\):
- si \(a>0\) la parábola es cóncava hacia arriba
- si \(a<0\) la parábola es cóncava hacia abajo
En la próxima unidad se estudiará una definición más precisa de este concepto.
Raíces
Las parábolas tienen a lo sumo dos raíces. Esto significa que podrían no tenerlas o podría ser solo una. La parábola del gráfico 3.22. tiene dos: \(-5\) y \( 1\). Las simbolizaremos \(x_1\) y \(x_2\).
Ya se estudió que la raíz de una función cumple con:
\[f\left(x\right)=0\]
En el caso de una función cuadrática, será:
\[ a x^2 + b x + c=0\]
Para resolver esta ecuación, se “completará el cuadrado”:
\[a\cdot\left(x^2+\frac{b}{a}x+\frac{c}{a}\right)=0\]
\[\left(x^2+\frac{b}{a}x+\frac{c}{a}\right)=\frac{0}{a}=0\]
Para poder escribir el primer miembro de esta expresión como un cuadrado perfecto, se deberá reescribir de la siguiente manera:
\[x^2+\frac{b}{a}x+\frac{c}{a}=0=\left(x+\frac{b}{2a}\right)^2+\frac{c}{a}-\left(\frac{b}{2a}\right)^2\]
En esta expresión, se puede despejar \(x\):
\[\left(x+\frac{b}{2a}\right)^2+\frac{c}{a}-\left(\frac{b}{2a}\right)^2=0\]
\[\left(x+\frac{b}{2a}\right)^2=0-\left[\frac{c}{a}-\left(\frac{b}{2a}\right)^2\right]=\left(\frac{b}{2a}\right)^2-\frac{c}{a}=\frac{b^2}{4\ a^2}-\frac{c}{a}=\frac{b^2-4ac}{4\ a^2}\]
En el siguiente paso, como conviene recordar que hay dos valores que podrían satisfacer el cuadrado del primer miembro de la ecuación anterior, se pone \(\pm\)adelante de la raíz cuadrada:
\[x+\frac{b}{2a}=\pm\sqrt{\frac{b^2-4ac}{4\ a^2}}=\pm\frac{\sqrt{b^2-4ac}}{\sqrt{4\ a^2}}=\pm\frac{\sqrt{b^2-4ac}}{2a}\]
Entonces:
\[x=\pm\frac{\sqrt{b^2-4ac}}{2a}-\frac{b}{2a}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
Se obtiene así la conocida fórmula de Bhaskara (lleva este nombre en honor al matemático y astrónomo indio, quien en el siglo XII dedujo esta fórmula).
En <https://www.biografiasyvidas.com/biografia/b/bhaskara.htm> se puede encontrar una breve biografía de Bhaskara.
El radicando de la raíz cuadrada de esta fórmula se llama discriminante, porque:
- Si \(b^2-4ac<0\), esa raíz no tiene soluciones reales y la parábola no tendrá raíces.
- Si \(b^2-4ac=0\), esa raíz valdrá cero y la parábola tendrá una única raíz.
- Si \(b^2-4ac>0\), esa raíz tiene solución y la parábola tendrá dos raíces: \[x_1=\frac{-b-\sqrt{b^2-4ac}}{2a}\text{ y } x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}\]
Las funciones cuadráticas que tienen raíces se pueden expresar en forma factorizada de la siguiente manera:
\[f\left(x\right)=a\ x^2\ +\ b\ x\ +\ c=a\cdot\left(x-x_1\right)\cdot\left(x-x_2\right)\]
Eje de simetría
Las parábolas tienen un eje de simetría vertical al que pertenece el vértice. Esto significa que, si se dobla la hoja en la que está graficada la parábola por esa recta, las dos ramas de la parábola coincidirán. El eje de simetría no es parte de la gráfica y su fórmula es la de una recta vertical:
\[Eje\ de\ simetría: x=x_v\]
En esta fórmula \(x_v\) simboliza la abscisa del vértice de la parábola.
En el gráfico 3.22., el eje de simetría es \(x=-2\).
En general, es:
\[x_v=\frac{x_1+x_2}{2}=-\frac{b}{2a}\]
En la fórmula anterior, \(x_1\ y\ x_2\) son las raíces, si las hubiera, de la parábola.
Vértice
El vértice es el punto a partir del cual la parábola cambia el sentido del crecimiento. En el gráfico 3.22., el vértice es \((-2;\ -1,8)\), porque en el intervalo \((-\infty;\ -2)\) la parábola es decreciente y en el intervalo \((-2;\ \infty)\), la parábola crece.
En general, se simbolizará así:
\[V=(x_v;\ y_v)\]
Para hallar la \(y_v\) se calcula la imagen de \(x_v\) por la función. Entonces, es:
\[V=\left(-\frac{b}{2a};f\left(-\frac{b}{2a}\right)\right)\]
Las funciones cuadráticas se pueden expresar en forma canónica de la siguiente manera:
\[f\left(x\right)=a\ x^2\ +\ b\ x\ +\ c=a\cdot\left(x-x_v\right)^2+y_v\]
Busque los elementos de la parábola \(f\left(x\right)=-x^2-4x-3\)
Comenzaremos por distinguir que \(a=-1, b=-4\), y \(c=-3\).
La gráfica de esta función es cóncava hacia abajo porque \(a=-1\).
Además, las raíces serán:
\[x_1=\frac{-(-4)-\sqrt{{(-4)}^2-4\cdot(-1)\cdot(-3)}}{2\cdot(-1)}=\frac{4-\sqrt{16-12}}{-2}=\frac{4-2}{-2}=-1\]
y
\[x_2=\frac{-\left(-4\right)+\sqrt{{(-4)}^2-4\cdot(-1)\cdot(-3)}}{2\cdot(-1)}=\frac{4+\sqrt{16-12}}{-2}=\frac{4+2}{-2}=-3\]
Entonces, esta función cuadrática se puede escribir en su expresión factorizada así:
\[f\left(x\right)=-1\cdot(x+1)\cdot(x+3)\]
La abscisa del vértice es:
\[x_v=-\frac{\left(-4\right)}{2\cdot\left(-1\right)}=-\frac{-4}{-2}=-2\]
Aquí se calculó con la fórmula \(x_v=-\frac{b}{2a}\). Por supuesto, si se utiliza \(x_v=\frac{x_1+x_2}{2}\) el resultado es el mismo:
\[x_v=\frac{-1+(-3)}{2}=\frac{-4}{2}=-2\]
Para buscar la ordenada del vértice, se calcula la imagen de \(x_v\):
\[f\left(-2\right)=-\left(-2\right)^2-4\cdot\left(-2\right)-3=-4+8-3=1\]
Por lo tanto, el vértice tiene coordenadas \((-2; 1)\). Y la expresión canónica de esta parábola es:
\[f\left(x\right)=-\left(x+2\right)^2+1\]
El eje de simetría es \(x=x_v\), por lo tanto, en este ejemplo es \(x=-2\).
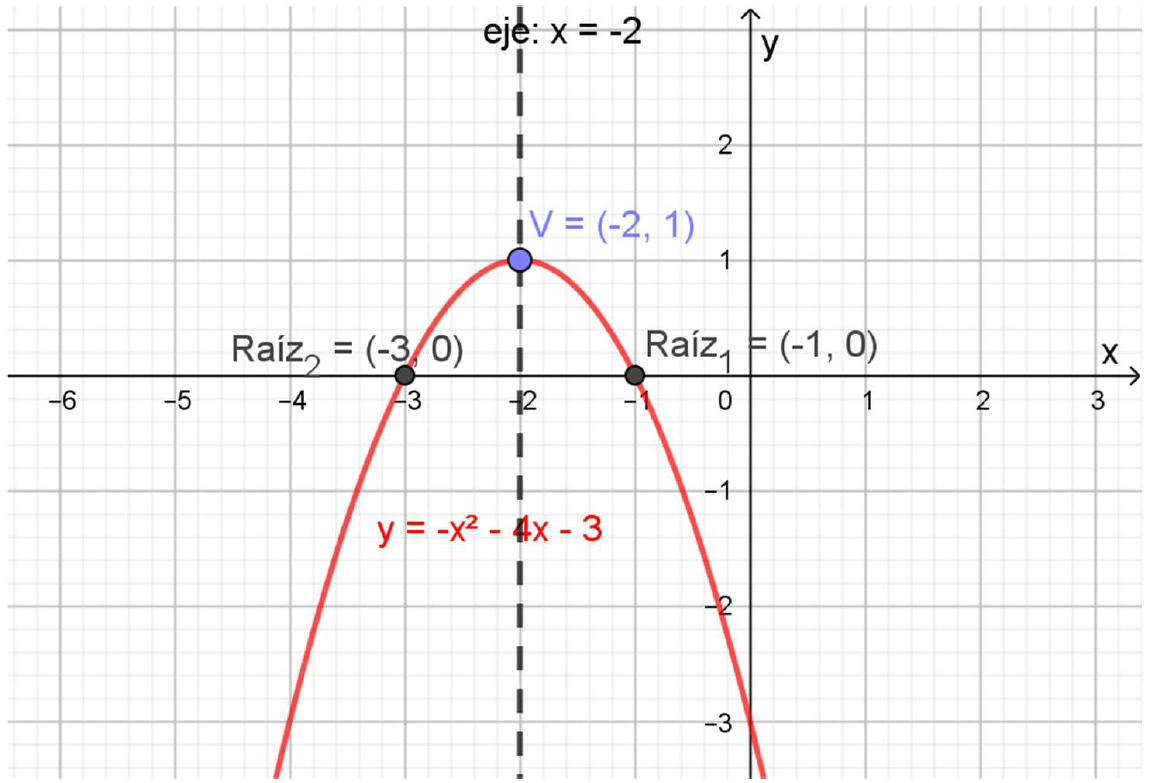
En el siguiente gráfico se destacaron los elementos que aquí se calcularon.
Parábola cóncava hacia abajo
En <https://www.youtube.com/watch?v=k9LdPkaGwhw> hay un video en el que se explica cómo armar tablas de valores en Excel. También se las utiliza para graficar funciones. Aquí se prefiere graficar con Geogebra, pero puede resultar de utilidad.
Una empresa monopólica enfrenta una función de demanda dada por:
\[D:q=2000-4\cdot p\]
Se necesita relacionar los ingresos totales con las cantidades producidas (y vendidas).
Como ya se vio en ejemplos anteriores, el ingreso total viene dado por:
\[IT=p\cdot q\]
En esta última fórmula se podría reemplazar q directamente de la función de demanda, ya que esta empresa es monopólica: ella sola provee a toda la demanda. Pero el ingreso total, en ese caso, quedaría expresado en función de los precios.
Para obtener el ingreso en función de las cantidades, se despejará el precio de la función de demanda:
\[q=2000-4\cdot p\]
\[4\cdot p=2000-q\]
\[p=\frac{2000-q}{4}=500-\frac{1}{4}\cdot q\]
Ahora sí, esta expresión se reemplaza en la de ingreso total:
\[IT=\left(500-\frac{1}{4}\cdot q\right)\cdot q\]
\[IT=500q-\frac{1}{4}q^2\]
Esta es la expresión buscada. A partir de ella, se puede buscar el máximo ingreso y para qué cantidades producidas y vendidas se obtendrá. Ese punto es el vértice de la parábola:
\[q_v=-\frac{500}{2\cdot\left(-\frac{1}{4}\right)}=1000\]
Y la ordenada correspondiente es:
\[p_v=f\left(q_v\right)=500\cdot1000-\frac{1}{4}{\cdot1000}^2=250000\]
¿Cuál será el precio de venta? Esa respuesta se obtiene al reemplazar 1000 en la función inversa de la demanda:
\[p=500-\frac{1}{4}\cdot1000=250\]
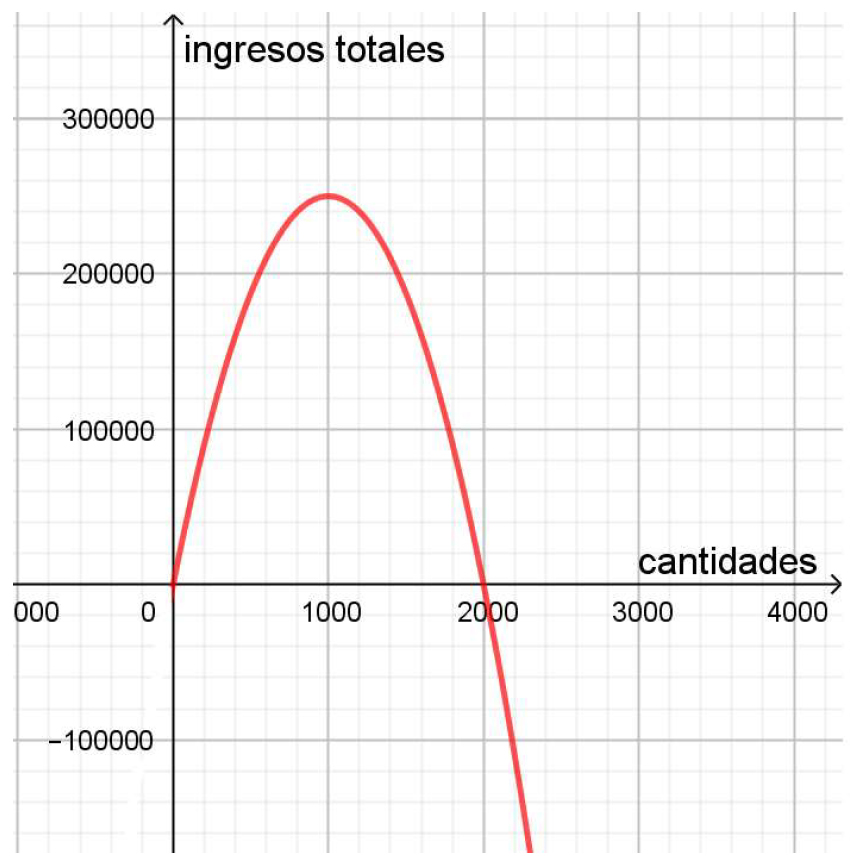
Es decir, el ingreso máximo será de $250000 y se obtendrá al producir y vender 1000 unidades a $250 cada una.
El ingreso total de la empresa monopolista es una parábola cuya gráfica es la siguiente:
Ingresos totales de empresa monopólica
Busque el punto (o los puntos) de intersección entre las funciones
\(f\left(x\right)=x^2+4x+8\ \ \ \) y \( \ \ \ g \left(x\right)={-x}^2-4x+2\)
Para resolver esta cuestión, planteamos la siguiente ecuación:
(1)\[f(x)=g(x)\]
Reemplazando por las fórmulas correspondientes a cada una de estas funciones, se obtiene:
(2)\[x^2+4x+8=-x^2-4x+2 \]
Y para resolver esta ecuación, se puede utilizar de la fórmula del cálculo de las raíces de la función cuadrática:
\[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
Esa fórmula es la manera de resolver una ecuación como la siguiente:
\[x^2+b\cdot x+c=0\]
Pero la ecuación 2 no está igualada a cero. De manera que es necesario comenzar por igualar a cero la expresión, antes de utilizar la fórmula. Agrupando los términos del segundo miembro, en el primero, se obtiene:
\[x^2+4x+8+x^2+4x-2=0\]
Al resolver las operaciones, se llega a:
\[2\cdot x^2+8\cdot x+6=0\]
En esta expresión resultan \(a=2\), \(b=8\) y \(c=6\).
Y cuando se reemplazan en la fórmula, se obtiene:
\[x_{1,2}=\frac{-8\pm\sqrt{8^2-4\cdot2\cdot6}}{2\cdot2}=\frac{-8\pm\sqrt{64-48}}{4}=\frac{-8\pm\sqrt{16}}{4}=\frac{-8\pm4}{4}\]
Al resolver este último cálculo, se concluye que los dos posibles valores de x son:
\(x_1=-1\ \ \ \) y \( \ \ \ \ x_2=-3\).
Así, ya se obtuvieron las abscisas de los puntos de intersección entre las funciones. Falta calcular las ordenadas correspondientes. Para ello, se reemplazan los valores de x en las fórmulas correspondientes:
\[f\left(-1\right)={(-1)}^2+4\cdot\left(-1\right)+8=5=g\left(-1\right)=-\left(-1\right)^2-4\cdot\left(-1\right)+2 \]
y
\[f\left(-3\right)={(-3)}^2+4\cdot\left(-3\right)+8=5=g\left(-1\right)=-\left(-3\right)^2-4\cdot\left(-3\right)+2\]
Entonces, los puntos de intersección entre las funciones \(f(x)\) y \(g(x)\) son \((-1;5)\) y \((-3;5)\).
Si se grafican ambas funciones en el mismo diagrama cartesiano, se puede comprobar que estas respuestas son correctas. Para hacer el gráfico manualmente, se puede confeccionar una tabla de valores, o, como en este ejemplo ambas funciones son cuadráticas, se puede buscar el vértice de cada una de ellas y sus raíces, para facilitar el trazado de la curva. (Nótese que \(f(x)\) no tiene raíces).
Intersección entre dos parábolas
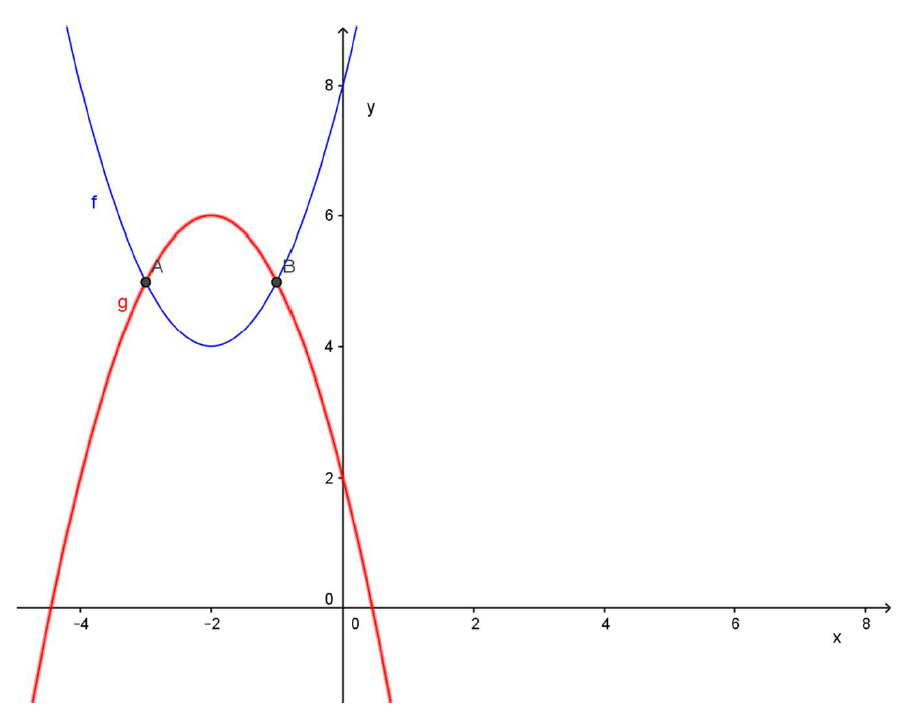
En el gráfico se aprecia que, efectivamente, las funciones se intersecan, se “cortan”, en los puntos encontrados analíticamente.
-
Encuentre los elementos, exprese en forma factorizada y canónica y grafique la función \(f\left(x\right)=-{\frac{1}{2}x}^2+2x+6\).
-
Halle los puntos en los que las siguientes funciones se intersecan, gráfica y analíticamente:
- \(f\left(x\right)=5x+1 \ \ \ \ \) y \( \ \ \ \ g\left(x\right)=x^2-2x+1\)
- \(f\left(x\right)=x^2-2x-8 \ \ \ \ \) y \( \ \ \ \ g\left(x\right)=-2x^2+4x-2\)
3.5. Funciones polinómicas
Se define la función polinómica como una función de la forma:
\[f\left(x\right)=a_0+a_1x+a_1x^1+a_2x^2+a_3x^3+a_4x^4+\ldots++a_nx^n\]
donde \(n\), la mayor potencia de la variable \(x\) con coeficiente \(a_n\) distinto de cero, es el grado de la función polinómica.
El dominio de estas funciones es el conjunto de todos los números reales \(\mathbb{R}\).
Por ejemplo, \(f\left(x\right)=6x-5\) es una función polinómica de grado 1. En esta función, sería \(a_0=-5\) y \(a_1=6\). La gráfica correspondiente es una recta creciente, como ya se estudió anteriormente en esta misma unidad.
Del mismo modo, la función \(g\left(x\right)=-4x^2+2x-1\) es una función polinómica de grado 2. Aquí, los valores que aquí toman los coeficientes son: \(a_0=-1\), \(a_1=2\) y \(a_2=-4\).
Grafique la función \(f\left(x\right)={-x}^3+x^2+14x-24\).
Esta función es polinómica de grado 3.
Para graficarla manualmente, se puede construir una amplia tabla de valores y luego ubicar los pares ordenados así obtenidos en un diagrama cartesiano y unirlos en orden:
| \(\boldsymbol{x}\) | \(\boldsymbol{f\left(x\right)={-x}^3+x^2+14x-24}\) |
| -6 | 144 |
| -5 | 56 |
| -4 | 0 |
| -3 | -30 |
| -2 | -40 |
| -1 | -36 |
| 0 | -24 |
| 1 | -10 |
| 2 | 0 |
| 3 | 0 |
| 4 | -16 |
| 5 | -54 |
| 6 | -120 |
Función polinómica (primera parte)

En este último gráfico se modificó la escala del eje y para poder apreciar los puntos con ordenadas tan alejadas del eje x.
En el gráfico siguiente, se unieron los puntos:
Función polinómica (segunda parte)
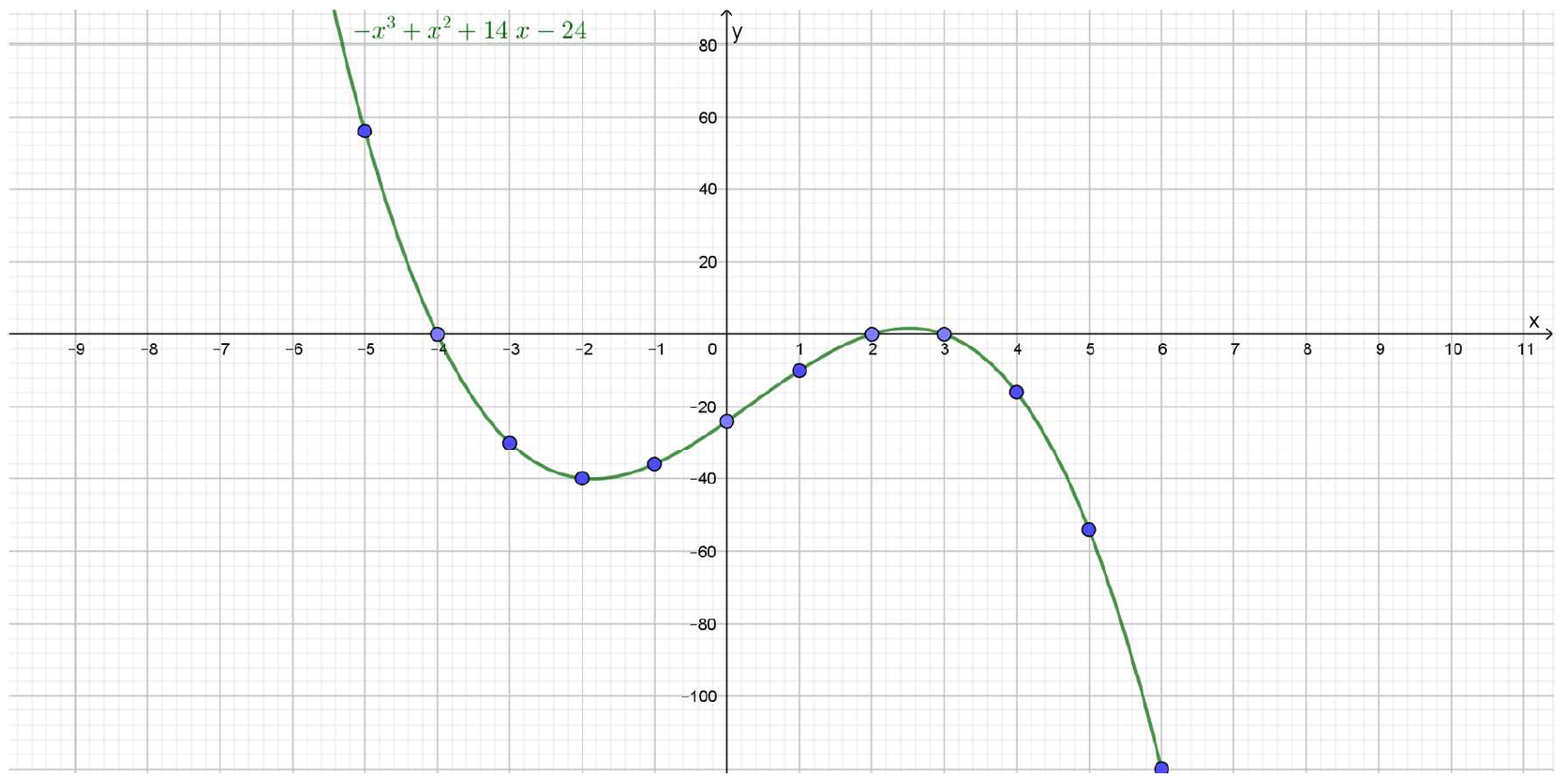
Como puede apreciarse en la tabla de valores y en el diagrama cartesiano, esta función tiene 3 raíces: \(x=-4\), \(x=2 \), y \( \ x=3\).
En <https://calculo.cc/temas/temas_bachillerato/primero_ciencias_sociales/funciones_elementales/teoria/polinomicas.html> hay un breve apunte con propiedades de las funciones polinómicas.
Grafique en un diagrama cartesiano e identifique las raíces de las siguientes funciones polinómicas:
- \(f\left(x\right)=x^4+2x^3-3x^2-4x+4\)
- \(g\left(x\right)=-x^4+2x^3+21x^2-22x+40\)
3.6. Funciones racionales
Las funciones racionales son aquellas cuyas fórmulas son un cociente de polinomios:
\[f\left(x\right)=\frac{b_0+b_1x+b_2x^2+b_3x^3+b_4x^4+\ldots+b_mx^m}{a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+\ldots+a_nx^n}\]
El dominio de estas funciones es el conjunto de los números reales \(\mathbb{R}\) que no anulan el polinomio del denominador.
Grafique \(f\left(x\right)=\frac{x+2}{3x-6}\)
Ante una función racional como esta, es muy necesario, antes de empezar a construir una tabla de valores, encontrar su dominio.
Como el denominador no puede anularse, será:
\[3x-6\neq0\]
\[3x\neq6\]
\[x\neq2\]
Por lo tanto, el dominio es \( Dom= \mathbb{R}-\left\{2\right\}\) es decir, todos los números reales excepto el dos.
Precisamente, porque hay que excluir al 2, en la tabla de valores se pondrá atención en qué sucede “cerca” de ese valor. Para eso, se calculará la imagen de valores de x en las proximidades de ese número:
| \(\boldsymbol{x}\) | \(\boldsymbol{fx}\) |
| -4 | 0,11111111 |
| -3 | 0,06666667 |
| -2 | 0 |
| -1 | -0,11111111 |
| 0 | -0,33333333 |
| 1 | -1 |
| 1,5 | -2,33333333 |
| 1,9 | -13 |
| 1,99 | -133 |
| 2 | no tiene imagen |
| 2,01 | 133,666667 |
| 2,1 | 13,6666667 |
| 2,5 | 3 |
| 3 | 1,66666667 |
| 4 | 1 |
| 5 | 0,77777778 |
| 6 | 0,66666667 |
En la tabla se aprecia que \(x=-2\) es raíz de esta función.
También se podría haber llegado a esa conclusión, al resolver la siguiente ecuación:
\[f\left(x\right)=0\]
\[\frac{x+2}{3x-6}=0\]
Para que un cociente resulte cero, deberá ser cero el numerador:
\[x+2=0\ \ \ \ \rightarrow\ \ \ \ x=-2\]
Los pares ordenados de la tabla se ubican en un diagrama cartesiano y se unen, sin olvidar que \(x=2\) no tiene imagen. Se obtiene el siguiente gráfico, en el que también se representó, en línea punteada la recta vertical \(x=2\), que es asíntota vertical de esta función.
Función racional y sus asíntotas
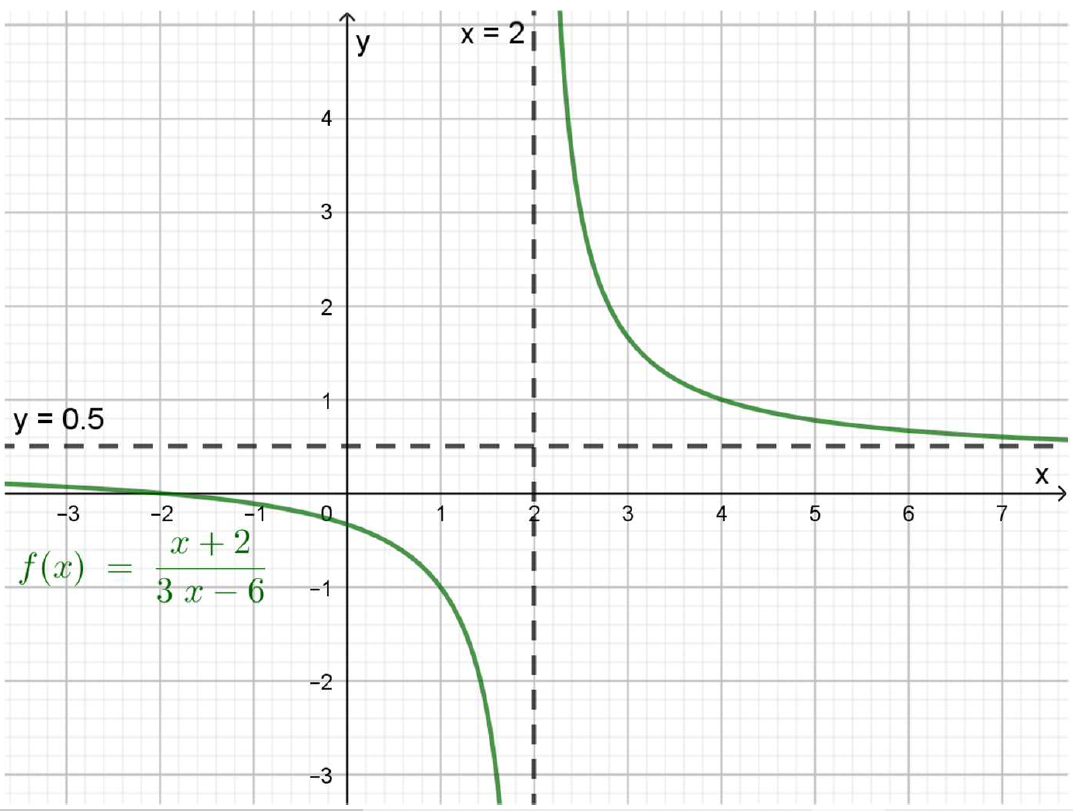
Aquí, también se ubicó la recta horizontal \(y=\frac{1}{2}\), que es asíntota horizontal de esta función.
Dada una función \(y=f(x)\) cuya gráfica es la curva \(C\) se dice que la recta \(r\) es una asíntota de \(f(x)\) si la curva \(C\) se acerca a \(r\) indefinidamente sin llegar a coincidir con la propia \(r\).
En la próxima unidad se volverá sobre este concepto con más precisiones.
Construya el gráfico y encuentre las asíntotas de las siguientes funciones racionales:
- \(f\left(x\right)=\frac{2x-1}{x^2+1}\)
- \(g\left(x\right)=\frac{x^2+4x}{x-2}\)
3.7. Funciones exponenciales y logarítmicas
En una función exponencial, la variable x está en el exponente. Es decir, es del tipo \(f(x)=a^x\), en la que la base
\[a\ \in\ (0;\infty)-\{1\}\]
El dominio de las funciones exponenciales es el conjunto \(\mathbb{R}\) de todos los números reales y su conjunto imagen, el de los reales positivos: \(\mathbb{R}^+ =\left(0;\ \infty\right)\).
Grafique la función \(f\left(x\right)={0,2}^x\)
Como puede apreciarse, la base de esta función exponencial es 0,2. Se trata de un número menor a 1.
Se construye una tabla y con base en ella, se confecciona el diagrama cartesiano
| \(\boldsymbol{x}\) | \(\boldsymbol{fx}\) |
| -6 | 15625 |
| -5 | 3125 |
| -4 | 625 |
| -3 | 125 |
| -2 | 25 |
| -1 | 5 |
| 0 | 1 |
| 1 | 0,2 |
| 2 | 0,04 |
| 3 | 0,008 |
| 4 | 0,0016 |
| 5 | 0,00032 |
| 6 | 0,000064 |
Función exponencial con base menor a 1
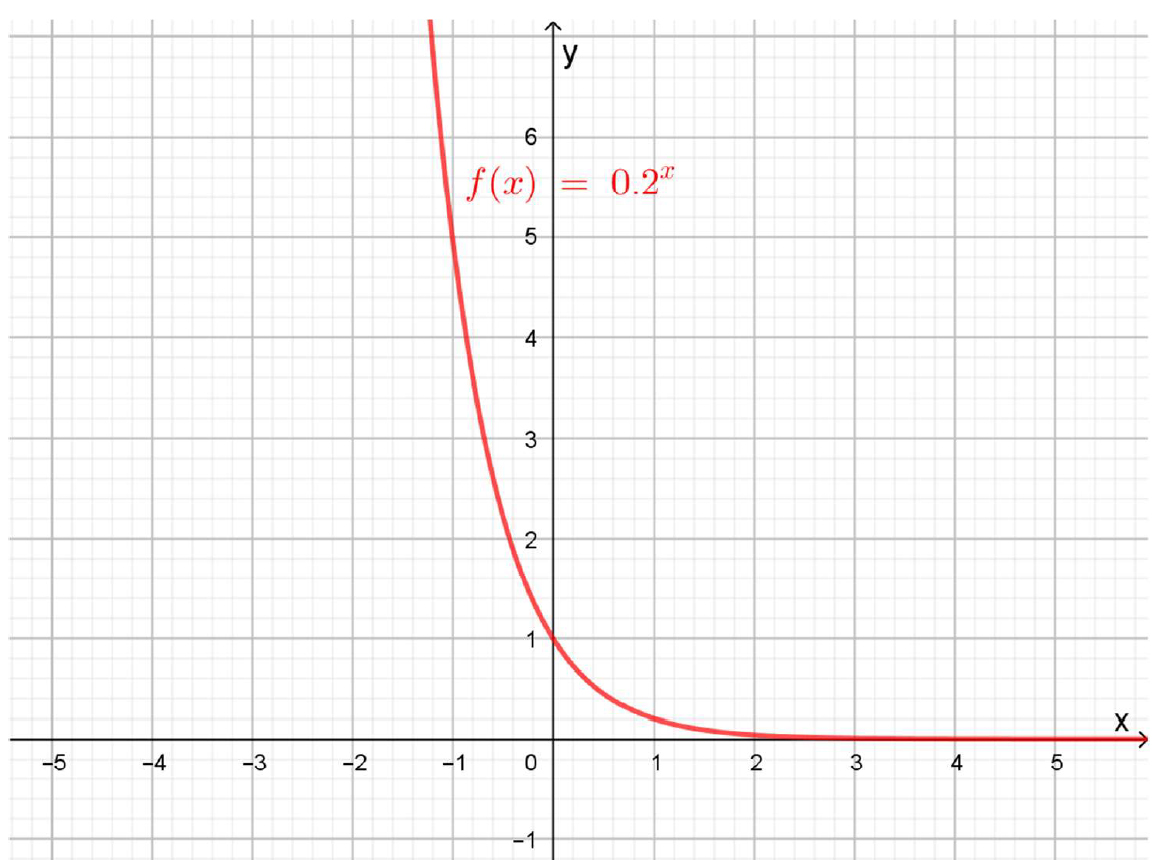
La gráfica resulta decreciente. Esto se debe a que la base de la exponencial es menor a 1.
Puede observarse que \(y=0\) es asíntota horizontal a derecha y que el conjunto imagen es el de los reales positivos: \(\mathbb{R}^+\).
Un caso particular de la función exponencial es la que tiene como base al número irracional \(e\) que en forma aproximada vale \(e\ =\ 2,718281828459\).........
Se trata de la función \(f(x)\ =\ e^x\), cuya importancia se apreciará en las siguientes unidades.
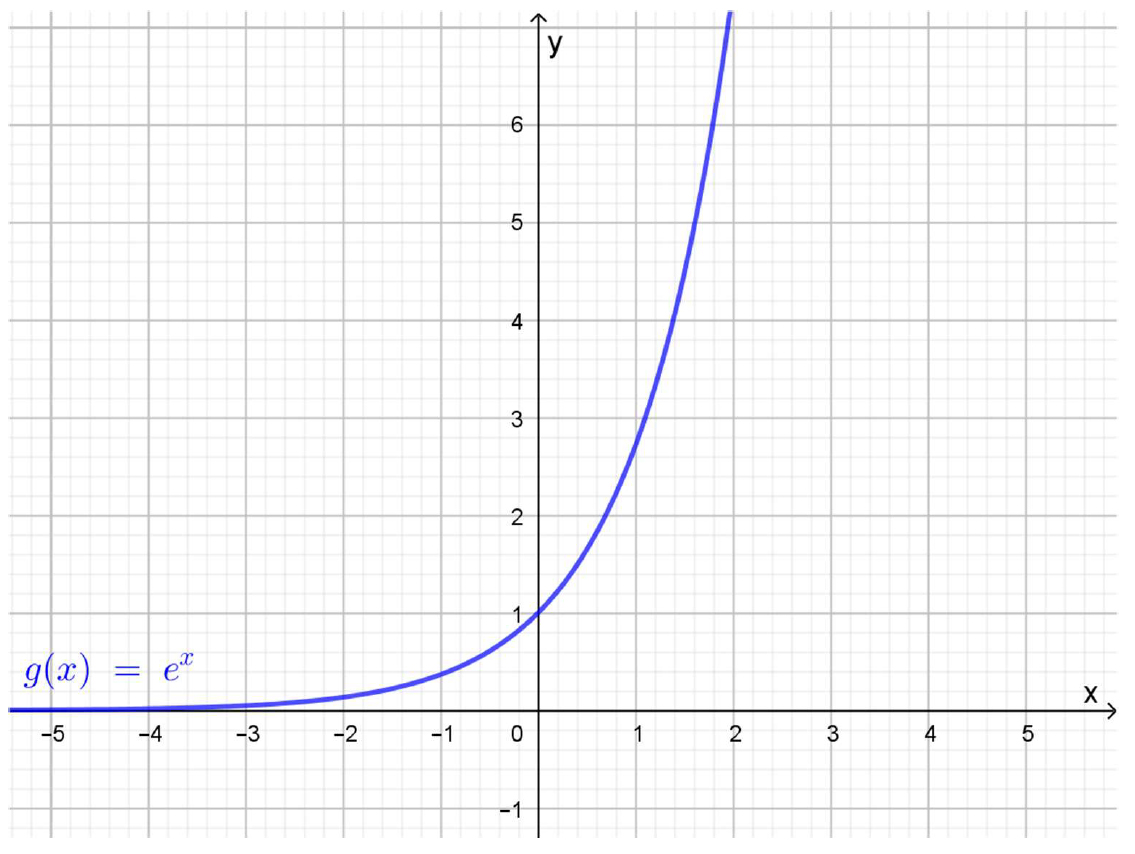
Su dominio es el conjunto \(\mathbb{R}\) de todos los números reales. Como la base de esta función exponencial es mayor a 1, su gráfica es creciente. Asimismo, \(y=0\) es asíntota horizontal a izquierda y su conjunto imagen es el de los reales positivos: \(\mathbb{R}^+\), como puede observarse en el siguiente gráfico.
Función \(e^x\)
En <https://www.universoformulas.com/matematicas/analisis/funcion-exponencial/> se pueden encontrar propiedades de las funciones exponenciales.
Se define logaritmo como el número al cual se debe elevar una base dada para obtener un resultado determinado. Es una de las operaciones inversas de la potenciación:
\[\log_a{c}=b\ \leftrightarrow\ \ a^b=c\]
La función logarítmica en base \(a\) es la función inversa a la exponencial en base \(a\):
\[f\left(x\right)={log}_ax\leftrightarrow x=a^{f(x)}\]
El dominio de las funciones logarítmicas es el conjunto de los reales positivos: \(\mathbb{R}^+\) y su conjunto imagen es el conjunto \(\mathbb{R}\) de todos los números reales.
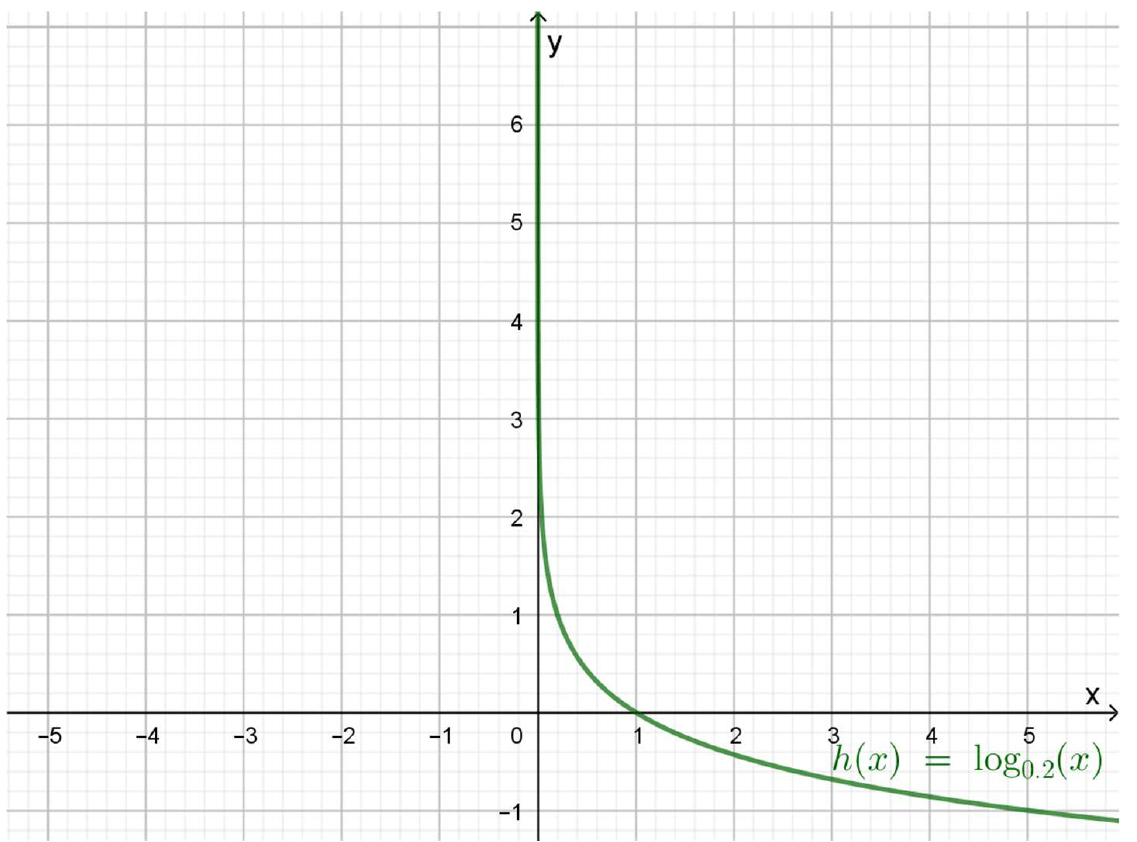
Grafique la función \(f\left(x\right)=\log_{0,2}{x}\)
Esta función es la función inversa de la del Ejemplo 3.20. Para confeccionar la tabla de valores, se invierten los pares ordenados de la tabla correspondiente:
| \(\boldsymbol{x}\) | \(\boldsymbol{fx}\) |
| 15625 | -6 |
| 3125 | -5 |
| 625 | -4 |
| 125 | -3 |
| 25 | -2 |
| 5 | -1 |
| 1 | 0 |
| 0,2 | 1 |
| 0,04 | 2 |
| 0,008 | 3 |
| 0,0016 | 4 |
| 0,00032 | 5 |
| 0,000064 | 6 |
Función logarítmica
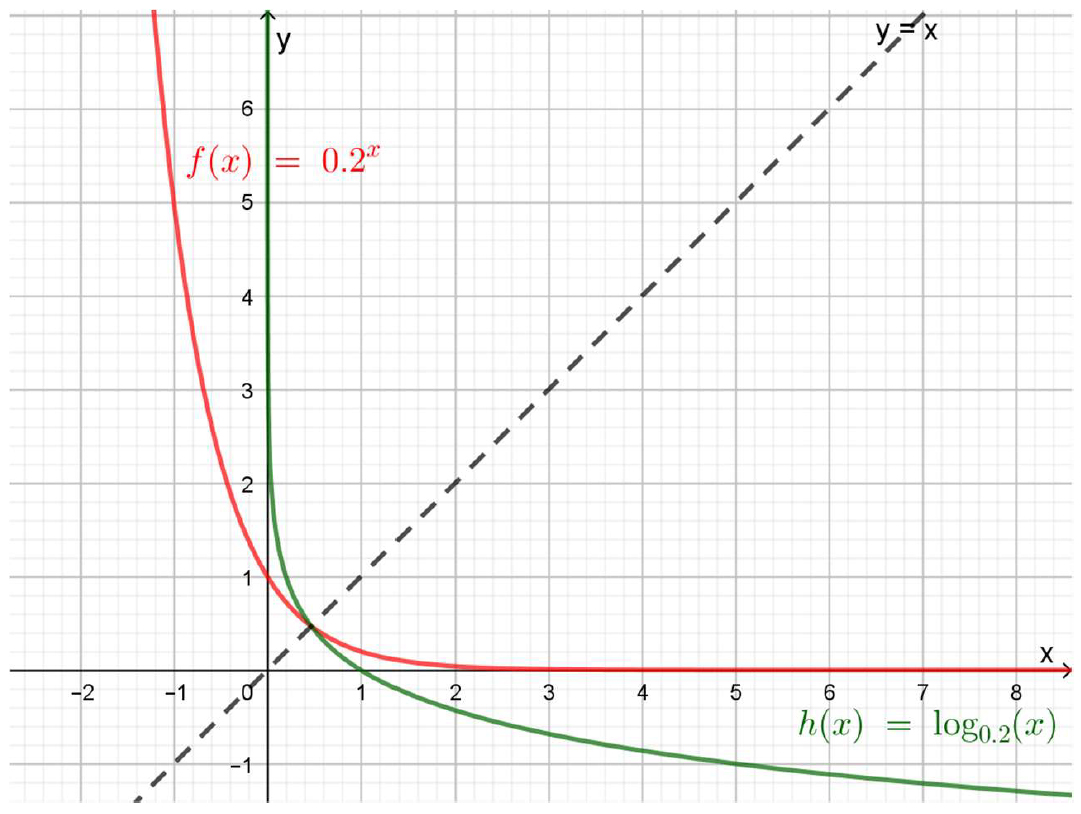
Si se grafican las funciones \({0,2}^x\) y \(\log_{{0,2}^x}\) en un mismo diagrama, se aprecia que ambas son simétricas respecto de la recta \(y=x\).
Función exponencial y su inversa
La función inversa de la \(f\left(x\right)=e^x\) es la función logaritmo natural (o logaritmo neperianoN ) que se simboliza: \(\log_e{(x)}=\ln{(x)}\)
Estas funciones tienen interesantes propiedades, que se estudiarán en la próxima unidad.
En honor a John Neper o Napier, matemático escocés del siglo XVI. Se pueden consultar más detalles sobre su vida y obra en

