5. Integración, métodos y aplicaciones
Objetivos
- Distinguir las integrales indefinidas de las definidas.
- Aplicar distintos métodos de integración: sustitución y partes
- Utilizar la integral de una función para el cálculo del área debajo de una curva
- Aplicar estos temas en la resolución de problemas económicos
Introducción
Los fundamentos asociados a la integración pueden ser abordados desde dos puntos de vistas diferentes. El primero de ellos, la integración indefinida, corresponde a analizar la operación recíproca de la derivación mientras que el segundo enfoque, la integración definida, se enfoca al cálculo del área debajo de la curva definida por una función en un dado intervalo, teniendo una interpretación gráfica más clara. El concepto importante en esta área a calcular radica en su relación con acumulación de valores que toma la función a lo largo de dicho intervalo. Ambos métodos se terminan relacionando por medio del teorema fundamental del cálculo.
5.1. Integral indefinida
Analizando la integración como el proceso inverso a la derivación, el resultado de esta operación debe ser tal que si lo derivamos volvamos a obtener la función que queremos integrar. Simbólicamente utilizamos para expresar el proceso de integración como \(\int f\left(x\right)dx\).
Luego definimos la integral indefinida, también llamada primitiva, a la función \(F\left(x\right)\) con:
(1)\[ F\left(x\right)=\int f\left(x\right)dx \]
siempre y cuando se cumpla \(F^\prime \left(x\right)=f\left(x\right)\)
La integral indefinida de la función \(f\left(x\right)=2x\) es la función \(F\left(x\right)=x^2\) puesto que \(F^\prime(x)=2x\), o lo que es lo mismo, \(\frac{d}{dx}\left(x^2\right) = 2x\).
Sin embargo, esta no es la única primitiva de \(\ f\left(x\right)=2x\). Las siguientes funciones \(F\left(x\right)=x^2+1\), \(F\left(x\right)=x^2\ -\ 3\) o \(F\left(x\right)=x^2+7\) son todas primitivas de \(f\left(x\right)\), dado que podemos sumar un valor constante a \(F\left(x\right)\), pues la derivada de una constante es 0 y la \(f\left(x\right)\) resultante no cambia por sumar una constante a la primitiva. Las funciones de la forma \(F\left(x\right)=x^2\ +C\), donde C es una constante, son primitivas de la función \(f\left(x\right)=2x\). Es decir que existen infinitas primitivas de la función \(f\left(x\right)=2x\).
Así, la ecuación (1) debe reescribirse considerando la constante indefinida que resulta del proceso de integración.
(2)\[\int f\left(x\right)dx=F\left(x\right)+C\]
5.1.1. Propiedades. Linealidad
Con la derivación vimos que la misma cumple con la propiedad de linealidad \( \frac{d\left(af\left(x\right)+bg\left(x\right)\right)}{dx} =\ a\ \frac{df\left(x\right)}{dx} +\ b\frac{dg\left(x\right)}{dx} \), en palabras la derivada de una suma es igual a la suma de las derivadas. Al ser la integración la operación inversa también cumple con esta propiedad. Formalmente lo expresamos como:
(3)\[\int\left(af\left(x\right)+bg\left(x\right)\right)dx=a\ \int f\left(x\right)dx+b\int g\left(x\right)dx \]
Calcule la integral indefinida de la función \(f\left(x\right)=3x^2-3x+1\). Para este problema debemos calcular: \(F\left(x\right)=\int f\left(x\right)dx=\int\left(3x^2-3x+1\right)dx\)
Aquí aplicamos la propiedad de la linealidad, por lo que la integral del polinomio, correspondiente a sumas de distintas potencias, la podemos calcular como la suma de las integrales individuales
\[F\left(x\right)=\int\left(3x^2-3x+1\right)dx=3\int{x^2\ dx}\ -\ 3\int{x\ dx}+1\int{1\ dx}\]
Calculando cada integral por separado resulta (sin considerar las contantes a sumar):
\[\int{x^2\ dx}\ =\ \frac{x^3}{3} \text{ pues } \frac{d}{dx}\left(\frac{x^3}{3}\right)=\frac{1}{3}\frac{d}{dx}\left(x^3\right)=\frac{1}{3}3x^2=x^2\]
\[\int{x\ dx}\ =\ \frac{x^2}{2} \text{ pues } \frac{d}{dx}\left(\frac{x^2}{2}\right)=\frac{1}{2}\frac{d}{dx}\left(x^2\right)=\frac{1}{2}2x=x \]
\[ \int{1\ dx}\ =\ x \text{ pues } \ \frac{d}{dx}\left(x\right)=1\]
Reemplazando estas integrales resulta
\[\begin{eqnarray} F\left(x\right)=3\int{x^2\ dx}\ -\ 3\int{x\ dx}+1\int{1\ dx}=3\ \frac{x^3}{3}\ -\nonumber\\ 3\ \frac{x^2}{2}+1x=x^3\ -\ \frac{3x^2}{2}+x\ +C \end{eqnarray} \]
Donde en este último resultado agregamos la constante para obtener la familia entera de integrales indefinidasN.
Dos integrales indefinidas cualesquiera de una función difieren sólo en una constante.
5.1.2. Algunas integrales indefinidas
En el siguiente cuadro se presenta una lista que vincula cada función con su primitiva.
| \(f\left(x\right)\) | \(F\left(x\right)=\int f\left(x\right)dx\) |
| \(1\) | \(x+C\) |
| \(x\) | \(\frac{x^2}{2}+C\) |
| \(x^{n}\) | \(\frac{x^{n+1}}{n+1}+C \text{ para todo } \ n\neq-1\) |
| \(\frac{1}{x^3}=x^{-3}\) | \(\frac{x^{-3+1}}{-3+1}+C=\frac{x^{-2}}{-2}+C=-\frac{1}{2x^2}+C \) |
| \(e^x\) | \(e^x+C\) |
| \(\frac{1}{x}\) | \(ln{\left(\left|x\right|\right)}+C\) |
| \( \sqrt x=x^\frac{1}{2} \) | \( \frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}+C=\frac{x^\frac{3}{2}}{\frac{3}{2}}+C=\frac{2}{3}\sqrt{x^3}+C \) |
Obsérvese que siempre puede verificarse la integral de una función derivando el resultado obtenido. Deberá llegarse a la función que se buscaba integrar.
Calcule las siguientes integrales indefinidas o primitivas:
- \(\ \int\left(3e^x+5\right)dx= \)
- \(\ \int\left(\frac{4}{\sqrt[3]{x^2}}+2x-\frac{1}{2x}\right)dx=\)
Para resolver esta primitiva se aplica la propiedad de linealidad:
\[\int\left(3e^x+5\right)dx=\int{3e^xdx}+\int5dx=3\cdot\int{e^xdx}+5\cdot\int d x\]
En el ultimo paso, se utilizan las integrales indefinidas de la tabla para hallar la respuesta:
\[\int\left(3e^x+5\right)dx=3\cdot e^x+5\cdot x+C\]
Al derivar la última expresión, se obtiene la función a integrar, lo que permite saber que el resultado es correcto.
Para hallar esta primitiva, conviene reescribir el primer término como una potencia y el último como un producto:
\[\int\left(\frac{4}{\sqrt[3]{x^2}}+2x-\frac{1}{2x}\right)dx=\int\left(4\cdot x^{-\frac{2}{3}}+2x-\frac{1}{2}\cdot\frac{1}{x}\right)dx=\]
Ahora, se resuelve por linealidad y las primitivas de la tabla anterior:
\[\int\left(\frac{4}{\sqrt[3]{x^2}}+2x-\frac{1}{2x}\right)dx=\int{4\cdot x^{-\frac{2}{3}}dx}+\int2xdx- \int{\frac{1}{2} \cdot\frac{1}{x} dx=}\]
\[\int\left(\frac{4}{\sqrt[3]{x^2}}+2x-\frac{1}{2x}\right)dx=4\cdot\int{x^{-\frac{2}{3}}dx}+2\cdot\int x d x-\frac{1}{2}\cdot\int{\frac{1}{x}dx=}\]
\[\int\left(\frac{4}{\sqrt[3]{x^2}}+2x-\frac{1}{2x}\right)dx=4\cdot\frac{x^{-\frac{2}{3}+1}}{-\frac{2}{3}+1}+2\cdot\frac{x^2}{2}-\frac{1}{2}\cdot ln\left|x\right|+C\]
\[\begin{eqnarray} \int\left(\frac{4}{\sqrt[3]{x^2}}+2x-\frac{1}{2x}\right)dx=4\cdot\frac{x^\frac{1}{3}}{\frac{1}{3}}+\nonumber\\ x^2-\frac{1}{2}\cdot ln\left|x\right|+C=12\cdot\sqrt[3]{x}+x^2-\frac{1}{2}\cdot ln\left|x\right|+C \end{eqnarray}\]
Si se deriva la última expresión se obtiene la función que se debía integrar. Así se comprueba que el resultado obtenido es correcto.
5.2. Integración con condiciones iniciales
La integración con condiciones iniciales es un caso particular de la integral indefinida. Al disponer de un valor de la función en un punto dado (llamado el de condición inicial) es posible calcular el valor de la constante \(C\).
Esto implica que la existencia de la condición inicial fija una correspondencia biunívoca entre la función a integrar y la integral, cuyo resultado es una única función y no una familia de funciones que se diferencian entre sí por el valor de la constante. Si se dispone de una función primitiva de la forma:
\[F\left(x\right)=\int{3x^4dx}\]
Luego
\[F\left(x\right)=3\ \frac{x^{4+1}}{4+1}+C=\ \frac{3x^5}{5}+C\]
Si además hay una condición que establece que \(F(1)\ =\ 4\), esta forma de escribir la función indica que: el valor de \(F\left(x\right)\) en el punto en el que \(x\) vale 1, es igual a 4. Si ese fuera el caso se puede reemplazar los valores de \(x\) y \(F\left(x\right)\) en la expresión anterior, para obtener:
\[F\left(x\right)=\ \frac{3x^5}{5}+C \text{ con } F(1)\ =\ 4 \]
\[F\left(1\right)=\ \frac{3{\ 1}^5}{5}+C=\ 4 \]
\[F\left(1\right)=\ \frac{3}{5}+C=\ 4\]
Despejando obtenemos el valor de \(C\)
\[C=\ 4\ -\ \frac{3}{5}\ = \frac{20 -\ 3}{5}\ =\frac{17}{5}\]
lo que permite escribir la expresión inicial como:
\[F\left(x\right)=\int{3x^4dx} \text{ con } F(1)\ =\ 4\]
Tiene como solución
\[F\left(x\right)=\ \frac{3x^5}{5}+\frac{17}{5}\]
Es decir, de todas las expresiones que se pueden obtener dando valores a \(C\), la que está determinada por una condición impuesta o condición inicial es aquella en la que \(C=\frac{17}{5}\ \).
Si \(y\) es una función de \(x\) tal que \(y\ \prime\ \left(x\right)=8x-4\) y además sabemos que \(y\left(2\right)=5\), encontrar \(y\left(x\right)\), calcular también \(y\left(4\right)\).
Para resolver el ejemplo se debe, en primer término, integrar la función derivada de \(y\left(x\right)\) que la anotamos como \(y\ \prime\ \left(x\right)\) y luego calcular el valor de la constante de integración como ya se ha hecho antes; finalmente, conocida la constante, se puede calcular \(\ y\left(4\right)\).
\[y\left(x\right)=\int\left(8x-4\right)dx=4x^2-4x+C\]
Además, se tiene que \(y\left(2\right)=5\), por lo que se pueden hacer los reemplazos correspondientes en la integral indefinida obtenida y luego calcular \(C\).
\[y\left(x\right)=4x^2-4x+C \text{ con } y\left(2\right)=5\]
\[y\left(2\right)=4\ 2^2-4\ 2+C\ =\ 5\]
\[y\left(2\right)=16-8+C\ =\ 5\]
Al reordenar queda:
\[C\ =\ 5\ -\ 8\ =\ -\ 3\]
La integral buscada será
\[y\left(x\right)=4x^2-4x\ -\ 3\]
El cálculo de \(\ y\left(4\right)\) resulta el siguiente:
\[y\left(4\right)=4\ 4^2-4\ 4\ – 3 \]
\[y\left(4\right)=64-16\ -\ 3 \]
Cuyo resultado numérico es:
\[y\left(4\right)=45\]
5.3. Integrales impropias
Un caso particular de integrales definidas se da cuando el intervalo de integración toma todos los posibles valores reales. A estas integrales se las llama impropias y el método para calcularlas es tomando como extremos de integración valores genéricos, como un parámetro, calcular la integral indefinida y evaluar esta primitiva en esos parámetros y luego tomar el límite cuando ese parámetro tiende a más y menos infinito, de esa manera estamos recorriendo todos los valores de los números reales. La expresión que representa a las integrales impropias es la siguiente:
\[\int\limits_{-\infty}^{\infty}f\left(x\right)dx\]
El método descripto previamente para calcular esta integral impropia en notación matemática es \[\int\limits_{-\infty}^{\infty}f\left(x\right)dx=\lim\limits_{R\rightarrow\infty}{\int\limits_{-R}^{R}f\left(x\right)dx}=\lim\limits_{R\rightarrow\infty}{(F(R)\ -\ F(-R))}\]
Estas integrales aparecen en las distribuciones de probabilidad, como la función normal, y temas de otras áreas del conocimiento, como análisis de señales con transformadas de Fourier, o estudios del comportamiento de sistemas dinámicos con la transformada de Laplace, etcétera.
5.4. Métodos de integración
Para integrar una suma de funciones se puede hacer la suma de las integrales de cada función como vimos anteriormente. Esto tiene sentido porque la integral indefinida es una antiderivada y la derivada de una suma de funciones es la suma de las derivadas de cada función, es decir que:
\[\small \int\left(af\left(x\right)+bg\left(x\right)\right)dx=a\int f\left(x\right)dx+b\int g\left(x\right)dx\ =a\ F\left(x\right)+b\ G\left(x\right)\ +\ C\ \]
pues
\[\left(a F\left(x\right)+b G\left(x\right) + C\right) \prime = a\left(\ F\left(x\right)\ + C\right) \prime +\\ b\left( G\left(x\right) + C\right) \prime=af\left(x\right)+bg\left(x\right) \]
El problema se presenta cuando se quiere integrar un producto o una composición de funciones. En este caso, dependiendo del producto que se tenga que integrar habrá que recurrir a algún procedimiento algebraico o para la composición a un cambio de variables.
Los métodos para resolver estos casos se conocen como el método de sustitución, que se basa en la regla de la cadena para composición de funciones y el método de integración por partes, que se basa en la derivada de un producto. Lo importante es reconocer en qué casos se puede aplicar cada uno de ellos.
5.4.1. Método de sustitución
Si se desea calcular la integral indefinida \(\int{x\ \left(3x^2+2\right)^3dx}\), en este caso se tiene un producto de funciones, pero este producto tiene una particularidad: la función \(\left(3x^2+2\right)^3\) es una composición de funciones \(f\left(g\left(x\right)\right)\) y la función x que aparece a la izquierda del paréntesis de la integral deseada, es la sexta parte de la derivada de \(g\left(x\right)\). Entonces, se tiene un producto donde una de las funciones es una composición y la otra es la derivada de la función de adentro de la composición multiplicada por una constante. Para poder integrar este tipo de producto se recurre a la regla de la cadena, donde:
\[\left(f\ o\ g\right)\ \prime\ \left(x\right)= f\ \prime\ \left(g\left(x\right)\right)\ g\ \prime\ \left(x\right)\]
con lo cual al integrar toda la ecuación se obtiene:
\[\int{\left(f\ o\ g\right)\ \prime\ \left(x\right)\ dx}=\int{\left(f\left(g\left(x\right)\right)\right)\ \prime\ dx}=\int{f\ \prime\ \left(g\left(x\right)\right)\ g\ \prime\ \left(x\right)\ dx} \]
Aquí podemos realizar el reemplazo \(u\ =\ g\left(x\right)\) y también \(du=g\ \prime\left(x\right)dx\) y resulta \(\ f\left(u\right)=f\left(g\left(x\right)\right)\) y \(f\ \prime\ \left(u\right)=f\ \prime\ \left(g\left(x\right)\right)\)
De esta forma se puede pasar a calcular simplemente la primitiva de
\[\int{f\ \prime\ \left(g\left(x\right)\right)\ g\ \prime\ \left(x\right)\ dx}=\ \int{f\ \prime\ \left(u\right)\ du}=f\left(u\right)+\ C\ =f\left(g\left(x\right)\right)\ +\ C\ \]
Apliquemos este método al problema presentado previamente.
\[\int{x \left(3x^2+2\right)^3dx} \]
En este caso tenemos la función \(\ u = g\left(x\right) = 3x^2+2\), que luego está compuesta con la función “elevar al cubo” \( f\left(x\right) = x^3\).
De esta manera calculamos \(du=g^\prime\left(x\right)dx =\left(\ 3x^2+2\right)^\prime dx=6\ x\ dx \) y por lo tanto resulta al despejar \(\frac{du}{6} = x\ dx \)
Al reemplazar estos datos en la integral anterior se tiene:
\[\int{x\ \left(3x^2+2\right)^3dx}=\int{\left(u\right)^3\frac{du}{6}}=\frac{1}{6}\int{u^3du}\]
Esta integral es más sencilla de integrar, resultando:
\[\int{x\ \left(3x^2+2\right)^3dx}=\frac{1}{6}\int{u^3du}\ =\frac{1}{6}\frac{u^4}{4}\ +\ C\]
Con esta primitiva podemos volver a la variable inicial reemplazando \(u = 3x^2+2\)
\[\int{x\ \left(3x^2+2\right)^3dx}=\frac{\ \left(3x^2+2\right)^4}{24}\ +\ C\]
Y así se termina de resolver el problema. Se puede confirmar el resultado derivando la integral indefinida encontrada y ver que obtenemos la función que teníamos que integrar
\[\begin{eqnarray} \left(\frac{\ \left(3x^2+2\right)^4}{24}\ +\ C\right)\ \prime=\ \frac{1}{24}\ \ {4\ \left(3x^2+2\right)}^{4-1}\ \left(6\ x+0\right)\ +\ 0\ =\nonumber\\ \frac{\ 1}{6}{\ \left(3x^2+2\right)}^3\ 6\ x=\ {\ \left(3x^2+2\right)}^3x \end{eqnarray} \]
Obteniendo la función que teníamos que integrar, con lo que se verifica que el resultado es correcto.
5.4.2. Método de integración por partes
Se desea calcular la integral de la función \(\int{ln\left(x\right)x^2dx}\). En este caso no tenemos una composición sino un producto de funciones sin composición por lo que no corresponde usar el método anterior. Por eso, y recordando que la derivada de un producto es:
\[\left(f\ .\ \ g\right)\ \prime\ \left(x\right)= f\ \prime\left(x\right)\ \ g\left(x\right)\ +f\left(x\right)\ \ g\ \prime\left(x\right)\]
Al integrar toda la ecuación se obtiene:
\[\begin{eqnarray} \int{\left(f\ .\ \ g\right)\ \prime\ \left(x\right)\ dx}\ = \int f\left(\ \prime\left(x\right)\ \ g\left(x\right)\ +f\left(x\right)\ \ g\ \prime\left(x\right)\right)dx= \nonumber\\ \int{f\ \prime\left(x\right)\ \ g\left(x\right)\ \ dx}\ +\int{f\left(x\right)\ \ g\ \prime\left(x\right)\ \ dx} \end{eqnarray}\]
Del lado izquierdo tenemos la integral de la derivada de una función, que nos da la misma función con lo que resulta:
\[\small f\left(x\right)\ .\ \ g\left(x\right)\ =\int{f\ \prime\left(x\right)\ \ g\left(x\right)\ \ dx}\ +\int{f\left(x\right)\ \ g\ \prime\left(x\right)\ \ dx}\]
Aquí podemos despejar una de las integrales del segundo término, si pasamos la otra al primer miembro de la identidad:
\[\small f\left(x\right)\ .\ \ g\left(x\right)\ -\int{f\ \prime\left(x\right)\ \ g\left(x\right)\ \ dx}\ =\int{f\left(x\right)\ \ g\ \prime\left(x\right)\ \ dx}\]
De esta manera, al calcular una integral producto entre dos funciones, se puede reemplazar por el cálculo de otra integral diferente.
\[\small \int{f\left(x\right)\ \ g\ \prime\left(x\right)\ \ dx}= f\left(x\right)\ .\ \ g\left(x\right)\ -\int{f\ \prime\left(x\right)\ \ g\left(x\right)\ \ dx}\]
Donde debemos buscar que la segunda integral. Lo que se busca es que sea más fácil de integrar con la derivada de \(f\left(x\right)\) que lo que resulta en la integral de la izquierda.
Veamos como lo aplicamos en la integral buscada, \(\int{ln\left(x\right)x^2dx}\).
Aquí sería mejor que en lugar de aparecer la función \(ln\left(x\right)\) en la integral, nos apareciera su derivada \(1/x\).
De esta manera tomamos en el método de integración por partes donde teníamos
\[\int{f\left(x\right)\ \ g\ \prime\left(x\right)\ \ dx}= f\left(x\right)\ .\ \ g\left(x\right)\ -\int{f\ \prime\left(x\right)\ \ g\left(x\right)\ \ dx}\]
\[f\left(x\right)=ln\left(x\right)\ \ \ g\ \prime\left(x\right)=x^2\]
Con ellas podemos calcular
\[f\ \prime\left(x\right)=\frac{1}{x}\ \ \ g\left(x\right)=\frac{x^3}{3}\]
De esta forma se puede calcular la integral anterior haciendo:
\[\int{f\left(x\right)\ \ g\ \prime\left(x\right)\ \ dx}=f\left(x\right)\ .\ \ g\left(x\right)\ -\int{f\ \prime\left(x\right)\ \ g\left(x\right)\ \ dx}\]
\[\int{ln\left(x\right)x^2dx}=ln\left(x\right)\frac{x^3}{3}-\int{\frac{1}{x}\frac{x^3}{3}dx}\]
Donde en la integral de la derecha podemos simplificar la fracción. Y resulta así una función más simple de integrar que la original:
\[\int{ln\left(x\right)x^2dx}=ln\left(x\right)\frac{x^3}{3}-\frac{1}{3}\int{x^2dx}\]
Integrando la función cuadrática del segundo término resulta:
\[\int{ln\left(x\right)x^2dx}=ln\left(x\right)\frac{x^3}{3}-\frac{1}{3}\frac{x^3}{3}+\ C \]
\[\int{ln\left(x\right)x^2dx}=\frac{x^3}{3}\left(ln\left(x\right)-\frac{1}{3}\right)+\ C \]
Resta la verificación: como siempre, se debe derivar la primitiva encontrada y obtener la función que se deseaba integrar al inicio del problema.
\[\left(\frac{x^3}{3}\left(ln\left(x\right)-\frac{1}{3}\right)+\ C\right)\ \prime= \frac{3x^{3-1}}{3}\left(ln\left(x\right)-\frac{1}{3}\right)+\frac{x^3}{3}\left(\frac{1}{x}-0\right)+0\]
\[\left(\frac{x^3}{3}\left(ln\left(x\right)-\frac{1}{3}\right)+\ C\right)\ \prime=x^2\left(ln\left(x\right)-\frac{1}{3}\right)+\frac{x^3}{3x}\\ =x^2ln\left(x\right)-\frac{x^2}{3}+\frac{x^2}{3}=x^2ln\left(x\right)\]
Al haber obtenido la función que teníamos que integrar, con lo que se verifica que el resultado es correcto.
5.5. Teoremas del cálculo
El teorema fundamental del cálculo define que la derivación y la integración son una la transformación inversa de la otra. De esta manera, toda función que se pueda integrar, si calculamos la derivada de su integral, obtenemos la misma función. El enunciado resulta así:
Dada una función \(f(x)\) integrable en un intervalo [a, b], y sea
\[F\left(x\right)=\int\limits_{a}^{x}f\left(x\right)dx \]
Si \(f(x)\) es continua en un punto \(c ∈ (a, b)\), entonces \(F(x)\) es derivable en \(x=c\) y además
\[F\ \prime\ \left(c\right)\ =f\left(c\right)\]
5.6. Integral definida
Así como las derivadas describen cómo son las variaciones de una función en cada punto, las integrales definidas nos darán idea de cómo se va acumulando los valores que toma la función. Como indica su nombre, la integral definida corresponde a la suma de todos los valores que toma la función que se está integrando, entre un valor inferior y otro superior.
Dado que estamos sumando todos estos valores de la función en el intervalo de la integral definida, podemos ver este resultado gráficamente como el área que queda determinada entre la curva que define la función y el eje horizontal.
Veamos el caso más sencillo, donde la función es un valor constante. Por ejemplo, si nuestros gastos fijos por mes son de 100$ y queremos saber cuánto gastaremos entre febrero y octubre, es decir en 8 meses, debemos multiplicar el valor de la función, los 100$, por ancho del intervalo de tiempo, en este caso 8 meses, por lo que el total será $100 x 8 meses, resultando en un total de 800 pesos. En la siguiente imagen mostramos este resultado y como corresponde al área entre la función constante y el eje horizontal dentro del intervalo definidos por los límites de la integral:
Área bajo y=100
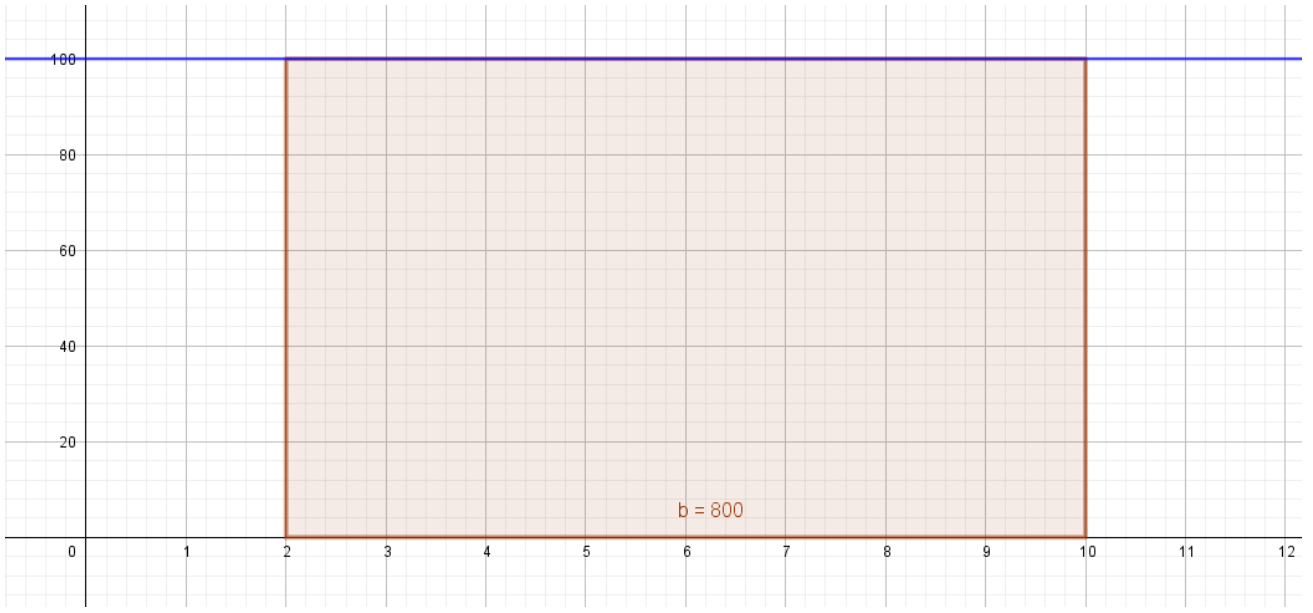
El símbolo de la integral corresponde a una S estirada, que nos recuerda que estamos sumando los valores de la función dentro del intervalo. Así en este caso tenemos:
\[\int\limits_{2}^{10}{100\ dx}=100\ .\ (10-2)\ =\ 100\ .\ 8\ =\ 800\]
El símbolo dx que aparece en la integral simboliza los intervalos de tiempo por los cuales estamos sumando los gastos fijos, en este caso cada uno de los meses, 100 pesos en el mes 2, febrero, más 100 pesos en el mes 3, marzo, etc. Gráficamente estamos sumando 8 rectángulos de base 1 mes y altura los 100 pesos que gastamos entre el mes 2 y el mes 10.
Si la función no es constante, la idea es similar, sumar rectángulos cuya altura es el valor que toma la función, y cuya base corresponde a un ancho de tiempo en cierto período que es el que se analiza. Consideremos una función donde los gastos aumentan en forma cuadrática a medida que va pasando el tiempo, \(f\left(x\right)=x^2\), ¿cuáles serán los gastos acumulados en este caso entre los meses 2 y 10 (la variable x representa los meses). En este caso el gráfico que resulta es:
Área bajo \(y=x^2\) (Primera parte)

Para aproximar el valor acumulado entre los meses 2 y 10, podemos multiplicar el valor de la función al comienzo de cada mes por el ancho del intervalo de ese mes, en este caso sería el valor de la función en 2 por el ancho de 1 mes, que nos da un rectángulo de 4, luego en el tercer mes la función toma el valor 9 por el ancho de 1 mes, y si continuamos así, tendremos los siguientes 6 rectángulos con valores 16, 25, 36, 49, 64 y 81 y obtendremos un total de gastos aproximados de 284, que gráficamente vemos en la siguiente imagen:
Área bajo \(y=x^2\) (Segunda parte)

Aquí podemos observar que, como el gasto aumenta día a día, calcularemos un gasto menor al verdadero pues solo tenemos en cuenta el gasto al principio de cada mes y no cómo aumenta a medida que avanza cada mes. Gráficamente corresponde a las áreas que faltan considerar en la parte que está arriba de cada rectángulo y la función graficada en rojo. Para mejorar esta aproximación, deberíamos tomar intervalos de tiempo más pequeños, por ejemplo, semana por semana o día por día, es decir rectángulos de base más pequeñas.
Con un deslizador de Geogebra podemos variar la cantidad de rectángulos de nuestra aproximación, y ver cómo, al tomar mayor cantidad de rectángulos con bases cada vez más pequeñas, va mejorando la aproximación.
Finalmente, obtenemos un gráfico que muestra el gasto total entre los meses 2 y 10, con un valor de $ 330.67, correspondiente al área debajo de la curva.
Área bajo y=x2 (Cuarta parte)
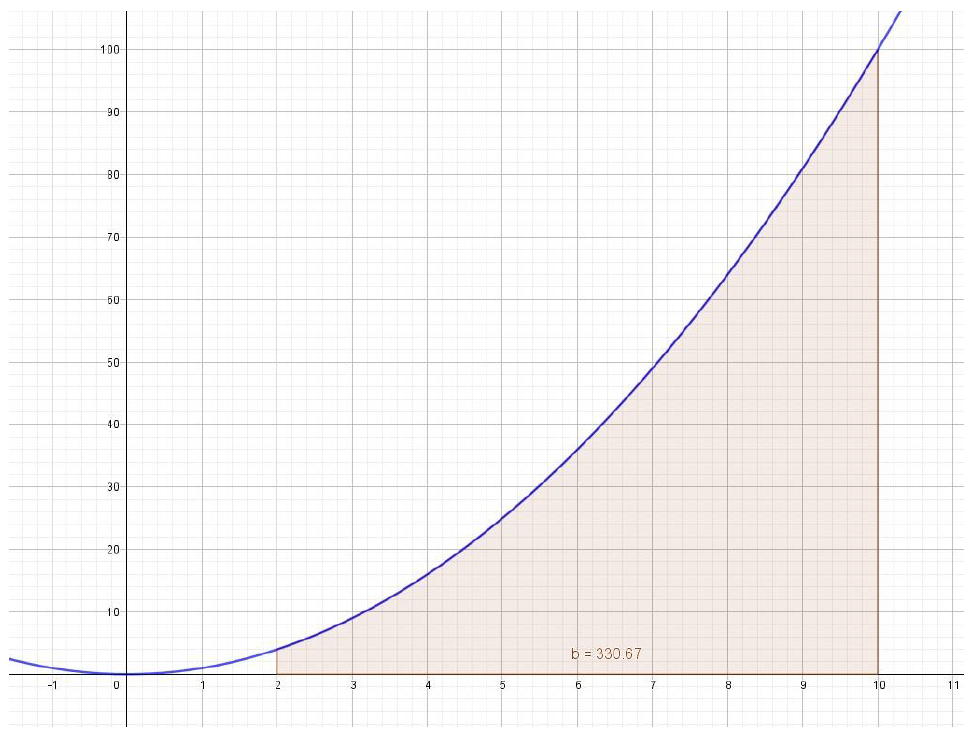
Valor exacto del área debajo de la curva
Afortunadamente existe una manera más simple de calcular las integrales definidas que relaciona las integrales definidas con las indefinidas, lo que se conoce como el Teorema fundamental del Cálculo:
Segundo Teorema Fundamental del Cálculo o Regla de Barrow
Sea \(F(x)\) una función continua en el intervalo \([a,b]\) y \(F(x)\) es una primitiva de \(f(x)\), entonces se verifica que:
(4)\[\int\limits_{a}^{b}f\left(x\right)dx=\left. F\left(x\right)\right|_a^b=F\left(b\right)-F\left(a\right)\]
Si \(f(x)\) es definida positiva, esta integral definida (un valor numérico) es igual al área delimitada entre la función y el eje \(x\) entre los límites a y b.
Usando el teorema fundamental del cálculo, calculemos nuevamente las dos áreas que hallamos antes en forma aproximada, cuando sumamos rectángulos.
En el primer caso la función \(f(x) = 100\) es constante por lo que su integral indefinida o primitiva es \(F(x) = 100 x + C\)
\[\int\limits_{2}^{10}{100\ dx}=F\left(10\right)-F\left(2\right)=100.10+C-\left(100.2+C\right)\]\[\int\limits_{2}^{10}{100\ dx}=1000\ +\ C\ -\ \ 200\ -\ C\ \ =\ 1000\ -\ 200\ =\ 800\]
El mismo resultado que obtuvimos sumando rectángulos.
Podemos observar que la constante de integración primero se suma y luego se resta al aplicar el teorema, por lo que el resultado no depende del valor que le asignemos a esta constante y podemos –si quisiéramos, por comodidad- tomarla igual a 0. Por su parte podemos remarcar que la integral definida tiene como resultado un valor numérico. En el caso particular en el que la función tome valores positivos, este valor será el resultado de la integral definida corresponde al área comprendida entre la función y el eje horizontal y entre los extremos de integración.
Veamos que sucede en el otro caso que ya calculamos la integral por la aproximación con rectángulos, con la función \(f\left(x\right)=x^2\) donde repetimos -para continuar con la idea- los límites de integración del ejemplo anterior. Para este caso la integral indefinida es \(F\left(x\right)=\frac{x^3}{3}+C\)
\[\int\limits_{2}^{10}{x^2dx}=\left. \frac{x^3}{3}\right|_2^{10}=\frac{{10}^3}{3}-\frac{2^3}{3}=\frac{1000\ -\ 8}{3}=\frac{992}{3} \sim 330,666\]
Que corresponde al valor numérico obtenido arriba y al que nos vamos aproximando al tomar mayor cantidad de rectángulos con bases cada vez más pequeñas.
5.7. Cálculo de áreas entre curvas
Podemos utilizar las integrales definidas para calcular el área encerradas entre un par de funciones. Así dadas las funciones \(f\left(x\right)\ =\ x\) y \(g\left(x\right)\ =\ x\ \left(x-2\right)^2\)calculemos el área encerrada entre ambas funciones. Para esto, calculamos el área debajo de la mayor de las funciones y le restamos el área de la función menor, quedando solamente el área que va desde la menor función a la mayor, siendo esta el área encerrada entre las dos funciones. El cálculo que debemos realizar entonces será \(\int_{a}^{b}{\left(f\left(x\right)-g\left(x\right)\right)\ dx\ }\) o \(\int_{a}^{b}{\left(g\left(x\right)-f\left(x\right)\right)\ dx}\), dependerá del intervalo en el que estemos integrando, cuál es la función mayor y cuál la menor para restar en ese orden. De la misma forma, los extremos del intervalo de integración quedan determinado por los valores de la variable independiente en los cuales las funciones toman el mismo valor (se cortan entre sí o se intersecan).
Área entre curvas (Primera parte)
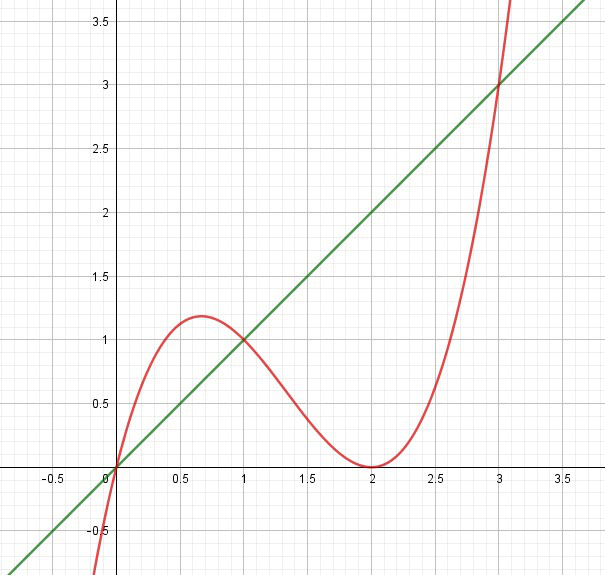
Para ver donde se cortan se igualan las funciones y resolvemos la ecuación que resulta de esta igualación.
\[f\left(x\right)=g\left(x\right) \]
En particular en este problema resulta:
\[x=x\ \left(x-2\right)^2\]
De aquí podemos ver que si \(x\ =\ 0\) se satisface la igualdad por lo que esta es una solución posible de la ecuación. Que sucede si \(x\ \neq\ 0\). En este caso podemos dividir toda la ecuación por \(\ x \) (por ser \(x\ \neq\ 0\)) resultando
\[\frac{x}{x}=\frac{x\ \left(x-2\right)^2}{x}\]
Si simplificamos las \(x \) que multiplican y dividen en ambos lados, tenemos:
\[1=\left(x-2\right)^2\]
Aquí podemos desarrollar el binomio y resolver la ecuación cuadrática o pensar: estamos buscando los valores de \(\left(x-2\right)\) que al elevarlos al cuadrado nos den como resultado 1. Los números que al elevar al cuadrado nos dan como resultado 1 son el 1 y el -1, por lo que buscamos los \(x \) que cumplan \(\left(x-2\right)=1\) y \(\left(x-2\right)=-1\)
\[\left(x-2\right)=1\]
\[x=1+2 \]
\[ x=3\]
O bien
\[\left(x-2\right)=-1 \]
\[ x=-1+2 \]
\[ x=1\]
Concluimos que las funciones se intersecan en los puntos \(x\ =\ 0, x\ =\ 1\) y \(x\ =\ 3\) como puede apreciarse en el gráfico 5.6.
Luego, para calcular el área encerrada entre las dos funciones, se debe integrar la diferencia de las funciones entre 0 y 1; y entre 1 y 3. Para ver cuál es mayor en cada caso se evalúan las funciones en un punto intermedio en cada intervalo.
Así, en el intervalo (0, 1) se evalúan \(f\left(x\right)\) y \(g\left(x\right)\) en, por ejemplo, \(x\ =½\) y se obtiene:
\[f(½)=½ \text{ y } g(½)=½ (½-2)^2=½ (-3/2)^2=½ (9/4)= 9/8 \]
Como \(9/8 > ½\) entonces \(g(½) >f(½)\) por lo que la función \(g\left(x\right)\) es mayor que la función \(f\left(x\right)\) en el intervalo (0, 1).
Por su parte en el intervalo (1, 3) evaluando \(f\left(x\right)\) y \(g\left(x\right)\) en \(x=2\) se obtiene:
\[f\left(2\right)=2 \text{ y } g\left(2\right)=2\ \left(2-2\right)^2=0\]
Como \(2 > 0\) entonces \(\ f\left(2\right)>g\left(2\right)\) por lo que la función \(f\left(x\right)\) es mayor que la función \(g\left(x\right)\) en el intervalo (1, 3). Todos estos resultados analíticos los podemos confirmar mirando el gráfico 5.6.
Luego, el área entre las funciones quedará determinada por:
\[\int\limits_{0}^{1}\left(g\left(x\right)-f\left(x\right)\right)dx+\int\limits_{1}^{3}\left(f\left(x\right)-g\left(x\right)\right)dx
\]
\[\int\limits_{0}^{1}\left(x\ \left(x-2\right)^2-x\right)dx+\int\limits_{1}^{3}\left(x-x\ \left(x-2\right)^2\right)dx\]
En ambas integrales desarrollamos los binomios al cuadrado:
\[\int\limits_{0}^{1}\left(x\ \left(x^2-4x+4\right)-x\right)dx+\int\limits_{1}^{3}\left(x-x\left(x^2-4x+4\right)\right)dx\]
\[\int\limits_{0}^{1}\left(\left(x^3-4x^2+4x\right)-x\right)dx+\int\limits_{1}^{3}\left(x-\left(x^3-4x^2+4x\right)\right)dx\]
\[\int\limits_{0}^{1}\left(x^3-4x^2+3x\right)dx+\int\limits_{1}^{3}{-\left(x^3-4x^2+3x\right)dx}\]
\[\int\limits_{0}^{1}\left(x^3-4x^2+3x\right)dx-\int\limits_{1}^{3}\left(x^3-4x^2+3x\right)dx\]
La primitiva de estas integrales es sencilla. Al ser un polinomio, es la suma de las primitivas de potencias de la variable independiente. Así:
\[\left. \left(\frac{x^4}{4}-4\frac{x^3}{3}+3\frac{x^2}{2}\right)\right|_0^1-\left. \left(\frac{x^4}{4}-4\frac{x^3}{3}+3\frac{x^2}{2}\right)\right|_1^3\]
\[\begin{eqnarray} \left(\frac{1^4}{4}-4\frac{1^3}{3}+3\frac{1^2}{2}\right)-\left(\frac{0^4}{4}-4\frac{0^3}{3}+3\frac{0^2}{2}\right)-\nonumber\\ \left(\left(\frac{3^4}{4}-4\frac{3^3}{3}+3\frac{3^2}{2}\right)-\left(\frac{1^4}{4}-4\frac{1^3}{3}+3\frac{1^2}{2}\right)\right) \end{eqnarray}\]
\[\left(\frac{1}{4}-\frac{4}{3}+\frac{3}{2}\right)-\left(0\right)-\left(\left(\frac{81}{4}-4\frac{27}{3}+3\frac{9}{2}\right)-\left(\frac{1}{4}-\frac{4}{3}+\frac{3}{2}\right)\right)\]
\[\left(\frac{1}{4}-\frac{4}{3}+\frac{3}{2}\right)-\left(\frac{81}{4}-4\frac{27}{3}+3\frac{9}{2}\right)+\left(\frac{1}{4}-\frac{4}{3}+\frac{3}{2}\right)\]
\[2\left(\frac{3-16+18}{12}\right)-\left(\frac{243-432+162}{12}\right)\]
\[2\left(\frac{5}{12}\right)-\left(-\frac{27}{12}\right)=\frac{10}{12}+\frac{27}{12}=\frac{37}{12}\]
Luego, el área encerrada entre las funciones \(f\left(x\right) = x\ \) y \( \ g\left(x\right) = x \left(x-2\right)^2\) es igual a \(\frac{37}{12}\)
Área entre curvas (Segunda parte)
El área en el caso de una función definida negativa, corresponderá a la diferencia entre la función que describe el eje horizontal \((y = 0)\) menos la función de interés \(f\left(x\right)\) . Como esta función es definida negativa (los valores de la función a sumar en la integral son todos negativos), la integral \(\int_{a}^{b}f\left(x\right)dx\) dará un valor negativo. En este caso, para el área debemos calcular la integral \(\int_{a}^{b}{\left(0-f\left(x\right)\right)\ dx\ }= -\int_{a}^{b}{f\left(x\right)\ dx\ }\)que resultará un valor positivo, como esperamos que nos dé un área.
5.8. Aplicaciones económicas y empresariales
Los siguientes ítems muestran algunas de las aplicaciones para Economía de los temas desarrollados en esta unidad.
5.8.1. Cálculo del costo total a partir del costo marginal
Las empresas pueden conocer el costo marginal \(C_m\left(q\right)\) de producir una unidad \(q\) más que las que fabrican actualmente. Como sabemos que el costo marginal es la derivada del costo total,
\[C_m\left(q\right)=\frac{dC_T\left(q\right)}{dq} \]
Luego la integral de la función de costo marginal nos permite obtener el costo total, su integral indefinida o primitiva, a menos de un valor constante:
\[C_T\left(q\right)=\int{C_m\left(q\right)dq} \]
Como ejemplo consideremos el caso \(C_m\left(q\right)=\ 7q+4\) . Para este caso integrando obtenemos:
\[C_T\left(q\right)=\int{C_m\left(q\right)dq}=\int\left(7q+4\right)dq=7\frac{q^2}{2}+4q+c\]
De esta manera, podemos calcular el costo total a menos de una constante que queda indeterminada. Decimos que los términos que dependen de la variable \(q\), \(7\frac{q^2}{2}+4q\), corresponden al costo variable, mientras que la constante indeterminada corresponderá a los costos fijos de producción.
Como vimos en el apartado 5.2, si se conocen lo que llamamos las condiciones iniciales - que en este caso sería un valor conocido de la función de costo total- podremos obtener el valor de la constante que aquí quedó indeterminada.
5.8.2. A partir del conocimiento de los ingresos marginales
De forma similar podemos a partir del conocimiento de los ingresos marginales, \(I_m\left(q\right)\), calcular los ingresos totales \(I_m\left(q\right)\)
\[I\left(q\right)=\frac{dI_T\left(q\right)}{dq}\]
Luego la integral de la función de ingreso marginal nos permite obtener el ingreso total, su integral indefinida o primitiva, a menos de un valor constante:
\[I_T\left(q\right)=\int{I_m\left(q\right)dq}\]
En el caso de los ingresos de una empresa, la constante de integración correspondería a todos los ingresos que no dependan de la cantidad producida y vendida. Por ejemplo, alquileres de propiedades, regalías por patentes o franquicias.
5.8.3. Excedentes del consumidor y del productor
En algunos problemas económicos, interviene el cálculo de áreas, por lo que se aplica lo estudiado hasta acá.
Ése es el caso del cálculo del excedente del consumidor y del productor. Son conceptos de la Teoría Marginalista, bastante discutidos, pero que aplican ideas matemáticas a los problemas económicos.
Definición de Excedentes:
Excedente del consumidor: “El excedente del consumidor, con relación a un bien determinado, es la diferencia entre la cantidad máxima que estaría dispuesto a pagar por el número de unidades que demanda de ese bien y la cantidad que realmente paga en el mercado.”
Excedente del productor: “El excedente del productor (...) puede definirse como la cantidad que los productores reciben por un bien, menos lo que les cuesta producirlo. En términos gráficos, está representado por el área total situada debajo del precio y encima de la curva de oferta.”
(Mochón y Beker, 2008: pp 71 y 126).
Gráficamente se trata de la siguiente situación:
Excedente del consumidor

En el gráfico se representaron las curvas de oferta y de demanda, y se indicó el punto de equilibrio del mercado. En ambas curvas, la variable independiente es el precio. Sin embargo, se graficó en el eje horizontal a las cantidades, como es habitual en los estudios de Economía.
En celeste, se sombreó el área que corresponde al excedente del consumidor. Está delimitada por la curva de demanda, graficada en verde, su límite inferior es la recta correspondiente al precio de equilibrio del mercado y verticalmente, va desde 0 hasta la cantidad de equilibrio. En fórmulas, es:
\[EC=\int_{0}^{QE}{\left(D-PE\right)\ dq}\]
Es importante notar que dq indica que la variable a integrar es q, que representa a las cantidades, tanto ofrecidas como demandadas.
En el gráfico siguiente se representa al excedente del productor. El gráfico es el mismo que el anterior, pero en esta nueva situación, el área es la que está comprendida entre la recta correspondiente al precio de equilibrio del mercado y la curva de oferta. Y verticalmente, va desde 0 hasta la cantidad de equilibrio. El excedente del productor también está sombreado en celeste y su fórmula es:
\[EP=\int_{0}^{QE}{\left(PE-O\right)\ dq}\]
Aquí también, la variable a integrar es \(q\).
Excedente del productor
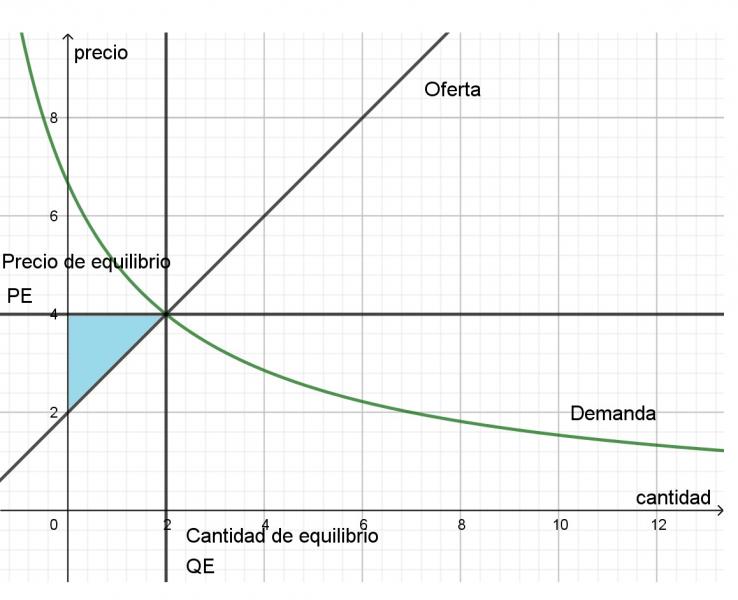
A continuación, se presentan ejemplos del cálculo de Excedentes:
En cierto mercado de bienes la curva de demanda es: \(D\rightarrow p=\frac{1400}{q+20}\) y la de oferta viene dada por: \(O\rightarrow p=\frac{1000}{100-q}\) .Calcule el excedente del consumidor y el del productor en este mercado.
Para resolver este problema, se debe primero hallar el punto de equilibrio del mercado, que informa sobre cuál es el precio al que se pagará este bien y cuántas unidades se venderán. Gráficamente, implica encontrar el punto de intersección de ambas curvas:
Cálculo de excedentes

En el diagrama anterior, confeccionado con Geogebra, se aprecia que el punto de equilibrio de mercado es Precio \(p = 20\) y Cantidad \(q = 50\), indicado por la intersección de las rectas rojas. Sombreado en verde claro, se aprecia el excedente del consumidor, y en celeste, el excedente del productor.
Para buscar analíticamente, el punto de equilibrio del mercado se debe resolver la siguiente ecuación:
\[precio\ demanda=precio\ oferta\]
\[\frac{1400}{q+20}=\frac{1000}{100-q}\]
\[1400=\left(\frac{1000}{100-q}\right)\cdot\left(q+20\right)=\frac{1000\cdot q+20000}{100-q} \]
\[1400\cdot\left(100-q\right)=1000\cdot q+20000\]
\[140000-1400\cdot q=1000\cdot q+20000 \]
\[ 140000-20000=1000\cdot q+1400\cdot q=2400\]
\[\frac{120000}{2400}=q=50 \]
Con este resultado, se reemplaza q en cualquiera de las dos funciones y se obtiene el precio de equilibrio:
\[p=\frac{1000}{100-50}=\frac{1000}{50}=20\]
En el gráfico 5.10., se pintó de color verde el excedente del consumidor y celeste el excedente del productor.
Para calcular el primero, se deberá calcular el área bajo la curva de demanda menos el precio de equilibrio entre 0 y la cantidad de equilibrio, 50:
(1)\[\begin{eqnarray} Excedente\ del\ Consumidor\ =\int_{0}^{50}{\left(\frac{1400}{q+20}-20\right)dq=\nonumber\\ \int_{0}^{50}{\left(\frac{1400}{q+20}\right)dq-20\int_{0}^{50}{dq=}}}\end{eqnarray}\]
En este cálculo, aparece dq indicando que la variable a integrar es q. La resolución del segundo término es muy sencilla:
(2)\[20\int_{0}^{50}{dq=}20\cdot\left. q\right|_0^{50}=20\cdot\left(50-0\right)=1000\ \]
Para resolver el primer término, se utilizará el método de sustitución. Se llamará
\[u=q+20\]
Por lo tanto,
\[du=dq\]
Los extremos de integración se modifican debido al cambio de variable. Por eso, ahora serán: cuando
\[q=0\ \ será \ u=0+20=20\]
y cuando
\[q=50\ \ será \ u=50+20=70 \]
Ahora se reemplaza en (1) y se tiene:
\[\int_{20}^{70}{\frac{1400}{u}du=}1400\ \int_{20}^{70}{\frac{1}{u}\ du}=1400\cdot\left. \ln (u)\right|_{20}^{70} \]
Y ahora, se aplica la regla de Barrow:
(3)\[Área \ bajo \ la \ demanda=1400\cdot [ln (70) -ln (20)] ≈1753,87 \]
Finalmente para obtener el Excedente del Consumidor, se reemplazan los resultados (3) y (2) en la expresión (1):
\[Excedente\ del\ Consumidor\ =\ 1753,87-1000=753,87\]
El excedente del consumidor en este mercado es de $753,87 por cada producto.
Para calcular el Excedente del Productor, el celeste en el gráfico, se hace:
\[Excedente\ del\ productor=\int_{0}^{50}\left(20-\frac{1000}{100-q}\right)dq\\ = \int_{0}^{50}{20\ dq}-\int_{0}^{50}\left(\frac{1000}{100-q}\right)dq\ \]
(4)\[\ =20\int_{0}^{50}dq-\int_{0}^{50}\left(\frac{1000}{100-q}\right)dq\]
El primer término ya se resolvió en (2). Para calcular el segundo, nuevamente es necesario aplicar el método de sustitución. Se llamará
\[u=100-q\]
Por lo tanto,
\[du=-dq \]
entonces,
\[dq=-du \]
Los extremos de integración, ahora serán: cuando
\[q=0\ será \ u=100-0=100\]
y cuando
\[q=50\ será \ u=100-50=50 \]
A pesar de que el “extremo superior” ahora es un número más chico que el nuevo “extremo inferior”, es importante mantener el orden al reemplazar en (2):
\[Área\ bajo\ la\ curva\ de\ oferta =1000\cdot \int_{100}^{50}\left(\frac{-1}{u}\right)du\\ =-1000\cdot \int_{100}^{50} \frac{1}{u}du=-1000\cdot (ln\ u) |_{100}^{50} \]
Y ahora se aplica la regla de Barrow
(5)\[Área\ bajo\ la\ curva\ de\ oferta\ =-1000\cdot(ln 50 -ln 100) =693,15 \]
Para calcular el Excedente del productor solo falta reemplazar (2) y (5) en (4):
\[Excedente\ del\ Productor\ =\ 1000-693,15=306,85\]
Por lo tanto, el excedente del productor es $306,85 por cada producto.
En el mercado del ejercicio anterior, el precio internacional más impuestos de importación es de $16. Si se abre la posibilidad de traer productos importados a ese precio, ¿qué sucederá?. Calcule los nuevos excedentes de consumidores y productores. La situación se puede representar gráficamente de la siguiente manera:
Cálculo de excedentes en una economía abierta al comercio internacional
Es importante notar que el precio de equilibrio de la situación anterior ya no es el precio de venta: a $50 se “vaciaba” el mercado interno: todas las personas que estaban dispuestas a comprar a ese precio podían hacerlo, y todo productor local que quisiera vender a ese precio conseguía vender. Pero al abrir el mercado al resto del mundo, habrá importaciones, porque el precio en el mercado internacional es menor. A ese nuevo precio, más personas querrán comprar. Pero menos productores locales podrán vender tan barato…
Por ese motivo, el excedente del consumidor aumenta y mientras disminuye el del productor. En estas circunstancias se destaca que el aumento en el excedente del consumidor es mayor que lo que disminuye el del productor. El “triángulo” comprendido entre la curva de oferta (en lila) y la de demanda (en verde), que se cruzan en el precio de equilibrio del mercado interno y el nuevo precio (representado por la recta roja) antes no formaba parte de ningún excedente, ni el del productor ni el del consumidor, y ahora se incorpora al del consumidor. En el siguiente gráfico se “agranda” esa zona, para que se vea mejor:
Detalle del gráfico 5.11.

Asimismo, las cantidades demandadas y las ofrecidas por la industria local ya no serán las mismas.
La cantidad demandada está graficada ahora por una recta vertical negra. Y la cantidad ofrecida por la industria local, por una azul.
La diferencia entre esos dos valores indican las cantidades importadas.
Para calcular la cantidad demandada, se deberá reemplazar en la fórmula de la demanda, el nuevo precio y, a partir de allí, calcular la nueva cantidad demandada, lo que implica resolver la siguiente ecuación:
\[D\rightarrow p=\frac{1400}{q+20}=16 \]
\[1400=16\cdot\left(q+20\right) \] \[\frac{1400}{16}=q+20=\ 87,5 \]
\[q=87,5-20=67,5\]
Por lo tanto, la cantidad demandada es 67,5 unidades.
De la misma manera, se busca, con la función de oferta, la cantidad ofrecida por la industria local:
\[O\rightarrow p=\frac{1000}{100-q}=16 \]
\[1000=16\cdot\left(100-q\right)=16\cdot100-16\cdot q=1600-16\cdot q \]
\[16\cdot q=1600-1000=600 \]
\[q=\frac{600}{16}=37,5\]
Entonces, en estas circunstancias la industria local sólo ofrecerá 37,5 unidades.
La diferencia entre las cantidades demandadas y las ofrecidas por la industria local se importan. Por lo tanto, se importarán 30 unidades.
En esta nueva situación, el excedente del consumidor se calcula de la siguiente manera:
\[Excedente\ del\ Consumidor\ =\int_{0}^{67,5}{\left(\frac{1400}{q+20}-16\right)dq\\ =\int_{0}^{67,5}{\left(\frac{1400}{q+20}\right)dq-16\int_{0}^{67,5}dq}}\]
Aquí el extremo superior de integración es la nueva cantidad demandada, 67,5. Y el precio ya no es el de equilibrio del mercado interno ya que se habilitaron las importaciones, sino el precio del mercado internacional más impuestos.
Se propone como ejercicio resolver este cálculo, que es similar al ya efectuado, pero en el que cambian algunas cifras. (Respuesta: excedente del consumidor en este mercado abierto a las importaciones es de $986,27 por cada producto).
Asimismo, el excedente del productor será:
\[Excedente\ del\ productor=\int_{0}^{37,5}\left(16-\frac{1000}{100-q}\right)dq\\ =\int_{0}^{37,5}{16\ dq}-\int_{0}^{37,5}\left(\frac{1000}{100-q}\right)dq\ \]
Otra vez, al precio de mercado (ahora $16) se le resta la función de oferta. Pero el extremo superior de integración cambió: en este caso corresponde a la cantidad ofrecida localmente.
Se propone resolver el cálculo.
Respuesta: el excedente del productor cuando el precio es de $16, es $170 por cada producto.
Como puede apreciarse, el excedente del consumidor aumentó de $753,87 a $986,27 por cada producto. Es decir: $232,40 por producto consumido. Mientras que el excedente del productor disminuyó de $306,85 a $170 por cada producto. Disminuyó en $ 136,85 por producto. O sea, el aumento del excedente del consumidor es mayor que la disminución del excedente del productor.
Anexo económico
Esta teoría de excedentes de consumidor y de productor se utiliza para justificar por qué resulta conveniente para toda la sociedad, por ejemplo, la apertura económica a las importaciones de productos que llegarían más económicos desde otro lugar del mundo, en lugar de fabricarlos localmente.
Si se hiciera esto, el precio local bajaría y aumentaría el excedente del consumidor más de lo que disminuye el excedente del productor. Entonces, aumentaría el excedente en toda la sociedad, más de lo que disminuiría. Aún en esta teoría (tan ortodoxa), se propone que parte de ese “excedente extra” se cobre en forma de impuestos al sector beneficiado por el comercio internacional y que ese dinero se utilice para redistribuirlo en forma de ayuda estatal al sector perjudicado.
La discusión se centra en que, en estas teorías, se concibe a quienes consumen sólo como consumidores. Y en realidad, cada uno de los actores y actrices económicos, puede consumir si puede pagar por sus consumos. Es decir, si tiene ingresos de alguna índole. Pero, para tener ingresos, la gran mayoría de la población debe trabajar. Entonces, si quien produce trabaja menos, porque trae los productos manufacturados en otro país, se contratará a menos cantidad de trabajadores en este país, y habrá, finalmente, menos consumidores. Estos “detalles” no son tenidos en cuenta en esta teoría.
Cuando se conciben las curvas de oferta y de demanda se explica que dependen de muchos factores, entre los que figuran los ingresos de quienes son consumidores. Pero después, con el fin de facilitar el análisis, se dejan fijos estos otros factores y ceteris paribusN se analiza qué sucede cuando van cambiando los precios en cada mercado.
Es decir, las curvas de oferta y de demanda suponen que esos otros factores se mantienen constantes y sólo cambian los precios. Pero, como se puede apreciar, si se abre el mercado a los bienes importados, sí se modifican esas condiciones subyacentes a las curvas. Para analizar correctamente esa situación, deberían recalcularse las curvas. Este es un paso que, en general, omiten quienes dicen que hay que abrirse al comercio internacional.
A pesar de que estas discusiones escapan al nivel del curso de Matemática, nos parece importante resaltar que, en cada problema, antes de generalizar una conclusión es necesario volver a revisar cuáles eran los supuestos iniciales.
Ceteris paribus es una expresión en latín que significa «todo lo demás constante». Es recurrente su uso en el análisis económico y financiero.
El término ceteris paribus sirve a un autor o expositor cuando explica el impacto de una variable económica sobre otra. Es una forma de indicar que todos los demás factores permanecen iguales.
En el mismo mercado en el que se estuvo trabajando, suponga ahora que el precio internacional menos impuestos a la exportaciones (retenciones) fuera $32. Se pide que grafique la situación y explique qué sucedería en este caso. Recalcule los excedentes.
La curva de oferta de un bien está dada por la función:
\[O:\ \ \ \ p=15+e^{0,03q}\]
+Sabiendo que el punto de equilibrio del mercado se alcanza para q = 115 y p=$46,50, calcule el excedente del productor en el mercado cerrado.
Explique qué sucederá en este mercado si se abre el comercio exterior, sabiendo que el precio internacional de este producto es de $40.
Además, calcule el nuevo excedente del productor.

