2. Temas de álgebra lineal
Objetivos
- Resolver un sistema de ecuaciones, usando matrices equivalentes y operaciones entre columnas.
- Comprender el concepto del determinante asociado a un matriz cuadrada y utilizarlo para caracterizar un sistema de ecuaciones.
- Calcular la matriz inversa, utilizando el método de Gauss o con determinantes, el método de Cramer y la matriz adjunta. Resolver un sistema compatible determinado, utilizando la matriz inversa.
Introducción
Cuando se tiene una ecuación con una incógnita, el objetivo generalmente es obtener los valores de la incógnita que satisfacen la ecuación. Así, en la ecuación \(x^2\ -\ 4\ =\ 0\), los valores buscados son \(x = 2\) y \(x = -2\). En esta unidad se verán problemas con varias incógnitas, como también varias ecuaciones, que se deberán satisfacer simultáneamente. A este conjunto de ecuaciones se lo llama sistema y el objetivo de la resolución de un sistema es hallar los valores de las incógnitas que satisfacen todas esas ecuaciones.
Sin embargo, solo se estudiará un tipo de sistema en particular: los sistemas lineales. Esto es una restricción importante sobre los requisitos para poder aplicar lo que aquí se verá. En los sistemas lineales todas las incógnitas en todas las ecuaciones aparecen a la primera potencia y solo pueden estar multiplicadas por un número. De esta forma, en la ecuación anterior \(x^2\ -\ 4\ =\ 0\), la incógnita está elevada a la potencia 2 por lo que a esa ecuación se la llama cuadrática y no es del tipo de ecuaciones que aparecerán en los sistemas lineales a estudiar.
Una propiedad importante que cumplen las ecuaciones lineales es que, si se multiplica por un número toda la ecuación, la nueva ecuación que se obtiene mantiene la misma solución, es decir, el valor de la incógnita que resolvía la ecuación original, también resuelve la nueva ecuación. Se dice que estas ecuaciones son equivalentes. Por ejemplo si dos kilos de pan cuestan cuatro pesos, entonces seis kilos ¿cuánto costarán? Como dos kilos cuestan cuatro pesos, entonces si se desean comprar tres veces más pan, se deberá pagar el triple de lo que se ha pagado por dos kilos. Por lo tanto, se abonarán 12 pesos por los seis kilos de pan. La incógnita aquí es el precio del kilo de pan, que en este caso es de dos pesos. Este procedimiento, que generalmente se resuelve mentalmente, es válido si el precio del pan es lineal con respecto a los kilos que se compran. Esto significa que si se compra el doble, se paga el doble.
En esta unidad, se estudiarán los sistemas lineales con varias incógnitas y cómo resolverlos. Y es importante recordar el significado de la palabra lineal. Pero, antes de enfrentar estos sistemas, se introducirán algunos conceptos de Álgebra lineal, que se utilizarán más adelante en esta misma unidad, para resolverlos.
2.1. Vectores y matrices
Se llama “matriz” a un arreglo ordenado de números, en filas y columnas.
En muchas situaciones se utilizan matrices. Por ejemplo, una lista de precios se puede expresar como una matriz, como se indica a continuación:
| Harina por kilo | Tipo de harina | ||
| Marca | 000 | 0000 | Leudante |
| Pureza | $ 70 | $ 71 | $ 75 |
| Morixe | $ 71 | $ 75 | $ 80 |
Aquí, la matriz de lista de precios es de \(2\times3\) (2 filas por 3 columnas). Se dice que \(2\times3\) es la dimensión de la matriz. La dimensión se podría pensar como el tamaño de la matriz. En forma general una matriz que tiene n filas y m columnas se dice que tiene una dimensión de \(n\times\ m\).
Las matrices se nombran con letras mayúsculas de imprenta. Y sus elementos se ordenan en filas y columnas, encerrados entre paréntesis. Por ejemplo, la matriz de la lista de precios de la tabla 2. 1. es:
\[ A= \left( \begin{array}{lcr} 70 & 71 & 75 \\ 71 & 75 & 80 \\ \end{array} \right) \]
A cada elemento de la matriz se lo identifica con la misma letra que la de su matriz, pero en minúscula y con dos números como subíndice. El primero refiere a la fila y el segundo a la columna.
Por ejemplo, el elemento \(a_{12}=71\) porque el número que se encuentra en la fila 1, columna 2, es 71. El número 80 está en la fila 2, columna 3, por eso es el elemento \(a_{23}\).
Cuando una matriz tiene una sola fila (o una sola columna) se llama vector. Por ejemplo, el vector V de precios de la harina Morixe es: \(V=\left(\begin{matrix}71&75&80\\\end{matrix}\right)\). Y también es un vector, que se puede llamar \(W\), el de los precios de las harinas leudantes:
\[W=\left(\begin{matrix}75\\80\\\end{matrix}\right)\]
Un concesionario de automóviles 0 km tiene dos sucursales, en las que se ofrecen cuatro modelos distintos (de un mismo fabricante). Para simplificar, se llamarán A y B a cada sucursal y Modelo 1, Modelo 2, Modelo 3 y Modelo 4 a cada tipo de automóvil. En la sucursal A tienen 1 unidad del Modelo 1, ninguna del Modelo 2, 2 del Modelo 3 y 3 del Modelo 4. En la sucursal B, tienen 2 autos de cada modelo. Ordene en una matriz la información anterior.
Antes de armar la matriz, conviene usar una tabla, en la que se pueden ubicar referencias:
| Cantidad de automóviles | Modelos | |||
| Sucursal | Modelo 1 | Modelo 2 | Modelo 3 | Modelo 4 |
| A | 1 | 0 | 2 | 3 |
| B | 2 | 2 | 2 | 2 |
Esta información se puede ordenar utilizando la siguiente matriz:
\[C=\left(\begin{matrix}1&0&2\\2&2&2\\\end{matrix}\begin{matrix}\ \ \ 3\\\ \ \ 2\\\end{matrix}\right)\]
Esta matriz es de \(2\times4\), es decir, dos filas por cuatro columnas.
2.1.1. Matriz traspuesta
Se define la matriz transpuesta \(A^t\) de una matriz \(A\) de dimensión \(n\times m\) a la matriz de dimensión \(m\times n\) cuyas filas serán las columnas de \(A\) y, por lo tanto, sus columnas serán las filas de \(A\). Sus elementos están definidos como:
\[a_{ij}^t\ ={\ a}_{ji}\]
Así, la matriz traspuesta de la de los precios de las harinas es:
\[ A^t=\left(\begin{matrix}70&71\\\begin{matrix}71\\75\\\end{matrix}&\begin{matrix}75\\80\\\end{matrix}\\\end{matrix}\right)\]
2.2. Suma de matrices y multiplicación por un escalar
Para poder sumar dos matrices, ambas deben tener la misma dimensión. La suma de dos matrices \(A\) y \(B\) de dimensión \(n\times m\) será una matriz \(C = A + B\), de dimensión \(n\times m\), cuyos elementos son iguales a la suma de los elementos correspondientes de \(A\) y de \(B\), esto es:
\[c_{ij}\ =\ a_{ij}\ +{\ b}_{ij}\]
A las sucursales de la concesionaria del Ejemplo 2.1. llega un cargamento con autos, según la siguiente información:
| Cantidad de automóviles | Modelos | |||
| Sucursal | Modelo 1 | Modelo 2 | Modelo 3 | Modelo 4 |
| A | 2 | 3 | 1 | 0 |
| B | 1 | 3 | 2 | 1 |
Ordene los datos en otra matriz y averigüe cuántos autos de cada modelo quedarán, luego de recibido el cargamento, en cada sucursal.
Esta nueva matriz se puede llamar N. Para poder operar más tarde con la matriz C, es importante mantener el orden de las sucursales (las filas) y los modelos (las columnas de la matriz) y que se correspondan en ambas matrices.
\[N=\left(\begin{matrix}2&3&1\\1&3&2\\\end{matrix}\ \ \ \begin{matrix}0\\1\\\end{matrix}\right)\]
Para calcular cuántos autos de cada modelo habrá en cada sucursal, se suman la matriz C del Ejemplo 1 con esta matriz N:
\( \begin{multline*} T=C+N=\left( \begin{matrix} 1 & 0 & 2 & 3 \\ 2 & 2 & 2 & 2 \end{matrix}\right) + \left( \begin{matrix} 2 & 3 & 1 & 0 \\ 1 & 3 & 2 & 1 \end{matrix}\right) = \\ = \left( \begin{matrix} 1+2 & 0+3 & 2+1 & 3+0 \\ 2+1 & 2+3 & 2+2 & 2+1 \end{matrix}\right) =\left( \begin{matrix} 3 & 3 & 3 & 3 \\ 3 & 5 & 4 & 3 \end{matrix}\right) \end{multline*} \)
Entonces, el total de autos en cada sucursal está indicado en la matriz:
\[T=\left(\begin{matrix}3&3&3\\3&5&4\\\end{matrix}\ \ \ \ \begin{matrix}3\\3\\\end{matrix}\right)\]
2.2.1. Matriz nula
La suma de matrices tiene elemento neutro llamado matriz nula. Se simboliza 0. Hay una matriz nula para cada dimensión de matrices. Por ejemplo, la matriz nula de \(2\times4\) es:
\[\mathbf{0}=\left(\begin{matrix}0&0\\0&0\\\end{matrix}\ \ \ \ \begin{matrix}0&0\\0&0\\\end{matrix}\right)\]
Y la de \(3\times3\) es:
\[\mathbf{0}=\left(\begin{matrix}0&0&0\\0&0&0\\0&0&0\\\end{matrix}\right)\]
Esta matriz tiene la siguiente propiedad:
Para cualquier matriz A, de la misma dimensión que la matriz nula, A + 0 = 0 + A = A
2.2.2. Multiplicación por un escalar
Las matrices pueden multiplicarse por números, a los que también se llaman escalaresN . La multiplicación de una matriz por un número da como resultado una nueva matriz. Cada uno de los coeficientes de la matriz resultado, se obtienen multiplicando a los coeficientes de la matriz original por el escalar.
En símbolos:
\[B = d \cdot A \text{ donde d es el escalar y } A\ \text{y } B\ \text{son matrices.}\]
Y cada uno de los coeficientes de \(B\) se obtienen mediante el siguiente cálculo:
\[b_{ij}\ =\ d\cdot{\ a}_{ij}\]
Se utiliza la expresión escalar, en lugar de número real, por ejemplo, porque los elementos de una matriz también son números reales. Este nuevo nombre lo incorporó al Álgebra Lineal el matemático irlandés William Rowan Hamilton. Más información sobre él en:
<https://www.buscabiografias.com/biografia/verDetalle/8226/William%20Rowan%20Hamilton>
Los precios de todas las harinas aumentaron el 10 %. Encuentre la nueva matriz de precios.
Los precios de las harinas están dados por la matriz \( A= \left( \begin{array}{lcr} 70 & 71 & 75 \\ 71 & 75 & 80 \\ \end{array} \right) \)
Para calcular cada nuevo precio se debería realizar el siguiente cálculo:
\(\begin{multline*}
precio\ nuevo=precio+aumento=precio+\frac{10}{100}\cdot precio=\\
=precio\cdot\left(1+\frac{10}{100}\right)=precio\ \cdot1,1=1,1\cdot precio
\end{multline*}\)
Como todos los precios aumentaron el mismo porcentaje, la nueva matriz de precios se obtiene multiplicando a la matriz original por el escalar 1,1:
\(\begin{multline*} B=1,1\cdot A=1,1\ \cdot A= \left( \begin{array}{lcr} 70 & 71 & 75 \\ 71 & 75 & 80 \\ \end{array} \right) = \\ = \left( \begin{array}{lcr} 1,1 \cdot 70 & 1,1 \cdot 71 & 1,1 \cdot 75 \\ 1,1 \cdot 71 & 1,1 \cdot 75 & 1,1 \cdot 80 \\ \end{array} \right) = \left( \begin{array}{lcr} 77 & 78,1 & 82,5 \\ 78,1 & 82,5 & 88 \\ \end{array} \right) \end{multline*} \)
Por lo tanto, la nueva matriz de precios es \( B= \left( \begin{array}{lcr} 77 & 78,1 & 82,5 \\ 78,1 & 82,5 & 88 \\ \end{array} \right) \)
2.3. Multiplicación de matrices
Para poder multiplicar dos matrices, la cantidad de columnas de la primera matriz debe ser la misma que la cantidad de filas de la segunda.
El producto de dos matrices \(A\) de dimensión \(n \times m\) y \(B\) de dimensión \(m \times k\) (la primera tiene n filas y m columnas y la segunda tiene m filas, es decir, la misma cantidad que columnas tiene la primera matriz, y k columnas) será una matriz \(C = A\) . \(B\) de dimensión \(n \times k\) (tantas filas como la primera matriz y tantas columnas como la segunda matriz) cuyos elementos \(c_{ij}\) son iguales a la suma de los productos de los elementos de la fila i de la primera matriz con los elementos correspondientes de la columna j de la segunda matriz, esto es:
\[ c_{ij}=a_{i1}\ b_{1j}+a_{i2}\ b_{2j}+a_{i3}\ b_{3j}+\ldots+a_{im}\ b_{mj}=\sum\nolimits_{p=1}^{m}{a_{ip}\ b_{pj}}\]
Es importante notar que el producto de matrices no es conmutativo.
Al resolver un producto de matrices, es necesario prestar atención a cuál es la primera y cuál es la segunda matriz, es decir, es importante el orden en que se efectúa la multiplicación. Entre las matrices, la multiplicación no es conmutativa.
En el siguiente ejemplo se multiplican dos matrices y se explica una disposición que facilita el uso de la fórmula anterior.
Multiplique las matrices \(A=\left(\begin{matrix}1&-2\\2&4\\0&-1\\\end{matrix}\right)\) y \(B=\left(\begin{matrix}3&-3&2\\4&1&6\\\end{matrix}\ \ \ \begin{matrix}0\\-2\\\end{matrix}\right)\)
La matriz \(A\) es de dimensión \(3\times2\) y la matriz \(B\) es de \(2\times4\). Por lo tanto, la matriz producto, a la que se llamará \(C\), será de \(3\times4\), la cantidad de filas de \(A\) por la cantidad de columnas de \(B\).
Para calcular cada elemento de \(C\), conviene disponer las matrices en un esquema como el siguiente. En el casillero inferior izquierdo se ubican los coeficientes de la matriz \(A\). En el superior derecho, los de la matriz \(B\) y en el inferior derecho, se calculan los de la matriz producto \(C\):
Tabla 2.4. Esquema para multiplicar matrices
En este ejemplo sería:
Tabla 2.5. Primera parte
Cada elemento de la matriz producto se obtendrá en el extremo inferior derecho, sumando el producto, elemento a elemento, de cada fila con cada columna que se crucen. Así, en la posición \(c_{11}\), se cruzan la fila 1 de \(A\) con la columna 1 de \(B\). Ese elemento se calculará sumando el producto de cada elemento de la fila 1 de \(A\) con el elemento correspondiente de la columna 1 de \(B\):
\[c_{11}=1\cdot3\ +\ \left(-2\right)\cdot4\ =3-8\ =\ -5\]
El 1 es el primer elemento de la fila 1 de \(A\) y se lo multiplica por el primer elemento de la columna 1 de \(B\), y se suma el producto entre el segundo elemento de la fila 1 de \(A\) por el segundo elemento de la columna 1 de \(B\).
Otro ejemplo: el elemento \(c_{34}\) se encuentra en el cruce de la fila 3 de \(A\) con la columna 4 de \(B\). Se calcula entonces como: \(c_{34}=0\cdot0\ +\ \left(-1\right)\cdot\left(-2\right)=0+2=2\) , es decir, al primer elemento de la fila 3 de A se lo multiplica por el primer elemento de la columna 4 de \(B\) y se le suma el producto entre el segundo elemento de la fila 3 de \(A\) y el segundo de la columna 4 de \(B\).
Completando todos los cálculos, se obtiene el resultado:
Tabla 2.6. Segunda parte
Por lo tanto, el producto de estas dos matrices es la matriz de dimensión \(3\times4 \) que llamamos \(C=\left(\begin{matrix}-5&-5&-10\\22&-2&28\\-4&-1&-6\\\end{matrix}\ \ \begin{matrix}4\\-8\\2\\\end{matrix}\right)\)
Es importante notar que el producto de estas matrices, en orden contrario, \(B\cdot A\) no se puede realizar, porque la cantidad de columnas de \(B\) no coincide con la cantidad de filas de \(A\).
La matriz \(B\) es de \(2\times4\) y la matriz \(A\), de \(3\times2\). Como 4 no es igual a 3, el producto no se puede realizar.
Como ejemplo de multiplicación entre matrices se verá la multiplicación entre dos matrices iguales, la matriz \(A\) por la misma matriz \(A\), obteniendo \(A^2\). La potencia de matrices se define del mismo modo que con los números. Así como \(2^3\) es \(2\cdot 2\cdot 2\), \(A^3\)será \(A \cdot A \cdot A\).
Sin embargo, como el producto de matrices solo se define cuando la cantidad de filas de la primera matriz coincide con la cantidad de columnas de la segunda, solo se podrán calcular potencias de matrices entre las que tengan igual número de filas que de columnas, es decir, matrices cuadradas.
Por ejemplo, calcule el cuadrado de la matriz \(A\):
\[A=\left(\begin{matrix}2&5\\2&-1\\\end{matrix}\right)\]
El cuadrado de esta matriz se calcula de la siguiente manera:
\[A^2=A.A=\left(\begin{matrix}2&5\\2&-1\\\end{matrix}\right)\cdot\left(\begin{matrix}2&5\\2&-1\\\end{matrix}\right)\]
Aquí se resolverá utilizando otra disposición, con colores y sombreado para ver cómo se combinan cada uno de los coeficientes, se los multiplica y suma para obtener la matriz producto.
\[ \begin{multline*} A^2=A\cdot A=\left(\begin{matrix}\color{yellow} 2 &\color{green} 5 \\ \color{orange} 2&\color{magenta}{-1}\\\end{matrix}\right)\cdot \left(\begin{matrix}\boldsymbol{\color{red} 2} & \boldsymbol{\color{blue} 5}\\ \boldsymbol{\color{brown}2}& \boldsymbol{\color{purple}{-1}} \\\end{matrix}\right)= \\ \left(\begin{matrix}\color{yellow} 2 \cdot \boldsymbol{\color{red} 2} +\color{green} 5 \cdot \boldsymbol{\color{brown}2}&\color{yellow} 2 \cdot \boldsymbol{\color{blue} 5} + \color{green} 5 \cdot(\boldsymbol{\color{purple}{-1}})\\\ \ \color{orange} 2 \cdot \boldsymbol{\color{red} 2} +(\color{magenta}{-1})\cdot \boldsymbol{\color{brown}2} \ \ & \ \ \color{orange} 2 \cdot \boldsymbol{\color{blue} 5}+(\color{magenta}{-1})\cdot(\boldsymbol{\color{purple}{-1}})\\\end{matrix}\right)=\ \left(\begin{matrix}14&5\\2&11\\\end{matrix}\right) \end{multline*} \]
2.3.1. Matriz identidad
El producto de matrices cuadradas tiene elemento neutro llamado matriz identidad. Se simboliza Id. Hay una matriz identidad para cada dimensión de matriz cuadrada. Por ejemplo, la matriz identidad de \(2\times2\) es:
\[Id=\left(\begin{matrix}1&0\\0&1\\\end{matrix}\right)\]
Y la de \(3\times3\) es:
\[Id=\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right)\]
Como puede apreciarse, los elementos son 0 y 1. Los 1 están en la diagonal de la matriz, formada por las posiciones en las que en número de la fila coincide con el número de la columna.
En general, los elementos de la matriz identidad de dimensión \(n\times n\) se definen de la siguiente manera:
\[\left\{\begin{matrix}{Id}_{ij}=1\ si\ i=j\\{Id}_{ij}=0\ si\ i\neq j\\\end{matrix}\right.\]
La matriz identidad, en el producto de matrices de su misma dimensión, cumple con la siguiente propiedad:
\[A\cdot Id=Id\cdot A=A\]
Muestre que la matriz identidad es el neutro de la multiplicación, realizando la siguiente operación:
\[A\cdot Id=\left(\begin{matrix}2&5\\2&-1\\\end{matrix}\right)\cdot\left(\begin{matrix}1&0\\0&1\\\end{matrix}\right) \]
Para realizar este cálculo se puede utilizar la disposición del Ejemplo 2.4.:
\[\begin{array}{r|rrrr} A\cdot Id & \left(\begin{matrix}1&0\\0&1\\\end{matrix}\right) \\ \hline \left(\begin{matrix}2&5\\2&-1\\\end{matrix}\right) & \left(\begin{matrix}2&5\\2&-1\\\end{matrix}\right) \end{array} \]Como puede apreciarse, el resultado es la matriz \(A\), es:
\[A\cdot Id=\left(\begin{matrix}2&5\\2&-1\\\end{matrix}\right)=A
\]
Es importante notar que no se ha demostrado la propiedad, sino que solo se ha presentado un ejemplo.
Halle los valores de a y b que resuelven la siguiente ecuación:
\[A^2+ a \cdot A + b \cdot Id = \mathbf{0}\]
Donde Id es la matriz identidad y \(A=\left(\begin{matrix}2&5\\2&-1\\\end{matrix}\right)\), la matriz del Ejemplo 2.5.
El problema requiere hallar los valores de a y b (dos escalares, es decir, números) que verifiquen la ecuación.
En ella, se reemplaza por lo que ya se conoce: el primer término de la ecuación a resolver es la matriz \(A^2\), que fuera calculada previamente:
\[A^2=\left(\begin{matrix}14 & 5\\2 & 11\\\end{matrix}\right) \]
el segundo término es igual al escalar a por la matriz \(A\), esto es:
\[a \cdot A = a \left(\begin{matrix}2 & 5\\2 & -1\\\end{matrix}\right) = \left(\begin{matrix}2a & 5a\\2a & -1a\\\end{matrix}\right) = \left(\begin{matrix}2a & 5a\\2a & -a\\\end{matrix}\right) \]
el tercer término de la ecuación es el producto de otro escalar b por la matriz identidad:
\[b \cdot Id = b \left(\begin{matrix}1 & 0\\0 & 1\\\end{matrix}\right) = \left(\begin{matrix}b & 0\\0 & b\\\end{matrix}\right) \]
solo resta sumar los tres términos (las tres matrices, componente a componente)
e igualar a la matriz nula de dimensión \( 2\times 2\): \[ A^2+\ a\cdot\ A\ +\ b\cdot\ Id\ =\ \mathbf{0} \] \[ \left(\begin{matrix}14&5\\2&11\\\end{matrix}\right)+\left(\begin{matrix}2a&5a\\2a&-a\\\end{matrix}\right)+\left(\begin{matrix}b&0\\0&b\\\end{matrix}\right)=\left(\begin{matrix}0&0\\0&0\\\end{matrix}\right)
\] \[ \left(\begin{matrix}14+2a+b&5+5a+0\\2+2a+0&11-a+b\\\end{matrix}\right)=\left(\begin{matrix}0&0\\0&0\\\end{matrix}\right)
\] para que
las dos últimas matrices sean iguales deben ser iguales componente a componente,
entonces debe ser: \[ \left\{ \begin{matrix}
14 + 2 a + b = 0\\
5 + 5 a = 0\\
2+2a=0\\
11 – a + b = 0
\end{matrix}
\right.
\] Este es un sencillo sistema de ecuaciones lineales. La llave que une a
todas las ecuaciones indica que se busca una única solución que debe cumplir
todas ellas. Se resolverá comenzando por la segunda ecuación. De ella, se obtiene
\(5a = -5\) entonces \(a = -1\),
resultado que coincide con el que se hubiera logrado si se comenzaba por
la tercera ecuación. Ya se tiene el valor de a. Ahora, en la ecuación 1,
se reemplaza este valor de a y se obtiene: \[14\ +\ 2\ a\ +\ b\ =\ 14\ +2\cdot(-1)\ +\ b\ =\ 0\]
entonces \(b = -12\), valor que también
satisface la ecuación 4: \[11\ -\ a\ +\ b\ =\ 11\ -\ (-1)\ +\ (-12)\ =\ 0\] Por lo tanto, los valores de a y b que satisfacen la ecuación a resolver
son: \[\left\{\begin{matrix}a=-1\\b=-12\\\end{matrix}\right.\]
2.4. Sistemas de ecuaciones lineales. Resolución por el Método de Gauss
Para resolver sistemas lineales, como los del Ejemplo 2.7. y de los que se habló en la introducción de esta Unidad, se puede trabajar con las matrices, sin utilizar las incógnitas y solo los coeficientes.
Suponga que en la verdulería se compran 2 kilos de manzanas, 1 kg de bananas y 3 de naranjas. Y no se preguntó el precio de cada fruta. El total de la compra resulta de $ 13. Al otro día se vuelve a comprar en el mismo lugar, pero diferentes cantidades, para obtener más información y deducir el precio del kilo de cada fruta. En esta ocasión se compraron 3 kilos de manzanas, 2 de bananas y 2 de naranjas y se pagó nuevamente $13. En tercer día se compran 2 kilos de manzanas, 3 kg de bananas y 1 kg de naranjas, y esta vez, la suma fue de $11. Simbolice estos datos con una matriz.
Esta información se puede resumir con 3 ecuaciones, considerando las siguientes incógnitas:
- el precio del kilo de manzanas, que se simbolizará con M,
- el de bananas, B y
- el de naranjas N.
Entonces, la suma de cada día se puede escribir como:
\[\left\{\ \ \begin{matrix} 2 M + 1 B + 3 N = 13 \\ 3 M + 2 B + 2 N = 13 \\ 2 M + 3 B + 1 N = 11 \end{matrix}\right.\]
La llave que une a todas las ecuaciones indica que se busca una única solución que deben cumplir todas ellas.
Más adelante, en esta misma la unidad, se verán diferentes métodos para resolver este sistema de ecuaciones lineales. Aquí el objetivo solo es simbolizar este sistema con una matriz.
A partir de un sistema de ecuaciones lineales con varias incógnitas (x, y, etc.) y los coeficientes (números) que las multiplican, se puede ordenar el sistema de forma tal que las incógnitas iguales en cada ecuación queden encolumnadas. De esta forma, se puede trabajar con los coeficientes por separado para hallar la solución del sistema y así no tener que mantener en los cálculos las incógnitas mientras se opera (aquí es importante notar que cada columna tiene asociada una incógnita con lo cual será conveniente no intercambiar las columnas).
A este ordenamiento de los coeficientes, separados del sistema, se lo llama matriz asociada al sistema. Luego, una matriz asociada es un conjunto de coeficientes (números) con tantas filas como ecuaciones tenga el sistema y tantas columnas como incógnitas tenga el sistema.
En este ejemplo, la matriz asociada es:
\[\left(\begin{matrix}2&1&3\\3&2&2\\2&3&1\\\end{matrix}\right)
\]
También se define la matriz ampliada asociada al sistema de ecuaciones a la matriz anterior a la que se le agrega una cuarta columna con los coeficientes independientes de cada ecuación (los números que no multiplican a ninguna incógnita). La matriz ampliada del sistema anterior será:
\[\left(\left. \begin{matrix}2&1&3\\3&2&2\\2&3&1\\\end{matrix}\ \ \right|\begin{matrix}13\\13\\11\\\end{matrix}\right)
\]
Esta última matriz asociada resume la información del texto de este ejemplo. Es importante recordar que los coeficientes de la primera columna corresponden a la incógnita M, los de la segunda a la B y los de la tercera a la N.
Halle la matriz asociada al siguiente sistema de ecuaciones:
\[\left\{\ \ \begin{matrix}3\ x\ +\ 2\ y\ =\ 12\\-\ y\ +\ 2\ z\ =\ -\ 5\\y\ +\ z\ +2\ x\ -6=0\\\end{matrix}\right.\]
Aquí, primero se encolumnan en forma ordenada las incógnitas en cada ecuación en el primer término y los términos independientes en el segundo. En algunas ecuaciones en las que no aparece alguna incógnita, será necesario agregarla, con coeficiente cero:
\[\left\{\begin{matrix}3\ x\ +\ 2\ y\ +\ 0\ z\ =\ 12\\0\ x-\ y\ +\ 2\ z\ =\ -\ 5\\2\ x\ +\ y\ +\ z\ =\ 6\\\end{matrix}\right.\]
Una vez ordenado el sistema se arma la matriz asociada, poniendo en la primera columna (la de las x) a los coeficientes que multiplican a esta variable en cada una de las ecuaciones), en la segunda columna los coeficientes que multiplican a las incógnitas y, y en la tercera columna los coeficientes que multiplican a las incógnitas z, y así quedan los coeficientes ordenados de la siguiente forma:
\[\left(\begin{matrix}3&2&0\\0&-1&2\\2&1&1\\\end{matrix}\ \ \left|\ \ \begin{matrix}12\\-5\\6\\\end{matrix}\right.\right)\]
Que es la matriz asociada a este sistema de ecuaciones.
2.4.1. El Método de Gauss
El método de Gauss propone operar con las ecuaciones del sistema, que son las filas de la matriz ampliada, para simplificar coeficientes y que sea más fácil encontrar la solución al sistema que se desea resolver.
Se trata de la generalización de uno de los métodos estudiados en el nivel medio para resolver sistemas de dos ecuaciones con dos incógnitas, donde se multiplican las ecuaciones por escalares, y se suman o restan entre sí para eliminar una de las incógnitas.
El objetivo del método de Gauss es precisamente ese, operar con las filas de la matriz ampliada, es decir, con las ecuaciones del sistema, de tal forma que aparezcan la mayor cantidad de ceros en cada una de las filas, ya que un cero corresponde a haber eliminado la incógnita de la ecuación correspondiente a esa fila. Pero es importante recordar que el nuevo sistema debe tener las mismas soluciones que el sistema original, es decir, el inicial y el final deben ser sistemas equivalentes.
Las dos operaciones más importantes que se pueden realizar para simplificar el sistema a resolver son:
- Multiplicar (o dividir) una fila por un escalar distinto de cero.
- Reemplazar una fila por la suma de esa fila con otra fila de la matriz.
También se pueden combinar ambas operaciones y permutar dos filas entre sí, lo que puede permitir ordenar mejor el sistema.
Se podría permutar las columnas si en algún caso facilita la resolución del sistema, pero esto trae el inconveniente de cambiar la asociación inicial entre columnas de la matriz y las incógnitas del problema, razón por la cual aquí no se recomienda esta operación.
Resuelva el siguiente sistema:
\[\left\{\begin{matrix}3x+2y=12\\-y+2z=-5\\y+z+2x-6=0\\\end{matrix}\right.\]
Este sistema de ecuaciones es el del Ejemplo 2.9., cuya matriz ampliada es:
\[\left(\left. \begin{matrix}3&2&0\\0&-1&2\\2&1&1\\\end{matrix}\ \right|\ \begin{matrix}12\\-5\\6\\\end{matrix}\right)\]
Se operará ahora con ella para resolverlo obteniendo matrices equivalentes a la original.
Aquí se puede multiplicar la fila 1 por 2 y, por otro lado, multiplicar la fila 3 por 3, lo que se simbolizará de la siguiente manera:
\[F^\prime1=2\cdot F1\]
\[F^\prime3=3\cdot F3\]
Y se obtiene la matriz equivalente:
\[\left(\left. \begin{matrix}6&4&0\\0&-1&2\\6&3&3\\\end{matrix}\ \right|\ \begin{matrix}24\\-5\\18\\\end{matrix}\right)\]
luego se reemplaza la \(F3\) por la \(F3\) menos la \(F1\), es decir: \(F´3=F3-F1\) . Resulta:
\[\left(\left. \begin{matrix}6&4&0\\0&-1&2\\0&-1&3\\\end{matrix}\ \right|\ \begin{matrix}24\\-5\\-6\\\end{matrix}\right)\]
Aquí hay una columna, la columna 1, con un solo elemento distinto de cero. Si se opera adecuadamente, esos ceros permanecerán allí hasta el final de la resolución.
El siguiente paso será tratar de que aparezcan ceros en la segunda columna. Para eso se puede utilizar la fila 2, que ya tiene un 0 en la columna de las x. Así no se alterna el 0 de la fila 3 y el 6 de la fila 1. Conviene mantener el -1 de la fila 2, columna 2, y operar para eliminar el 4 de la posición 1-2 y el -1 de la posición 3-2. Las operaciones que se realizarán serán:
\(F´1=F1 + 4 \cdot F2\) (la nueva fila 1 será la \(F1 + 4 \cdot F2\)). A veces se simboliza como \(F1+4 \cdot F2\rightarrow F1\)
\(F´3=F3-F2\) (la nueva fila 3 será la \(F3 – F2)\). También se puede escribir así: \(F3-F2\rightarrow F3\)
Así, se obtiene la matriz equivalente:
\[\left(\left. \begin{matrix}6&0&8\\0&-1&2\\0&0&1\\\end{matrix}\ \right|\ \begin{matrix}4\\-5\\-1\\\end{matrix}\right)\]
Hasta aquí se ha obtenido una matriz triangular, o subtriangular, porque tiene un “triángulo de ceros” en el extremo inferior izquierdo.
En este punto, ya se podría volver al sistema de ecuaciones y sería más sencillo de resolver que el original. Sin embargo, se puede continuar operando, para simplificar aún más el sistema, hasta obtener lo que se llama una matriz diagonal, es decir, una matriz en la cual todos los elementos \( a_{ij} \) con i \( \neq \) j son ceros. En el ejemplo solo resta obtener ceros en la columna 3. Para ello, se realizan los reemplazos:
\[F´1=F1 - 8 \cdot F3\]
\[F´2=F2 - 2 \cdot F3\]
Con lo que se llega a:
\[\left(\left. \begin{matrix}6&0&0\\0&-1&0\\0&0&1\\\end{matrix}\ \right|\ \begin{matrix}12\\-3\\-1\\\end{matrix}\right)\]
Aquí ya resulta una matriz diagonal. Si se quiere simplificar del todo el sistema, se pueden dividir las filas de tal forma que queden solo unos en la diagonal, mientras se conservan los ceros fuera de esta, con lo que se obtiene la matriz identidad en la primera parte de la matriz asociada. Para lograrlo, se divide la fila 1 por 6 y se multiplica la fila 2 por (-1):
\[F´1=F1/6\]
\[F´2=F2 \cdot (-1)\]
El resultado es:
\[\left(\left. \begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\ \right|\ \begin{matrix}2\\3\\-1\\\end{matrix}\right)\]
Ahora, se recuerda que la columna 1 corresponde a la incógnita x, la columna 2 a la incógnita y, y la columna 3 a la incógnita z y se reescribe el sistema equivalente:
\[\left\{\begin{matrix}1x + 0y + 0z = 2 \\ 0x + 1y + 0z = 3 \\ 0x + 0y + 1z = -1\end{matrix}\right.\]
\[\text{Lo que equivale a }\left\{\begin{matrix}x = 2\\ y= 3\\ z =-1\end{matrix}\right.\]
con lo cual, ya se tiene la solución del sistema.
Es muy conveniente adquirir la costumbre, después de resolver un problema, de realizar la verificación de la solución. En este caso la idea es reemplazar los valores obtenidos para \(x, y\) y \( z\), en el sistema original y comprobar si satisfacen todas las ecuaciones del sistema. El sistema original era:
\[\left\{\begin{matrix}3x+2y=12\\-y+2z=-5\\y+z+2x-6=0\\\end{matrix}\right.\]
Entonces, con los valores hallados, se obtiene.
\[\begin{split} & Primera\ ecuaci\acute{o}n:\ 3 x + 2 y = 3 \cdot2 + 2\cdot3 = 6 + 6 = 12 &\ \ verificada\\ & Segunda\ ecuaci\acute{o}n:\ - y + 2 z = - 3 + 2 \cdot(-1) = -3 -2 = -5 &\ \ verificada\\ & Tercera\ ecuaci\acute{o}n:\ y + z + 2 x = 3 + (-1) + 2 \cdot2 -6= 3 -1 + 4-6 =0 &\ \ verificada \end{split}\]
De esta manera se ha verificado que el resultado obtenido es correcto.
A los sistemas que admiten solución se los denomina compatibles. Aquellos sistemas compatibles que tienen una sola solución como el ejemplo anterior se los llama compatibles determinados.
También hay sistemas que tienen más de una solución denominados compatibles indeterminados.
Por último, hay sistemas que no tienen solución, porque no hay valores que reemplazados en las incógnitas satisfagan todas las ecuaciones del sistema. A estos sistemas sin soluciones se los llama incompatibles.
Resuelva el sistema:
\[\left\{\begin{matrix} x +y=z \\-2 x + 3 z=5 \\ x + 5 y + z=10\end{matrix}\right.\]
Como ya se ha visto, primero se ordena y completa el sistema:
\[\left\{\begin{matrix}x+y-z=0\\-2x+0y+3z=5\\x+5y+z=10\\\end{matrix}\right.\]
Y se escribe la matriz asociada ampliada:
\[\left(\begin{matrix}1&1&-1\\-2&0&3\\1&5&1\\\end{matrix}\left|\begin{matrix}0\\5\\10\\\end{matrix}\right.\right) \]
Para diagonalizar la matriz asociada al sistema, conviene elegir un coeficiente de la matriz, al que se lo llamará pivote, para hacer ceros los coeficientes de su columna. Se puede seleccionar cualquier coeficiente y no hay una regla general. Es muy importante que una vez que se tiene una columna con todos ceros menos uno de sus elementos, seleccionar luego otro pivote en otra columna diferente y que sea de una fila distinta en donde quedó el número diferente de cero de la columna anterior. Por lo general, si hay algún elemento que valga 1 es más fácil de usar como pivote.
Las operaciones que se pueden hacer sin cambiar el problema, como ya se ha visto, es multiplicar las filas por cualquier número distinto de cero y reemplazar una fila por la misma fila sumada a otra fila distinta, a la que se puede haber multiplicado por un número previamente, o, por lo general se hacen ambos pasos a la vez. El objetivo final es tratar de que, al hacer el paso recién descripto, aparezcan en la fila que se está reemplazando algún coeficiente igual a cero. Por lo general, son los coeficientes de la columna del pivote que busca que se transformen en cero.
En este ejemplo, se toma el 1 que aparece en la posición 1-1 y se realizan las operaciones y reemplazos siguientes:
\( F´2 = F2 + 2 F1 \) (la nueva fila 2 será la \(F2 + 2 F1)\) y \(F´3 = F3 - F1\) (la nueva fila 3 será la \(F3 - F1\))
\[\left(\begin{matrix}1&1&-1\\0&2&1\\0&4&2\\\end{matrix}\left|\begin{matrix}0\\5\\10\\\end{matrix}\right.\right)\]
El siguiente paso es realizar el reemplazo \(F3 - 2 F2 \rightarrow F3\)
\[\left(\begin{matrix}1&1&-1\\0&2&1\\0&0&0\\\end{matrix}\left|\ \begin{matrix}0\\5\\0\\\end{matrix}\right.\right)\]
En este caso, la tercera fila no contiene ninguna información dado que se la puede reescribir como: \( 0 x + 0 y + 0 z = 0 \) que no impone ninguna condición sobre las incógnitas. Cualquier valor de x, de y o de z puede satisfacer esta ecuación. Es decir, el sistema queda con una ecuación menos. En este paso, el sistema que ya está triangulado, es decir, hay ceros debajo de la diagonal que es lo que busca realizar el método de Gauss. A partir de allí hay que rearmar las ecuaciones y despejar.
\[\left\{\begin{matrix}x+y-z=0\\2y+z=5\\0=0\\\end{matrix}\right.\]
De la segunda ecuación se obtiene:
\[z = 5 - 2 y\]
Ahora se puede reemplazar z por el valor obtenido de la ecuación anterior en la primera ecuación. Y conviene que la otra incógnita a despejar, en este caso la x, quede también en función de y. Entonces:
\[\begin{gather*} x\ +\ y\ -\ z\ =\ 0\\ x+y-\left(5-2y\right)=0\\ \ x\ +\ y\ -\ 5\ +\ 2\ y\ =\ 0\\ x\ +\ 3\ y\ -\ 5\ =\ 0\\ x\ =\ 5\ -\ 3\ y \end{gather*}\]
De modo que la solución de este sistema es:
\[\left\{\begin{matrix}x=5-3y\\y=y\\z=5-2y\end{matrix}\right.\]
Este es un sistema compatible indeterminado, porque las incógnitas quedan dependiendo de los valores que toman las otras incógnitas, en este caso, por ejemplo, z será igual a 5 menos dos veces el valor que tome y.
¿Qué significa este resultado? Que existen muchas soluciones para el sistema, por ejemplo tomando \(y = 7\), resulta:
\[\ x = 5 - 3 y = 5 – 3 . 7 = 5 - 21 = -16\]
\[z = 5 - 2 y = 5 – 2 . 7 = 5 - 14 = - 9\]
Si se toma otro valor cualquiera de y, se obtendrán valores de x y de z que también serán solución del sistema. La solución general se suele escribir, en forma matricial, de la siguiente manera:
\[\boldsymbol{x} =\ \left(\begin{matrix}x\\y\\z\\\end{matrix}\right)= \left(\begin{matrix}5-3y\\y\\5-2y\\\end{matrix}\right)\]
El vector columna \(\boldsymbol{x}\), de las soluciones del sistema, se puede escribir como la suma de dos vectores columna uno que tenga los términos con la y y otro con los términos independientes:
\[\boldsymbol{x} =\ \left(\begin{matrix}x\\y\\z\\\end{matrix}\right)=\ \left(\begin{matrix}5-3y\\y\\5-2y\\\end{matrix}\right)=\left(\begin{matrix}5\\0\\5\\\end{matrix}\right)+\ \left(\begin{matrix}-3y\\y\\-2y\\\end{matrix}\right)=\left(\begin{matrix}5\\0\\5\\\end{matrix}\right)+\ y\left(\begin{matrix}-3\\1\\-2\\\end{matrix}\right)\]
Este es el resultado general donde, como vimos antes, la y puede tomar cualquier valor. En general, a ese cualquier valor lo simboliza con la letra \(t\) para evitar confundirlo con la variable. Luego, la solución del sistema es:
\(\boldsymbol{x} =\left(\begin{matrix}5\\0\\5\\\end{matrix}\right)+\ t\left(\begin{matrix}-3\\1\\-2\\\end{matrix}\right)\) donde \(t\) puede tomar cualquier valor.
Lo único que resta de este ejercicio es realizar la verificación. Se insiste en esto porque se pretende que se adquiera la costumbre, ya que es una posibilidad muy importante que nos brindan las matemáticas para saber si realizamos las cosas bien.
Para ello se debe reemplazar en el sistema original los valores de x, y y z que se obtuvieron. Aquí se hará usando matrices y productos de matrices.
El sistema original se puede escribir como:
\(\left\{\begin{matrix} x + y - z = 0\\ -2 x + 0 y + 3 z = 5 \\ x + 5 y + z = 10\end{matrix}\right.\) equivalente a \[\left(\begin{matrix}1&1&-1\\-2&0&3\\1&5&1\\\end{matrix}\right)\left(\begin{matrix}x\\y\\z\\\end{matrix}\right)=\left(\begin{matrix}0\\5\\10\\\end{matrix}\right)\]
Ahora se reemplaza por la solución encontrada \(\boldsymbol{x} =\left(\begin{matrix}5\\0\\5\\\end{matrix}\right)+\ t\left(\begin{matrix}-3\\1\\-2\\\end{matrix}\right)\)
\[ \left( \begin{matrix}1 & 1 & -1\\-2 & 0 & 3\\1 & 5 & 1\end{matrix}\right) \left[ \left( \begin{matrix}5\\0\\5\end{matrix} \right) + t \left( \begin{matrix}-3\\1\\-2\end{matrix} \right) \right] = \left( \begin{matrix}0\\5\\10\end{matrix} \right) \]
donde los corchetes están colocados porque la matriz \(A\) multiplica a la suma de los dos vectores columna. Aquí se suma para obtener solo un vector columna:
\[\left(\begin{matrix}1&1&-1\\-2&0&3\\1&5&1\\\end{matrix}\right)\left(\begin{matrix}5\ -\ 3\ t\\0\ +\ 1\ t\\5\ -\ 2\ t\\\end{matrix}\right)=\left(\begin{matrix}0\\5\\10\\\end{matrix}\right)\]
Y se efectúa el producto \( A \cdot x \)
\[\left(\begin{matrix}1&1&-1\\-2&0&3\\1&5&1\\\end{matrix}\right)\left(\begin{matrix}5\ -\ 3\ t\\0\ +\ 1\ t\\5\ -\ 2\ t\\\end{matrix}\right)=\left(\begin{matrix}1\ .\ (5\ -\ 3\ t)\ +1\ .\ (\ 0\ +\ 1\ t)\ +\ (-1)\ .\ (5\ -\ 2\ t)\\(-2)\ .\ (5\ -\ 3\ t)\ +0\ .\ (\ 0\ +\ 1\ t)\ +\ 3\ .\ (5\ -\ 2\ t)\\1\ .\ (5\ -\ 3\ t)\ +5\ .\ (\ 0\ +\ 1\ t)\ +\ 1\ .\ (5\ -\ 2\ t)\\\end{matrix}\right)\]
\[\left(\begin{matrix}5\ -\ 3\ t\ +\ \ t\ -\ \ 5\ \ +\ 2\ t\\-10\ +6\ t\ +15\ -\ 6\ t\\5\ -\ 3\ t+5\ t\ +\ 5\ -\ 2\ t\\\end{matrix}\right)=\left(\begin{matrix}0\\5\\10\\\end{matrix}\right)\]
Al resolver, se obtiene el vector columna con los coeficientes independientes, lo que verifica la solución general obtenida.
Al resolver un sistema de ecuaciones por el método de Gauss, se puede clasificar la solución del sistema en función del número de incógnitas del sistema, el número de ecuaciones distintas de cero de la matriz asociada resultante y también de las de la matriz ampliada. Lo más sencillo es hacerlo cuando se obtiene la matriz subtriangulada.
En el caso de tener un sistema compatible determinado, luego de diagonalizar el sistema, se tiene la misma cantidad de ecuaciones tanto, para la matriz asociada como para la matriz ampliada y, a su vez, la misma cantidad de incógnitas.
Puede suceder, en cambio, que luego de la diagonalización, algunas de las ecuaciones se anulan, y quedan todos los coeficientes en cero, como en el Ejemplo 2.11., tanto los de las incógnitas como el término independiente. En este caso quedan más incógnitas que ecuaciones independientes por lo que existirán muchas soluciones posibles ya que algunas de las incógnitas quedarán indeterminadas. Y el sistema será un sistema compatible indeterminado.
Por último, si luego de la diagonalización hay ecuaciones con los coeficientes de las incógnitas igual a cero, pero el término independiente distinto de cero, en ese caso se llega a una contradicción por lo que no existirá solución para ese sistema. El sistema será incompatible.
Resuelva el siguiente sistema de ecuaciones:
\[\left\{\begin{matrix}2x+y=5\\-4x=9+2y\\\end{matrix}\right.\]
Como en los ejemplos anteriores, se comienza por ordenar el sistema y hallar la matriz asociada ampliada:
\[\left\{\begin{matrix}2x+y=5\\-4x-2y=9\\\end{matrix}\right.\]
\[\left(\begin{matrix}2&1\\-4&-2\\\end{matrix}\ \middle|\ \begin{matrix}5\\9\\\end{matrix}\right)\]
Para obtener un cero en la posición \(2,1\) (fila 2 columna 1), se realiza \(F2+2F1\rightarrow F2\)
\[\left(\begin{matrix}2&1\\0&0\\\end{matrix}\ \middle|\ \begin{matrix}5\\19\\\end{matrix}\right)\]
En este caso, la segunda fila de la matriz ampliada se anula en su primera parte, pero la columna de los términos independientes no se anuló. Al volver a escribir, a partir de esta matriz, el sistema equivalente es:
\[\left\{\begin{matrix}2x+y=5\\0x+0y=19\\\end{matrix}\right.\]
Es decir:
\[\left\{\begin{matrix}2x+y=5\\0=19\\\end{matrix}\right.\]
Claramente, la segunda ecuación es absurda. Cero no es igual a diecinueve. Por eso, este sistema no tiene ninguna solución posible.
Se trata de un sistema incompatible.
Resuelva el siguiente sistema de ecuaciones:
\[\left\{\begin{matrix}3x+4y-2z=-13\\x+5y+z=-5\\3+z=2-y+3x\\\end{matrix}\right.\]
2.5. Sistemas homogéneos
Los sistemas homogéneos son sistemas de ecuaciones en los que el término independiente de todas las ecuaciones es cero.
La particularidad que tienen es que son siempre compatibles.
Pueden ser determinados. En ese caso, la única solución es que todas las incógnitas valgan cero, llamada solución trivial.
O pueden resultar compatibles indeterminados con infinitas soluciones.
Resuelva el siguiente sistema de ecuaciones:
\[\left\{\begin{matrix}-2x+10y-2z=0\\2x+3y-z=0\\18x+y-3z=0\\\end{matrix}\right.\]
Se trata de un sistema homogéneo, ya que todos los términos independientes de las ecuaciones son nulos. Por lo tanto, ya se sabe que será un sistema compatible. Falta averiguar si es determinado o no.
La matriz ampliada es:
\[\left(\begin{matrix}-2&10&-2\\2&3&-1\\18&1&-3\\\end{matrix}\ \ \middle|\ \ \ \begin{matrix}0\\0\\0\\\end{matrix}\right)\]
Para anular las posiciones 2-1 y 3-1, se realizarán las siguientes operaciones:
\[F´2=F2+F1\]
\[F´3=F3+9\cdot F1\]
Con lo que queda:
\[\left(\begin{matrix}-2&10&-2\\0&13&-3\\0&91&-21\\\end{matrix}\ \ \middle|\ \ \ \begin{matrix}0\\0\\0\\\end{matrix}\right)\]
Ahora se desea obtener un 0 en la posición 3-2, a partir de operaciones con la segunda fila, donde ya hay un 0 en la primera columna. ¿Qué operación será necesaria? Para averiguarlo, se puede escribir la siguiente ecuación:
\[91+x\cdot13=0\]
Y despejar x:
\[x=\frac{-91}{13}=-7\]
Entonces, la operación que se busca es:
\[F´3=F3-7\cdot F2\]
Con lo que queda:
\[\left(\begin{matrix}-2&10&-2\\0&13&-3\\0&0&0\\\end{matrix}\ \ \middle|\ \ \ \begin{matrix}0\\0\\0\\\end{matrix}\right)\]
Como esta última matriz ampliada tiene una fila completa de ceros, el sistema es indeterminado. Se puede volver a escribir este sistema equivalente para buscar la solución general:
\[\left\{\begin{matrix}-2x+10y-2z=0\\13y-3z=0\\0=0\\\end{matrix}\right.\]
De la segunda ecuación resulta:
\[y=\frac{3}{13}z\]
Este resultado se reemplaza en la primera ecuación.
\[-2x+10\cdot\frac{3}{13}z\ -2z=0\]
\[-2x+\frac{4}{13}z\ =0\]
\[x=\frac{4}{26}z=\frac{2}{13}z\ \]
La solución general es, entonces:
\(\boldsymbol{x} = z\cdot\left(\begin{matrix}^2/_{13}\\^3/_{13}\\1\end{matrix}\right)\) donde z puede tomar cualquier valor. Para evitar confundir este número con la variable, se puede escribir:
\[\boldsymbol{x} =\ t \cdot \left( \begin{matrix}^2/_{13}\\^3/_{13}\\1\end{matrix}\right)\]
Como siempre, conviene comprobar esta respuesta. Aquí se hará con un ejemplo. Se toma un valor posible de t, por facilidad de cálculos, 13, y se efectúan los cálculos para hallar las demás incógnitas:
Si \(t\) vale 13, \(x\) será 2 y la y valdrá 3. Entonces, en el sistema original, será:
\(-2x+10y-2z=-2\cdot2+10\cdot3-2\cdot13=-4+30-26=0\) verifica la primera ecuación.
\(2x+3y-z=2\cdot2+3\cdot3-13=4+9-13=0\) verifica la segunda ecuación.
\(18x+y-3z=18\cdot2+3-3\cdot13=36+3-39=0\) verifica la tercera ecuación.
Efectivamente, esta es una solución de las infinitas posibles que admite este sistema.
2.6. Determinante de una matriz cuadrada
El determinante es un número real que se puede asociar a una matriz cuadrada. Para obtener el determinante de una matriz, hay que trabajar con sus elementos, sumando y restando distintos productos entre ellos. Y el resultado es un número.
La forma en que se calcula el determinante de una matriz cuadrada depende de las dimensiones de la matriz \(n\ \times\ n\). Es importante recordar que solamente las matrices cuadradas permiten el cálculo del determinante.
2.6.1. Determinante de una matriz de 2×2
Para el caso de una matriz de \(2\times2\) el determinante es igual al producto de los elementos de la diagonal menos el producto de los elementos fuera de la diagonal. Es decir:
Si A = \(\left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right)\) su determinante será:
\[det(A)\ =\left|A\right|=\left|\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right|=a_{11}\cdot a_{22}-a_{12}\cdot a_{21}\]
2.6.2. Determinante de una matriz de 3×3
En el caso de matrices cuadradas de dimensión \(3\times3\), se puede calcular el determinante utilizando la “Regla de Sarrus”. Si la matriz es:
\[A=\left(\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right)\]
Su determinante se puede calcular agregando dos filas más, repitiendo las dos primeras filas de la matriz:
\[\left(\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\\begin{matrix}a_{31}\\a_{11}\\a_{21}\\\end{matrix}&\begin{matrix}a_{32}\\a_{12}\\a_{22}\\\end{matrix}&\begin{matrix}a_{33}\\a_{13}\\a_{23}\\\end{matrix}\\\end{matrix}\right)\]
A continuación, se multiplican entre sí los componentes de las “diagonales”, y se suman los resultados de las que van de izquierda a derecha y se restan los de las que van de derecha a izquierda:
\[\begin{multline*} \left|A\right|=a_{11}\cdot a_{22}\cdot a_{33}+a_{21}\cdot a_{32}\cdot a_{13}+a_{31}\cdot a_{12}\cdot a_{23}-\\-a_{13}\cdot a_{22}{\cdot a}_{31}-a_{23}\cdot a_{32}\cdot a_{11}-a_{33}\cdot a_{12}\cdot a_{21}\cdot\end{multline*}\]
También se puede escribir de esta manera:
\[\begin{multline*} \left|A\right|=a_{11}\cdot a_{22}\cdot a_{33}+a_{21}\cdot a_{32}\cdot a_{13}+a_{31}\cdot a_{12}\cdot a_{23}-\\-(a_{13}\cdot a_{22}{\cdot a}_{31}+a_{23}\cdot a_{32}\cdot a_{11}+a_{33}\cdot a_{12}\cdot a_{21})\end{multline*}\]
En <https://www.youtube.com/watch?v=8OnOZvc5rFQ> , Alexánder Gómez, de Colombia, el “Profe Alex”, calcula el determinante de una matriz de \(3\times3\) utilizando la Regla de Sarrus.
2.6.3. Determinante de una matriz de n×n
Para calcular determinantes de matrices de mayor dimensión, se utiliza la siguiente propiedad:
\( \det{\left(A\right)}=\left|A\right|= \left|\begin{matrix} a_{11} & a_{12}\dots & a_{1n} \\ a_{21} & a_{22}\dots & a_{2n} \\ \dots & \dots \ \dots & \dots \\ a_{n1} & a_{n2}\dots & a_{nn} \end{matrix}\right| = \) \[ = (-1)^{1+1} \cdot a_{11} \cdot \left|\begin{matrix} a_{22} & a_{23}\dots & a_{2n} \\ a_{32} & a_{33}\dots & a_{3n}\\ \dots & \dots \ \dots & \dots \\ a_{n2} & a_{n3}\dots & a_{nn} \end{matrix}\right| + \] \[ +(-1)^{1+2} \cdot a_{12} \cdot \left|\begin{matrix} a_{21} & a_{23}\dots & a_{2n}\\ a_{31} & a_{33}\dots & a_{3n}\\ \dots & \dots \ \dots & \dots \\ a_{n1} & a_{n3}\dots & a_{nn} \end{matrix}\right| +\dots+ \]
\[+(-1)^{1+n}\cdot a_{1n}\cdot \left|\begin{matrix} a_{21} & a_{22}\dots & a_{1(n-1)} \\a_{31} & a_{32}\dots & a_{2(n-1)} \\ \dots & \dots \ \dots & \dots \\ a_{n1} & a_{n2}\dots & a_{n(n-1)} \end{matrix}\right| \]
Aquí se “desarrolló el determinante” por la primera fila. Pero vale también hacerlo por otra fila o por una columna.
Con este método un determinante de \(n \times n\) se calcula como sumas y restas de determinantes de \((n-1) \times (n-1)\), multiplicados por los coeficientes de esa fila o columna.
El desarrollo por una fila o columna se realiza multiplicando los coeficientes de la fila o columna por el determinante de la matriz que se obtiene quitando la fila y columna a la cual pertenece el coeficiente en cuestión. Cada uno de esos determinantes de \((n-1) \times (n-1)\) se llama menor complementario.
Estos términos van sumados o restados según la posición del coeficiente \(a_{ij}\); si la suma \(i + j\) es par, entonces va sumando, si la suma \(i + j\) es impar, entonces va restando. En general el término tiene el signo que determina la expresión \({(-1) }^{i + j}\). Al producto de \({(-1) }^{i + j} \) por el menor complementario correspondiente se la denomina adjunto \(A_{ij}\).
Si se calcula el determinante de la matriz de \(3 \times 3\) con este método, desarrollándolo por la fila 3, es:
\[det(A)=\left|A\right|=\left|\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right|\]
Los signos de cada término sumar están determinados por el factor \({(-1)\ }^{i\ +\ j}\). Cuando \(i+j\) es un número par, quedarán sumando. Y si \(i+j\) es impar, quedarán restando. Entonces es:
\[\left(-1\right)^{3+1}a_{31}\left|\begin{matrix}a_{12}&a_{13}\\a_{22}&a_{23}\\\end{matrix}\right|=1\cdot a_{31}\cdot\left(a_{12}\cdot a_{23}-a_{22}\cdot a_{13}\right)=a_{12}\cdot a_{23}\cdot a_{31}-a_{13}\cdot a_{22}\cdot a_{31}\]
\[\begin{multline*} {(-1)}^{3+2} a_{32} \left|\begin{matrix}a_{11}&a_{13}\\a_{21}&a_{23}\\\end{matrix}\right| = {(-1)\cdot a}_{32}\cdot (a_{11}\cdot a_{23} - a_{21}\cdot a_{13}) = a_{13}\cdot a_{21}\cdot a_{32} -a_{11}\cdot a_{23}\cdot a_{32} \end{multline*}\]
\[\begin{multline*} {(-1)}^{3+3} a_{33} \left|\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right| =1\cdot a_{33}\cdot (a_{11}\cdot a_{22} - a_{21}\cdot a_{12}) = a_{11}\cdot a_{22}\cdot a_{33}- a_{12}\cdot a_{21}\cdot a_{33} \end{multline*}\]
que sumados y reordenados dan:
\[ \begin{multline*} det(A)=\left|A\right|=a_{11}\cdot a_{22}\cdot a_{33}+a_{12}\cdot a_{23}\cdot a_{31}+a_{13}\cdot a_{21}\cdot a_{32}-\\-a_{11}\cdot a_{23}\cdot a_{32}-\ a_{12}\cdot a_{21}\cdot\ a_{33}-a_{13}\cdot a_{22}\cdot a_{31} \end{multline*}\]
Lo interesante del desarrollo por una fila o columna es que, si se tiene un determinante con una fila o columna con varios ceros salvo algún coeficiente, al desarrollar por esa fila o columna requerirá calcular pocos determinantes, que además tienen una fila y columna menos que el determinante original.
Calcule el determinante de la siguiente matriz, utilizando el desarrollo por filas o columnas:
\[B=\left(\begin{matrix}12&2&0\\-17&-3&0\\6&1&1\\\end{matrix}\right)\]
Aquí conviene hacer el desarrollo por la tercera columna, en la que hay dos ceros. En el cálculo que sigue, se “tacharon” las filas y las columnas que se eliminan de la matriz para calcular cada término:
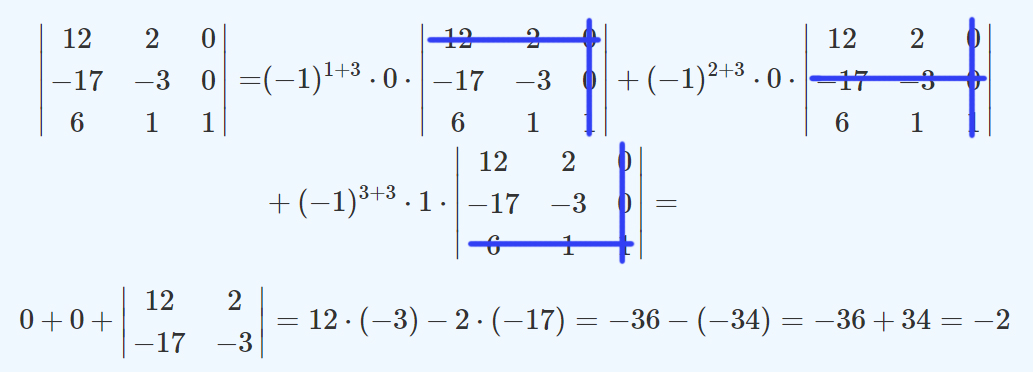
El determinante pedido es igual a -2.
Como puede apreciarse, en algunas matrices, este método puede facilitar los cálculos.
Calcule el determinante de la siguiente matriz:
\[A= \left( \begin {matrix} 1 & -1 & 3 & 2 \\0 & 4 & -2 & 1\\ 2 & 3 & 1 & -3 \\ 0 & -1 & 0 & 2 \end{matrix} \right) \]
Tanto en la primera columna como en la cuarta fila hay dos ceros. Por ese motivo, conviene desarrollar el determinante por alguna de ellas. Aquí se hará de las dos maneras, para mostrar que, obviamente, el resultado que se obtiene es el mismo:
Desarrollo por la cuarta fila:
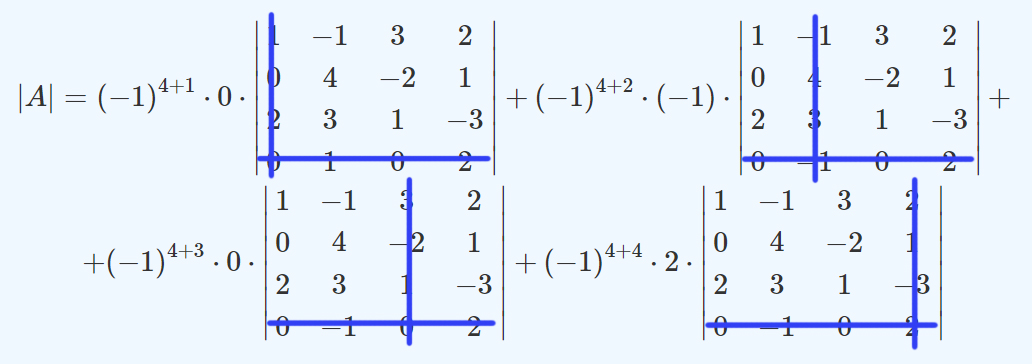
\[ \begin{gather*} \left|A\right|=\left(-1\right)^{4+1}\cdot0\cdot\left|\begin{matrix}-1&3&2\\4&-2&1\\3&1&-3\\\end{matrix}\right| +\left(-1\right)^{\cdot4+2}\cdot\left(-1\right) \cdot \left|\begin{matrix}1&3&2\\0&-2&1\\2&1&-3\\\end{matrix}\right| + \\ + \left(-1\right)^{4+3}\cdot0\cdot \left|\begin{matrix}1&-1&2\\0&4&1\\2&3&-3\\\end{matrix}\right| + {(-1)}^{4+4}\cdot2\cdot\left|\begin{matrix}1&-1&3\\0&4&-2\\2&3&1\\\end{matrix}\right| = \end{gather*} \]
\[=0-1\ .\ 1\ .\ 19+0+2\ .\ 1\ .\ \left(-10\right)=-39\]
Desarrollo por la primera columna (en la que directamente se escribieron los menores complementarios correspondientes):
\[ \begin{align*} \left|A\right|=\left(-1\right)^{1+1}\cdot1\cdot\left|\begin{matrix}4&-2&1\\3&1&-3\\-1&0&2\\\end{matrix}\right|+\left(-1\right)^{2+1}\cdot 0 \cdot \\ \cdot \left|\begin{matrix}-1&3&2\\3&1&-3\\-1&0&2\\\end{matrix}\right|+\left(-1\right)^{3+1}\cdot2\cdot\left|\begin{matrix}-1&-3&2\\4&-2&1\\-1&0&2\\\end{matrix}\right|+ \end{align*}\]
\[ +\left(-1\right)^{4+1}\cdot0\cdot\left|\begin{matrix}-1&3&2\\4&-2&1\\3&1&-3\\\end{matrix}\right|=1\cdot1\cdot15-0+1\cdot2\cdot(-27)+0=-39 \]
Por lo tanto, el determinante de la matriz A es -39, como ya se había calculado.
En el siguiente video <https://www.youtube.com/watch?v=avFmc3RvVGo> se muestra el uso de Excel para calcular determinantes.
2.6.4. Propiedades de los determinantes
-
Si se multiplica una fila (o una columna) de una matriz A por un escalar, el determinante de la nueva matriz será igual al producto del determinante de A por ese escalar.
En símbolos:
Para todo número \(\lambda \neq0\) se cumple que:
\[\left|\begin{matrix}\lambda\mathrm{\ \ }a_{11}&\lambda\mathrm{\ \ }a_{12}&\lambda\mathrm{\ \ }a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right|=\lambda\cdot\left|\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right|\]
O, lo que es lo mismo:
\[\left|\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right|=\frac{1}{\lambda}\cdot\left|\begin{matrix}\lambda\mathrm{\ \ }a_{11}&\lambda\mathrm{\ \ }a_{12}&\lambda\mathrm{\ \ }a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right|\]
-
Si en una matriz se reemplaza una fila por la suma de esa fila con otra fila de la matriz, el determinante no varía.
En símbolos, para todo número \(\lambda \neq0\)se cumple que:
\[\left|\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right|=\left|\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}+\lambda\mathrm{\ \ } a_{11}&a_{32}+\lambda\mathrm{\ \ } a_{12}&a_{33}+\lambda\mathrm{\ \ } a_{13}\\\end{matrix}\right| \]
Estas propiedades, pueden utilizarse para obtener una matriz con filas o columnas con muchos ceros, lo que facilitará calcular el determinante por el último método visto. Se puede operar con las filas (o columnas en los determinantes) de forma similar a como se hizo con el método de Gauss con las matrices. Pero es importante recordar que, a diferencia del método de Gauss, si solo se multiplica una fila o columna por un escalar distinto de cero, para que el nuevo determinante sea igual que el anterior se debe dividir el resultado por ese escalar, según la propiedad 1. Sin embargo, sigue siendo válido reemplazar una fila o columna por la suma de ella más otra paralela, que sí puede estar multiplicada por un escalar, sin que cambie el valor del nuevo determinante.
-
Un sistema de ecuaciones es compatible determinado si, y solo si, el determinante de su matriz asociada es distinto de cero
Esta propiedad permite clasificar un sistema de ecuaciones antes de comenzar a resolverlo. Si el determinante de la matriz asociada al sistema no es cero, será compatible determinado, es decir, tendrá una única solución.
Si el determinante fuera cero, podría ser que el sistema fuera indeterminado o que fuera incompatible. Pero no tendrá solución única.
-
El determinante del producto de dos matrices cuadradas es igual al producto de los determinantes de esas matrices. En símbolos:
\[\left|A\cdot B\right|=\left|A\right|\cdot\left|B\right| \]
Calcule el determinante de la matriz del Ejemplo 15, aplicando las propiedades anteriores:
\[A= \left( \begin {matrix} 1 & -1 & 3 & 2 \\0 & 4 & -2 & 1\\ 2 & 3 & 1 & -3 \\ 0 & -1 & 0 & 2 \end{matrix} \right) \]Aquí se va a desarrollar por la cuarta fila, pero antes, se reemplazará la cuarta columna por la siguiente combinación : \(\ C4+2C2\rightarrow C4\)
\[\left|A\right|= \left|\begin{matrix} 1 & -1 & 3 & 2\\ 0 & 4 & -2 & 1\\ 2 & 3 & 1 & -3 \\ 0 & -1 & 0 & 2 \end{matrix}\right| = \left|\begin{matrix} 1 & -1 & 3 & 0 \\ 0 & 4 & -2 & 9\\ 2 & 3 & 1 & 3 \\ 0 & -1 & 0 & 0 \end{matrix}\right| \]
Ahora, el desarrollo por la cuarta fila es:
\[ \left|A\right|=\left(-1\right)^{4+1}\cdot0\cdot\left|\begin{matrix}-1&3&0\\4&-2&9\\3&1&3\\\end{matrix}\right|+\left(-1\right)^{4+2}\cdot\left(-1\right)\cdot\left|\begin{matrix}1&3&0\\0&-2&9\\2&1&3\\\end{matrix}\right|+ \]
\[ +\left(-1\right)^{4+3}\cdot0\cdot\left|\begin{matrix}1&-1&0\\0&4&9\\2&3&3\\\end{matrix}\right|+{(-1)}^{4+4}\cdot0\cdot\left|\begin{matrix}1&-1&3\\0&4&-2\\2&3&1\\\end{matrix}\right|=0-1\cdot39=-39 \]
Por supuesto, el resultado es el mismo que el que se obtuvo anteriormente, pero en este caso, solo hubo que calcular un único determinante de \(3\times3\).
Calcule los determinantes de las matrices asociadas al sistema de ecuaciones del Ejemplo 2.10. y al del Ejemplo 2.11. y compruebe la propiedad 3 de los determinantes.
La matriz asociada al sistema del Ejemplo 2.10. es:
\[A=\left(\begin{matrix}3&2&0\\0&-1&2\\2&1&1\\\end{matrix}\right)
\]
Para calcular su determinante, se desarrollará por la segunda fila. Pero antes, se realizará el siguiente reemplazo, para que los cálculos sean más sencillos: \(C3+2C2\rightarrow C3\)
\[ \begin{gather*} \left|A\right|=\left|\begin{matrix}3&2&0\\0&-1&2\\2&1&1\\\end{matrix}\right|=\left|\begin{matrix}3&2&4\\0&-1&0\\2&1&3\\\end{matrix}\right|= \\ = \left(-1\right)^{2+1}\cdot0\cdot\left|\begin{matrix}2&4\\1&3\\\end{matrix}\right|+\left(-1\right)^{2+2}\cdot\left(-1\right)\cdot\left|\begin{matrix}3&4\\2&3\\\end{matrix}\right|+\left(-1\right)^{2+3}\cdot0\cdot\left|\begin{matrix}3&2\\2&1\\\end{matrix}\right|= \end{gather*} \]
\[=0-1\cdot1=-1\]
De modo que el determinante de la matriz es distinto de cero, lo que garantiza que este sistema es compatible determinado. Esta información ya estaba disponible, pues se había resuelto el sistema por el método de Gauss.
La matriz asociada al sistema del Ejemplo 2.11. es \(A=\left(\begin{matrix}1&1&-1\\-2&0&3\\1&5&1\\\end{matrix}\right)\)
Para calcular su determinante, se desarrollará por la segunda columna. Pero, para facilitar los cálculos, primero se hará el siguiente reemplazo: \(F3-5\cdot F1\rightarrow F3\)
\[\left|A\right|=\left|\begin{matrix}1&1&-1\\-2&0&3\\1&5&1\\\end{matrix}\right|=\left|\begin{matrix}1&1&-1\\-2&0&3\\-4&0&6\\\end{matrix}\right|\]
En el siguiente desarrollo no se escribieron todos los términos, porque los que faltan son nulos:
\[\left|A\right|=\left(-1\right)^{1+2}\cdot1\cdot\left|\begin{matrix}-2&3\\-4&6\\\end{matrix}\right|=(-1)\cdot0=0\]
Como el determinante de esta matriz es cero, el sistema de ecuaciones no es compatible determinado, pudiendo con esta herramienta solamente decir que el sistema será o bien incompatible o bien compatible indeterminado.
En este caso será compatible indeterminado como vimos anteriormente al haber resuelto el sistema anteriormente por el método de Gauss.
2.7. Regla de Cramer
La Regla de Cramer es un método alternativo al de Gauss para resolver sistemas de ecuaciones lineales cuadrados, es decir, con la misma cantidad de incógnitas que de ecuaciones, compatibles determinados.
Como se mencionó, si el determinante de la matriz asociada es distinto de cero, un sistema es compatible determinado. Su solución se puede obtener utilizando determinantes.
Así, la solución para un sistema de ecuaciones de \( 2 \times 2 \) genérico:
\[ \left\{ \begin{matrix} a_{11} x_1 + a_{12} x_2 = b_1 \\ a_{21} x_1 + a_{22} x_2 = b_2 \\ \end{matrix} \right. \]
o, si se lo escribe en forma de producto de matrices \(A \cdot x = b\)
\[\left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right)\left(\begin{matrix}x_1\\x_2\\\end{matrix}\right)=\left(\begin{matrix}b_1\\b_2\\\end{matrix}\right) \]
Si el \(det(A) =\left|A\right|= \left|\begin{matrix} a_{11}\ \ a_{12}\\ a_{21}\ \ a_{22} \end{matrix}\right| = a_{11} \cdot a_{22}-a_{12} \cdot a_{21} \neq 0\), entonces las soluciones se pueden escribir como
\[ \begin{array}{lr} x_1=\frac{\Delta x_1}{\left|A\right|}=\frac{\left|\begin{matrix}b_1 \ \ a_{12}\\ b_2 \ \ a_{22}\end{matrix}\right|} {\left|\begin{matrix}a_{11} \ \ a_{12}\\ a_{21} \ \ a_{22}\end{matrix}\right|} \ & \ x_2=\frac{\Delta x_2}{\left|A\right|}=\frac{\left|\begin{matrix}a_{11} \ \ b_1\\ a_{21} \ \ b_2\end{matrix}\right|} {\left|\begin{matrix}a_{11} \ \ a_{12}\\ a_{21} \ \ a_{22}\end{matrix}\right|} \end{array} \]
Los determinantes que aparecen en los numeradores de las expresiones anteriores se obtienen reemplazando, en la matriz asociada, los coeficientes de la incógnita correspondiente por los términos independientes de la ecuación.
Este es el denominado método de Cramer para hallar las soluciones de un sistema compatible determinado. Para el sistema de \( 2 \times 2 \) (dos ecuaciones y dos incógnitas) las soluciones \( x_1 \) y \( x_2 \) del sistema se pueden hallar calculando 3 determinantes:
-
el determinante de la matriz del sistema:
\[\left|\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right| \]
-
el determinante de la matriz que se obtiene al reemplazar la columna asociada a la variable \(x_1\) por la columna de los términos independientes, al que llamaremos \(\Delta x_1\)
\[\Delta x_1=\left|\begin{matrix}b_1 \ \ a_{12} \\ b_2 \ \ a_{22} \end{matrix}\right| \]
-
y el determinante de la matriz que se obtiene al reemplazar la columna asociada a la variable \(x_2\) por la columna de los términos independientes, al que se denominará \(\Delta x_2\)
\[\Delta x_2=\left|\begin{matrix}a_{11}&b_1\\a_{21}&b_2\\\end{matrix}\right| \]
Esta regla se puede aplicar para la resolución de cualquier sistema de ecuaciones cuadrado, compatible determinado, como se verá al final del siguiente apartado.
Resuelva el sistema de ecuaciones del Ejemplo 2.8. utilizando el método de Cramer:
\[ \left\{ \begin{matrix} 2 M + 1 B + 3 N = 13 \\ 3 M + 2 B + 2 N = 13 \\ 2 M + 3 B + 1 N = 11 \end{matrix} \right. \]
La matriz asociada a este sistema es:
\[A=\left(\begin{matrix}2&1&3\\3&2&2\\2&3&1\\\end{matrix}\right)\]
El vector de términos independientes es \(V=\left(\begin{matrix}13\\13\\11\\\end{matrix}\right)\)
Ahora, con Excel, se calcularán los siguientes determinantes:
\[\left|A\right|=\left|\begin{matrix}2&1&3\\3&2&2\\2&3&1\\\end{matrix}\right|=8
\]
\[ \Delta M=\left|\begin{matrix}13&1&3\\13&2&2\\11&3&1\\\end{matrix}\right|=8
\]
\[ \Delta B=\left|\begin{matrix}2&13&3\\3&13&2\\2&11&1\\\end{matrix}\right|=16
\]
\[ \Delta M=\left|\begin{matrix}2&1&13\\3&2&13\\2&3&11\\\end{matrix}\right|=24
\]
Entonces, el precio de las manzanas es:
\[M=\frac{\Delta M}{\left|A\right|}=\frac{8}{8}=1\]
El de las bananas:
\[B=\frac{\Delta N}{\left|A\right|}=\frac{16}{8}=2\]
Y el de las naranjas:
\[N=\frac{\Delta N}{\left|A\right|}=\frac{24}{8}=3\]
Entonces, el vector solución es:
\[X=\left(\begin{matrix}1\\2\\3\\\end{matrix}\right)\]
Se propone como actividad comprobar que estos resultados satisfacen el sistema de ecuaciones, que podría escribirse en forma matricial, así:
\[\left(\begin{matrix}2&1&3\\3&2&2\\2&3&1\\\end{matrix}\right)\cdot\left(\begin{matrix}1\\2\\3\\\end{matrix}\right)=\left(\begin{matrix}13\\13\\11\\\end{matrix}\right)\]
2.7.1. Clasificación del tipo de sistema utilizando determinantes
La regla de Cramer también se puede utilizar para clasificar los sistemas de ecuaciones.
Cuando la cantidad de ecuaciones es igual a la cantidad de incógnitas, se puede clasificar el sistema teniendo en cuenta el valor de los determinantes que se utilizan en la regla de Cramer.
Un sistema de ecuaciones será:
- Compatible determinado, es decir, tendrá una única solución, si el determinante de la matriz asociada es distinto de cero.
- Compatible indeterminado, es decir, tendrá infinitas soluciones, si todos los determinantes, \(\left|A\right|\) y todos los \(∆x_i\) correspondientes a las distintas variables son iguales a cero.
- Incompatible, es decir, no tendrá soluciones, si el determinante de la matriz asociada es igual a cero y alguno de los otros determinantes \(∆x_i\), correspondiente a alguna de las variables tiene un valor diferente a cero.
Determine para qué valores de k el siguiente sistema es compatible determinado, para cuáles es compatible indeterminado y para cuáles es incompatible.
\[ \left\{ \begin{matrix} x+k \cdot y+3 \cdot z=12 \\ k.z=-7+2 \cdot x+y \\ 2 \cdot k.z=0 \end{matrix} \right. \]
Si un sistema de ecuaciones lineales es compatible, el determinante de la matriz de coeficientes debe ser diferente a cero. Pero antes, es necesario ordenar y completar el sistema de ecuaciones:
\[ \left\{ \begin{matrix} x+k.y+3\cdot z=12 \\ -2\cdot x-y+k.z=-7 \\ 0\cdot x+0\cdot y+2\cdot k.z=0 \end{matrix} \right. \]
Ahora sí, se calculará el determinante de la matriz de coeficientes, utilizando la regla de Sarrus.
\[ \left|\begin{matrix}1&k&3\\-2&-1&k\\0&0&2k\\1 & k & 3\\-2 & -1 & 2k\end{matrix}\right|= 1.(-1).2k+(-2).0.3+0.k.2k-[3.(-1).0+k.0.1+2k.k.(-2)=\]
\[=-2k+0+0-\left(0+0-4k^2\right)=4k^2-2k\neq0\]
Para que este determinante no resulte igual a cero, deberá ser \(k\neq0\) o \(k\neq\frac{1}{2}\) que son los valores que anulan la expresión anterior (calculados, por ejemplo, con la fórmula de la resolvente).
Por lo tanto, si \(k\) pertenece al conjunto \(R -\left\{0;\frac{1}{2}\right\}\), el sistema de ecuaciones será compatible y determinado.
Para averiguar qué sucede cuando \(k=\frac{1}{2}\), se calculará el determinante correspondiente a la variable x, cuando \(k\) toma este valor.
\[\Delta x= \left|\begin{matrix}12&^1/_2&3\\-7&-2&^1/_2\\0&0&1\end{matrix}\right|= -8,5 \neq 0 \]
Como hay al menos un determinante de coeficientes que es distinto de cero, el sistema será incompatible cuando \(k=\frac{1}{2}\).
Falta averiguar qué sucede cuando \(k=0\). Con ese objetivo, se calcularán los determinantes correspondientes a todas las variables, cuando \(k\) toma este valor:
\[\Delta x= \left|\begin{matrix}12&0&3\\-7&-1&0\\0&0&0\end{matrix}\right|=0 \]
\[\Delta y= \left|\begin{matrix}1&12&3\\-2&-7&0\\0&0&0\end{matrix}\right|=0 \]
\[\Delta z= \left|\begin{matrix}1&0&12\\-2&-1&-7\\0&0&0\end{matrix}\right|=0 \]
Como todos los determinantes son nulos, el sistema es indeterminado cuando \(k=0\).
Resumiendo todo lo dicho hasta aquí es:
Si \(k=0\), el sistema resulta indeterminado (infinitas soluciones).
Si \(k=\frac{1}{2}\), el sistema resulta incompatible (no tiene solución).
Si \(k\in\ \mathbb{R} -\left\{0;\frac{1}{2}\right\}\), el sistema es compatible determinado (tiene solución única).
2.8. Matriz inversa
Se define matriz inversa de una matriz cuadrada \(A\), a la matriz \(A^{-1}\) que cumple:
\[A .{ A}^{-1} = { A}^{-1}\ . A = Id\]
donde Id es la matriz identidad, que ya se definió en esta misma Unidad.
La propiedad 4 de los determinantes, la del producto de matrices, permite obtener una condición necesaria para la existencia de la matriz inversa:
\(\left|A .{ A}^{-1}\right| = \left| Id\right| = 1\), porque el determinante de cualquier matriz identidad es uno.
Entonces,
\(\left|A \right| . \left|{ A}^{-1}\right| = 1\), entonces debe ser \(\left|A \right|\neq0\) y \[\left|{ A}^{-1}\right|\neq0\]
Una condición necesaria para que exista la matriz inversa de una matriz A es que el determinante de A debe ser distinto de cero
La matriz inversa \(A^{-1}\) es, por su definición, la inversa multiplicativa de la matriz A dado que al multiplicarlas da como resultado el elemento neutro de la multiplicación de matrices, es decir, la matriz identidad. La definición de matriz inversa viene dada por \(A A^{-1}= I\).
Para hallar la matriz inversa es necesario resolver la ecuación matricial:
\[A A^{-1} = A^{-1} A = I\]
Encuentre la matriz inversa de \(A=\left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\right)\)
En este caso, la ecuación matricial a resolver es:
\[A A^{-1} = \left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\ \ \right)\left(\begin{matrix}c_{11}&c_{12}&c_{13}\\c_{21}&c_{22}&c_{23}\\c_{31}&c_{32}&c_{33}\\\end{matrix}\right)=\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right) = I \]
Donde los coeficientes \(c_{ij}\) son los elementos de la matriz inversa, \(A^{-1}\). Al realizar el producto de las matrices se obtiene el siguiente sistema de 9 ecuaciones y nueve incógnitas:
\[ \left\{ \begin{matrix} 1 \cdot c_{11}+ 1 \cdot c_{21}+(-1) \cdot c_{31}=1 \\ 1 \cdot c_{12}+ 1 \cdot c_{22}+(-1) \cdot c_{32}=0 \\ 1 \cdot c_{13}+ 1 \cdot c_{23}+(-1) \cdot c_{33}=0 \\ 2 \cdot c_{11}+ 2 \cdot c_{21}+(-1) \cdot c_{31}=0 \\ 2 \cdot c_{12}+ 2 \cdot c_{22}+(-1) \cdot c_{32}=1 \\ 2 \cdot c_{13}+ 2 \cdot c_{23}+(-1) \cdot c_{33}=0 \\ -2 \cdot c_{11}+(-1) \cdot c_{21}+1 \cdot c_{31}=0 \\ -2 \cdot c_{12}+(-1) \cdot c_{22}+1 \cdot c_{32}=0 \\ -2 \cdot c_{13}+(-1) \cdot c_{23}+1 \cdot c_{33}=1 \end{matrix} \right. \]
Si se observa el sistema cuidadosamente, se puede advertir que, en realidad, este gran sistema es equivalente a 3 sistemas separados cada uno con 3 incógnitas.
Escribiendo para el sistema particular que se quiere calcular la inversa de A resulta:
\[\left\{\begin{matrix}1\cdot\ c_{11}+\ \mathrm{1\cdot} \ \ \ c_{21}+(-1)\cdot\ c_{31}=1\\\ 2\cdot\ c_{11}+\ 2\cdot\ c_{21}+(-1)\cdot\ c_{31}=0\\-2\cdot\ c_{11}+(-1)\cdot\ c_{21}+1\cdot\ c_{31}=0\\\end{matrix}\right. \]
\[\left\{\begin{matrix}1\cdot\ c_{12}+\ \mathrm{1\cdot} \ \ \ c_{22}+(-1)\cdot\ c_{32}=0\\\ 2\cdot\ c_{12}+\ 2\cdot\ c_{22}+(-1)\cdot\ c_{32}=1\\-2\cdot\ c_{12}+(-1)\cdot\ c_{22}+1\cdot\ c_{32}=0\\\end{matrix}\right. \]
\[\left\{\begin{matrix}1\cdot\ c_{13}+\ \mathrm{1\cdot} \ \ \ c_{23}+(-1)\cdot\ c_{33}=0\\\ 2\cdot\ c_{13}+\ 2\cdot\ c_{23}+(-1)\cdot\ c_{33}=0\\-2\cdot\ c_{13}+(-1)\cdot\ c_{23}+1\cdot\ c_{33}=1\\\end{matrix}\right. \]
o bien en forma matricial hay que resolver los tres sistemas dados por:
\[\left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\ \ \right)\left(\begin{matrix}c_{11}\\c_{21}\\c_{31}\\\end{matrix}\right)=\left(\begin{matrix}1\\0\\0\\\end{matrix}\right) \]
\[\left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\ \ \right)\left(\begin{matrix}c_{12}\\c_{22}\\c_{32}\\\end{matrix}\right)=\left(\begin{matrix}0\\1\\0\\\end{matrix}\right) \]
\[\text{ y } \]
\[\left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\right)\left(\begin{matrix}c_{13}\\c_{23}\\c_{33}\\\end{matrix}\right)=\left(\begin{matrix}0\\0\\1\\\end{matrix}\right)\]
Nótese que los tres sistemas tienen la misma matriz asociada solo cambia el vector de los términos independientes. De esta forma, para hallar la matriz inversa se tienen que resolver estos tres sistemas.
Como siempre, se pueden resolver de varias maneras. Primero se resolverá utilizando el método de Gauss.
-
Con el método de Gauss
Estos tres sistemas tienen las siguientes matrices ampliadas a las que se les aplicará el método de Gauss:
\[ \left(\left. \begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\ \ \right|\begin{matrix}1\\0\\0\\\end{matrix}\right) \text{ ; } \left(\left. \begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\ \ \right|\begin{matrix}0\\1\\0\\\end{matrix}\right) \text{ y } \left(\left. \begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\ \ \right|\begin{matrix}0\\0\\1\\\end{matrix}\right) \]
Dado que los tres tienen la misma matriz asociada, se pueden resolver los tres sistemas simultáneamente si se reescriben en una única matriz ampliada con los vectores de términos independientes, formando una nueva matriz de tres columnas, de esta manera:
\[\left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\left|\ \begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right.\right) \]
Es importante notar que, en esta nueva distribución, a la izquierda aparece la matriz asociada al sistema de ecuaciones, ampliada a la derecha con la matriz identidad:
\[\left(A \middle| Id\right) \]
A partir de aquí, se aplica el método de Gauss para esta matriz.
Para hacer ceros en la primera columna se realiza \(F2 – 2 F1 \rightarrow F2 \text{ y } F3 + 2 F1 \rightarrow F3\)
\[\left(\begin{matrix}1&1&-1\\0&0&1\\0&1&-1\\\end{matrix}\left| \begin{matrix}1&0&0\\-2&1&0\\2&0&1\\\end{matrix}\right.\right) \]
En este punto, como en la segunda fila hay dos ceros y un 1, que es lo deseado para la tercera fila, conviene intercambiar de lugar entre ellas, es decir, \(F2 \leftrightarrow F3\)
\[\left(\begin{matrix}1&1&-1\\0&1&-1\\0&0&1\\\end{matrix}\left|\ \begin{matrix}1&0&0\\2&0&1\\-2&1&0\\\end{matrix}\right.\right) \]
Falta lograr un 0 en la posición \(1-2: F1-F2 \rightarrow F1\):
\[\left(\begin{matrix}1&0&0\\0&1&-1\\0&0&1\\\end{matrix}\left|\ \begin{matrix}-1&0&-0\\2&0&1\\-2&1&0\\\end{matrix}\right.\right) \]
Ahora, solo falta un cero en la posición \(2-3: F2+F3 \rightarrow F2\):
\[\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\left|\ \begin{matrix}-1&0&-1\\0&1&1\\-2&1&0\\\end{matrix}\right.\right) \]
Al reescribir con este resultado, los tres sistemas de arriba se transforman en:
\[\left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\left|\ \begin{matrix}1\\0\\0\\\end{matrix}\right.\right)\ \rightarrow\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\left|\begin{matrix}-1\\0\\-2\\\end{matrix}\right.\right) \]
Entonces, \(c_{11} =-1, c_{21}=0 \text{ y } c_{31}=-2\).
\[\left(\begin{matrix}3&2&0\\0&-1&2\\2&1&1\\\end{matrix}\ \left|\ \begin{matrix}0\\1\\0\\\end{matrix}\right.\right)\rightarrow\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\left|\ \begin{matrix}0\\1\\1\\\end{matrix}\ \right.\right) \]
Entonces, \(c_{12} =0, c_{22}=1 \text{ y } c_{32}=1 \text{ y:}\)
\[ \left(\begin{matrix}3&2&0\\0&-1&2\\2&1&1\\\end{matrix}\ \left|\ \begin{matrix}0\\0\\1\\\end{matrix}\right.\right)\rightarrow\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\left|\ \begin{matrix}-1\\1\\0\\\end{matrix}\ \right.\right) \]
Entonces, \(c_{13} =-1, c_{23}=1 \text{ y } c_{33}=0\)
con lo que la matriz inversa \(A^{-1}\) será:\(\left(\begin{matrix}-1&0&-1\\0&1&1\\-2&1&0\\\end{matrix}\right)\), que es la matriz que queda a la derecha después de aplicar el método de Gauss.
Se parte de la matriz ampliada con la identidad y se llega a la identidad ampliada con la inversa
\[\left(A\ \middle|\ Id\right)\rightarrow\left(Id\ \middle|\ A^{-1}\right) \]
En este ejemplo es:
\[ \left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\left|\ \begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right.\right)\rightarrow\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\left|\ \begin{matrix}-1&0&-1\\0&1&1\\-2&1&0\\\end{matrix}\right.\right) \]
Es conveniente verificar que la matriz hallada es la inversa de la matriz A. Para ello, se multiplican ambas matrices debiéndose obtener la matriz identidad.
\[\left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\right).\left(\begin{matrix}-1&0&-1\\0&1&1\\-2&1&0\\\end{matrix}\right)=\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right) \]
con lo cual, se verifica que la matriz inversa calculada es correcta.
-
Con la regla de Cramer
También se pueden resolver los sistemas
\[\left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\left|\ \begin{matrix}1\\0\\0\\\end{matrix}\right.\right)\ ; \left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\ \left|\ \begin{matrix}0\\1\\0\\\end{matrix}\right.\right) y\ \ \left(\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\ \left|\ \begin{matrix}0\\0\\1\\\end{matrix}\right.\right) \]
con la regla de Cramer.
Para todos ellos será necesario calcular el determinante de A:
\[\left|A\right|=\left|\begin{matrix}1&1&-1\\2&2&-1\\-2&-1&1\\\end{matrix}\right|= \]
\[ \begin{multline*} =1\cdot2\cdot1+2\cdot\left(-1\right)\cdot\left(-1\right)+\left(-2\right)\cdot1\cdot\left(-1\right)- \\ - \left[\left(-2\right)\cdot2\cdot\left(-1\right)+2\cdot\left(-1\right)\cdot\left(-1\right)+1\cdot\left(-1\right)\cdot\left(-1\right)\right]= \end{multline*} \]
\[2+2+2-\left(4+2+1\right)=-1 \]
Para el primer sistema:
se puede calcular \(c_{11}\) utilizando el determinante que resulta al reemplazar el vector de los términos independientes en la primera columna de la matriz A dividido por el determinante de A (que ya se calculó previamente y dio \({\left|A\right|} = -1\)). Esto da:
\[c_{11}=\frac{\Delta c_{11}}{{\left|A\right|}}=\frac{\left|\begin{matrix}1&1&-1\\0&2&-1\\0&-1&1\\\end{matrix}\right|}{\left|A\right|} \]
Para resolver el determinante del numerador, conviene desarrollarlo por la primera columna:
\[ \small{ \begin{multline*} c_{11}=\frac{\left|\begin{matrix}1&1&-1\\0&2&-1\\0&-1&1\\\end{matrix}\right|}{\left|A\right|}= \\ = \frac{(-1)^{\left(1+1\right)}\cdot1\cdot\ \left|\begin{matrix}2&-1\\-1&1\\\end{matrix}\right|+(-1)^{\left(2+1\right)}\cdot0\cdot\ \left|\begin{matrix}1&-1\\-1&1\\\end{matrix}\right|+(-1)^{\left(3+1\right)}\cdot0\cdot\left|\ \begin{matrix}1&-1\\2&-1\\\end{matrix}\right|}{-1}= \end{multline*} } \]
En este paso es importante notar que el numerador es igual al adjunto del elemento \(a_{11}\) de la matriz asociada:
\[=\frac{(-1)^{\left(1+1\right)}\cdot\ \left|\begin{matrix}2&-1\\-1&1\\\end{matrix}\right|}{-1}=\frac{A_{11}}{\left|A\right|}=\frac{2.1-(-1).(-1)}{-1}=\frac{2-1}{-1}=-1 \]
Lo mismo se realiza para los demás coeficientes de la matriz inversa, es decir, se desarrolla el determinante por la columna más conveniente:
\[ \begin{multline*} c_{21}=\frac{\left|\begin{matrix}1&1&-1\\2&0&-1\\-2&0&1\\\end{matrix}\right|}{\left|A\right|}=\frac{0+\ (-1)^{(2+1)}\cdot1\cdot\left|\begin{matrix}2&-1\\-2&1\\\end{matrix}\right|+0\ }{-1}= \\ \frac{-1\cdot\ \left|\begin{matrix}2&-1\\-2&1\\\end{matrix}\right|}{-1}=\frac{A_{21}}{\left|A\right|}=0 \end{multline*}\]
Advierta que para calcular el elemento \(c_{21}\) se utiliza el \(A_{12}\). En general, para calcular el elemento \(c_{ij}\), resulta necesario calcular el adjunto de el elemento \(c_{ji}\).
No se repetirá acá, para el resto de los elementos, todo el desarrollo; simplemente se calcularán mediante el uso de los adjuntos correspondientes de A:
\[c_{31}=\frac{A_{13}}{\left|A\right|}=\frac{(-1)^{\left(1+3\right)}\ \cdot\left|\begin{matrix}2&2\\-2&-1\\\end{matrix}\right|}{-1}=\frac{-2-\left(-4\right)}{-1}=-2 \]
\[c_{12}=\frac{A_{21}}{\left|A\right|}=\frac{(-1)^{(1+2)}\cdot\left|\begin{matrix}1&-1\\-1&1\\\end{matrix}\right|\ }{-1}=\frac{-1\cdot(1-1)}{-1}=0 \]
\[c_{22}=\frac{A_{22}}{\left|A\right|}=\frac{(-1)^{(2+2)}\cdot\ \left|\begin{matrix}1&-1\\-2&1\\\end{matrix}\right|}{-1}=\frac{1\cdot(1-2)}{-1}=1 \]
\[c_{23}=\frac{A_{32}}{\left|A\right|}=\frac{(-1)^{(2+3)}\ \cdot\ \left|\begin{matrix}1&1\\2&1\\\end{matrix}\right|}{-1}=\frac{(-1)\cdot(1-2)}{-1}=1 \]
\[c_{13}=\frac{A_{31}}{\left|A\right|}=\frac{(-1)^{(3+1)}\cdot\left|\begin{matrix}1&-1\\2&-1\\\end{matrix}\right|\ }{-1}=\frac{-1-(-2)}{-1}=-1 \]
\[c_{23}=\frac{A_{32}}{\left|A\right|}=\frac{(-1)^{(3+2)}\ \left|\begin{matrix}1&-1\\2&-1\\\end{matrix}\right|}{-1}=\frac{(-1)\cdot\left[-1-(-2)\right]}{-1}=1 \]
\[c_{33}=\frac{A_{33}}{\left|A\right|}=\frac{(-1)^{(3+3)}\ \left|\begin{matrix}1&1\\2&2\\\end{matrix}\right|}{-1}=\frac{1\cdot(2-2)}{-1}=0 \]
con lo cual, nuevamente se obtiene la matriz inversa:
\[A^{-1} = \left(\begin{matrix}-1&0&-1\\0&1&1\\-2&1&0\\\end{matrix}\right) \]
En el siguiente video se muestra cómo aprovechar Excel para calcular matrices inversas.
2.8.1. Uso de las matrices inversas para resolver sistemas de ecuaciones
La matriz inversa, permite obtener la solución sistema de ecuaciones lineales, multiplicando dos matrices, la matriz inversa por el vector de los coeficientes independientes del sistema.
Dado el sistema en forma matricial:
\[A\cdot x = b\]
si se multiplica a izquierda cada miembro de esta ecuación por la matriz inversa de la matriz asociada es:
\[ A^{-1} \cdot A \cdot x = A^{-1} \cdot b\]
\[Id \cdot x = A^{-1} \cdot b\]
\[ x = A^{-1} \cdot b\]
Al utilizar este método, es muy importante recordar que en el producto de matrices es importante el orden, ya que en general no cumplen con la propiedad conmutativa. Si bien
\[ A \cdot A^{-1} = A^{-1} \cdot A \text{, en general } x \cdot A^{-1} \neq A^{-1} \cdot x \]
Entonces la solución del sistema se puede calcular directamente como el producto de la matriz inversa de la asociada al sistema, por el vector de los coeficientes independientes, b.
Dado el sistema de ecuaciones:
\[\left\{\begin{matrix}y=9+4z-2x\\x-2y+2z=-7\\3x+3z=4y-12\\\end{matrix}\right.\]
Se pide que: calcule el determinante de la matriz asociada al sistema, halle la matriz inversa de dicha matriz y utilícela para resolver el sistema.
Para calcular el determinante, antes es necesario reordenar el sistema:
\[\left\{\begin{matrix}2x+y-4z=9\\x-2y+2z=-7\\3x-4y+3z=-12\\\end{matrix}\right.\]
Por lo tanto, la matriz asociada al sistema es:
\[A=\left(\begin{matrix}2&1&-4\\1&-2&+2\\3&-4&3\\\end{matrix}\right)\]
Su determinante se puede calcular por la regla de Sarrus:
\[\left|A\right|=\left|\begin{matrix}2 & 1 & -4\\ 1 & -2 & 2\\ 3 & -4 & 3 \\ 2 & 1 & -4 \\ 1 & -2 & 2 \end{matrix}\right|= \]
\[ \begin{gather*} =2\cdot\left(-2\right)\cdot3+1\cdot\left(-4\right)\cdot\left(-4\right)+3\cdot1\cdot2-\left[\left(-4\right)\cdot\left(-2\right)\cdot3+2\cdot\left(-4\right)\cdot2+3\cdot1\cdot1\right]=\\ =-12+16+6-\left(24-16+3\right)=10-11=-1 \end{gather*} \]
Por lo tanto, el determinante de la matriz es igual a \(-1\).
Ahora se buscará la matriz inversa mediante el método de Gauss. Para ello, se amplía la matriz con la matriz identidad:
\[\left(\begin{matrix}2&1&-4\\1&-2&2\\3&-4&3\\\end{matrix}\ \ \middle|\ \ \begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right)\]
Para obtener un 1 en la posición 1-1, se puede dividir toda la fila por 2. Pero también se pueden cambiar de lugar las filas uno y dos. Aquí, se prefiere esta última opción para evitar trabajar con fracciones:
\[F1\leftrightarrow F2 \]
\[\left(\begin{matrix}1&-2&2\\2&1&-4\\3&-4&3\\\end{matrix}\ \ \middle|\ \ \begin{matrix}0&1&0\\1&0&0\\0&0&1\\\end{matrix}\right)\]
Ya hay un 1 en la posición 1-1. Hacen falta un cero en la posición 2-1 y otro en la posición 3-1 para que quede lista la primera columna. Por eso, se hace:
\[F`2=F2-2\cdot F1\]
\[F´3=F3-3\cdot F1\]
\[\left(\begin{matrix}1&-2&2\\0&5&-8\\0&2&-3\\\end{matrix}\ \ \middle|\ \ \begin{matrix}0&1&0\\1&-2&0\\0&-3&1\\\end{matrix}\right)\]
Para obtener un 1 en la posición 2-2, se divide toda la fila por 5: \[F`2=F2/5\]
\[\left(\begin{matrix}1&-2&2\\0&1&-1,6\\0&2&-3\\\end{matrix}\ \ \middle|\ \ \begin{matrix}0&1&0\\0,2&-0,4&0\\0&-3&1\\\end{matrix}\right) \]
Para completar de ceros la columna 2, se hace: \(F´1=F1+2\cdot F2\) y \(F´3=F3-2\cdot F2\)
\[\left(\begin{matrix}1&0&-1,2\\0&1&-1,6\\0&0&0,2\\\end{matrix}\ \ \middle|\ \ \begin{matrix}0,4&0,2&0\\0,2&-0,4&0\\-0,4&-2,2&1\\\end{matrix}\right)\]
Así, queda lista la columna 2. Ahora, para tener un 1 en la posición 3-3, se hace:
\[F´3=F3/(0,2)\]
\[\left(\begin{matrix}1&0&-1,2\\0&1&-1,6\\0&0&1\\\end{matrix}\ \ \middle|\ \ \begin{matrix}0,4&0,2&0\\0,2&-0,4&0\\-2&-11&5\\\end{matrix}\right) \]
Para completar con ceros el resto de la tercera columna, hacemos:
\[F´1=F1+1,2\cdot F3\cdot \]
\[F´2=F2+1,6\cdot F3\]
\[\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\ \ \middle|\ \ \begin{matrix}-2&-13&6\\-3&-18&8\\-2&-11&5\\\end{matrix}\right)\]
Por lo tanto, la matriz inversa buscada es: \[A^{-1}=\left(\begin{matrix}-2&-13&6\\-3&-18&8\\-2&-11&5\\\end{matrix}\right)\]
Conviene chequear que este cálculo esté bien, realizando el producto
\(A.A^{-1}\), que aquí se sugiere realizar como actividad. Para resolver el sistema, utilizando el método de la matriz inversa, conviene
escribirlo primero como un producto de matrices: \[\left(\begin{matrix}2&1&-4\\1&-2&2\\3&-4&3\\\end{matrix}\right)\cdot\left(\begin{matrix}x\\y\\z\\\end{matrix}\right)=\left(\begin{matrix}9\\-7\\-12\\\end{matrix}\right)\]
Para resolverlo, se multiplica a izquierda por la matriz inversa encontrada: \[\left(\begin{matrix}-2&-13&6\\-3&-18&8\\-2&-11&5\\\end{matrix}\right)\cdot\left(\begin{matrix}2&1&-4\\1&-2&+2\\3&-4&3\\\end{matrix}\right)\cdot\left(\begin{matrix}x\\y\\z\\\end{matrix}\right)=\left(\begin{matrix}-2&-13&6\\-3&-18&8\\-2&-11&5\\\end{matrix}\right)\cdot\left(\begin{matrix}9\\-7\\-12\\\end{matrix}\right)\]
Y se resuelven los productos en ambos miembros: \[\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right)\cdot\left(\begin{matrix}x\\y\\z\\\end{matrix}\right)=\left(\begin{matrix}1\\3\\-1\\\end{matrix}\right)\]
\[\left(\begin{matrix}x\\y\\z\\\end{matrix}\right)=\left(\begin{matrix}1\\3\\-1\\\end{matrix}\right) Por lo tanto, la solución del sistema de ecuaciones es: \[\left\{\begin{matrix}x=1\\y=3\\z=-1\\\end{matrix}\right.\]
\]
Siendo A \(=\left(\begin{matrix}1&1&-3\\-1&0&2\\0&2&-1\\\end{matrix}\right)\), \(B=\left(\begin{matrix}3&2&1\\-1&5&0\\2&-7&4\\\end{matrix}\right)\) y \(C=\left(\begin{matrix}4&6&-4\\-6&4&11\\5&-3&-5\\\end{matrix}\right)\) se pide que halle la matriz \(X\) para que \(X.A+B=C\)
Para resolver esta ecuación matricial, se resta en ambos términos la matriz B:
\[A\cdot X+B-B=C-B\]
\[A\cdot X + 0 = A \cdot X = C-B\]
\[X.A=C-B=\left(\begin{matrix}4&6&-4\\-6&4&11\\5&-3&-5\\\end{matrix}\right)-\left(\begin{matrix}3&2&1\\-1&5&0\\2&-7&4\\\end{matrix}\right)=\left(\begin{matrix}1&4&-5\\-5&-1&11\\3&4&-9\\\end{matrix}\right)\]
Ahora se multiplica a la derecha a ambos miembros por la matriz inversa de A:
\[X\cdot A\cdot A^{-1}=\left(\begin{matrix}1&4&-5\\-5&-1&11\\3&4&-9\\\end{matrix}\right)\cdot A^{-1} \]
Operando en el primer miembro, se obtiene:
\[X\cdot A\cdot A^{-1}=X.I=X=\left(\begin{matrix}1&4&-5\\-5&-1&11\\3&4&-9\\\end{matrix}\right)\cdot A^{-1}\]
Por lo tanto, para hallar la matriz X, se debe hallar antes la matriz inversa de A.
Aquí se hará mediante el método de Gauss.
Se amplía la matriz A con la matriz identidad:
\[\left(\begin{matrix}1&1&-3\\-1&0&2\\0&2&-1\\\end{matrix}\ \middle|\ \begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right)\]
Luego, se busca obtener un 0 en la 2° fila, 1° columna y 3° fila, 1° columna (pero ahí ya hay un cero). Por lo tanto,
\[F2´=F2 + F1\]
\[\left(\begin{matrix}1&1&-3\\0&1&-1\\0&2&-1\\\end{matrix}\middle|\ \begin{matrix}1&0&0\\1&1&0\\0&0&1\\\end{matrix}\right)\]
Ahora es necesario seguir por la segunda columna. Se comienza con un 1 en la posición 2-2. Como ya hay uno, se buscará hacer 0 las posiciones 1-2 y 3-2. Para esto, se realizan las siguientes operaciones:
\[F1´=F1 – F2\]
\[F3´=F3 – 2 F2\]
\[\left(\begin{matrix}1&0&-2\\0&1&-1\\0&0&1\\\end{matrix}\middle|\ \begin{matrix}0&-1&0\\1&1&0\\-2&-2&1\\\end{matrix}\right)\]
Ya hay un 1 en la 3° fila, 3° columna. Para dejar lista la tercera columna, hace falta un 0 en la posición 1-3 y otro en la posición 2-3. Para eso, se hace:
\[F1´=F1 + 2 F3\]
\[F2´=F2 + F3\]
\[\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\middle|\ \begin{matrix}-4&-5&2\\-1&-1&1\\-2&-2&1\\\end{matrix}\right)\]
Por lo tanto, la matriz inversa de A será:
\[A^{-1}=\left(\begin{matrix}-4&-5&2\\-1&-1&1\\-2&-2&1\\\end{matrix}\right)\]
Antes de proseguir, es conveniente comprobar, mediante la multiplicación con A, que no se hayan cometido errores en este cálculo. Tarea que se sugiere como actividad.
Ahora se retoma la ecuación matricial que se está resolviendo. Es:
\[X\cdot A\cdot A^{-1}=\left(\begin{matrix}1&4&-5\\-5&-1&11\\3&4&-9\\\end{matrix}\right)\cdot A^{-1}\]
Al operar en el primer miembro, se obtiene:
\[X\cdot A\cdot A^{-1}=X.I=X=\left(\begin{matrix}1&4&-5\\-5&-1&11\\3&4&-9\\\end{matrix}\right)\cdot A^{-1}\]
Por lo tanto, para hallar la matriz X, se debe realizar la multiplicación que ha quedado en el último miembro:
\[\begin{array}{r|rrrr} & \left(\begin{matrix}-4&-5&2\\-1&-1&1\\-2&-2&1\\\end{matrix}\right) \\ \hline \left(\begin{matrix}1&4&-5\\-5&-1&11\\3&4&-9\\\end{matrix}\right) & \left(\begin{matrix}2&1&1\\-1&4&0\\2&-1&1\\\end{matrix}\right) \end{array} \]
Entonces, la matriz X buscada será:
\[X=\left(\begin{matrix}2&1&1\\-1&4&0\\2&-1&1\\\end{matrix}\right)\]
Como siempre, es conveniente reemplazar esta matriz en la ecuación original y comprobar que los cálculos coincidan con el resultado del enunciado.
Resuelva el siguiente problema.
En la fabricación de un producto X se utilizan 5 unidades del insumo A y 3 del B. En la fabricación del producto Y, se utilizan 2 unidades de A y 4 de B. Si se disponen de 71 unidades de A y 79 unidades del insumo B, calcule cuántos productos X y cuántos Y se pueden fabricar, utilizando la totalidad de los insumos disponibles.
Para plantear un problema es muy importante comenzar preguntándose ¿qué hay que averiguar en este problema? Para responder, suele ser necesario leer otra vez el enunciado y pensar bien.
En este caso, la pregunta está explícita. Pide averiguar cuántos productos X y cuántos productos Y se pueden calcular. Por eso, el siguiente paso es ponerle nombre a esas incógnitas. Y se escribe con claridad de qué se habla:
x: cantidad del producto X a fabricar.
y: cantidad del producto Y a fabricar.
Es importante notar que no dice “x: producto x” sino que se explicita que se busca la cantidad del producto x a fabricar. Se detalla bien.
El resto de la información que ofrece el enunciado, conviene acomodarlo en una tabla. Se habla allí de insumos, que son las materias primas que hacen falta para la producción y productos, que serán el resultado de esa producción. Cada producto requiere una combinación distinta de esos insumos, según el siguiente detalle:
| Productos | X | Y |
| Insumos | ||
| A | 5 | 2 |
| B | 3 | 4 |
La restricción a la cantidad de productos que se pueden fabricar la impone la cantidad de insumos disponibles. Se puede agregar una columna con ese dato:
| Productos | X | Y | Total |
| Insumos | |||
| A | 5 | 2 | 71 |
| B | 3 | 4 | 79 |
Entonces, para el insumo A se tienen 71 unidades, que se pueden utilizar de la siguiente manera:
5 por cada producto X que vayan a producir (en total sería 5 por x) y 2 por cada producto Y (en total, sería 2 por y).
De la misma manera, para el insumo B, se pueden utilizar 3 unidades por cada producto X y 4 por cada producto Y. Y, en total, se pueden gastar 79 unidades.
Es decir:
\[ \left\{\begin{matrix}5\cdot x+2\cdot y=71 \\ 3\cdot x+4\cdot y=79 \end{matrix}\right. \]
Como ambas deben tener la misma solución, forman un sistema de ecuaciones, que se puede resolver por cualquiera de los métodos ya estudiados. Por ejemplo, por la regla de Cramer.
La matriz asociada al sistema es:
\[A=\left(\begin{matrix}5&2\\3&4\\\end{matrix}\right)\]
y su determinante es \(\left|A\right|=5\cdot4-3\cdot2=20-6=14\).
Por lo tanto, será:
\[x=\frac{\Delta x}{\left|A\right|}=\frac{\left|\begin{matrix}71 & 2\\ 79 & 4 \end{matrix}\right|}{14}=\frac{71 \cdot 4 - 79 \cdot 2}{14}=\frac{126}{14}=9 \]
y
\[y=\frac{\Delta y}{\left|A\right|}=\frac{\left|\begin{matrix}5 & 71\\ 3 & 79 \end{matrix}\right|}{14}=\frac{5 \cdot 79 - 3 \cdot 71}{14}=\frac{182}{14}=13 \]
Por lo tanto, si se desea utilizar la totalidad de los insumos disponibles, se pueden fabricar 9 unidades del producto X y 13 del producto Y.
Resuelva los siguientes ejercicios:
-
Dado el sistema de ecuaciones:
\[\left\{\begin{matrix}x=-5-2y-5z\\\ y=-x-z\ \\z=3-4x-3y\\\end{matrix}\right.\]
Se pide que calcule el determinante de la matriz asociada al sistema, clasifíquelo y resuélvalo.
-
Siendo \(A=\left(\begin{matrix}3&10&-2\\2&2&2\\1&4&-1\\\end{matrix}\right)\), \(B=\left(\begin{matrix}-50&0&-3\\5&1&3\\-15&6&-1\\\end{matrix}\right)\)y \(C=\left(\begin{matrix}9&6&1\\9&7&1\\9&8&1\\\end{matrix}\right)\)se pide que halle la matriz X que cumpla:
\[A\cdot X+B=C\]
-
Dado el sistema de ecuaciones:
\[\left\{\begin{matrix}k\cdot x+y+7z=-4\\ -5x+(k+3) \cdot y+z=-15 \\ y+2z=-1\end{matrix}\right.\]
Determine para qué valores de k el siguiente sistema es compatible determinado, indeterminado o incompatible.
-
Resuelva el problema siguiente, mediante un sistema de ecuaciones.
Un cuaderno tiene 100 hojas con diferentes colores. Algunas son blancas, otras azules y otras, rojas. La mitad de las hojas blancas y la tercera parte de las azules, ya se escribieron, pero todavía no se utilizó el 60 % del cuaderno. También se sabe que hay tres veces más hojas azules que rojas. Calcule cuántas hojas de cada color tiene el cuaderno.