6. Programación lineal
Objetivos
- Plantear problemas de programación lineal.
- Resolver por métodos gráficos y analíticos problemas de programación lineal.
Introducción
La programación lineal es un modelo matemático que data de mediados del siglo XX. Se creó durante la Segunda Guerra Mundial (1939-1945), cuando se necesitó planificar los gastos y envíos tratando de minimizar los costos y maximizar las pérdidas del enemigo.
El objetivo de la programación lineal es el de optimizar un sistema con ecuaciones lineales, sujeto además a restricciones también lineales expresadas como desigualdades. Es decir, busca un máximo o un mínimo valor que satisfaga a la vez ciertas desigualdades y ciertas ecuaciones.
6.1. Formulación de modelos
La Programación Lineal (PL) es una de las principales ramas de la Investigación Operativa. En esta categoría se consideran todos aquellos modelos de optimización donde las funciones que lo componen, es decir, función objetivo y restricciones, son funciones lineales en las variables de decisión. Los modelos de Programación Lineal, por su sencillez, son frecuentemente usados para abordar una gran variedad de problemas de ingeniería y ciencias sociales, lo que ha permitido a empresas y organizaciones lograr importantes beneficios y ahorros asociados a su utilización.
Aquí se manejarán algunos nombres específicos que se describen a continuación.
Se llama función objetivo a la función lineal que se desea optimizar, es decir, buscar que logre un máximo o un mínimo.
Se llaman restricciones a un conjunto de inecuaciones que deben satisfacerse en el problema.
Los puntos del dominio de la función objetivo, que además satisfacen las restricciones del problema, se llaman puntos factibles: puntos permitidos por las restricciones, en donde será factible hallar el máximo o el mínimo de la función objetivo. El punto factible que cumple la condición de optimizar la función objetivo –máximo o mínimo, dependiendo del problema a resolver– se llama solución óptima y es el resultado final al que se desea llegar.
En Economía, la idea es asignar recursos escasos (que se expresan mediante inecuaciones), para lograr maximizar (por ejemplo, los beneficios que obtiene una empresa) o minimizar (por ejemplo, sus costos) cierta función objetivo.
Un modelo de Programación Lineal (PL) considera que las variables de decisión tienen un comportamiento lineal, tanto en la función objetivo como restricciones del problema. En este sentido, la Programación Lineal es una de las herramientas más utilizadas en la Investigación Operativa debido a que por su naturaleza se facilitan los cálculos y en general permite una buena aproximación de la realidad.
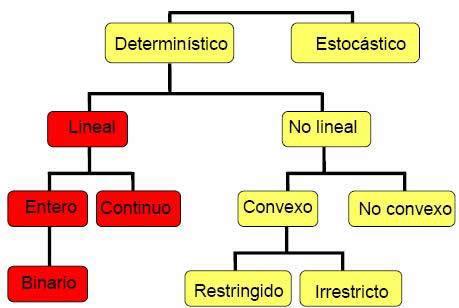
Los Modelos Matemáticos se dividen básicamente en Modelos Deterministas (MD) o Modelos Estocásticos (ME). En el primer caso (MD) se considera que los parámetros asociados al modelo son conocidos con certeza absoluta, a diferencia de los Modelos Estocásticos, donde la totalidad o un subconjunto de los parámetros tienen una distribución de probabilidad asociada.
En los cursos introductorios a la Investigación Operativa generalmente se enfocan solo en Modelos Deterministas. Aquí, en donde solo se ofrece un breve panorama de estos temas, también.
En una carpintería se producen mesas y sillas que requieren diferente cantidad de tiempo de trabajo y de materia prima.
Asimismo, por la venta de cada silla se obtiene un beneficio de 11 y por cada mesa, uno de 20.
Se busca decidir con la producción de qué cantidad de sillas y de mesas se logra el máximo beneficio.
En el siguiente cuadro se presentan los datos de este problema:
| Recursos | Productos | ||
| Silla | Mesa | Disponibilidad por día | |
| Tiempo de trabajo | 3 | 5 | 150 |
| Materias primas | 2 | 7 | 133 |
| Beneficio | 11 | 20 | |
Exprese matemáticamente este problema.
A la cantidad de sillas que se vayan a producir, se la representará con s. Y a la cantidad de mesas, con m. Para el tiempo de trabajo, se pueden utilizar hasta 150 unidades (que, por ejemplo, podrían medirse en horas). Entonces, la información de la tabla anterior se puede expresar con la siguiente desigualdad o inecuación:
\[3 \cdot s + 5 \cdot m ≤ 150\]
Y, dado que se dispone de hasta 133 unidades de materia prima, será:
\[2 \cdot s + 7 \cdot m ≤ 133\]
Estas dos inecuaciones forman un sistema, en el que también está implícito que ni la cantidad s de sillas, ni la cantidad m de mesas pueden tomar un valor negativo. Por lo tanto, el sistema de restricciones es:
\[ \left\lbrace \begin{gather*} s ≥ 0\\ m ≥ 0 \\ 3 \cdot s + 5 \cdot m ≤ 150\\ 2 \cdot s + 7 \cdot m ≤ 133 \end{gather*} \right. \]
Como el objetivo es maximizar el beneficio, la función objetivo es:
\[B\ (s; m) = 11 \cdot s + 20 \cdot m\]
El conjunto de inecuaciones y la función objetivo forman el modelo matemático de este problema. A lo largo de esta unidad se estudiarán diferentes formas de resolverlo.
Un resultado importante de estos problemas es que la solución óptima se encuentra en la periferia de la región factible, ya que las restricciones dadas por desigualdades, corresponden a semiplanos, con lo cual la intersección de las restricciones, o sea, la intersección de los semiplanos, es necesariamente una región convexa.
La solución óptima de un problema de programación lineal se encuentra en la periferia de la región factible.
Si la solución óptima es uno de los vértices de la región factible, será única. Pero podría suceder que haya infinitas soluciones únicas, si la función objetivo alcanza su extremo en todo lo largo de uno de los lados de la región factible.
Represente en un diagrama cartesiano la región factible del Ejemplo 6.1.
Las inecuaciones son:
\[ \begin{gather*} s ≥ 0\\ m ≥ 0 \\ 3 \cdot s + 5 \cdot m ≤ 150\\ 2 \cdot s + 7 \cdot m ≤ 133 \end{gather*} \]
Para representarlas en un diagrama cartesiano, en el eje horizontal se ubicará la variable \(s\) y en el vertical, la \(m\).
Las dos primeras desigualdades se superponen en el primer cuadrante, donde tanto s como m son positivas. En el siguiente gráfico, se sombrearon, de diferente color, cada una de las regiones del plano correspondientes. En rosado queda la superposición de ambas, que coincide con el primer cuadrante del diagrama:
Primer cuadrante
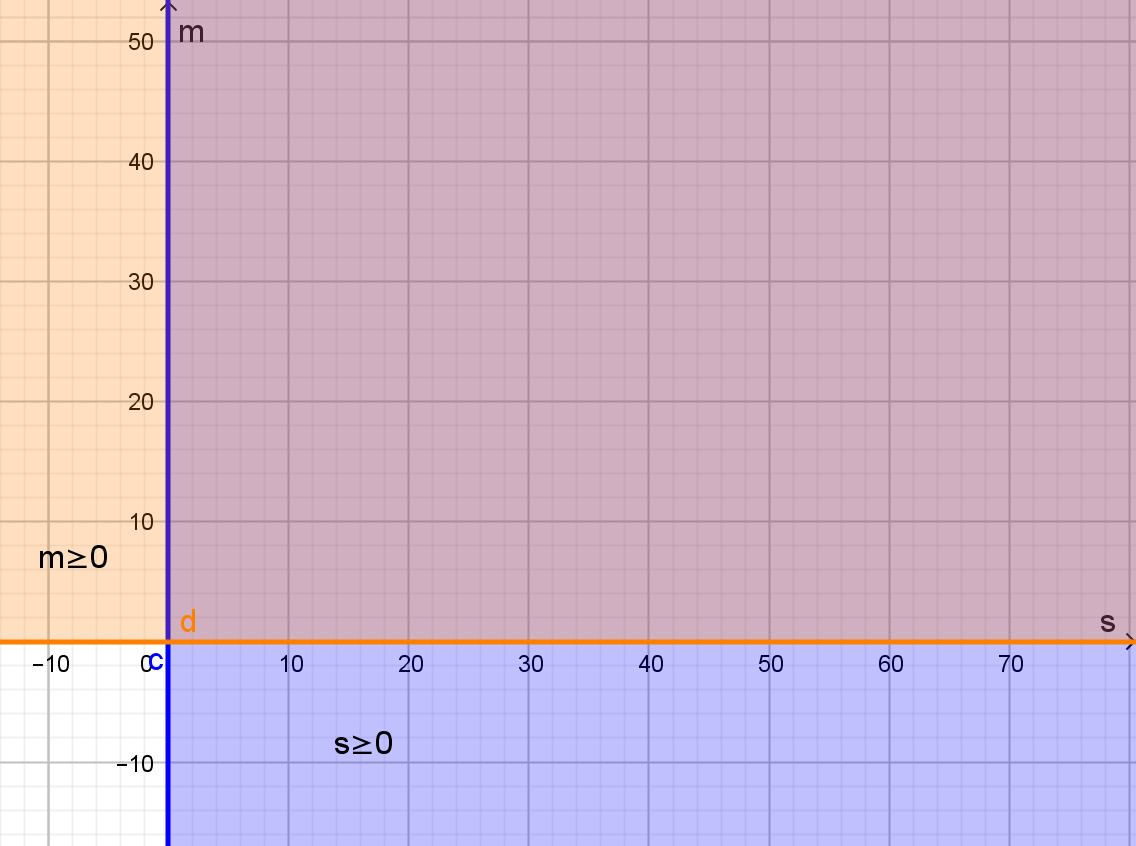
Como este resultado es sencillo de recordar, y con el fin de no complicar más este diagrama, las otras dos desigualdades se graficarán aparte, teniendo en cuenta esta primera conclusión: que la región factible deberá ser del primer cuadrante.
Para representar manualmente las demás desigualdades, conviene comenzar representando la recta borde de cada una. Las rectas borde vienen dadas por las siguientes ecuaciones:
\[3 \cdot s + 5 \cdot m = 150 \]
\[2 \cdot s + 7 \cdot m = 133\]
De ellas, se puede despejar la variable que se representa en el eje vertical. De la primera ecuación es:
\[m = 30 – 3/5 \cdot s\]
Después de representar en el diagrama, se eligen dos puntos, uno de cada semiplano en los que queda dividido por la recta:
Recta borde
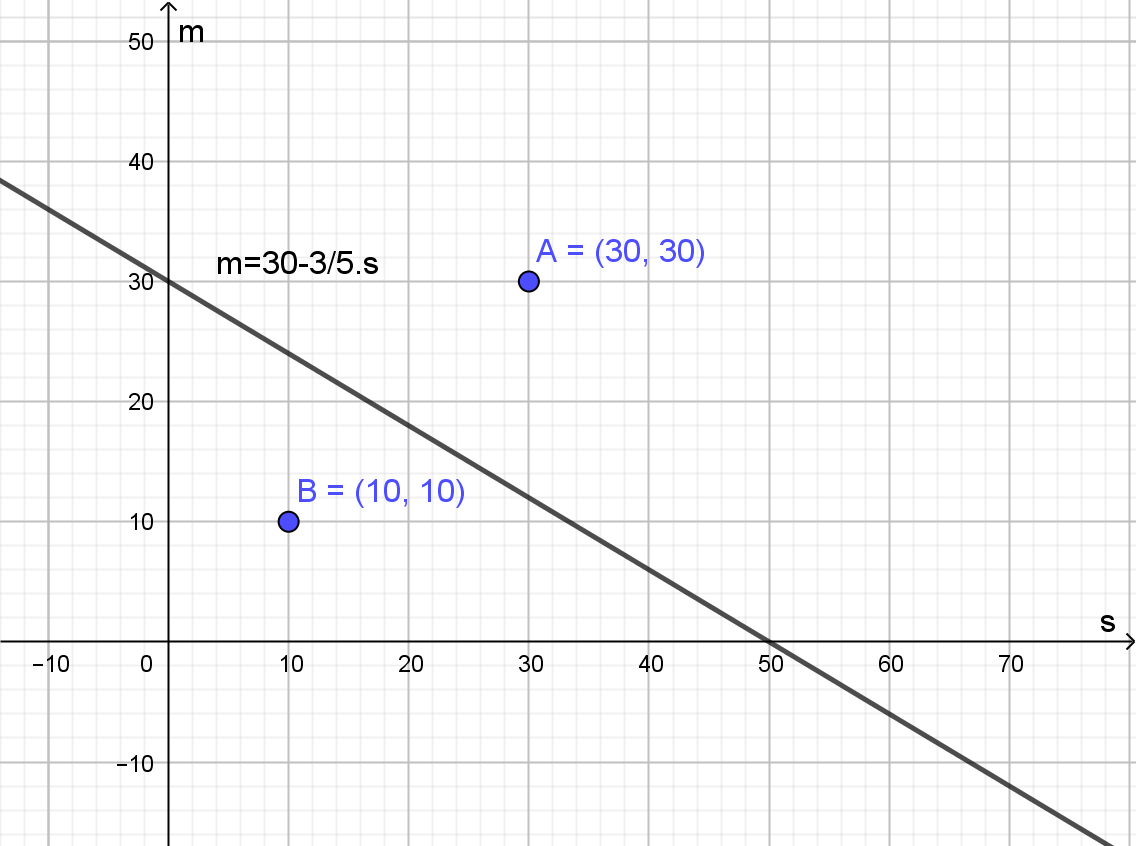
Con esos puntos, se decidirá cuál de los dos semiplanos corresponde a la inecuación. Para el punto A, de coordenadas (30;30), la inecuación queda:
\[3 \cdot 30 + 5 \cdot 30 = 90 + 150 = 240 ≥ 150\]
Que no es lo que se busca, porque no se dispone de tantas horas de trabajo.
Para el punto B, de coordenadas (10;10), es:
\[3 \cdot 10 + 5 \cdot 10 = 30 + 50 = 80 ≤ 150\]
Aquí sí se satisface la ecuación. De modo que el semiplano que representa a esta desigualdad es el siguiente:
Semiplano
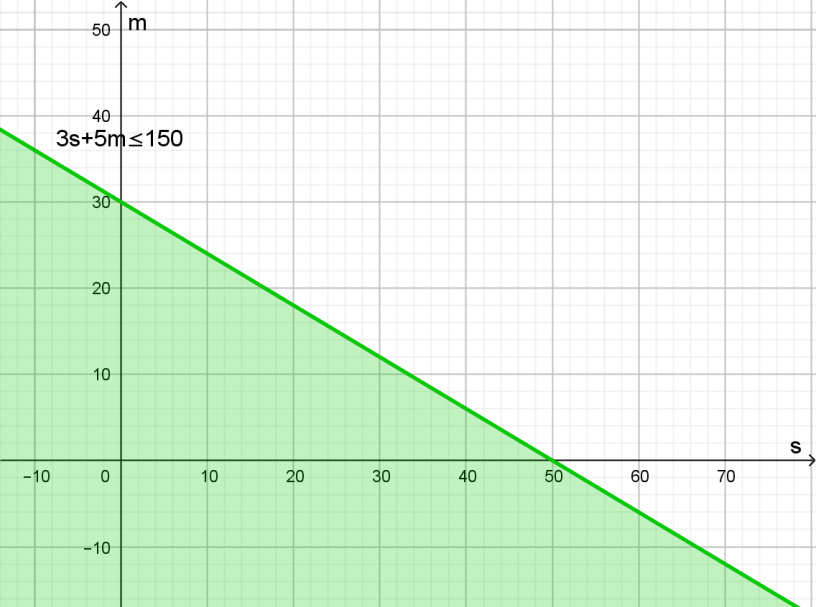
Este procedimiento se repite para la otra inecuación y se representó en el diagrama anterior.
Semiplanos superpuestos
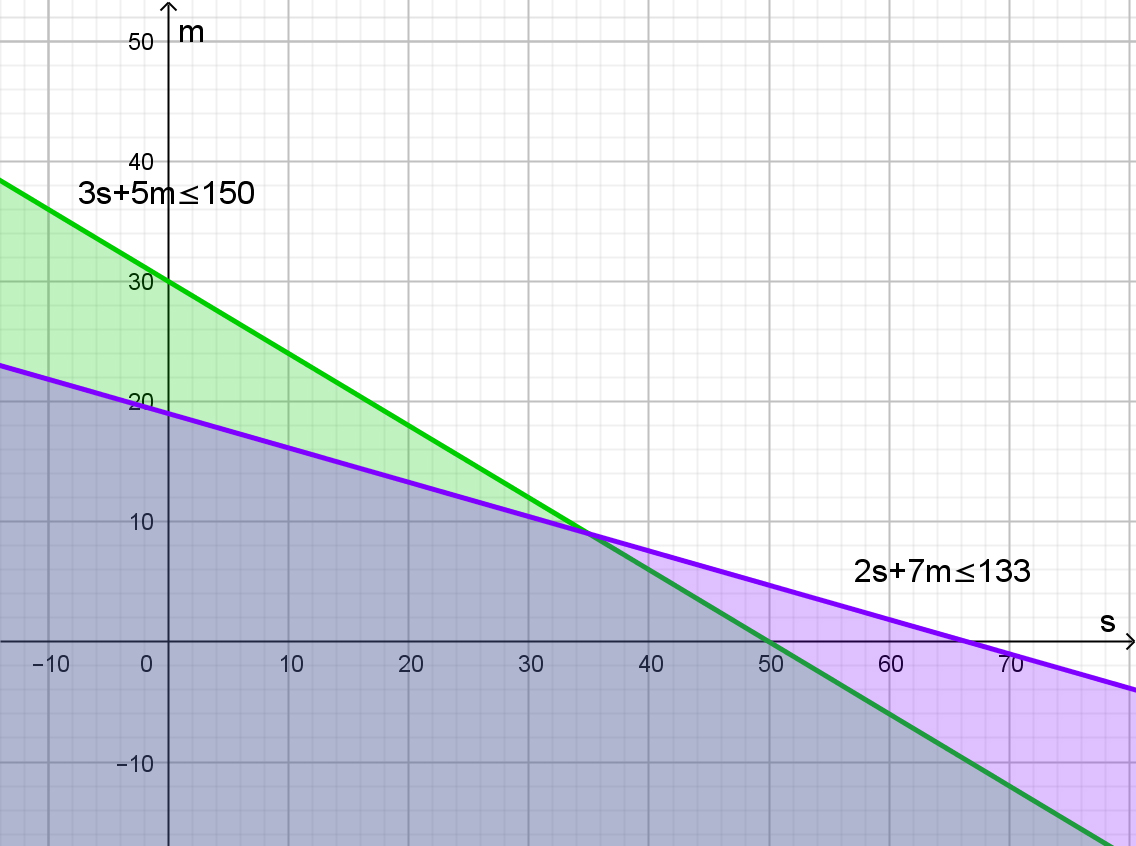
GeoGebra permite graficar directamente el semiplano, al escribir la desigualdad en la barra de fórmulas.
En este punto, es necesario recordar que la región factible debe estar en el primer cuadrante. Por lo tanto, será la siguiente:
Región factible
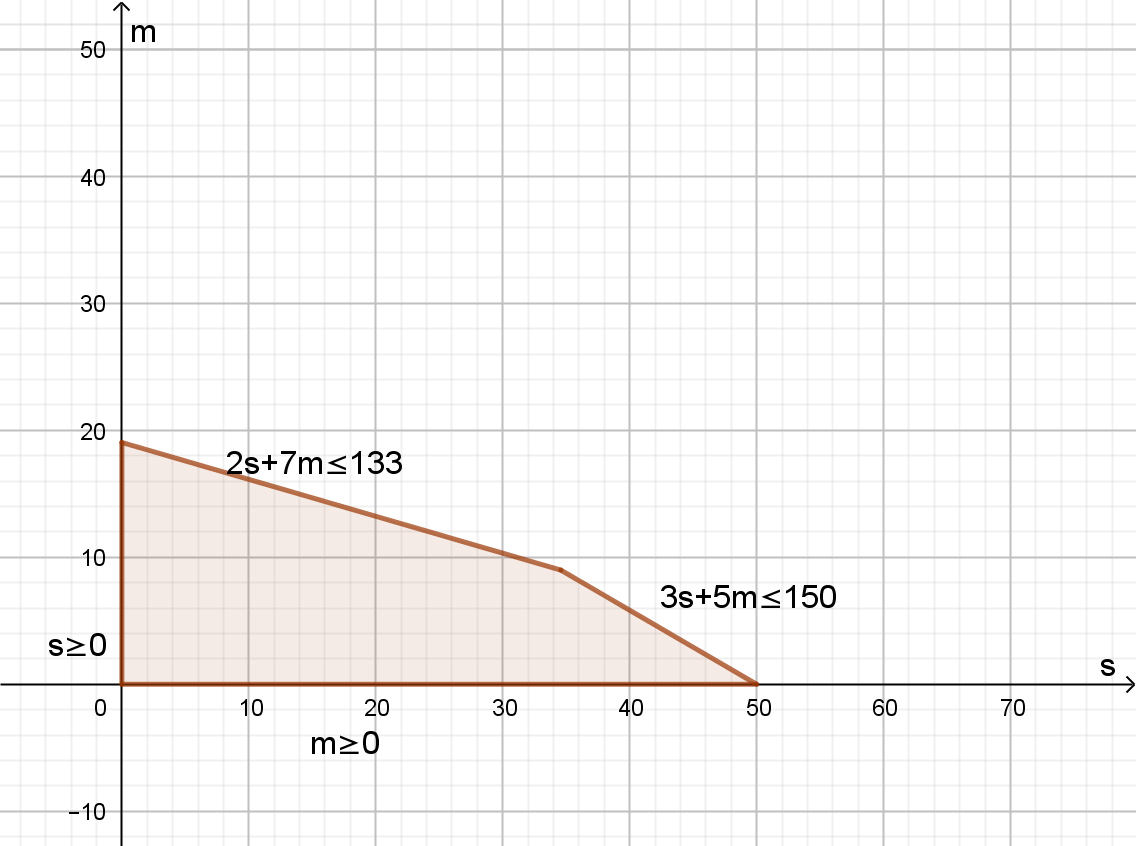
En este último gráfico solo se representó la región factible. Se dejaron las inecuaciones al lado de cada segmento de las rectas bordes, que forman los lados de este polígono.
Todos los puntos que están incluidos en este polígono satisfacen todas las desigualdades del sistema. Por ejemplo, el punto B, de coordenadas (10,10). Se sugiere como actividad, comprobarlo.
La región de validez del problema anterior es convexa, es decir que, dados dos puntos de la región, el segmento que los une está incluido en la región.
6.2. Método de resolución gráfica y analítica
En el caso de dos variables, la función objetivo estará representada por una recta móvil que se desplaza paralela a sí misma al ir cambiando el término independiente, que alcanzará su valor óptimo en el último o en el primer punto que toque dentro de la región de validez que contiene a los puntos factibles.
Por ser la región de validez convexa, la solución óptima estará en un vértice del conjunto factible o bien en un lado del conjunto factible. En ese caso, habrá infinitas soluciones óptimas.
En la empresa de los ejemplos anteriores, ¿con la producción de qué cantidad de sillas y de mesas se logra el máximo beneficio?
Ya se estableció qué conjunto de combinaciones de producción son factibles con los recursos disponibles, es decir, ya se conocen las coordenadas de todos los puntos que satisfacen el sistema de inecuaciones. Pero falta decidir cuál de todas esas combinaciones es la que conviene económicamente, según la fórmula de la función objetivo:
\[B(s; m) = 11 \cdot s + 20 \cdot m\]
Como la región factible es convexa, la solución óptima estará en uno de sus vértices o en uno de sus lados. Por ese motivo, se buscan las coordenadas de los vértices de la región factible. En el siguiente diagrama, se nombran cada uno de ellos:
Vértices de la región factible
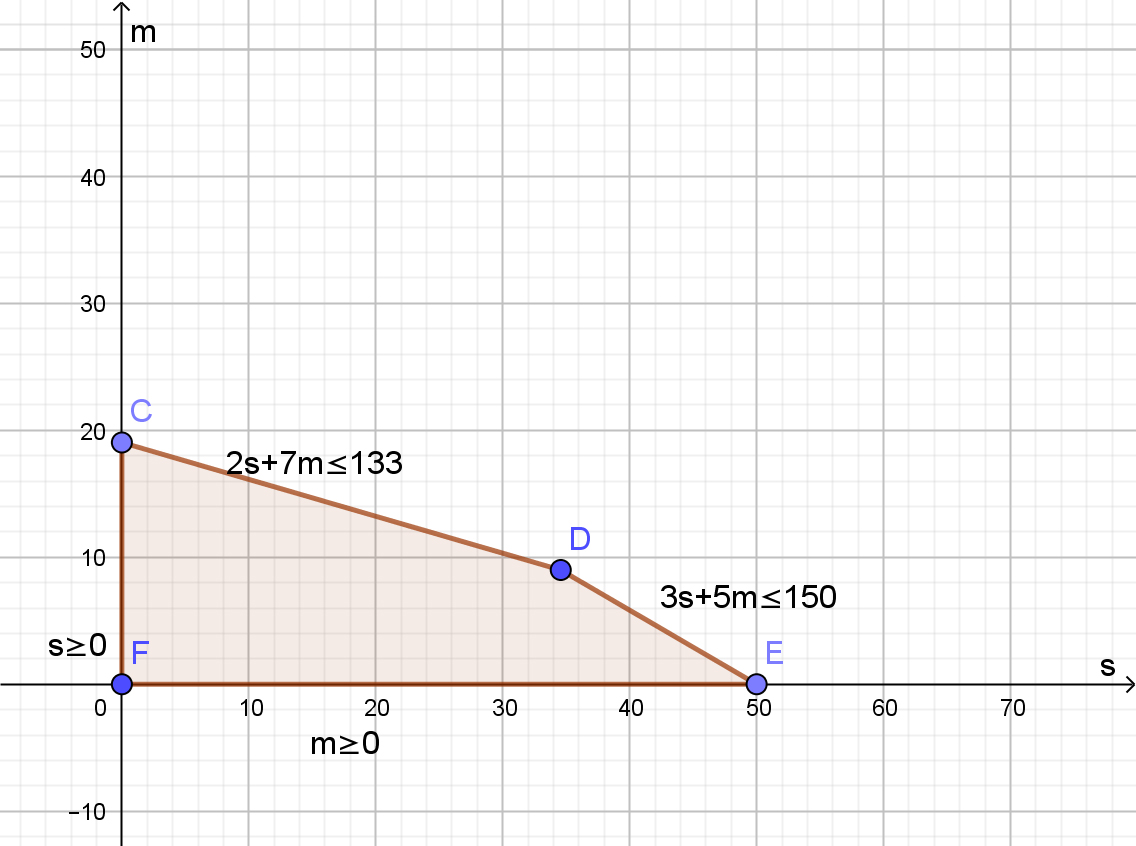
Con GeoGebra pueden calcularse automáticamente sus coordenadas. Para hacerlo manualmente, se busca la solución a la intersección de las rectas bordes que cada vértice une. Por ejemplo, en el caso de D, se unen las rectas:
\[3 \cdot s + 5 \cdot m = 150\]
\[2 \cdot s + 7 \cdot m = 133\]
Para hallar sus coordenadas, se resuelve este sistema de ecuaciones. Por ejemplo, utilizando la regla de Cramer, ya estudiada:
\[s=\frac{\Delta s}{\left| A \right|} = \frac{\left|\begin{matrix}150 & 5 \\133 & 7 \end{matrix}\right|}{\left|\begin{matrix}3 & 5\\2 & 7\end{matrix}\right|} =\frac{385}{11}=35\]
\[m=\frac{\Delta m}{\left| A \right|}= \frac{\left|\begin{matrix}3 & 150 \\2 & 133 \end{matrix}\right|}{\left|\begin{matrix}3 & 5\\2 & 7\end{matrix}\right|} =\frac{99}{11}=9\]
Por lo tanto, las coordenadas de D son (35;9)
Al repetir este procedimiento con cada vértice de la región factible, se obtiene la primera columna de la siguiente tabla, en donde se calculó el beneficio que se obtiene con cada combinación en la segunda columna:
| Vértice | Beneficio |
|---|---|
| \(C\ =(0;19)\) | \(B\ (0;19) = 11 \cdot 0 + 20 \cdot 19 = 380\) |
| \(D\ =(35;9)\) | \(B\ (35;9) = 11 \cdot 35 + 20 \cdot 9= 565\) |
| \(E\ =(50;0)\) | \(B\ (50;0) = 11 \cdot 50 + 20 \cdot 0 = 550\) |
| \(F\ =(0;0)\) | \(B\ (0;0) = 11 \cdot 0 + 20 \cdot 0 = 0\) |
Al comparar los beneficios que se obtienen en cada vértice, se puede apreciar que serán máximos cuando se produzcan 35 sillas y 9 mesas. En las demás combinaciones de producción, el beneficio es menor.
A esta misma conclusión se puede llegar trazando rectas sobre el diagrama en el que está representada la región factible, para distintos valores del beneficio.
Por ejemplo, para un beneficio de 500, la función objetivo se transforma en la siguiente identidad:
\[B\ (s; m) = 11 \cdot s + 20 \cdot m = 500\]
De aquí se despeja m
\[m\ = 25 - 11/20 \cdot s\]
Y en el gráfico queda como sigue:
Función objetivo
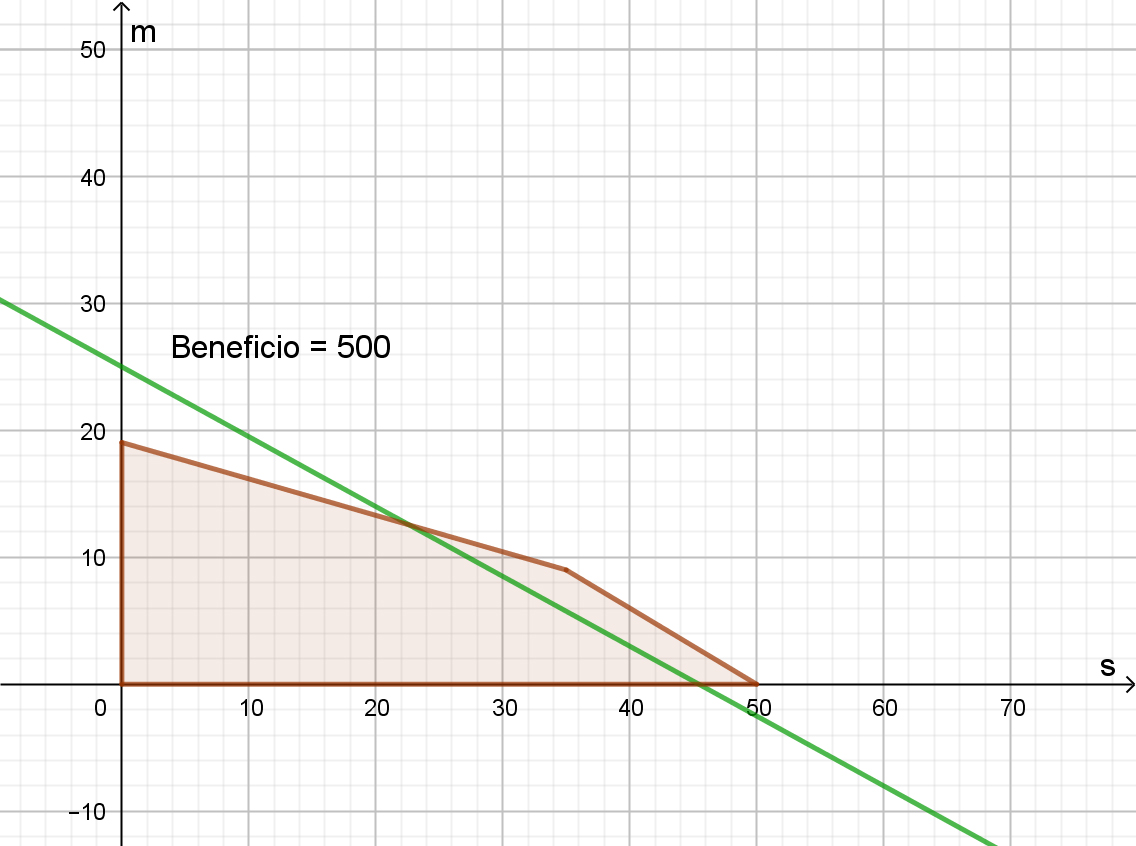
Como puede apreciarse, esta recta atraviesa a la región factible. Dado que la solución óptima será uno de sus vértices o uno de sus lados, el beneficio puede ser mayor.
En el siguiente diagrama interactivo de GeoGebra, se pueden cambiar los valores del “deslizador” Beneficio, de color rojo arriba de la región factible, lo que permite ver el desplazamiento de la recta correspondiente para cada valor. Se puede apreciar que, cuando el beneficio es mayor a 565, la recta sale de la región factible, no tiene puntos de intersección con ella. Esto significa que, con estas restricciones, no se puede obtener un beneficio mayor a ese número.
El último de los puntos de la región factible que la recta móvil interseca es el vértice D, cuyas coordenadas ya se buscaron. Y corresponde al mayor beneficio posible, dadas las condiciones de producción planteadas.
Una empresa de muebles tiene 2 fábricas A y B donde se elaboran los cortes del material para los distintos módulos que se venden en el mercado y 3 plantas de armado I, II y III donde ensamblan los muebles para ser vendidos al público.
Las fábricas A y B producen 2000 y 3000 piezas por año respectivamente, las que deben enviarse a las plantas I, II y III cuyas capacidades máximas de procesamiento son 500, 3500 y 1000 piezas de muebles por año.
Los costos de transporte de los cortes desde las fábricas A y B a las plantas I, II y III en pesos por pieza cortada son:
| Plantas | Fábricas | ||
| I | II | II | |
| A | 10 | 20 | 30 |
| B | 15 | 17,5 | 20 |
¿Cómo conviene distribuir las piezas cortadas en las fábricas a las plantas de armado, de modo tal que los costos de transporte sean lo mínimo posible?
El primer paso es traducir el problema al lenguaje que se utiliza en este curso, plantearlo como ecuaciones matemáticas con variables y funciones que se desea optimizar. Es decir, escribir el modelo matemático.
Se llamará x a la cantidad de piezas que se envían de la fábrica A hacia la planta I e y a la cantidad de muebles que se envían de la fábrica A para la planta II, el resto de los envíos quedan determinados con estas incógnitas y las condiciones del problema: como la planta I puede procesar hasta 500 piezas, si recibe x piezas de la fábrica A, podrá recibir a lo sumo
\[500 - x \text{ piezas de la fábrica } B\]
De la misma manera, si la planta II puede procesar hasta 3500 piezas, entonces si recibe y piezas de la fábrica A, podrá recibir a lo sumo:
\[3500 - y \text{ piezas de la fábrica } B\]
Solo resta determinar cuántos muebles recibe la planta III.
Si la planta A produce 2000 piezas y envía \(x\) a la planta I e \(y\) piezas a la planta II, entonces deberá enviar:
\[2000 – x - y \text{ a la planta III.}\]
Con el mismo razonamiento se puede determinar cuántas piezas recibe de la fábrica B. Si esta planta produce 3000 piezas y envía 500 - x a la planta I y 3500 - y piezas a la planta II, entonces deberá enviar
\[3000 - (500 - x) - (3500 - y)= x + y - 1000 \text{ piezas a la planta III}\]
En este caso, este mismo resultado se puede obtener del mismo modo que se hizo para averiguar cuántas piezas reciben las plantas I y II de la fábrica B dadas las que recibe de la fábrica A y cuál es la máxima producción de la planta III.
La planta III puede procesar hasta 1000 muebles, entonces si recibe 2000 – x - y piezas de la fábrica A, podrá recibir a lo sumo
\[1000 - (2000-x-y) = 1000 - 2000 + x + y = x + y - 1000 \text{ piezas de la fábrica B}\]
Esta información se puede resumir en un cuadro como el siguiente:
| \( I \leq 500\) | \( II \leq 3500\) | \( III \leq 1000\) | |
| \( A=2000\) | \( x\) | \( y\) | \( 2000-x-y\) |
| \( B=3000\) | \( 500 - x\) | \( 3500 - y\) | \( x + y - 1000\) |
Esta tabla representa la cantidad de piezas que serán enviadas a cada planta de armado de muebles, con lo cual las restricciones surgen de pedir que estas cantidades sean mayores o iguales a cero (no tienen sentido las cantidades negativas en este problema). Nuevamente, la solución debe estar incluida en el primer cuadrante.
La función objetivo combina estas cantidades, con los valores indicados en la Tabla 6.3.
El costo resulta entonces:
\[\begin{gather*} C(x, y)= 10 x + 20 y + 30 (2000 – x - y) + 15 (500 - x) +\\ +17,5 (3500 - y) + 20 (x + y - 1000) = \\ =108750 - 15 x – 7,5 y \end{gather*} \]
Esta función objetivo, que se busca minimizar, debido a que la cantidad de piezas nunca puede ser negativa, estará sujeta a las siguientes restricciones:
\[\begin{gather*} x \geq 0 \\ y \geq 0 \\ 500 - x \geq 0 \\ 3500 - y \geq 0 \\ 2000 - x - y \geq 0 \\ x + y - 1000 \geq 0 \end{gather*} \]
Este sistema se puede escribir despejando las variables del lado izquierdo y los números del derecho de las desigualdades:
\[\begin{gather*} x \geq 0 \\ y \geq 0 \\ x \leq 500\\ y \leq 3500 \\ x + y \leq 2000 \\ x + y \geq 1000 \end{gather*}\]
Queda así traducido todo el problema al lenguaje matemático: con la función objetivo, es decir, los costos a minimizar y las restricciones planteadas.
Ahora, se buscará la región factible. Las dos primeras inecuaciones, según ya se vio en el ejemplo anterior, equivale a decir que la solución debe estar incluida en el primer cuadrante.
Junto con las siguientes dos desigualdades, determinan el cuadrilátero cuyos vértices son A, B, C y D en el siguiente gráfico:
Ejemplo 4 – Primera parte
.jpg)
Para facilitar la comprensión, en el siguiente gráfico sólo se ubicaron las últimas dos restricciones. La zona común a ambas, dentro del primer cuadrante, es el cuadrilátero con vértices E, F, G y H.
Ejemplo 4 – Segunda parte
.jpg)
Al combinar los dos últimos resultados parciales, se logra visibilizar la región solución del sistema de inecuaciones, que será donde ambos se superponen. En el siguiente diagrama, aparecen indicadas las inecuaciones de las rectas borde. La región factible tiene como vértices a los puntos E, F, I y J.
Ejemplo 4 – Región factible
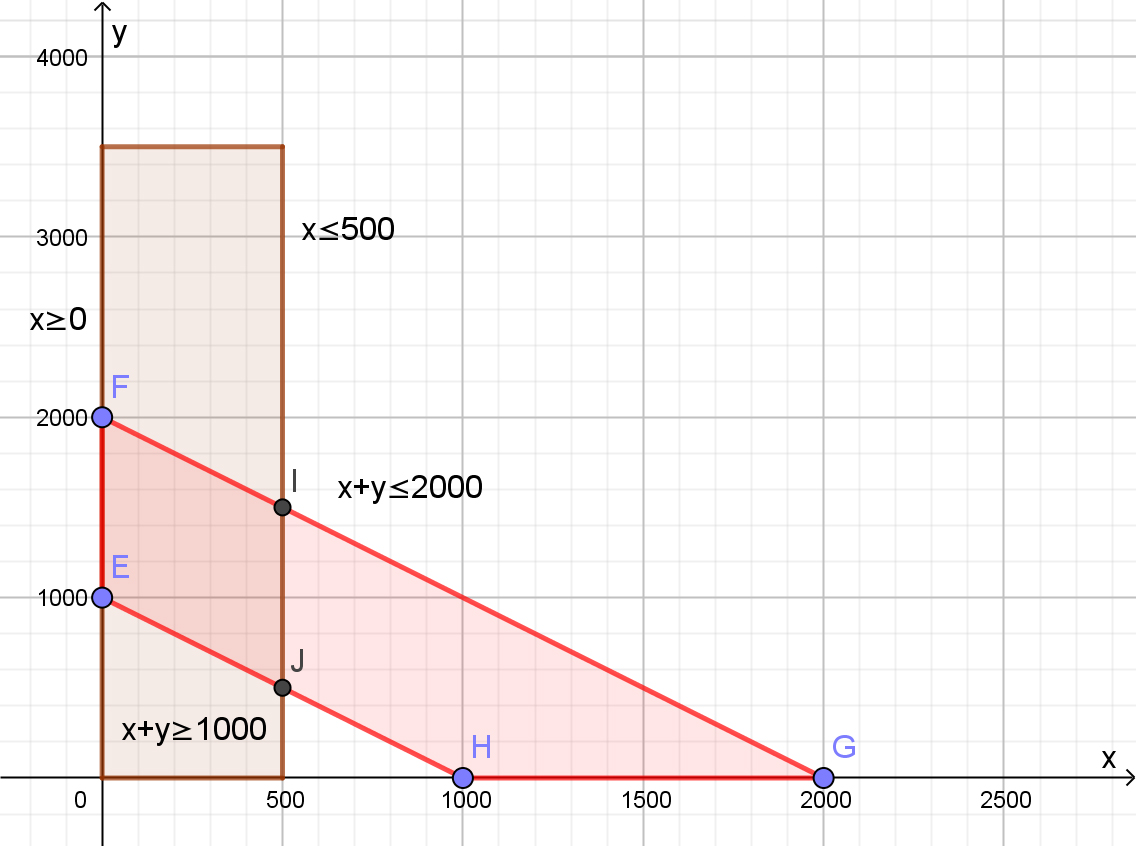
En el próximo gráfico interactivo se ubicó únicamente la región solución y se agregó la función objetivo:
\[C(x, y)= 108750 - 15 x - 7,5 y\]
mediante un deslizador ubicado arriba a la derecha, de color azul, se puede mover la recta roja que representa a los costos.
Como puede apreciarse, los costos bajan a medida que la recta se desplaza hacia arriba. Gráficamente, se puede afirmar que la solución óptima está en el punto I, cuyas coordenadas se pueden encontrar cuando se resuelve el siguiente sistema de ecuaciones:
\[\begin{gather*} x = 500\\ x + y = 2000 \end{gather*} \]
Entonces, la solución óptima es cuando x=500, y=1500. Y los costos llegan a:
\[Costos= 108750 - 15 . 500 - 7,5 . 1500 =90000\]
La respuesta a este problema se completa al ubicar en la tabla cuántas piezas de las fábricas A y B se destinarán a cada una de las plantas de armado I, II y III:
| \( I \leq 500\) | \( II \leq 3500\) | \( III \leq 1000\) | |
| \( A=2000\) | \( 500\) | \( 1500\) | \( 0\) |
| \( B=3000\) | \( 1000\) | \( 2000\) | \( 1000\) |
Hasta aquí, en este ejemplo se ha repetido el método gráfico de resolución de problemas de programación lineal.
6.2.1. Método analítico
La resolución analítica del problema anterior permite resolver cualquier problema (incluso con más de dos o tres variables, casos que no podrán resolverse gráficamente). La idea radica en modificar las restricciones de menor o mayor e igual, es decir, las inecuaciones, por restricciones de igualdad, o sea, ecuaciones, con lo que se pasará a tener un sistema de ecuaciones lineales para resolver.
Se resolverá el mismo problema del Ejemplo 6.4., pero analíticamente.
Las inecuaciones del problema son:
\[ \begin{gather*} x \leq 500\\ y \leq 3500\\ x + y \leq 2000\\ x + y \geq 1000 \end{gather*} \]
Y se transformarán en ecuaciones de la siguiente manera:
La restricción \(x \leq 500\), puede escribirse como
\[x + x_3 = 500\]
En la que se agrega una nueva variable al problema: \( x_3\)
A las variables que se agregan al problema se las llama variables de holgura o exceso. Se eligió el subindice 3 porque es una nueva variable del problema y ya existen las dos variables de decisión originales, \( x\) e \( y\) por lo que esta es la tercer variable para nuestro problema, una variable agregada para convertir la inecuación en una igualdad.
Esta variable de holgura \( x_3\) indica cuánto le falta a \( x\) para llegar a \(500\). Si \( x\) vale \(500\), \( x_3\) será cero. En caso contrario, será mayor a cero. Esta variable, igual que \( x\) y que \( y\), debe ser positiva o nula.
Los pares ordenados de la región factible en los que \( x_3\) vale cero, son los de la recta borde \( x=500\), para cualquier valor de \( y\).
La restricción \(y \leq 3500 \) se puede escribir como
\[y + x_4 = 3500\]
Donde se agregó la variable \(x_4\) que será la que tenga en cuenta cuánto le falta a \(y\) para llegar a \(3500\). Los pares ordenados de la región factible en los que \(x_4\) vale cero, son los de la recta borde \(y = 3500\), para cualquier valor de \(x\).
La restricción \(x + y \leq 2000\), puede escribirse como
\[x + y + x_5 = 2000\]
En esta ecuación \( x_5\) será la que tenga en cuenta cuánto le falta a la suma \( x + y\) para llegar a \(2000\), dado que la inecuación \(x + y \leq 2000 \) dice que \(x + y \) es menor o igual que \(2000\). En el caso en que sumen \(2000\), \(x_5\) valdrá cero y, si no, será mayor que cero. Cuando \(x_5\) vale cero, los pares ordenados de la región factible son los de la recta borde \(x + y = 2000\).
Por último, resta considerar la restricción \(x + y \geq 1000\). Esta se puede escribir como
\[x + y - x_6 = 1000\]
La variable \(x_6\) que será la que tenga en cuenta cuánto le sobra a la suma \(x + y\) respecto de \(1000\). En el caso en que sumen \(1000\), \(x_6\) valdrá cero y, si no, será mayor que cero.
Nótese que, como la desigualdad era del tipo mayor o igual, la variable de holgura aparece restando, pues representa cuánto le sobra a la suma \(x + y\) respecto de \(1000\).
En esta ecuación, cuando en la resolución se tengan resultados con \(x_6 = 0\), significa que se está moviendo a lo largo de la recta \(x + y = 1000\).
El sistema a resolver queda en la forma canónica o aumentada:
\[\begin{gather*} Z = C\ (x, y) = 108750 -15 x -7,5\ y\ \ \ \text{ que se desea minimizar }\\ x + x_3 = 500\\ y + x_4 = 3500\\ x + y + x_5 = 2000\\ x + y - x_6 = 1000\\ x,\ y,\ x_3,\ x_4,\ x_5,\ x_6 \geq 0 \end{gather*} \]
Como ya se mencionó, se debe mover por los bordes de la región factible, ya que alguno de ellos será la solución óptima. Por eso, deberán ir valiendo cero las variables del sistema que, como antes se mostró, permiten moverse por estos bordes. Las posibles variables que tendrán que valer cero en este problema son \(x\), \(y\), \(x_3\), \(x_4\) y \(x_6\). Cuando dos de las variables valen cero, se está en un vértice de la zona factible, que son los puntos donde estarán los valores óptimos. Alguno de los vértices de la zona factible será la solución óptima.
Entonces, una forma de resolver el problema es hallar las soluciones del sistema lineal, igualando a cero dos de las variables del sistema, \(x,\ y,\ x_3,\ x_4,\ x_5,\ x_6\).
Para cada solución que se obtenga, se debe ver si los valores de \(x\) e \(y\) obtenidos pertenecen a la zona factible, y luego, de todos ellos, cuál maximiza o minimiza la función objetivo. En este problema, se busca el mínimo.
Las posibilidades serán considerar los vértices de la zona factible, los valores para \((x, y)\) iguales a \((0,\ 1000),\ (0,\ 2000),\ (500,\ 500)\ o\ (500,\ 1500)\). Los valores de \( x_3,\ x_4,\ x_5\) y \(x_6\) se calculan a partir de las ecuaciones donde se definieron estas variables
\[\begin{gather*} x = 0 \ \ \ \ \ \ y = 1000 \ \ \ \ \ \ x_3 = 500 \ \ \ \ \ \ x_4 = 2500 \ \ \ \ \ \ x_5 = 1000 \ \ \ \ \ \ x_6 = 0 \\ C\ (0, 1000)= 108750 - 7500 = 101250 \end{gather*} \]
\[\begin{gather*} x = 0 \ \ \ \ \ \ y = 2000 \ \ \ \ \ \ x_3 = 500 \ \ \ \ \ \ x_4 = 1500 \ \ \ \ \ \ x_5 = 0 \ \ \ \ \ \ x_6 = 1000\\ C\ (0, 2000)= 108750 - 15000 = 93750 \end{gather*} \]
\[\begin{gather*} x = 500 \ \ \ \ \ \ y = 500 \ \ \ \ \ \ x_3 = 0 \ \ \ \ \ \ x_4 = 3000 \ \ \ \ \ \ x_5 = 1000 \ \ \ \ \ \ x_6 = 0\\ C\ (500, 500)= 108750 - 7500 - 3750 = 97500 \end{gather*} \]
\[\begin{gather*} x = 500 \ \ \ \ \ \ y = 1500 \ \ \ \ \ \ x_3 = 0 \ \ \ \ \ \ x_4 = 2000 \ \ \ \ \ \ x_5 = 0 \ \ \ \ \ \ x_6 = 1000\\ C\ (500, 1500)= 108750 - 7500 -11250 = 90000 \end{gather*} \]
Al comparar el valor de los costos en cada par ordenado \((x, y)\), se puede apreciar que los costos son máximos cuando \(x = 0\) e \(y= 1000\). Y que la distribución que más conviene realizar entre los armados de elaboración de muebles será con
\[x = 500 ;\ y = 1500:\]
Por supuesto, se arriba a la misma conclusión que con el método gráfico.
Este método puede utilizarse, pero puede ser tedioso, complicado o imposible de llevar a la práctica cuando se tienen muchas variables.
En el caso del Ejemplo 6.5., se tienen 6 variables que, tomadas de a dos, abren 15 posibilidades distintas para seleccionar un par de variables e igualarlas a cero. Por esta dificultad es que se desarrollaron otros métodos, como el Simplex, que se estudiará a continuación.
6.3. Método Simplex
El método del simplex fue creado en 1947 por el matemático George Dantzig.N Se utiliza, principalmente, para resolver problemas de programación lineal en los que intervienen tres o más variables, que complican su resolución gráfica. El álgebra matricial y el proceso de eliminación de Gauss-Jordan para resolver un sistema de ecuaciones lineales constituyen su base.
El método Simplex es un procedimiento iterativo que permite ir mejorando la solución a cada paso. El proceso concluye cuando no es posible seguir mejorando más dicha solución. Se parte del valor de la función objetivo en un vértice cualquiera de la región factible. El método consiste en buscar sucesivamente otro vértice que mejore al anterior. La búsqueda se hace siempre a través de los lados del polígono (o de las aristas del poliedro, si el número de variables es mayor a dos). Como el número de vértices (y de aristas) es finito, siempre se podrá encontrar la solución.
El método del Simplex se basa en la siguiente propiedad: si la función objetivo, f, no toma su valor máximo en el vértice A, entonces hay una arista que parte de A, a lo largo de la cual f aumenta.
A continuación, se utiliza este método para resolver el problema del Ejemplo 6.1., que gráficamente o calculando solo en los 4 vértices se resuelve de forma mucho más simple. De todos modos, su sencillez permite mostrar el método.
En <http://www.phpsimplex.com/biografia_Dantzig.htm> se puede leer una biografía de este matemático estadounidense.
Con el siguiente sistema de restricciones:
\[\begin{gather*} s \geq 0\\ m \geq 0\\ 3 \cdot s + 5 \cdot m \leq 150\\ 2 \cdot s + 7 \cdot m \leq 133 \end{gather*} \]
Se busca maximizar la función objetivo, así:
\[B\ (s; m) = 11 \cdot s + 20 \cdot m\]
Para aplicar este método se transforma la función objetivo en una ecuación:
\[B - 11 \cdot s – 20 \cdot m = 0\]
Y las restricciones se escriben con las variables de holgura, de la siguiente manera:
\[\begin{gather*} 3 \cdot s + 5 \cdot m + x_3 = 150\\ 2 \cdot s + 7 \cdot m + x_4 =133\\ s,\ m,\ x_3,\ x_4 \geq 0 \end{gather*} \]
La última inecuación, que es la condición de no negatividad de las variables, no se utilizará. Con las demás, se arma un sistema de ecuaciones, que, ordenado y completo, en este caso es:
\[\begin{gather*} 1 \cdot B - 11 \cdot s\ – 20 \cdot m + 0 \cdot x_3 + 0 \cdot x_4 = 0\\ 0 \cdot B +3 \cdot s + 5 \cdot m + 1 \cdot x_3 + 0 \cdot x_4 = 150\\ 0 \cdot B +2 \cdot s + 7 \cdot m + 0 \cdot x_3 + 1 \cdot x_4 =133 \end{gather*} \]
Con este sistema de ecuaciones se puede trabajar con la matriz ampliada, con el método de Gauss o con tablas. Aquí se hará de las dos maneras:
\[\left(\begin{matrix}1&-11&-20\\0&3&5\\0&2&7\\\end{matrix}\ \ \ \ \ \begin{matrix}0&0\\1&0\\0&1\\\end{matrix}\ \ \left|\ \ \ \begin{matrix}0\\150\\133\\\end{matrix}\right.\right)
\]
| \(\mathbf{B}\) | \(\mathbf{s}\) | \(\mathbf{m}\) | \(\mathbf{x_3}\) | \(\mathbf{x_4}\) | \(\mathbf{R}\) |
| \(1\) | \(-11\) | \(-20\) | \(0\) | \(0\) | \(0\) |
| \(0\) | \(3\) | \(5\) | \(1\) | \(0\) | \(150\) |
| \(0\) | \(2\) | \(7\) | \(0\) | \(1\) | \(133\) |
La disposición en forma de tabla permite seguir visualizando a qué variable corresponde cada coeficiente.
Es importante notar que en este punto hay tres columnas en las que un único coeficiente es 1 y todos los demás son 0. Son las que corresponden a las variables \(B\), \(x_3\) y \(x_4\). Si las demás variables del problema, es decir s y m, valen cero, \(B\), de acuerdo con la primera fila, sería 0, \(x_3\) valdría 150 (fila 2) y \(x_4\), 133 (fila 3). A estas conclusiones se llega observando la última columna, la que corresponde a los resultados del sistema de ecuaciones.
Esta posibilidad:
\[\begin{gather*} B = s = m = 0\\ x_3 = 150\\ x_4 = 133 \end{gather*} \]
es una solución, pero no es la óptima, porque \(B\) puede tomar valores mayores a cero.
Para encontrar una mejor solución se buscará obtener una matriz equivalente a la anterior, pero en la que sean otras las variables no nulas. Para elegir cuál es la variable que dejará de valer 0, se busca, en la fila correspondiente a la función objetivo, que en esta disposición es la primera, el menor de los coeficientes. En este ejemplo es -20, que es menor que -11, y que corresponde a la variable \(m\). Para elegir en qué fila de dejará un 1 en el coeficiente de la \(m\), se dividen los resultados por los coeficientes positivos de esa variable en las demás filas. Y se selecciona la fila en la que se obtenga el menor cociente:
| \(\mathbf{B}\) | \(\mathbf{s}\) | \(\mathbf{m}\) | \(\mathbf{x_3}\) | \(\mathbf{x_4}\) | \(\mathbf{R}\) | Cocientes |
| \(1\) | \(-11\) | \(-20\) | \(0\) | \(0\) | \(0\) | |
| \(0\) | \(3\) | \(5\) | \(1\) | \(0\) | \(150\) | \(150/5=30\) |
| \(0\) | \(2\) | \(7\) | \(0\) | \(1\) | \(133\) | \(133/7=19\) |
Como 19 es menor que 30, se utilizará la tercera fila.
Ahora se procede como en el método de Gauss. Para conseguir un 1 en la posición 3-3, se hace \(F3 /7 \rightarrow F3\) y se obtiene:
\[\left(\begin{matrix}1&-11&-20\\0&3&5\\0&2/7&1\\\end{matrix}\ \ \ \ \ \begin{matrix}0&0\\1&0\\0&1/7\\\end{matrix}\ \ \left|\ \ \ \begin{matrix}0\\150\\19\\\end{matrix}\right.\right) \]
O, en forma de tabla:
| \(\mathbf{B}\) | \(\mathbf{s}\) | \(\mathbf{m}\) | \(\mathbf{x_3}\) | \(\mathbf{x_4}\) | \(\mathbf{R}\) |
|---|---|---|---|---|---|
| \(1\) | \(-11\) | \(-20\) | \(0\) | \(0\) | \(0\) |
| \(0\) | \(3\) | \(5\) | \(1\) | \(0\) | \(150\) |
| \(0\) | \(2/7\) | \(1\) | \(0\) | \(1/7\) | \(19\) |
Ya hay un 1 en la posición 3-3. Para anular los demás coeficientes de esa columna, se hace:
\[F1 + 20 \cdot F3 \rightarrow F1 \text{ y } F2 -5 \cdot F3 \rightarrow F2:\]
\[\left(\begin{matrix}1&-37/7&0\\0&11/7&0\\0&2/7&1\\\end{matrix}\ \ \ \ \ \begin{matrix}0&0\\1&-5/7\\0&1/7\\\end{matrix}\ \ \left|\ \ \ \begin{matrix}380\\55\\19\\\end{matrix}\right.\right) \]
O, en forma de tabla:
| \(\mathbf{B}\) | \(\mathbf{s}\) | \(\mathbf{m}\) | \(\mathbf{x_3}\) | \(\mathbf{x_4}\) | \(\mathbf{R}\) |
| \(1\) | \(-37/7\) | \(0\) | \(0\) | \(0\) | \(380\) |
| \(0\) | \(11/7\) | \(0\) | \(1\) | \(-5/7\) | \(55\) |
| \(0\) | \(2/7\) | \(1\) | \(0\) | \(1/7\) | \(19\) |
En este paso, el beneficio \(B\) creció hasta 380, como puede verse en la columna de resultados. La variable \(m\) dejó de ser nula y se hizo cero a \(x_4\). Aquí, las variables toman los siguientes valores:
\[\begin{gather*} s = x_4 = 0\\ B = 380\\ m = 19\\ x_3 = 55 \end{gather*} \]
Como aún queda un coeficiente negativo en la primera ecuación (en la primera fila), se puede seguir operando para que \(B\) tome un valor mayor. Ese coeficiente negativo corresponde a la variable \(s\), que ahora dejará de ser nula. Nuevamente, para saber con qué fila conviene trabajar, se dividen los resultados por sus coeficientes positivos y se elige la fila en la que el cociente sea menor:
| \(\mathbf{B}\) | \(\mathbf{s}\) | \(\mathbf{m}\) | \(\mathbf{x_3}\) | \(\mathbf{x_4}\) | \(\mathbf{R}\) | Cocientes |
| \(1\) | \(-37/7\) | \(0\) | \(0\) | \(0\) | \(380\) | |
| \(0\) | \(11/7\) | \(0\) | \(1\) | \(-5/7\) | \(55\) | \(55/(11/7)=35\) |
| \(0\) | \(2/7\) | \(1\) | \(0\) | \(1/7\) | \(19\) | \(19/(2/7)=133/2\) |
Dado que 35 es menor que 133/2, se utilizará la segunda fila. Se buscará primero un 1 en la posición 2-2, mediante la siguiente operación:
\[F2 \cdot 7/11 \rightarrow F2\]
\[\left(\begin{matrix}1&-37/7&0\\0&1&0\\0&2/7&1\\\end{matrix}\ \ \ \ \ \begin{matrix}0&0\\7/11&-5/11\\0&1/7\\\end{matrix}\ \ \left|\ \ \ \begin{matrix}380\\35\\19\\\end{matrix}\right.\right) \]
Para lograr anular las posiciones 1-2 y 3-2, se hace:
\[F1 + 37/7 \cdot F2 \rightarrow F1 \text{ y } F3 – 2/7 \cdot F2 \rightarrow F3\]
\[\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\ \ \ \ \ \begin{matrix}37/11&5/11\\7/11&-5/11\\-2/11&3/11\\\end{matrix}\ \ \left|\ \ \ \begin{matrix}565\\35\\9\\\end{matrix}\right.\right) \]
| \(\mathbf{B}\) | \(\mathbf{s}\) | \(\mathbf{m}\) | \(\mathbf{x_3}\) | \(\mathbf{x_4}\) | \(\mathbf{R}\) |
| \(1\) | \(0\) | \(0\) | \(37/11\) | \(5/11\) | \(565\) |
| \(0\) | \(1\) | \(0\) | \(7/11\) | \(-5/11\) | \(35\) |
| \(0\) | \(0\) | \(1\) | \(-2/11\) | \(3/11\) | \(9\) |
Aquí se llegó al resultado óptimo, dado que no quedan coeficientes negativos en la primera fila. Ese resultado óptimo es:
\[\begin{gather*} B = 565\\ s = 35\\ m = 9\\\ x_3 = x_4 = 0 \end{gather*} \]
Por supuesto, es la misma solución a la que se había llegado oportunamente. Pero este método sirve para una mayor cantidad de variables. Y es fácilmente programable para que los cálculos los haga una computadora.
En el siguiente sitio se explica el uso del Sistema Simplex a través de la resolución de un problema.
<http://thales.cica.es/rd/Recursos/rd98/Matematicas/29/simplex.html>
En el siguiente video el Profesor Marcel Ruiz resuelve paso a paso un problema de maximización, utilizando el Método Simplex:
Encuentre el máximo de la función \(B = 2 \cdot x + 3 \cdot y\), sujeta a las siguientes restricciones:
\[ \begin{gather*} 2 \cdot x + y \leq 800\\ x + 3 \cdot y \leq 900\\ y – x \leq 100 \end{gather*} \]
En este problema ya se tiene la expresión del modelo matemático. Para utilizar el método Simplex, se reescriben la función objetivo y las inecuaciones, utilizando variables de holgura, aquí serán \(h_1\), \(h_2\) y \(h_3\)
\[ \begin{gather*} B – 2 \cdot x - 3 \cdot y = 0\\ 2 \cdot x + y + h_1 = 800\\ x + 3 \cdot y + h_2 = 900\\ -x + y + h_3 = 100 \end{gather*} \]
La primera tabla Simplex queda así:
| \(\mathbf{B}\) | \(\mathbf{x}\) | \(\mathbf{y}\) | \(\mathbf{h_1}\) | \(\mathbf{h_2}\) | \(\mathbf{h_3}\) | \(\mathbf{R}\) |
| \(1\) | \(-2\) | \(-3\) | \(0\) | \(0\) | \(0\) | \(0\) |
| \(0\) | \(2\) | \(1\) | \(1\) | \(0\) | \(0\) | \(800\) |
| \(0\) | \(1\) | \(3\) | \(0\) | \(1\) | \(0\) | \(900\) |
| \(0\) | \(-1\) | \(1\) | \(0\) | \(0\) | \(1\) | \(100\) |
Se comienza a trabajar por variable cuyo coeficiente en la primera ecuación es menor. Como \(-3 < -2\), se utilizará la \(y\).
Para elegir en qué fila se buscará que la y tenga coeficiente 1, se dividen los resultados por sus coeficientes positivos:
\(\begin{align*} &\text{De la fila 2 es } 800 / 1 = 800\\ &\text{De la fila 3, } 900 / 3 = 300\\ &\text{De la fila 4, } 100 / 1 = 100\\ \end{align*} \)
Como 100 es el menor valor, se buscará utilizar la fila 4 para operar. Ya hay un 1 en la posición 4-3. Para anular el resto de esta columna, se hace:
\[\begin{gather*} F´1 = F1 + 3 \cdot F4\\ F´2 = F2 – F4\\ F´3 = F3 – 3 \cdot F4 \end{gather*} \]
Así, se obtiene la segunda tabla, en la que ya se hicieron las divisiones correspondientes a la variable x, cuyo coeficiente en la primera fila, es negativo:
| \(\mathbf{B}\) | \(\mathbf{x}\) | \(\mathbf{y}\) | \(\mathbf{h_1}\) | \(\mathbf{h_2}\) | \(\mathbf{h_3}\) | \(\mathbf{R}\) |
| \(1\) | \(-5\) | \(0\) | \(0\) | \(0\) | \(3\) | \(300\) |
| \(0\) | \(3\) | \(0\) | \(1\) | \(0\) | \(-1\) | \(700\) |
| \(0\) | \(4\) | \(0\) | \(0\) | \(1\) | \(-3\) | \(600\) |
| \(0\) | \(-1\) | \(1\) | \(0\) | \(0\) | \(1\) | \(100\) |
\[\begin{gather*} 700/3=233,33\\ 600/4=150\\ coeficiente\ negativo \end{gather*} \]
Como en la fila 4 la \(x\) tiene coeficiente negativo, no se realiza la división. El menor cociente es 150, en la fila 3. Por eso, ahora se busca obtener un 1 en la posición 3-2, dividiendo toda la fila por \(4: F´2 = F2/4\)
| \(\mathbf{B}\) | \(\mathbf{x}\) | \(\mathbf{y}\) | \(\mathbf{h_1}\) | \(\mathbf{h_2}\) | \(\mathbf{h_3}\) | \(\mathbf{R}\) |
| \(1\) | \(-5\) | \(0\) | \(0\) | \(0\) | \(3\) | \(300\) |
| \(0\) | \(3\) | \(0\) | \(1\) | \(0\) | \(-1\) | \(700\) |
| \(0\) | \(1\) | \(0\) | \(0\) | \(0,25\) | \(-0,75\) | \(150\) |
| \(0\) | \(-1\) | \(1\) | \(0\) | \(0\) | \(1\) | \(100\) |
Ahora se procede a anular el resto de la columna 2, mediante las siguientes operaciones:
\[\begin{gather*} F´1 = F1 + 5 \cdot F3\\ F´2 = F2 – 3 \cdot F3\\ F´4 = F4 + F3 \end{gather*}\]
Y se obtiene la siguiente tabla:
| \(\mathbf{B}\) | \(\mathbf{x}\) | \(\mathbf{y}\) | \(\mathbf{h_1}\) | \(\mathbf{h_2}\) | \(\mathbf{h_3}\) | \(\mathbf{R}\) |
| \(1\) | \(0\) | \(0\) | \(0\) | \(1,25\) | \(-0,75\) | \(1050\) |
| \(0\) | \(0\) | \(0\) | \(1\) | \(-0,75\) | \(1,25\) | \(250\) |
| \(0\) | \(1\) | \(0\) | \(0\) | \(0,25\) | \(-0,75\) | \(150\) |
| \(0\) | \(0\) | \(1\) | \(0\) | \(0,25\) | \(0,25\) | \(250\) |
Aquí todavía queda un coeficiente negativo en la primera fila: el que corresponde a la variable de holgura \(h_3\).
Para decidir con qué fila se trabajará, se realizan las divisiones de los resultados por sus coeficientes postitivos:
En la fila 2 es \(250 / 1,25 = 200\)
La fila 3 no se considera, pues el coeficiente de \(h_3\) es negativo.
En la fila 4 es \(250 / 0,25 = 1000\)
Como el menor valor es \(200\), se utiliza la fila 2. Y para lograr un 1 en la posición 2-6, se reemplaza \(F´2 = F2 / 1,25:\)
| \(\mathbf{B}\) | \(\mathbf{x}\) | \(\mathbf{y}\) | \(\mathbf{h_1}\) | \(\mathbf{h_2}\) | \(\mathbf{h_3}\) | \(\mathbf{R}\) |
| \(1\) | \(0\) | \(0\) | \(0\) | \(1,25\) | \(-0,75\) | \(1050\) |
| \(0\) | \(0\) | \(0\) | \(0,8\) | \(-0,6\) | \(1\) | \(200\) |
| \(0\) | \(1\) | \(0\) | \(0\) | \(0,25\) | \(-0,75\) | \(150\) |
| \(0\) | \(0\) | \(1\) | \(0\) | \(0,25\) | \(0,25\) | \(250\) |
Y para anular el resto de la sexta columna, es:
\[\begin{gather*} F´1 = F1 + 0,75 \cdot F2\\ F´3 = F3 + 0,75 \cdot F2\\ F´4 = F4 – 0,25 \cdot F2 \end{gather*}\]
Con lo que se obtiene:
| \(\mathbf{B}\) | \(\mathbf{x}\) | \(\mathbf{y}\) | \(\mathbf{h_1}\) | \(\mathbf{h_2}\) | \(\mathbf{h_3}\) | \(\mathbf{R}\) |
| \(1\) | \(0\) | \(0\) | \(0,6\) | \(0,8\) | \(0\) | \(1200\) |
| \(0\) | \(0\) | \(0\) | \(0,8\) | \(-0,6\) | \(1\) | \(200\) |
| \(0\) | \(1\) | \(0\) | \(0,6\) | \(-0,2\) | \(0\) | \(300\) |
| \(0\) | \(0\) | \(1\) | \(-0,2\) | \(0,4\) | \(0\) | \(200\) |
Esta es la tabla final, pues ya no hay coeficientes negativos en la primera fila.
El valor máximo de \(B\) es \(1200\), según queda expresado en la columna de los resultados de la primera fila. Y se logra cuando \(x\) es \(300\), valor que aparece en la tercera fila, y cuando \(y\) es \(200\), dato que se halla en la cuarta fila. Además, la variable de holgura \( h_3\) vale \(200\), de acuerdo con la información de la segunda fila. Esto significa que en la tercera inecuación, la diferencia entre \(y\) y \(x\) es \(200\) unidades menor que \(100\).
Resuelva este mismo ejemplo, utilizando el método gráfico.
En estos pocos ejemplos no resulta fácil apreciar la practicidad del método Simplex. Pero cuando intervienen más variables, no es posible utilizar el método gráfico y el método analítico resulta engorroso. Sin embargo, los problemas más complejos en los que este método demuestra su potencia, exceden al nivel introductorio de este material.