4. Las ideas básicas del cálculo
Objetivos
- Utilizar el concepto de límite de una función para analizar su continuidad en un valor dado y para calcular su derivada.
- Describir la gráfica de una función, utilizando derivadas.
- Aplicar las propiedades de las derivadas de funciones a la solución de problemas económicos.
Introducción
En esta unidad se analizarán funciones a partir de sus fórmulas.
El método que se seguirá tiene raíces en ideas que se desarrollaron desde el siglo III a. C., pero empezó a formalizarse recién en el siglo XVII. Isaac Newton desde Inglaterra y Gottfried Leibniz nacido en Leipzig (actual territorio de Alemania), quienes investigaron independientemente, son considerados sus creadores. Durante los siglos XIX y XX matemáticos como Karl Weierstrass, Georg Riemann y David Hilbert contribuyeron para lograr su actual axiomatización.
Aquí se dará un tratamiento intuitivo de los temas, teniendo presente el contexto de esta materia en las carreras universitarias en las que se incluye.
4.1. Límites de funciones
En la unidad anterior se trató el tema de las funciones racionales y se enfatizó en la necesidad de comenzar buscando su dominio porque podía ser que no todos los números reales tuvieran imagen. Ese problema se abordará en el siguiente ejemplo:
Grafique la función \(f\left(x\right)=\frac{x^3+7x^2+14x+8}{x^2+3x-4} \)
Como se recomendó en la Unidad 3, es necesario hallar el dominio de las funciones antes de ocuparse de graficar. Al tratarse de una función racional, el denominador no se puede anular, por lo que:
\[x^2+3x-4\neq0 \]
Cuando se resuelve la ecuación \(x^2+3x-4=0 \) se obtienen los valores que deberán extraerse del Dominio. En este caso es \( Dom= \mathbb{R} - \{-4;1\} \)
Debido a que la función no está definida en \(x=-4\ \) y en \(x=1\) es importante averiguar qué sucede cerca de esos valores. Hay varias maneras de lograrlo. Aquí se explicarán dos.
-
Construir una tabla de valores de la función en la que se incorporarán cifras de \(x\) en las proximidades de \(x=-4\) y de \(x=1\)
Tabla 4.1. Límites de una función racional
x f(x) -6 -2,85714286 -5 -2 -4,5 -1,59090909 -4,1 -1,27647059 -4,01 -1,20760479 -4 No tiene imagen -3,99 -1,19240481 -3,9 -1,1244898 -3,5 -0,83333333 -3 -0,5 -2 0 x f(x) -1 0 0 -2 0,5 -7,5 0,9 -55,1 0,99 -595,01 1 No tiene imagen 1,01 605,1 1,1 65,1 1,5 17,5 2 12 3 10 Con estos datos se puede comenzar a graficar, como se muestra en el Gráfico 4.1. en el que se ubicaron los pares ordenados de la tabla 4.1. en un diagrama cartesiano.
Gráfico 4.1.+Límites de una función racional (primera parte)

En la escala de este gráfico, no llegan a entrar los valores que la función toma en las cercanías de \(x=1\). Sucede que allí la función presenta una asíntota vertical. En cambio, en las proximidades de \(x=-4\), hay una acumulación de puntos que pertenecen a la gráfica de la función. Si se buscara más precisión, se podría seguir ampliando la tabla en la zona aún más cercana a \(x=-4\) . Las imágenes de esos valores son cada vez más cercanos a \( y=-1,2 \).
En este caso se dice que el límite de \(f(x)\) cuando \(x\) tiende a \(-4\) es \(-1,2\). Se anota así:
\[\lim\limits_{x\rightarrow-4}f\left(x\right)=-1,2\]
LLeer con atención+El límite de una función \(f(x)\) cuando el valor de \(x\) tiende a un cierto valor \(a\) es \(L\) cuando \(f(x)\) es arbitrariamente cercano a \(L\) para toda \(x\) suficientemente cercana a (pero distinta de) \(a\).
Se anota:
\[\lim\limits_{x\rightarrow a}f\left(x\right)=L\]
Es importante notar que \(x\) no toma nunca el valor de \(a\), sino que se acerca tanto como se desee a él.
Con este análisis numérico, se encontró que \(x=1\) en la función presenta una asíntota vertical. Y que en \(x=-4\) , la gráfica se aproxima tanto como se desee al punto de coordenadas \((-4;-1,2)\) .
-
Ahora veremos un tratamiento algebraico de la fórmula de la función que nos permitirá llegar a las mismas conclusiones que con tabla, pero con menos necesidad de cálculos.
La fórmula de la función se puede factorizar de la siguiente manera:
\[\frac{{x^3+7x}^2+14x+8}{x^2+3x-4}=\frac{\left(x+4\right)\cdot (x+2)\cdot (x+1)}{\left(x+4\right).(x-1)}\]
En este paso es importante evitar cancelar el factor \((x+4)\). Si así se hiciera, se estaría cambiando la función, porque se modifica el dominio.
Sin embargo, en la definición de límite dice que se busca qué pasa cuando x “tiende” a un cierto valor, se “acerca” a ese valor, pero sin “tocarlo”. Entonces, si se calcula el límite cuando x tiende a \(-4\) , la x no va a tomar ese valor, que no pertenece al dominio. Por lo tanto, en ese caso vale “simplificar” la expresión anterior:
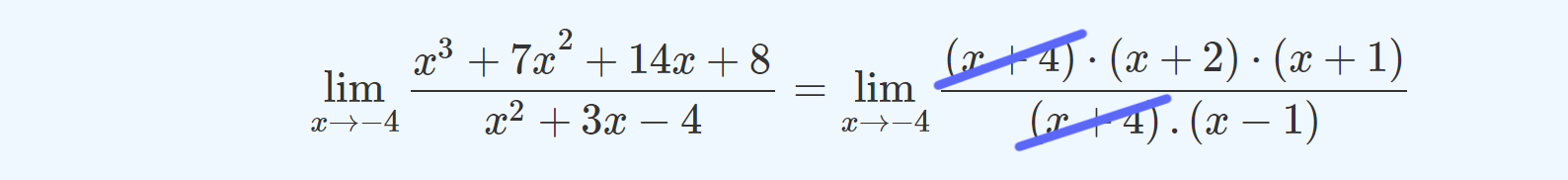
Es importante notar que en la expresión anterior se especifica que se está calculando el límite. Por eso es válida la simplificación. Después de hacerla, se pueden realizar los cálculos porque ya no habrá un cero en el denominador:
\[\lim\limits_{x\rightarrow-4}\frac{(x+2)\cdot (x+1)}{x-1}=\frac{-2\cdot (-3)}{-5}=\frac{6}{-5}=-1,2\]
Esto significa que, en la gráfica de la función, “falta el punto” \(\left(-4;-1,2\right)\). No se puede reemplazar el \(-4\) en la fórmula de la función, pero la gráfica pasa muy, muy cerca de este punto que “falta”.
Ahora veamos qué pasa cuando se calcula el límite para x tendiendo a 1:
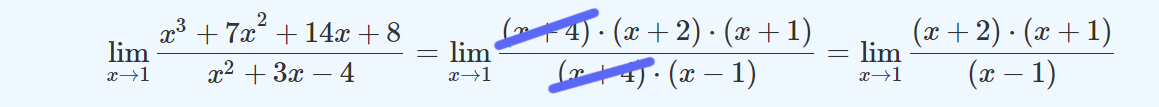
En este caso, la imposibilidad de efectuar la división persiste. Por eso se dice que no existe el límite. Se indica de la siguiente manera:
\[\lim\limits_{x\rightarrow1}\frac{(x+2)\cdot(x+1)}{x-1}=\infty\]
Y significa que la función presenta una asíntota vertical en \(x=1\).
Con la información que se obtuvo aquí (de dos maneras distintas) se puede realizar el gráfico, que queda como se muestra a continuación:
Gráfico 4.2.+Límites de una función racional (segunda parte)
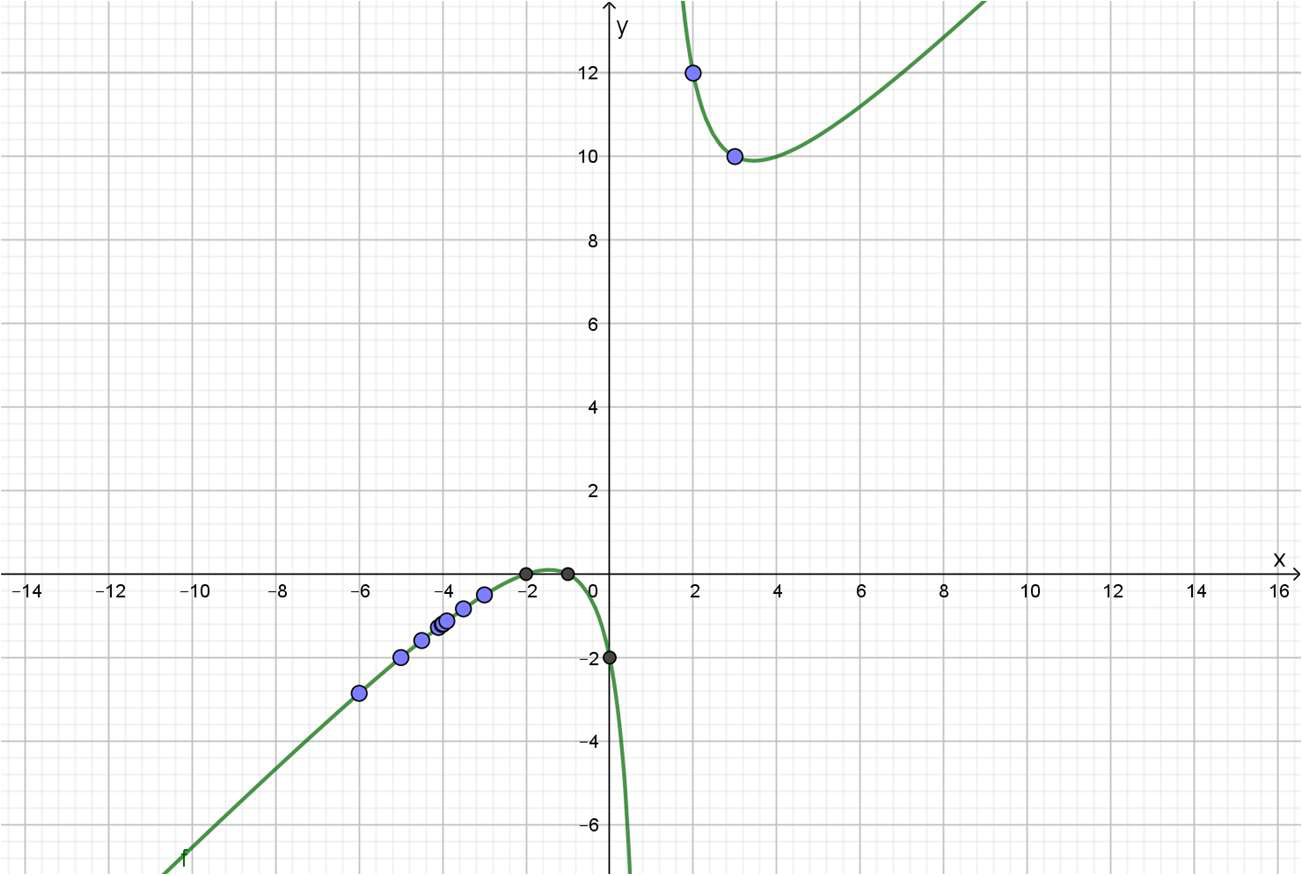
Este gráfico, realizado en GeoGebra, no toma en cuenta que falta el punto \(\left(-4;-1,2\right)\) . Por ese motivo, es necesario agregar un círculo verde con relleno blanco “a mano” con “insertar formas” de Word. Si bien el gráfico que realiza Geogebra no muestra que falta un punto, en cambio, sí permite apreciar la asíntota, debido a que ella lo divide en dos "ramas".
Límites de una función racional parte final

4.1.1. El número e
Calcule el límite para x tendiendo a cero de la siguiente función:
\[f\left(x\right)=\left(1+x\right)^\frac{1}{x}\]
Como puede apreciarse, esta función no está definida en \(x=0\). Y por no tratarse de una función racional, el límite pedido no se puede hallar por los métodos algebraicos utilizados en el ejemplo anterior. Por ese motivo, se prepara una tabla de valores acercándose a cero, tanto “por la izquierda”, con valores de \(x\) negativos, como “por la derecha”, con valores de \(x\) positivos, muy cercanos a cero. En la siguiente tabla, que se completó utilizando Excel, se aprecia que a medida que x tiende a cero, la imagen tiende a 2,71828…:
| x | f(x) |
|---|---|
| -0,5 | 4 |
| -0,3 | 3,28352152 |
| -0,2 | 3,05175781 |
| -0,1 | 2,86797199 |
| -0,01 | 2,73199903 |
| -0,001 | 2,71964222 |
| -0,0001 | 2,71841776 |
| -0,00001 | 2,71829542 |
| -0,000001 | 2,71828319 |
| 0 | No existe la imagen |
| 0,000001 | 2,71828047 |
| 0,00001 | 2,71826824 |
| 0,0001 | 2,71814593 |
| 0,001 | 2,71692393 |
| 0,01 | 2,70481383 |
| 0,1 | 2,59374246 |
| 0,2 | 2,48832 |
El verdadero valor del límite es un número de los denominados trascendentes, con infinitas cifras decimales y con el que ya se trabajó en la unidad anterior. El límite en este caso es el famoso número e que se utiliza como base de la función exponencial \(e^x\) o en la base de los logaritmos neperianos y de hecho, este límite, es una de las formas de definir este número:
\[\lim\limits_{x\rightarrow0}{\left(1+x\right)^\frac{1}{x}}=e\]
En <https://soymatematicas.com/numero-e/> se pueden encontrar algunas referencias a la historia del número e y algunos datos curiosos sobre él. En <https://economipedia.com/definiciones/logaritmo-natural.html> se muestra su relación con los logaritmos neperianos o naturales (que se simbolizan ln, las dos primeras letras de esas palabras).
4.2. Continuidad de funciones
La idea de continuidad es muy intuitiva: una función es continua cuando se puede graficar completa en un solo trazo, sin “levantar el lápiz”. Es decir, cuando no presenta “saltos” o “puntos faltantes”.
Por ejemplo, la función del Ejemplo 4.1. no es continua porque “se corta” en \(x=1\), presentando dos “ramas” y, además, no existe la imagen ni de \(x=-4\) ni de \(x=1\) (al graficar, es necesario “levantar el lápiz” para no “tocar” ni el punto \(\left(-4;-1,2\right)\) ni la recta \(x=1)\).
En cambio, las funciones polinómicas y las funciones exponenciales, que se estudiaron en la unidad anterior, son continuas.
Para que una función sea continua, deberá serlo en todos los puntos de acumulación de su dominioN.
Y, para que una función sea continua en un punto \(x=a\) , deberá cumplir con:
-
que exista la imagen del número \(a\) por la función \(f\):
\[f(a)\]
-
que exista el límite de \(f(x) \) cuando \(x\) tiende a \(a\):
\[\lim\limits_{x\rightarrow a}{f(x)}\]
-
que la imagen de \(a\) y el límite de \(f(x)\), cuando \(x\) tiende a \(a\), sean iguales:
\[\lim\limits_{x\rightarrow a}{f(x)}\ =f(a)\]
Punto de acumulación (también denominado punto límite o punto de aglomeración) de un conjunto es un punto que está arbitrariamente próximo a ese conjunto sin pertenecer necesariamente a él.
Cuando una función no es continua en un determinado punto de acumulación del dominio, se dice que allí esa función es discontinua.
Si en una función racional hay que excluir valores del dominio, la función no será continua, porque en esos valores no se cumple la condición a. de la definición anterior.
En esos valores habrá discontinuidad de la función.
Las discontinuidades pueden ser:
- discontinuidad evitable: cuando existe el límite de la función en el valor para el cual no está definida. Así, en el Ejemplo 4.1., hay una discontinuidad evitable en \(x=-4\)
- discontinuidad esencial: cuando no existe el límite de la función en el valor para el cual no está definida. En el Ejemplo 4.1. hay una discontinuidad esencial en \(x=1\)
Encuentre el dominio, calcule los límites cuando x tiende a los valores que de él deben excluirse, clasifique las discontinuidades que allí se presentan y grafique las siguientes funciones:
- \(f\left(x\right)=\frac{x^2-1}{2x-2}\)
- \(g\left(x\right)=\frac{x+3}{x^2+4x+3}\)
4.3. Derivadas
En esta sección se estudiarán las derivadas de las funciones, que es uno de los temas del análisis matemático más utilizados en Economía.
La idea es averiguar, a partir de su fórmula, si una función, en uno de sus puntos, crece o decrece.
Si la función fuera lineal esa tarea resultaría sencilla, porque el signo de la pendiente brinda esa información, como se ha estudiado en el punto 3.3. de la unidad anterior. Si la función no fuera lineal, se pueden aprovechar las propiedades de las rectas utilizando los cocientes incrementales, que ya se han definido y se verán a continuación con mayor detalle.
4.3.1. Cociente incremental
Con el objetivo de analizar el crecimiento (o decrecimiento) de una función en un punto \((x_1;f\left(x_1\right))\), se considera otro punto, también perteneciente a la gráfica de la función \((x_2;f\left(x_2\right))\). A la pendiente del segmento que los une se la denomina cociente incremental, que también se llama tasa de variación media o tasa de variación promedio, y viene dado por la siguiente fórmula:
\[\frac{\Delta y} {\Delta x}= \frac{f(x_2)-f(x_1)}{x_2-x_1}\]
A continuación, en los gráficos se puede apreciar que, cuando la función es creciente, el cociente incremental probablemente tendrá signo positivo, y negativo en caso contrario.
Cociente incremental positivo
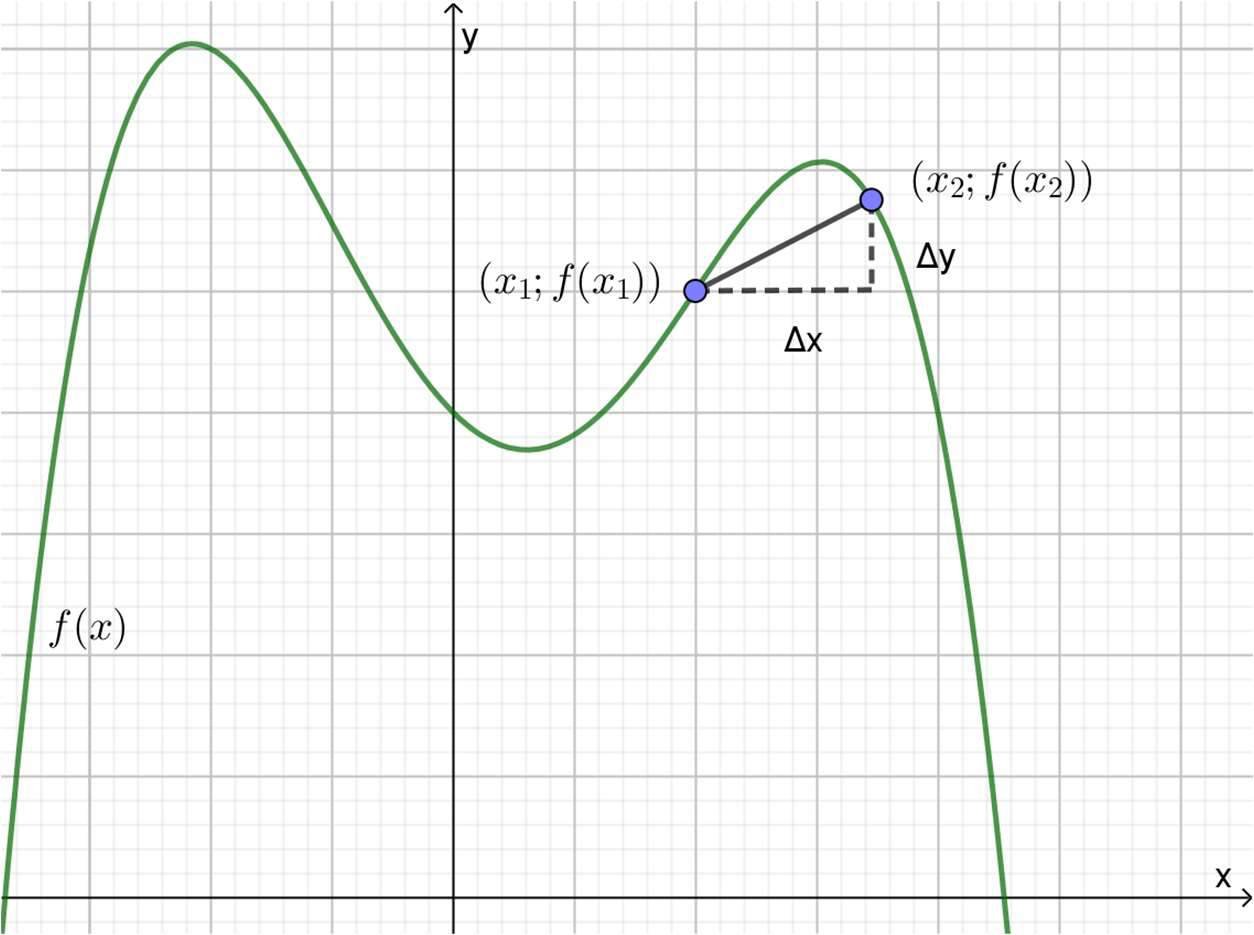
Cociente incremental negativo
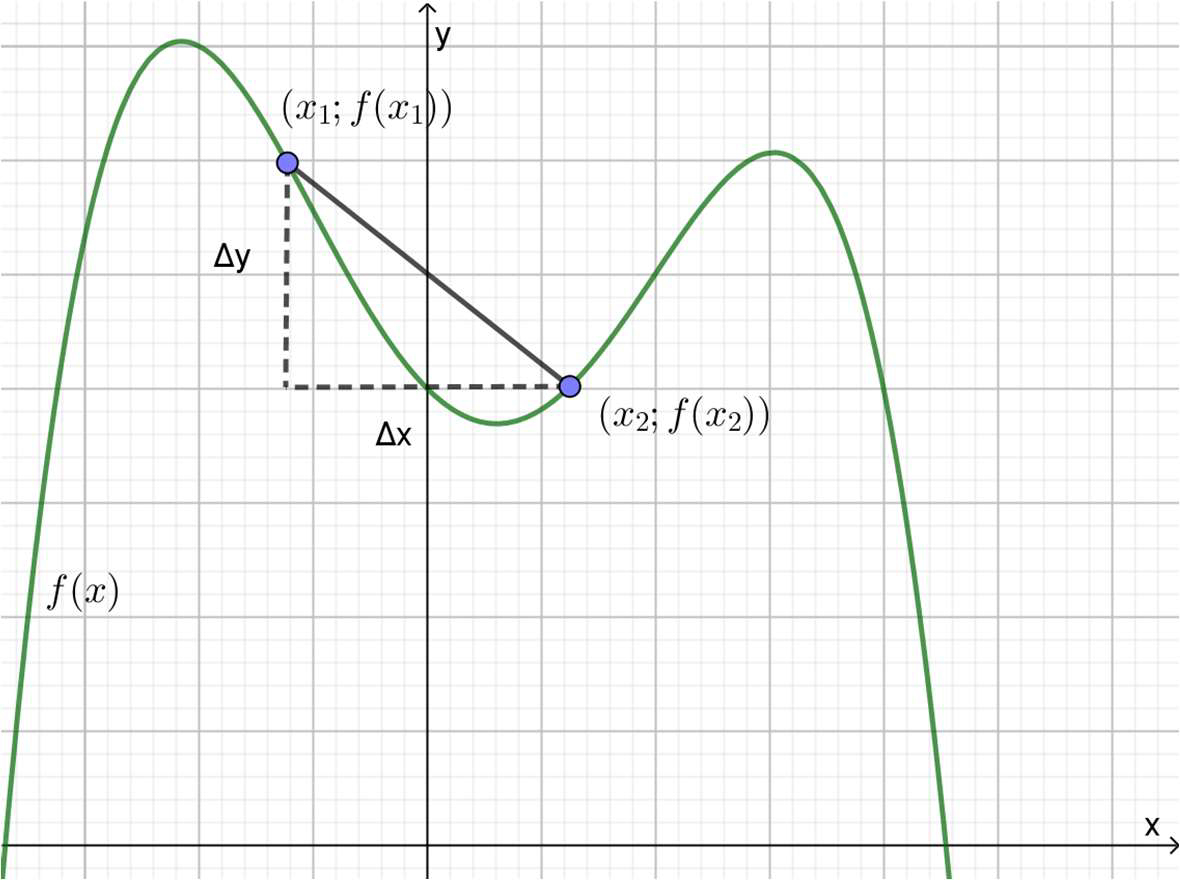
En ambos ejemplos, \(\Delta x\) es positivo. Entonces, el signo de \(\Delta y\) determina el del cociente incremental.
Para enfatizar que el estudio se hace en el punto \((x_1;f\left(x_1\right))\), la fórmula del cociente incremental se puede reescribir teniendo en cuenta que \(x_2=x_1+\Delta x \), por lo que queda:
\[\frac{\Delta y} {\Delta x}=\frac{f(x_2)-f(x_1)}{x_2-x_1}=\frac{f(x_1+ \Delta x) -f(x_1)}{(x_1+ \Delta x)-x_1}=\frac{f(x1+ \Delta x)-f(x_1)}{\Delta x}\]
4.3.2. Derivada de una función en un punto
En el apartado anterior se afirmó que “cuando la función es creciente, el cociente incremental probablemente tendrá signo positivo, y negativo en caso contrario”. ¿Por qué probablemente? Porque la función \(g(x)\), graficada en rojo en el siguiente diagrama, presenta el mismo cociente incremental de uno de los gráficos anteriores. Si bien ese cociente incremental es positivo, \(g(x)\) es decreciente en el punto \((x_1;f(x_1 ))\).
Cociente incremental confuso

Para evitar este inconveniente, lo que se hace es buscar un punto de intersección de la recta con la función, muy próximo al punto en que se investiga el crecimiento. La idea es que la diferencia entre \(x_1\) y \(x_1+∆x\) sea infinitamente pequeña. En ese caso, para la función graficada en verde el cociente seguirá siendo positivo y para la función en rojo, en cambio, será negativo.
Esto se logra calculando el límite cuando \(\Delta x \) tiende a cero del cociente incremental.
Se define entonces la derivada de \(f(x) \) en el punto de abscisa \(x_1\) , y se simboliza \(f\ `\left(x_1\right)\ o\ {\ \left. \frac{dy}{dx}\right|}_{x_1}\) de la siguiente manera:
\[f\ `\left(x_1\right)\ = {\ \left. \frac{dy}{dx}\right|}_{x_1}= \lim\limits_{\Delta x\rightarrow 0} \frac{f(x_1+\Delta x)-f(x_1)}{\Delta x}\]
El signo de este número indica el crecimiento o decrecimiento de la función \(f(x)\) en el punto de abscisa \(x_1\). Indica entonces la variación instantánea de \(f(x)\) en ese lugar. Hay dos maneras de simbolizar la derivada (y casi todos los conceptos del Análisis Matemático) porque, como se explicó con anterioridad, estas ideas fueron desarrolladas por dos autores diferentes en forma simultánea (y sin coordinación entre ellos).
Investigue si la función \(f\left(x\right)=x^2\) es creciente o decreciente en el punto de abscisa \(x=-2\).
Esta sencilla función cuadrática tiene una gráfica muy conocida, por la que ya sabemos que es decreciente en ese punto. Pero aquí se utilizará la derivada para comprobarlo.
El punto \((x_1;f\left(x_1\right))\) en este caso es \(\left(-2;f\left(-2\right)\right)=(-2;4)\).
Para encontrar la derivada de \(f(x)\) allí, se deberá calcular, entonces:
\[f\ `\left(-2\right)={\ \left. \frac{dy}{dx}\right|}_{-2}= \lim\limits_{\Delta x\rightarrow 0} \frac{f(-2+\Delta x)-f(-2)}{\Delta x}\]
Conviene calcular \(f(-2+\Delta x)=(-2+\Delta x)^2=4-4\Delta x+(\Delta x)^2\) aparte y luego reemplazar:
\[f\ `\left(-2\right)={\ \left. \frac{dy}{dx}\right|}_{-2}= \lim\limits_{\Delta x\rightarrow 0} \frac{4-4\Delta x+(\Delta x)^2-4}{\Delta x} =\lim\limits_{\Delta x\rightarrow 0} \frac{-4\Delta x+(\Delta x)^2}{\Delta x}\]
Este límite es indeterminado, por lo que se factoriza el numerador:
\[f\ `\left(-2\right)={\ \left. \frac{dy}{dx}\right|}_{-2}= \lim\limits_{\Delta x\rightarrow 0} \frac{\Delta x\cdot (-4+\Delta x)}{\Delta x}=\lim\limits_{\Delta x\rightarrow 0}-4+\Delta x=-4\]
Por lo tanto, como el signo de la derivada de la función en el punto de abscisa \(x=-2\) es negativo, la gráfica de la función es decreciente en ese punto.
4.3.3. Función derivada de una función
Para analizar una función sería imposible realizar el procedimiento del Ejemplo 4.3. para cada valor del dominio. Por eso, se define la derivada de la función, para todo valor de \(x\) de ese conjunto:
La derivada de \(f(x) \) en el punto de abscisa \(x\), se simboliza \(f\ `\left(x\right) \text{ o } \frac{dy}{dx}\) es:
\[f\ `\left(x\right)= \frac{dy}{dx}= \lim\limits_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \]
Este número indica el crecimiento o decrecimiento de la función \(f(x)\) en cualquier punto \(x\) del dominio de la función. Indica entonces la variación instantánea de \(f(x)\) en cada punto. Geométricamente es la pendiente de la recta tangente a la función en el punto de abscisa \(x\).
En <https://www.youtube.com/watch?t=6&v=RgJ5slNXBOM&feature=youtu.be> una de las autoras de este texto explica la definición de derivada, a partir de la interpretación geométrica.
Encuentre la función derivada de \(f\left(x\right)=x^2\).
Para esto hay que calcular \(f\ ´(x)= \frac{dy}{dx}= \lim\limits_{\Delta x\rightarrow 0} \frac {f(x+\Delta x)-f(x)}{\Delta x} \). Conviene calcular aparte \(f(x+\Delta x)=(x+\Delta x)^2=x^2+2\cdot x\cdot \Delta x+(\Delta x)^2\) y luego reemplazar:
\[ \begin{multline*} f\ ´(x)=\frac{dy}{dx}=\lim\limits_{\Delta x\rightarrow 0} \frac{x^2+2\cdot x\cdot \Delta x+(\Delta x)^2-x^2}{\Delta x}= \\ = \lim\limits_{\Delta x\rightarrow 0} \frac{\Delta x\cdot (2\cdot x+\Delta x)}{ \Delta x} = \lim\limits_{\Delta x\rightarrow 0} (2\cdot x+\Delta x)=2\cdot x \end{multline*} \]
Entonces, la derivada de la función \(f\left(x\right)=x^2\) es \(f\ ´(x)=2x\).
Con esta fórmula se podría haber hecho el ejercicio anterior inmediatamente: cuando \(x=-2,\ f\ `\left(x\right)=2\cdot \left(-2\right)= -4\) que es el resultado al que ya se había llegado.
4.3.4. Reglas de derivación
A continuación, se demostrarán algunas reglas de derivación que facilitarán aún más la búsqueda de la derivada de una función.
-
La derivada de una función constante \(f(x)=k \) es cero:
\(f ´(x)=\frac{dy}{dx}=\lim\limits_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} =\lim\limits_{\Delta x\rightarrow 0} \frac{k-k}{\Delta x}=\lim\limits_{\Delta x\rightarrow 0} \frac{0}{\Delta x}=0\)
Entonces, si \(\ f\left(x\right)=k,\ f\ ´(x)=0\)
-
La derivada de una suma (o de una resta) de funciones es igual a la suma (o a la resta) de las derivadas de esas funciones:
\[\begin{gather*} \left(f+g\right)´(x)=\frac{d(f+g)}{dx}=\lim\limits_{\Delta x\rightarrow 0} \frac{(f+g)(x+\Delta x)-(f+g)(x)}{\Delta x} = \\ = \lim\limits_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)+g(x+\Delta x)-[f(x)+g(x)]}{\Delta x} = \\ = \lim\limits_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)+g(x+\Delta x)-f(x)-g(x)}{\Delta x} \end{gather*}\]
Esta última expresión se puede reordenar.
\[\begin{gather*} \lim\limits_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)+g(x+\Delta x)-g(x)}{\Delta x}= \\ = \lim\limits_{\Delta x\rightarrow 0} \left[ \frac{f(x+\Delta x)-f(x)}{\Delta x}+ \frac{g(x+\Delta x)-g(x)}{\Delta x} \right]= \\ =\lim\limits_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}+ \lim\limits_{\Delta x\rightarrow 0} \frac{g(x+\Delta x)-g(x)}{\Delta x} = \\ =f´(x)+g´(x) \end{gather*}\]
Realice la demostración correspondiente a la derivada de la resta de funciones:
\[\left(f-g\right)´(x)=\frac{d(f-g)}{dx}=f´(x)-g´(x)=\frac{df}{dx}-\frac{dg}{dx}\]
Las siguientes reglas no se demostrarán, pero son válidas:
-
Derivada de una constante por una función:
\[\left(k\cdot f(x)\right)´=k\cdot f´(x)\]
Con la otra notación sería:
\[\frac{d(k\cdot f)}{dx}=k\cdot\frac{df}{dx}\]
-
Derivada de una potencia:
\[f\left(x\right)=x^n \text{ su derivada es } f´(x)=n\cdot x^{n-1}\]
-
Derivada de un producto de funciones:
\[\left(f\cdot g\right)´(x)=f´(x)\cdot g(x)+f(x)\cdot g´(x)\]
Si se utiliza la otra notación sería:
\[\frac{d(f\cdot g)}{dx}=\frac{df}{dx}\cdot g\left(x\right)+f(x)\cdot\frac{dg}{dx}\]
-
Derivada de un cociente de funciones:
\[\left(\frac{f}{g}\right)´(x)=\frac{f´(x)\cdot g(x)-f(x)\cdot g´(x)}{g(x)^2}\]
Utilizando la otra notación sería:
\[\frac{d\left(\frac{f}{g}\right)}{dx}=\frac{\frac{df}{dx}\cdot g\left(x\right)-f(x)\cdot\frac{dg}{dx}}{{g(x)}^2}\]
-
Derivada de la composición de funciones:
\[\left(f\ o\ g\right)´(x)=f´(g(x)) \cdot g´(x)\]
Utilizando la otra notación sería:
\[\frac{d(fo\ g)}{dx}=\frac{df}{dg}\cdot\frac{dg}{dx}\]
-
Derivada de la función exponencial:
\[\frac{d\left(a^x\right)}{dx}=a^x\cdot\ln{a}\]
Si la base de la función exponencial fuera e, la derivada es:
\[\frac{d\left(e^x\right)}{dx}=e^x\cdot\ln{e}=e^x\]
-
Derivada del logaritmo natural:
\[\frac{d(\ln{x})}{dx}=\frac{1}{x}\]
Derive las siguientes funciones:
- \( f\left(x\right)=x^3-3x^2-9x+4\)
- \( g\left(x\right)=(x^2+3)\cdot\ln{x}\)
- \( h\left(x\right)=\frac{x^2+2x+3}{e^x}\)
- \( i\left(x\right)=8^{4x^2-5}\)
-
\(f\left(x\right)=x^3-3x^2-9x+4\)
Esta función es un polinomio, por lo que hay sumas y restas de potencias. Para derivarla, se utilizarán las reglas 2, 3, 4 y 1, en ese orden:
\[f´(x)=3\cdot x^{3-1}-3\cdot 2\cdot x^{2-1}-9\cdot x^{1-1}+0\]
Solo resta resolver los cálculos:
\[f´(x)=3\cdot x^2-6\cdot x^1-9\cdot x^0+0=3x^2+6x-9\]
-
\( g\left(x\right)=(x^2+3)\cdot\ln{x}\)
Aquí hay un polinomio que multiplica a una función logarítmica. Se utilizará la regla 5, pero antes, se buscarán las derivadas de los factores:
\[\frac{d\left(x^2+3\right)}{dx}=2\cdot x^{2-1}+0=2x\] \[ \frac{d\left(\ln{x}\right)}{dx}=\frac{1}{x}\]
En este último paso, se usó la regla 9.
Entonces, es:
\[g´(x)=2x\cdot ln\ x + (x^2+3)\cdot \frac{1}{x}\]
-
\(\ h\left(x\right)=\frac{x^2+2x+3}{e^x}\)
Esta función es un cociente. Se utilizará la regla 6 y conviene calcular primero las derivadas de las funciones dividendo y divisora. En ese cálculo se usa la regla 8:
\[\frac{d\left(x^2+2x+3\right)}{dx}=2\cdot x^{2-1}+2\cdot x^{1-1}+0=2x+2 \] \[\frac{d\left(e^x\right)}{dx}=e^x\]
Por lo tanto, la derivada de \(h(x)\) será:
\[h´(x)=\frac{(2x+2)\cdot e^x-(x^2+2x+3)\cdot e^x}{(e^x)^2}\]
Esta es la derivada pedida. Pero se puede factorizar esta expresión para lograr una más sencilla:
\[h´(x)=\frac{e^x \cdot \left[ (2x+2)-(x^2+2x+3)\right]} {(e^x)^2}= \frac {(2x+2)-(x^2+2x+3)}{e^x}=\] \[ \frac{2x+2-x^2-2x-3}{e^x}=\frac{-x^2-1}{e^x}\]
Entonces,
\[h´(x)=\frac{-x^2-1}{e^x} \]
-
\(\ i\left(x\right)=8^{4x^2-5} \)
La función \(i(x)\) es una composición entre dos funciones: \(g\left(x\right)=4x^2-5\) y \(f\left(x\right)=8^x\)
\[i\left(x\right)=f\ o\ g(x)\]
Para buscar su derivada, se utilizará la regla 7.
\[\left(f\ o\ g\right)´(x)=f´(g(x))\cdot g´(x)\]
La derivada de la función \(f(x)\) es: \(f´(x)=8^x\cdot ln\ 8 \)
Pero, como es necesario calcularla en \(g(x)\), será: \(f´(g(x))=8^{4x^2-5} \cdot ln\ 8 \)
Falta calcular la derivada de \(g(x)\): \(g´(x)=4\cdot 2\cdot x^{2-1}-0=8x\)
Con estos pasos previos, ya se puede “armar” la derivada pedida:
\[i´(x)=\frac{di}{dx}=8^{4x^2-5} \cdot ln\ 8 \cdot 8x=(8\cdot ln\ 8) \cdot x\cdot 8^{4x^2-5}\]
En el último paso se reordenó la expresión.
Calcule las derivadas de las siguientes funciones:
- \(f(x)=\sqrt[3]{x^4+2x-1}\)
- \(g(x)= ln\ (x^2+x+3)\)
- \(h(x)=\frac{e^x+8}{x^2+2}\)
4.4. Derivadas de orden superior
Hasta aquí se calcularon derivadas de funciones. Pero, a su vez, las derivadas también son funciones. Y, por lo tanto, se pueden volver a derivar. Por ejemplo, la derivada que se obtuvo en el Ejemplo 4.4., \(f´(x)=2x\) puede volver a derivarse y obtenerse la derivada segunda de la función \(f(x) : f´´(x)=\frac{d^2f}{dx^2}=2\).
Esta derivada segunda podría volver a derivarse. Será la derivada tercera. En este caso, sería \(f´´´(x)=\frac{d^3f}{dx^3}=0\).
Obtenga las derivadas segundas de las funciones del Ejemplo 4.5.
-
\(f(x)=x^3-3x^2-9x+4\)
Su derivada es:
\[f´(x)=\frac{df}{dx}=3x^2+6x-9\]
La derivada segunda es:
\[f´´(x)=\frac{d^2f}{dx^2}=6x+6\]
-
\(g(x)=(x^2+3)\cdot \ln{x}\)
La derivada es:
\[g´(x)=2x\cdot ln\ x +(x^2+3)\cdot \frac{1}{x}\]
Para calcular la derivada segunda es importante notar que esta función tiene dos términos y en cada uno de ellos hay un producto. En la siguiente tabla se calculan las derivadas de cada factor, para luego “armar” la derivada segunda, de acuerdo con la regla de derivación del producto:
Tabla 4.3. Derivadas ejemplo 4.6. b) Función Derivada \(2x\) \(2\) \(\ln{x}\) \(\frac{1}{x}\) \(x^2+3\) \(2x\) \(\frac{1}{x}=x^{-1}\) \(-1\cdot x^{-2}=-\frac{1}{x^2}\) \[\begin{gather*} g´´(x)=\frac{d^2g}{dx^2}=2\cdot ln\ x +2x\cdot \frac{1}{x}+2x\cdot \frac{1}{x}+(x^2+3)\cdot \left(-\frac{1}{x^2}\right)= \\ g´´(x)=\frac{d^2g}{dx^2}=2\cdot ln\ x +2+2+x^2 \cdot \left(-\frac{1}{x^2}\right)+3\cdot \left(-\frac{1}{x^2}\right)= \\ g´´(x)=\frac{d^2g}{dx^2}=2\cdot ln\ x +2+2-1+3\cdot \left(-\frac{1}{x^2}\right) =2\cdot ln\ x -\frac{3}{x^2} +3 \end{gather*} \]
En los últimos pasos se resolvieron cálculos y se reordenó el resultado.
-
\( h(x)=\frac{x^2+2x+3}{e^x}\)
Su derivada es:
\[h´(x)=\frac{-x^2-1}{e^x}\]
Es un cociente, entonces, para volver a derivar, se utilizará la regla correspondiente. Nuevamente, conviene calcular primero las derivadas del divisor y del dividendo y luego escribir la derivada segunda. Aquí se hará directamente:
\[h´´(x)=\frac{d^2h}{dx^2}=\frac{-2x\cdot e^x-(-x^2-1)\cdot e^x}{(e^x)^2}=\frac{x^2-2x+1}{e^x}\]
-
\(\ i\left(x\right)=8^{4x^2-5}\)
Su derivada es:
\[i´(x)=\frac{di}{dx}=(8\cdot ln\ 8) \cdot x\cdot 8^{4x^2-5}\]
Aquí hay un producto de dos funciones. En la siguiente tabla se buscan sus derivadas antes de expresar la derivada segunda:
Tabla 4.4. Derivadas ejemplo 6 d) Función Derivada \(\left(8\cdot\ln{8}\right)\cdot x\) \(\left(8\cdot\ln{8}\right)\) \(8^{4x^2-5}\) \(\left(8\cdot\ln{8}\right)\cdot x\cdot8^{4x^2-5}\) Entonces, será:
\[\begin{gather*} i´´(x)=\frac{d^2i}{dx^2}=(8\cdot ln\ 8)\cdot 8^{4x^2-5}+(8\cdot ln\ 8) \cdot x\cdot (8\cdot ln\ 8) \cdot x\cdot 8^{4x^2-5}= \\ =(8\cdot\ln\ 8)\cdot 8^{4x^2-5}\cdot (1+8\cdot \ln{8}\cdot x^2) \end{gather*} \]
4.4.1. Derivada segunda y concavidad
Gráficamente, el signo de la derivada segunda informa sobre la concavidad de una función en cada punto.
Clasificaremos a las concavidades en “hacia arriba” o “hacia abajo”, según el signo de la derivada segunda en cada punto. El detalle se encuentra en el Cuadro 4.1.

En el Gráfico 4.7. hay un ejemplo de cada caso:

Para profundizar sobre la interpretación geométrica de la segunda derivada, se puede consultar la siguiente página: <http://thales.cica.es/rd/Recursos/rd97/UnidadesDidacticas/deriva6.htm>
En el siguiente video explicamos la interpretación geométrica de la derivada segunda.
El geogebra que se utiliza en el video es el siguiente:
4.5. Polinomios de Taylor
En esta sección se utilizarán los conceptos desarrollados hasta aquí, para aproximar el valor de funciones en las cercanías de cierto valor dado.
Se comenzará por la aproximación lineal.
4.5.1. Aproximación lineal
Cuando se conocen las coordenadas de un punto \((a;f(a))\) perteneciente a la gráfica de una función y se desea conocer el valor que toma la función en las cercanías del valor de \(x = a\), se puede utilizar la aproximación lineal.
Gráficamente, la situación es la que se presenta en el Gráfico 4.8.
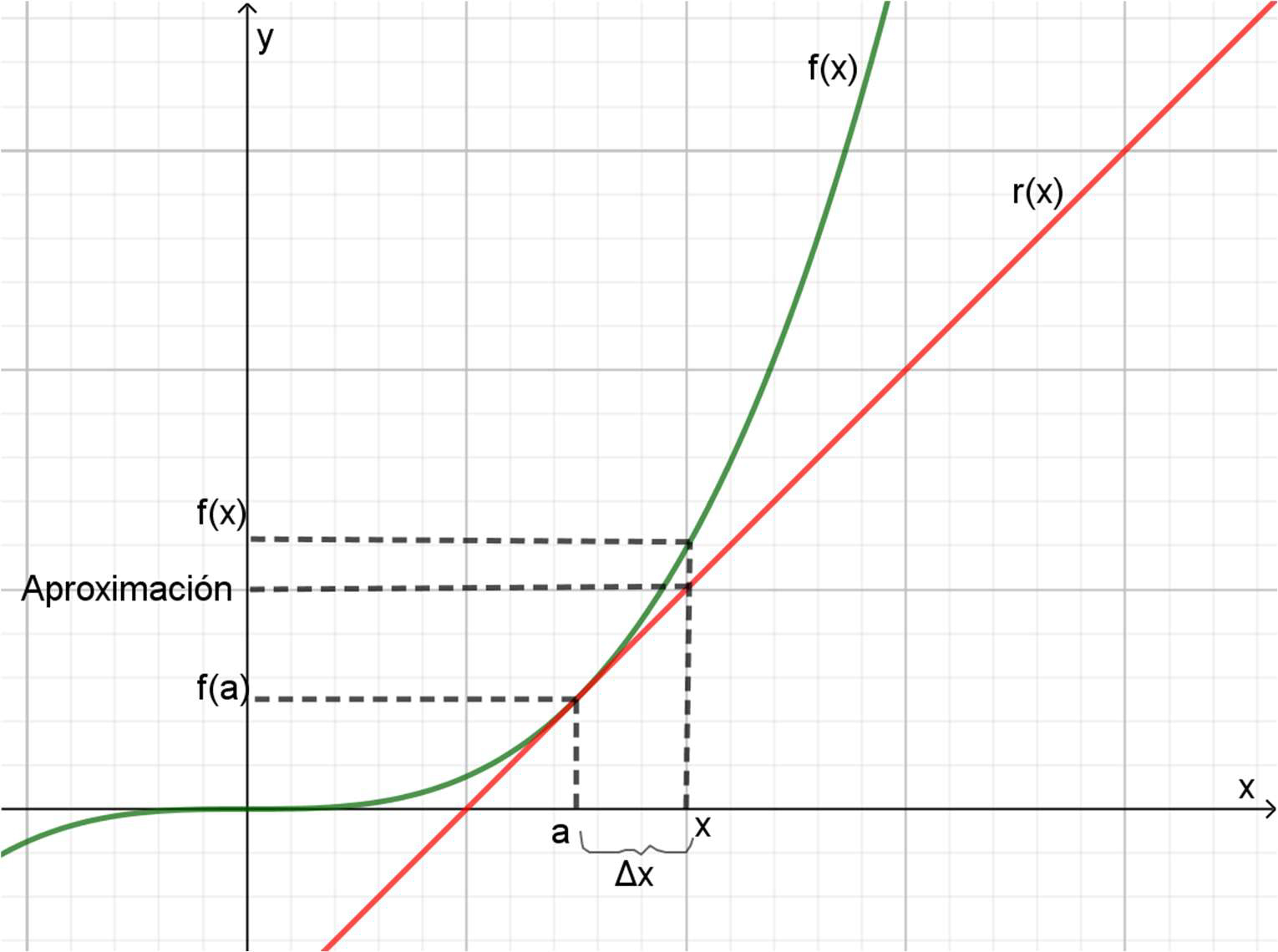
Aún en ese gráfico, en el que \(\Delta x\) es un número bastante grande, se aprecia que el valor aproximado (que se indica con el nombre de “Aproximación”) es cercano al valor de \( f(x)\).
Para calcular el valor de “aproximación”, es necesario tener presente que la recta de color rojo, a la que llamaremos r, es la tangente a la función \(f(x)\) en el punto de abscisa \(x = a\). De modo que su pendiente será \(f`(a)\) , de acuerdo con lo estudiado en el apartado 4.3.3.
Como, además, esa recta pasa por el punto de coordenadas \((a; f(a))\), su ecuación será tal que se cumplan, a la vez, las siguientes ecuaciones:
(1)(2)\[ \left\lbrace \begin{array}{ll} r(x)= f´(a)\cdot x+b\\ r(a)= f(a) \end{array} \right. \]
Este sistema de ecuaciones se resuelve de la siguiente manera: se reemplaza x por a en (1) y se tiene en cuenta (2):
\[r\left(a\right)=f´(a)\cdot a+b=f(a)\]
Despejando b, se obtiene:
\[b=f\left(a\right)-f´(a)\cdot a\]
Reemplazando este valor en (1), se logra la ecuación de la recta:
\[r(x)=f´(a)\cdot x+f(a)-f´(a) \cdot a=f´(a) \cdot (x-a)+f(a)\]
Entonces, es:
\[r(x)=f´(a) \cdot (x-a)+f(a)\]
El valor que toma la recta en x es aproximado al que toma la función, por eso se puede decir que:
\[f(x)\approx f´(a) \cdot (x-a)+f(a)\]
Para valores de \(x\) cercanos a \(a\).
La función del gráfico 4.8. tiene la siguiente fórmula: \(f\left(x\right)=\frac{1}{27}\cdot x^3\). Allí se puede observar que \(f\left(3\right)=1\).
Se pueden utilizar estos datos y la fórmula de la aproximación lineal para hallar \(f(3,01):\)
La derivada de la función es: \(f´(x)=\frac{1}{27}\cdot 3\cdot x^2=\frac{1}{9} \cdot x^2\), entonces, \(f´(3)=1\). De este modo, la recta tangente a la gráfica en el punto \((3; 1)\) es:
\[r\left(x\right)=1\cdot\left(x-3\right)+1=x-2\]
Para hallar \(f(3,01)\) aproximadamente, se utiliza \(r(3,01)\):
\[r\left(3,01\right)=3,01-2=1,01\]
Se puede comprobar que este valor es muy cercano a
\[f\left(3,01\right)=1,01003337\widehat{037}\]
Este último resultado se obtuvo con una calculadora científica (recurso que, claramente, no estaba disponible cuando estos temas fueron originalmente desarrollados).
Con esta fórmula se puede aproximar el valor que toma una función en cierto valor de x, a partir del dato de su valor en un punto cercano, mediante una recta. Esta aproximación se puede mejorar tanto como se desee utilizando los polinomios de Taylor, que se estudiarán a continuación.
4.5.2. Polinomios de Taylor
Cuando fuera necesaria una mejor aproximación del valor que una función toma para cierto valor de x, a partir de un punto conocido \((a;f\left(a\right))\), se puede utilizar el polinomio de Taylor o serie de Taylor, que viene dado por la siguiente expresión:
\[\begin{multline*} f(x)\approx t(x)=f(a)+f´(a) \cdot (x-a) + \frac{f´´(a)}{2!} \cdot (x-a)^2+ \\ + \frac{f´´´(a)}{3!} \cdot (x-a)^3+…+\frac{f^n(a)}{n!} \cdot (x-a)^n \end{multline*}\]
Como puede apreciarse es una suma de infinitos sumandos, una serie según la definición vista en la Unidad 1.
Los dos primeros sumandos son los de la fórmula de la aproximación lineal. Se desglosará el último para comprender de qué se trata.
\(f^n\left(a\right)\)es la derivada enésima de la función, calculada en el punto de abscisa a.
\(n!\) es el factorial de \(n\). Se define de la siguiente manera:
Para todo \(n\in N\):
\[ \left\lbrace \begin{array}{ll} n=0 →n!=1\\ n>0→n!=n\cdot (n-1)! \end{array} \right. \]
Busque una mejor aproximación para \(f\left(x\right)=\frac{1}{27}\cdot x^3\) que la hallada en el Ejemplo 4.7., para \(x=3,01.\)
Aquí se agregará un término a la aproximación lineal. Con ese objetivo, se calcula la derivada segunda de la función: \(f´´(x)=\frac{1}{9}\cdot 2\cdot x=\frac{2}{9}\cdot x\). Entonces, \(f´´(3)=\frac{2}{9}\cdot 3=\frac{2}{3}\). La serie de Taylor correspondiente es:
\[t\left(x\right)=1+1\cdot\left(x-3\right)+\frac{\frac{2}{3}}{2\cdot1\cdot1}\cdot\left(x-3\right)^2=1+x-3 + \frac{1}{3} \cdot (x-3)^2\]
Al desarrollar los cálculos expresados, se obtiene la serie de Taylor de orden 2 (porque llega hasta la derivada segunda):
\[t\left(x\right)=\frac{1}{3}\cdot x^2-x+1\]
Para hallar la aproximación pedida, resta hallar \( t(3,01)\):
\[t\left(3,01\right)=\frac{1}{3}\cdot{3,01}^2-3,01+1=1,0100\hat{3}\]
Como puede apreciarse, esta aproximación es mucho más exacta que la obtenida en el apartado anterior. En el Gráfico 4.9. se graficó la serie de Taylor de orden 2 (en azul) junto con la función (en verde) y la recta tangente (en rojo). Allí se aprecia que la serie de Taylor, en las cercanías de \( x=3\) prácticamente se superpone a la función, lo que muestra la buena calidad de la aproximación que se logra.

Es importante notar que el polinomio de Taylor será diferente, si se busca una aproximación cerca de otro punto.
Por ejemplo, si se considera al punto \((-2;-\frac{8}{27})\), también perteneciente a la función, el polinomio de Taylor de orden 2 será:
\[\begin{multline*} t(x)=f(-2)+f´(-2) \cdot (x+2)+\frac{f´´(-2)}{2!}\cdot (x+2)^2= \\ = -\frac{8}{27}+\frac{4}{9} \cdot (x+2) + \frac{\frac{-4}{9}}{2}\cdot (x+2)^2= \\ \end{multline*} \] \[ t(x)=-\frac{2}{9}x^2-\frac{4}{9}x-\frac{8}{27} \]
En el gráfico 4.10. se representó la función (en verde), y los polinomios de Taylor de orden 2 para \( x=3\) (en azul) y para \( x=-2\) (en rojo).
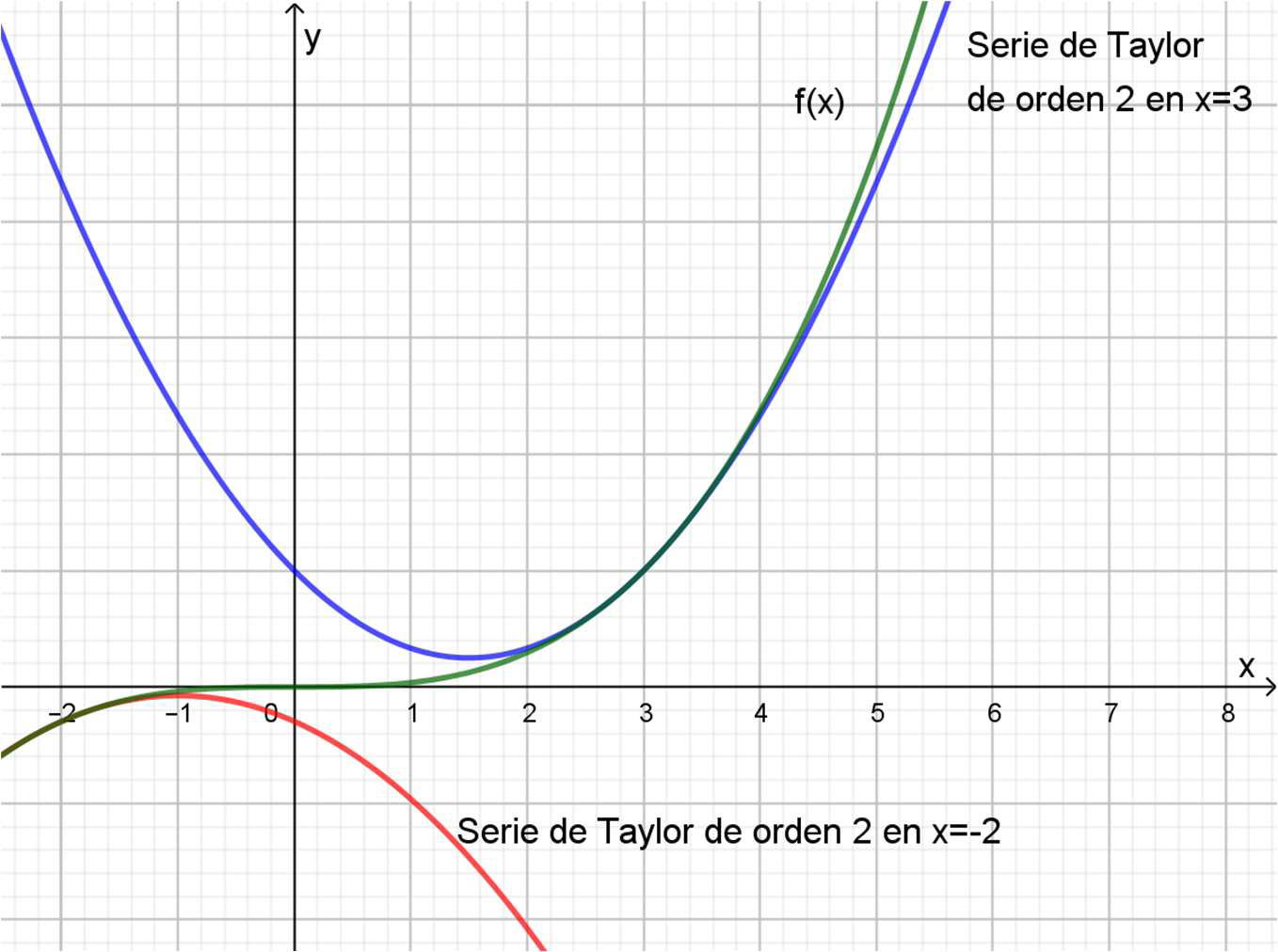
Como puede apreciarse en el gráfico, ambas series de Taylor son muy distintas, pero las dos se ajustan muy bien a la gráfica de la función \( f(x)\) en las cercanías del punto \(a\) considerado en cada caso.
4.6. Estudio de funciones y trazado de curvas
Con los conceptos desarrollados hasta aquí, se estudiarán funciones para encontrar sus puntos destacados, como extremos relativos.
4.6.1. Extremos relativos
En el apartado 4.3.1. se introdujo el concepto de derivada para estudiar el crecimiento (o decrecimiento) de una función. Aquí se realizará ese análisis para identificar en qué puntos la gráfica alcanza extremos relativos.
Gráficamente un extremo relativo es muy sencillo de identificar. En el diagrama cartesiano del Gráfico 4.11. se identificaron un mínimo relativo y un máximo relativo de una función. Pero hay otro mínimo, que se sugiere identificar.
Extremos relativos
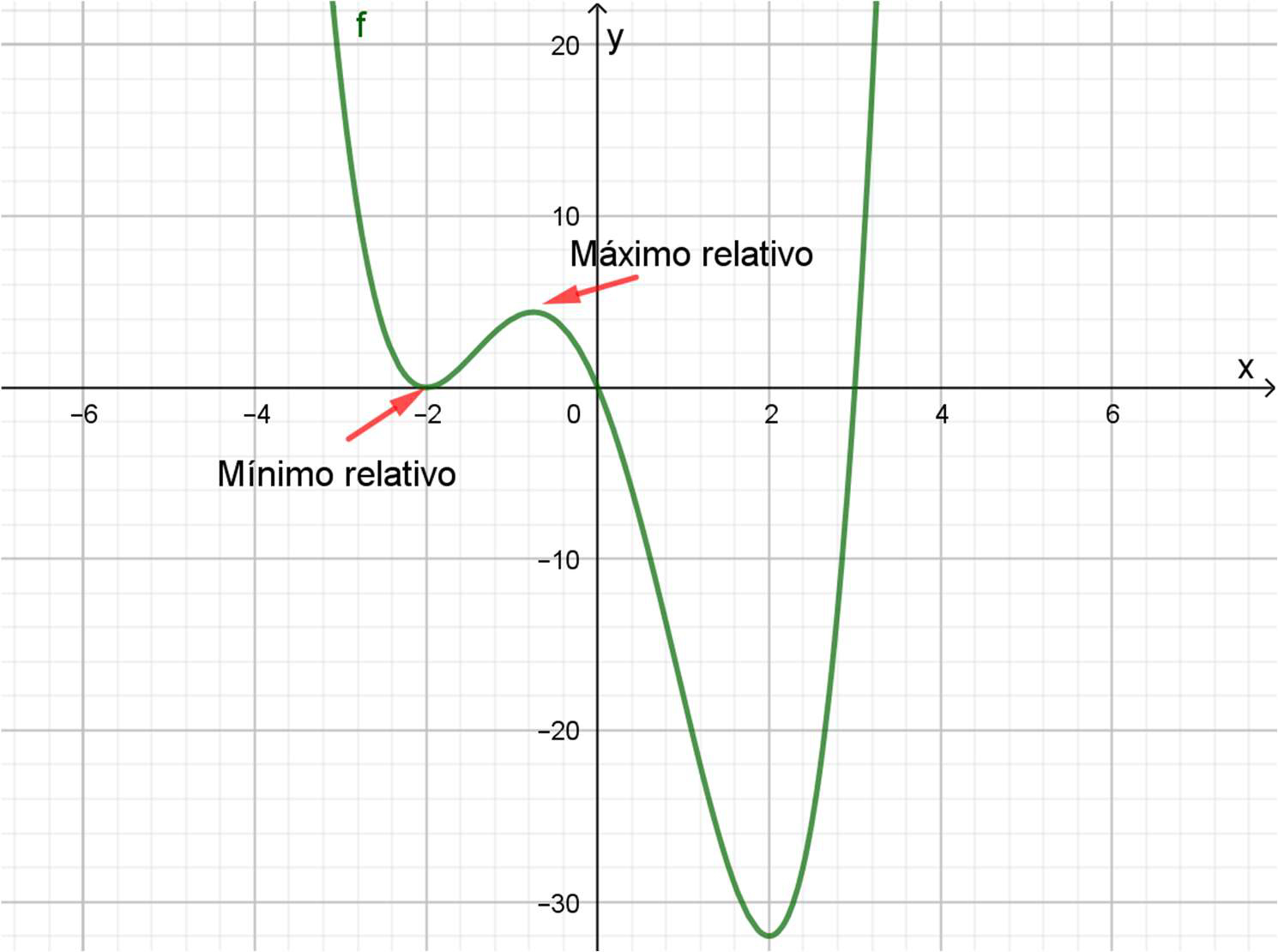
Es importante notar que en \(x=2\) hay otro mínimo relativo. Para ese valor, además, el mínimo es absoluto, porque la función f no presenta valores menores a la imagen de 2 en todo el resto de la gráfica.
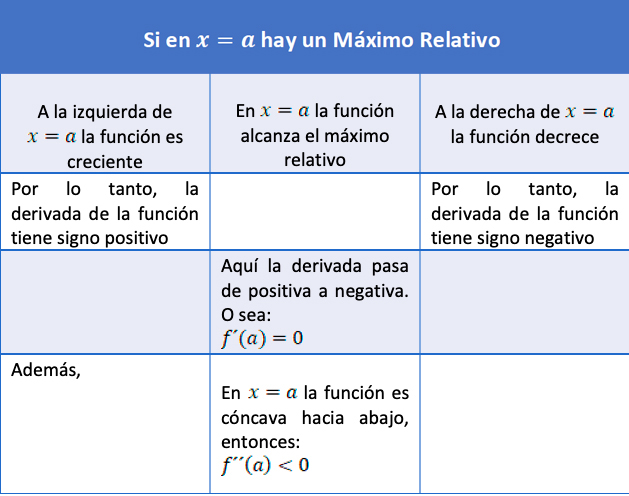
Una función tiene un máximo relativo en \(x=a\), si existe un intervalo abierto que contenga a \(a\) sobre el cual \(f(a)\geq f(x)\) para toda x en el intervalo. El máximo relativo es \(f(a)\).
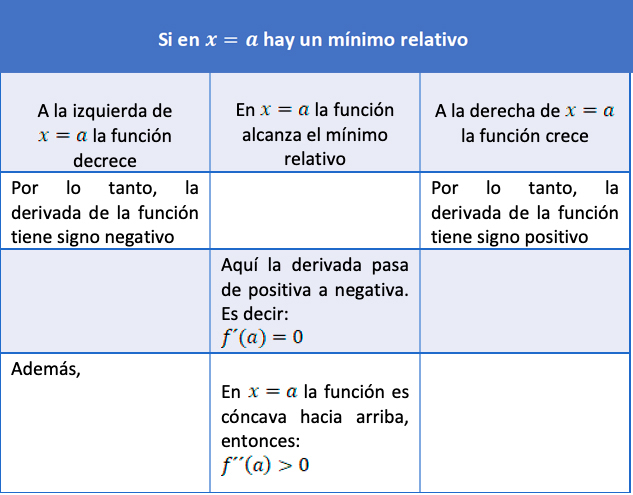
Una función tiene un mínimo relativo en \(x=a\), si existe un intervalo abierto que contenga a \(a\) sobre el cual \(f(a)\le f(x)\) para toda x en el intervalo. El mínimo relativo es \(f(a)\).
Si en \(x=a\) hay un máximo relativo es porque hasta ese punto la función está creciendo. Allí “se estanca” y luego, comienza a decrecer. Como la derivada de la función (según lo visto en el apartado 4.3.) es positiva cuando la función crece, deberá ser positiva “antes de” \(x=a\) y, como después decrece, la derivada será negativa “después de” \(x=a\). Entonces, \(x=a\) en la derivada deberá valer cero, porque cambia de signo.
Pasa lo contrario cuando en \(x=a\) la función presenta un mínimo relativo. Pero allí también hay cambio de signo de la derivada, y también deberá valer cero en \(x=a\).
Además, la concavidad de la curva es negativa cuando hay un máximo relativo. Y es positiva cuando hay un mínimo.
En los siguientes cuadros se sintetiza esto:
Condición para máximo relativo
Condición para mínimo relativo
4.6.2. Puntos de inflexión
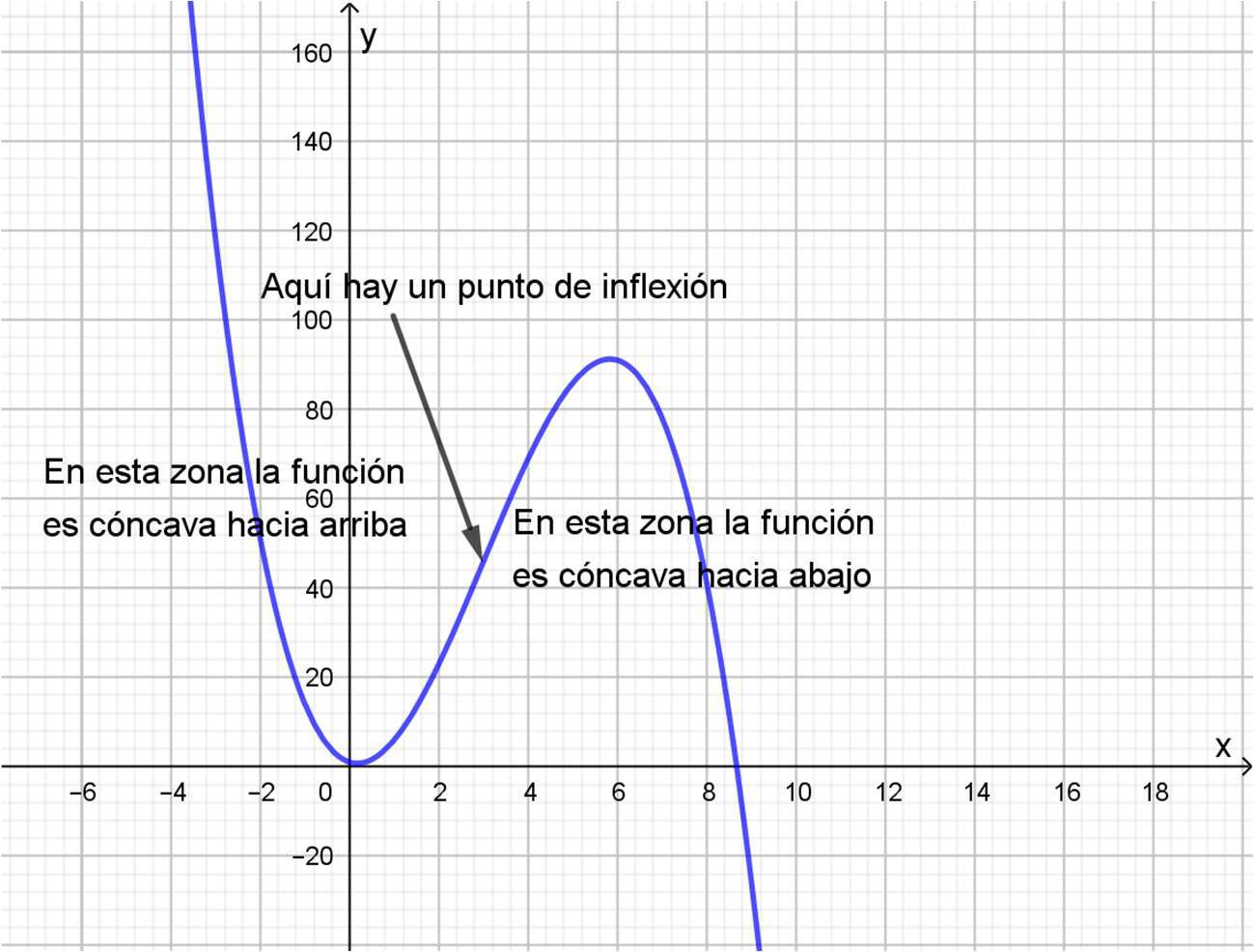
En el gráfico 4.7. del apartado 4.4.1 se aprecia que en un punto de inflexión la concavidad de la curva cambia de signo.
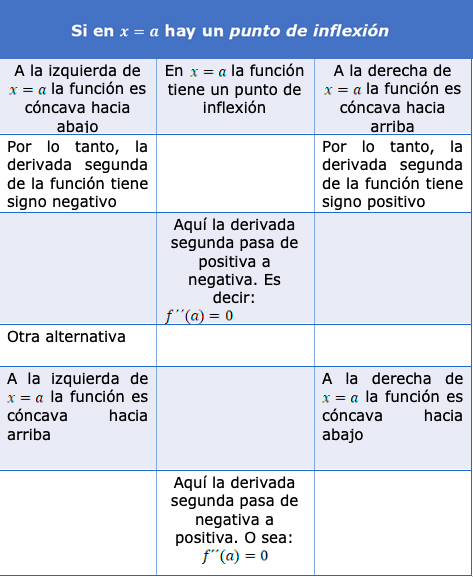
Una función \(f\) tiene un punto de inflexión en \(x=a\), si \(f\) es continua en \(a\) y \(f\) cambia de concavidad en \(x=a\).
Entonces, si en \(x=a\) hay un punto de inflexión es porque hasta ese punto la función era, por ejemplo, cóncava hacia abajo. Allí “se aplana” y luego, comienza a ser cóncava hacia arriba. Como la derivada segunda de la función (según lo visto en el apartado 4.4.1) es negativa cuando la función es cóncava hacia abajo, deberá ser negativa si \(x < a\) y, como después es cóncava hacia arriba, la derivada segunda será positiva si \(x>a\). Entonces, en \(x=a\) la derivada segunda deberá valer cero.
Pero podría pasar como en el gráfico 4.12., en el que las concavidades también cambian, pero en orden contrario.
Punto de inflexión
Para resumir, en el siguiente cuadro se consideran las dos posibilidades:
Puntos de inflexión
4.6.3. Trazado de curvas
A continuación, se utilizarán todos estos conceptos en el trazado de curvas:
Dada la siguiente función se pide que:
- Encuentre su dominio
- Indique si tiene puntos de discontinuidad y, en caso afirmativo, clasifíquelos.
- Encuentre si tiene extremos relativos y, en caso afirmativo, indique sus coordenadas.
- Encuentre si tiene puntos de inflexión y, en caso afirmativo, indique sus coordenadas.
- Grafique la función.
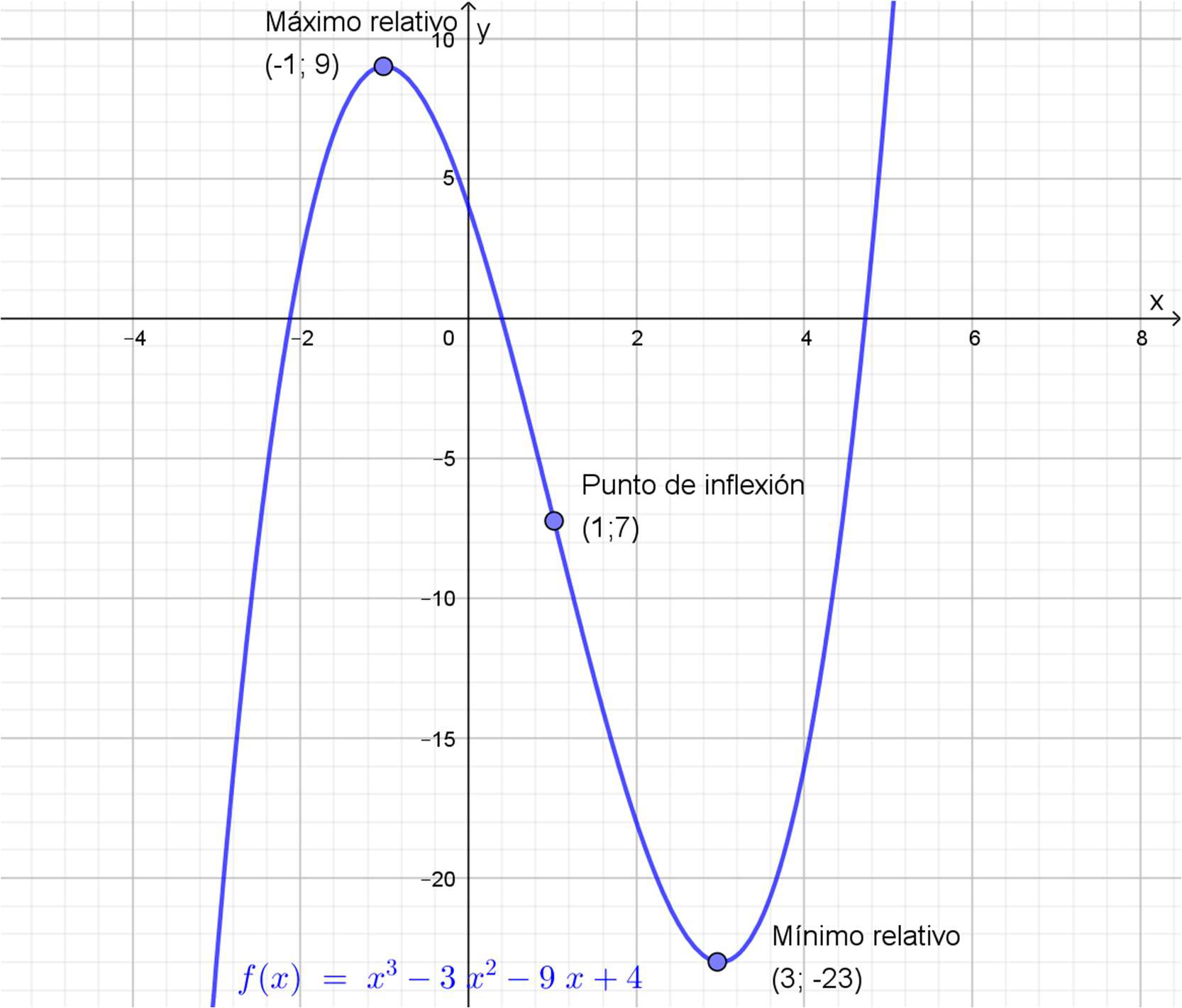
\[f\left(x\right)=x^3-3\cdot x^2-9\cdot x+4\]
-
Como la función es polinómica, su dominio son todos los números reales:
\[Dom= \mathbb{R}\]
-
No tiene puntos de discontinuidad, porque está definida para todos los números reales.
-
Para encontrar extremos relativos se procede de la siguiente manera:
- se deriva la función,
- se buscan los valores de \(x\) para los cuales se anula la derivada,
- Luego se investiga si esos valores corresponden a un máximo, un mínimo o ninguna de las dos cosas. Se puede investigar observando los intervalos de crecimiento y de decrecimiento o utilizando la concavidad de la función.
-
En este caso, la derivada es:
\[f´(x)=3\cdot x^2-3\cdot 2\cdot x-9+0=3\cdot x^2-6\cdot x-9 \]
-
Se iguala a cero la derivada y se buscan los “valores críticos”:
\[3\cdot x^2-6\cdot x-9=0\]
Esa ecuación se resuelve:
\[\begin{gather*} x=\frac{-(-6)\pm\sqrt{{(-6)}^2-4\cdot3\cdot(-9)}}{2\cdot3}=\frac{6\pm12}{6} \\ x_1=\frac{18}{6}=3 \\ x_2=\frac{-6}{6}=-1 \end{gather*} \]
Estos dos valores son los “valores críticos” en los que podría haber extremos relativos.
-
Ahora se investigará si en esos valores críticos la función cambia el sentido de crecimiento. Esos valores dividen al eje x en intervalos en los que el signo de la derivada no cambia. Esos intervalos son \(\left(-\infty;-1\right)\ \left(-1;3\right)\text{ y } \ (3;\ +\infty)\). Para analizar el signo que tiene la derivada en cada uno de ellos, conviene ordenar la información en un cuadro. Para cada uno de estos intervalos se elige un número que pertenezca a ellos y en ese número se calcula la derivada. En el Cuadro 4.5. se presentan todos los cálculos, pero en realidad solo interesa el signo de la derivada, que es lo que indica el sentido del crecimiento de la función.
Luego se compara un intervalo con el siguiente para escribir las conclusiones que se presentan escritas en color azul.
Cuadro 4.5.+Estudio del crecimiento

Otra manera de determinar si hay extremos relativos en esos valores críticos es analizar el signo de la derivada segunda. Para usar este otro método se busca la derivada segunda de esta función:
\[f´´(x)=3\cdot 2\cdot x-6+0=6\cdot x-6\]
A continuación, se calcula el signo que esta segunda derivada tiene en cada valor crítico. Es lo que se muestra en la Cuadro 4.6.
Cuadro 4.6.+Criterio de la derivada segunda

Por supuesto, las conclusiones son las mismas con ambos criterios.
Falta buscar las coordenadas de los extremos relativos.
Siempre que se piden coordenadas de un punto de una función, hay que reemplazar el valor de x en la fórmula de la función correspondiente.
El máximo relativo está en:
\(f\left(-1\right)={(-1)}^3-3\cdot\left(-1\right)^2-9\cdot(-1)+4=9 \). Sus coordenadas son \((-1;\ 9)\).
El mínimo relativo está en : \(f\left(3\right)=3^3-3\cdot3^2-9\cdot3+4=-23\). Sus coordenadas son \((3; -23)\).
-
Para buscar puntos de inflexión, se procede de la siguiente manera:
- se busca la derivada segunda de la función,
- se buscan los valores de x para los cuales se anula la derivada segunda,
-
Luego se investiga si esos valores corresponden a punto inflexión, observando si se modifica el sentido de la concavidad en los intervalos determinados por esos valores críticos.
La derivada segunda ya se calculó:
\[f´´(x)=6\cdot x-6\]
Ahora se busca resolver la ecuación:
\[\begin{gather*} f´´(x)=6\cdot x-6=0 \\ x=1 \end{gather*} \]
Este valor es el “valor crítico” en el que podría haber punto de inflexión.
- Ahora se investigará si en ese valores críticos la función cambia la concavidad.
Ese valor divide al eje x en intervalos en los que el signo de la derivada segunda no cambia. Esos intervalos son \( \left(-\infty;1\right)\ \ \ \ y\ \ \ (1;\ +\infty) \).
Como en el análisis del punto anterior, al ubicar los datos en un cuadro, se facilita la comprensión. La conclusión en rojo se obtiene comparando los resultados que se obtuvieron en los intervalos anterior y posterior:
Cuadro 4.7.+Puntos de inflexión

Falta buscar las coordenadas del punto de inflexión.
Siempre que se piden coordenadas de un punto de una función, hay que reemplazar el valor de x en la fórmula de la función: En este caso es: \(f(1)=1^3-3\cdot 1^2-9\cdot 1+4=7\). Por lo tanto, el punto de inflexión está en (1;7).
-
El Gráfico 4.13., hecho en Geogebra, es la representación de esta función. Es importante notar que coincide con la información que se obtuvo más arriba.
Gráfico 4.13.+Gráfica de la función del Ejemplo 4.9.
Dada la función \(f\left(x\right)=\frac{x^2+1}{x}\) se pide que:
- Encuentre su dominio
- Indique si tiene puntos de discontinuidad y, en caso afirmativo, clasifíquelos.
- Encuentre si tiene extremos relativos y, en caso afirmativo, indique sus coordenadas.
- Encuentre si tiene puntos de inflexión y, en caso afirmativo, indique sus coordenadas.
- Grafique la función.
4.7. Extremos aplicados. Optimización. Aplicaciones económicas y empresariales
Algunos de los conceptos desarrollados en esta unidad se utilizan en Economía. En esa ciencia la terminología se modifica. Así, en lugar de hablar de la derivada de la función de costos, hablan de los costos marginales. Para referirse a la derivada de la función ingresos, dicen ingresos marginales. Además, la notación también difiere. Por ejemplo, el costo marginal se anota:
\[C´=CMg\]
La derivada del producto total, a la que llaman producto marginal, es:
\[Q´=PMg\]
Teniendo en cuenta esas particularidades, se mostrarán algunas de las aplicaciones, a través de ejemplos.
Demuestre el siguiente teorema:
Para maximizar el beneficio, es necesario que el ingreso marginal sea igual al costo marginal.
Demostración:
El beneficio es el ingreso total menos los costos totales:
\[B=IT-CT\]
Si se desea buscar el máximo de la función beneficio, deberá procederse como en el Ejercicio 4.9.: se deriva y se iguala a cero la derivada. En este caso en particular:
\(B´=(IT-CT)´=IT´-CT´\) y esta expresión deberá ser igual a cero en el máximo.
(Se utilizó la propiedad de la derivada de una sustracción).
Aquí hace falta recordar que la derivada del ingreso total se llama ingreso marginal y que la derivada del costo total se llama costo marginal, así
\[IMg-CMg=0\]
lo que es lo mismo:
\[IMg=CMg \text{ (1) que es lo que se quería demostrar.}\]
A esta condición los economistas la llaman “condición de primer orden”, que significa que es una condición necesaria pero no suficiente para que haya un máximo en el beneficio.
Matemáticamente, esto significa que falta demostrar que el punto crítico que satisface la ecuación (1) se trata realmente de un máximo.
También es importante comprender que, para que esta condición que se ha demostrado sea válida, se deben cumplir los axiomas de la teoría en la que está inserta. En este caso en particular, el mercado debe ser de competencia perfecta. Por lo tanto, esta condición no es válida en mercados oligopólicos o monopólicos, por ejemplo.
La función de producción de corto plazo de una empresa es una función que vincula la cantidad producida con la cantidad de trabajo incorporado a la producción.
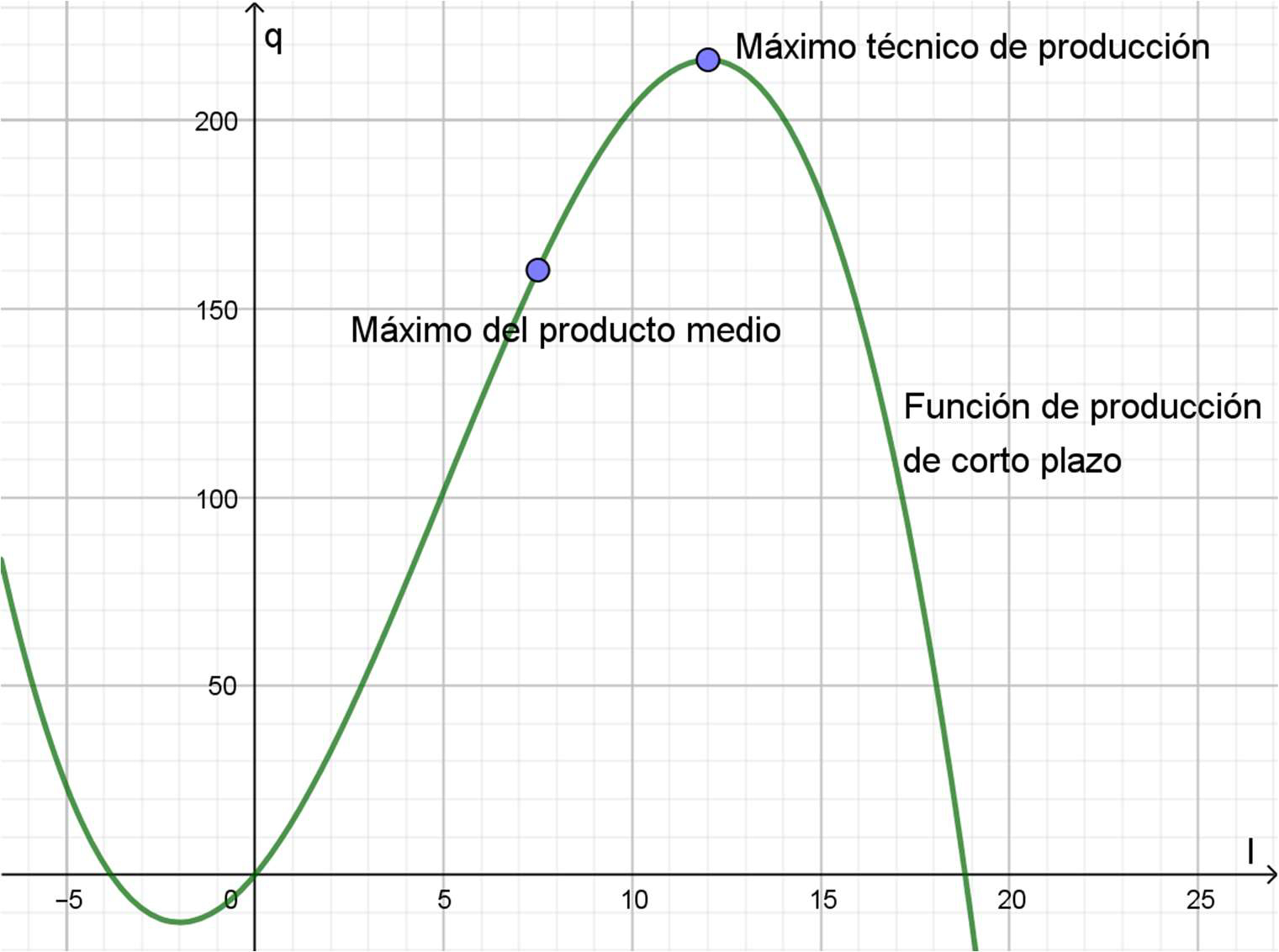
Una fábrica produce, en el corto plazo, según la función \(Q(l)=-\frac{1}{6}\cdot l^3+\frac{5}{2}\cdot l^2+12\cdot l\) donde \(l\) representa la cantidad de horas que trabaja por día el personal contratado (por labor, que es su nombre en inglés) y \(Q\) (de quantity) la cantidad producida diariamente con las máquinas y herramientas que la empresa posee actualmente.
Se pide que encuentre:
- La cantidad diaria que produce esta fábrica cuando se contratan 8 horas de trabajo diario.
- La función producto medio, que se define como la cantidad producida por hora de trabajo contratado: \(P_{me}=\frac{Q(l)}{l}\)
- La función producto marginal, que es la derivada de la función de producción \(Q\left(l\right)\).
- La máxima cantidad que puede producir esta fábrica sin incorporar más máquinas, y la cantidad de horas que el personal debería trabajar para lograrlo.
- La cantidad de horas por las que será necesario contratar al personal actual para que se obtenga el máximo del producto medio.
- Compruebe que ese máximo del producto medio sea igual al producto marginal para esa cantidad de horas trabajadas.
- La cantidad de producto que se obtiene con la cantidad horas diarias que trabaja el personal que maximiza el producto medio.
- ¿Cuántas horas al día le conviene a la empresa que trabaje su personal?
-
La cantidad pedida se obtiene reemplazando \(l=8\) en la fórmula de \(Q\):
\[Q\left(8\right)=-\frac{1}{6}\cdot8^3+\frac{5}{2}\cdot8^2+12\cdot8=\frac{512}{3}=170,66\]
Entonces, cuando el personal trabaja 8 horas diarias, se producen 170,66 unidades.
-
La función producto medio indica cuántas unidades se producen por hora de trabajo del personal. Y, en este ejemplo, se calcula de la siguiente manera:
\[P_{me}=\frac{Q(l)}{l}=\frac{-\frac{1}{6}\cdot l^3+\frac{5}{2}\cdot l^2+12\cdot l\ }{l}=-\frac{1}{6}\cdot l^2+\frac{5}{2}\cdot l\ +12 \]
-
La función producto marginal indica cuánto aumenta el producto a medida que se incrementa marginalmente el tiempo de trabajo. Su fórmula es la derivada de la función del producto.
\[PMg=Q´(l)=-\frac{1}{6} \cdot 3\cdot l^2+\frac{5}{2}\cdot 2\cdot l+12=-\frac{1}{2}\cdot l^2+5\cdot l+12\]
-
Para encontrar la cantidad máxima que puede producir esta fábrica, se debe encontrar el máximo de la función \(Q(l)\). Para ello, se deriva y se iguala a cero la derivada.
La derivada \(Q(l)\) de ya se calculó en c): \(\ Q´(l)=-\frac{1}{2}\cdot l^2+5\cdot l+12\). Al igualar a cero esta fórmula, se obtiene la ecuación:
\(-\frac{1}{2}\cdot l^2+5\cdot l+12=0\) que tiene dos soluciones:
- \(l=-2\) (lo que no tiene sentido económico, ya que no se puede trabajar una cantidad negativa de horas), o
- \(l=12\)
Para investigar si en \( l=12\) hay un extremo relativo (y si es realmente un máximo), se puede utilizar el criterio de la derivada segunda. Para ello, se vuelve a derivar la derivada de \(Q(l):\)
\[Q´´(l)=-\frac{1}{2}\cdot 2\cdot l+5=-l+5\]
Y se calcula el valor de la derivada segunda en \(l=12\):
\[Q´´(12)=-12+5=-7<0\]
por lo tanto, la función es cóncava hacia abajo y en \(l=12\) presenta un máximo.
El máximo que puede producir se consigue reemplazando este valor de en la función de producción \(Q(l)\):
\[Q\left(12\right)=-\frac{1}{6}{\cdot12}^3+\frac{5}{2}\cdot{12}^2+12\cdot12=216\]
Entonces, esta fábrica, sin incorporar más máquinas, puede producir a lo sumo 216 productos al día, cuando su personal trabaje 12 horas diarias.
-
Ahora hay que buscar el máximo de la función de producto medio. El procedimiento es el mismo que el aplicado en el apartado anterior, pero cambia la función. Habrá que derivar la función producto medio: \(P_{me}=\frac{Q(l)}{l}=-\frac{1}{6}\cdot l^2+\frac{5}{2}\cdot l+12\)
Se obtiene: \(P_{me}´=-\frac{1}{6}\cdot 2\cdot l+\frac{5}{2}=-\frac{1}{3}\cdot l+\frac{5}{2}\)
Para buscar el máximo del producto medio, se deberá igualar a cero esta derivada, o sea:
\[-\frac{1}{3}\cdot l+\frac{5}{2}=0\rightarrow l=\frac{5}{2}\cdot3=7,5\]
El valor crítico es, entonces, \(l=7,5\). Nuevamente, utilizando el criterio de la derivada segunda, se evaluará si se trata de un máximo o un mínimo:
\(P_{me}´´=-\frac{1}{3}<0\) para cualquier valor de \(l\). Por lo tanto, en la función es cóncava hacia abajo y en \( l=7,5\) hay un máximo relativo.
Entonces, habrá que acordar que el personal trabaje 7,5 horas al día para obtener el máximo del producto medio.
-
Para comprobar esta afirmación es necesario calcular el producto medio y el producto marginal cuando la cantidad de horas trabajadas es 7,5:
\[\begin{gather*} P_{me}=\frac{Q(7,5)}{l}=-\frac{1}{6}\cdot{7,5}^2+\frac{5}{2}\cdot7,5+12=21,375 \\ PMg=Q´(7,5)=-\frac{1}{2}\cdot 7,5^2+5\cdot 7,5+12=21,375 \end{gather*} \]
Como ambos resultados coinciden, cuando se trabajan 7,5 horas al día el producto medio y el producto marginal son iguales.
-
Con esa cantidad de personal, la producción será:
\[Q\left(7,5\right)=-\frac{1}{6}{\cdot7,5}^3+\frac{5}{2}\cdot{7,5}^2+12\cdot 7,5=160,3125\]
Nótese que esta cifra se obtiene reemplazando el valor obtenido en e) en la función de producción \(Q\left(l\right)\)
-
La respuesta a esta pregunta depende de qué quiere la empresa dueña de la fábrica.
Si necesitara obtener el máximo de producción, le convendrá contratar al personal para que trabaje 12 horas al día (o contratar a más gente). Pero si pretende maximizar su beneficio, podría preferir contratar 7,5 horas al día, ya que así obtiene la mayor cantidad de producto por hora.
De todos modos, para contestar con certeza, es necesario tomar en cuenta los costos, que no se consideran en este problema.
Si bien el problema no lo pide, en el Gráfico 4.14 se representó la función de producción.
En ese diagrama se ubicaron los puntos correspondientes al máximo técnico de producción (el máximo que se puede lograr, dadas las condiciones iniciales de máquinas, herramientas y personal contratado actualmente) y el máximo del producto medio.
Si bien la gráfica incluye los valores de la función para \(l<0\) y \(l>12\), es importante notar que no tienen sentido, económicamente hablando, debido a que:
- para \(l<0\) no se puede trabajar una cantidad de horas negativas, y
- para \(l>12\): a la empresa no le va a convenir contratar al personal por más tiempo, si es que va a ver reducida la cantidad que produce.
Por esos motivos, económicamente el dominio de esta función es \(Dom=\left[0\right.;\left. 12\right]\), que corresponde al tramo en el que la función es creciente.
En este ejemplo se supuso que la empresa conoce la fórmula de la función de producción de corto plazo. Sin embargo, es solo una fantasía matemática, ya que en la práctica no se dispone de dicha información.
Función de producción de corto plazo
La función \(I_{me}\left(q\right)=\frac{Ingreso\ total}{q}=-2q^3+24q^2\) representa el Ingreso medio de una empresa en función de la cantidad q de bienes producidos y vendidos.
- Encuentre la función de Ingreso total y la función de Ingreso marginal.
Calcule qué cantidad de bienes se deben producir y vender para lograr el máximo del Ingreso total. ¿Cuál es el máximo ingreso total?
Justifique sus respuestas.

