1. Números reales. Temas de repaso

Objetivos

Operar con números reales.
Resolver ecuaciones y problemas aplicando las propiedades de las operaciones con números reales.
Reconocer y utilizar sucesiones y series de números reales.

Introducción

En esta primera unidad se explican brevemente los conceptos con los que ya se ha trabajado en los estudios de nivel secundario (o polimodal), y que resultan indispensables para avanzar con este curso.

Trabajaremos especialmente con ejemplos de economía y administración por el anclaje disciplinar de las carreras en que se ofrece este material.

1.1. Los números reales

Texto

Desde hace más de 5000 años la humanidad “cuenta”, es decir, utiliza alguna manera de cuantificar y registrar diferentes cosas (piezas de caza, herramientas o personas). Los números que se utilizan para “contar” son los elementos del conjunto $ \mathbb{N} $ de los números naturales. Este conjunto tiene infinitos elementos, pero entre dos consecutivos de ellos no hay otro número natural:

\[\mathbb{N} = \{1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; \ldots \}\]

Como, por ejemplo, entre el 1 y el 2 (o entre cualquier par de números naturales consecutivos) no hay ningún otro número natural, se dice que el conjunto es discreto. Con la difusión del comercio, aparecieron las deudas y con ellas los números negativos, que, junto con los naturales y el cero, son los elementos del conjunto $\mathbb{Z}$ de los números enteros, que también tiene infinitos elementos y también es discreto.

Como algunos problemas prácticos requerían de divisiones cuyos resultados no son números enteros, se incorporaron (alrededor del año 2000 a. C.) las “fracciones”, que son los elementos del conjunto $\mathbb{Q}$ de los números racionales. Este conjunto también tiene infinitos elementos, pero es denso, que significa que no es discreto. Porque entre dos números racionales cualesquiera siempre hay otro.

También fue mediante problemas que la humanidad se enfrentó con los números irracionales. Tal vez, el primero de ellos haya sido $\pi$, pero también $ \sqrt{2} $ es irracional.

La palabra irracional indica que se trata de números que no se pueden escribir como una razón -es decir como una división- entre dos enteros; pero también connota que carece de razón, que no puede entenderse. Porque eso fue lo que sucedió. Durante siglos los números irracionales no se comprendieron, aunque se utilizaron.

La unión entre el conjunto de los números racionales y el de los irracionales es el conjunto $\mathbb{R}$ de los números reales que se utilizará a lo largo de todo el curso. Se trata de un conjunto denso, pero también continuo, porque completa la recta numérica, es decir, hay un punto por cada número real y un número real por cada punto de la recta.

1.1.1. La recta numérica

Texto

Los números reales se pueden representar sobre una recta. Generalmente, se grafica en forma horizontal, con una flecha hacia la derecha, que indica hacia dónde es el orden creciente de los números. Asimismo, es importante indicar la escala, marcando la posición del 0 y del 1 (por lo menos):

Gráfico 1.1.

Recta numérica

Audiovisual

En el siguiente video, Alexánder Gómez, de Colombia, explica cómo ubicar números racionales en la recta numérica:

<https://www.youtube.com/watch?v=UiJZwbqT06U>

Si alguien tuviera interés en representar en la recta raíces cuadradas irracionales, en el siguiente video se explica cómo hacer:

<https://www.youtube.com/watch?v=alzItrqvPhI>

1.1.2. Intervalos de números reales

Texto

Un intervalo es un subconjunto de números reales situado entre dos valores extremos. Los extremos de los intervalos pueden ser abiertos o cerrados.

Intervalo cerrado:

Conjunto de los números reales mayores o iguales a $a$ y menores o iguales a $b$:

\[\left[a;b\right]=\left\{x\in\ \mathbb{R} / a\le x\le b\right\}\]

Como puede apreciarse, se indican los extremos entre corchetes.

Su representación en la recta numérica es un segmento que incluye a sus extremos. En el gráfico siguiente se representó la situación mostrando los extremos como puntos rellenos.

Gráfico 1.2.

Intervalo cerrado

Texto

Intervalo abierto:

Conjunto de los números reales mayores a $a$ y menores a $b$:

\[ \left(a;b\right)=\left\{ x\in \mathbb{R} / a < x < b \right\} \]

Como en este caso los extremos del intervalo no pertenecen a él, se indican entre paréntesis.

Su representación en la recta es un segmento al que NO pertenecen a sus extremos, como se muestra a continuación, utilizando puntos huecos (sin relleno de color).

Gráfico 1.3.

Intervalo abierto

Texto

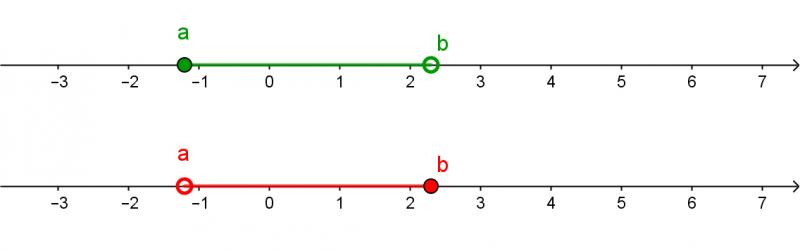
Intervalos semiabiertos (o semicerrados):

Son aquellos en los que uno de los extremos pertenece al intervalo y el otro no:

\[ \left[a; b\right) = \left\{ x \in \mathbb{R} / a \le x < b \right\} \] o \[\left(a; b\right] = \left\{ x \in \mathbb{R} / a < x \le b \right\} \]

El extremo perteneciente al intervalo se indica con un corchete y el que no, con paréntesis.

En el siguiente gráfico vemos ambos segmentos, el primer caso en color verde y el segundo caso en color rojo.

Gráfico 1.4.

Intervalos semiabiertos

Ejemplo 1.1.

Los siguientes ejemplos son casos particulares de intervalos:

$\left[a;\ \right.\left. +\infty\right)=\left\{x\in\ \mathbb{R} / a\le x \right\}$ en este caso, el subconjunto corresponde a una semirrecta con origen en a, que pertenece al intervalo:

Gráfico 1.5.

Semirrecta ejemplo 1 a)

$ \left(-\infty; 0\right) = \mathbb{R}^- =\left\{x \in \mathbb{R} / x < 0 \right\} $ es el conjunto de los reales negativos.

Del mismo modo, $\mathbb{R}^+$ es el conjunto de los números reales positivos, que se puede escribir como el intervalo $\left(0;\ +\infty\right)$.

La representación gráfica de la semirrecta $\left(-\infty;\ \right.\left. 4\right)$ es la del gráfico siguiente, en el que se indicó mediante un punto hueco que el 4 no pertenece al intervalo. También se puede escribir a este intervalo como el conjunto $\left\{x\in\ \mathbb{R} / x < 4 \right\} $

Gráfico 1.6.

Semirrecta ejemplo 1 d)

1.2. Operaciones con números reales

1.2.1. Suma y producto de números reales

Texto

En el conjunto de los números reales se definen las operaciones suma, que se simboliza con +, y producto, que se simboliza $\cdot $ o $\times$ (aquí se utilizará el punto).

Estas operaciones cumplen con las siguientes propiedades:

La suma y el producto son “cerradas” en $\mathbb{R}$:

Para todo número $a,\ b\ \in\ \mathbb{R}$ se verifica

\begin{gather*} a+b\ \in \mathbb{R} & a\cdot b\in \mathbb{R}\\ El\ resultado\ de\ la\ suma\ de\ & \ \ El\ resultado\ del\ producto\ de\ \\ n\acute{u}meros\ reales\ es\ otro\ n\acute{u}mero\ real\ \ \ & \ \ \ n\acute{u}meros\ reales\ es\ otro\ n\acute{u}mero\ real \end{gather*}

Asociatividad

Para todo número $a,\ b,\ c\ \in\ \mathbb{R}$ se verifica:

\begin{gather*} \left(a+b\right)+c=a+(b+c) \ \ \ & \ \ \ \left(a\cdot b\right)\cdot c=a\cdot(b\cdot c) \end{gather*}

Conmutatividad

Para todo número $a,\ b\ \in\ \mathbb{R}$ se verifica:

\begin{gather*} a+b=b+a \ \ \ \ \ \ & \ \ \ \ \ \ a\cdot b=b\cdot a \end{gather*}

Existencia de elemento neutro

Existe el número $0\ \in \mathbb{R}$ tal que para todo número $a\ \in\ \mathbb{R}$ se verifica:

\[a+0=0+a=a\]

Existe el número $1\ \in \mathbb{R}$ tal que para todo número $a\ \in\ \mathbb{R}$ se verifica:

\[a\cdot1=1\cdot a=a\]

El 0 es el elemento neutro para la suma y el 1 es el elemento neutro para el producto.

Existencia de elementos inversos

Para todo número $a\ \in\ \mathbb{R}$ existe un único número $(-a)\ \in\ \mathbb{R}$ tal que sumado $a$ es igual 0, elemento neutro de la suma:

\[a+(-a)=(-a)+a=0\]

Al número $-a$ se lo llama opuesto de $a$.

Para todo número $a\ \in\ \mathbb{R}-\left\{0\right\}$ existe un único número $a^{-1}\ \in\ \mathbb{R}$ tal que multiplicado por $a$ es igual $1$, elemento neutro del producto:

\[a\cdot a^{-1}=a^{-1}\cdot a=1\]

Aquí es importante notar que el 0, elemento neutro de la suma, no tiene inverso multiplicativo.

Al número $a^{-1}$ se lo llama inverso de $a$.

El producto es distributivo respecto de la suma

Para todo número $a,\ b,\ c\ \in\ \mathbb{R}$ se verifica:

\[a\cdot\left(b+c\right)=a\cdot b+a\cdot c\]

En un curso universitario como este, es necesario conocer estas propiedades y saber utilizarlas para resolver cálculos, tanto a mano como con calculadora.

1.2.2. Potencia, radicación y logaritmación de números reales

Texto

Potencia

Dado un número real $a$ y un número natural $n$, se llama potencia enésima de $a$ a:

\[a^n=\underbrace{a\cdot a\cdot\ldots\ \cdot a} _{n\ veces}\]

es decir, a la multiplicación de $a$ por sí mismo, $n$ veces.

Al número $a$ se lo llama base de la potencia, al número $n$ se lo denomina exponente y al resultado de la cuenta, potencia.

Esta operación cumple con las siguientes propiedades:

El producto de dos potencias de igual base es otra potencia de la misma base cuyo exponente es la suma de los exponentes de los factores:

\[a^m\cdot a^n=a^{m+n}\]

El cociente de dos potencias de igual base es otra potencia de igual base, cuyo exponente es la resta del exponente del dividendo menos el exponente del divisor. En símbolos:

\[a^m:a^n=\frac{a^m}{a^n}=a^{m-n}\]

La potencia de una potencia es otra potencia con la misma base, cuyo exponente es el producto de los exponentes:

\[\left(a^m\right)^n=a^{m\cdot n}\]

Propiedad distributiva de la potencia respecto del producto y del cociente: la potencia de un producto (o de un cociente) es igual al producto (o al cociente) de las potencias de los factores. En símbolos:

\[\left(a\cdot b\right)^n=a^n\cdot b^n\]

y también,

\[\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}\]

Leer con atención

Es importante notar que la potencia:

No es conmutativa. Por ese motivo habrá dos operaciones inversas: la radicación (que se verá a continuación) cuando se busca la base de una potencia y la logaritmación (que se estudiará más adelante, en esta misma unidad) cuando se desconozca el exponente.

No es distributiva respecto de la suma o de la resta.

\[\left(a+b\right)^n\neq a^n+b^n\]

\[ {(a+b)}^n \text{ es distinto a } a^n+b^n \]

Texto

Radicación

Sean un número real $b$ y un número natural $n$, se define la raíz enésima del número de la siguiente manera:

\[\sqrt[n]{b}=a\leftrightarrow b=a^n\]

Esto se lee “la raíz enésima de $b$ es un número $a$ sí y solo si $b$ es igual a la potencia enésima de $a$”.

Al número $n$ se lo llama índice de la raíz, al número $b$, radicando y al resultado, raíz.

Generalización de la definición de potenciación

Se define la potenciación con exponente negativo de la siguiente manera: siendo $n$ un número natural,

\[a^{-n}=\frac{1}{a^n}\]

Con esta notación, se puede apreciar que el inverso multiplicativo de un número real $a\neq0$, es:

\[a^{-1}=\frac{1}{a^1}=\frac{1}{a}\]

También se define la potenciación con exponente 0, siempre que la base no sea cero:

Si \[a\neq0,\ {\ \ a}^0=1\]

La potenciación con exponente racional se define de la siguiente manera:

\[a^\frac{p}{q}=\sqrt[q]{a^p} \]

donde $p$ y $q$ son números enteros (o sea, $\frac{p}{q}$ es un número racional).

Con base en la última definición, se generaliza la definición para exponentes irracionales. Pero la explicación excede las pretensiones de este curso.

Logaritmación

Se define logaritmo como el número al cual se debe elevar una base $a$ distinta de 0 dada para obtener un resultado determinado. Es una de las operaciones inversas de la potenciación cuando se desconoce el exponente:

\[\log_a{c}=b\ \leftrightarrow\ \ a^b=c \]

Esto se lee “logaritmo en base $a$ de $c$ es un número $b$ sí y solo si la potencia $b$ de $a$ es igual a $c$”.

Al número $a$ se lo llama base del logaritmo, al número $c$, argumento y al resultado, logaritmo.

Esta operación cumple con las siguientes propiedades:

El logaritmo de un producto es igual a la suma de los logaritmos de los factores:

\[\log_a{(b\cdot c)}=\log_a{b}+\log_a{c}\]

El logaritmo de un cociente es igual a la resta del logaritmo del dividendo menos el logaritmo del divisor. En símbolos:

\[\log_a{\left(\frac{b}{c}\right)}=\log_a{b}-\log_a{c}\]

El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base:

\[\log_a{b^c}=c\cdot\log_a{b}\]

Esta propiedad incluye a las raíces, porque se pueden escribir como potencias de exponente fraccionario. En símbolos:

\[{\log_a{\sqrt[c]{b}}=\log}_a{b^\frac{1}{c}}=\frac{1}{c}\cdot\log_a{b}\]

Además, $\log_a{a}=1$ y $\log_a{1}=0$.

En las calculadoras científicas suelen haber dos teclas para calcular logaritmos: log y ln. Esta última se refiere a los logaritmos naturales, con los que se trabajará en la Unidad 3.

La tecla log calcula logaritmos en base 10. Si hiciera falta calcular un logaritmo en otra base, se utiliza la siguiente fórmula:

\[\log_a{b}=\frac{\log_c{b}}{\log_c{a}}\]

1.3. Ecuaciones con números reales

Texto

Una ecuación es una igualdad en la que aparece por lo menos una incógnita. Y se necesita averiguar su valor de modo que la ecuación resulte una proposiciónN verdadera.

En este curso se trabajará con ecuaciones con números reales y, para resolverlas, se aplican las propiedades recién estudiadas de las operaciones.

Ejemplo 1.2.

Resuelva las siguientes ecuaciones:

$\left(x+5\right)^2-4=\frac{10}{2} $

$\frac{5}{6}\cdot\left(3x-1\right)+\frac{1}{2}=2x-\frac{1}{6}$

$4x^2-2x+5=8x-1 $

$4x^2\cdot\left(x+3\right)=6-5x $

${25}^x=0,008$

$\left(x+5\right)^2-4=\frac{10}{2} $

El signo igual separa a la ecuación en dos miembros.

En este caso, es conveniente resolver los cálculos del segundo miembro antes de comenzar.

\[\left(x+5\right)^2-4=\frac{10}{2}=5 \]

En este punto, es importante reconocer el orden de prelación de las operaciones del primer miembro. Si se conociera el valor de $x$, habría que comenzar sumando 5, luego, al resultado se lo elevaría al cuadrado y finalmente se restaría 4. En orden contrario a la enunciación anterior se despeja la incógnita.

Para eliminar el 4 que resta, se suma a ambos miembros esa misma cifra (opuesto aditivo):

\begin{align*} \left(x+5\right)^2-4+4&=5+4=9\\ \left(x+5\right)^2+0&=9 \\ \left(x+5\right)^2&=9 \end{align*}

Aquí se aplica la definición de radicación:

\[\left(x+5\right)^2=9\leftrightarrow x+5=\sqrt[2]{9}\]

En este punto hay que recordar que existen dos números que, elevados al cuadrado, dan 9. Por eso, la ecuación tendrá dos resultados.

Finalmente, para eliminar el 5 se suma su opuesto aditivo a cada miembro:

\begin{align*} x+5 &=\sqrt[2]{9}=3 & x+5&=\sqrt[2]{9}=-3\\ x+5-5&=3-5=-2 & x+5-5&=-3-5=-8\\ x+0&=-2 & x+0&=-8\\ x&=-2 & x&=-8 \end{align*}

Entonces, hay dos valores posibles de x que hacen de la ecuación una proposición verdadera: $x=-2$ y $x=-8$.

Se puede comprobar, resolviendo los cálculos:

\begin{align*} \left(-2+5\right)^2-4&= & \left(-8+5\right)^2-4&=\\ \left(3\right)^2-4=9-4&=5 & \left(-3\right)^2-4=9-4&=5 \end{align*}

En este primer ejemplo de ecuaciones se explicó con propiedades de los números reales cada paso. En general, se pueden omitir esas explicaciones. Se podría haber resuelto la misma ecuación como sigue:

\begin{align*} \left(x+5\right)^2-4&=\frac{10}{2}=5\\ \left(x+5\right)^2&=5+4=9 \end{align*}

\begin{align*} x+5&=3 & x+5&=-3\\ x=3-5&=-2 & x=-3-5&=-8\\ x&=-2 & x&=-8 \end{align*}

Entonces, hay dos valores posibles de x: $x=-2$ y $x=-8$.

L

Leer con atención

Cuando se resuelven cálculos, problemas o ecuaciones es importante responder con una oración la cuestión planteada en el enunciado. No basta con hacer cálculos y redondear (o resaltar, o destacar) un resultado.

$\frac{5}{6}\cdot\left(3x-1\right)+\frac{1}{2}=2x-\frac{1}{6}$

En este caso, la incógnita está en ambos miembros. Para poder despejarla es necesario antes agrupar los dos términos en los que se encuentra.

En el primer miembro, la incógnita está afectada por un producto. Para poder agruparla con la que se encuentra en el segundo miembro, se utiliza la propiedad distributiva del producto respecto de la suma y se resuelven los cálculos. Así, la ecuación queda:

\begin{align*} \frac{5}{6}\cdot3x-\frac{5}{6}\cdot1+\frac{1}{2}&=2x-\frac{1}{6}\\ \frac{5}{2}\cdot x-\frac{5}{6}+\frac{1}{2}&=2x-\frac{1}{6}\\ \frac{5}{2}\cdot x-\frac{5}{6}+\frac{3}{6}&=2x-\frac{1}{6}\\ \frac{5}{2}\cdot x-\frac{2}{6}&=2x-\frac{1}{6}\\ \frac{5}{2}\cdot x-\frac{1}{3}&=2x-\frac{1}{6} \end{align*}

En el próximo paso se agrupan los dos términos con incógnita en el primer miembro y los que no la tienen, en el segundo:

\begin{align*} \frac{5}{2}\cdot x-\frac{1}{3}+\frac{1}{3}-2x&=2x-2x-\frac{1}{6}+\frac{1}{3}\\ \frac{5}{2}\cdot x-2x&=-\frac{1}{6}+\frac{1}{3}\\ x\cdot\left(\frac{5}{2}-2\right)&=-\frac{1}{6}+\frac{2}{6}=\frac{1}{6}\\ x\cdot\frac{1}{2}&=\frac{1}{6}\\ x\cdot\frac{1}{2}\cdot2&=\frac{1}{6}\cdot2=\frac{1}{3}\\ x&=\frac{1}{3} \end{align*}

Por lo tanto, el valor de la incógnita que satisface esta ecuación es $x=\frac{1}{3}$

Como en el ejemplo anterior, se podría comprobar resolviendo los cálculos de la ecuación. Y también se podría resolver omitiendo pasos. Aquí se detallaron para facilitar la comprensión de los procesos que llevan a la solución.

$4x^2-2x+5=8x-1$

En esta ecuación nuevamente aparecen términos con la incógnita en ambos miembros. Se comienza por agruparlos en el primer miembro. En este ejemplo se abreviarán pasos:

\begin{align*} 4x^2-2x+5-8x&=-1\\ 4x^2-10x+5&=-1 \end{align*}

Esta expresión es una ecuación de segundo grado, porque la incógnita tiene potencia 2, y, además, está completa, porque también hay un término en el que la incógnita tiene grado 1. Para resolverla, se utiliza la fórmula de Baskara o Bhaskara o fórmula de la resolvente.

L

Leer con atención

Fórmula de Baskara o BhaskaraN o fórmula de la resolvente

En una ecuación del siguiente tipo:

\[a\cdot x^2+b\cdot x+c=0\]

Las dos soluciones posibles se encuentran realizando los siguientes cálculos:

\[x_1=\frac{-b+\sqrt{b^2-4ac}}{2a}\ y\ x_2=\frac{-b-\sqrt{b^2-4ac}}{2a}\]

Esta expresión suele escribirse, en forma abreviada, así:

\[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]

Y el polinomio queda factorizado del siguiente modo:

\[a\cdot x^2+b\cdot x+c=a\cdot\left(x-x_1\right)\cdot\left(x-x_2\right)\]

W

Web

En el enlace siguiente se puede ver la demostración de esta fórmula: < http://www.denumeros.com/bhaskara.html>

Para poder aplicar esta fórmula, será necesario igualar a cero el primer miembro de la ecuación que se está resolviendo:

\begin{align*} 4x^2-10x+5+1&=0 \\ 4x^2-10x+6&=0 \end{align*}

En este caso particular, es $a=4,\ \ \ b=-10\ $ y $c=6$. Por lo que la fórmula queda:

\[x=\frac{-(-10)\pm\sqrt{{(-10)}^2-4\cdot4\cdot6}}{2\cdot4}\]

En este paso es importante recordar que se debe separar en términos antes de efectuar cálculos:

\[x=\frac{10\pm\sqrt{100-96}}{8}=\frac{10\pm\sqrt4}{8}\]

En este punto, se desdoblan las dos soluciones:

\begin{align*} x=\frac{10+2}{8}=\frac{12}{8}=\frac{3}{2} & & & & & x=\frac{10-2}{8}=\frac{8}{8}=1 \end{align*}

Entonces, esta ecuación tiene dos posibles soluciones: $x=1$ o $x=\frac{3}{2}$.

$4x^2\cdot\left(x+3\right)=6-5x$

Aquí se comienza por distribuir el producto en el primer miembro:

\[4x^3+12x^2=6-5x\]

Y se iguala a cero toda la expresión:

\[4x^3+12x^2+5x-6=0\]

Esta ecuación es polinómica de grado mayor a dos. Para hallar sus resultados se factorizará el polinomio, teniendo en cuenta el teorema de GaussN:

L

Leer con atención

Si un polinomio de coeficientes enteros de grado $n$ admite una raíz racional $\frac{p}{q}$ (siendo $p$ y $q$ coprimosN), entonces $p$ es divisor del término independiente y $q$ lo es del coeficiente principal.

En este caso, el término independiente $-6$ tiene los siguientes divisores: $\pm1;\ \pm2;\ \pm3 ;\ \pm6$ y los del coeficiente principal 4 son: $\pm1;\ \pm2;\ \pm4$.

Entonces, las posibles raíces del polinomio de la ecuación son: $\pm1;\ \pm\frac{1}{2};\ \pm\frac{1}{4};\pm2;\ \pm3;\ \pm\frac{3}{2};\ \pm\frac{3}{4};\ \pm6$.

Como el polinomio es de grado 3, a lo sumo tendrá 3 raíces reales. Para comprobar cuáles de todos estos valores es raíz, se aplica la regla de la división de RuffiniN.

W

Web

En la siguiente página se detalla cómo utilizar esa regla:

<https://www.superprof.es/apuntes/escolar/matematicas/algebra/polinomios/ruffini.html>

Se puede comenzar con el 1:

\begin{array}{r|rrrr} & 4 & 12 & 5 & -6\\ 1 & & 4 & 16 & 21\\ \hline & 4 & 16 & 21 & \fbox{15} \end{array}

Como el resto de la división no es 0, sino 15, 1 no es raíz de este polinomio.

Se probará con el $-1$:

\begin{array}{r|rrrr} & 4 & 12 & 5 & -6\\ -1 & & -4 & -8 & 3\\ \hline & 4 & 8 & -3 & \fbox{-3} \end{array}

Tampoco es raíz.

Se sigue, por ejemplo con $-2$:

\begin{array}{r|rrrr} & 4 & 12 & 5 & -6\\ -2 & & -8 & -8 & 6\\ \hline & 4 & 4 & -3 & \fbox{0} \end{array}

Aquí se obtuvo resto 0, por lo que $-2$ es raíz del polinomio y se puede reescribir de la siguiente manera:

\begin{gather*} 4x^3+12x^2+5x-6=\left[x-\left(-2\right)\right]\cdot\left(4x^2+4x-3\right)=0\\ \left(x+2\right)\cdot\left(4x^2+4x-3\right)=0 \end{gather*}

Con el polinomio del segundo factor se podría seguir utilizando la regla de Ruffini. Pero, al ser de segundo grado, también se puede aplicar la fórmula de Baskara. En este caso, es $a=4;\ b=4\ y\ c=-3$:

\[x=\frac{-4\pm\sqrt{4^2-4\cdot4\cdot(-3)}}{2\cdot4}=\frac{-4\pm8}{8}\]

Las dos posibles soluciones son $x=\frac{1}{2}\ y\ x=-\frac{3}{2}$:

El polinomio queda factorizado de la siguiente forma:

\[\left(x+2\right)\cdot\left(4x^2+4x-3\right)=\left(x+2\right)\cdot4\cdot\left(x-\frac{1}{2}\right)\cdot\left(x+\frac{3}{2}\right)=0\]

En general, se ubican primero los números. Por lo que se acostumbra escribir así: \[4\cdot\left(x+2\right)\cdot\left(x-\frac{1}{2}\right)\cdot\left(x+\frac{3}{2}\right)=0\]

Las soluciones a esta ecuación son $x=2; x=\frac{1}{2}$ y $x=-\frac{3}{2}$, porque al reemplazar cada uno de esos valores en la expresión anterior, valdrá cero uno de los factores, anulando también todo el producto. Como puede apreciarse, los dos últimos resultados eran parte de la lista de posibles raíces del polinomio, según se había previsto por el teorema de Gauss.

Esta forma de resolver ecuaciones polinómicas de grado superior a dos es la que se utilizará en este material.

E

Audiovisual

En <https://www.youtube.com/watch?v=ZlVfjM8aJZo> la ingeniera Mariana explica cómo se factorizan los polinomios, utilizando el teorema de Gauss y la regla de Ruffini, como se hizo en este ejemplo.

${25}^x=0,008$

En esta ecuación la incógnita está en el exponente. Por definición de logaritmo es:

\[\log_{25}{0,008=x}\]

Para resolver el cálculo del primer miembro, se cambia la base de los logaritmos a 10, para poder utilizar la calculadora (tecla LOG):

\[\log_{25}{0,008=}\frac{\log_{10}{0,008}}{\log_{10}{25}}=\frac{-2,09691}{1,39794}=-1,5=x\]

Entonces, el valor de x es $-1,5$.

1.3.1. Problemas

Texto

Al resolver problemas, particularmente de Economía y de Administración, pero de otras ciencias también, se suelen plantear ecuaciones. En este apartado, se presenta una introducción a estas cuestiones, que se retomarán en todas las unidades.

Para ello, resulta importante definir algunos conceptos.

El ingreso total es el dinero que recibe por la venta de sus productos la persona que los vende. Suponiendo que solo haya una clase de producto y que se venda siempre al mismo precio, se puede calcular como la multiplicación entre el precio por cada unidad y el número de unidades vendidas:

\[Ingreso\ Total=precio\ por\ unidad\ \cdot n\acute{u}mero\ de\ unidades\ vendidas\]

Lo podemos simbolizar, usando menos palabras de la siguiente manera:

\[IT=p\cdot q\]

En esta última fórmula, $ IT $ significa “ingreso total”, p representa al precio de cada unidad y q representa el número de unidades vendidas.

El costo total es la suma de los costos fijos y variables de la producción. El costo fijo es la suma de todos los costos que son independientes del nivel de producción (como, por ejemplo, el alquiler del local, los seguros, el costo fijo de la factura de electricidad, entre otros). El costo variable es la suma de todos los costos que sí dependen del nivel de producción (como la mano de obra, las materias primas, el precio de la electricidad que varía con la cantidad de energía utilizada, etcétera).

\[Costo\ Total\ =\ Costo\ Fijo\ +\ Costo\ Variable\]

Simbolizando más abreviadamente sería:

\[CT=CF+CV\]

A su vez, el costo variable se puede calcular como el producto entre el costo por unidad, que se simboliza c, por la cantidad de unidades producidas:

\[CV=c\cdot q\]

Con esta última fórmula, se puede reescribir la de costos totales de la siguiente manera:

\[CT=CF+c\cdot q\]

El beneficio que le queda a la empresa surge de la diferencia entre el ingreso total y el costo total:

\[Beneficio=Ingreso\ Total-Costo\ Total\]

Que se puede simbolizar:

\[B=IT-CT\]

Al combinar todas estas expresiones, también se puede calcular el beneficio así:

\[B=p\cdot q-\left(CF+c\cdot q\right)=p\cdot q-CF-c\cdot q=q\cdot\left(p-c\right)-CF\]

A lo largo de este material, se volverá, en reiteradas ocasiones, a utilizar las fórmulas recién vistas en problemas como los de los ejemplos a continuación.

Ejemplo 1.3.

La empresa A fabrica un producto para el cual el costo variable por unidad es $150 y el costo fijo es de $120000. Cada unidad tiene un precio de venta de $200. Determine la cantidad de artículos que deben venderse para obtener un beneficio de $200000.

En este ejemplo, debemos encontrar la cantidad de unidades (q) que se necesitan vender para que la fábrica obtenga un beneficio de $200000. Como vimos, q representa la cantidad de unidades.

Ahora, se usa la última versión de la fórmula del beneficio:

\[B=q\cdot\left(p-c\right)-CF\]

Y en ella se reemplazan los datos de este problema:

\[200000\ =\ q\cdot\left(200-150\right)-\ 120000\]

Se resuelve el paréntesis y se reordena:

\[200000\ =\ 50\cdot q\ -\ 120000\]

Y se resuelve la ecuación:

\begin{align*} 200000+\ 120000&=\ 50\cdot q\ \\ 320000&=50\cdot q \\ \frac{320000}{50}&=q \\ 6400&=q \end{align*}

Por lo tanto, esta empresa deberá vender 6400 unidades de su producto para obtener un beneficio de $200000.

Ejemplo 1.4.

Cierto emprendimiento tiene costos fijos mensuales por $150000. Sus productos tienen $240 de costo unitario. ¿A qué precio deberán venderse, si se desea cubrir costos produciendo y vendiendo 1200 unidades al mes?

Cubrir costos significa que los beneficios serán nulos. Aparentemente, no sería económicamente viable que una empresa no genere beneficios. Sin embargo, es importante tener en cuenta que los costos de los que se hablan en Economía, incluyen los costos de oportunidad, es decir, la retribución al capital propietario del emprendimiento. Los beneficios mayores a cero son beneficios extraordinarios, superiores a los que se calcularon como “de oportunidad”.

Entonces, para resolver este problema, se iguala a cero el beneficio. Y se reemplazan en la fórmula, los datos del problema:

\begin{gather*} B=q\cdot\left(p-c\right)-CF\\ 0=1200\cdot\left(p-240\right)-150000 \end{gather*}

Y se resuelve la ecuación, en la que la incógnita es el precio del producto:

\begin{gather*} 150000=1200\cdot\left(p-240\right)\\ \frac{150000}{1200}=125=p-240\\ 125+240=365=p \end{gather*}

Por lo tanto, será necesario cobrar $365 por cada producto para cubrir los costos, produciendo y vendiendo 1200 unidades al mes.

Actividad 1.1.

Se sugiere como actividad resolver el siguiente problema:

En el mes de abril una empresa vendió 3000 productos y obtuvo un ingreso total de $570000 y un beneficio de $20000. El costo unitario de cada uno de sus productos es de $150. Con estos datos, calcule:

¿A qué precio vendió sus productos en abril?
¿Cuáles fueron los costos totales de esta empresa?
¿Cuánto son los costos fijos de esta empresa?

1.4. Sucesiones y series

1.4.1. Sucesiones

Texto

En algunos problemas surge la necesidad de expresar listas de números escritos en un orden definido. A cada uno de ellos se los llama términos. Se simboliza así:

\[ a_1\ \ \ a_2\ \ \ a_{3\ \ \ }a_4\ \ \ a_5\ \ \ a_6\ \ \ldots\ \ \ a_n\ \ldots\ =\left\{a_n\right\}\ \]

A $a_n$ se lo llama: término enésimo de la sucesión.

Ejemplo 1.5.

La sucesión de Fibonacci, $\left\{f_n\right\}$, de la que se habla hasta en novelas y películasN , es:

\[1\ \ \ 1\ \ \ 2\ \ \ 3\ \ \ 5\ \ \ 8\ \ \ 13\ \ \ 21\ \ \ 34\ \ \ 55\ \ \ 89\ \ \ldots\]

En esta sucesión es fácil encontrar cuál es el siguiente número. A partir de los dos primeros, los siguientes términos son la suma de los dos anteriores:

\begin{gather*} f_{3\ }=f_1+ f_2=1+1=2 \\ f_{4\ }=f_2+ f_3=1+2=3 \\ f_{5\ }=f_3+ f_4=2+3=5 \\ f_{6\ }=f_4+ f_5=3+5=8 \end{gather*}

En general, esto se simboliza así:

\[f_1=1;\ f_2=1;\ f_n=f_{n-2}+f_{n-1}\ \ cuando\ n\geq3\]

Ejemplo 1.6.

Escriba los primeros 5 términos de la sucesión $\left\{\frac{n}{n+1}\right\}$.

Aquí se va reemplazando n por los primeros 5 números naturales:

\begin{gather*} a_1=\frac{1}{1+1}=\frac{1}{2}\\ a_2=\frac{2}{2+1}=\frac{2}{3}\\ a_3=\frac{3}{3+1}=\frac{3}{4}\\ a_4=\frac{4}{4+1}=\frac{4}{5}\\ a_5=\frac{5}{5+1}=\frac{5}{6} \end{gather*}

Entonces, los primeros términos de la sucesión son:

\[\frac{1}{2}\ \ \ \ \ \frac{2}{3}\ \ \ \ \ \frac{3}{4}\ \ \ \ \ \frac{4}{5}\ \ \ \ \ \frac{5}{6}\]

Ejemplo 1.7.

Encuentre una posible fórmula para el término enésimo de la siguiente sucesión:

\[2\ \ \ \ 5\ \ \ \ 10\ \ \ \ 17\ \ \ \ 26\ \ \ \ 37\ \ \ \ 50\ \ \ \ 65\ \ \ \ 82\ \ \ \ 101\ \ \ldots\]

Esto requiere de un poco de imaginación. Pero es fácil notar que cada término se podría escribir así:

\[1^2+1\ \ \ \ \ 2^2+1\ \ \ \ \ 3^2+1\ \ \ \ \ 4^2+1\ \ \ \ \ 5^2+1\ \ \ \ \ 6^2+1\ \ \ \ \ 7^2+1\ \ \ \ \ 8^2+1\ \ \ \ \ 9^2+1\ \ \ \ \ {10}^2+1
\]

Entonces, la fórmula del término enésimo podría ser:

\[a_n=n^2+1\]

1.4.2. Series

Texto

Se llama serie, o también serie infinita, a la suma de todos los términos de una sucesión. Se simboliza de la siguiente manera:

\[\sum_{n=1}^{\infty}a_n=a_1+a_2+a_3+a_4+a_5+a_6+\ \ldots+a_n+\ \ldots\]

Es una suma de infinitos sumandos. ¿Cuál es el resultado?

Este problema se ha planteado desde las “paradojas de Zenón”, en el siglo V a. C. en Grecia.

Web

A quien le interese la historia, puede leer en la siguiente página, la “paradoja de Aquiles y la tortuga”:

<https://www.xatakaciencia.com/matematicas/aquiles-y-la-tortuga>

Texto

La respuesta es que algunas series tienen un resultado infinito, como la serie que se obtiene con la sucesión de Fibonacci. Cuando eso sucede, se llaman divergentes.

Pero otras no. A esas, cuya suma es un número real (finito), se las llama convergentes.

Ejemplo 1.8.

La suma parcial hasta el quinto término de la serie de Fibonacci es:

\[\sum_{n=1}^{5}f_n=f_1+f_2+f_3+f_4+f_5=1+1+2+3+5=12\]

La suma parcial hasta el sexto término es:

\[\sum_{n=1}^{6}f_n=f_1+f_2+f_3+f_4+f_5=1+1+2+3+5+8=20\]

Como cada nuevo término es mayor que el anterior, esta serie es divergente. Esto no es una demostración. Simplemente, se muestra un ejemplo de serie divergente.

Ejemplo 1.9.

Si se considera la sucesión cuyo término general es:

\[a_n=\left(\frac{1}{2}\right)^n\]

Los primeros términos son:

\[\frac{1}{2}\ \ \ \ \ \frac{1}{4}\ \ \ \ \ \frac{1}{8}\ \ \ \ \ \frac{1}{16}\ \ \ \ \frac{1}{32}\ \ \ \ \frac{1}{64}\ \ \ \ \frac{1}{128}\ \ \ \ \ \frac{1}{256}\ \ \ \ \frac{1}{512}
\]

En este ejemplo, cada término es menor que el anterior.

La suma parcial hasta el quinto término de esta serie es:

\[\sum_{n=1}^{5}\left(\frac{1}{2}\right)^n=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=\frac{31}{32}
\]

Se puede demostrar que esta serie es convergente y su suma es 1:

\[\sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^n=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\ldots=1
\]

Pero esa demostración excede las pretensiones de este curso.