4. El procesamiento y análisis de datos cuantitativos
Objetivos
Que cada estudiante:
-
Reconozca los aportes y posibilidades de la estadística en la construcción y análisis de problemas sociales y educativos.
-
Se aproxime a herramientas conceptuales y procedimientos para la medición desde las ciencias sociales.
-
Identifique fuentes oficiales y formas de presentación y comunicación de datos estadísticos educativos mediante informes, tablas, gráficos, mapas y tableros interactivos.
4.1. Medir desde las ciencias sociales
En esta última unidad presentaremos una aproximación al análisis de datos cuantitativos, en el cruce entre la investigación social en educación y la estadística. A partir de lo trabajado en las unidades anteriores, podemos reconocer que el enfoque epistemológico cuantitativo habilitó algunas veces un marco estereotipado y rígido que ha concebido que la realidad conocible e investigable es –a partir de la articulación de fundamentos teóricos y empíricos– solo aquella que puede ser cuantificada o traducida en valores numéricos o, en otros términos, que la única realidad social que puede ser abordada desde las ciencias sociales es la realidad objetivable, observable, medible y matematizable. En esta línea de sentido, y en una reflexión desde la epistemología de las ciencias sociales, Gregorio Klimovsky y Cecilia Hidalgo plantearon el siguiente interrogante.
Pero en ciencias sociales, ¿el uso de la matemática es imprescindible y conveniente? En particular, y modificando ligeramente la pregunta, ¿el uso de lo cuantitativo es imprescindible y conveniente en ciencias sociales? [...]
Son muchos los cultores de las ciencias sociales que han considerado lícito y positivo el empleo de conceptos matemáticos en sus disciplinas. [...]
Lo cual no prueba que éste sea un método imprescindible que convenga utilizar sistemáticamente. Bien podría ser tan sólo una de las tantas cosas que pueden intentarse, y la respuesta final la proporcionará la historia futura de las ciencias sociales.
(Klimovsky e Hidalgo, 1998: 237-238)
En línea con esta primera reflexión abierta y el recorrido de las unidades anteriores –que le dan contexto a la producción científica en educación y nos permiten pensar los datos como construcciones– vale también presentar una lectura reflexiva sobre la idea de medición. Desde la producción de conocimiento sobre problemáticas sociales, podemos encontrar versiones ampliadas de la medición más allá de la estricta matematización del mundo y de la forma científica de conocerlo. Por ejemplo, Néstor Cohen y Gabriela Gómez Rojas (2019) nos proponen una definición que va más allá de la mera cuantificación y así lo señalan: “Cada vez que incluimos un objeto o sujeto en una clase de objetos o sujetos, en tanto esa clase fuera definida teóricamente, entendemos que estamos midiendo (p. 18).
Es decir que las tareas de clasificación dentro de un sistema de categorías y de comparación, sobre la base de la identificación de semejanzas y/o diferencias, constituyen ya procedimientos propios de la producción de conocimiento en ciencias sociales y pueden pensarse como una parte inicial de la medición. Ahora bien, el enfoque cuantitativo implica también trabajar desde un abordaje estadístico sobre aquello que se categorizó y/o comparó. Encontramos así una idea de la medición que nos permite trabajar sobre cualidades o sobre valores numéricos, es decir, sobre entidades que pueden ser cualitativas o cuantitativas.
Ante todo, medir es comparar una o varias cosas: 1) entre sí, 2) respecto a un patrón constante o 3) en relación con otro objeto de la misma clase. Por ello, todo trabajo de comparación implica alguna forma de medición. En algunos casos, esa comparación puede ser auxiliada por la cuantificación, en otras no. Esto da lugar a la existencia de dos sistemas de medición: la cualitativa y la cuantitativa. En ambos casos, la medición se puede realizar con ventajas relativas: en cada una de ellas se gana y se pierde algo. La ventaja de la cuantificación es que permite el uso de técnicas estadísticas que facilitan mucho el procesamiento de la información y el trabajo con grandes cantidades de casos. Pero es necesario saber cuándo se puede legítimamente usar números mediante procedimientos estadísticos y cuándo no lo es.
(Saltalamacchia, 2014: 122)
Entonces, desde el enfoque cuantitativo de hacer ciencia (según lo trabajado en la Unidad 1), la búsqueda de una medición que conecte con sentido válido un conjunto de categorías o de variables con la información recabada empíricamente a través del trabajo de campo (mediante una encuesta o un censo) es una parte fundamental del trabajo de construcción de conocimiento. Por ello resultan igualmente importantes las etapas previas de diseño del problema y su abordaje metodológico dentro de un proyecto de investigación (según lo trabajado en la Unidad 2) y la de construcción de un instrumento válido y confiable para el relevo empírico y basado en la operacionalización de aquello que se quiere medir (según lo trabajado en la Unidad 3). Como parte necesaria del proceso de investigación, la etapa siguiente será la del trabajo analítico con la información y la construcción e interpretación de los datos. Es así que, en esta mirada cuantitativa sobre los asuntos sociales y educativos, entran a jugar conceptos y procedimientos propios de la estadística.
4.1.1. Los aportes y posibilidades de la estadística
Los abordajes de la investigación social desde la cuantificación y la estadística reconocen algunos primeros intentos hacia mediados del siglo XVII en Inglaterra y Alemania, y un desarrollo más sostenido entre finales del siglo XIX y principios del XX. De hecho, están quienes definen al siglo XX como “el siglo de la estadística” (Batanero, 2001: 7). En ese largo devenir de los usos de la estadística, se han encontrado dentro de la producción de conocimiento en ciencias sociales, posicionamientos de sentido común entre un “rechazo (dogmático)” y una “aceptación (acrítica)” (Piovani, 2007: 8) de sus aportes. De esto último se deriva una necesaria mirada en contexto sobre las posibilidades efectivas de la producción y uso de la estadística para construir e investigar problemas sociales y educativos.
Las estadísticas como objetos culturales
En una lectura sociológica de las estadísticas producidas por entidades estatales e incluso privadas, Claudia Daniel propone entenderlas como “objetos culturales, elaboraciones expertas que resultan de prácticas sociales de clasificación, registro, recuento, comparación de distintos aspectos o dimensiones de la realidad” (Daniel, 2013: 11). Desde ese enfoque, se destaca el prestigio social que cargan por su supuesto vínculo con una realidad manifiestamente “verdadera”, pero también los procesos de consenso y disputa de los que se derivan y, finalmente, su carácter performativo. Esto último quiere decir que el lenguaje estadístico que da forma a los “números públicos” tiene la capacidad de darle forma inteligible a fragmentos de la realidad que son a su vez aquello que precisamente se busca medir. De este modo, para Daniel, las estadísticas “constituyen una gramática compartida, puesto que las cifras aportan las categorías y los esquemas a partir de los cuales pensamos e interpretamos la realidad. Por lo tanto, como códigos de lectura de la realidad, contribuyen también a la formación de un imaginario acerca de quiénes somos y qué nos pasa como sociedad” (p. 34).
El quehacer científico en perspectiva estadística aborda lo social (comportamientos, actitudes, opiniones, relaciones sociales, trayectorias, políticas educativas, etc.) construyendo primordialmente un enfoque general y agregado, en base al lenguaje de las variables (ver Unidad 3, subapartado 3.1.1). Es decir que trabajar estadísticamente en la investigación social supone construir una mirada panorámica, holística e integral que busca estudiar empíricamente, caracterizar y analizar un fragmento colectivo de la realidad social (identificando regularidades, tendencias, aunque también excepciones y rarezas) para construir síntesis y, eventualmente, explicaciones o bien predicciones científicamente fundamentadas según parámetros cuantitativos.
Ese enfoque general y panorámico es el que plantea Ferris Ritchey (2002) en su libro Estadística para las ciencias sociales, cuando nos propone articular la idea de la “imaginación sociológica” –que retoma de un trabajo clásico del sociólogo estadounidense Charles Wright Mills– con su planteo clave de la “imaginación estadística”.
Ritchey, F. (2002). La imaginación estadística. En: Estadística para las ciencias sociales (pp. 1-19). México: McGraw-Hill.
Hacia finales de la década de 1950 y dentro de una discusión en la disciplina sociológica sobre las formas de entender la relación entre individuo y sociedad, C. Wright Mills definió a la imaginación sociológica como una forma sistemática de “captar la historia y la biografía y la relación entre ambas dentro de la sociedad. Esa es su tarea y su promesa” (Mills, 2003: 18). Es decir, como un modo de entender la estructura social –sus dinámicas culturales, económicas, políticas, educativas, etc.– sin dejar de lado las experiencias individuales en su vínculo necesario con condicionantes sociales e históricos más amplios que podrían influenciarlas o afectarlas. Basándose en esta primera idea, Ritchey propone pensar la investigación social en clave de la imaginación estadística, definida según sus palabras como “una apreciación de qué tan usual o inusual es un evento, circunstancia o comportamiento, en relación con un conjunto mayor de eventos similares y una apreciación de las causas y consecuencias del mismo” (Ritchey, 2002). Esto quiere decir que ante un fenómeno social se deberá poner en perspectiva su singularidad o rareza, o ponderar si se trata de la expresión de regularidades colectivas más abarcativas.
Una vía de entrada para poner en práctica esta forma de artesanía intelectual es ubicar el conjunto de eventos o prácticas sociales en su sentido de proporción, es decir, en relación con una totalidad social de la cual forman parte en mayor o menor grado. Será una de las tareas de la estadística caracterizar o ponerle un valor a esa medida proporcional, darle un significado y sacar las conclusiones pertinentes.
Sobre la base de estos aportes, Ritchey (2002) identifica el campo de la estadística como sigue: “Conjunto de procedimientos para reunir, medir, clasificar, codificar, computar, analizar y resumir información numérica adquirida sistemáticamente” (p. 2). Ante ese abanico de tareas posibles, una forma de enfocarlas ha sido la distinción entre la estadística descriptiva y la estadística inferencial.
La estadística descriptiva se enfoca en resumir y describir las características básicas de un conjunto amplio de información estandarizada recabada sistemáticamente (mediante una encuesta, un censo, un operativo de evaluación, etc.). Su objetivo es, por tanto, proporcionar una lectura global de las variables seleccionadas, a partir de la identificación de regularidades y tendencias, o de singularidades y excepcionalidades, en el conjunto de casos bajo estudio.
Entre los procedimientos típicos de la estadística descriptiva (ver más adelante el apartado 4.2) se incluyen el cálculo y la presentación ordenada en tablas y/o gráficos de:
-
Medidas de tendencia central (media, mediana, moda).
-
Medidas de dispersión (rango, varianza, desviación estándar).
-
Medidas de posición (quintiles, cuartiles, deciles y percentiles).
-
Frecuencias (absolutas y relativas).
Como paso más complejo dentro del análisis cuantitativo, la estadística inferencial se enfoca en elaborar conclusiones sobre una población a partir de los datos tomados de una muestra construida de manera probabilística (según lo trabajado en la Unidad 2, apartado 2.2). Su objetivo primordial es así analizar en qué medida los resultados obtenidos en la muestra son estadísticamente representativos –junto a un necesario y calculable margen de error– de la población en su conjunto y poder plantear generalizaciones válidas.
Algunos de los procedimientos propios de la estadística inferencial (ver más adelante el subapartado 4.2.2) incluyen:
-
La prueba de hipótesis sobre relaciones entre variables.
-
El cálculo de intervalos de confianza.
-
El análisis de regresión lineal (simple o múltiple) para analizar la relación entre variables dependientes e independientes.
-
El análisis de varianza para comparar grupos.
En la mirada general que propone la estadística, los casos particulares interesan solo como parte proporcional dentro de una totalidad. Sin embargo, este modo de enfocar los asuntos sociales y educativos no debería dejar de tomar en consideración que lo que se busca abordar básicamente son prácticas y espacios sociales de aprendizaje, trabajo, convivencia y existencia de sujetos situados en el cruce entre sus propios contextos biográficos y las configuraciones sociales, económicas, culturales, políticas e históricas que los atraviesan.
En el sistema educativo, la producción y los usos de la estadística están presentes en distintas instancias que pueden ir desde el diseño de políticas educativas basadas en evidencias y su monitoreo, el relevamiento de las condiciones materiales y pedagógicas de trabajo en las instituciones, la negociación de los salarios docentes, la evaluación estandarizada de los aprendizajes, los insumos, procesos y resultados de la gestión en un jardín de infantes, escuela, instituto superior o universidad, hasta el registro cotidiano de asistencias, calificaciones o características socioeducativas de los y las estudiantes y sus familias.
¿Se puede medir la educación?
“Aunque a primera vista parezcan formas directas de reflejar los hechos y las cosas, las estadísticas jamás están dadas en la realidad, sino que son construidas. Decimos que los datos estadísticos son construcciones sociales, en el mismo sentido en el que nos referimos, por ejemplo, a un edificio, que por construido no deja de ser real, producto de una amalgama de decisiones, acciones y materiales que intervienen en su construcción. Un dato estadístico es la síntesis de un complejo proceso, tanto técnico como político, que involucra una larga cadena de personas, prácticas y decisiones. Al igual que con un edificio, lo mismo ocurre con las estadísticas, según los materiales y el diseño que se elija, puede arrojar resultados de lo más disímiles.
El modo en que se mide un fenómeno social es uno entre muchos posibles. Allí hay decisiones, más o menos arbitrarias, más o menos sustentadas en consensos, pero siempre susceptibles de controversia. Esto no quiere decir que las estadísticas sean falsas, inútiles por tendenciosas o que no podamos tomarlas en serio para analizar o administrar la realidad. Pero muchas veces, en su uso cotidiano, tomamos las informaciones que arrojan como piezas de evidencia indiscutida, ignorando que son el producto de una construcción compleja y parcial, útiles para generar una representación de la realidad, pero no la realidad misma. De hecho, pareciera ser que ese olvido es una condición necesaria para el funcionamiento social de las estadísticas, en cuanto les permite ganar autoridad y transformarse en referencias sólidas para el conjunto de la sociedad”.
(Bottinelli, Tenti Fanfani, Sleiman, Daniel, Grandoli y Pasin, 2018: I)
Según lo trabajado en las unidades anteriores, sabemos que todo abordaje de lo educativo desde el quehacer científico y sus herramientas cuantitativas supone una serie de definiciones precisas para la construcción de un objeto de estudio, y decisiones teóricas y metodológicas rigurosas para su abordaje. Estas pautas son parte del fundamento para entender el carácter construido de los datos, la definición amplia de la idea de medición y el lugar definitorio de quien investiga, así como su posicionamiento ante la realidad. La siguiente reflexión introductoria de Flavia Terigi acompaña esta trama de ideas a partir de una explicación de los usos posibles de los indicadores cuantitativos en el campo educativo.
Los datos estadísticos se construyen con información referida a nosotros, pero lo que dicen sobre nosotros no está en ellos: lo construye quien los interpreta, quien pone en juego lo que sabe, lo que le preocupa, lo que le interesa, en su análisis. Detrás está la gente, como dice Serrat; pero, para encontrarla, hay que saber mirar. Y a mirar, como a tantas otras cosas, se aprende.
(Terigi, 2008: 2)
Terigi, F. (2008). “Detrás, está la gente”. Clase 1 del Seminario Virtual de Formación “Lecturas de las políticas educativas de inclusión e igualdad”. Organización de Estados Americanos, Proyecto Hemisférico Elaboración de Políticas y Estrategias para la Prevención del Fracaso Escolar. https://elvs-tuc.infd.edu.ar/sitio/nuestra-escuela-formacion-situada/upload/Detras_esta_la_gente-_Terigi.pdf
4.1.2. Trabajar con los datos
La sistematización del material empírico construido desde la encuesta, operativo censal o evaluación que se haya planteado como estrategia metodológica, requiere su carga y codificación dentro de lo que se denomina matriz de datos.
La matriz de datos ordena –a partir de una disposición visual básica organizada en filas y columnas– la información relevada en el trabajo de campo para cada una de las variables definidas. Facilita así las tareas estadísticas de procesamiento, tabulación, graficación y análisis.
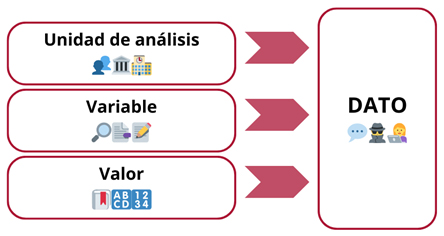
La matriz permite trabajar con lo que se conoce como la “forma tripartita del dato” –según la formulación original del sociólogo noruego Johan Galtung en su libro Theory and Methods of Social Research (Teoría y métodos de investigación social) de 1967–. Para Galtung (1978), los tres componentes fundamentales de los datos sociológicos que buscan expresarse mediante el lenguaje de las variables son: 1) las unidades de análisis, 2) las variables y 3) los valores.
La matriz de datos hace visible esta forma tripartita, ya que en aquella se disponen las unidades de análisis en las filas, las variables en las columnas y, en cada celda que las cruza, se presentan los valores específicos. La matriz de datos tiene entonces esta forma bidimensional básica:
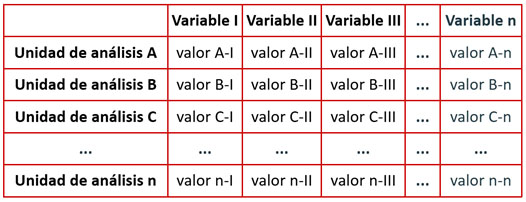
Esto quiere decir que un dato emerge solamente en el cruce entre unas unidades de análisis (que podrán ser individuos, grupos, instituciones, países, etc.) y unas variables (que solo cobran relevancia a partir del problema de conocimiento, el marco teórico y la forma de operacionalización que se haya definido dentro un proyecto de investigación). A su vez, cada una de las variables adquiere determinados valores (en forma de números o categorías) para cada unidad de análisis. En el cruce entre esos tres componentes, un dato se expresa en una proposición u oración con sentido.
Del planteo original de Galtung (1978) se derivan tres principios para construir una matriz de datos robusta que facilite luego su procesamiento estadístico:
-
Debe dar cuenta de una relación con sentido entre las unidades de análisis y las variables, de modo que los casos sean comparables entre sí. Por ejemplo, no tendría sentido que, si las unidades de análisis fueran escuelas de nivel primario, una de las variables fuera “Antigüedad en el cargo docente”.
-
Cada variable debe permitir una clasificación con sentido, es decir que los valores posibles que puede tomar una variable deben ser exhaustivos y excluyentes entre sí (sin posibilidad de superposición ni ambigüedad en la respuesta recibida).
-
Debe tener una composición integral, es decir que no deben existir celdas vacías (sin respuestas), o estas deberían ser la menor cantidad posible.
La imputación de valores faltantes
En el largo camino entre el diseño de un cuestionario, el trabajo de campo de una encuesta y la carga en una matriz de datos de esa información relevada, puede darse una pérdida o falta de respuestas.
Las respuestas faltantes son muy comunes (preguntas no respondidas o respondidas parcialmente). Entre las causas de esa falta de respuesta, pueden estar el cansancio o negación de quien debía responder, su desconocimiento efectivo de la información solicitada, el rechazo a responder sobre determinados temas, así como el criterio para la selección de casos de la muestra que fueran efectivamente pertinentes (Medina y Galván, 2007). En una matriz, a esos casos a veces se les adjudica el valor “No sabe” o “No contesta”. En tales ocasiones, habrá que distinguir entre las respuestas legítimas y las fallas en la etapa de recopilación de los datos, así como considerar si las respuestas faltantes se suceden al azar o si se asocia a algún subgrupo dentro de la muestra (Zeisel, 1990).
También puede darse el caso de respuestas que no son faltantes pero son evidentemente ilógicas, pues fueron anotadas erróneamente en la carga de datos. Por ejemplo, si en una matriz de datos nos encontráramos que un estudiante de nivel primario de la modalidad común respondió “125” en la variable edad, estaríamos claramente ante una respuesta mal registrada. A estos valores atípicos o anómalos se los puede clasificar como outliers.
Las respuestas faltantes o atípicas requieren una revisión y tratamiento porque pueden afectar los resultados del análisis. Desde la estadística, hay varias posibilidades o métodos de imputación para tratarlos. En el trabajo con matrices de datos, imputar significa asignarle un valor válido a una celda con un valor faltante.
-
La alternativa previa y más simple de ejecutar es la eliminación de los casos con respuestas faltantes. Sin embargo, se correría el riesgo de reducir el tamaño de la muestra con la que se trabaja y sesgar los resultados. También podrá explicitarse en la presentación de los datos en tablas o gráficos (ver más adelante el subapartado 4.2.3) la cantidad de valores faltantes con los que no se trabajó estadísticamente (para todo el conjunto de datos o para determinadas variables).
-
Desde las herramientas estadísticas, se puede generar una imputación simple basándose en: 1) una sustitución de los valores faltantes por lo que se llaman medidas de tendencia central, esto es, la media, la mediana y la moda (ver más adelante el subapartado 4.2.1). Por ejemplo, ante celdas vacías, puede imputarse como valor válido la media (o promedio) o también la moda (o valor que más se repite) de la variable que esté en consideración. 2) Imputación por regresión, que se realiza sobre la base de una predicción estadística de los valores faltantes de una variable a partir de los valores de otras variables y su patrón de correlación con la primera. Por ejemplo, imputar el valor faltante del nivel socioeconómico de estudiantes en función de la correlación general de esa variable con la cantidad de años de escolaridad de la madre o padre. 3) La asignación de un valor válido en función de los valores observados en otros casos similares o tomados de una fuente externa.
-
De manera más elaborada, existen formas de imputación múltiple a partir de la creación de distintas simulaciones estadísticas con imputaciones para el conjunto de datos, que luego se analizan y combinan para generar valores válidos ante los valores faltantes.
Zeisel, H. (1990). Cómo tratar los “No sé” y los “Sin respuesta”. En: Dígalo con números (pp. 65-80). Buenos Aires: Fondo de Cultura Económica.
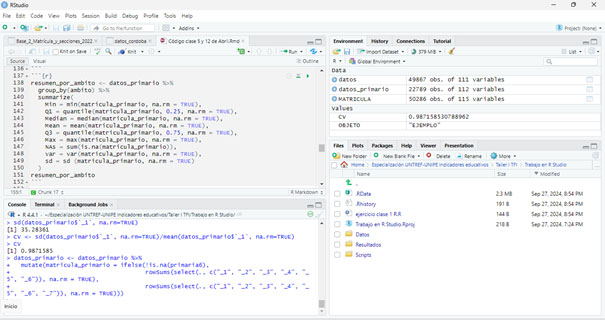
Programas para el procesamiento de datos cuantitativos
Una mención aparte merece el procesamiento cuantitativo de las matrices de datos con programas específicos.
Algunas posibilidades básicas las presenta Excel (como parte del paquete Office) (Microsoft Corp., 2019). Permite trabajar en el formato de hojas de cálculo con archivos de extensión *.xlsx (o *xls en sus primeras versiones) y con otros formatos genéricos que presentan los valores separados por comas, con la extensión *.csv y que pueden ser también abiertos con Excel. Estos tipos de archivos también son manipulables de manera online y colaborativa a través de Google Sheets (como parte del paquete de Google Docs) (Google LLC, 2025). O con el uso de software libre con funciones similares, como LibreOffice (The Document Foundation, 2025). Algunos cálculos y graficaciones son posibles con estos programas, aunque los procedimientos estadísticos más complejos y específicos han sido programados como opciones de fácil acceso en otro tipo de software para el análisis cuantitativo.
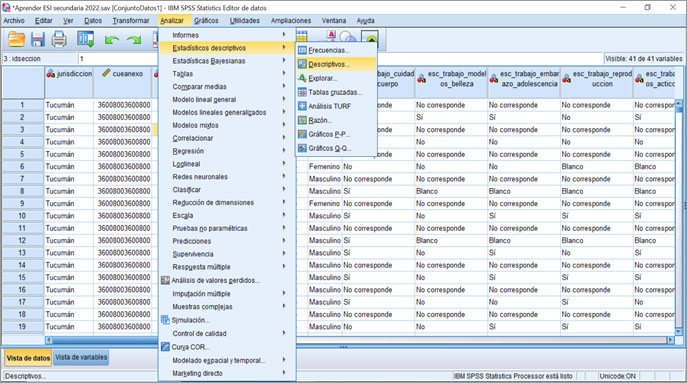
Particularmente para el trabajo estadístico en ciencias sociales, uno de los primeros programas destacados ha sido el SPSS (Statistical Package for the Social Sciences, esto es, paquete estadístico para las ciencias sociales) de la empresa IBM (IBM Corp., 2017). Es un programa con una licencia paga, aunque permite acceder a una versión de prueba con límite temporal. Sus archivos para el manejo de matrices de datos tienen la extensión *.sav y, en su pestaña de vista de datos, muestran una interfaz y presentación visual similar al Excel. El SPSS permite generar cálculos más complejos entre la estadística descriptiva y la estadística inferencial, así como la presentación de tablas y graficaciones elementales para el conjunto de datos que se esté trabajando.
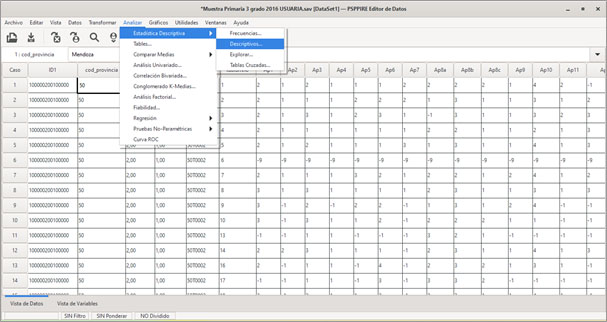
Una alternativa de acceso libre es el programa PSPP (Public domain Statistical Package for Social Sciences, es decir, paquete estadístico de dominio público para ciencias sociales) (Free Software Foundation, 2024). Está basado en un código abierto y ofrece muchas de las herramientas de análisis estadístico del SPSS de IBM. PSPP es compatible con una variedad de formatos de archivo, incluyendo los propios de SPSS (*.sav) y otros formatos comunes (como los de extensión *.csv).
Otra herramienta de uso recurrente en el análisis de datos cuantitativos es el entorno de trabajo RStudio (Posit PBC, 2025), que permite trabajar mediante un lenguaje de programación especializado denominado R, ampliamente utilizado para el análisis estadístico (en estudios sobre economía, sociología, educación, epidemiología, etc.). Es una herramienta de uso gratuito y generada dentro de un marco colaborativo y abierto. Su utilización facilita procesar, analizar y graficar datos desde los parámetros de la estadística descriptiva e inferencial.
Parte del potencial de este tipo de lenguaje está en que, mediante la codificación escrita, es posible automatizar tareas, replicar pasos en el análisis de los datos y compartirlos con otros colegas o grupos de investigación. Al tratarse de una plataforma de código abierto, cuenta también con una comunidad activa de usuarios y desarrolladores que actualiza funciones y complementos (en forma de “paquetes” y “librerías”).
4.1.3. Los niveles de medición de las variables
Como señalamos al inicio, trabajar desde una perspectiva amplia de la medición en ciencias sociales, pero también desde el lenguaje de las variables para abordar la realidad social y educativa, implica trabajar con entidades que podemos clasificar como cualidades o cantidades. Dentro de la investigación social con apoyo en la estadística, esto quiere decir que las variables pueden tener distintos niveles de medición.
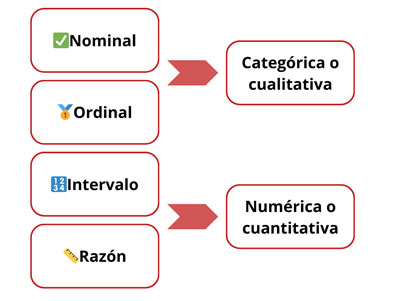
La idea de los niveles de medición de las variables en ciencias sociales fue planteada por primera vez por el psicólogo estadounidense Stanley S. Stevens en un artículo “On the Theory of Scales of Measurement” (Sobre la teoría de escalas de medición) publicado en 1946. La clasificación que propuso Stevens –y que sigue vigente en el análisis cuantitativo de datos– supone cuatro niveles de medición para las variables:
-
Nominal
-
Ordinal
-
Intervalo
-
Razón
Las variables nominales y ordinales también pueden clasificarse como categóricas o cualitativas, mientras que las variables de intervalo y de razón son de tipo numérico o cuantitativo.
Esta clasificación resulta útil para determinar qué tipo de análisis estadístico y modos de graficación son posibles y apropiados para los distintos tipos de variables.
Variables nominales
Las variables nominales suponen el primer paso básico de clasificación en categorías (etiquetas, tipologías, nombres o atributos para el mismo tipo de unidades de análisis). Entre esas categorías no existe una jerarquía ni una distancia medible o comparable.
Un criterio básico en la definición de sus valores es que ellos sean exhaustivos y excluyentes entre sí. Asimismo, las variables nominales pueden ser dicotómicas (solo con dos opciones) o politómicas (con más de dos opciones).
Variables ordinales
Las variables ordinales suponen también categorías, aunque entre ellas se reconoce un orden, gradación, secuencia, escalonamiento o progresión.
Esto quiere decir que puede plantearse una comparación de las diferencias entre sus categorías. Pero, dado que la distancia entre las categorías no es uniforme, no puede plantearse su medición cuantitativa. Por caso, no tendría sentido decir que, en una variable que mida niveles de acuerdo con una afirmación a partir de una escala Likert, el valor “Totalmente de acuerdo” representa el doble de “Ni en acuerdo ni en desacuerdo”. Pero sí podrá establecerse una comparación que ubique e interprete la gradación u orden de esos valores.
Variables de intervalo
En las variables de intervalo, la distancia entre cada uno de los valores expresados cuantitativamente es uniforme, medible y comparable. La particularidad de este tipo de variables es que tienen un cero arbitrario como punto de origen. Es decir que el valor “0” (cero) no implica ausencia de lo que se mide, sino un corte arbitrario establecido de manera convencional como punto de referencia. De este modo, se pueden realizar comparaciones, establecer un orden entre sus valores y medir la distancia existente entre ellos (mediante operaciones de suma y resta).
Variables de razón
Las variables de razón (o de proporción o de cociente) también se expresan cuantitativamente. La distancia entre sus valores es igual, constante, proporcional, comparable y medible. La diferencia con las variables de intervalo es que las variables de razón tienen un cero absoluto como punto de origen. Es decir que el cero es una referencia única y absoluta (y no arbitraria o establecida por convención). El valor “0” (cero) indica así la ausencia de aquello que se quiere medir. Por ello, este tipo de variables no puede tener valores negativos.
A partir de este parámetro común, es posible realizar con este tipo de variables operaciones matemáticas como suma, resta, multiplicación y división.
Estos cuatro niveles de medición de las variables tienen entre sí una lógica acumulativa, es decir que cada nivel comparte las propiedades de los niveles de medición que le anteceden (Cea D’Ancona, 1996). Esto posibilita que, si fuera necesario para facilitar el análisis o su presentación, las variables cuantitativas (de intervalo o de razón) podrían recategorizarse como variables ordinales o nominales, basándose en un agrupamiento de sus valores cuantitativos según puntos de corte que establezcan intervalos de clase y se reclasifiquen categóricamente. Por ejemplo, la variable cuantitativa de razón “Salario mensual” (medida en cantidad de pesos) puede ser agrupada en intervalos de clase (“$1 a $999 999”, “$1 000 000 a $3 000 000” y “Más de $3 000 000”) que, a su vez, pueden tomar las respectivas etiquetas de “Salario bajo”, “Salario medio” y “Salario alto”, haciendo así de la variable “Salario mensual” una de tipo categórico y ordinal.
Por tanto, una clave para definir el nivel de medición de una variable es el tipo de valores que puede adquirir y el alcance de los objetivos de investigación.
Es en función de los tipos de valores adjudicados a la variable que se definirá cuál es su nivel de medición. Es decir que una variable no es intrínsecamente nominal, ordinal, de intervalo o de razón, sino que ella podrá tomar distintos tipos de valores (según se haya definido en su operacionalización).
Por ejemplo, la variable “Edad” puede tomar como valor para su medición la cantidad de años de vida cumplidos (1, 2, 3, 4, etc.). En tal caso, se tratará de una variable cuantitativa con nivel de medición de razón. Pero desde otra perspectiva alternativa, podrían asignársele a la variable “Edad” los siguientes valores cualitativos: “Recién nacido”, “Infante”, “Preadolescente”, “Adolescente”, “Joven”, “Adulto/a” y “Adulto/a mayor”. Estas categorías harían de la “Edad” una variable ordinal.
O bien podríamos considerar como caso la variable referida al “Nivel educativo de la madre” de estudiantes en edad escolar. Esta variable podría reflejarse en valores del tipo “Sin instrucción”, “Primario incompleto”, “Primario completo”, “Secundario incompleto”, “Secundario completo”, “Superior incompleto” y “Superior completo”. Sería así una variable categórica con un nivel de medición ordinal. Aunque otra decisión metodológica podría ser la de otorgarle a esta variable valores cuantitativos en la forma de cantidad de años de escolaridad (más allá de los niveles del sistema educativo), haciendo del “Nivel educativo de la madre” una variable de razón.
García Ferrando, M. (1985). El análisis estadístico de los datos sociológicos. En: Socioestadística. Introducción a la estadística en sociología (pp. 23-43). Madrid: Alianza.
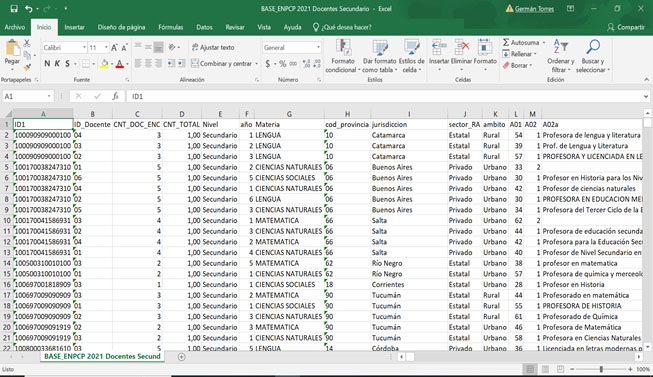
A partir de la siguiente matriz de datos, identifique:
-
Cuáles son las unidades de análisis.
-
Qué variables se presentan.
-
Qué tipo de valores (numéricos o categóricos) toman las variables.
-
Cuál es el nivel de medición de cada una de las variables.
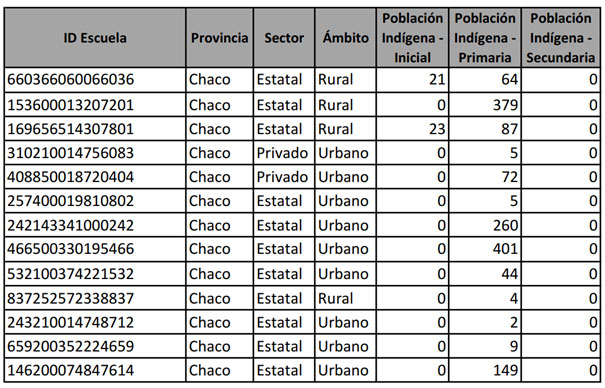 Fuente: selección adaptada del Relevamiento Anual 2023. Base 6: Educación Común - Población. RedFIE-DIE.
Fuente: selección adaptada del Relevamiento Anual 2023. Base 6: Educación Común - Población. RedFIE-DIE.
4.2. Análisis estadístico y presentación de datos
La idea de los datos como construcciones (ver Unidad 3, apartado 3.1) marca la necesaria impronta teórica que fundamenta a toda pregunta investigativa, el relevamiento de información empírica y su posterior análisis, interpretación y discusión. Al decir de Ruth Sautu (2011): “Los datos sin teoría, cualquiera sea la manera como fueron recogidos, no tienen un interés académico”, esto quiere decir que es la teoría la que “permite la construcción de la evidencia empírica” (p. 69), y es uno de los elementos claves para diferenciar a la investigación científica de un ensayo, el relato de un caso periodístico o un conjunto de estadísticas compiladas.
En una línea de sentido complementaria, María Teresa Sirvent y Luis Rigal (2023) plantean que lo que denominan como “marco de referencia teórico conceptual” (ver Unidad 2, subapartado 2.1.5) tiene un valor fértil al “darle voz al corpus empírico”. Es decir, plantean una superación de la idea empirista de que “los datos hablan por sí solos” (p. 224) sin una intervención de quien investiga y su elección teórica, la que le permite decir algo nuevo sobre aquello que se investiga.
En esta mirada cobra sentido el trabajo con herramientas y procedimientos de la estadística para analizar, presentar y comunicar los datos construidos, según se presentará en los siguientes apartados. Como señalamos, las tareas estadísticas pueden entenderse según su alcance descriptivo dando cuenta de frecuencias, medidas de tendencia central, de posición y de dispersión. Y también puede trabajarse en función de su alcance inferencial, enfocándose en las relaciones entre variables y la puesta a prueba de las hipótesis con vistas a la construcción de generalizaciones válidas.
4.2.1. Medidas de tendencia central, de dispersión y de posición
Ante una matriz de datos, interesa destacar algunas características de las variables. Desde la estadística descriptiva, se puede enfocar en la forma en que se distribuyen los valores de las variables a partir de sus medidas de tendencia central, de dispersión y de posición. Estas medidas buscan resumir un conjunto amplio de valores tomados de una muestra o población.
Medidas de tendencia central
En primer lugar, se puede dar cuenta de las medidas de tendencia central de una variable: 1) la media, 2) la mediana y 3) la moda.
Ritchey, F. (2002). Estimación de promedios. En: Estadística para las ciencias sociales (pp. 107-135). México: McGraw-Hill.
La media
La media aritmética es el valor promedio de una variable. Se calcula sumando los valores de todos los casos y dividiéndolos por el número total de casos (o unidades de análisis).
Así calculada, la media es sensible a valores extremos o atípicos (outliers) que podrían hacer que tome un valor poco significativo para entender cómo se distribuye la variable.
Por su naturaleza cuantitativa, la media puede ser calculada solo en variables con un nivel de medición de intervalo o de razón. Y no tiene sentido calcularla en variables categóricas nominales u ordinales.
La mediana
La mediana es el valor central de un conjunto de datos ordenados. Es decir que es el valor que divide a los datos –ordenados de menor a mayor– en dos partes iguales, de modo que el 50 % de los casos está por debajo y el otro 50 % por encima.
La mediana resulta útil cuando hay valores extremos o atípicos (outliers) que pueden distorsionar el valor de la media y su significado.
El cálculo de la mediana es aplicable a variables con un nivel de medición ordinal, de intervalos y de razón, pero no a variables nominales porque en ellas no hay un orden o jerarquía lógica entre sus valores categóricos.
La moda
La moda (también denominada como modo) es el valor que más se repite en un conjunto de datos. Puede suceder que exista más de una moda (distribución bimodal o multimodal) o ninguna moda si todos los valores son diferentes. Su utilidad radica en que permite identificar tendencias o patrones comunes.
El cálculo de la moda puede utilizarse con variables de todos los niveles de medición.
¿Media o mediana?
En una nota de divulgación matemática titulada “De cómo Bill Gates altera el promedio: Buenas tardes… ¿Puedo hablar con la mediana por favor?”, Adrián Paenza nos advierte sobre las distorsiones de la media (o promedio) ante valores extremos y el aporte de la mediana para interpretar la distribución real de los datos.
[...] Volvamos al ejemplo de las 100 personas que trabajan en la oficina de manera tal que todas cobran 100 mil pesos por mes. Supongamos por un instante que uno de los trabajadores sale de la oficina, y entra Bill Gates. Sigue habiendo 100 personas, todos siguen cobrando 100 mil pesos, con la excepción de uno: el nuevo integrante del grupo. ¿Cuánto dará el promedio ahora?
[...]
Como usted advierte, el promedio ha sufrido un brutal incremento: ahora, el salario promedio de las personas que están dentro de la oficina es de 10.099.000, mientras que sin Bill Gates, ese salario promedio era de 100 mil pesos.
[...]
Es decir, la aparición de Bill Gates, distorsionó el promedio y ofrece una muy mala idea de lo que uno querría estimar (cuánto cobran en promedio las personas que trabajan en la oficina). Técnicamente, es irreprochable: el promedio con Bill Gates se eleva a más de 10 millones de pesos mensuales, pero es la mediana la que evita que la aparición de un solo integrante que percibe un número TAN diferente de todos los otros, decía… este integrante NO ALTERA la percepción que querríamos tener.
[...]
Moraleja: cuando usted lea en un diario o escuche por televisión o por radio cuando alguien quiera evaluar el promedio de los salarios en alguna región o ciudad o barrio (o lo que fuere), piense que este particular número (el promedio), ¡no es el único que debería usarse! Uno debería llamar al medio de comunicación que ofreció ese dato y pedirles que le ofrezcan un segundo número: ¡la mediana! Los mismos datos que les permitieron obtener el promedio sirven para calcular la mediana. Con ambos números, las conclusiones que uno saque serán decididamente más cercanas a la realidad.
(Paenza, 2021)
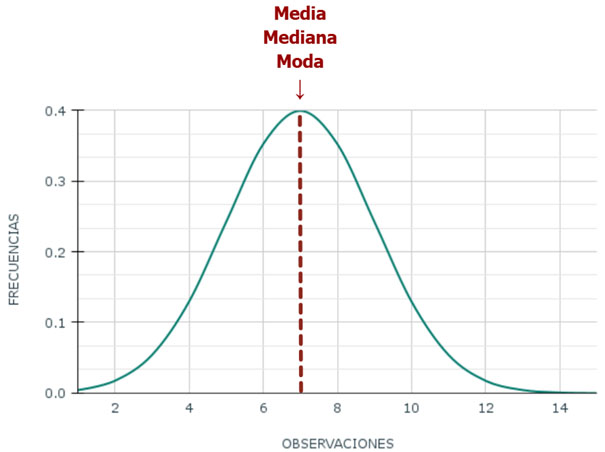
En la representación de la distribución normal de una variable cuantitativa, la media, la mediana y la moda coinciden. En caso contrario, se tratará de distribuciones asimétricas. La graficación de la distribución normal es una curva simétrica (es decir, que se reparte en mitades iguales hacia su izquierda y derecha), unimodal (es decir, con un solo pico o moda) y tiene forma acampanada.
La distribución normal es un elemento relevante en el análisis estadístico. Existen algunos fenómenos o características que efectivamente tienden a una distribución normal, como el coeficiente intelectual (CI) o la altura de las personas. Pero, fundamentalmente, la mayoría de los procedimientos de la estadística inferencial (ver más adelante el subapartado 4.2.2 sobre la prueba de hipótesis) asumen como supuesto teórico que los valores de una variable tienen una distribución normal. Es el caso del teorema del límite central que indica que, por un lado, si se extrajeran repetidas muestras aleatorias simples a partir de una población (ver lo trabajado en la Unidad 2, apartado 2.2), las medias de tales muestras se distribuirán normalmente; y, por otro lado, que sobre la base de la denominada ley de los grandes números, si la muestra es suficientemente grande, independientemente de la distribución de la población, también tenderá a distribuirse normalmente. Este planteo es el que está en la base de la inferencia de parámetros poblaciones a partir de los valores estadísticos de una muestra aleatoria o probabilística.
Blalock, H. (1986). Escalas de intervalo: medidas de tendencia central. En: Estadística Social (pp. 67-89). México: Fondo de Cultura Económica.
García Ferrando, M. (1985). Características de una distribución de frecuencias: tendencia central, distribución y forma. La distribución normal. En: Socioestadística. Introducción a la estadística en sociología (pp. 85-117). Madrid: Alianza.
Medidas de dispersión
En segundo lugar, el trabajo estadístico en clave descriptiva puede indicar también las medidas de dispersión de una variable en una población, muestra o conjunto de muestras. Las medidas de dispersión más utilizadas son: 1) el rango, 2) la desviación estándar y 3) la varianza.
En términos generales, su cálculo permite visualizar qué tan homogéneos o heterogéneos son los valores de una variable en un conjunto de datos y también comparar distintas muestras.
Pérez-Tejada, H. (2008). Medidas de dispersión o variabilidad. En: Estadística para las ciencias sociales, del comportamiento y de la salud (pp. 63-69). México: Cengage Learning.
Ritchey, F. (2002). Medición de la dispersión o variación en una distribución de puntuaciones. En: Estadística para las ciencias sociales (pp. 136-156). México: McGraw-Hill.
El rango
El rango (también denominado recorrido o amplitud de variación) es la diferencia entre el valor máximo y el valor mínimo que toma una variable. Cuanto mayor sea el rango, la dispersión de los datos también será más alta.
Por ejemplo, en una muestra supuesta de docentes de nivel superior de formación docente, las edades varían entre un valor mínimo de 24 y un valor máximo de 59 años. Por tanto, el rango es: 59 – 24 = 35.
Esta medida aporta así un primer panorama sobre la amplitud de la distribución de los datos, tomando sus extremos.
La desviación estándar
La desviación estándar expresa cuánto se desvían, en promedio, los valores de la variable en relación con su media (o promedio). Es decir que permite visualizar cómo los valores de una variable cuantitativa se dispersan a lo largo de todo el conjunto de datos tomando como punto de referencia la media o promedio de esa variable. Por ello, la desviación estándar se interpreta siempre en relación con la media.
La desviación estándar se denomina así porque ofrece una unidad de medida común (o estandarizada) expresada precisamente en unidades de desviación estándar (Ritchey, 2002). Una de sus ventajas es que ofrece una medida de comparación con otros grupos o muestras.
Una desviación estándar alta indicará que la dispersión y variabilidad de los valores es mayor, mientras que una desviación estándar baja mostrará que los valores son similares entre sí y tienden a estar cerca del promedio.
La varianza
La varianza es una medida expresada al cuadrado que indica cuánto se dispersan los datos respecto a la media. Se puede obtener su valor elevando al cuadrado la desviación estándar. Por tanto, se simboliza como s².
Permite distinguir si los valores de una variable tienen una distribución homogénea (varianza baja) o si existen amplias diferencias entre ellos (varianza alta).
Es una parte del cálculo de la desviación estándar, entonces no es fácil interpretarla directamente ya que está expresada en unidades al cuadrado. La varianza es la base para métodos estadísticos más avanzados en ciencias sociales, tales como el análisis de la varianza (o ANOVA por el acrónimo en inglés de analysis of variance), la regresión lineal o las pruebas de hipótesis (ver más adelante subapartado 4.2.2).
Medidas de posición
En tercer lugar, otros elementos estadísticos descriptivos son las medidas de posición (también denominadas como medidas de tendencia no central y definidas genéricamente como cuantiles). Ellas son los cuartiles, quintiles, deciles y percentiles.
Estas medidas de posición requieren que se ordenen los valores de una variable de menor a mayor. Son útiles para entender la distribución de los datos y para realizar comparaciones dentro del conjunto. Ayudan así a identificar tendencias y regularidades, así como valores atípicos o anómalos (outliers) que podrían influir en la interpretación de los resultados.
Cuartiles
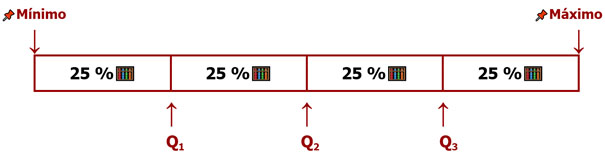
Los cuartiles son puntos de corte que dividen el conjunto de valores ordenados en cuatro partes iguales, resultando en tres cuartiles. El primer cuartil (que se denomina Q₁) es el valor que divide el 25 % inferior de los datos, el segundo cuartil (Q₂) es equivalente a la mediana (es decir que divide a los datos ordenados en dos mitades) y el tercer cuartil (Q₃) incluye el 75 % inferior de los datos y marca el inicio del 25 % superior.
Los cuartiles, junto a los quintiles, son las medidas de posición más usadas en el análisis y presentación de datos en la investigación social, especialmente en perspectiva cuantitativa. Su uso típico se presenta en los análisis de los niveles de ingresos económicos de una población, donde el cuartil menor da cuenta de los grupos con menos ingresos y el cuartil superior agrupa a la población con mayores ingresos.
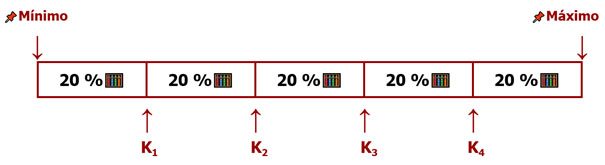
Quintiles
Esta medida de posición divide al conjunto de datos ordenados en cinco subconjuntos iguales (cada uno representa el 20 % de los valores). Se marcan así cuatro quintiles. El primer quintil (denominado K₁) marca el límite del 20 % de los valores más bajos, es decir que el 20% de los valores son menores o iguales a ese punto. El segundo quintil (K₂) deja por debajo al 40 % de los valores. El tercer quintil (K₃) divide el 60 % inferior. Y, finalmente, el cuarto quintil (K₄) indica hasta el 80 % de los valores y marca que el 20 % restante está por encima.
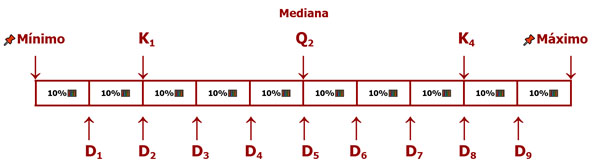
Deciles
Dividen a los datos en diez partes iguales, siendo nueve deciles. El primer decil (D₁) deja el 10 % de los valores ordenados por debajo y el resto por encima, y así sucesivamente hasta el decil 9. El quinto decil (D₅) es también la mediana (y el cuartil 2 o Q₂). Siguiendo esta lógica, el decil 2 (D₂) es también el quintil 1 (K₁), a la vez que el decil 8 (D₈) está en la misma posición que el quintil 4 (K₄).
Percentiles
Dividen los datos en 100 partes iguales. De este modo, el percentil 50 (P₅₀) es la mediana y es también el segundo cuartil (Q₂).
4.2.2. Relaciones entre variables y prueba de hipótesis
En el proceso de investigación en perspectiva cuantitativa, uno de sus alcances más elaborados es la construcción de inferencias que expliquen o incluso predigan el comportamiento de las variables respecto de determinado recorte de la realidad social bajo estudio (ver en la Unidad 2 el subapartado 2.1.3 en relación con el alcance posible de los objetivos dentro de un proyecto de investigación).
Con ese propósito, el análisis de las relaciones entre variables supone la puesta a prueba de hipótesis en términos estadísticos.
Variables independientes y dependientes
Una forma de categorizar a las variables dentro de un estudio que busca poner a prueba hipótesis es la relación que existe entre ellas; por tanto, pueden ser:
- Variables independientes
- Variables dependientes
A la variable independiente se la denomina también variable explicativa, es decir que se la plantea como factor causal en el contexto de una pregunta de investigación y su correspondiente hipótesis.
Mientras que a la variable dependiente también se la denomina variable explicada. Precisamente, la variable dependiente es lo que se busca entender y medir estadísticamente como efecto posible de la variable independiente.
Otras definiciones alternativas de las variables independiente y dependiente se presentan en la siguiente tabla.
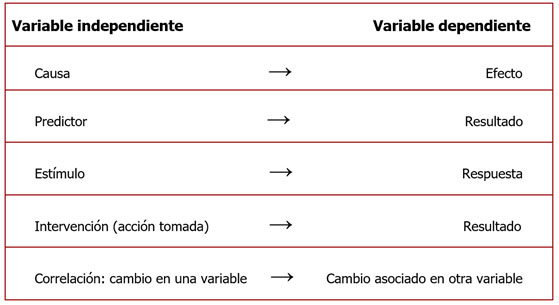
Interesa así analizar de qué modo una variable se encuentra afectando a otra (u otras) o, en otras palabras, cómo se correlacionan. La definición de la hipótesis que relaciona una variable independiente con otra dependiente estará dada principalmente por el marco teórico y los antecedentes de investigación que guían su formulación. Ese mismo marco teórico será el que luego oriente la interpretación de los resultados.
Si bien en las pruebas de hipótesis (ver el siguiente apartado) se busca calcular la magnitud y dirección de la relación entre variables, debe advertirse que incluso una fuerte correlación estadística entre ellas no implica necesariamente una asociación automática de causa y efecto. Es decir que una fuerte correlación entre una variable X y una variable Y no puede constituirse en prueba suficiente de una relación causal, dado que pueden existir otros factores que no están siendo considerados o porque podría tratarse de una relación espuria (sin conexión lógica). En ese mismo sentido, tampoco sería posible asumir linealmente que, si la variable X se sucedió luego de la variable Y, Y sea la causa de X.
Marradi, A., Archenti, N. y Piovani, J. (2012). El análisis bivariable. En: Metodología de las ciencias sociales (pp. 223-254). Buenos Aires: Cengage Learning.
Prueba de hipótesis
En el quehacer científico en perspectiva cuantitativa, una prueba de hipótesis es un procedimiento estadístico que se usa para determinar si hay suficiente evidencia empírica para aceptar o rechazar la hipótesis planteada en vínculo con una pregunta de investigación de alcance explicativo o predictivo (ver en la Unidad 2, el subapartado 2.1.2).
En el cruce entre el método hipotético-deductivo y el análisis estadístico, a la hipótesis de investigación que guía al proyecto se la invierte para plantear como punto de partida una hipótesis nula.
En la hipótesis nula (representada como H0) se plantea que no existe relación, efecto o diferencia significativa entre las variables definidas en la hipótesis de investigación. A partir de pruebas estadísticas estandarizadas, lo que se busca finalmente es recolectar evidencias para rechazar la hipótesis nula y así poder corroborar lo que se define como hipótesis alternativa (representada como H1) que no es otra cosa que la hipótesis de investigación que se busca sostener. En palabras del epistemólogo Gregorio Klimosky: “La corroboración significa, simplemente, que si bien seguimos sin saber nada acerca de la verdad de la hipótesis, ésta ha resistido un intento de refutarla y ha probado, hasta el momento, no ser falsa” (Klimovsky, 1994: 138).
Como parte de las tareas de la estadística inferencial, existen técnicas correlacionales que buscan responder si dos variables están efectivamente relacionadas entre sí. Y, si la respuesta es positiva, se buscará saber también cuál es la dirección de esa relación y cuál es su fuerza, intensidad o magnitud (Cohen, Manion y Morrison, 2007).
En la investigación cuantitativa en ciencias sociales existen múltiples pruebas o tests estadísticos para analizar las relaciones entre variables y entre grupos (Hidalgo, 2019). Entre las pruebas más utilizadas se encuentran las siguientes:
- Chi-cuadrado (χ²): para analizar relaciones entre variables categóricas.
- Coeficiente de correlación de Pearson: mide la fuerza y dirección de una relación entre dos variables cuantitativas y continuas.
- Coeficiente de correlación de Spearman: utilizado para variables categóricas ordinales o cuando las variables no se ajustan a un modelo teórico de distribución normal.
- Coeficiente de correlación de Kendall: para variables categóricas ordinales.
- Regresión lineal simple y múltiple: para predecir una variable dependiente cuantitativa.
Yendo del chorizo al chancho. El análisis de regresión
“Una de las patas flojas de las ciencias sociales es su dificultad para realizar experimentos, como los que hacen los biólogos o los agrónomos. No es por falta de imaginación. Muchas veces la experimentación en ciencias sociales se topa con barreras éticas o legales, antes que con dificultades metodológicas. [...]
Si quisiéramos aprender acerca de los efectos de la educación sobre los salarios [...] podríamos asignar distintos niveles de educación a distintas personas y luego medir sus performances, en términos de cuánto dinero ganan o de sus logros profesionales. Claramente, impedir que una persona continúe su educación solo porque queremos implementar un experimento es éticamente aberrante, además de ridículo. Entonces, la inhabilidad de llevar a cabo este experimento se enfrenta con una restricción moral y también legal, antes que con una restricción lógica o metodológica. El experimento es fácil de pensar, y lógicamente coherente, pero no es implementable en la práctica.
Por otro lado, existe el análisis de regresión, el “automóvil de la estadística moderna”, que, al decir del reconocido historiador de la estadística George Stigler, es una herramienta ampliamente usada (y abusada) para medir efectos causales sin necesidad de apelar a experimentos, lo cual explica su enorme popularidad en las ciencias sociales. [...]
El gran desafío de las técnicas de regresión, que nos permiten ir de lo observado a sus determinantes, implica tener un buen conocimiento de qué es lo que explica lo que nos interesa, y de que aquello que se quedó afuera no molesta. Pavada de desafío, ya que implica conocer muy bien cómo funcionan las cosas”.
(Sosa Escudero, 2022: 64-68)
Kelmansky, D. (2009). Decisiones en el campo de la estadística. En: Estadística para todos (pp. 231-244). Buenos Aires: Ministerio de Educación de la Nación - Instituto Nacional de Educación Tecnológica.
Ritchey, F. (2002). Prueba de hipótesis I. Los seis pasos de la inferencia estadística. En: Estadística para las ciencias sociales (pp. 267-302). México: McGraw-Hill.
Realice la siguiente actividad a partir de la información a nivel nacional presentada en la página 6 del informe “Mujeres en la ETP. Algunos datos sobre la participación de las mujeres en la secundaria técnica” (INET, 2020).
-
Elabore una hipótesis que correlacione dos de las variables presentadas (tipo de escuela secundaria –común o técnica–, matrícula, género, porcentaje de varones y mujeres en 1° año, porcentaje de varones y mujeres que egresan, y especialidad elegida) para una eventual investigación explicativa.
-
Establezca cuál es la variable independiente y cuál la dependiente.
-
Defina la hipótesis nula y la hipótesis alternativa a poner a prueba.
-
Comparta y compare su respuesta con colegas del curso. Y realice ajustes si lo cree necesario.
 Fuente: INET (2020: 6).
Fuente: INET (2020: 6).
Enlace al informe: https://www.inet.edu.ar/wp-content/uploads/2020/07/ETP_Mujeres-en-la-Secundaria-T--cnica_2020.pdf
4.2.3. El análisis y presentación de datos en tablas, gráficos e informes
La etapa de presentación y comunicación de los resultados de una investigación es un componente necesario de todo proceso de investigación. El diálogo entre colegas de una comunidad académica, así como con otros públicos, hace que deba prestarse especial atención a la tarea de presentación de los datos y la discusión de las conclusiones.
De igual modo, la interpretación crítica de informes de investigación producidos por otras entidades también requiere ejercitarse en un modo específico de lectura de elementos gráficos o tabulados insertados dentro del recorrido de un reporte escrito o visual.
Como parte del trabajo estadístico, las tablas y gráficos resultan útiles para organizar, representar y comunicar datos de manera clara y resumida. Según su disposición, permiten la visualización de patrones y tendencias. Y pueden también convertirse en facilitadores para ulteriores análisis y lecturas alternativas.
Ritchey, F. (2002). Tablas y gráficas: una imagen dice más que mil palabras. En: Estadística para las ciencias sociales (pp. 78-95). México: McGraw-Hill.
Indicaremos, en primer lugar, algunas características de tablas de frecuencia y tablas bivariadas (o también llamadas tablas de contingencia) y sus usos en la presentación y análisis de los datos.
Tablas de frecuencias
Una tabla de frecuencias es una herramienta que organiza datos estadísticos para una sola variable. En este tipo de tabla, se le asigna a cada valor o categoría de la variable la cantidad de casos en los que se presenta o repite, es decir, su frecuencia.
Las tablas de frecuencia presentan usualmente estos tipos de información:
Para variables con un nivel de medición nominal, la organización de las categorías es indistinta (por ejemplo, si fuera el caso de la variable “Provincia” en una muestra de escuelas a nivel nacional). En cambio, para la presentación de variables ordinales, corresponde en la tabla seguir el orden de las categorías que toma la variable para facilitar su lectura. Finalmente, para variables cuantitativas (de razón o de intervalo), puede resultar conveniente agrupar los datos en intervalos de clase para que la tabla no sea extensa y pueda cumplir con su función de resumen de los datos. Por ejemplo, en la siguiente tabla se agrupa en cuatro intervalos la variable “Edad” para el conjunto de directores/as que respondieron el censo docente de 2004, expresada en frecuencias relativas en porcentajes.
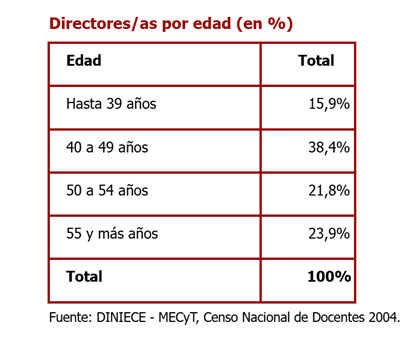
Baranger, D. (2009). Técnicas elementales de análisis. En: Construcción y análisis de datos. Introducción al uso de técnicas cuantitativas en la investigación social (pp. 43-78). Posadas: Editorial Universitaria.
Tablas bivariadas
En la investigación social en educación nos interesa trabajar también con los cruces posibles entre al menos dos variables, para analizar relaciones, correspondencias, regularidades o tendencias.
Las tablas bivariadas se construyen para el cruce de dos variables categóricas: presentan la relación entre una variable con nivel de medición nominal junto a otra variable también nominal o con una variable ordinal. Si fuera que se quiere incluir una variable cuantitativa (de intervalo o razón), podrá agrupársela en intervalos para convertirla en una variable ordinal.
Para establecer comparaciones con sentido –en línea con el sentido de proporción indicado antes en el subapartado 4.1.1 sobre la “imaginación estadística”– en las tablas bivariadas se trabaja con los valores de las frecuencias relativas expresadas en porcentajes.
La construcción de este tipo de tablas es ya un procedimiento de análisis estadístico inferencial. Pues al cruzar dos variables, está en juego alguna hipótesis sobre la asociación o la relación entre esas variables. Por ejemplo, se podrá examinar si los porcentajes de una variable se distribuyen de manera uniforme en las distintas categorías de la otra variable. Por ello es importante definir, dentro del contexto de la investigación, cuál es la variable independiente (o explicativa) y cuál la dependiente (o variable a explicar) (según lo trabajado en el subapartado 4.2.2).
En general, aunque no de manera estricta, se estipula que en una tabla bivariada la variable independiente se coloca en las columnas y la variable dependiente en las filas.
Recomendaciones para la lectura de tablas bivariadas
Es importante tener una clave de lectura que permita analizar la información presentada en las tablas bivariadas y derivar así conclusiones pertinentes. En la lectura de una tabla bivariada que supone una hipótesis a poner a prueba, se sugiere:
-
Calcular los porcentajes en el sentido de la variable independiente. Es lo que Zeisel definió como “la regla de la causa y el efecto”, indicando que –salvo excepciones en muestras que no son estadísticamente representativas– se obtendrá mejor información si los porcentajes se calculan en la dirección del “factor causal” (Zeisel, 1990: 52).
-
Efectuar la lectura y el análisis de los datos en el sentido de la variable dependiente. Por ejemplo, comparando cómo se distribuye dentro de la variable independiente.
Tipos de gráficos
En segundo lugar, desde la investigación social en educación en perspectiva cuantitativa, la graficación apoya también la presentación de los resultados y el propio análisis e interpretación de los datos. Destacaremos a continuación las características de algunos de los recursos gráficos que pueden resultar más útiles: gráficos de torta o sectores, de barras, histogramas, de líneas o polígonos, box plot o de “caja y bigotes”, pictogramas y mapas.
Según veremos, una clave para la elección del tipo de gráfico es la definición del nivel de medición de la variable (según lo trabajado en el subapartado 4.1.3) que se quiere presentar visualmente.
Gráfico de torta (o “pastel” o de sectores)
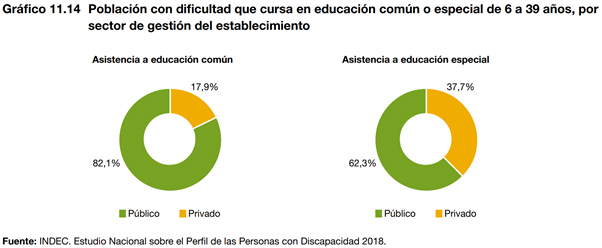
Se utiliza para representar datos en forma de “porciones" como parte de un total que representa el 100 % (las porciones pueden estar expresadas como frecuencias absolutas o relativas en porcentajes).
Los gráficos de torta, “pastel”, sectores, son pertinentes para la graficación de variables nominales.
Se recomienda que el número de categorías (cantidad de “porciones”) sea de hasta cinco elementos, para no recargar visualmente el diseño y sumar claridad. Si hubiera más categorías a considerar, podrían agruparse algunas de menor peso en una categoría de “Otros”. O, si no se pueden descartar categorías para su visualización, es conveniente realizar un gráfico de barras (ver más adelante).
Gráfico de barras (horizontales o verticales)
En este tipo de gráficos, las variables y sus valores se visualizan en barras rectangulares (en forma vertical u horizontal) cuya longitud es proporcional dentro del conjunto total de datos. Permite así visualizar magnitudes y comparaciones.
El uso de los gráficos de barras (horizontales o verticales) está recomendado para la representación de datos de variables nominales (categorías sin orden) y especialmente para variables ordinales (categorías con un orden o secuencia) y algunas variables cuantitativas.
Histograma
Es una representación gráfica de datos numéricos. Para cada valor (o intervalos de clase establecidos) se construye un rectángulo vertical cuya altura es proporcional a la frecuencia absoluta. La suma de la superficie de todas las barras es igual al total.
El histograma se recomienda especialmente para variables cuantitativas (de intervalo o razón). Por ello, entre cada barra no hay espacios, para graficar la continuidad de los valores de la variable.
Polígonos (gráfico de líneas)
El gráfico de polígonos es una variante del histograma. La diferencia está en que, en lugar de barras contiguas, se utilizan como elementos visuales los puntos (unidos a su vez por líneas rectas que, por debajo de ellas, pueden formar un área).
Gráfico box plot (o de “caja y bigotes”)
Este es un tipo de gráfico útil para tener una lectura de algunos datos principales desde la estadística descriptiva, pues permite identificar características de una variable cuantitativa (de razón o intervalo), como la distribución y la dispersión de sus valores. En un solo gráfico se resumen estas medidas de posición:
-
Valor mínimo (sin contar los outliers)
-
Primer cuartil (Q₁)
-
Mediana (Q₂)
-
Tercer cuartil (Q₃)
-
Valor máximo (sin contar los outliers)
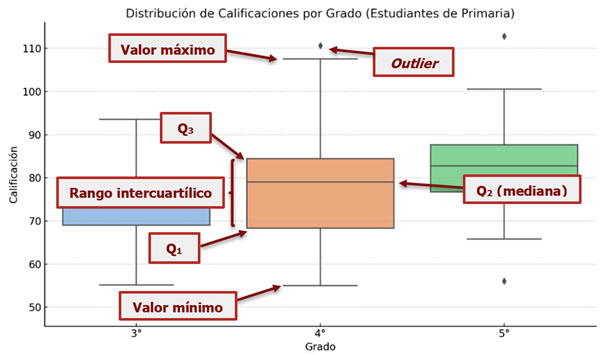
La siguiente imagen representa un caso simulado de las distribuciones de calificaciones escolares en una muestra de 3°, 4° y 5° grado de nivel primario. Para el gráfico box plot de 4° grado, se indican sus componentes:
El límite inferior de la caja corresponde al valor del primer cuartil (Q₁), que agrupa al primer 25 % de los casos. Y su límite superior está marcado por el tercer cuartil (Q₃), que indica el tope del 75 % de los valores ordenados. La caja representa así el rango intercuartílico (esto es, la diferencia entre el Q₃ y el Q₁), donde se encuentra el 50 % central de los datos.
Dentro de la caja se agrega una línea que indica el valor de la mediana (equivalente al Q₂, es decir, las dos mitades en que se distribuyen los valores).
Por encima y debajo de la caja se derivan dos líneas (de allí la figura de los “bigotes”), que en su extensión muestran la dispersión de la distribución de la variable graficada entre el valor mínimo y el valor máximo. Por fuera de esos valores que marcan los “bigotes”, son fácilmente identificables los valores atípicos o extremos (o outliers).
Así organizada la información, este tipo de gráfico permite entender rápidamente la dispersión de los datos, comparar distribuciones entre distintos grupos e identificar los valores extremos.
Pictograma
Es un tipo de representación gráfica que utiliza íconos, dibujos, imágenes o símbolos (en lugar de barras, líneas o puntos) que representan una unidad de conteo. Permite acercar la lectura de los datos a entidades reconocibles más allá de los meros números (absolutos o porcentajes). Tiene así el potencial de simplificar la presentación de datos estadísticos que pueden ser complejos y ofrecer un aporte visual de fácil comprensión.
Recomendaciones para la presentación de tablas bivariadas y gráficos
Toda presentación de tablas y gráficos dentro de un informe deberá incluir estos elementos:
-
Título. La forma sugerida de organizar el título de una tabla bivariada y de gráficos es la siguiente:
[Universo] por [Variable dependiente] según [Variable independiente]. Referencia espacio-temporal.
Por ejemplo: “Estudiantes de 6° año de nivel secundario por desempeño en matemática según género. Total país. Año 2024”.
-
Numeración. Especialmente si se presentan varios elementos (tablas o gráficos), agregar antes del título de cada uno de ellos su numeración consecutiva para hacerlos fácilmente identificables.
-
Fuente. Indicar debajo de la tabla o gráfico la fuente de los datos.
Mapas
Otra forma de acceso y presentación de la información estadística es a través de mapas. La presentación cartográfica de las variables (cuyos valores se corresponden a su vez con distintos colores) permite visualizar y comparar su distribución espacial en territorios amplios.
A partir de la lectura exploratoria del capítulo 1 “¿Qué muestran los datos estadísticos?”, del libro Igualdad de género y educación media en América Latina y el Caribe: estadísticas, políticas e investigaciones, de Gloria Bonder (2021):
-
Elija uno de los apartados y haga un listado de todos los elementos estadísticos que se utilizan para la presentación de los datos. Indique en ese listado los usos de:
-
Medidas de tendencia central.
-
Medidas de posición.
-
Tablas.
-
Gráficos.
-
Fuentes de datos estadísticos.
-
-
Señale para qué variables se utilizan esos recursos y cuál cree que es su aporte en la presentación de los datos.
La escritura de informes de investigación
El proceso de investigación supone como instancia necesaria, la puesta en discusión de los resultados en informes de investigación que pueden estar dirigidos a distintos públicos (investigadores/as, decisores de políticas educativas, comunidades educativas, público en general, etc.). Allí se pone en juego el desafío, como operación intelectual, de “tejer nuestra voz autoral” y establecer un diálogo con otras voces en un registro académico (Rosso, Camargo y Pozzo, 2024: 31).
Los géneros de la escritura académica para dar cuenta de resultados (de avance o finales) de una investigación pueden tomar la forma de:
-
Informes ejecutivos (en ámbitos de gobierno y decisión de políticas).
-
Informes de proyectos acreditados (en universidades u organismos públicos de ciencia y tecnología).
-
Tesis (de grado o posgrado).
-
Artículos de investigación en revistas académicas.
-
Ponencias en encuentros académicos (congresos, jornadas, simposios, etc.).
Más allá de los criterios y requisitos específicos para cada uno de estos géneros académicos, un informe de investigación tendrá en su estructura estos elementos comunes:
Para ahondar en la práctica de la elaboración de resúmenes, recomendamos el siguiente artículo: Amezcua, M. (2020). Diez claves para la elaboración del resumen en un artículo científico. Index de Enfermería, 29(1-2), 36. https://ciberindex.com/index.php/ie/article/view/e32912/e32912
Como parámetro posible para la presentación de información cuantitativa en informes, tablas y gráficos, puede consultarse el Manual de estilo elaborado por el Instituto Nacional de Estadística y Censos: Instituto Nacional de Estadística y Censos - INDEC (2024). Manual de estilo. 5a edición. Buenos Aires: INDEC. https://www.indec.gob.ar/ftp/cuadros/publicaciones/manual_estilo_quinta_edicion.pdf
En la plataforma normas-apa.org se detallan los criterios para la confección de referencias en formato APA: Sánchez, C. (11 de febrero de 2020). Ejemplos de Referencias Bibliográficas APA. Normas APA (7a. edición). https://normas-apa.org/referencias/ejemplos/
En el siguiente enlace se encuentran ejemplos de informes de investigación producidos desde la cartera educativa nacional: https://www.argentina.gob.ar/educacion/evaluacion-e-informacion-educativa/investigaciones
También puede accederse a informes elaborados por el Instituto Nacional de Educación Técnica (INET) en el siguiente enlace: https://www.inet.edu.ar/index.php/estudios-investigaciones/
4.3. La información estadística para la investigación social en educación
La producción de conocimiento puede tomar la propia construcción de datos desde, por ejemplo, un estudio basado en una encuesta elaborada en el marco de un proyecto de investigación (según lo trabajado en las unidades 2 y 3). O puede tomar como fuente la información estadística producida por entidades oficiales desde los organismos de gobierno.
En la investigación social en educación se reconoce una mayor disponibilidad y accesibilidad a esas fuentes estadísticas, por lo que se renueva el interés en su uso. Esto ha ido de la mano de políticas de acceso abierto a la información educativa y social, que hacen posible el acceso mediante portales y repositorios al público en general y especialmente a la comunidad científica (Suasnábar y Valencia, 2022).
Big data y educación
Más allá de los datos estadísticos producidos centralmente desde las áreas de definición de las políticas educativas (a partir de, por caso, censos, relevamientos, estudios específicos de monitoreo u operativos de evaluación estandarizada), puede existir otro cúmulo de información que es posible englobar bajo el concepto de big data. Es decir, una cantidad masiva de información digital cuantificable, no estructurada, generada espontáneamente en la interacción con dispositivos interconectados y abordable desde métodos algorítmicos (Sosa Escudero, 2020). Ante su constante desarrollo, transformación y eventual expansión en el terreno educativo, el fenómeno de los big data resulta un novedoso foco de interés.
La aparición de este tipo de información se origina en procesos de dataficación (Williamson, 2018), es decir, la generación y almacenamiento de un volumen grande de información digital en forma de “macrodatos”, junto a su procesamiento, análisis y visualización desde herramientas estadísticas avanzadas.
En los ámbitos educativos –a diferencia de la información derivada de los censos, encuestas o evaluaciones– los big data emergen en el “interior de la maquinaria didáctica” (Williamson, 2018: 11) especialmente en contextos digitales de enseñanza y aprendizaje. Por ejemplo, se genera información cuando un/a estudiante cliquea y deja la huella de su recorrido en determinados contenidos y vínculos, accede a materiales educativos digitales, interactúa en línea con otros estudiantes o sube sus respuestas a ejercicios de evaluación. Aunque también podrían sumarse los registros digitales de asistencia escolar y calificaciones para cada estudiante y curso.
Entre los usos posibles que se podrían derivar de una dataficación de los entornos de enseñanza y aprendizaje, pueden reseñarse los siguientes: 1) la retroalimentación digital en tiempo real, en una replicación de la respuesta posible de un/a docente a partir de dispositivos de inteligencia artificial; 2) la individualización y personalización del proceso educativo (por ejemplo, adecuando, mediante un análisis automatizado, los materiales a las particularidades de cada estudiante); y 3) la generación de predicciones probabilísticas que, a partir de la reunión de datos de las acciones de cada estudiante, prevea desempeños o resultados futuros (por ejemplo, mediante “sistemas de alerta temprana” para el trabajo institucional sobre trayectorias escolares en riesgo de verse interrumpidas).
Datos, información y educación en un mundo digitalizado
Para ampliar sobre los sentidos, posibilidades y desafíos de los big data en el campo educativo, recomendamos la visualización del panel sobre “Datos, información y educación en un mundo digitalizado”, organizado por la UNIPE en 2024. En su exposición, Juan Suasnabar y Gabriel Estrada nos presentan qué se entiende por big data (minuto 07:00 en adelante) y avanzan sobre los desafíos presentes (01:10 en adelante):
Fuente: Ciencias Sociales y Educación - UNIPE [@socialesyeducacion] (5 de marzo de 2024). Datos, información y educación en un mundo digitalizado [Video]. https://www.youtube.com/watch?v=86BezizQG4s
Si bien existen antecedentes puntuales en Argentina (ver en la Unidad 1, el subapartado 1.1.3 sobre la investigación, la estadística y la evaluación desde el Estado), el sistema de información estadística y educativa a nivel nacional tiene sus orígenes en la década de 1990 con la creación de la Dirección General Red Federal de Información Educativa (RedFIE) dentro de la cartera educativa nacional, en 1993 (Pascual, 2016). La RedFIE está conformada por las áreas de estadística educativa de las provincias y la Ciudad Autónoma de Buenos Aires. Entre sus responsabilidades está el operativo del relevamiento anual (RA) en todos los establecimientos de los niveles inicial, primario, secundario y superior no universitario de todo el país (ver más adelante), la realización de censos docentes (en 1994, 2004 y 2014, y el que se realizará en 2025 al momento de edición de este material) y otros operativos como los censos de infraestructura escolar. Progresivamente, estos esfuerzos se han orientado hacia la construcción de un sistema nacional de indicadores educativos con criterios metodológicos compartidos a nivel nacional (Ministerio de Educación, Ciencia y Tecnología, 2005).
A partir de 2012 se buscó, desde la entonces Dirección Nacional de Información y Evaluación de la Calidad Educativa (DiNIECE), la consolidación de un Sistema Integral de Información Digital Educativa (SInIDE) que sistematizara información nominal (es decir, por estudiante) del sistema educativo a nivel central en todos los niveles obligatorios de la educación común y las modalidades de educación especial y educación permanente de jóvenes y adultos (UNICEF-OEI, 2024). En esta línea de trabajo, se desarrolló en 2020 una plataforma de visualización y acceso a información estadística a través del Sistema de Consulta de Datos Educativos Nacionales (SICDIE), a cargo de la Dirección de Evaluación e Información Educativa a nivel nacional (ver más adelante).
Apuntaremos a continuación algunos de los recursos estadísticos disponibles, según dependan de áreas propiamente educativas y también otras fuentes que aportan información relevante para temas y preocupaciones del campo de la educación.
4.3.1. Fuentes estadísticas educativas a nivel nacional
Entre las principales fuentes a nivel nacional, encontramos: 1) el padrón de establecimientos educativos, 2) el relevamiento anual (RA), 3) las pruebas Aprender, 4) el tablero de visualización del Sistema Integrado de Consulta de Datos e Indicadores Educativos (SICDIE) y 5) los anuarios estadísticos universitarios.
El padrón de establecimientos educativos
Es un nomenclador institucional unificado que presenta información sobre los establecimientos educativos de los niveles inicial hasta superior no universitario (su ubicación, contacto y ofertas educativas), en todo el país. Es actualizado en forma continua por cada una de las áreas de estadística educativa de las jurisdicciones.
Padrón de establecimientos educativos: https://www.argentina.gob.ar/educacion/evaluacion-e-informacion-educativa/padron-oficial-de-establecimientos-educativos
El relevamiento anual (RA)
Desde 1996 genera datos a partir de un operativo censal en las instituciones educativas de los niveles inicial hasta superior no universitario de todo el país. Incluye información relevada hasta el 30 de abril de cada año. Abarca las principales variables del sistema educativo, según la información que completa cada jardín, escuela o instituto superior (establecimientos y su infraestructura, estudiantes y sus características, cargos docentes, etc.). La mayor parte de su información se publica en bases de datos abiertas a la consulta y también en anuarios estadísticos.
Relevamiento anual (RA): https://www.argentina.gob.ar/educacion/evaluacion-e-informacion-educativa/relevamiento-anual-ra
Las pruebas Aprender
Las pruebas Aprender son el operativo nacional de evaluación estandarizada de los aprendizajes de estudiantes de los últimos años de los niveles primario y secundario, en las áreas básicas de conocimiento escolares (Lengua y Matemática). Está a cargo de la Secretaría de Evaluación e Información Educativa de la cartera educativa nacional, en acuerdo con las jurisdicciones subnacionales y se ha realizado desde el año 2016 en adelante. Genera además información de contexto sobre algunas condiciones socioeducativas. Este operativo se ha implementado a partir de muestras representativas y también en forma censal, sobre la población de estudiantes de 6° grado del nivel primario y de 5° o 6° año del nivel secundario, en todo el país.
El Sistema Integrado de Consulta de Datos e Indicadores Educativos (SICDIE)
Es una plataforma web que, basada en tableros interactivos, permite consultar información estadística relevada por distintos los operativos ya mencionados de información educativa y evaluación implementados por el área de Evaluación e Información Educativa y otros organismos del Estado. Permite acceder a información según los niveles educativos y modalidades (mayormente tomados del relevamiento anual) y también a una presentación de los resultados de las pruebas Aprender.
Sistema Integrado de Consulta de Datos e Indicadores Educativos (SICDIE): https://data.educacion.gob.ar/
Los anuarios estadísticos universitarios
Presentan información sobre las instituciones universitarias de gestión pública y privada de todo el país (población estudiantil, recursos humanos, presupuesto, programas de becas, incentivos docentes, etc.). Su elaboración está a cargo del área de políticas universitarias de la cartera educativa nacional, a partir de la consulta a cada una de las universidades.
Anuarios estadísticos universitarios: https://www.argentina.gob.ar/educacion/universidades/informacion/publicaciones/anuarios
4.3.2. Otras fuentes estadísticas para el abordaje de lo educativo
Además de la producción y difusión estadística de las propias carteras educativas (a nivel nacional y jurisdiccional), puede encontrarse información importante para el relevamiento y la investigación sobre asuntos educativos en otras fuentes oficiales. Entre ellas, podemos destacar: 1) el Sistema de Información de Tendencias Educativas en América Latina (SITEAL), 2) la Coordinación General de Estudio de Costos del Sistema Educativo (CGECSE), 3) la plataforma Presupuesto Abierto y 4) el Censo Nacional de Población, Hogares y Vivienda.
El Sistema de Información de Tendencias Educativas en América Latina (SITEAL)
Es un observatorio regional de políticas educativas del Instituto Internacional de Planeamiento de la Educación (IIPE-UNESCO). Presenta perfiles de los países, en los que se sistematizan, analizan y difunden documentos de políticas y normativas, investigaciones y estadísticas educativas.
Sistema de Información de Tendencias Educativas en América Latina (SITEAL): https://siteal.iiep.unesco.org/
La Coordinación General de Estudio de Costos del Sistema Educativo (CGECSE)
Es un área dependiente de la cartera educativa nacional. Genera documentos y reportes regulares con información sobre los salarios docentes y el gasto educativo en cada una de las jurisdicciones provinciales y la Ciudad Autónoma de Buenos Aires.
Coordinación General de Estudio de Costos del Sistema Educativo (CGECSE): https://www.argentina.gob.ar/educacion/evaluacion-e-informacion-educativa/cgecse
La plataforma Presupuesto Abierto
Presenta información oficial sobre la ejecución presupuestaria de la administración pública nacional. Permite distinguir los gastos por jurisdicción, finalidad, función y objeto al que se los destina (incluida la inversión en educación, ciencia y tecnología), así como aplicar filtros por año.
Presupuesto Abierto: https://www.presupuestoabierto.gob.ar/sici/
El Censo Nacional de Población, Hogares y Vivienda
El operativo del Censo Nacional de Población, Hogares y Vivienda está a cargo del Instituto Nacional de Estadística y Censos (INDEC). Su última edición fue en 2022. Entre la información educativa que nos permite conocer y complementar con la información estadística de las áreas educativas oficiales están la tasa de alfabetismo (incluida hasta el censo de 2010), las trayectorias educativas (según máximo nivel educativo alcanzado) y la asistencia escolar (actual y pasada) de la población del país.
Censo Nacional de Población, Hogares y Vivienda 2022 - Educación: https://censo.gob.ar/wp-content/uploads/2023/12/censo2022_educacion.pdf
Redatam - INDEC. Sistema de procesamiento estadístico de censos y encuestas: Esta plataforma web permite trabajar con la información estadística disponible en los censos nacionales de población. De manera interactiva, pueden ejecutarse filtros y cruces entre variables y accederse a su resumen en tablas en formato de hojas de cálculo para su posterior procesamiento. https://redatam.indec.gob.ar/
Los censos nacionales de población y las variables educativas
Los aportes y decisiones metodológicas de los censos nacionales de población en Argentina para abordar temas educativos pueden profundizarse a partir de los trabajos de Di Pietro y Tófalo (2013) y Massé (2022). Ambos articulan una perspectiva histórica de los antecedentes junto a las características actuales de los censos nacionales de población para relevar y comparar variables tales como el analfabetismo, el máximo nivel educativo alcanzado y la expansión de la cobertura escolar obligatoria.
Otro recurso es el tablero web construido por el Observatorio Educativo y Social de la Universidad Pedagógica Nacional (UNIPE). A partir de una visualización interactiva, se puede acceder a la información educativa de los censos en series históricas, con desagregaciones por jurisdicción y otras variables sociodemográficas.
La Educación en los Censos Nacionales de Población: https://observatorio.unipe.edu.ar/tableros/la-educacion-en-los-censos
Finalmente, se pueden retomar las presentaciones del panel “El censo 2022 y la educación”, organizado en 2022 por la Especialización en Estadísticas e Indicadores Educativos (UNIPE y UNTREF) y con la participación de funcionarios/as y especialistas del INDEC y del Ministerio de Educación de la Nación.
El Censo 2022 y la Educación. Especialización en Estadísticas e Indicadores Educativos, UNIPE-UNTREF
Fuente: Ciencias y Tecnología - UNIPE [@unipecienciasytecnologia] (6 de mayo de 2022). El Censo 2022 y la Educación. Especialización en Estadísticas e Indicadores Educativos, UNIPE-UNTREF [Video]. https://www.youtube.com/live/mKXeTM9QOSE?si=W67Rwb2jl-Tvim6i