5. Programación lineal
Objetivos
- Reconocer problemas de programación lineal.
- Resolver problemas de programación lineal por métodos gráficos.
- Resolver problemas de administración, utilizando programación lineal.
5.1. Sistemas de inecuaciones lineales
Ejercicio 1
Una empresa productora de muebles fabrica sillas y mesas, combinando madera con caño cromado en diferentes procesos, en los que intervienen distintas máquinas. El tiempo de uso de las máquinas y los insumos de cada producto están dados por la siguiente tabla:
|
Insumo Producto |
Madera |
Caño cromado |
Máquina 1 |
Máquina 2 |
|
Silla |
3 |
2 |
3 |
4 |
|
Mesa |
5 |
7 |
3 |
3 |
Si en un momento determinado se disponen de 110 unidades de madera, 140 de caño cromado y la máquina 1 se puede utilizar 81 horas y la máquina 2 durante 100 horas, ¿cuántas sillas y cuántas mesas se pueden producir?
Este problema es similiar a los que se resolvieron en la unidad 4 con sistemas de ecuaciones. Pero hay más ecuaciones que incógnitas. Para utilizar todos los insumos disponibles, sería:
s: cantidad de sillas que se pueden producir.
m: cantidad de mesas que se pueden producir.
\[ \begin{equation} \left\lbrace \begin{array}{ll} 3s + 5m = 110 \ (ecuación \ a)\\ 2s + 7m = 140 \ (ecuación \ b)\\ 3s + 3m = 81 \ (ecuación \ c)\\ 4s + 3m = 100 \ (ecuación \ d) \end{array} \right. \end{equation}\]
Como solo hay dos incógnitas, se pueden representar estas ecuaciones en un diagrama cartesiano. El siguiente, confeccionado con Geogebra, muestra la situación:
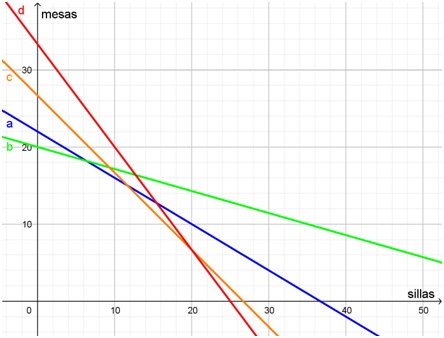
Como puede apreciarse, las rectas no se intersecan en un único punto. Esto significa que el sistema no tiene solución.
Sin embargo, la región de las posibilidades de producción se puede representar matemáticamente mediante el siguiente sistema de inecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 3s + 5m \le 110 \ (inecuación \ a)\\ 2s + 7m \le 140 \ (inecuación \ b)\\ 3s + 3m \le 81 \ (inecuación \ c)\\ 4s + 3m \le 100 \ (inecuación \ d) \end{array} \right. \end{equation}\]
La primera, por ejemplo, significa que se pueden usar en la producción “hasta” 110 unidades de madera. La representación gráfica de estas inecuaciones es la que se aprecia en el siguiente diagrama:
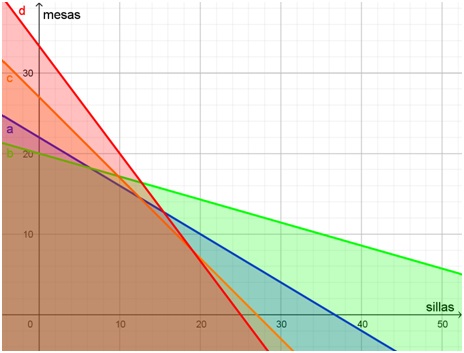
Solo los puntos ubicados en el primer cuadrante tienen sentido económico e integran la “región solución” del sistema. En el siguiente gráfico están sombreados en gris:
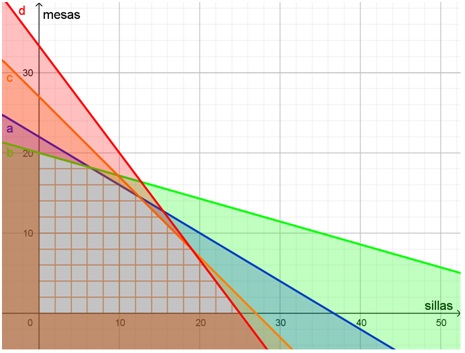
Cualquiera de las combinaciones de sillas y mesas que representan los puntos de esa región puede fabricarse con los insumos disponibles. Si se elige alguno de los puntos de los bordes de esa región, se agotará completamente alguno de los insumos, pero siempre sobrará de algún otro recurso, porque el sistema de ecuaciones no tiene solución.
Por ejemplo, si se eligiera producir 20 mesas y ninguna silla, se agotarían los caños cromados, pero sobrarán 10 unidades de madera, 21 horas de uso de la máquina 1 y 40 de la máquina 2.
5.2. Función objetivo
Ejercicio 2
La empresa del problema anterior obtiene un beneficio de $35 por cada silla y de $30 por cada mesa que vende. Si se mantienen las condiciones, ¿cuánto le conviene producir para maximizar sus beneficios?
Esta nueva condición se denomina “función objetivo” y, en este caso se busca que resulte máxima la expresión:
f(s, m) = 35 · s + 30 · m (expresión 1)
Si existe una solución única, que maximiza o minimiza la función objetivo, tal solución corresponde a un vértice de la “región solución” del sistema de inecuaciones.
Para encontrar el punto que maximiza la expresión (1), es necesario identificar los vértices de la región solución.
En el siguiente gráfico se aprecia que la región solución tiene seis vértices. El A corresponde a la intersección entre la representación gráfica de la ecuación b y el eje de ordenadas. Sus coordenadas se pueden hallar resolviendo el sistema de ecuaciones formado por la ecuación b y la que corresponde a dicho eje, es decir s = 0:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 2s + 7m = 140 \ (ecuación \ b)\\ s = 0 \ (ecuación \ 2) \end{array} \right. \end{equation}\]
Sustituyendo la ecuación 2 en la b, es:
2 · 0 + 7m = 140
0 + 7m = 140
\[ m = \frac{140}{7} = 20 \]
Por lo que las coordenadas del punto A son A = (0; 20).
Las del punto B son la solución del sistema de ecuaciones formado por las ecuaciones a y b:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 3s + 5m = 110 \ (ecuación \ a)\\ 2s + 7m = 140 \ (ecuación \ b) \end{array} \right. \end{equation}\]
Que se puede resolver por el método de Cramer:
\[ s = \frac{|^{110}_{140} \ \ ^5_7|}{|^3_2 \ \ ^5_7|} = 6,36 \]
\[ m = \frac{|^3_2 \ \ ^{110}_{140}|}{|^3_2 \ \ ^5_7|} = \frac{200}{11} = 18,18 \]
Entonces, las coordenadas del punto B son (6,36; 18;18).
De esta misma manera se buscan las coordenadas de los puntos:
- C: intersección entre las ecuaciones a y c, (12,5; 14,5)
- D: intersección entre c y d, (19; 8)
- E: intersección entre d y el eje x (25; 0)
- F: intersección entre los dos ejes (0; 0).
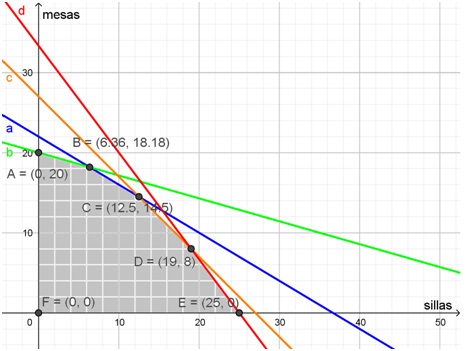
Con estos datos, se evalúa la función objetivo en cada uno de estos puntos. En la siguiente tabla se presenta la información de cada punto y se muestra qué cuenta se efectúa en cada caso.
|
Puntos |
s |
m |
f(s; m) |
|
A |
0 |
20 |
35 · 0 + 30 · 20 = 600 |
|
B |
6,36 |
18,18 |
35 · 6,36 + 30 · 18,18 = 768 |
|
C |
12,5 |
14,5 |
35 · 12,5 + 30 · 14,5 = 872,5 |
|
D |
19 |
8 |
35 · 19 + 30 · 8 = 905 |
|
E |
25 |
0 |
35 · 25 + 30 · 20 = 875 |
|
F |
0 |
0 |
35 · 0 + 30 · 0 = 0 |
Finalmente, después de reunir toda esta información, se puede apreciar que el beneficio máximo es de $905, y es el que se obtiene en el punto D, fabricando 19 sillas y 8 mesas.
Por lo tanto, y respondiendo a la pregunta del problema, para maximizar el beneficio, en las condiciones actuales deberían fabricarse 19 sillas y 8 mesas. Así, se obtendrá un beneficio de $905. Se utilizarán las máquinas 1 y 2 todas las horas disponibles, pero sobrarán 13 unidades de madera y 46 de caños cromados.
A esta misma conclusión se puede llegar gráficamente. Con ese fin, se grafica la función objetivo, dándole arbitrariamente valores al beneficio. En el siguiente gráfico, en el que, para simplificar, solo se representó la región solución y sus vértices, se representaron diferentes valores del beneficio:
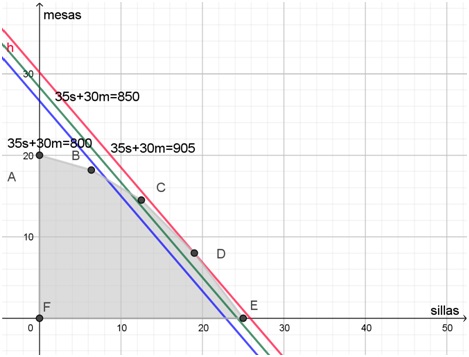
Por ejemplo, la que está graficada en color azul corresponde a un beneficio de $800, la que está en verde, corresponde a $900. Se obtienen de este modo rectas paralelas y, a medida que el beneficio aumenta, dichas rectas se “desplazan” alejándose del origen de coordenadas. En este desplazamiento, el último vértice de la región solución que tocan es el D. Es allí en donde el beneficio será máximo. Como ya se vio, corresponde a fabricar 19 sillas y 8 mesas. En color rojo se representó esa recta, que implica un beneficio de $905.
Ejercicio 3
Encuentre gráficamente la región solución del siguiente sistema de inecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} x \ge 0 \\ y \ge 40 \\ 2x + y \ge 100\\ 4y - x \ge 80 \end{array} \right. \end{equation}\]
- Encuentre el mínimo de la función objetivo C = 2x + 3y + 500 dentro de la región solución del sistema anterior, gráfica y analíticamente.
Con Geogebra se grafica el sistema de ecuaciones para hallar la zona solución de ese sistema.
La zona sombreada con todos los colores (se ve en marrón) es la región de las soluciones posibles del sistema:
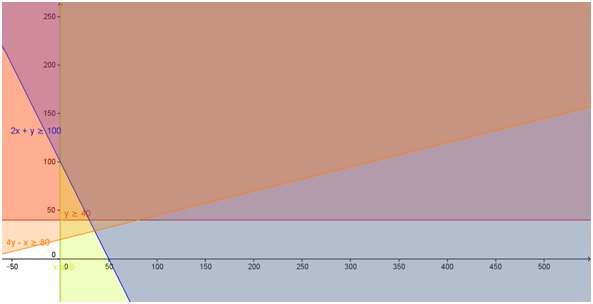
b) Encuentre el mínimo de la función objetivo C = 2x + 3y + 500 dentro de la región solución del sistema anterior, gráfica y analíticamente.
Para hallar la solución al problema, se grafican ahora las rectas correspondientes a diferentes valores de C, por ejemplo:
- C1 = 600 = 2x + 3y + 500 (en negro)
- C2 = 800 = 2x + 3y + 500 (en rojo)
- C3 = 680 = 2x + 3y + 500 (en verde)
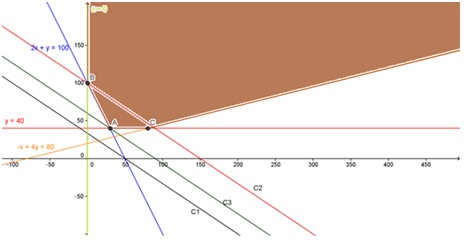
Como se aprecia en el gráfico, en el que la región solución se sombreó en color marrón, el valor de C disminuye a medida que las rectas se desplazan hacia el “sudoeste” del diagrama. La recta en color verde, correspondiente a C = 680 es la última en intersecar la zona solución del sistema de inecuaciones en el punto A, en el que se intersecan dos de las rectas borde de la región solución. Para encontrar sus coordenadas, se deberá resolver el sistema:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 2x + y = 100 (1)\\ y = 40 (2) \end{array} \right. \end{equation}\]
Que son las dos rectas borde que se intersecan allí. Se resolverá por sustitución.
Reemplazando la ecuación (2) en (1):
2x + 40 = 100
2x = 100 - 40
2x = 60
\[ x = \frac{60}{2} = 30 \]
Por lo tanto, el valor mínimo de C es 680 y se logra cuando x = 30 e y = 40.
A este mismo resultado se puede llegar evaluando C en cada vértice de la región solución. En el siguiente cuadro, se aprecian los resultados que se obtienen en cada uno de ellos:
|
Punto |
x |
y |
C(x; y) |
|
A |
30 |
40 |
2 · 30 + 3 · 40 + 500 = 680 |
|
B |
0 |
100 |
2 · 0 + 3 · 100 + 500 = 800 |
|
C |
80 |
40 |
2 · 80 + 3 · 40 + 500 = 780 |
El menor valor de C(x; y) es 680 y se obtiene cuando x es 30 y y es 40.
Encuentre el máximo de la función f(x; y) = 5x + 2y dadas las condiciones expresadas por el siguiente sistema de inecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 2x + 3y \le 600 \\ 10x + 3y \le 1800 \\ x \ge 0\\ y \ge 0 \end{array} \right. \end{equation}\]
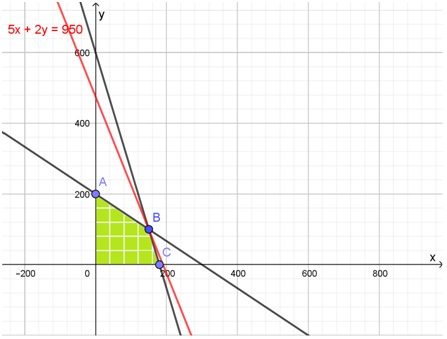
Respuesta: la región solución está sombreada en verde en el siguiente gráfico. El máximo de la función f(x; y) es 950, representada en rojo y se obtiene en el vértice B, cuando x=150 y y=100.
5.3. Método Simplex
Ejercicio 4
Resuelva el siguiente problema utilizando el método Simplex.
Encuentre el máximo de la función objetivo f(x,y) = 4x + 5y sujeta a las siguientes condiciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 3x + 5y \le 2250 \ (1) \\ 3x + y \le 1050 \ (2) \\ x \ge 0 \ (3)\\ y \ge 0 \ (4) \end{array} \right. \end{equation}\]
El método Simplex permite resolver un problema de maximización (o minimización) algebráicamente.
En el siguiente enlace: <https://www.ingenieriaindustrialonline.com/herramientas-para-el-ingeniero-industrial/investigaci%C3%B3n-de-operaciones/m%C3%A9todo-simplex/> se explica en qué consiste y cómo resolver un problema de maximización utilizando el método Simplex.
En el siguiente video <https://www.youtube.com/watch?v=CCud7rAIi8A> se resuelve un problema como este por el método Simplex.
Este problema se podría resolver gráficamente, como los anteriores, porque solo hay dos variables. Pero se pide utilizar el método Simplex para aprender a utilizarlo y luego aplicarlo a otros en los que no resulte posible graficar debido a una mayor cantidad de variables involucradas.
Entonces, para comenzar, se revisan las inecuaciones. Las dos últimas se llaman “de no negatividad” y piden que tanto x como y resulten nulas o positivas. Estas no son tenidas en cuenta en la tabla Simplex.
En la función objetivo, se agrupan todas las variables en el primer término:
f - 4x - 5y = 0
Y las inecuaciones (1) y (2) se transforman en ecuaciones, incorporando “variables de holgura” si en donde i indica en qué inecuación se incorporan:
3x + 5y + s1 = 2250
3x + y + s2 = 1050
Con estos datos se arma la primera tabla. En ella, se identifican en una primera fila las variables que entran en el problema, incluyendo f y los resultados, en la primera y la última columnas.
En las siguientes tres filas, se acomodan los coeficientes de las ecuaciones anteriores:
|
f |
x |
y |
s1 |
s2 |
R |
|
1 |
-4 |
-5 |
0 |
0 |
0 |
|
0 |
3 |
5 |
1 |
0 |
2250 |
|
0 |
3 |
1 |
0 |
1 |
1050 |
En las tablas Simplex se puede identificar a las variables que no son nulas porque son aquellan en cuya columna hay un único 1 y todos los demás valores son ceros. El valor que toma la variable se observa en la columna de los resultados, en la fila en la que aparece el 1.En la tabla anterior, por ejemplo, las variables no nulas son f, s1 y s2, cuyos valores son 0, 2250 y 1050 respectivamente. Como se busca maximizar f, que en este momento toma el valor 0, se sacará una de las otras variables y se incorporará otra. Para elegir la variable que entra, en la primera fila (la que corresponde a la función objetivo) se elige el número negativo. Si hubiera más de uno (como en esta tabla), se selecciona el de mayor valor absoluto. Aquí es -5 y corresponde a la variable y. Para seleccionar qué fila se usará, se dividen los resultados por los coeficientes de esa variable y en cada una. En la que se obtenga el menor de los cocientes será la seleccionada. En este caso, es la segunda fila, porque 450<1050:
|
f |
x |
y |
s1 |
s2 |
R |
|
|
1 |
-4 |
-5 |
0 |
0 |
0 |
|
|
0 |
3 |
5 |
1 |
0 |
2250 |
2250/5= 450 |
|
0 |
3 |
1 |
0 |
1 |
1050 |
1050/1=1050 |
En la tabla anterior, aparece esa posición sombreada en gris. Con ese fin, toda la fila 2 se divide por 5 (que es el valor que ahora ocupa esa posición):
|
f |
x |
y |
s1 |
s2 |
R |
|
1 |
-4 |
-5 |
0 |
0 |
0 |
|
0 |
0,6 |
1 |
0,2 |
0 |
450 |
|
0 |
3 |
1 |
0 |
1 |
1050 |
A continuación, se anularán los coeficientes de la variable y en las demás columnas. Para ello se hará: F'1 = F1 + 5F2 y F'3 = F3 - F2:
|
f |
x |
y |
s1 |
s2 |
R |
|
1 |
-1 |
0 |
1 |
0 |
2250 |
|
0 |
0,6 |
1 |
0,2 |
0 |
450 |
|
0 |
2,4 |
0 |
-0,2 |
1 |
600 |
Esta es la 2° tabla terminada. Aquí se ve que las nuevas variables no nulas son f, y y s2, con valores 2250, 450 y 600, respectivamente. El valor de la función objetivo f ahora es mayor que en la primera tabla. Pero como en la primera fila aún quedan coeficientes negativos, todavía se puede mejorar.
El único coeficiente negativo que queda es el que corresponde a la variable x. Para ver con qué fila se trabajará ahora, se dividen los resultados por los coeficientes de x:
|
f |
x |
y |
s1 |
s2 |
R |
|
|
1 |
-1 |
0 |
1 |
0 |
2250 |
|
|
0 |
0,6 |
1 |
0,2 |
0 |
450 |
450/0,6=750 |
|
0 |
2,4 |
0 |
-0,2 |
1 |
600 |
600/2,4=250 |
Como el menor cociente se obtiene en la última fila, se tomará como pivote a la posición sombreada en gris. Para transformar ese coeficiente en un 1, se divide a toda la fila por 2,4:
|
f |
x |
y |
s1 |
s2 |
R |
|
1 |
-1 |
0 |
1 |
0 |
2250 |
|
0 |
0,6 |
1 |
0,2 |
0 |
450 |
|
0 |
1 |
0 |
-1/12 |
5/12 |
250 |
En esta última tabla, se expresaron como fracción algunos resultados para evitar los números decimales periódicos. Para terminar, hay que anular los coeficientes correspondientes a la variable x de las otras filas. Entonces, se hará: F'1 = F1 + F3 y F'2 = F2 - 0,6 · F3:
|
f |
x |
y |
s1 |
s2 |
R |
|
1 |
0 |
0 |
11/12 |
5/12 |
2500 |
|
0 |
0 |
1 |
0,25 |
-0,25 |
300 |
|
0 |
1 |
0 |
-1/12 |
5/12 |
250 |
Esta es la 3º tabla terminada. Aquí son no nulas las variables f, x y y, que toman los valores 2500, 250 y 300, respectivamente. Esto se puede ver en la tabla considerando que las columnas correspondientes a esas variables tienen un único 1 y todos los demás lugares son ceros. En la fila en la que se encuentra el 1, en la columna de los resultados, está el valor que toma la variable. Por ejemplo, la variable y vale 300 porque, siguiendo las flechas rojas en la siguiente tabla, vemos que en la fila en la que está el 1, el resultado es 300:
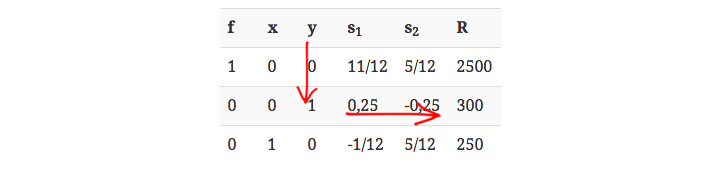
Como en la primera fila ya no quedan coeficientes negativos, se ha llegado a la solución. El máximo de la función objetivo es 2500 y se logra cuando x es 250 y y es 300.
Este resultado se puede comprobar con el método gráfico, que es lo que se sugiere como Ejercicio propuesto.
Compruebe utilizando el método gráfico, que el máximo de la función objetivo f(x,y) = 4x + 5y sujeta a las siguientes condiciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 3x + 5y \le 2250 \ (1) \\ 3x + y \le 1050 \ (2) \\ x \ge 0 \ (3) \\ y \ge 0 \ (4) \end{array} \right. \end{equation}\]
es 2500, cuando x es 250 y y es 300.
Ejercicio 5
Encuentre el máximo de la función objetivo f(x, y, z) = 2x + 3y + 4z sujeta a las siguientes condiciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 4x + y + 2z \le 400 \ (1) \\ 3x + 4y + 2z \le 535 \ (2) \\ x + 2y + 3z \le 405 \ (3) \\ x \ge 0 \ (4) \\ y \ge 0 \ (5) \end{array} \right. \end{equation}\]
Como este ejercicio involucra a tres variables, no existe la posibilidad de resolverlo gráficamente.
Las ecuaciones (4) y (5) son de “no negatividad” y no se incorporan en la tabla Simplex. Despejando la función objetivo e incorporando las variables de holgura, se tienen las siguientes 4 ecuaciones:
f - 2x - 3y - 4z = 0
4x + y + 2z + s1 = 400
3x + 4y + 2z + s2 = 535
x + 2y + 3z + s3 = 405
Con ellas, se arma la primera tabla Simplex, en la que resultan no nulas las variables s1, s2 y s3, que toman los valores 400, 535 y 405 respectivamente.
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
-2 |
-3 |
-4 |
0 |
0 |
0 |
0 |
|
0 |
4 |
1 |
2 |
1 |
0 |
0 |
400 |
|
0 |
3 |
4 |
2 |
0 |
1 |
0 |
535 |
|
0 |
1 |
2 |
3 |
0 |
0 |
1 |
405 |
En la tabla anterior para comenzar la transformación, se elige a la variable z, ya que tiene el menor coeficiente negativo en la primera fila. Para elegir en qué fila ubicar el pivote, se calculan los cocientes entre cada resultado y los coeficientes de z. El que resulte menor será el indicado. En este caso es \( \frac{400}{2} =200 \) en la fila 2, \( \frac{535}{2} = 267,5 \) en la 3 y \( \frac{405}{3}= 135 \) en la fila 4. Por eso, como pivote, se selecciona la casilla de la columna z, fila 4. Para transformar esa casilla en un 1, se divide a toda la fila por 3:
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
-2 |
-3 |
-4 |
0 |
0 |
0 |
0 |
|
0 |
4 |
1 |
2 |
1 |
0 |
0 |
400 |
|
0 |
3 |
4 |
2 |
0 |
1 |
0 |
535 |
|
0 |
1/3 |
2/3 |
1 |
0 |
0 |
1/3 |
135 |
Ahora hay que anular todos los coeficientes de la columna z. Para ello, se hace: F'1 = F1 + 4 · F4 F'2 = F2 - 2 · F4 y F'3 = F3 - 2 · F4
Así se obtiene la 2º tabla Simplex:
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
-2/3 |
-1/3 |
0 |
0 |
0 |
4/3 |
540 |
|
0 |
10/3 |
-1/3 |
0 |
1 |
0 |
-2/3 |
130 |
|
0 |
7/3 |
8/3 |
0 |
0 |
1 |
-2/3 |
265 |
|
0 |
1/3 |
2/3 |
1 |
0 |
0 |
1/3 |
135 |
Aquí son no nulas las variables f, s1, s2 y z, que toman valores 540, 130, 265 y 135 respectivamente. Como puede verse, f aumentó su valor respecto de la primera tabla, que es lo que se busca. Pero como todavía quedan coeficientes negativos en la primera fila, se puede seguir mejorando.
Para continuar, se elige la variable con el menor coeficiente negativo en la primera fila. En este caso es x. Para seleccionar la fila que se utilizará de pivote, se dividen los resultados, que están en la última columna, por los coeficientes de x. En la siguiente tabla, se anotaron las cuentas y sus resultados al costado de cada fila. Allí se observa que el menor cociente es el que corresponde a la fila 2:
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
|
1 |
-2/3 |
-1/3 |
0 |
0 |
0 |
4/3 |
540 |
|
|
0 |
10/3 |
-1/3 |
0 |
1 |
0 |
-2/3 |
130 |
130/(10/3)=39 |
|
0 |
7/3 |
8/3 |
0 |
0 |
1 |
-2/3 |
265 |
265/(7/3)=113,571429 |
|
0 |
1/3 |
2/3 |
1 |
0 |
0 |
1/3 |
135 |
135/(1/3)=405 |
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
-2/3 |
-1/3 |
0 |
0 |
0 |
4/3 |
540 |
|
0 |
1 |
-1/10 |
0 |
3/10 |
0 |
-2/10 |
39 |
|
0 |
7/3 |
8/3 |
0 |
0 |
1 |
-2/3 |
265 |
|
0 |
1/3 |
2/3 |
1 |
0 |
0 |
1/3 |
135 |
Ahora, para anular el resto de los coeficientes de la columna x se hace:
\[ F´1 = F1 + \frac{2}{3} \cdot F2 \]
\[ F´3 = F3 - \frac{7}{3} \cdot F2 \]
\[ F´4 = F4 - \frac{1}{3} \cdot F2 \]
Con lo que se obtiene la 3º tabla Simplex:
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
0 |
-0,4 |
0 |
0,2 |
0 |
1,2 |
566 |
|
0 |
1 |
-0,1 |
0 |
0,3 |
0 |
-0,2 |
39 |
|
0 |
0 |
2,9 |
0 |
-0,7 |
1 |
-0,2 |
174 |
|
0 |
0 |
0,7 |
1 |
-0,1 |
0 |
0,4 |
122 |
En este paso, son no nulas las variables f, x, s2 y z, que toman los valores 566, 39, 174 y 122, respectivamente. Nuevamente, f aumentó su valor con respecto a la segunda tabla Simplex. Pero aún queda un coeficiente negativo, por eso, se debe continuar modificando la variable y.
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
|
1 |
0 |
-0,4 |
0 |
0,2 |
0 |
1,2 |
566 |
|
|
0 |
1 |
-0,1 |
0 |
0,3 |
0 |
-0,2 |
39 |
39/-0,1=-390 |
|
0 |
0 |
2,9 |
0 |
-0,7 |
1 |
-0,2 |
174 |
174/2,9=60 |
|
0 |
0 |
0,7 |
1 |
-0,1 |
0 |
0,4 |
122 |
122/0,7=174,286 |
Como el menor cociente (no negativo) corresponde a la fila 3, se usará esa y se buscará un 1 en la posición fila 3 columna y. Para lo que se divide toda la fila por 2,9:
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
0 |
-0,4 |
0 |
0,2 |
0 |
1,2 |
566 |
|
0 |
1 |
-0,1 |
0 |
0,3 |
0 |
-0,2 |
39 |
|
0 |
0 |
1 |
0 |
-0,24 |
0,3448 |
-0,07 |
60 |
|
0 |
0 |
0,7 |
1 |
-0,1 |
0 |
0,4 |
122 |
Falta hacer ceros a todos los coeficientes de la columna y. Para ello, se hace:
F'1 = F1 + 0,4 · F3
F'2 = F3 + 0,1 · F3
F'4 = F4 - 0, 7 · F3
Con lo que se obtiene la cuarta tabla Simplex:
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
0 |
0 |
0 |
0,1034 |
0,1379 |
1,1724 |
590 |
|
0 |
1 |
0 |
0 |
0,2759 |
0,0345 |
-0,207 |
45 |
|
0 |
0 |
1 |
0 |
-0,241 |
0,3448 |
-0,069 |
60 |
|
0 |
0 |
0 |
1 |
0,069 |
-0,241 |
0,4483 |
80 |
Aquí ya no quedan coeficientes negativos para las variables del problema en la primera fila, con lo que se llegó a la solución. Son no nulas las variables f, x, y y z, con valores 590, 45, 60 y 80, respectivamente. Esto significa que la función objetivo f(x, y, z) alcanza un valor máximo de 590 cuando:
\[ \begin{equation} \left\lbrace \begin{array}{ll} x = 45 \\ y = 60 \\ z = 80 \end{array} \right. \end{equation}\]
- Resuelva utilizando el método Simplex el ejercicio 2, ya hecho mediante el método gráfico.
- Encuentre el máximo de la función objetivo f(x;y;z) = 3x + 4y + 3z sujeta a las siguientes condiciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} x + 2y + x \le 120 \\ 2x + 4y + 5z \le 420 \\ x + y + 2z \le 155 \\ x \ge 0; y \ge 0; z \ge 0 \end{array} \right. \end{equation}\]
Respuesta ii) El máximo de f(x;y;z) es 310 y se alcanza cuando x vale 10, y vale 25 y z vale 60. Las tablas Simplex que se van obtieniendo son las siguientes:
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
-3 |
-4 |
-3 |
0 |
0 |
0 |
0 |
|
0 |
1 |
2 |
1 |
1 |
0 |
0 |
120 |
|
0 |
2 |
4 |
5 |
0 |
1 |
0 |
420 |
|
0 |
1 |
1 |
2 |
0 |
0 |
1 |
155 |
Se toma la variable y y queda:
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
-1 |
0 |
-1 |
2 |
0 |
0 |
240 |
|
0 |
0,5 |
1 |
0,5 |
0,5 |
0 |
0 |
60 |
|
0 |
0 |
0 |
3 |
-2 |
1 |
0 |
180 |
|
0 |
0,5 |
0 |
1,5 |
-0,5 |
0 |
1 |
95 |
Se toma la variable z:
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
-1 |
0 |
0 |
1,3333 |
0,3333 |
0 |
300 |
|
0 |
0,5 |
1 |
0 |
0,8333 |
-0,167 |
0 |
30 |
|
0 |
0 |
0 |
1 |
-0,667 |
0,3333 |
0 |
60 |
|
0 |
0,5 |
0 |
0 |
0,5 |
-0,5 |
1 |
5 |
Y finalmente, la variable x:
|
f |
x |
y |
z |
s1 |
s2 |
s3 |
R |
|
1 |
0 |
0 |
0 |
2,3333 |
-0,667 |
2 |
310 |
|
0 |
0 |
1 |
0 |
0,3333 |
0,3333 |
-1 |
25 |
|
0 |
0 |
0 |
1 |
-0,667 |
0,3333 |
0 |
60 |
|
0 |
1 |
0 |
0 |
1 |
-1 |
2 |
10 |
Ejercicio 6
Utilice el método Simplex para minimizar la función f(x;y) = 3 · x + 2 · y sujeta a las siguientes restricciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 5 \cdot x + 2 \cdot y \ge 30 \\ 2 \cdot x + 4 \cdot y \ge 28 \end{array} \right. \end{equation}\]
En este caso, como las restricciones son de “mayor o igual”, las variables auxiliares s1 y s2 aparecerán restando en las ecuaciones. Por lo demás, el método ya visto se aplica de igual manera. Las ecuaciones son:
f - 3 · x - 2 · y = 0
5 · x + 2 · y - s1 = 30
2 · x + 4 · y - s2 = 28
Con estos datos la primera tabla Simplex será la siguiente, en la que ya se calcularon los cocientes entre los resultados y los coeficientes de la variable x, que se elige para comenzar porque su coeficiente en la primera fila es el de mayor valor absoluto:
|
f |
x |
y |
s1 |
s2 |
R |
|
|
1 |
-3 |
-2 |
0 |
0 |
0 |
|
|
0 |
5 |
2 |
-1 |
0 |
30 |
30/5=6 |
|
0 |
2 |
4 |
0 |
-1 |
28 |
28/2=14 |
Como el menor cociente corresponde a la fila 2, es esa la que se tomará como pivote. Se la divide por 5 para lograr un 1 en la posición sombreada, que será el pivote:
|
f |
x |
y |
s1 |
s2 |
R |
|
1 |
-3 |
-2 |
0 |
0 |
0 |
|
0 |
1 |
0,4 |
-0,2 |
0 |
6 |
|
0 |
2 |
4 |
0 |
-1 |
28 |
Para anular los demás coeficientes de la fila x, se hace: F'1 = F1 + 3 · F2 Y F'3 = F3 - 2 · F2:
|
f |
x |
y |
s1 |
s2 |
R |
|
1 |
0 |
-0,8 |
-0,6 |
0 |
18 |
|
0 |
1 |
0,4 |
-0,2 |
0 |
6 |
|
0 |
0 |
3,2 |
0,4 |
-1 |
16 |
Esta es la segunda tabla Simplex. Aquí no son nulas las variables f, x y s2, que valen respectivamente 18, 6 y -16. Pero como en la primera fila aún hay coeficientes negativos, no se ha llegado a la solución. En la tabla anterior se sombreó la casilla de la columna y, fila 3, porque esa es la que se deberá tomar como pivote para el siguiente paso. Para lograr un 1 en esa posición, se divide toda la fila por 3,2:
|
f |
x |
y |
s1 |
s2 |
R |
|
1 |
0 |
-0,8 |
-0,6 |
0 |
18 |
|
0 |
1 |
0,4 |
-0,2 |
0 |
6 |
|
0 |
0 |
1 |
0,125 |
-0,313 |
5 |
Para anular los restantes coeficientes de esa columna, se hace:
F'1 = F1 + 0,8 · F3 y F'2 = F2 - 0,4 · F3:
|
f |
x |
y |
s1 |
s2 |
R |
|
1 |
0 |
0 |
-0,5 |
-0,25 |
22 |
|
0 |
1 |
0 |
-0,25 |
0,125 |
4 |
|
0 |
0 |
1 |
0,125 |
-0,313 |
5 |
En esta, que es la segunda tabla Simplex, ya no quedan coeficientes negativos para las variables del problema. Eso significa que se llegó al valor mínimo de f, que es 22, cuando la x vale 4 y la y vale 5.
- Resuelva el ejercicio anterior por el método gráfico y compruebe el resultado obtenido.
- Resuelva el ejercicio 3 utilizando el método Simplex.

