2. Introducción al cálculo
Objetivos
- Calcular límites de funciones.
- Encontrar puntos de discontinuidad de funciones y clasificarlos.
- Calcular derivadas.
- Aplicar el concepto de derivada para analizar funciones y estimar sus gráficas.
- Aplicar derivadas para resolver problemas económicos.
2.1. Límite funcional y continuidad
Ejercicio 1
Calcule el límite de \( f(x) = \frac{2x+4}{x^2-4}\) cuando x tiende a los puntos que no pertenecen al dominio.
En este ejercicio primero se determina el dominio. Como no se puede dividir por cero, el denominador no puede tomar ese valor:
\[ x^2 - 4 \ne 0\]
Al resolver esta ecuación, se obtiene: \( Dom = \Re - \{-2;2 \}\)
Por lo tanto, lo que se pide es calcular el límite cuando x tiende a -2 y a 2.
Existen al menos dos maneras de calcular estos límites: a través de tablas de valores suficientemente detalladas o al factorizar los polinomios del numerador y del denominador, analizar si es posible hallarlos algebraicamente. A continuación, se realizarán las dos resoluciones aquí mencionadas.
Por tabla de valores
La siguiente tabla se confeccionó con Excel. Los valores de x se cargan manualmente, de acuerdo con los valores que interesan analizar. En este caso, se toman muchos números cerca de -2 y 2, tanto mayores como menores.
En la segunda casilla de la primera fila, se copió la fórmula tal como debe escribirse en Excel. Al ubicar el mouse en la celda correspondiente a f(-4), se escribe la fórmula. Donde dice casilla, se indica la posición del -4 (por ejemplo, A2). Después, cuando ya se calculó el valor correspondiente a f(-4), se copia la misma fórmula para todos los demás valores, arrastrando hacia abajo la cruz que aparece al posicionar el mouse sobre el borde inferior derecho de la casilla con el resultado.
|
x |
f(x)=(2*casilla+4)/(casilla*casilla-4) |
x |
f(x) |
|
-4 |
-0,333333333 |
1 |
-2 |
|
-3 |
-0,4 |
1,5 |
-4 |
|
-2,5 |
-0,444444444 |
1,9 |
-20 |
|
-2,1 |
-0,487804878 |
1,99 |
-200 |
|
-2,01 |
-0,498753117 |
1,999 |
-2000 |
|
-2,001 |
-0,499875031 |
1,9999 |
-20000 |
|
-2,0001 |
-0,4999875 |
2 |
#¡DIV/0! |
|
-2 |
#¡DIV/0! |
2,0001 |
20000 |
|
-1,9999 |
-0,5000125 |
2,001 |
2000 |
|
-1,999 |
-0,500125031 |
2,01 |
200 |
|
-1,99 |
-0,501253133 |
2,1 |
20 |
|
-1,99 |
-0,501253133 |
2,5 |
4 |
|
-1,5 |
-0,571428571 |
3 |
2 |
|
-1 |
-0,666666667 |
4 |
1 |
|
0 |
-1 |
5 |
0,666666667 |
En las celdas correspondientesa f(-2) y f(2) aparece la leyenda “#¡DIV/0!”, que es el mensaje de error que indica que se intentó dividir por cero.
Al observar los valores que toma la función en las cercanías de -2 se puede apreciar que los resultados están cada vez más cerca de… ¿qué valor? (Respuesta: -0,5).
Esto se expresa así:
\[ lím_{x\to-2} \frac{2x+4}{x^2-4}=-0,5\]
Y se lee “el límite para x tendiendo a -2 de la función es -0,5".
En cambio, en las proximidades a 2 se puede apreciar que no existe el límite, ya que al acercarse a ese valor por la izquierda (es decir, desde valores menores a 2), los resultados son cada vez más chicos y al acercarse por la derecha (es decir, desde valores mayores a 2), cada vez más grandes.
Esto se expresa de la siguiente manera:
\[ lím_{x\to2} \frac{2x+4}{x^2-4}= \infty\]
Cálculo algebraico
Para realizar algebraicamente estos límites, se pueden factorizar los polinomios del numerador y el denominador:
\[ lím_{x\to-2} \frac{2x+4}{x^2-4}= lím_{x\to-2} \frac{2 \cdot (x+2)}{(x+2) \cdot (x-2)}= \]
En este punto N, se puede simplificar la expresión y efectuar las cuentas correspondientes:
\[ lím_{x\to-2} \frac{2 \cdot (x+2) } {(x+2) \cdot (x-2)} = \frac{2}{-4} = - \frac{1}{2} = -0,5 \]
Recordemos que al calcular el límite se están considerando valores de x cercanos, muy cercanos, pero no iguales a -2.
Gráficamente, esto significa que “falta” el punto (-2; -0,5) en la traza de la función, porque x no puede tomar el valor -2.
Cuando se utiliza el mismo procedimiento para el límite de x que tiende a 2, se observa que el denominador sigue igual a cero. Por lo tanto, continúa sin poder realizarse la división. Esto implica que el límite no existe:
\[ lím_{x\to-2} \frac{2 \cdot (x+2) } {(x+2) \cdot (x-2)} = \infty \]
En el gráfico esto significa que la función presenta una asíntota vertical en x=2.
En el siguiente diagrama, construido con Geogebra, se puede observar la asíntota mencionada en línea punteada. Sin embargo, el punto faltante no aparece.
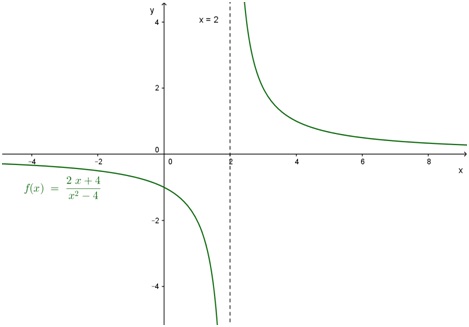
Como se mencionó en los ejercicios sobre funciones racionales en la Unidad 1, es necesario destacar los “puntos faltantes”, agregando manualmente círculos con relleno blanco:
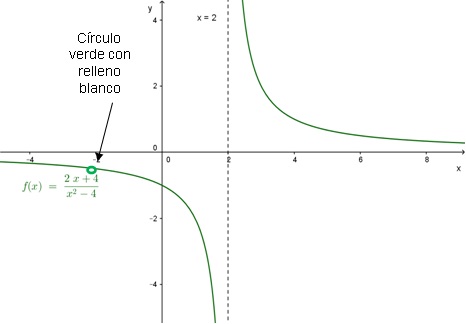
A partir de los resultados de estos dos ejercicios, se puede concluir que cuando se busca el límite de una función racional y x tiende a un valor que anula el denominador, pueden pasar dos situaciones:
- que ese valor anule también el numerador: en ese caso, se factorizan ambos polinomios y se simplifican, para luego calcular el límite;
- que ese valor no anule el numerador. Ahí, el límite no existe.
Ejercicio 2
Dada la función \( \large f(x) = \frac{x^2 - 9} {x^2 + 2x - 3} \), se pide:
- Encuentre su dominio y los puntos de intersección de la función con los ejes cartesianos.
- Indique los puntos en los que la función es discontinua y clasifique esas discontinuidades de acuerdo con si son evitables o no. Justifique su respuesta.
- Grafique la función.
- El Dominio de la función está formado por los valores de x para
los que la función está definida. Como se trata de una función racional,
no puede calcularse cuando el denominador se anula. Esos valores se buscan resolviendo la ecuación x2 + 2x - 3 = 0.
Al utilizar la fórmula de la resolvente, se obtienen x = -3 y x = 1, que deberán excluirse del dominio.
Por lo tanto, \( Dom = \Re - \{-3;1 \} \)
La intersección con el eje de las ordenadas se obtiene al reemplazar, en la fórmula de la función f(x), la x por cero. En este caso se obtiene 3. Por lo tanto, la intersección con el eje y es en (0; 3).
La intersección con el eje de las abscisas se encuentra cuando se iguala a cero la función:
\[ \frac {x^2 -9}{x^2 + 2x -3}=0 \]
Al despejar, será:
\[ x^2 -9 = 0 \cdot (x^2 + 2x -3 ) \]
Esto solo se puede hacer si \( x \neq -3 \) o si \( x \neq 1 \), porque esos dos valores no pertenecen al dominio de la función.
Cuando se continúa, se obtiene:
\[ x^2 - 9 = 0 \]
Y, por lo tanto, x = 3 o x = -3. Pero este último valor no pertenece al dominio. Por eso, la única intersección de la función con el eje de las abscisas es en (3; 0).
Si la función no está definida para algún valor de x, la función no será continua en ese punto.
Esta función no está definida para los valores de x que anulan el denominador. En esos valores, la función es discontinua. En este caso, hay discontinuidades en x = -3 y x = 1. Y, para analizar esas discontinuidades, se calcula el límite de la función cuando x tiende a esos valores:
- \( \large lím_{x \to -3} \frac {x^2 -9}{x^2 +2x-3} = lím_{x \to -3} \frac {(x-3)\cdot (x+3)}{(x+3) \cdot (x-1)} = lim_{x \to -3} \frac{x-3}{x-1} = \frac {3}{2} = 1,5\)
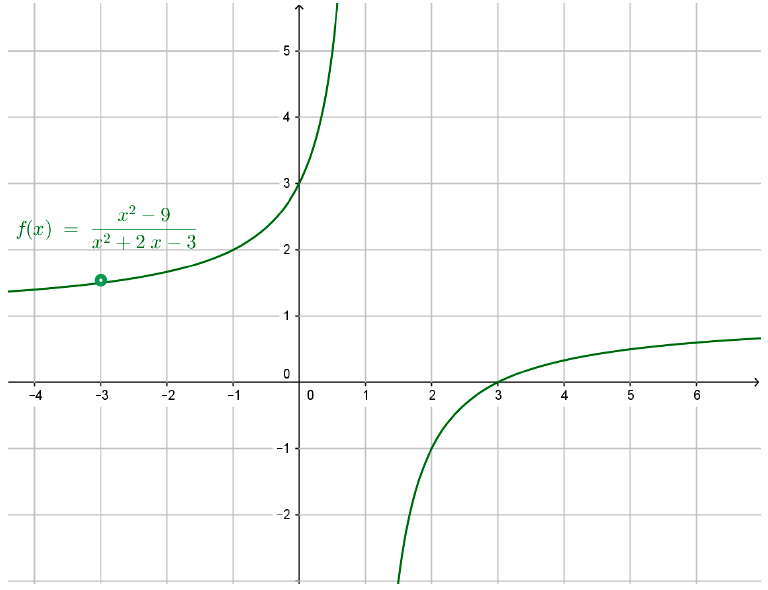
Esto significa que, en la gráfica de la función “falta” el punto (-3; 1,5). De modo que esta discontinuidad se puede evitar si definimos la imagen de x = -3 como y = 1,5.
- \( \large lím_{x \to 1} \frac {x^2 -9}{x^2 +2x-3} = lím_{x \to 1} \frac {(x-3)\cdot (x+3)}{(x+3) \cdot (x-1)} = lim_{x \to 1} \frac{x-3}{x-1} = \infty \), es decir, este límite no existe.
Como no existe el límite para la función en las proximidades de x = 1, la discontinuidad no se puede salvar, ya que esta función tiene una asíntota vertical en x = 1.
- \( \large lím_{x \to -3} \frac {x^2 -9}{x^2 +2x-3} = lím_{x \to -3} \frac {(x-3)\cdot (x+3)}{(x+3) \cdot (x-1)} = lim_{x \to -3} \frac{x-3}{x-1} = \frac {3}{2} = 1,5\)
- En Geogebra se obtiene el siguiente gráfico al que se le agregó un círculo verde relleno de color blanco, para destacar que falta el punto (-3; 1,5). N
Como ya se mencionó en la Unidad 1, los programas que grafican no indican esta discontinuidad.
En los siguientes videos, el Profesor Julio Ríos Gallego resuelve límites como los de estos ejercicios.
Dada la función \[ f(x) = \frac{x^2 + 7x + 12}{x^2 + x -6} : \]
- Encuentre su dominio y los puntos de intersección de la función con los ejes cartesianos.
- Indique los puntos en los que la función es discontinua y clasifique esas discontinuidades (si son evitables o no). Justifique su respuesta.
- Grafique la función f(x).
- \( Dom = \Re - \{ -3;2\} \) Intersección con x: (-4; 0) con y (0; -2).
- La función tiene una discontinuidad evitable en \( \left( -3 ; - \frac{1}{5} \right) \) y una asíntota vertical en x = 2. Esta última es una discontinuidad no evitable.
Respuestas:
2.2. Derivadas
Ejercicio 3
En el siguiente diagrama, construído con Geogebra, al mover con el mouse el deslizador(en azul, en el centro del gráfico), cambian los puntos de intersección de la recta roja con la parábola y = x2 + 1.
Observe el diagrama y responda las siguientes cuestiones.
- Al mover el deslizador, hay uno de los puntos de intersección que se mantiene fijo, ¿cuál es?
- ¿Cuál es el otro punto de intersección cuando el deslizador d = 1? ¿ y cuando d = -1? ¿Cuánto vale la pendiente de la recta roja en cada uno de esos casos? Compruebe el valor indicado en el gráfico, correspondiente al cálculo \( \large \frac{\Delta y}{\Delta x} \)
- ¿Qué indica el deslizador d?
- ¿Qué sucede con los puntos de intersección cuando d = 0? ¿Cómo es la recta roja respecto de la parábola en este caso? ¿Cuál es su pendiente?
- El punto que se mantiene fijo al mover el deslizador es el punto (1; 2)
Cuando d = -1, el otro punto de intersección es (0; 1). En ese momento, la pendiente de la recta secante es 1.
Este valor se puede calcular como Pendiente = \( \large \frac{\Delta y}{\Delta x} = \frac {1-2}{0-1} = \frac {-1}{-1} = 1 \)
Cuando d = 1, la recta secante interseca a la parábola en (1; 2) y en (2; 5), y su pendiente es 3, que se puede calcular como
Pendiente = \( \large \frac{\Delta y}{\Delta x} = \frac {5-2}{2-1} = \frac {3}{1} = 3 \)
El deslizador d indica la diferencia entre la abscisa del otro punto de intersección y la abscisa del punto que permanece fijo, es decir 1. Por ejemplo, cuando d = 0,5, el otro punto de intersección es 1,5::
d = 1,5 - 1 = 0,5
Por lo tanto, el deslizador d es el mismo valor que \( \Delta x\)
- Cuando d = 0, los dos puntos de intersección ya no son dos, sino uno: (1;2). La recta roja es tangente a la parábola en ese punto. Su pendiente es 2. Pero este valor no se puede calcular como \( \large \frac {\Delta y}{\Delta x} \), ya que \( \Delta x\) es 0. Se calcula como \( \large lím_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \).
En la siguiente animación, se generalizan los resultados de este ejercicio para cualquier función, y se define la derivada de una función en punto.
Entonces, la derivada de una función f(x) es:
\[ f´(x) = lím_{\Delta x \to 0} \frac {f (x + \Delta x)- f (x)}{\Delta x}\]
En el desarrollo de estos temas, se utilizan distintas notaciones. En particular, el \( lím_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \) también se anota \( \frac{d y}{d x} \) por lo que también se escribe:
\[ f´(x) = \frac{d y}{d x} \]
Cuando se utiliza más de una función, para distinguir entre ellas también se puede anotar:
\[ f´(x) = \frac{d f}{d x} \]
Demuestre la fórmula de la derivada de un producto de funciones.
Sea i(x) = f(x) · g(x) . La derivada de i(x) es lo que se está buscando. Por definición de derivada, es:
\[ i´(x) = lím_{h \to 0}\frac{i (x + h) - i (x)}{h} \]
Por definición de i(x) , es:
\[ i´(x) = [ f (x) \cdot g(x)]´ = lím_{h \to 0}\frac{f (x + h) \cdot g (x + h) - f(x) \cdot g(x)}{h} = \]
\[ lím_{h \to 0}\frac{f (x + h) \cdot g (x + h) - f(x) \cdot g(x) + 0}{h} = \]
\[ = lím_{h \to 0}\frac{f (x + h) \cdot g (x + h) - f(x) \cdot g(x) - f(x) \cdot g(x+h) + f(x) \cdot g(x+h)}{h} \]
\[ = lím_{h \to 0}\frac{f (x + h) \cdot g (x + h) - f(x) \cdot g(x+h) + f(x) \cdot g(x+h) - f(x) \cdot g(x)}{h} \]
En este último paso se reagruparon los términos que se agregaron en el paso anterior. Ahora, se sacarán factores comunes entre los dos primeros y los dos últimos:
\[ = lím_{h \to 0}\frac{g (x + h) \cdot [f (x + h) - f(x)] + f(x) \cdot [g(x+h) - g(x)]}{h} = \]
\[ = lím_{h \to 0} \left \{ \frac{g (x + h) \cdot [f (x + h) - f(x)]}{h} + \frac {f(x) \cdot [g(x+h) - g(x)]}{h} = \right \} \]
Esta expresión se puede calcular de la siguiente manera:
\[ = lím_{h \to 0} \frac{g (x + h) \cdot [f (x + h) - f(x)]}{h} + lím_{h \to 0} \frac {f(x) \cdot [g(x+h) - g(x)]}{h} = \]
\[ = lím_{h \to 0} g (x + h) \cdot lím_{h \to 0} \frac{f (x + h) - f(x)} {h} + lím_{h \to 0} f(x) \cdot lím_{h \to 0} \frac { g(x+h) - g(x)}{h} \]
Ahora, se calcularán estos límites, teniendo presente las definiciones de derivada de f(x) y de g(x):
\[ = g(x) \cdot f´(x) + f(x) \cdot g´(x)\]
Al reordenar los términos, se obtiene la fórmula de la derivada de un producto:
\[ [f(x) \cdot g(x)]´ = (f \cdot g)´(x) = f´(x) \cdot g(x) + f(x) \cdot g´(x)\]
Ejercicio 5
A continuación, se pide derivar las siguientes funciones. Es importante, tener en cuenta las reglas de derivación.
|
a) \[ f(x) = 4x^5 + 9x^2 +8 \] |
b) \[ g(x) = \sqrt[4]{3x^2 + 1} \] |
|
c) \[ h(x) = e^{4x^3 + 3x} \] |
d) \[ i(x) = ln(2x^5 + 5 x^3) \] |
|
e) \[ j(x) = e^x \cdot (2x^3 + 5x^2 + 6x) \] |
f) \[ k(x) = \frac {7x^3 + 4x^2 -2x}{ln(x)} \] |
f(x) = 4x5 + 9x2 + 8
La función f es un polinomio, de modo que se deriva término a término. Recordemos tres reglas de derivación:
- La derivada de una constante es cero.
- La derivada de \( \large a \cdot f(x) \) es \( a \cdot f´(x) \)
- La derivada de xn es n · xn-1
\[ f´(x) = 4 \cdot 5 \cdot x^{5-1}+ 9 \cdot 2 \cdot x^{2-1} + 0 \]
Al resolver los cálculos es:
\[ f´(x) = 20 \cdot x^4 + 18 \cdot x^1 + 0 = 20 \cdot x^4 + 18 \cdot x \]
\[ g(x) = \sqrt[4]{3x^2 + 1} \]
La función de este ejercicio es compuesta, porque hay una raíz (que conviene expresar como exponente racional) que afecta a un polinomio. Para derivarla, se aplica la regla de derivación de funciones compuestas:
\[ (fog)´(x) = f´[g(x)] \cdot g´(x)\]
Conviene identificar las funciones. En este ejercicio la función que en la fórmula anterior es g(x) es 3x2+ 1 . Su derivada es 3 · 2 · x2-1 + 0 = 6 · x
La función f es la raíz que abarca a g(x). Entonces resulta:
\[ g(x) = \sqrt[4]{3x^2 + 1} = (3x^2 + 1)^{\frac{1}{4}} \]
Y su derivada es: \( g´(x) = \frac{1}{4} \cdot (3x^2 + 1)^{\frac{1}{4}-1} \cdot (6x) \)
Se resuelven los cálculos del exponente y se resuelven de otra manera:
\[ g´(x) = \frac{1}{4} \cdot (3x^2 + 1)^{-\frac{2}{4}} \cdot (6x) = \frac {6x}{4 \cdot (3x^2 + 1)^{\frac{2}{4}}} \]
- \( h(x) = e^{4x^3 +3x} \)
Esta función también es compuesta porque un polinomio es el exponente de una función exponencial.
Es necesario aplicar la derivada de la función exponencial, que es la misma función exponencial por el logaritmo natural de la base (que en este caso, es 1) y la misma regla que en el ejercicio anterior. Así, se obtiene:
\[ h´(x) = e^{4x^2 +3x} \cdot (4 \cdot 3 \cdot x^{3-1} + 3 \cdot x^{1-0}) \]
Cuando se resuelven los cálculos, se llega al resultado:
\[ h´(x) = e^{4x^2 +3x} \cdot (12 \cdot x^2 + 3) \]
Es importante notar que el uso de los paréntesis es indispensable.
- \( i(x) = ln(2x^5 + 5x^3) \)
Esta función también es compuesta, porque se calcula el logaritmo de un polinomio. Además de la regla de derivación de las funciones compuestas, se utiliza la derivada del logaritmo natural, que es:
\[ [ln(x)]´ = \frac{1}{x} \]
Como aquí hay una función compuesta, la fórmula anterior indica que la derivada del logaritmo es la inversa del argumento:
\[ i´(x) = \frac{1}{2x^5 + 5x^3} \cdot (2\cdot 5 \cdot x^{5-1} + 5 \cdot 3 \cdot x^{3-1}) \]
Cuando realizamos los cálculos:
\[ i´(x) = \frac{1}{2x^5 + 5x^3} \cdot (10 \cdot x^4 + 15 \cdot x^2) \]
En el siguiente video el profesor Julio Ríos Gallego calcula una derivad de una función compuesta.
Disponible en: <https://www.youtube.com/watch?v=5qs-GIIJUy0>
- \( j(x) = e^x \cdot (2x^3 + 5x^2 + 6x)\)
Aquí hay un producto entre dos funciones. Se utiliza la derivada del producto, cuya demostración se realizó en el ejercicio 4:
\[ j´(x) = e^x \cdot (2x^3 + 5x^2 + 6x) + e^x \cdot (2 \cdot 3 \cdot x^{3-1}+ 5 \cdot 2 \cdot x + 6) \]
\[ j´(x) = e^x \cdot (2x^3 + 5x^2 + 6x) + e^x \cdot (6 \cdot x^{2}+ 10 \cdot x + 6) \]
\[ j´(x) = e^x \cdot (2x^3 + 5x^2 + 6x + 6 \cdot x^{2}+ 10 \cdot x + 6) = \]
\[ = e^x \cdot (2 \cdot x^3 + 11 \cdot x^{2}+ 16x + 6) \]
En los últimos pasos se sacó factor común y se sumaron los términos semejantes.
En el siguiente video el profesor Julio Ríos Gallego calcula una derivad de una función que es producto de otras dos.
Disponible en: <https://www.youtube.com/watch?v=C1kvg19s6Yk>
- \( k(x) = \frac {7x^3 + 4x^2 -2x}{ln(x)}\)
Esta función es una división. La regla de la derivada de una división es la siguiente:
\[ \left( \frac{f(x)}{g(x)}\right)´= \frac {f´(x) \cdot g(x) - f(x) \cdot g´(x)}{g(x)^2}\]
En este ejercicio, serían:
\[ f(x) = 7x^3 + 4x^2 - 2x\]
\[ g(x) =ln(x) \]
Y sus derivadas:
\[ f´(x) = 7 \cdot 3 \cdot x^{3-1} + 4 \cdot 2 \cdot x - 2 = 21x^2+ 8x - 2\]
\[ g´(x) = \frac{1}{x} \]Aquí se arma la derivada de k:
\[ k´(x) = \frac {(21x^2 + 8x - 2) \cdot ln(x) - (7x^3 + 4x^2 -2x) \cdot \frac{1}{x}}{[ln(x)]^2} \]
En el segundo término del numerador, se puede distribuir y simplificar:
\[ k´(x) = \frac {(21x^2 + 8x - 2) \cdot ln(x) - (7x^3 \cdot \frac{1}{x} + 4x^2 \cdot \frac{1}{x} -2x \cdot \frac{1}{x})}{[ln(x)]^2} \]
\[ k´(x) = \frac {(21x^2 + 8x - 2) \cdot ln(x) - (7x^2 + 4x -2)}{[ln(x)]^2} \]A continuación, se puede suprimir el paréntesis:
\[ k´(x) = \frac {(21x^2 + 8x - 2) \cdot ln(x) - 7x^2 - 4x + 2}{[ln(x)]^2} \]
En el siguiente video el profesor Julio Ríos Gallego calcula una derivad de una función que es cociente de otras dos:
Disponible en: <https://www.youtube.com/watch?v=CZ6CBlsKif8>
2.3. Derivadas para el estudio de funciones
Ejercicio 6
En el siguiente gráfico, realizado con Geogebra, está representada la función. Al mover el deslizador que se encuentra abajo, a la izquierda, se grafican distintas rectas que resultan tangentes a la curva por diferentes puntos.
Con base en la observación del gráfico, contestar las siguientes cuestiones.
- Mueva el deslizador e indique qué representa. ¿Cuál es la relación entre las distintas rectas rojas y la función?
- Cuando el deslizador está en a = 1, ¿cuál es el punto de tangencia? Indique sus coordenadas.
- Encuentre la ecuación de la recta tangente a la función por el punto encontrado en a).
- Repita las partes a) y b) cuando a = -2.
- ¿Qué sucede con la recta r cuando a = -1? ¿Sucede lo mismo para algún otro valor de? ¿Cuál es la pendiente de la recta tangente en esos casos?
- Generalice esta observación para cualquier función.
El deslizador indica la abscisa del punto de intersección de la recta roja con la función. Cuando hay dos puntos de intersección, a es la abscisa del punto de tangencia.
Las rectas rojas son tangentes a la función. Al mover el deslizador, se grafica la recta tangente por el punto cuya abscisa es el valor del deslizador.
Como puede observarse en el gráfico, cuando el deslizador está en a=1, la recta roja es tangente a la función f(x) por el punto (1; 10).
Si no se dispusiera del gráfico, se podría encontrar reemplazando el 1 en la fórmula de la función:
\[ f(1) = -1^3+ 3 \cdot 1^2 + 9 \cdot 1 - 1 = -1 + 3 + 9 - 1 = 10\]
Para encontrar la ecuación de una recta, es necesario hallar su pendiente y su ordenada al origen.
La pendiente de esta recta es el valor de la derivada de f(x) en el punto de tangencia, es decir, en 1, de acuerdo con lo estudiado en el ejercicio 3. Por lo tanto, se derivará la función f(x) y se calculará f´(x):
\[ f´(x) = -3x^2 + 6x + 9\]
\[ f´(1) = -3 \cdot 1^2 + 6 \cdot 1 + 9 = -3 + 6 + 9 = 12\]
De modo que la ecuación de la recta es r(x) = 12 · x + b y falta hallar el valor de b. Pero se sabe que la recta buscada pasa por el punto de tangencia (1,10), de modo que r(1) = 10. Con este dato, se puede hallar b:
r(1) = 12 · 1 + b = 10
12 + b = 10
b = 10 - 12 = -2
Por lo tanto, la ecuación buscada es:
r(x) = 12 · x - 2
Este resultado se puede generalizar:
\[ r(x) = f´(a) \cdot x + [f(a) - f´(a) \cdot a]= f´(a) \cdot x + f(a) - f´(a) \cdot a\]
Reagrupando, se obtiene la fórmula de la recta tangente a una curva, por el punto de abscisa x = a:
\[ r(x) = f´(a) \cdot (x-a) + f(a)\]
En a = -2 el punto de tangencia es (-2; 1). Es decir, f(a) = 1.
Cuando x = -2, la pendiente de la recta tangente es el valor de la derivada en esa abscisa:
\[ f´(-2) = -3 \cdot (-2)^2 + 6 \cdot (-2) + 9 = -12 - 12 + 9 = -15\]
Reemplazando estos valores en la fórmula deducida en el punto b) es:
r(x) = -15 · [x - (-2)] + 1 = -15 · (x + 2) + 1 = -15 · x - 30 + 1
Resolviendo los cálculos resulta la fórmula buscada:
r(x) = -15 · x - 29
Es importante notar que, como ya se sabía, la recta tangente tiene pendiente negativa cuando la función decrece y pendiente positiva cuando la función crece.
Cuando a = -1 la recta tangente es horizontal. Sucede lo mismo cuando a = 3. Esto se debe a que la función alcanza, en ambas abscisas, “extremos relativos”. Cuando a = -1 hay un mínimo relativo y cuando a = 3 hay un máximo relativo.
Si la recta es horizontal, su pendiente es nula. Como la pendiente de la recta tangente es el valor de la derivada en esa abscisa, significa que f'(-1) = 0 y que f'(3) = 0, lo que se puede comprobar cuando se efectúan los cálculos correspondientes:
f'(-1) = -3 · (-1)2 + 6 · (-1) + 9 = -3 - 6 + 9 = 0
f'(3) = -3 · 32 + 6 · 3 + 9 = -27 + 18 + 9 = 0
El resultado anterior se puede generalizar para encontrar las abscisas de los extremos relativos de una función.
En las abscisas de los extremos relativos de una función, la derivada se anula.
Sin embargo, podría suceder que la derivada resulte nula en cierto valor de x (al que se le llamará valor crítico) y aún así, la función no presente extremo relativo en esa abscisa.
Para asegurar que un valor crítico de x corresponde a un extremo relativo, se deberá investigar si cambia el signo de la derivada de la función en los intervalos determinados por ese valor. Si a la derecha del valor crítico la derivada es positiva, y a su izquierda es negativa, significa que la función crece antes del valor crítico y después decrece, por lo tanto, la función presenta un máximo relativo cuya abscisa es el valor crítico. Si el cambio de signo de la derivada es en sentido contrario, habrá un mínimo relativo. Si no hay cambio de signo en la derivada, el valor crítico no es un extremo relativo.
Ejercicio 7
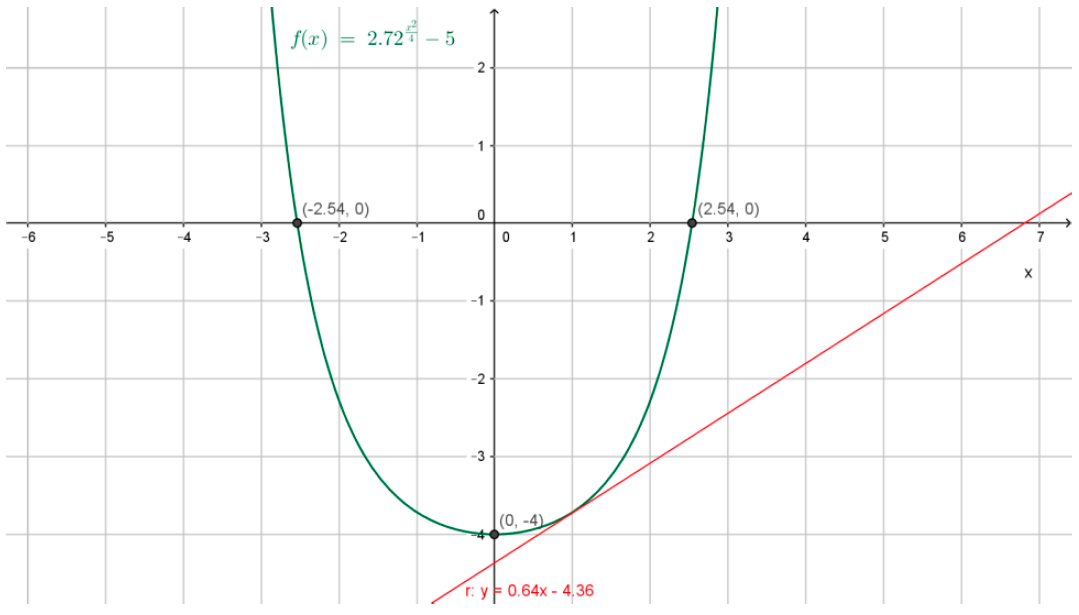
Dada la función \( f(x) = e^{ \left( \frac{x^2}{4} \right)}- 5\) se pide que:
- Encuentre su dominio.
- Indique las intersecciones de la gráfica con los ejes cartesianos.
- Calcule su derivada.
- Busque sus extremos relativos, los intervalos de crecimiento y los de decrecimiento.
- Encuentre la ecuación de la recta tangente a la función en x=1.
- Grafique ambas funciones en un mismo diagrama.
- La función f(x) es una exponencial, de manera que su dominio son todos los números reales \( Dom = \Re\)
La intersección con el eje x ocurre cuando la imagen es 0:
\[ e^{ \left( \frac{x^2}{4} \right)}- 5 = 0\]
\[ e^{ \left( \frac{x^2}{4} \right)} = 5 \]
Cuando se aplican los logaritmos naturales en ambos lados de esta identidad:
\[ ln \left[ e^{ \left( \frac{x^2}{4} \right)} \right] = ln(5) \]
Si utilizamos las propiedades de los logaritmos, se puede reescribir:
\[ \frac{x^2}{4} \cdot ln(e) = ln(5) \approx 1,60944 \]
\[ \frac{x^2}{4} \cdot 1 \approx 1,60944 \]
Al despejar x en esta última expresión se obtienen los dos valores para los cuales la gráfica interseca al eje x: \( x \approx -2,537 \) y \( x \approx 2,537 \). Los puntos de intersección se indican con sus correspondientes coordenadas, por eso son: (-2,537;0) y (2,537;0).
Falta buscar cuál es la intersección con el eje y , para lo que se reemplaza la x con cero:
\[ f(0) = e^{ \left( \frac{0^2}{4} \right)} - 5 = 1 - 5 = -4 \]
Entonces, la intersección con el eje y es el punto (0;-4)
La función es una exponencial compuesta, por lo tanto,
\[ f´(x) = e^{ \left( \frac{x^2}{4} \right)} \cdot \frac{1}{4} \cdot 2x = \frac{x}{2} \cdot e^{ \left( \frac{x^2}{4} \right)} \]
Aquí se utilizó la derivada de la función exponencial y la de la función compuesta.
Como ya se vio en el ejercicio anterior, en los extremos relativos, la derivada se anula. Como la derivada es un producto entre una función exponencial (que nunca vale cero) y un polinomio, la derivada valdrá cero cuando se anule el polinomio. Este polinomio se anula cuando x = 0.
Para averiguar si en x = 0 hay realmente un extremo relativo, es necesario estudiar si la derivada cambia de signo en los intervalos que este valor determina. Este valor divide al eje x en dos intervalos \( (- \infty ; 0 )\) y \( (0 ; + \infty )\).
Se debe investigar si en esos intervalos la función f(x) crece o decrece. Con ese fin, se averigua el signo de la derivada primera en cada uno de esos intervalos, tomando un punto interior a cada uno de ellos y calculando allí la derivada:
En \( (- \infty ; 0 )\), se puede tomar, por ejemplo x = -1:
\[ f´(-1) = \frac{-1}{2} \cdot e^{ \left( \frac{(-1)^2}{4} \right)} = - \frac{1}{2} \cdot e^{\frac{1}{4}} \approx -0,64 < 0 . \] Como la derivada es negativa, f(x) es decreciente en este intervalo. (1)
En el intervalo \( (0 ; + \infty )\), se puede tomar, por ejemplo x = 1:
\( f´(1) = \frac{1}{2} \cdot e^{ \left( \frac{1^2}{4} \right)} = \frac{1}{2} \cdot e^{\frac{1}{4}} \approx 0,64 > 0 \). La dervida es positiva y, por lo tanto,(x) es creciente en este intervalo. (2)
Teniendo en cuenta (1) y (2), se concluye que en x = 0, la función presenta un mínimo relativo. La ordenada del punto mínimo relativo se obtiene al reemplazar este valor crítico de x en la fórmula de la función f(x). Ese valor ya se obtuvo en el punto b) (0; -4).
En resumen. La función f(x) presenta un mínimo relativo en el punto de coordenadas (0; -4).
Es decreciente en el intervalo \( (- \infty ; 0 )\) y creciente en el intervalo \( (0 ; + \infty )\)
Para encontrar la ecuación de la recta tangente en x = 1, se requiere calcular el valor de la función y de la derivada en esa abscisa:
\[ f(1) = e^{ \left( \frac{1^2}{4} \right)} - 5 \approx 1,28 - 5 = -3,72\]
La derivada en x = 1 ya se calculó en la parte d): \( f´(1) \approx 0,64 \)Al reemplazar estos valores en la fórmula deducida en el ejercicio anterior es:
\[ r(x) = f´(1) \cdot (x-1) + f(1) = 0,64 \cdot (x-1) + (-3.72) \]
Si se realizan las operaciones indicadas, se obtiene la fórmula buscada:
\[ r(x) = 0,64 \cdot x - 4,36\]
- Utilizando Geogebra, se obtiene el siguiente gráfico:
Para confeccionar manualmente el gráfico de f(x) , se pueden ubicar los puntos de intersección con los ejes y calcular una breve tabla de valores. Es conveniente considerar que, como la variable está elevada al cuadrado, no hace falta poner en la tabla los valores negativos, porque los resultados serán iguales a los que se obtengan con x positivas. Por ejemplo:
|
x |
1 |
2 |
3 |
4 |
|
f(x) |
-3,716 |
-2,280 |
4,501 |
49,736 |
Al ubicar en el diagrama los puntos encontrados en la primera parte del ejercicio y estos puntos de la tabla, junto con los simétricos, se logra un buen gráfico. Como puede verse, la función crece muy rápidamente, ya que para x = 4 y para x = -4 alcanza valores cercanos a 50, que no podrán graficarse si se utiliza la misma escala en los dos ejes.
Ejercicio 8
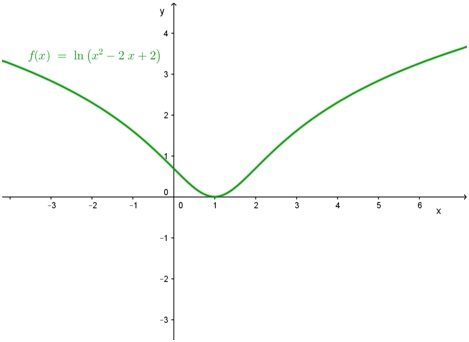
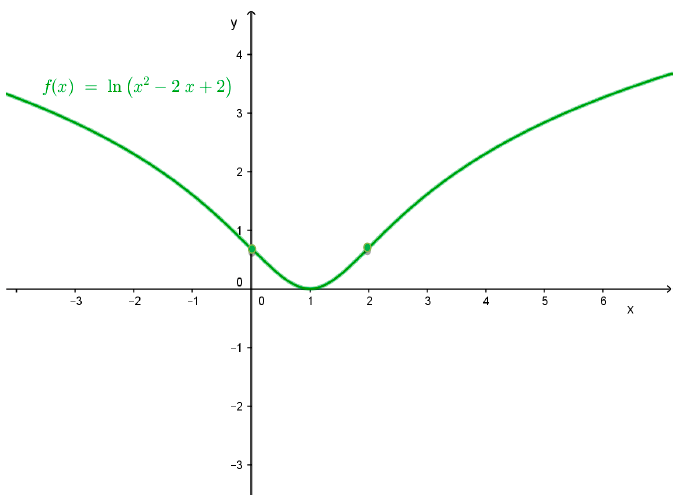
Dada la función f(x) = ln (x2 - 2x + 2), se pide que:
- Indique el dominio.
- Investigue si existen puntos de discontinuidad y en caso afirmativo, clasificarlos.
- Analice si presenta extremos relativos y en caso afirmativo, clasifíquelos e indique sus coordenadas.
Grafíquela.
f(x) = ln (x2 - 2x + 2)
Esta función es un logaritmo. Por eso, el argumento debe ser mayor a cero:
x2 - 2x + 2 > 0
Para resolver esta inecuación, se puede utilizar la fórmula de la resolvente de la ecuación de segundo grado y, a partir de allí, investigar para qué valores de x esa expresión es mayor a cero.
\[ x_{1,2} = \frac{-(-2) \pm \sqrt{(-2)^2 - 4.1.2}}{2.1} \]
Como esta expresión no tiene solución, no hay valores de x que la anulen. Si se reemplaza x por cero, se obtiene 2, que es mayor que cero. Como no hay cambios de signos (porque para ninguna x, este polinomio vale cero), el dominio será: \( Dom = \Re \)
- Como todos los números reales tienen imagen, la función f(x) no presenta discontinuidades.
Para buscar extremos relativos, se procede como en los ejercicios anteriores: se deriva la función y se buscan los valores de x para los cuales se anula la derivada. Luego se investiga mediante intervalos si esos valores corresponden a un máximo, un mínimo o ninguna de las dos cosas.
Entonces, primero se deriva la función:
\[ f´(x) = \frac{1}{x^2 - 2x + 2} \cdot (2x - 2) = \frac {2x -2}{x^2 - 2x + 2} \]
Aquí se utilizó la fórmula de la derivada de un logaritmo natural y la de una función compuesta.
Ahora, se buscan los valores de x para los cuales se anula la derivada:N
\[ \frac {2x - 2}{x^2 - 2x + 2} = 0 \]
Para que un cociente resulte cero, debe ser cero el numerador. Por lo tanto, deberá ser:
2x - 2 = 0
x = 1
Por lo tanto, la derivada se anula cuando x = 1. El punto crítico correspondiente se obtiene al reemplazar el 1 en la función original, con lo que resulta ser (1; 0). En él, la función puede presentar algún extremo relativo.
Para investigar si es un máximo o un mínimo, se estudian los dos intervalos en los que queda dividido el eje x por este valor: \( (- \infty ; 1) \) y \( (1; + \infty) \). En cada uno de estos intervalos se elegirán números y se calculará el valor de la derivada en esos números. Según el signo de la derivada, se podrá saber si la función f(x) crece o decrece en el intervalo correspondiente:
\( 0 \in (- \infty ; 1) \to f´(0) = -1 < 0 \) por lo tanto, f(x) es decreciente en este intervalo. (1)
\( 2 \in (1; + \infty) \to f´(2) = 1 > 0 \) por lo tanto, f(x) es creciente en este intervalo. (2)
De (1) y (2), se puede decir que en el punto de abscisa x = 1, la función presenta un mínimo relativo. Sus coordenadas, como se vio, son (1; 0).
- Con Geogebra se obtiene el siguiente gráfico, donde se aprecia claramente el mínimo relativo encontrado analíticamente:
Aquí se resolvió la ecuación, que es muy sencilla.
Ejercicio 9
Dada la función \( f(x) = \left[ \frac {x^2}{2} - 6 \ ln (x + 1) + 2x - \frac{5}{2}\right] \) se pide que:
- Halle el dominio.
- Calcule la derivada e indique los intervalos de crecimiento y decrecimiento.
- Ubique, si es que la función tiene, sus máximos y mínimos.
- Grafique la función.
- Esta función es la suma de un polinomio con un término que es un logaritmo. Por lo tanto, su argumento debe ser positivo. Por eso, para buscar el dominio, se plantea la siguiente inecuación: x + 1 > 0. Su conjunto solución es el dominio: \( Dom = (-1; \infty) \).
- Como la función es una suma, se deriva término a término:
\[ f´(x) = \frac {2x}{2} - 6 \cdot \frac{1}{x+1} \cdot 1 + 2 - 0 = x - \frac{6}{x+1} + 2\]
Por lo tanto, la derivada pedida es:
\[ f´(x) = x- \frac{6}{x+1}+ 2 \]
Para hallar los intervalos de crecimiento y decrecimiento, conviene comenzar por buscar los valores de x que anulan a la derivada. Con ese propósito, se deberá resolver la siguiente ecuación:
\[ f´(x) = 0 \]
\[ x- \frac{6}{x+1}+2=0 \]
\[ x+2 = \frac{6}{x+1} \]
\[ (x+2) \cdot (x+1) = 6 \]
\[ x^2 + 2x + 1x + 2 = 6 \]
\[ x^2 + 3x + 2 - 6 = 0 \]
\[ x^2 + 3x - 4 = 0 \]
Las soluciones a esta última expresión son x = -4 y x = 1. Pero, si tenemos en cuenta que el dominio de esta función es \( Dom = (-1; \infty) \), la primera solución no corresponde porque no pertenece a él. De modo que el único valor de x que anula la derivada es x = 1. Este valor divide al dominio en dos intervalos (-1; 1) y \( (1; + \infty) \). Se debe investigar si en esos intervalos la función f(x) crece o decrece; para ello se averigua el signo de la derivada primera en cada uno de esos intervalos, tomando un punto interior a cada uno de ellos y calculando allí la derivada. En el primer intervalo, por ejemplo, se puede considerar x = 0
\( f´(0) = 0 - \frac{6}{0+1} + 2 = - 6 + 2 = - 4 < 0 \) por lo tanto, la función es decreciente en todo el intervalo (-1; 1).
Para el segundo intervalo, se puede tomar x = 2:
\( f´(0) = 2 - \frac{6}{2+1} + 2 = 2 - 2 + 2 = + 2 > 0 \) por lo tanto, la función crece en todo el intervalo \( (1; + \infty) \). En x =1 la función, que era decreciente hasta ese valor, comienza a crecer a partir de él. Por lo tanto, la función tiene un mínimo cuando la abscisa es x = 1. Para ubicar ese mínimo, falta encontrar la ordenada que se obtiene al reemplazar ese valor de x en la función analizada:N
\[ f(1) = \left[ \frac{1^2}{2} - 6 \ ln (1+1) + 2 \cdot 1 - \frac {5}{2} \right] \approx -4,16 \]
- El siguiente gráfico se realizó con Geogebra:
Imagen+
Imagen 07
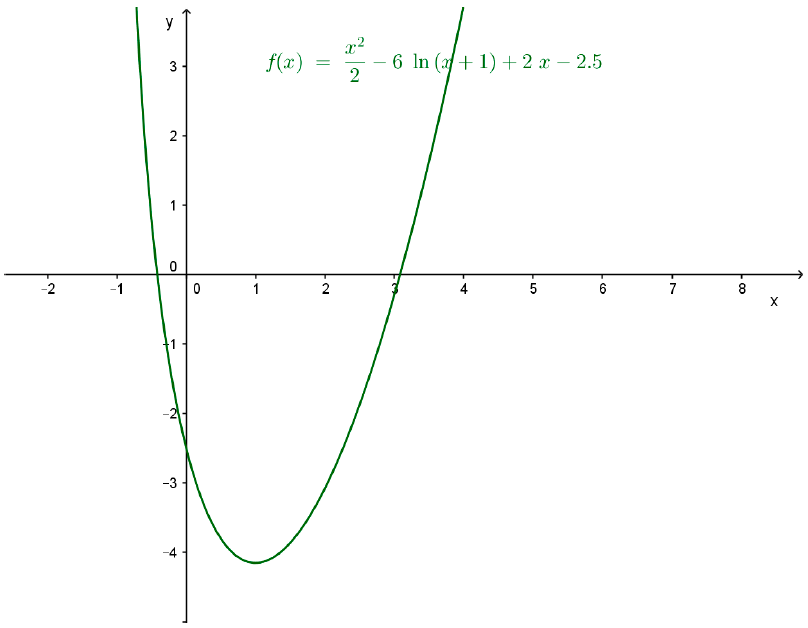
Entonces, esta función no tiene máximos relativos. Pero presenta un mínimo relativo en el punto (1; -4,16).
Este último valor se obtuvo al realizar los cálculos con calculadora.
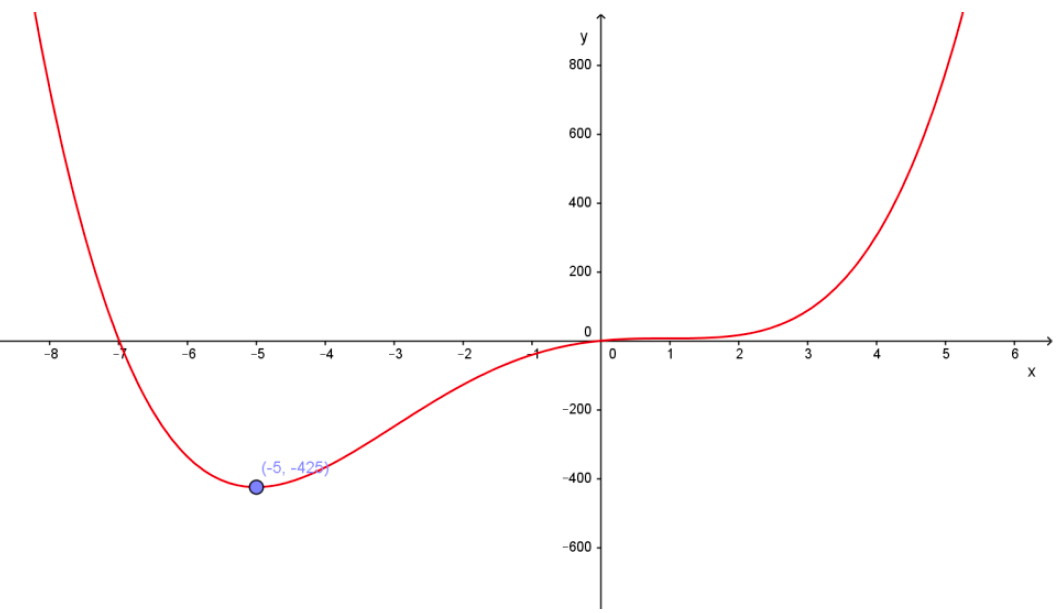
Sea f(x) = x4 + 4x3 - 18x2 + 20x . Se pide hallar el dominio, la derivada de la función, máximos y mínimos relativos y graficar aproximadamente.
Respuestas: \( Dom = \Re \), \( f´(x) = 4x^3 + 12 x^2 - 36x + 20 \). La función solo presenta un mínimo relativo en (-5; -425), a pesar de que su derivada se anula también en x = 1.
El siguiente gráfico fue confeccionado con Geogebra:
En los siguientes videos el Profesor Julio Ríos Gallego realiza el estudio completo de la función f(x) = x · ln(x), y utiliza el análisis de concavidad (que aún no se introdujo en este curso):
Disponible en: <https://www.youtube.com/watch?v=B3A1Ge9udvI> (1ª parte)
<https://www.youtube.com/watch?v=XEzbU-EMkx0> (2ª parte)
Fuente: <https://julioprofe.net/>
2.4. Aplicaciones económicas de las derivadas
Ejercicio 10
Suponemos que en un mercado el único productor de un bien enfrente una función de demanda dada por:
D : q = 176 - 4 · p
Se pide que:
- Encuentre la expresión que vincula los ingresos totales de ese único productor con el precio de venta.
- Encuentre a qué precio se obtiene el máximo ingreso total y cuántas unidades de este bien venderá.
- Los ingresos totales de un productor se calculan al multiplicar el precio de venta por la cantidad de artículos vendidos. Esto se expresa mediante la siguiente fórmula:
IT = p · q (1)
En este ejercicio, la cantidad vendida depende del precio. Si reemplazamos su fórmula en la expresión (1) y se efectúan los cálculos, es:
IT = p · (176 - 4 · p) = 176 · p - 4 · p2
Entonces, la expresión que vincula los ingresos totales con el precio de venta es:
IT = 176 · p - 4 · p2
Para encontrar el máximo ingreso total, se analizará matemáticamente esta función IT = 176 · p - 4 · p2
Se calcula su derivada: \( IT´= 176 - 4 \cdot 2 \cdot p \)
En un extremo relativo, deberá ser nula su derivada:
176 - 8 · p = 0
Al resolver esta ecuación es:
176 = 8 · p
\[ \frac{176}{8} = p = 22 \]
Entonces, el valor crítico es p = 22, que divide al dominio en dos intervalos (0; 22) y \( (22; + \infty) \). Se analizará a continuación qué signo tiene la derivada en cada uno de ellos:
\( 3 \in (0;22) \to IT´(3) = 176 - 8 \cdot 3 = 152 > 0 \) por lo tanto, IT es creciente en este intervalo. (1)
\( 25 \in (22; + \infty) \to IT´(25) = 176 - 8 \cdot 25 = -24 < 0 \) por lo tanto, IT es decreciente en este intervalo. (2)
De (1) y (2), se puede decir que en el punto de abscisa p = 22, la función ingreso total presenta un máximo relativo. Con un precio de $22, el ingreso total de la empresa será máximo.
Para averiguar cuántas unidades del producto se venden, se utiliza la fórmula de las cantidades demandadas:
D : q = 176 - 4 · 22 = 88
Es decir que al precio de $22 se venden 88 unidades y se maximiza el ingreso total del único productor (o sea, se trata de un productor monopolista). En esas condiciones, su ingreso total será de $1936.
Ejercicio 11
La siguiente función representa el total producido de una fábrica en función de la cantidad l de trabajo contratado: \( Q(l) = 45. l^2 - l^3 + 1200 . l \)
Se pide que:
- Calcule la función producto medio y la función producto marginal.
- Calcule qué cantidad de trabajadores/as se debe contratar para lograr el máximo de producción posible. ¿Cuál es el máximo de producción?
- Indique cuáles es el máximo del producto medio.
En todos los casos justifique sus respuestas.
- En Economía, la función producto medio, se define como la cantidad producida por cada trabajador/a contratado/a:
\[ Q_{me} = \frac{Q(l)}{l} \]
En este ejercicio es:
\[ Q_{me} = \frac{Q}{l}= \frac{45 \cdot l^2 - l^3 + 1200 \cdot l}{l} = 45 \cdot l-l^2 + 1200 \]
La función producto marginal es la derivada de la función de producción Q(l).
\[ Q_{mg} = Q´ \]
En este ejercicio es:
\[ Q_{mg} = Q´ = 90 \cdot l - 3l^2 + 1200 \]
- El máximo de producción se encuentra al buscar el máximo de la función de producción
\( Q_{(l)} = 45 \cdot l^2 - l^3 + 1200 \cdot l \)
Para ello, se procede como en los ejercicios anteriores. Se deriva la función que se analiza. En este caso, esto ya se realizó en a) porque la derivada de la función de producción es la función producto marginal:
\[ Q_{mg} = Q´ = 90 \cdot l - 3l^2 + 1200 \]
En los extremos relativos, la derivada debe ser igual a cero:
\[ 90 \cdot l - 3l^2 + 1200 = 0 \]
Esa es una ecuación de grado dos. Para resolverla se utilizará la fórmula de la resolvente:
\[ 1 = \frac{-90 \pm \sqrt{90^2 - 4 \cdot (-3) \cdot 1200}}{2 \cdot (-3)} \]Y al realizar las cuentas, se llega a que \( l = 40 \) o \( l = -10 \). El último resultado carece de sentido económico, porque no se pueden contratar a -10 personas. Por eso, se descarta esa solución. El único valor crítico es \(l = 40 \) que divide al dominio en dos intervalos: \( (0 ; 40) \) y \( (40 ; + \infty ) \). Para comprobar que se trata de un máximo relativo, se analiza el comportamiento de la derivada en esos intervalos:
\( 3 \in (0; 40) \to Q´(3) = 90 \cdot 3 - 3 \cdot 3^2 + 1200 = 1443 > 0 \) por lo tanto, Q es creciente en este intervalo. (1)
\( 50 \in (40, +\infty) \to Q´(25) = 90 \cdot 50 - 3 \cdot 50^2 + 1200 = -1800 < 0 ) \) por lo tanto, Q es decreciente en este intervalo. (2)
De (1) y (2), se puede decir que en el punto de absisa l = 40, la función de producción presenta un máximo relativo. Al contratar 40 personas, la empresa producirá al máximo. Para encontrar la producción máxima, se reemplaza en valor crítico en la función de producción:
\[ Q(40) = 45 \cdot 40^2 - 40^3 + 1200 \cdot 40 = 8000 \]
Por lo tanto, en estas condiciones de producción, esta empresa puede producir un máximo de 8000 unidades, cuando contrata 40 personas.
- El máximo del producto medio se busca analizando la función
producto medio, que se buscó en a):
\[ Q_{me} = 45 \cdot l - l^2 + 1200 \]
Se deriva:
\[ Q_{me}´ = 45 - 2l \]
La derivada se iguala a cero:
\[ 45 - 2l = 0 \]
\[ \frac{45}{2} = l = 22,5 \]
Este valor crítico determina dos intervalos, \( (0 ; 22,5 ) \) y \( (22,5; + \infty ) \). Se analiza el signo de la derivada en ellos:
\( 1 \in (0; 22,5) Q_{me}´(1) = 45 - 2 \cdot 1 = 43 > 0 \) entonces la función producto medio crece en este intervalo.
\( 30 \in (22,5 ; + \infty) Q_{me}´(30) = 45 - 2 \cdot 30 = -15 < 0 \) entonces la función producto medio decrece en este intervalo.
Por lo tanto, hay un máximo en 22,5. El máximo del producto medio se obtiene al reemplazar este valor en la función producto medio:
\( Q_{me} (22,5) = 45 \cdot 22,5 - 22,5^2 + 1200 = 1706,25 \)
Es decir, el máximo del producto medio se alcanza cuando se contratan 22,5 personas y se obtiene 1706,25 productos por persona.
En este ejercicio aparece un resultado extraño… ¿cómo se hace para contratar a 22,5 personas?
En la resolución de estos ejercicios se considera que las variables son continuas, es decir, que la cantidad de trabajadores/as no salta entre 1 y 2, sino que pasa entre ambas cifras de modo continuo. Es decir, 1,3 es una cantidad válida de personas a contratar. La corriente del pensamiento económico que plantea estos ejercicios argumenta que se puede medir el trabajo incorporado a la producción en horas de trabajo y, de este modo, la variable sí resulta continua. De esa forma, 22,5 personas se podrían pensar como 22 personas contratadas y el resto son horas extra que pueden realizar diferentes trabajadores/as en distintos días.
Ejercicio 12
La función costo medio, que se define como el costo promedio de producción es:
\[ C_{me} = \frac{C(q)}{q} \]
En esta fórmula que expresa la cantidad de productos fabricados.
Una empresa que solo puede producir hasta 20 productos, se encuentra con una función de costos medios dada por la siguiente fórmula:
\[C_{me} = -\frac{1}{2} \cdot q^2 + 28q + \frac{2304}{q} \]
donde q representa la cantidad de unidades producidas y Cme, el costo medio correspondiente. Se pide que encuentre:
- El costo medio que tiene producir 5 unidades.
- Encuentre la fórmula de la función de costos C(q).
- La función costo marginal, que es la derivada de la función de costos C(q).
- El mínimo costo medio que esta fábrica puede tener y cuántas unidades deberá producir para tenerlo.
- El costo medio pedido se obtiene reemplazando q = 5 en la fórmula de Cme:
\( C_{me}(5) = -\frac{1}{2} \cdot 5^2 + 28 \cdot 5 + \frac{2304}{5} = 588,3 \)
Por lo tanto, el costo medio de producir 5 unidades es $588,3.
Como
\[ C_{me}(q) = \frac{C(q)}{q} \]De aquí se puede despejar la función de costos:
\[ C_{me}(q) \cdot q = C(q)\]
Y, por lo tanto, la función de costos es:
\[ C_ {(q)} = C_{me}(q) \cdot q = \left( - \frac{1}{2} \cdot q^2 + 28q + \frac{2304}{q} \right) \cdot q \]\[ C_ {(q)} = - \frac{1}{2} \cdot q^3 + 28q^2 + 2304 \]
Aquí se remplazó la fórmula de Cme en la del costo y se realizaron las operaciones algebraicas correspondientes.
- Costo marginal = \( - \frac {3}{2} \cdot q^2 + 28 \cdot q \). Se derivó la función C(q) obtenida en b).
Para encontrar el mínimo costo medio que esta fábrica puede tener, se debe encontrar el mínimo de la función Cme(q). Para ello, se deriva e iguala a cero la derivada.
\[ C´_ {me} = -q + 28 + 2304 \cdot (-1) \cdot q^{-2} \]
Por lo tanto, \( C_ {me}´(q) = -q + 28 - \frac{2304}{q^2}\)
En los extremos relativos, esta fórmula debe dar cero:
\[ -q + 28 - \frac{2304}{q^2} = 0\]
\[ -q + 28 = 0 + \frac{2304}{q^2} = \frac{2304}{q^2} \]
\[ (-q + 28) \cdot q^2 = 2304 \]
\[ -q^3 + 28 \cdot q^2 - 2304 = 0 \]
Esta es una ecuación polinómica de grado tres, cuyas soluciones se pueden encontrar con una calculadora científica o al factorizar (cuando se utiliza el teorema del resto).
En <https://www.youtube.com/watch?v=Sc4E8mGO2Vg> el profesor Julio Ríos Gallego factoriza un polinomio con el teorema del resto.
En este caso, los resultados posibles son:
q = 12 o
q = -8 o
..q = 24
El segundo valor no tiene sentido económico, ya que no es posible producir una cantidad negativa de unidades. Y el último está por encima de las posibilidades de producción de esta fábrica (que solo puede producir hasta 20 unidades).
Para investigar si en q = 12 hay un extremo relativo, se analiza el signo de la derivada en los intervalos que este valor determina:
\( 1 \in (0;12) \ C_{me}´(1) = -1 + 28 - \frac{2304}{1^2} = - 2277 < 0 \) entonces la función costo medio decrece en este intervalo.
\( 13 \in (12; 20) \ C_{me}´(13) = -13 + 28 - \frac{2304}{13^2} = 1,37 > 0 \) entonces la función costo medio crece en este intervalo.
Por lo tanto, hay un mínimo en 12. El mínimo del costo medio se obtiene al reemplazar este valor en la función costo medio:
\[ C_{me} (12) = - \frac{1}{2} \cdot 12^2 + 28 \cdot 12 + \frac{2304}{12} = 456 \]
Así, esta empresa, puede tener un costo medio mínimo de producción de $456, cuando produce 12 unidades.
Una fábrica enfrenta la función de costos medios dada por la siguiente fórmula:
\[ C_{me} = \frac{1}{2} \cdot q^2 + 5q + \frac{4500}{q} \]
donde q representa la cantidad de unidades producidas y Cme, el costo medio correspondiente. Se pide que encuentre:
- La fórmula de la función de costos C(q).
- La función costo marginal, que es la derivada de la función de costos C(q).
- El mínimo costo medio que esta fábrica puede tener y cuántas unidades deberá producir para tenerlo.
Respuestas:
- \( C_{(q)} = \frac{1}{2} \cdot q^3 + 5q^2 + 4500 \)
- \( C_{mg} = \frac{3}{2} \cdot q^2 + 10 \cdot q \)
- Esta fábrica tiene un costo medio mínimo de producción de $487,50 cuando produce 15 unidades.
2.5. Derivada segunda y concavidad
Ejercicio 13
El siguiente gráfico, confeccionado con Geogebra, ya fue utilizado en el Ejercicio 6. En él se aprecia el gráfico de la función:
f(x) = -x3+ 3x2+ 9x - 1.
Ahora, aparece junto a la recta tangente a la curva en cada punto, su fórmula:
Se pide que:
- Compare la pendiente de la recta tangente a la función para los valores de abscisas x = -2 ; x = -1 ; x = 0 y x = 1 . Saque conclusiones y relacione este resultado con la forma de la función f(x) = -x3+ 3x2+ 9x - 1.
- Repita la comparación para x = 1 ; x = 2 ; x = 3 ; x = 4 . Saque conclusiones y relacione este resultado con la forma de la función f(x) .
- ¿Cómo podría analizarse donde cambia la concavidad de la función? [donde]
Como puede apreciarse, cuando el deslizador toma el valor -2, la recta tangente es y = -15x - 29. Por lo tanto, la pendiente de esta recta es -15.
Al repetir esta observación, se obtiene la siguiente tabla:
x
recta tangente
pendiente
-2
y = -15x - 29
-15
-1
y = -6
0
0
y = 9x - 1
9
1
y = 12x - 2
12
Como puede apreciarse en la tercera columna, las pendientes de las rectas tangentes son crecientes: -15 < 0 < 9 < 12.
En el gráfico, se puede ver que en el intervalo \( ( - \infty ; 1) \) la función es convexa.
Si se mueve el deslizador, ahora entre 1 y 4, se puede completar la siguiente tabla:
x
recta tangente
pendiente
1
y = 12x - 2
12
2
y = 9x + 3
9
3
y = 3
0
4
y = -15x + 79
-15
En este caso, puede notarse que las pendientes de las rectas tangentes decrecen: 12 > 9 > 0 > -15. En el gráfico puede verse que corresponde al intervalo \( ( 1 ; \infty) \), en el que la función es cóncava.
Con base en lo visto en los ítems a) y b) se puede concluir que cuando las pendientes de las rectas tangentes a una función son crecientes, la gráfica es convexa. Y que cuando las pendientes de las rectas tangentes son decrecientes, la gráfica es cóncava.
Las pendientes de las rectas tangentes son las derivadas de la función en cada punto. Si se quiere analizar el crecimiento (o decrecimiento) de ellas, deberá derivarse a la función que informa sobre la pendiente de las rectas tangentes. Es decir, deberá derivarse la derivada de la función.
Volvemos al caso del ejercicio que se está resolviendo. Aquí se deberá derivar la derivada de:
\[ f(x) = -x^3 + 3x^2 + 9x - 1 \]
Como ya se calculó, la derivada de f(x) es:
\[ f(x) = -3 \cdot x^2 + 3 \cdot 2 \cdot x + 9 = -3x^2 + 6x + 9 \]
Y su derivada será:
\[ f´´(x) = -3 \cdot 2 \cdot x + 6 = -6x + 6 \]
A esta expresión se la denomina derivada segunda de f y, como se acaba de ver, está relacionada con la concavidad de la gráfica de la función f.
Cuando la derivada segunda de una función se anula, en ese punto, la función no es ni cóncava ni convexa. Allí la función puede presentar un punto de inflexión, es decir, un punto en el que cambia la concavidad. Para buscar puntos de inflexión, entonces, se resuelve la ecuación:
\[ f´´(x) = 0 \]
En este ejercicio sería:
\[ -6x + 6 = 0 \]
\[ -6x = -6 \]
\[ x = \frac{-6}{-6} = 1 \]
Este valor divide al dominio de la función en dos intervalos. Para confirmar que se trata de un punto de inflexión, es necesario demostrar que cambia la concavidad. Con ese fin, se analiza el signo de la derivada segunda en cada uno de esos dos intervalos.
En \( (- \infty ; 1) \), se puede considerar el valor x = 0:
\( f´´(0) = -6 \cdot 0 + 6 = 6 > 0 \) por lo tanto, la función (como ya se había visto) es convexa en el intervalo.
En \( (1 ; + \infty ) \), se elige un número, por ejemplo x = 6:
\( f´´(6) = -6 \cdot 6 + 6 = - 30 < 0 \) por lo tanto, la función (como ya se había visto) es cóncava en este intervalo.Dado que la concavidad de la función cambia en x = 1, habrá allí un punto de inflexión. Falta buscar su ordenada, para lo que se reemplaza este valor en la fórmula de la función f:
f(1) = -13+ 3 · 12+ 9 · 1 - 1 = 10
De este modo se demostró que en (1; 10) la función presenta un punto de inflexión.
Ejercicio 14
Investigue si las funciones de los ejercicios 7 y 8 presentan puntos de inflexión.
La función del ejercicio 7 es \( f(x) = e^\left( {\frac{x^2}{4}} \right) - 5 \). Su derivada primera ya fue calculada: \( f´(x) = \frac{x}{2} \cdot e^\left( {\frac{x^2}{4}} \right) \)
Para investigar si presenta puntos de inflexión, se debe calcular la derivada segunda. Aquí hay un producto de funciones, la segunda de las cuales es compuesta. Por eso, la derivada segunda será:
\[ f´´(x) = \frac{1}{2} \cdot e^\left( {\frac{x^2}{4}} \right) + \frac{x}{2} \cdot e^\left( {\frac{x^2}{4}} \right) \cdot \frac{x}{2} \]
Como esta última expresión debe igualarse a cero, conviene expresarla como un producto:
\[ f´´(x) = \frac{1}{2} \cdot e^\left( {\frac{x^2}{4}} \right) \cdot \left( 1 + \frac{x^2}{2} \right) \]
Por lo tanto, debería ser:
\[ \frac{1}{2} \cdot e^\left( {\frac{x^2}{4}} \right) \cdot \left( 1 + \frac{x^2}{2} \right) = 0 \]
Para que un producto dé 0, tendría que ser igual a cero alguno de sus factores. Los dos primeros nunca se anulan, por lo tanto, debería ser:
\[ 1 + \frac{x^2}{2} = 0 \]
Pero esta expresión no tiene raíces reales. Por lo tanto, esta función no presenta puntos de inflexión. Como puede apreciarse en el gráfico (en el ejercicio 7), esta función es convexa en todo su dominio.
La función del ejercicio 8 es: \( f(x) = ln (x^2 - 2x + 2) \)
Y su derivada: \( f´(x) = \frac {2x -2}{x^2 - 2x + 2} \)
Para encontrar sus puntos de inflexión, es necesario volver a derivar. Como la derivada primera es una división, se utilizará esa fórmula para calcular la derivada segunda. Luego, se realizan los cálculos del numerador:
\[ f´(x) = \frac {2 \cdot (x^2 - 2x -2) - (2x - 2) \cdot (2x - 2)}{(x^2 - 2x + 2)^2} = \]
\[ = \frac {2 x^2 - 4x + 4 - 4x^2 + 8x - 4}{(x^2 - 2x + 2)^2} = \frac{-2x^2 + 4x}{(x^2 - 2x + 2)^2} \]
Puede haber puntos de inflexión en los que tienen abscisas que anulan esta última expresión:
\[ \frac {- 2x^2 + 4x}{(x^2 - 2x + 2)^2} = 0 \]
\[ - 2x^2 + 4x = 0 \cdot (x^2 - 2x + 2)^2 \]
\[ 2x \cdot (-x + 2) = 0 \]
Por lo tanto, los valores críticos son x = 0 y x = 2.
Estos valores dividen al dominio de la función en tres intervalos. Para confirmar que se tratan de puntos de inflexión, es necesario demostrar que cambia la concavidad. Con ese fin, se analiza el signo de la derivada segunda en cada uno de esos tres intervalos.
En \( (- \infty ; 0) \), se puede considerar el valor x = -1:
\( f´´(-1) = \frac {- 2 (-1)^2 + 4 (-1)}{[(-1)^2 - 2 (-1) + 2]^2} = \frac{-6}{25} < 0 \) por lo tanto, la función es cóncava en el intervalo \( (- \infty ; 0) \)
En (0; 2) se considerará el valor x = 1:
\( f´´(1) = \frac {- 2 \cdot 1^2 + 4 \cdot 1}{(1^2 - 2 \cdot 1 + 2)^2} = \frac{2}{1} > 0 \) por lo tanto, la función es convexa en todo este intervalo.
Como la concavidad cambió en x = 0, hay punto de inflexión. Sus coordenadas serán: (0; f(0)) = (0; ln 2)
Finalmente, en \( f´´(3) = \frac {- 2 \cdot 3^2 + 4 \cdot 3}{(3^2 - 2 \cdot 3 + 2)^2} = \frac{-6}{25} < 0 \) se investigará el valor x = 3: \( (- \infty ; 0) \) por lo tanto, la función es cóncava en el intervalo.
Como vuelve a cambiar la concavidad, en (2; f(2)) también hay otro punto de inflexión: (2; ln 2)
Estos puntos de inflexión se pueden apreciar en la gráfica (la misma del ejercicio 8 en la que se destacaron los puntos hallados en este ejercicio):
Sea f(x) = x4 + 4x3 - 18x2 + 20x. Se pide que halle los intervalos de concavidad e indique si presenta puntos de inflexión.
Respuestas: esta función es cóncava en \( (- \infty ; -4) \) y en \( ( 1 ; \infty) \). Y es convexa en el intervalo (-4; 1) . Por lo tanto, tiene dos puntos de inflexión: (-4; -368) y (1; 7) .

