1. Funciones de una variable
Objetivos
- Determinar el dominio de una función.
- Representar funciones en diagramas cartesianos, a mano y con sistemas graficadores.
- Calcular la función inversa de una función.
- Componer funciones.
- Distinguir las diferentes funciones por sus gráficas.
1.1. Las funciones en economía
Una función es una relación entre dos conjuntos -el de partida y el de llegada– que a cada elemento del conjunto de partida le asigna un único elemento del conjunto de llegada, al que se llamará “imagen”.
En esta definición se destacan dos ideas: “cada elemento del conjunto de partida”, es decir, que todos los elementos del conjunto de partida deben tener asignado “un único elemento del conjunto de llegada”, lo que significa que la imagen debe existir y además debe ser única.
¿Por qué se estudian funciones en una carrera económica? Son muchas las situaciones económicas en las que se analiza cómo una variable se relaciona con otra (u otras). En muchas de ellas, se puede hallar un modelo matemático que incluya funciones. La manera más sencilla es utilizando tablas de valores, pero también se pueden expresar con fórmulas.
Ejercicio 1
La tarifa de taxi en la Ciudad Autónoma de Buenos Aires es de $27,20 al momento de partir (“bajada de bandera”) más el 10% de esa cifra por cada 200 metros de recorrido, en viajes en horario diurno, sin tiempos de espera y sin salir de la ciudad. Exprese con una tabla la relación entre la tarifa y la cantidad de metros recorridos y represéntela en un diagrama cartesiano (considere múltiplos de 200 metros de recorrido).
La tabla que se pide es de dos columnas. En la primera se ubican los elementos del “conjunto de partida” y en la segunda los del “conjunto de llegada”. Como la tarifa depende de los metros recorridos, se considerará “conjunto de partida” a la distancia que recorrió el taxi. Pero solo se utilizarán los múltiplos no negativos de 200 metros, porque únicamente allí “cae la ficha” y el “conjunto de llegada” es el de los precios que deberán abonarse.
|
Distancia recorrida |
Precio del taxi |
|
0 |
27,70 |
|
200 |
30,47 |
|
400 |
33,24 |
|
600 |
36,01 |
|
800 |
38,78 |
|
1000 |
41,55 |
|
1200 |
44,32 |
|
1400 |
47,09 |
|
1600 |
49,86 |
|
1800 |
52,63 |
|
2000 |
55,40 |
|
2200 |
58,17 |
|
2400 |
60,94 |
|
2600 |
63,71 |
|
2800 |
66,48 |
|
3000 |
69,25 |
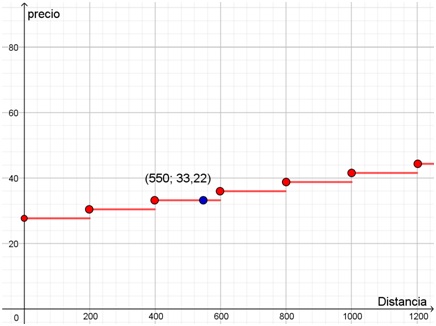
Si el taxi recorre una distancia intermedia entre cada uno de estos “renglones” de la tabla, por ejemplo, 550 metros, deberá abonar la tarifa correspondiente a 400 metros, porque todavía “no cayó” la ficha correspondiente a los 600 metros. Gráficamente la situación se representa considerando a los elementos del conjunto de partida en el eje horizontal, y a los del conjunto de llegada en el vertical. Cada punto de la función representa un par ordenado de la tabla. Pero la representación gráfica ofrece mucha más información. Aquí sí puede verse cuánto deberá pagarse por un viaje de 550 metros.
Como puede apreciarse en el gráfico siguiente, el punto azul corresponde a 550 metros de distancia recorrida y $33,22 que deberán abonarse.
Ejercicio 2
Un banco paga un interés del 15 % por un plazo fijo a 30 días. El mínimo que debe depositarse es de $500. Confeccione una tabla que relacione cuánto se ganará de interés, en función de la cantidad de dinero depositada. Represente en un diagrama cartesiano dicha función.
En este ejercicio, el conjunto de partida es el monto del dinero que se deposita y el conjunto de llegada, la cantidad de dinero que se cobrará como interés al finalizar el período de 30 días. Nuevamente, la tabla es de dos columnas. En la primera se eligen los valores arbitrariamente, por eso se llama “variable independiente”. Los números correspondientes a la segunda columna se calculan, y por eso se llama “variable dependiente”. En este ejercicio, debe ser el 15 % de la cifra de la primera columna. Si se llama x a la variable independiente e y a la dependiente:
\[y = x \cdot \frac{15}{100} = 0,15 \cdot x \]
Resolviendo los cálculos para varias cifras, cada una de las cuales representa cuánto dinero se deposita en el banco, se obtiene la tabla de valores que pide el ejercicio. En este caso, la cantidad de dinero depositado puede ser cualquier valor (a partir del monto mínimo):
|
Dinero depositado |
Interés a cobrar |
|
500 |
75 |
|
1000 |
150 |
|
1500 |
225 |
|
2000 |
300 |
|
2500 |
375 |
|
3000 |
450 |
|
3500 |
525 |
|
4000 |
600 |
|
4500 |
675 |
|
5000 |
750 |
|
5500 |
825 |
|
6000 |
900 |
|
6500 |
975 |
|
7000 |
1050 |
|
7500 |
1125 |
|
8000 |
1200 |
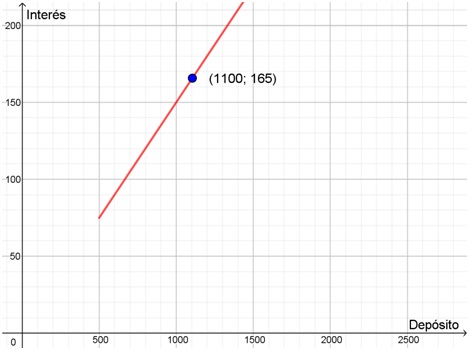
Para la representación gráfica se consideran los valores calculados en la tabla, pero los intereses no “saltan” (como en el ejercicio 1), sino que van ascendiendo en forma continua. En el gráfico siguiente se destacó, por ejemplo, el punto (1100; 165), que corresponde a un depósito de $1100, que al cabo de 30 días cobrará $165 de interés.
1.1.1. Dominio de una función
Cuando una relación asigna un único elemento del conjunto de llegada a no todos los elementos del conjunto de partida, se puede definir una función restringiendo el conjunto de partida para considerar únicamente los elementos que sí tienen imagen. Se define así el dominio de una función: el conjunto de los elementos pertenecientes al conjunto de partida que sí tienen imagen.
Ejercicio 3
Encuentre el dominio de la función del ejercicio 2.
En este caso, como ya se comentó, se puede depositar cualquier suma, a partir de un mínimo de $500. Por lo tanto, el dominio de esta función es:
\[Dom = [ 500; + \infty ) \]
Ejercicio 4
Determine el dominio de la función\[ f(x) = 3 x^3 - 3x^2 + 5x -1\]
En la función de este ejercicio, la regla de asignación es un polinomio. Cada una de las operaciones tiene siempre un único resultado, para cada valor de la variable independiente x.
Por ese motivo, todos los valores reales de la variable x tendrán una imagen única. Es decir, el \( Dom = \mathfrak{R} \)
Ejercicio 5
Determine el dominio de la función \( f(x) = \frac {x+2}{x^2-2x}\)
Para que la relación de este ejercicio cumpla con las condiciones requeridas para ser función se debe definir su Dominio, que es el conjunto de números que tienen imagen.
Como la regla de asignación es una división entre dos polinomios y no se puede dividir por cero, la variable no puede tomar valores que hagan que el polinomio divisor se anule. Esta condición se puede simbolizar con la fórmula:
\[ x^2 - 2x \neq 0\]
En el primer miembro de esta desigualdad, se escribió el polinomio del denominador de la función. Ahora, es necesario resolver esta desigualdad para encontrar los valores de x que no pertenecen al Dominio de la función.
Para hallar la solución se pueden elegir, por lo menos, dos caminos:
- factorizando el polinomio, o
- utilizando la fórmula de la resolvente de la ecuación de segundo grado, también conocida como fórmula de Bhaskara.
En este caso, se verán las dos maneras.
- Factorizando el polinomio
- Utilizando la fórmula de la resolvente de la ecuación de segundogrado.
En este caso, hay dos términos que comparten un factor: x. “Sacando” ese factor común, se obtiene:
\[ x \cdot (x - 2) \neq 0 \]
Se expresó, entonces, el polinomio como un producto. Para que un producto no sea igual a cero, no deberán ser 0 ninguno de los factores.
\[ x \neq 0 \text { y } x - 2 \neq 0\]
De la segunda expresión se despeja x:
\[ x \neq 2 \]
Por lo tanto, hay dos valores que deben extraerse del conjunto de los números reales para definir el Dominio:
\[ Dom = \mathfrak{R} - \{0;2\}\]
Los valores que se extraen del conjunto ℜ se escriben entre llaves, para indicar que se trata de una diferencia entre dos conjuntos: el de los reales y el que tiene dos elementos, en este caso, el 0 y el 2.
En <https://www.vitutor.com/ecuaciones/2/ecu_Contenidos.html> se puede consultar qué son y cómo se resuelven las ecuaciones de segundo grado.
En la ecuación \( x^2 - 2x \neq 0\) se deben distinguir los números a, b y c.
a = 1 ya que hay una x2
b = - 2 porque x aparece multiplicada por este valor.
Como no hay un término independiente, c = 0.
Estos valores se reemplazan en la fórmula de la resolvente:
\[ x = \frac {-b \pm \sqrt {b^2-4ac}}{2a}\]
\[ x = \frac {-(-2) \pm \sqrt {(-2)^2-4\cdot 1 \cdot 0}}{2 \cdot 1} = \frac {2 \pm \sqrt{4}}{2} \]
Resolviendo esta última expresión, se obtienen dos valores: x = 0 y x = 2 que son los que hay que extraer del conjunto de los números reales, ya que ambos anulan al denominador.
Por lo tanto, se llega al mismo resultado que en 1): \( Dom = \mathfrak{R} - \{0;2\}\)
Generalizando lo realizado hasta aquí, se puede decir que cuando se busca el dominio de una función cuya regla de asignación es una división, del conjunto de los números reales se deben extraer aquellos valores de x que anulan el denominador, porque ellos no tendrían imagen.
Ejercicio 6
Determine el dominio de la función \( f (x) = ln \ (2x^2 + 4x - 16) \)
En este caso, la regla de asignación es un logaritmo natural. Es decir:
si \( f (x) = ln \ (2x^2 + 4x - 16) \) , entonces, \( e ^{f(x)} = 2x^2 + 4x -16\) por la definición de logaritmo natural.
Para más información sobre los logaritmos naturales, se puede consultar: <https://matematica.laguia2000.com/general/logaritmos-naturales-o-neperianos>
Como \( 2x^2 + 4x -16 \) es una potencia de e, su resultado debe ser positivo. Por lo tanto, al buscar el dominio de esta función, se deberán considerar todos los valores de x que hagan positivo el resultado de ese cálculo. En símbolos:
\[ 2x^2 + 4x -16 > 0\]
Para resolver esta inecuación, se factoriza el polinomio.
En general, un polinomio de grado dos, puede factorizarse de la siguiente manera:
\[ a \cdot x^2 + b \cdot x + c = a \cdot (x - x_1) \cdot (x - x_2) \] (1)
En la que x1 y x2 son las raíces del polinomio.
En <https://www.vitutor.com/ab/p/a_12.html> “Trinomio de segundo grado” hay ejemplos resueltos de este tema.
Utilizando la fórmula de la resolvente de la ecuación de segundo grado, se encuentran las raíces x1 y x2. En este ejercicio, es a = 2, b = 4 y c = -16.
\[ x = \frac {-b \pm \sqrt {b^2-4ac}}{2a}\]
\[ x = \frac {-4 \pm \sqrt {4^2-4\cdot 2 \cdot (-16)}}{2 \cdot 2} = \frac {-4 \pm \sqrt{16 + 128}}{4} = \frac {-4 \pm 12}{4} \]
De donde se obtienen x1 = 2 y x2 = -4. Reemplazando estos valores en la fórmula (1), queda:
\[ 2 x^2 + 4x - 16 = 2 \cdot (x - 2) \cdot [x - (-4)] = 2 \cdot (x- 2) \cdot (x + 4) \]
Y esta última expresión deberá ser mayor a cero:
\[ 2 \cdot (x - 2) \cdot (x + 4) > 0 \]
Se tiene, entonces, una multiplicación cuyo resultado es mayor a cero. ¿Cuándo es mayor a cero el resultado de una multiplicación entre dos factores? Recordando la “regla de los signos”, se obtiene la respuesta: cuando ambos factores son positivos o ambos negativos. Por lo tanto, se tienen dos alternativas:
- Cuando ambos factores son positivos: x - 2 > 0 y también x + 4 > 0. De la primera inecuación, deberá ser x > 2 y de la segunda, x > -4. Representando estas situaciones en una recta numérica, se observa que suceden ambas condiciones a la vez cuando x > 2:
- Cuando ambos factores son negativos: x - 2 < 0 y también x + 4 < 0.
De la primera inecuación, deberá ser x < 2 y de la segunda, x < -4.
Representando estas situaciones en una recta numérica, se observa que suceden ambas a la vez cuando x < -4:

Entonces, el intervalo de números reales \( (2; + \infty ) \) está incluido en el dominio.
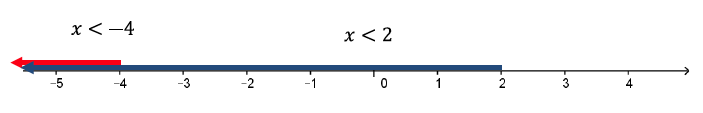
Entonces, el intervalo de números reales \( (- \infty ; -4) \) está incluido en el dominio.
Por lo tanto, de 1) y 2), se deduce que el dominio de esta función es:
\[ Dom = (- \infty ; -4) \cup (2 ; + \infty) \]
Este dominio se expresó como una unión entre intervalos de números reales. También se puede expresar como \( Dom = \Re - [-4;2] \), es decir, del conjunto de los números reales se resta el intervalo cerrado de reales [-4;2].
Generalizando este resultado, se puede afirmar que el dominio de una función logarítmica es el conjunto de números reales que hace positivo el argumento del logaritmo.
Determine el dominio de las siguientes funciones:
- \( g (x) = \frac {2x+1}{x^3 -x^2 -2x}\)
- \( h (x) = + \sqrt {3x - 6} \)
Respuestas:
- \( Dom = \Re - \{-1; 0; 2 \} \)
- En este caso, la regla de asignación de la función es una raíz cuadrada, para poder calcularla, su argumento deberá ser positivo o nulo. Por eso, el \( Dom = [2; + \infty ] \).
En <https://www.youtube.com/watch?v=qOCMPXoxJyg> el profesor colombiano Julio Ríos Gallego explica este tema. En todos sus videos desarrolla contenidos que pueden resultar muy útiles en el estudio de esta materia. Son muy claros y, aunque a veces utiliza una terminología diferente a la de este curso, son para recomendar.
1.2. Composición de funciones
Ejercicio 7
Dadas las funciones \( f (x) = 2x^2 + 3x - 1 \) y \( g (x) = 4x - 1 \) se pide que encuentre:
- f (3) =
- g (4) =
- (gof) (x) =
- (fog) (x) =
Las dos primeras partes se resuelven de manera muy sencilla, reemplazando la x por la cifra correspondiente y resolviendo los cálculos:
- f (3) = 2 · 32 + 3 · 3 - 1 = 2 · 9 + 9 - 1 = 18 + 9 - 1 = 26
- g (4) = 4 · 4 - 1 = 16 - 1 = 15
Las partes c) y d) corresponden a composición de funciones.
Se puede pensar a la composición de funciones como una línea de producción, en la que la materia prima pasa sucesivamente por dos máquinas:
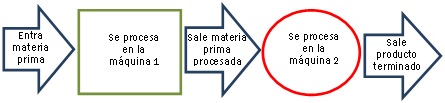
A cada una de esas máquinas se las puede pensar como funciones. Entra “materia prima” que en el caso de las funciones es x. Cuando esa materia prima “sale” de la primera máquina, ya no es lo mismo... ahora es f (x), es decir, el número que se obtiene al hacer la cuenta f con el número x. Esto es lo que entra en la segunda máquina como “materia prima procesada”. Ahora, en la “máquina” g no entra x, sino f (x). Y lo que de ella sale es (gof) (x) = g [f (x)].
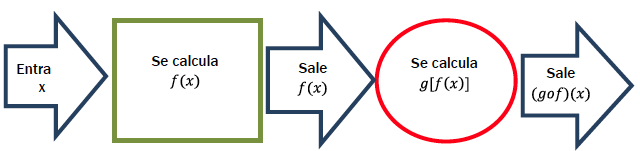
En este ejercicio es:
(gof) (x) = g [f (x)] = g [2x2 + 3x - 1]
La “máquina” g, en este ejercicio, multiplica por 4 y resta 1 a lo que “entra” en ella. Por lo tanto, será:
(gof) (x) = g [2x2 + 3x - 1] = 4 · (2x2 + 3x - 1) - 1
Solo resta distribuir y hacer cuentas:
(gof) (x) = 8x2 + 12x - 4 - 1 = 8x2 + 12x - 5
es la respuesta correspondiente a c)
Aquí, la composición es en orden inverso:
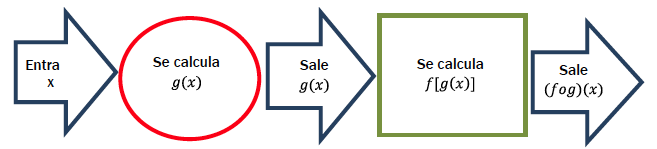
Por lo tanto, será:
\[ (fog) (x) = f [g (x)] = f [4x - 1] \]
En la “máquina” f de este ejercicio, la “materia prima” aparece en dos términos, por lo que se reemplaza en esos dos términos el resultado de la cuenta obtenida por g:
\[ (fog) (x) = f [4x - 1] = 2 \cdot (4x - 1)^2 + 3 \cdot (4x - 1) - 1\]
Falta hacer las cuentas indicadas. En el primer término, es importante recordar cómo resolver el cuadrado de un binomio. En los siguientes pasos se distribuye y se suman los términos semejantes:
\[ (fog) (x) = 2 \cdot (16x^2 - 8x + 1) + 12x - 3 - 1\]
\[ (fog) (x) = 32x^2 - 16x + 2 + 12x - 4\]
Esta es la fórmula buscada.
En este ejercicio no se pide que se calculen los dominios de (gof) (x) y (fog) (x). Pero como se trata de funciones polinómicas, en ambos casos, el dominio es \( \Re \).
(fog) (x) = 32x2 - 4x - 2
Ejercicio 8
A un comerciante le facturaron $400 por una caja de 10 botellas de aceite comestible. Si desea cobrar un 15 % de mark up (o margen de comercialización, que es lo que quiere ganar el comerciante), y debe pagar 21 % de IVA sobre todo el costo, calcule el precio de venta que ofrecerá a sus clientes. Desarrolle una fórmula para calcular lo mismo para otro producto con otro precio y diferente cantidad de unidades por paquete.
En este caso, se puede considerar una composición de tres funciones porque son tres los pasos a seguir para encontrar el precio de venta:
- cálculo del precio unitario que el comerciante abonó.
- cálculo costo total, incluido el margen de comercialización
- cálculo del precio, incluido el impuesto.
Si llamamos x al precio de la caja que contiene n unidades, el primer paso se puede calcular de la siguiente manera:
\[ f (x) = \frac {x}{n} \]
El segundo paso consiste en sumar el 15 % al precio de compra. Si llamamos x al precio de compra, el costo total sería:
\[ g (x) = x + \frac {15}{100} \cdot x = x \cdot \left( 1 + \frac{15}{100} \right) = x \cdot 1,15 = 1, 15 \cdot x \]
En el último paso se suma el impuesto al costo total. Si llamamos x al costo total, será:
\[ h (x) = x + \frac {21}{100} \cdot x = x \cdot \left( 1 + \frac{21}{100} \right) = x \cdot 1,21 = 1, 21 \cdot x \]
Falta ahora “componer” estas funciones
\[ (hogof) (x) = h [(gof)](x) = h \{ g[f(x)] \} = h \left[ g \left( \frac {x}{n} \right) \right] = h \left( 1,15 \cdot \frac{x}{n} \right) = 1,21 \cdot \left( 1,15 \cdot \frac{x}{n} \right) \]
Como la multiplicación es asociativa, esta última cuenta se puede calcular así:
\[ 1,21 \cdot \left( 1,15 \cdot \frac{x}{n} \right) = (1,21 \cdot 1,15) \cdot \left( \frac {x}{n} \right) = 1, 3915 \cdot \frac {x}{n} \]
Por lo tanto, la expresión que permite calcular el precio de venta al público que ofrece el comerciante conociendo el precio x del mayorista por una caja de n productos es:
\[ (hogof) (x) = 1,3915 \cdot \frac{x}{n} \]
En el caso particular del aceite comestible, por el que se pagaron $400 por una caja de 10 botellas, será:
\[ (hogof) (x) = 1,3915 \cdot \frac{400}{10} = 55,66 \]
Entonces, el comerciante ofrecerá cada botella de aceite comestible por $55,66.
Ejercicio 9
Dadas las funciones \( f (x) = 2^{x+3} \) y \( g (x) = + \sqrt {3x + 1} \) se pide que encuentre (fog)(x) y (gof)(x) e indique sus dominios.
Como se puede observar en un ejemplo anterior, la composición de funciones no es conmutativa. Por lo tanto:
\[ (fog) (x) = f [g(x)] = f [ + \sqrt{3x + 1}] = 2^{+\sqrt{3x + 1}+ 3} \]
\[ (gof) (x) = g [f(x)] = g [ 2^{x + 3}] = +\sqrt{3 \cdot 2^{x + 3} + 1} \]
Es importante tener en cuenta que, en esta última expresión, no se puede efectuar la multiplicación de 3 · 2x+3 ya que el 2 es base de una potencia. Si se efectuara ese producto, se modificaría la base de la potencia.
Se calculará ahora el dominio de (fog) (x). Como en el exponente hay una raíz cuadrada, el radicando debe ser mayor o igual a cero:
\[ 3x + 1 \geq 0 \]
\[ 3x \geq 0 - 1 = -1\]
\[ x \geq \frac {-1}{3} \]
Por lo tanto, el \( Dom = \left[ - \frac{1}{3}; + \infty \right) \) para \( (fog)(x) \)
En el caso de (gof) (x), la regla de asignación es una raíz, por lo tanto, el radicando deberá ser mayor o igual a cero:
\[ 3 \cdot 2^{x + 3}+ 1 \geq 0 \]
\[ 3 \cdot 2^{x + 3}+ 1 \geq -1 \]
\[ 2^{x + 3} \geq -\frac{1}{3} \]
Como en el primer miembro de esta desigualdad se tiene una potencia de 2, el resultado siempre dará positivo, independientemente del valor de x. De modo que esta desigualdad se cumplirá siempre. Por eso, en el caso de (gof) (x), el \( Dom = \Re \).
- Dadas las funciones f (x) = 32x y g (x) = x2 + 1 se pide que encuentre (fog) (x) y (gof) (x) y sus dominios.
- La función del ejercicio 3, f(x) = ln (2x2 + 4x - 16), se puede pensar como una función compuesta. ¿Cuáles serían las funciones que se compusieron para obtener este resultado?
Respuestas:
- \( (fog)(x) = 3^{2x^2 + 2}(gof)(x) = 3^{4x} + 1 \) (para resolver este último ejercicio es necesario recordar las propiedades de la potencia de una potencia, que se pueden consultar en <https://contenidosdigitales.ulp.edu.ar/exe/matematica1/propiedades_de_la_potenciacin.html>). Ambos dominios son \( \Re \).
- Como primero hay que calcular el polinomio, la x debería “entrar en la máquina” g primero: g(x) = 2x2 + 4x - 16 y luego se calcula el logaritmo de este resultado. Considerando a h(x) = ln(x), la función se puede escribir: f(x) = ln (2x2 + 4x - 16) = h [g(x)] = hog(x)
En <https://www.youtube.com/watch?v=fLiwtU-8KN4> el profesor Julio Ríos Gallego resuelve ejercicios de este tema.
1.3. Función inversa
Ejercicio 10
Encuentre la función inversa de f(x) = 3x + 2
La función inversa f -1 de otra f(x) = y es la relación y con x de manera inversa a la que x está relacionada con y.
Gráficamente se podría representar de la siguiente manera:
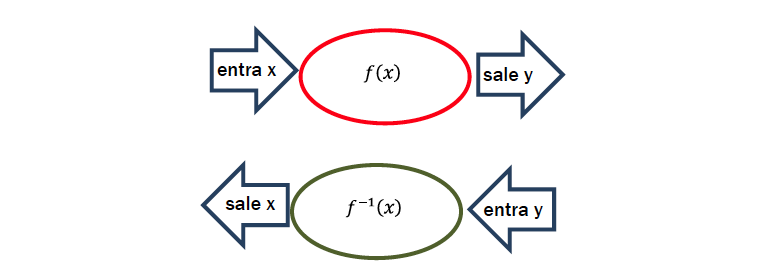
La idea es buscar qué cuenta hay que hacer con y para obtener x. Que equivale a resolver para x la siguiente ecuación:
f(x) = y
En este ejercicio es:
f(x) = 3x + 2 = y
Y en ella, hay que “despejar” la x:
\[ 3x + 2 = y \]
\[ 3x = y - 2 \]
\[ x = \frac {y - 2}{3} = f^{-1} (y) \]
Esta es la fórmula correspondiente a f -1(y). Pero se pide f -1(x). Tanto x como y son simplemente nombres que representan a la variable. Por eso, solo es necesario “cambiar la variable”:
\[ f^{-1}(x) = \frac{x - 2}{3} \]
que es la fórmula buscada.
Se puede comprobar esto buscando pares ordenados correspondientes a f(x) y a f-1(x), para comprobar que son inversos. Por ejemplo,
f(3) = 3 · 3 + 2 = 11
De modo que el par ordenado \( (3; 11) \ \in\ f(x)\). Es decir, en f(x) “entró” 3 y “salió” 11. Entonces, el par (11; 3) debería pertenecer a f -1(x), es decir, si en f -1(x) “entra” 11, debe “salir” 3:
\[ f^{-1}(11) = \frac {11 - 2}{3} = \frac {9}{3} = 3\]
Efectivamente, \[ (11; 3) \ \in \ f^{-1}(x) \]
Ejercicio 11
Encuentre la función inversa de f(x) = x2 - x + 2
Como en el ejercicio anterior, es necesario despejar x en la siguiente ecuación:
x2 - x + 2 = y
La dificultad radica en que la x aparece en dos términos.
Para resolver esta ecuación es necesario “completar el cuadrado”. En <https://www.disfrutalasmatematicas.com/algebra/completar-cuadrado.html> está explicado paso a paso el procedimiento.
\[ x^2 - 2 \cdot \frac {1}{2} \cdot x + \left( \frac {1}{2} \right)^2 - \left( \frac {1}{2} \right)^2 + 2 = y \]
En este paso se reescribió el primer miembro de la ecuación, de manera que quede el cuadrado de un binomio en los tres primeros términos. Si se cancela el tercer término con el cuarto, se vuelve al paso anterior. Pero la idea es expresarlo de la siguiente manera:
\[ \left( x - \frac {1}{2} \right)^2 - \left( \frac {1}{2} \right)^2 + 2 = y \]
En esta nueva expresión, la x aparece solo una vez y es más fácil de despejar. Ahora se resuelven los cálculos y se despeja:
\[ \left( x - \frac {1}{2} \right)^2 - \frac {1}{4} + 2 = y \]
\[ \left( x - \frac {1}{2} \right)^2 + \frac {7}{4} = y \]
\[ \left( x - \frac {1}{2} \right)^2 = y - \frac {7}{4} \]
\[ x - \frac {1}{2} = \sqrt{y - \frac {7}{4} } \]
\[ x = \sqrt{y - \frac {7}{4} } + \frac {1}{2} \]
Cambiando la variable, se obtiene la fórmula buscada:
\[ f^{-1}(x) = \sqrt{x - \frac {7}{4} } + \frac {1}{2} \]
Es de destacar que, como f(x) no es una función biyectiva, no tiene inversa para todo su dominio. Además, para que f -1(x) sea una función, se debe considerar solo el resultado positivo de la raíz cuadrada (de otra forma, algunos valores de x tendrían dos imágenes). Esto se debe a que f(x) no es inyectiva.
Se sugiere encontrar el dominio de f -1(x).
Respuesta: \[ Dom = \left[ \frac {7}{4}; + \infty \right) \]
Ejercicio 12
Sabiendo que los productos pagan 21 % de IVA sobre el costo, calcule cuánto es el costo conociendo el precio de venta.
Si se llama x al precio de costo, el precio de venta f(x) se calcula de la siguiente manera:
\[ f (x) = y = x + x \cdot \frac {21}{100} = 1,21 \cdot x \]
Para resolver este problema, se debe encontrar f -1(x), que vincula el precio de venta con el de costo:
\[ y = 1,21 \cdot x \]
\[ \frac {y}{1,21} = x \]
\[ \frac {1}{1,21} \cdot y = x \]
\[ 0,826 \cdot y = x \]
Si cambiamos la variable, se obtiene la fórmula buscada:
0,826 · x = y
f -1(x) = 0,826 · x
Ejercicio 13
Encuentre la función inversa de f(x) = 32x
Es necesario despejar x en la siguiente ecuación:
y = 32x
Cuando la x está en el exponente, se aplican logaritmos y sus propiedades (en los dos primeros pasos) y luego se despeja:
\[ ln (y) = ln (3^{2x}) \]
\[ ln (y) = 2x \cdot ln \ 3 \]
\[ \frac {ln (y)}{ln \ 3}= 2x \]
\[ \frac {ln (y)}{ln \ 3} \div 2 = x \]
\[ \frac {ln (y)}{2 \cdot ln \ 3} = x \]
Solo resta cambiar variables:
\[ f^{-1}(x) = \frac {ln (x)}{2 \cdot ln \ 3} \]
Se sugiere encontrar el dominio de f -1(x).
Respuesta: \[ Dom = (0; + \infty) \]
Encuentre las funciones inversas de: f(x) = x3 + 4, g(x) = ln(x + 2) y h(x) = x + 1 y sus dominios.
Respuestas:
\( f^{-1}(x) = \sqrt [3]{x - 4}, g^{-1}(x) = e^x - 2 \text { y } h^{-1}(x) = x - 1 \). Todos los dominios son \( \Re \).
1.4. Representación gráfica de funciones
Uso de Geogebra
Geogebra es un software libre de matemáticas dinámicas muy sencillo de utilizar. Se puede descargar gratuitamente.
Como se actualiza permanentemente, algunas de las pantallas que siguen podrían verse algo diferente en cada versión del programa. Pero, de todas maneras, las ideas principales siguen siendo válidas.
La pantalla inicial es:
Al pie de ella dice “Entrada” y allí se escribe la fórmula de la función que se desea graficar. A la derecha de ese “renglón” hay un “botón” [redondeado en azul] que se despliega al clickear sobre él y permite introducir símbolos especiales, como los exponentes, o funciones, como raíz cuadrada: sqrt(x) o logaritmo natural: ln(x).
En el sitio de Geogebra <https://www.geogebra.org/help/geogebraquickstart_es.pdf> hay una Guía Rápida de Referencia de este programa.
En YouTube hay muchos videos para aprender a usarlo, por ejemplo:
<https://www.youtube.com/watch?v=CGXy7G9b_5s>: en este enlace se indica cómo descargarlo. Es importante tener en cuenta que en este ejemplo utiliza aplicaciones de geometría que no se usarán en este curso.
<https://www.youtube.com/watch?v=R8tm5tL1_4w> en este enlace se grafican funciones, esta aplicación sí se utiliza en esta materia.
1.4.1. Gráfica de funciones lineales
Las funciones lineales son aquellas cuya representación gráfica es una recta. Su regla de asignación es un polinomio de grado uno:
f(x) = a · x + b
El número a se denomina “pendiente” y el número b “ordenada al origen”.
En el siguiente gráfico, construido con Geogebra, se puede observar qué sucede con la gráfica de las rectas, al modificar los valores de la pendiente y de la ordenada al origen. Moviendo los “deslizadores” llamados “ordenada” y “pendiente” (en color verde y en color azul respectivamente, arriba, a la derecha), va cambiando la fórmula de la recta roja.
Como puede apreciarse, al cambiar la ordenada al origen, se obtienen rectas paralelas, que se intersecan con el eje vertical en diferentes lugares. Mientras que, al cambiar la pendiente, se mantiene fijo el punto de intersección de las rectas con el eje y, pero se modifica la inclinación de las rectas.
Ejercicio 14
Si utilizamos el gráfico anterior, se pide que:
- Describa la recta f(x) = - 5x + 1
- Compárela con la recta g(x) = - 4x + 1 y con h(x) = - 5x + 2
- ¿Qué sucede con las rectas cuya pendiente es igual a cero?
- ¿Cómo son las rectas con pendiente positiva? Compárelas con las de pendiente negativa.
- Observe la recta f(x) = - 2x + 1 y relacione su fórmula con su gráfico.
- La recta f(x) = - 5x + 1, considerando el gráfico de izquierda a derecha, “decrece”, es decir, para todos los números reales, es:
- La recta g(x) también es decreciente, se interseca con el eje y en el mismo punto que f(x), pero, como su pendiente es mayor, se interseca con el eje x en \( \left( \frac{1}{4}; 0 \right) \). La recta h(x) es paralela a f(x), pero se interseca con el eje vertical en (0; 2).
- Las rectas de pendiente nula son horizontales.
- Las rectas de pendiente positiva son “crecientes”, es decir, para todos los números reales \( \text {si a } < b \to f (a) \leq f (b) \). Y las de pendiente negativa son “decrecientes”.
- La recta f(x) = - 2x + 1 tiene el siguiente gráfico, en el que se destacaron dos puntos: el que corresponde a la intersección con el eje y, es decir, el punto (0; 1) y el punto (1; -1).
\[ \text {si a } < b \to f (a) \geq f (b) \]
Además, se interseca con el eje vertical en el punto (0, 1). Y con el eje horizontal en \( \left( \frac{1}{5}; 0 \right) \).
En <https://www.ditutor.com/funciones/funcion_creciente.html> se pueden encontrar más datos sobre las funciones crecientes y decrecientes.
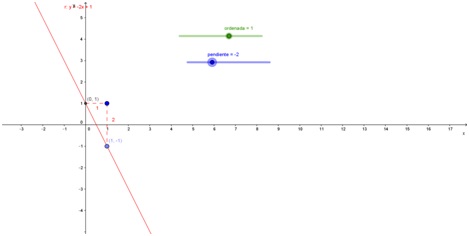
Si tenemos la fórmula de la función, se deduce que su intersección con el eje vertical será en (0; 1) porque su “ordenada al origen” es 1.
La “pendiente” de la recta es -2, es decir, \( \frac {-2}{1} \), que, en general, se puede escribir como \( \frac {\Delta y}{\Delta x} \), es decir, cuánto se “mueve verticalmente” dividido “cuánto se mueve horizontalmente”. A partir del punto de intersección con el eje vertical, teniendo en cuenta la pendiente, se puede obtener el segundo punto destacado, “moviéndose” un lugar a la derecha (por el denominador de la pendiente) y “bajando” dos lugares (por el numerador de la pendiente).
Esta regla práctica facilita la construcción de rectas a partir de su fórmula.
La pendiente de una recta se puede escribir como \( a = \frac {\Delta y}{\Delta x} = \frac {y_2 - y_1}{x_2 - x_!} \), siendo (x1; y1) y (x2; y2) dos puntos de la recta.
Ejercicio 15
Grafique las siguientes funciones lineales:
- f(x) = x
- g(x) = x + 1
- h(x) = x + 2
- i(x) = x - 1
- j(x) = x - 2
En este ejercicio se busca observar qué sucede con el gráfico de la función al modificar la ordenada al origen, manteniendo fija a la pendiente, que en este caso es: (respuesta: a = 1).
En el siguiente gráfico, construido con Geogebra, al “mover” el deslizador “ordenada” (en color verde, arriba a la derecha), van graficándose todas estas rectas, y otras más, al ir cambiando la ordenada al origen.
Como puede observarse, al costado de cada recta, aparece la fórmula correspondiente. Todas ellas son paralelas, porque se mantiene constante la pendiente. La ordenada al origen se corresponde con la ordenada del punto de intersección entre cada recta y el eje vertical, que es el eje de las ordenadas.
Proponemos, como ejercicio, encontrar los puntos de intersección de cada una de estas rectas con los ejes cartesianos.
Para construir estos gráficos “con lápiz y regla”, es importante recordar que, por tratarse de polinomios de grado uno, todos serán rectas. Y para trazar una recta, solo hacen falta dos puntos.
Para encontrar dos puntos, se pueden elegir por lo menos dos caminos.
- Se puede armar una “tabla de valores”. Esto es lo que se hará para la función f(x) = x:
- Se puede graficar con base en la ordenada al origen y a la pendiente. Es lo que se hará con la función g(x) = x + 1:
Se eligen arbitrariamente dos valores de x y se calcula el valor de y para cada uno de ellos:
|
x |
f(x) = x |
|
0 |
0 |
|
3 |
3 |
Con esta información, se ubican estos puntos en un diagrama cartesiano (conviene utilizar hojas cuadriculadas, que facilitan la tarea):
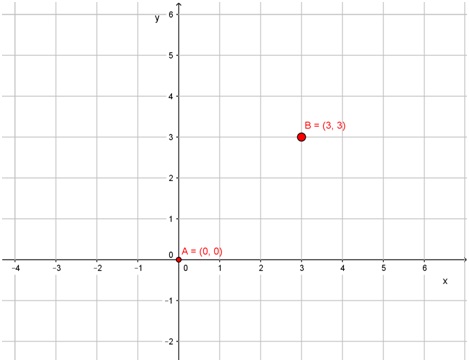
Al graficar un diagrama cartesiano, se nombra a cada uno de los ejes, y se indica una escala. En el gráfico anterior, por ejemplo, se ubicaron los números enteros. Y, en color rojo, los pares ordenados que corresponden a la recta que se va a graficar.
Una vez hecho esto, se unen ambos puntos con una regla y se obtiene la recta f(x) = x.
Como la ordenada al origen es 1, esto significa que la recta se interseca con el eje vertical en el par ordenado (0; 1). Este será el primer punto.
Como su pendiente es 1, que se puede escribir como \( \frac {1}{1} \), se puede obtener el segundo punto a partir del anterior, “moviéndose” un lugar a la derecha y “subiendo” un lugar. Se llega así al punto (1, 2).
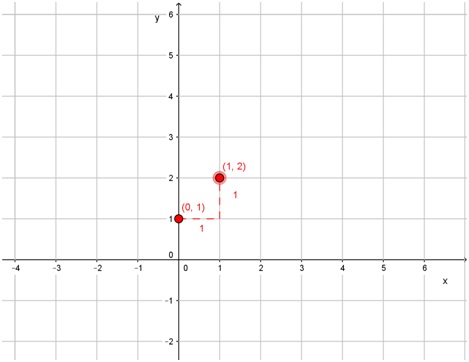
Nuevamente, resta unirlos con una regla para obtener la gráfica buscada.
Puntos de intersección de una función con los ejes cartesianos
El punto de intersección de una función f(x) con el eje y tiene las coordenadas (0; f(0)). Como f(x) es una función, hay un único punto de intersección con el eje y, ya que la imagen de 0 es única (por la definición de función).
Por ejemplo, para la función h(x) = x + 2, es h(0) = 0 + 2 = 2, por lo tanto, el punto de intersección de h(x) con el eje de ordenadas es (0; 2).
El/los punto/s de intersección de una función con el eje x tiene/n como coordenadas (x; 0). Es decir, es/son el/los puntos cuya abscisa anula a la función.
Para encontrar el/los valores de x, se debe resolver la ecuación
f(x) = 0
En el caso de funciones lineales, la ecuación tendrá un único resultado. Por ejemplo, para la función h(x) = x + 2 es
x + 2 = 0
x = - 2
Entonces, el punto de intersección de la recta h(x) con el eje de las abscisas es (-2; 0)
Respuestas a los puntos de intersección con los ejes cartesianos de las rectas del ejercicio 10:
|
Función |
Intersección con eje y |
Intersección con eje x |
|
f(x) |
(0; 0) |
(0; 0) |
|
g(x) |
(0; 1) |
(-1; 0) |
|
h(x) |
(0; 2) |
(-2; 0) |
|
i(x) |
(0; -1) |
(1; 0) |
|
j(x) |
(0; -2) |
(2; 0) |
Ejercicio 16
Encuentre la fórmula de:
- la recta que pasa por los puntos (1; 5) y (3; 6)
- la recta paralela a la anterior que pasa por el punto (-1; 6)
- la recta perpendicular a las dos primeras y a la que pertenece el punto (-2; 2)
- grafique todas las rectas en un mismo diagrama cartesiano.
- Si tenemos dos puntos de la recta, se puede calcular su pendiente:
- La recta que se busca ahora tiene la misma pendiente que la de la parte a), porque son paralelas. Solo diferirán en su ordenada al origen. Por eso, sigue siendo:
- Para obtener una recta perpendicular, los desplazamientos de la pendiente deben ser “al revés”:
\[ a = \frac {\Delta y}{\Delta x} = \frac {y_2 - y_1}{x_2 - x_1} = \frac {6 - 5}{3 - 1} = \frac {1}{2} \]
De este modo, ya se sabe que la fórmula buscada será:
\[ y = \frac {1}{2} \cdot x + b \]
Y falta hallar el valor de la ordenada al origen b. Con este objetivo, se reemplazan en esta fórmula los datos de uno (cualquiera) de los puntos. Por ejemplo, para (1; 5) es:
\[ 5 = \frac {1}{2} \cdot 1 + b \]
Resolviendo la ecuación, se obtiene el valor de b:
\[ b = \frac {9}{2} \]
Se sugiere comprobar que al reemplazar con los datos del otro punto, se llega al mismo resultado.
Por lo tanto, la fórmula buscada es:
\[ y = \frac {1}{2} \cdot x + \frac {9}{2} \]
O, lo que es lo mismo, y = 0,5 · x + 4,5
\[ y = \frac {1}{2} \cdot x + b \]
Para buscar esta nueva ordenada al origen, se reemplazan los datos del punto (-1; 6) y se resuelve la ecuación:
\[ 6 = \frac {1}{2} \cdot (-1) + b \]
\[ b = \frac {13}{2} \]
Entonces, esta nueva recta tiene como fórmula:
\[ y = \frac {1}{2} \cdot x + \frac {13}{2} \]
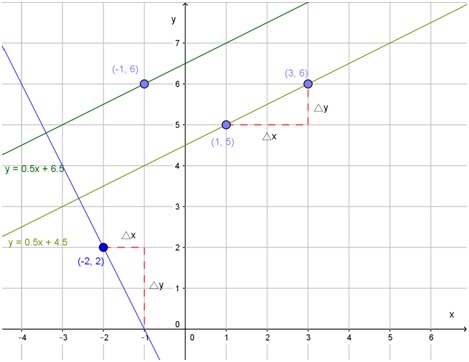
El gráfico anterior sirve de respuesta para la parte d). Allí se indicaron los “desplazamientos” que corresponden a la recta de la parte a) y los que corresponden a la recta perpendicular que se está buscando ahora. Allí se aprecia que la pendiente correspondiente es \( a = \frac {-2}{1} = -2 \).
De modo que esta nueva recta tendrá la siguiente fórmula:
y = -2 · x + b
Y como el punto (-2; 2) pertenece a ella, deberá ser:
2 = -2 · (-2) + b
Despejando b, se obtiene b = - 2
Y la fórmula de la recta perpendicular es y = -2 · x - 2
Encuentre la fórmula de la recta que pasa por los puntos (2; 0) y (-1; 9), y de la perpendicular a ella por el origen de coordenadas. Grafique ambas en un mismo diagrama.
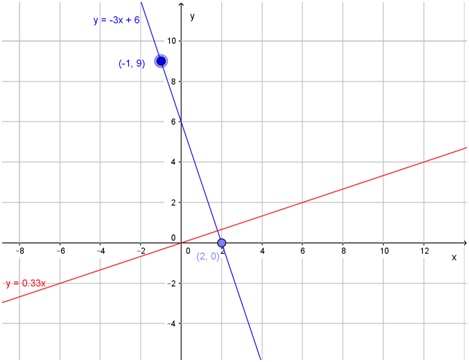
Respuestas: la recta es y = -3 · x + 6 y su perpendicular es \( y = \frac {1}{3} \cdot x \)
1.4.2. Gráfica de funciones polinómicas de grado 2
Las funciones polinómicas de grado dos, también llamadas “funciones cuadráticas” son aquellas cuya regla de asignación tiene la forma:
f(x) = a · x2 + b · x + c
Los números a, b y c son números reales cualesquiera, pero a debe ser distinto de cero: ¿por qué? (Respuesta: si fuera cero, se trataría de una recta, y no de una función cuadrática).
En el siguiente gráfico, construido con Geogebra, se puede variar el valor de a, moviendo el “deslizador” de color azul que se encuentra arriba, a la derecha. Para cada valor de a, se grafica una función cuadrática distinta, en este caso, tanto b como c son cero ya que se desea observar qué sucede al variar a.
Como se puede apreciar, la representación gráfica es una parábola.
Ejercicio 17
Observando el gráfico anterior, se pide que:
- Conteste las siguientes preguntas:
- ¿Cómo son las parábolas cuando a es un número positivo?
- ¿Cómo son las parábolas cuando a es un número negativo?
- Compare las funciones f(x) = 3,5x2 y f(x) = -3,5x2.
- Compare las funciones f(x) = 4x2 y f(x) = 1x2.
- Indique los intervalos de crecimiento y de decrecimiento para todas las parábolas del gráfico. Generalice su resultado.
En la siguiente página se puede leer más sobre concavidad y convexidad: <https://recursostic.educacion.es/descartes/web/materiales_didacticos/aplicaciones_derivada/concavidad_1.htm>
-
- Todas las parábolas con a > 0 tienen forma de \( \cup \). Se dice que estas parábolas son “convexas”.
- Todas las parábolas con a < 0 tienen forma de \( \cap \). Se dice que son “cóncavas”.
Estas dos funciones tienen gráficos “simétricos” respecto del eje x.
Esto significa que si se grafica f(x) = 3,5x2 en un papel con tinta y, mientras la tinta está fresca se dobla el papel por el eje x, la mancha que se produce corresponde a la gráfica de f(x) = -3,5x2. La situación sería la siguiente:
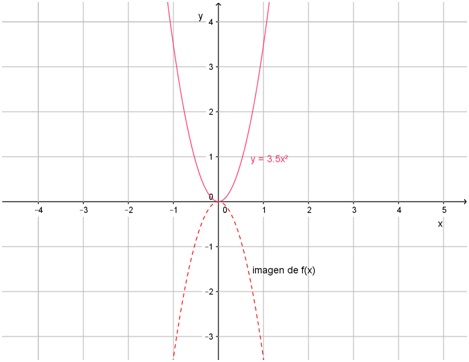
Esto sucede con todos los pares de parábolas en las que los correspondientes valores de a son opuestos: sus gráficas son simétricas respecto del eje x.
Además, todas las parábolas son “simétricas” respecto del eje vertical que pasa por su vértice.
La función f(x) = 4x2 tiene una forma de \( \cup \) más “cerrada” que f(x) = 1x2 . En general, cuanto más grande es el módulo de a, el gráfico de la parábola es más “cerrada”.
Todas las parábolas con a > 0 crecen en el intervalo \( ( 0 ; \infty )\) y decrecen en el intervalo \( ( - \infty ; 0 )\).
Todas las parábolas con a < 0 crecen en el intervalo \( ( - \infty ; 0 )\) y decrecen en el intervalo \( ( 0 ; \infty )\).
El punto (0; 0) en todas estas parábolas, es el vértice. En las que presentan a > 0, este punto se trata de un mínimo. En las otras, de un máximo.
En el gráfico siguiente, construido con Geogebra, se pueden modificar todos los valores de las constantes a, b y c. Como puede apreciarse, lo estudiado sobre la relación entre a y la concavidad o convexidad de la parábola vale aunque cambien b y c. Pero la posición del vértice y de las raíces de la función se modifica.
Ejercicio 18
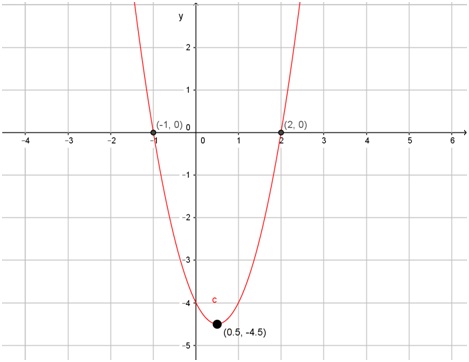
Dada la función f(x) = 2x2 - 2x - 4 se pide que:
- encuentre las coordenadas de su vértice y sus raíces
- se construya su gráfico
- se escriban sus ecuaciones factorizada y canónica y
- que encuentre los puntos de intersección de f(x) con la recta r(x) = 3x - 1
- La abscisa del vértice de una parábola está dado por la siguiente fórmula:
- Para construir manualmente el gráfico, conviene comenzar por ubicar estos puntos que se encontraron en la parte a) y unirlos, teniendo en cuenta que las parábolas son “redondeadas” en su vértice:
- La ecuación factorizada de una función polinómica tiene la forma:
\[ x_v = \frac {-b}{2a} \]
En este ejercicio, es:
\[ x_v = \frac {-b}{2a} \]
\[ x_v = \frac {-(-2)}{2 \cdot 2} = \frac {1}{2} \]
Para encontrar la ordenada, se reemplaza este valor en la fórmula de la función:
\[ f \left( \frac {1}{2} \right) = 2 \cdot \left( \frac {1}{2} \right)^2 - 2 \cdot \frac{1}{2} - 4 = - \frac {9}{2} \]
Por lo tanto, el vértice de f(x) está en el punto \( \left( \frac{1}{2}; - \frac{9}{2} \right) )\). También se puede indicar utilizando números decimales: (0,5; -4,5).
Para encontrar sus raíces, se utiliza la fórmula de la resolvente de la ecuación de segundo grado:
2x2 - 2x - 4 = 0
\[ x = \frac {-(-2) \pm \sqrt {(-2)^2 - 4 \cdot 2 \cdot (-4)}}{2 \cdot 2} = \frac{2 \pm 6}{4} \]
Por lo tanto, resolviendo los cálculos, se tiene que las raíces son x1 = -1 y x2 = 2. Como se piden las coordenadas de las raíces, la respuesta es: (-1; 0) y (2; 0).
f(x) = an · (x - x1) · (x - x2) · ... · (x - xn)
Donde x1, x2, …, xn son las raíces del polinomio.
De este modo, para la función del ejercicio, la ecuación factorizada será:
f(x) = 2 · [x - (-1)] · (x - 2) = 2 · (x + 1) · (x - 2)
La ecuación canónica de una parábola tiene la siguiente forma:
\[ f (x) = a \cdot (x - \alpha)^2 - \beta \]
Donde \( \alpha \) y \( \beta \) son, respectivamente, la abscisa y la ordenada del vértice.
Por eso, en la funciónN del ejercicio actual es:
\[ f (x) = 2 \cdot \left( x - \frac{1}{2} \right)^2 - \left( - \frac{9}{2} \right) = 2 \cdot \left( x - \frac{1}{2} \right)^2 + \frac{9}{2} \]
Se sugiere, como práctica adicional, desarrollar las operaciones indicadas en ambas expresiones, la factorizada y la canónica, para confirmar que se trata de la misma función f(x) con la que se estuvo trabajando.
En las abscisas de los puntos de intersección entre dos funciones, se obtendrá el mismo resultado con la cuenta f(x) como con la cuenta r(x). En símbolos, se puede expresar:
f(x) = r(x)
En este ejercicio, sería:
2x2 - 2x - 4 = 3x - 1
Esta es una ecuación de grado dos. Para resolverla, se puede utilizar la fórmula de la resolvente. Pero antes, es necesario igualarla a cero:
2x2 - 2x - 4 - 3x + 1 = 0
2x2 - 5x - 3 = 0
Ahora si:
\[ x = \frac {-(-5) \pm \sqrt {(-5)^2 - 4 \cdot 2 \cdot (-3)}}{2 \cdot 2} = \frac {5 \pm 7}{4} \]
De este modo, se obtienen las dos abscisas, \( x_1 = \frac {-1}{2} \) y x2 = 3, de los puntos de intersección buscados. Para encontrar las ordenadas correspondientes, se reemplazan estos valores en las fórmulas de las funciones. En ambas, se debe obtener el mismo resultado:
Para \( x_1 = \frac {-1}{2} \text{ es } f \left( - \frac{1}{2} \right) = 2 \cdot \left( - \frac{1}{2} \right)^2 - 2 \cdot \left( - \frac{1}{2} \right) - 4 = - \frac {5}{2} \)
Y \( r \left( - \frac{1}{2} \right) = 3 \cdot \left( - \frac{1}{2} \right) - 1 = - \frac{5}{2} \)
Por lo tanto, uno de los puntos de intersección es \( \left( - \frac{1}{2} ; - \frac{5}{2} \right) \).
Para x2 = 3 es f(3) = 2 · (3)2 - 2 · 3 - 4 = 8
Y r(3) = 3 · 3 - 1 = 8
El otro punto de intersección es (3; 8).
Gráficamente se pueden obtener estos puntos representando la recta r(x) = 3x - 1 en el diagrama cartesiano realizado en el punto c):
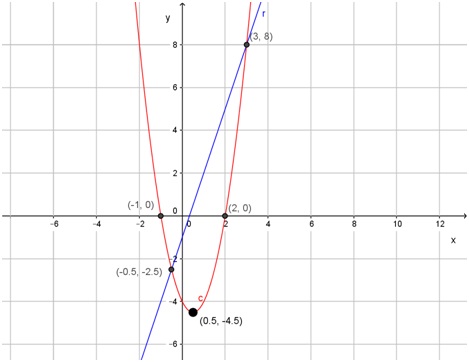
Ejercicio 19
Construya el gráfico de la función f (x) = x2+ 2x + 2 y encuentre su función inversa.
Para construir manualmente un gráfico de una parábola, conviene encontrar las coordenadas del vértice y de las raíces.
En este caso, la abscisa del vértice será:
\[ x_v = \frac {-b}{2a} = \frac {-2}{2 \cdot 1} = -1 \]
Y su ordenada:
f (-1) = (-1)2 + 2 · (-1) + 2 = 1
Por lo tanto, el vértice está en el punto (-1; 1).
Como a = 1 > 0, la parábola es convexa. Por ese motivo, el intervalo de decrecimiento será \( (- \infty ; -1) \) y el de crecimiento será \( (-1 ; - \infty) \).
Como la ordenada correspondiente a - 1 es 1, se deduce que esta parábola no tomará valores menores a 1. Entonces, no tendrá raíces.
Para poder graficar la función de este ejercicio, se puede considerar también el punto en que se interseca con el eje y:
f(0) = (0)2 + 2 · (0) + 2 = 2
Por lo tanto, el punto (0; 2) también pertenece al gráfico.
Como todas las parábolas son “simétricas” respecto del eje vertical que pasa por su vértice, se puede ver que también pertenece al gráfico el punto (-2; 2), simétrico del anterior respecto del eje x = -1.
Con estos tres puntos, y considerando que las parábolas son “redondeadas” en su vértice, se puede construir el gráfico pedido:
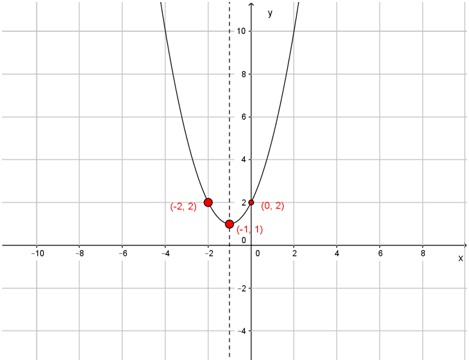
En este diagrama se graficó en línea punteada el eje de simetría de la parábola.
Para hallar la función inversa, conviene escribir la función en su expresión canónica:
f(x) = x2 + 2x + 2 = 1 · [x - (-1)]2 + 1 = (x + 1)2 + 1
De esta última expresión es más sencillo despejar la x:
y = (x + 1)2 + 1
y - 1 = (x + 1)2
\[ \sqrt {y - 1} = x + 1 \]
\[ \sqrt {y - 1} - 1= x \]
Solo resta cambiar las variables:
\[ f ^{-1} (x) = \sqrt {x - 1} - 1 \]
Cuyo dominio es \( Dom = [1 ; \infty ) \). Es necesario considerar solamente el resultado positivo de la raíz para que f-1(x) sea una función.
Si se grafican ambas funciones en un mismo diagrama cartesiano se puede apreciar una propiedad de las funciones inversas: ambos gráficos son simétricos respecto de la bisectriz del primer y tercer cuadrante, es decir, de la recta y = x:
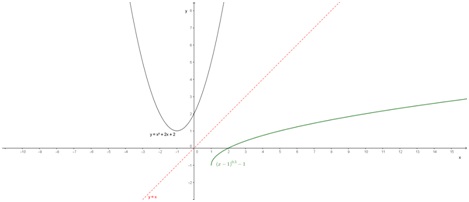
1.4.3. Gráfico de funciones polinómicas de grado mayor a 2
A lo largo del desarrollo de este material, se verán estrategias para facilitar la construcción de los gráficos de las funciones. De todos modos, siempre se pueden construir aproximadamente, utilizando una tabla de valores.
Ejercicio 20
Dada la función f(x) = 2 · x3 - 2 · x2 - 34x - 30 se pide que indique su dominio y construya aproximadamente su gráfico.
Como esta función es polinómica, su dominio son todos los números reales:
\[ Dom = \Re . \]
Para construir aproximadamente su gráfico con lápiz, regla y calculadora, se puede hacer una amplia tabla de valores:
|
x |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
f(x) |
-330 |
-160 |
-54 |
0 |
14 |
0 |
-30 |
-64 |
-90 |
-96 |
-70 |
0 |
126 |
320 |
Como puede observarse en la tabla anterior, los valores que toma la función son grandes, comparados con los valores de x. Por eso, conviene cambiar la escala del eje vertical, por ejemplo, que cada “cuadrito” de la hoja cuadriculada, sea 50 unidades. De este modo, se pueden ubicar los puntos obtenidos:
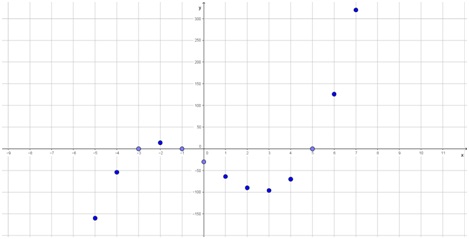
Solo resta unirlos, teniendo en cuenta que las funciones polinómicas tienen formas suaves y redondeadas:
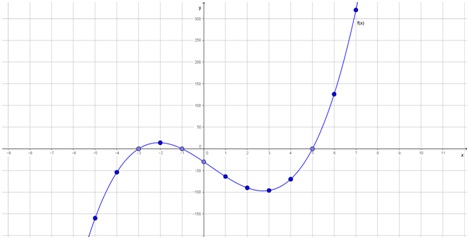
Si observamos el gráfico y la tabla de valores, parece que esta función tiene un máximo relativo en el punto (-2; 14) y un mínimo relativo en (3; -96). En la próxima unidad se verá que esto es solo una aproximación.
Se dice que el punto (a; f(a)) es un máximo relativo de la función f(x) si en las proximidades de x = a la función toma valores menores o iguales a f(a), es decir, \( f (x) \leq f (a)\). Es importante notar que la función puede tomar valores mayores a f(a) en zonas alejadas a a.
Siguiendo esta explicación, ¿cómo explicaría qué es un “mínimo relativo”?
Respuesta: el punto (a; f(a)) es un mínimo relativo de la función f(x) si en las proximidades de x = a la función toma valores mayores o iguales a f(x), o sea, \( f (x) \geq f (a)\).
En las próximas unidades, se aprenderá a encontrar los “extremos relativos”, es decir, los máximos relativos y los mínimos relativos de la función, y, graficar a partir de ellos, para que no haga falta construir una tabla de valores tan larga.
1.4.4. Gráfico de funciones racionales
Las funciones racionales son aquellas cuya regla de asignación es el cociente entre dos polinomios:
\[ f (x) = \frac {P(x)}{Q(x)}\]
Como ya se estudió en el ejercicio 5, el dominio de las funciones polinómicas son todos los valores de x que no anulan al denominador.
Ejercicio 21
Construya el gráfico de la función \( f (x) = \frac {x + 2}{x^2 - 2x}\) [vista en el ejercicio 5].
Ya se conoce el dominio de esta función \( Dom = \Re - \{ 0 ; 2 \}\):
Como siempre, para graficar se puede construir una tabla de valores. En este caso, es interesante averiguar qué sucede en las proximidades de los puntos que hay que excluir del dominio:
|
x |
-4 |
-3 |
-2 |
-1 |
-0,5 |
-0,1 |
-0,01 |
|||||||
|
f(x) |
-0,1 |
-0,1 |
0 |
0,33 |
1,2 |
9,05 |
99 |
|||||||
|
x |
0,01 |
0,1 |
0,5 |
1 |
1,5 |
1,9 |
1,99 |
|
||||||
|
f(x) |
-101 |
-11 |
-3,3 |
-3 |
-4,7 |
-20,5 |
-201 |
|||||||
|
x |
2,01 |
2,1 |
2,5 |
3 |
4 |
5 |
6 |
|||||||
|
f(x) |
200 |
19,5 |
3,6 |
1,67 |
0,75 |
0,47 |
0,33 |
|||||||
Al graficar es importante recordar que el gráfico no pasará por los valores de x = 0 y x = 2. Para enfatizar esta cuestión se presenta la tabla anterior en tres “tramos”, porque el gráfico también tendrá tres tramos.
Como se aprecia, al acercarse al cero desde los números menores a él, es decir, desde la izquierda, la función toma valores cada vez más grandes. Y al acercarse desde la derecha, la función toma valores cada vez menores. Lo contrario pasa al acercarse al dos. Así es como se ven en la tabla las asíntotas verticales. En la siguiente unidad se verá este tema con más detalle.
El siguiente gráfico, construido con Geogebra corresponde al diagrama de esta función. En él se ubicaron, con líneas de puntos, las asíntotas y sus ecuaciones:
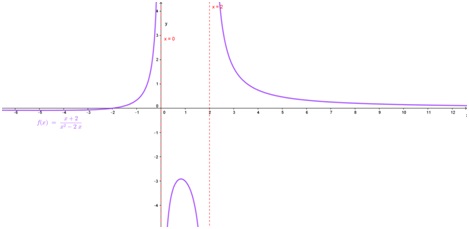
En el gráfico se aprecia además que y = 0 es asíntota horizontal tanto a derecha como a izquierda.
En este ejercicio, los dos valores de x que no pertenecen al dominio son asíntotas verticales. No siempre sucede así.
Ejercicio 22
Construya el gráfico de la función \( g(x) = \frac {2x^2 - 4x - 6}{x^2 - 4x -5} \)
Para comenzar, es importante buscar el dominio de la función, para luego poder construir una tabla tomando valores cercanos a los números que anulan el denominador.
Entonces, debe ser \( x^2 - 4x - 5 \neq 0 \)
Resolviendo esa ecuación, es \( Dom = \Re - \{ -1 ; 5 \} \)
Con base en este resultado, se construye una tabla de valores, acercándose a -1 y a 5, en tres tramos:
|
x |
-4 |
-3 |
-2 |
-1,5 |
-1,1 |
-1,01 |
|
g(x) |
1,556 |
1,5 |
1,429 |
1,385 |
1,344 |
1,334 |
|
x |
-0,99 |
-0,9 |
-0,5 |
0 |
1 |
2 |
3 |
4 |
4,9 |
4,99 |
|
g(x) |
1,332 |
1,322 |
1,273 |
1,2 |
1 |
0,667 |
0 |
-2 |
-38 |
-398 |
|
x |
5,01 |
5,1 |
5,5 |
6 |
7 |
8 |
|
g(x) |
402 |
42 |
10 |
6 |
4 |
3,333 |
A medida que los valores se acercan a -1, tanto desde la izquierda como desde la derecha, la función toma valores cercanos a…: (respuesta: 1,33). Aquí no hay asíntota.
En cambio, cuando la x se aproxima a 5 por la izquierda, los valores de la función decrecen muchísimo. Y aproximándose por la derecha, la función toma valores cada vez mayores. Es decir, hay una asíntota vertical en x = 5.
Cuando se grafica “con lápiz, regla y calculadora” esta función, es importante recordar que tiene tres tramos que no se pueden unir porque la x no puede tomar el valor -1, ni el valor 5.
El siguiente gráfico se confeccionó con Geogebra. Y es incorrecto…
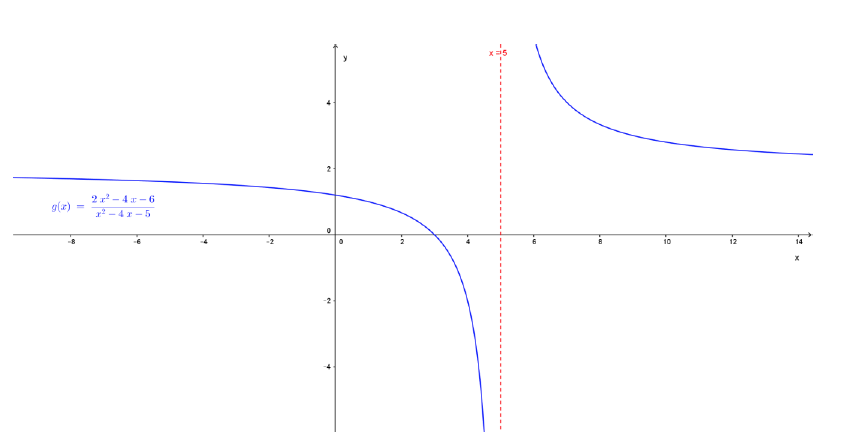
Nótese que no aparece indicado de ninguna manera que no existe la imagen de x = -1.
Cuando se hace con “lápiz, regla y calculadora”, se indica la inexistencia de la imagen de x = -1 con un “circulito” en el punto que falta en el gráfico de la siguiente manera:
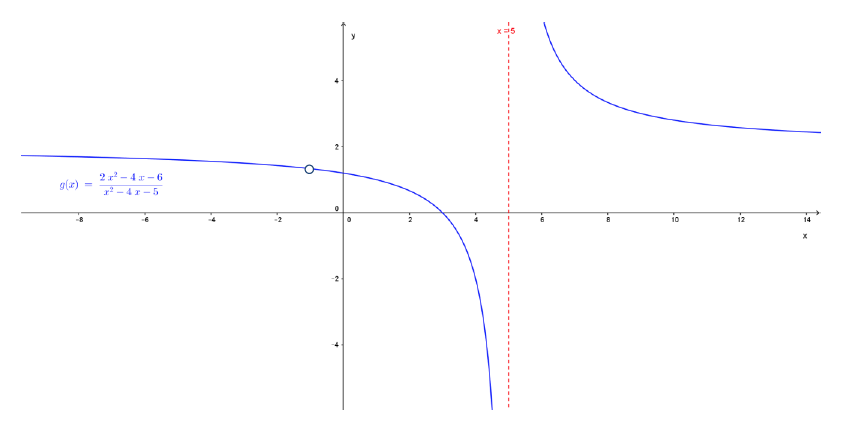
[Aquí, sobre el gráfico de Geogebra, se “insertó” un círculo de contorno azul y relleno blanco, para “tapar” el punto (-1; 1,33), que no pertenece al gráfico de la función g]
En la siguiente unidad se verá con detenimiento cómo encontrar estos “puntos de discontinuidad” que presentan algunas funciones.
En <https://www.youtube.com/watch?v=NADZ1qa_zRw> el profesor Julio Ríos Gallego resuelve un ejercicio de funciones racionales y brinda algunas pistas que se desarrollarán en la próxima unidad.
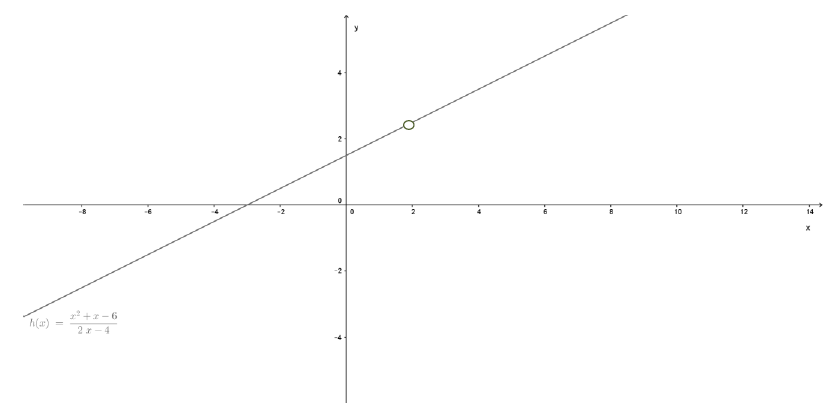
Encuentre el dominio y construya el gráfico de la función \( h(x) = \frac{x^2 + x - 6}{2x - 4} \)
Respuesta: \( Dom = \Re - \{ 2 \} \) El gráfico es:
1.4.5. Gráfico de funciones exponenciales
En una función exponencial, la variable x está en el exponente. Es decir, es del tipo f(x) = ax, en la que la base \( a \in (0 ; \infty ) - \{ 1 \} \).
Ejercicio 23
En el siguiente diagrama, confeccionado con Geogebra, se obtienen gráficos de diferentes funciones exponenciales al mover el “deslizador” de color rojo ubicado arriba, a la derecha:
Observando los gráficos que se obtienen, resuelva las siguientes cuestiones:
- ¿Qué forma tiene el gráfico de la función f(x) = 1x?
- Todos los gráficos de las funciones exponenciales tienen un punto en común. ¿Cuál es?
- Describa las diferentes funciones exponenciales, según su base.
- La función f(x) = 1x es una recta horizontal, ya que, para todo valor de x, 1x = 1. Por eso, no se la considera una “función exponencial”.
- Todos los gráficos de las funciones exponenciales tienen en común al punto (0; 1), ya que cualquier valor de \( a \neq 0 \) es \( a^0 = 1 \). Y, como ya se estudió en la definición de funciones exponenciales, la base de la función nunca es 0.
- En todos los casos, y = 0 es asíntota horizontal de la función.
Ninguna función presenta extremos relativos.
Si la base de la función exponencial es un número entre 0 y 1, la función es decreciente y asintótica a derecha.
Si la base de la función exponencial es un número mayor a 1, la función es creciente y asintótica a izquierda.
En las próximas unidades se aprenderá cómo encontrar asíntotas verticales y horizontales.
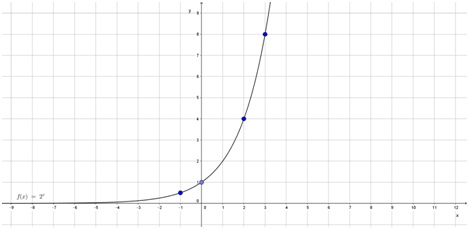
Ejercicio 24
Dada la función f(x) = 2x se pide que indique su dominio y construya aproximadamente su gráfico con lápiz, regla y calculadora.
Por el ejercicio anterior, ya se sabe que esta función es creciente, que pasa por el punto (0; 1) y que el eje horizontal es asíntota a izquierda.
Con esta información se pueden buscar algunos puntos más y graficar:
|
x |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
f(x) |
0,5 |
1 |
2 |
4 |
8 |
16 |
32 |
1.4.6. Gráfico de funciones logarítmicas
La función logarítmica en base a es la función inversa a la exponencial en base a:
\[ f(x) = log _ax \leftrightarrow x = a^{f(x)} \]
Por lo tanto, la base de los logaritmos debe cumplir las mismas restricciones que se le imponen a la base de las funciones exponenciales, es decir, \( a \in (0 ; \infty ) - \{ 1 \} \).
Como x es el resultado de una potencia, siempre será un número positivo. Por este motivo, el dominio de las funciones logarítmicas es:
\[ Dom = (0 ; \infty ) \]
Ejercicio 25
En el siguiente diagrama, confeccionado con Geogebra, se obtienen gráficos de diferentes funciones logarítmicas al mover el “deslizador” de color gris ubicado arriba, a la derecha:
Observando los gráficos que se obtienen, resuelva las siguientes cuestiones:
- ¿Qué forma tiene el gráfico de la función \( f(x) = log_1x \)?
- Todos los gráficos de las funciones logarítmicas tienen un punto en común. ¿Cuál es?
- Describa las diferentes funciones logarítmicas, según su base.
- Geogebra no grafica la función \( f(x) = log_1x \) ya que no es una función. Se trataría de la recta vertical de ecuación x = 1. En este ejercicio se aprecia por qué es importante recordar que la base de los logaritmos no puede ser 1.
- Todos los gráficos de las funciones logarítmicas tienen en común al punto (1; 0).
- En todos los casos, x = 0 es asíntota vertical de la función.
Ninguna función presenta extremos relativos.
Si la base de la función logarítmica es un número entre 0 y 1, la función es decreciente y asintótica hacia arriba.
Si la base de la función logarítmica es un número mayor a 1, la función es creciente y asintótica hacia abajo.
Ejercicio 26
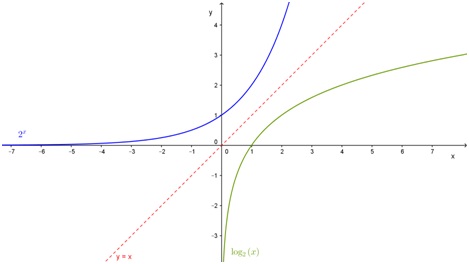
Construya el gráfico de la función \( f(x) = log_2x \) considerando que es la inversa de g(x) = 2x y la propiedad de los gráficos de las funciones inversas (vista en el ejercicio 19).
En el ejercicio 24 ya se construyó el gráfico de g(x) = 2x. Como los gráficos de las funciones inversas son simétricos respecto del eje y = x, basta buscar esa simetría para graficar:
Este ejercicio no es fácil de resolver con calculadora, ya que no tienen una tecla para calcular logaritmos en base 2.

