3. Primitivas e integrales definidas
Objetivos
- Calcular primitivas de funciones.
- Utilizar distintos métodos para integrar funciones.
- Calcular áreas comprendidas entre curvas.
- Aplicar integrales para resolver problemas económicos.
3.1. Primitiva de una función
Ejercicio 1
Encuentre una función primitiva de f(x) = 2 · x3
Se dice que F(x) es una primitiva de una función f(x)
si la derivada de F(x) es la función f(x) . En símbolos:F'(x) = f(x)
Otra notación, que resulta adecuada en estos temas es la siguiente:
\[ \frac{d}{dx} (F(x))= f(x) \]
Que se lee “la derivada respecto de la variable x de la función F(x) es igual a f(x)”.
Para resolver este ejercicio hay que pensar qué función derivada da como resultado 2 · x3. Teniendo presente la regla de la derivada de la potencia, se puede ver que la función buscada está relacionada con x4, porque la derivada de x4 es 4 · x3. Pero en el ejercicio actual, no aparece el 4 sino un 2. Para que pueda simplificarse, se multiplica a esta función por 2 y por el inverso de 4:
\[ F(x) = 2 \cdot \frac{1}{4} \cdot x^4 = \frac{1}{2} \cdot x^4 \]
Como puede apreciarse la derivada de esta función es f(x) = 2 · x3.
Sin embargo, esta es una primitiva. Pero existen infinitas. Por ejemplo:
\[ F_1(x) = \frac{1}{2} \cdot x^4 + 8 \]
\[ F_2(x) = \frac{1}{2} \cdot x^4 - 1 \]
\[ F_3(x) = \frac{1}{2} \cdot x^4 + 3 \]
En general, una primitiva difiere de otra solo en una constante. A todas ellas se las puede simbolizar de la siguiente manera:
\[ \int f(x) dx = F(x) \]
\( \int f(x) dx \) se lee “integral indefinida de f respecto de la variable x”. Simboliza a todas las primitivas de una función. El símbolo \( \int \) se escribe al comienzo de la función a la que se le va a buscar la integral y dx (que se lee “diferencial x”) se escribe al final. Esta última expresión indica cuál es la variable a integrar.
Cuando ya se resolvió la integral, no se escriben más ninguno de los dos símbolos.
En este ejercicio, sería:
\[ \int 2 \cdot x^3 dx = \frac{1}{2} \cdot x^4 + C \]
Donde C simboliza a una constante y se denomina “constante de integración”.
Generalizando este resultado, se obtiene que
\[ \int a \cdot x^n dx = a \cdot \frac{1}{n + 1} \cdot x^{n+1} + C \]
Es importante notar que esta fórmula solo es válida si \( n \not= -1 \) . (Si ese fuera el caso, el denominador daría cero. Por eso, la fórmula no es válida cuando el exponente es -1)
3.2. Integral indefinida de una función
Ejercicio 2
Calcule las siguientes integrales indefinidas:
- \( \int (x^3 + 3x^2 - x + 1) dx = \)
- \( \int 4t^5 dt = \)
- \( \int \frac{1}{x^2} dx = \)
- \( \int \sqrt[4]{x} \ dx = \)
- \( \int \frac{1}{x} dx = \)
- \( \int \frac{2x^5 - 5x^2 + 3}{x} dx =\)
En este ejercicio, la función f(x) es una suma. Como la derivada de una suma es la suma de las derivadas de cada término, se puede pensar que la primitiva F(x) es también una suma. Entonces, se puede escribir:
\[ \int (x^3 + 3x^2 - x + 1) dx = \]
\[ = \int x^3 dx + \int 3x^2 dx - \int x \ dx + \int 1 dx \]
Para resolver las primitivas de cada uno de estos términos, se puede utilizar la fórmula del final del ejercicio 1. El último término se interpreta como 1 = 1 · X0. Entonces:
\[ \int (x^3 + 3x^2 - x + 1) dx = \]
\[ = \frac{1}{4} \cdot x^4 + C_1 + 3 \cdot \frac{1}{3} \cdot x^3 + C_2 - \frac{1}{2} \cdot x^2 + C_3 + 1 \cdot \frac{1}{1} \cdot x^1 + C_4 \]
En esta expresión ya no aparecen el símbolo \( \int \) ni la expresión dx, porque ya se encontraron las primitivas de cada término. Solo faltan resolver los cálculos y se pueden reemplazar todas las constantes por una sola: k = C1 + C2 + C3 + C4. Entonces, la respuesta es:
\[ \int (x^3 + 3x^2 - x + 1) dx = \frac{1}{4} \cdot x^4 + x^3 - \frac{1}{2} \cdot x^2 + x + k \]
Se puede comprobar, derivando el segundo miembro, que la integral es correcta.
En este ejercicio, la variable a integrar es t, ya que el diferencial es dt. Como la función a integrar es una potencia, podemos utilizar la fórmula vista:
\[ \int 4t^5 dt = 4 \cdot \frac{1}{5+1} \cdot t^{5+1} + C = 4 \cdot \frac{1}{6} \cdot t^6 + C = \frac{2}{3} \cdot t^6 + C \]
En este caso, se puede reescribir la función para expresarla como una potencia, utilizando un exponente negativo:
\[ \int \frac{1}{x^2} dx = \int x^{-2} dx \]
Expresada de esta manera, se utiliza la fórmula aprendida:
\[ \int \frac{1}{x^2} dx = \int x^{-2} dx = 1 \cdot \frac{1}{-2+1} \cdot x^{-2+1} + C \]
Resolviendo los cálculos llegamos al resultado buscado:
\[ \int \frac{1}{x^2} dx = -1 \cdot x^{-1} + C = - \frac{1}{x} + C \]
Como en el caso anterior, conviene reescribir la función para expresarla como una potencia. Ahora, es con exponente racional:
\[ \int \sqrt[4]{x} \ dx = \int x^{1/4} dx \]
De este modo, solo resta utilizar la fórmula vista:
\[ \int \sqrt[4]{x} \ dx = \int x^{1/4} dx = 1 \cdot \frac{1}{1/4 + 1} \cdot x^{(1/4 +1)} + C \]
El resultado se obtiene efectuando los cálculos:
\[ \int x^{1/4} dx = \frac{1}{5/4} \cdot x^{5/4} + C = \frac{4}{5} \cdot x^{5/4} + C \]
Este caso podría parecerse a los anteriores. Sin embargo, es importante notar que si se expresa la función como una potencia negativa, obtenemos:
\[ \int \frac{1}{x} dx = \int x^{-1} dx \]
Si se utilizara la fómula vista, en el denominador quedaría un cero. Y ya se estudió que no está definida la división por cero.
Para resolver este ejercicio solo hace falta recordar que la derivada del logaritmo natural es \( \frac{1}{x} \)N. Por eso,
\[ \int \frac{1}{x} dx = ln|x| + C \]
En este ejercicio hay una división. Antes de calcular la primitiva, conviene distribuir el denominador a cada uno de los términos del numerador para obtener una expresión más sencilla:
\[ \int \frac{2x^5 - 5x^2 + 3}{x} dx = \int \left( \frac{2x^5}{x} - \frac{5x^2}{x} + \frac{3}{x} \right) dx = \int \left( 2x^4 - 5x + \frac{3}{x} \right) dx = \]
\[ = \int \left( 2x^4 - 5x + \frac{3}{x} \right) dx \]
Ahora sí se puede calcular la primitiva de cada término:
\[ \int \frac{2x^5 - 5x^2 + 1}{x} dx = 2 \cdot \frac{1}{4+1} \cdot x^5 - 5 \cdot \frac{1}{1+1} \cdot x^2 + 3 \cdot ln|x| + C = \]
\[ \int \frac{2x^5 - 5x^2 + 1}{x} dx = \frac{2}{5} \cdot x^5 - \frac{5}{2} \cdot x^2 + 3 \cdot ln|x| + C \]
Se puede comprobar, derivando el segundo miembro, que la integral es correcta.
La función \( f(x) = \frac{1}{x} \) tiene como dominio al conjunto \( Dom = \Re - \{ 0 \} \), mientras que el dominio de la función F(x) = ln(x) es \( Dom = (0 ; \infty) \). Para que coincida el dominio de la función que se integra con el de su primitiva, se usa el módulo de x como argumento de la función logaritmo natural.
En <https://www.youtube.com/watch?v=Fj8SHHJIElU> la profesora Nancy Saín resuelve varios ejercicios de este tipo y explica algunas de las propiedades de la integración.
Calcule las siguientes integrales indefinidas:
- \( \int \left( 3t^4 + \frac{2}{t} \right) dt \)
- \( \int \left( \frac{2}{\sqrt{x}} + 3x \right) dx \)
- \( \int \left( \frac{3}{x} + \frac{4}{x^2} + \frac{5}{x^3} - 1 \right) dx \)
Respuestas:
- \( \int \left( 3t^4 + \frac{2}{t} \right) dt = \frac{3}{5} \cdot t^5 + 2 \cdot ln|t| + C \)
- \( \int \left( \frac{2}{\sqrt{x}} + 3x \right) dx = 4 \cdot x^{1/2} + \frac{3}{2} \cdot x^2 + C = 4 \cdot \sqrt{x} + \frac{3}{2} \cdot x^2 + C \)
\( \int \left( \frac{3}{x} + \frac{4}{x^2} + \frac{5}{x^3} - 1 \right) dx = 3 \cdot ln|x| - 4 \cdot x^{-1} - \frac{5}{2} \cdot x^{-2} - x + C = \)
\( = 3 \cdot ln|x| - \frac{4}{x} - \frac{5}{2 \cdot x^2} - x + C \)
3.3. Métodos de integración
3.3.1. Integración por sustitución
Ejercicio 3
Calcule la siguiente integral indefinida:
\[ \int (x^2 + 1) \cdot \sqrt[2]{x^3 + 3x} \cdot dx = \]
En este caso, la función a integrar es un producto entre un polinomio y una función compuesta: la raíz cuadrada de otro polinomio. Aquí es importante recordar que la derivada del producto no es el producto de las derivadas. Sin embargo, al derivar una función compuesta, aparece un producto de funciones:
\[ (fog)´(x) = f´[g(x)] \cdot g´(x) \]
El argumento de la función compuesta de este ejercicio es:
\[ g(x) = x^3 + 3x \](1)
Entonces, será:
\[ g´(x) = \frac{dg}{dx} = 3 \cdot x^2 + 3 \]
Por lo tanto,
\[ dg = ( 3 \cdot x^2 + 3) dx = 3 \cdot (x^2 + 1) dx \]
Al despejar la expresión que aparece en la integral, el ejercicio es:
\[ (x^2 + 1) dx = \frac{dg}{3} \](2)
A continuación se sustituyen las expresiones (1) y (2) en la integral y se resuelve:
\[ \int (x^2 + 1) \cdot \sqrt[2]{x^3 + 3x} \cdot dx = \int \sqrt[2]{x^3 + 3x} \cdot (x^2 + 1) \cdot dx = \]
\[ \int \sqrt[2]{g} \cdot \frac{dg}{3} = \frac{1}{3} \cdot \int g^{1/2} dg = \frac{1}{3} \cdot \frac{1}{1/2 + 1} \cdot g^{1/2 + 1} + C = \frac{2}{9} \cdot g^{3/2} + C \](3)
Es importante notar que al integrar solo quedan funciones con la varible g (ya no hay x).
Finalmente, en la expresión (3) se reemplaza la expresión (1):
\[ \int (x^2 + 1) \cdot \sqrt[2]{x^3 + 3x} \cdot dx = \frac{2}{9} \cdot (x^3 + 3x)^{3/2} + C \]
Y esta es la solución buscada.
Se puede comprobar, derivando el segundo miembro, que la integral es correcta.
En los siguientes videos el profesor Julio Ríos resuelve integrales por sustitución.
<https://www.youtube.com/watch?v=4JHHE99fsKY>
Ejercicio 4
Calcule las siguientes integrales indefinidas:
- \[ \int \left[ \frac{x^2 + x}{2x^3 + 3 x^2 - 1} \right] dx = \]
- \[ \int (5 + e ^{2x+1}) \ dx = \]
- \[ \int \left[ \frac{3 \cdot x^2 + 5x - 2}{\sqrt{2x^3 + 5x^2 - 4x + 1}} \right] dx = \]
En este ejercicio la función a integrar es un cociente. Pero su divisor no es un único término, como en el ejercicio 2. f). En este caso, se puede escribir como un producto de una función compuesta por otra función:
\[ \int \left[ \frac{1}{2x^3 + 3x^2 - 1} \cdot (x^2 + x) \right] dx = \]
Aquí, el primer factor se puede pensar como una función compuesta: (2x3 + 3x2 - 1)-1 y la otra función es “parecida” a la derivada de la base de la potencia negativa. Por eso, se puede resolver por “sustitución” o “cambio de variable”.
Se llamará:
\[ u = 2x^3 + 3 \cdot x^2 - 1 \](1)
En esta expresión, u es una función de x . Derivando esta función es:
\[ u`= \frac{du}{dx} = 6 \cdot x^2 + 6x \]
Por lo tanto,
\[ du = (6 \cdot x^2 + 6x) \cdot dx = 6 \cdot (x^2 + x) \cdot dx \to \frac{du}{6} = (x^2 + x) \ dx \](2)
Teniendo presente (1) y (2), conviene reescribir la integral solicitada, sustituyendo de la siguiente manera:
\[ \int \left[ \frac{1}{2x^3 + 3x^2 - 1} \cdot (x^2 + x) \right] dx = \int \left[ \frac{1}{2x^3 + 3x^2 - 1} \right] \cdot (x^2 + x) \ dx \] \[ = \int \left( \frac{1}{u} \right) \cdot \frac{1}{6} \cdot du \]
En esta nueva expresión, que es más sencilla que la original, hay que integrar respecto de la variable u. Es importante notar que dentro de la integral ya no hay ninguna x, por eso se puede resolver:
\[ \int \left( \frac{1}{u} \right) \cdot \frac{1}{6} \cdot du = \frac{1}{6} \cdot \int \frac{1}{u} du = \frac{1}{6} \cdot \int \frac{1}{u} du = \frac{1}{6} \cdot ln|u| + C \]
Una vez resuelta la integral en la nueva variable, se reemplaza (1) en esta última expresión, y se llega a la solución buscada:
\[ \int \left[ \frac{x^2 + x}{2x^3 + 3x^2 -1} \right] dx = \frac{1}{6} \cdot ln|2^3 + 3x^2 -1| + C \]
En este caso, la función a integrar es una suma. Por eso, se puede hacer:
\[ \int (5 + e^{2x + 1}) dx = \int 5 dx + \int e^{2x + 1} dx = \]
\[ = 5x + C_1 + \int e^{2x + 1} dx \](1)
Para resolver la última integral, conviene cambiar la variable en el exponente y llamar:
\[ v = 2x + 1 \](2)
Al derivar es: \( v`= \frac{dv}{dx} = 2 \). Por lo tanto, será \( dv = 2dx \) y \( \frac{dv}{2} = dx \).(3)
Reemplazando las expresiones (2) y (3) en la integral es:
\[ \int e^{2x + 1} dx = \int e^v \cdot \frac{dv}{2} = \int \frac{1}{2} \cdot e^v dv = \frac{1}{2} \cdot \int e^v dv = \frac{1}{2} e^v + c_2 \](4)
Nuevamente, es importante destacar que esta integral se puede resolver porque solo quedó como variable v.
Al reemplazar la expresión (2) en (4) es:
\[ \int e^{2x + 1} dx = \frac{1}{2} e^{2x + 1} + c_2 \](5)
Finalmente, el resultado se obtiene cuando reemplazamos (5) en (1):
\[ \int (5 + e^{2x + 1}) dx = 5x + C_1 + \frac{1}{2} e^{2x + 1} + c_2 \]
Por último, las dos constantes se pueden resumir en una única:
\[ k = C_1 + C_2 \]
\[ \int (5 + e^{2x + 1}) dx = 5x + \frac{1}{2} e^{2x+1} + k \]/span>
En esta primitiva conviene escribir toda la función como un producto entre una potencia negativa y el polinomio del numerador:
\[ \int \left[ (3 \cdot x^2 + 5x - 2)(2x^3 + 5x^2 - 4x + 1)^{-1/2} \right] dx = \]
Así, se puede apreciar que la base de la potencia tiene una derivada similar al polinomio del numerador. Por eso, se aplicará sustitución. Se llamará:
\[ m = 2x^3 + 5x^2 - 4x + 1 \](1)
Derivando es:
\[ m´= \frac{dm}{dx} = 6x^2 + 10x - 4 \]
Por lo tanto,
dm = (6 · x2 + 10x - 4)dx = 2 ·(3x2 + 5x - 2)dx
Entonces,
\[ \frac{dm}{2} = (3x^2 + 5x - 2) dx \](2)
Teniendo presente (1) y (2), conviene reescribir la integral solicitada de la siguiente manera:
\[ \int \left[ (3 \cdot x^2 + 5x - 2)(2x^3 + 5x^2 - 4x + 1)^{-1/2} \right] dx = \]
\[ \int \frac{dm}{2} \cdot m^{-1/2} = \int m^{-1/2} \frac{dm}{2} = \frac{1}{2} \int m^{-1/2} dm = \frac{1}{2} \cdot \frac{1}{\frac{-1}{2} + 1} \cdot m^{-1/2 + 1} \]
\[ = m^{1/2} + C = \sqrt{m} + C \]
Al reemplazar (1) en esta última expresión, se llega a la solución:
\[ \int \left[ \frac{3 \cdot x^2 + 5x - 2}{\sqrt{2x^3 + 5x^2 -4x + 1}} \right] dx = \sqrt{2x^3 + 5x^2 - 4x + 1} + C \]
Resuelva las siguientes integrales indefinidas:
- \( \int \left[ 1 + \frac{x+3}{x^2 + 6x} \right] dx \)
- \( \int e^{3x^2+1} \cdot x \ dx = \)
- \(\int \left( \frac{x^4 + 1}{(x^5 + 5x + 2)^2} + \sqrt[3]{x} + 2 \right) dx \)
Respuestas:
- \( \int \left[ 1 + \frac{x+3}{x^2 + 6x} \right] dx = x + \frac{1}{2} \cdot ln|x^2 + 6x| + C \)
- \( int e^{3x^2+1} \cdot x \ dx = \frac{1}{6} \cdot e^{3x^2+1} + C \)
\( \int \left( \frac{x^4 + 1}{(x^5 + 5x + 2)^2} + \sqrt[3]{x} + 2 \right) dx \) \( = - \frac{1}{5} \cdot (x^5 + 5x + 2)^{-1} + \frac{3}{4} \cdot x^{4/3} + 2x + C \)
3.3.2. Integración por partes
Ejercicio 5
Calcule la siguiente primitiva:
\[ \int x \cdot ln \ x \ dx = \]
En esta integral también hay un producto de dos funciones. Sin embargo, ninguna de las dos es compuesta, ni es una la derivada de la otra. Por eso, para resolverla se requiere de otro procedimiento.
Se comenzará por reescribir la regla de derivación de un producto, utilizando la notación de diferenciales:
\[ [f(x) \cdot g(x)]´= (f \cdot g)´(x) = f´(x) \cdot g(x) + f(x) \cdot g´(x) \]
\[ \frac{d(f \cdot g)}{dx} = \frac{df}{dx} \cdot g + f \cdot \frac{dg}{dx} \]
Aquí se puede despejar d(f · g):
\[ d (f \cdot g) = \left( \frac{df}{dx} \cdot g + f \cdot \frac{dg}{dx} \right) \cdot dx = \frac{df}{dx} \cdot g \cdot dx + f \cdot \frac{dg}{dx} \cdot dx = df \cdot g + f \cdot dg \]
En resumen es:
d(f · g) = df · g + f · dg
Si a esta expresión se la integra, obtenemos:
\[ \int d (f \cdot g) = \int (df \cdot g + f \cdot dg) = \int df \cdot g + \int f \cdot dg \]
El primer miembro se puede resolver, y es conveniente reordenar el primer término del segundo, por lo que queda:
\[ f \cdot g = \int g \cdot df + \int f \cdot dg \]
Al despejar el segundo término del segundo miembro, se obtiene la fórmula de la integración por partes:
\[ \int f \cdot dg = f \cdot g - \int g \cdot df \](1)
Cuando se tiene un producto de dos funciones, se puede considerar que una de ellas es el diferencial de una cierta función g. Al encontrar la fórmula de g y el diferencial del otro factor, aplicando la fórmula anterior, se cambia la integral a resolver. Por lo tanto, a una de las funciones se la integra y a la otra, se la deriva. La nueva integral a resolver, seguirá siendo un producto. Pero se espera que resulte más sencilla que la original.
En el ejercicio que se está resolviendo, uno de los factores que aparecen en la integral es la función x, y el otro, la función ln(x). Es necesario elegir a cuál de las dos se la llamará f y a cuál, dg. Hay que tener en cuenta que se deberá calcular a continuación la función g. Como es más fácil integrar el factor x, a esa función se la llamará dg:
dg = x · dx
Entonces, será f = ln(x).
Para utilizar la fórmula es necesario calcular:N
\[ g = \int dg = \int x \cdot dx = \frac{1}{2} \cdot x^2 \]
En estos ejercicios, la constante de integración se agrega al finalizar.
También será necesario encontrar df:
\[ df = \frac{1}{x} \cdot dx \]
En este punto se reemplaza en la fórmula (1):
\[ \int x \cdot ln \ x \ dx = ln (x) \cdot \frac{1}{2} x^2 - \int \frac{1}{2} \cdot x^2 \cdot \frac{1}{x} \cdot dx \]
Aquí es muy importante comprobar que la nueva integral a resolver es más sencilla que la original. En este ejercicio, se puede simplificar x:
\[ \int x \cdot ln \ x \ dx = ln (x) \cdot \frac{1}{2} x^2 - \int \frac{1}{2} \cdot x^{\not{2}} \cdot \frac{1}{\not{x}} \cdot dx \]
\[ \int x \cdot ln \ x \ dx = ln (x) \cdot \frac{1}{2} x^2 - \int \frac{1}{2} \cdot x \cdot dx \]
\[ \int x \cdot ln \ x \ dx = ln (x) \cdot \frac{1}{2} x^2 - \frac{1}{2} \cdot \int x \cdot dx \]
\[ \int x \cdot ln \ x \ dx = ln (x) \cdot \frac{1}{2} x^2 - \frac{1}{2} \cdot \frac{1}{2} \cdot x^2 + C \]
Es importante notar que, como ya se resolvió la nueva integral, aparece la constante de integración.
Solo resta efectuar los cálculos. Entonces, la integral buscada es:
\[ \int x \cdot ln \ x \ dx = ln (x) \cdot \frac{1}{2} x^2 - \frac{1}{4} \cdot x^2 + C \]
Se puede comprobar, derivando el segundo miembro, que la integral está bien hecha. En este caso, se hará la demostración.
La función integral es \( h(x) = ln (x) \cdot \frac{1}{2} x^2 - \frac{1}{4} x^2 + C \). El primer término es un producto. La derivada se obtiene aplicando la fórmula de la derivada de un producto. Y el segundo término es una potencia que se derivará también.
\[ h´(x) = \frac{1}{x} \cdot \frac{1}{2} \cdot x^2 + ln(x) \cdot \frac{1}{2} \cdot 2 \cdot x - \frac{1}{4} \cdot 2 \cdot x + 0 \]
Al simplificar queda:
\[ h´(x) = \frac{1}{2} \cdot x + ln(x) \cdot x - \frac{1}{2} \cdot x \]
Como el primer y el tercero término son iguales y con distinto signo, se llega a que: h'(x) = ln(x) · x = x · ln(x) que es la expresión original. Es decir, la integral estaba bien resuelta.
Ejercicio 6
Encuentre las siguientes integrales indefinidas:
- \( \int [5 + e^x \cdot (x-1)] \ dx = \)
- \( \int [(x^2 + 2x) \cdot ln (2x)] \ dx = \)
- \( \int ln \ x \ dx = \)
En esta primitiva hay una suma y un producto. Primero, se distribuye el producto y luego, aplicando la propiedad, queda:
\[ \int [5 + e^x \cdot (x-1)] \ dx = \int [5 + e^x \cdot x-e^x] \ dx = \]
\[ = \int 5dx + \int e^x \cdot xdx - \int e^x dx \]
Al resolver la primera y la última integral, que son inmediatas, queda:
\[ = \int 5dx + \int e^x \cdot xdx - \int e^x dx = 5x + \int e^x \cdot xdx - e^x \](1)
Falta resolver el término central. Para ello, se utilizará el método por partes. Primero es necesario elegir a uno de los factores para integrar y al otro para derivar. Como la derivada de f = x es más sencilla, se tomará como dg = ex dx. Entonces, serán df = 1 · dx y
\[ g= \int dg = \int e^x dx = e^x \]
Al reemplazar estos valores en la fórmula de la integral por partes, se obtiene:
\[ \int e^x \cdot xdx = x \cdot e^x - \int 1 \cdot e^x dx = x \cdot e^x - e ^x \](2)
Si sustituimos este resultado en la expresión (1), se obtiene la primitiva pedida en a):
\[ \int [5 + e^x \cdot (x-1)] dx = 5x + x \cdot e^x - e^x - e^x + C \]
Se puede sacar factor común entre los últimos tres términos para obtener una expresión más sencilla:
\[ \int [5 + e^x \cdot (x-1)] dx = 5x + e^x \cdot (x-2) + C \]
Y, para comprobar que la expresión obtenida es la integral buscada, se puede derivar.
En esta primitiva, si bien hay una función compuesta: ln (2x), no aparece su derivada. Por eso, debe realizarse utilizando la fórmula de integración por partes.
Se elige f = ln (2x) porque su derivada es más sencilla (y va a permitir simplificar la integral de dg). Por lo tanto,
\[ df = \frac{1}{2x} \cdot 2 \cdot dx = \frac{1}{x} dx \]
Entonces será: dg = (x2 + 2x) de modo que,
\[ g = \int dg = \int (x^2 + 2x) dx = \frac{1}{3} \cdot x^3 + \frac{1}{2} \cdot 2 \cdot x^2 = \frac{1}{3} \cdot x^3 + x^2 \]
Si reemplazamos estos valores en la fórmula, se tiene:
\[ \int [(x^2 + 2x) \cdot ln (2x)] dx = ln (2x) \cdot \left( \frac{1}{3} \cdot x^3 + x^2 \right) - \int \left( \frac{1}{3} \cdot x^3 + x^2 \right) \cdot \frac{1}{x} dx \]
En esta expresión es muy importante el uso de paréntesis. En la nueva integral, se puede distribuir y simplificar:
\[ \int [(x^2 + 2x) \cdot ln (2x)] dx = ln (2x) \cdot \left( \frac{1}{3} \cdot x^3 + x^2 \right) - \int \left( \frac{1}{3} \cdot x^3 \cdot \frac{1}{x}+ x^2 \cdot \frac{1}{x} \right) \cdot dx \]
\[ = ln(2x) \cdot \left( \frac{1}{3} \cdot x^3 + x^2 \right) - \int \left( \frac{1}{3} \cdot x^2 + x \right) \cdot dx \]
Esta nueva integral es más sencilla que la original. Resolviéndola, se obtiene:
\[ \int [(x^2 + 2x) \cdot ln (2x)] dx = ln (2x) \cdot \left( \frac{1}{3} \cdot x^3 + x^2 \right) - \left( \frac{1}{3} \cdot \frac{1}{3} \cdot x^3 + \frac{1}{2} \cdot x^2 \right) + C \]
Cuando resolvemos los cálculos, se obtiene la expresión final:
\[ \int [(x^2 + 2x) \cdot ln (2x)] dx = ln (2x) \cdot \left( \frac{1}{3} \cdot x^3 + x^2 \right) - \left( \frac{1}{9} \cdot x^3 + \frac{1}{2} \cdot x^2 \right) + C \]
En esta integral no hay ningún producto. Sin embargo, se puede considerar f = ln x y dg = dx. Entonces, será:
\( df = \frac{1}{x} dx \) y \( g = \int dg = \int dx = x \)
Al reemplazar en la fórmula se obtiene:
\[ \int ln \ x \ dx = ln \ x \cdot x - \int x \cdot \frac{1}{x} \cdot dx = ln \ x \cdot x - \int dx \]
En el último paso se simplificaron las x. Y cuando resolvemos queda:
\[ \int ln \ x \ dx = ln \ x \cdot x - x + C \]
Se puede sacar factor común x para obtener una expresión más sencilla:
\[ \int ln \ x \ dx = x \cdot (ln \ x - 1) + C \]
Si se deriva esta última expresión, se puede comprobar que la integral está bien resuelta.
En los siguientes videos el profesor Julio Ríos resuelve integrales por partes.
<https://www.youtube.com/watch?v=CavjhBTYma8>
Resuelva las siguientes integrales indefinidas:
- \( int (7x + ln \ x) dx = \)
- \( \int [e^{3x+1} \cdot (3x + 1) - \sqrt{x} + 4] dx = \)
- \(int e^x \cdot x^2 dx = \)
Respuestas:
- \( \int (7x + ln \ x) dx = \frac{7}{2} x^2 + x \cdot (ln \ x - 1) + C \)
- \( \int [e^{3x+1} \cdot (3x + 1) - \sqrt{x} + 4] dx = x \cdot e^{3x+1} - \frac{2}{3} \cdot x^{3/2} + 4x + C \)
\( \int e^x \cdot x^2 dx = e^x \cdot x^2 - \int 2x \cdot e^x dx \)
En este ejercicio es necesario volver a aplicar la fórmula de la integración por partes en la segunda integral. Así, el resultado final es:
\[ \int e^x \cdot x^2 dx = e^x \cdot (x^2 - 2x + 2) + C \]
3.4. Integrales definidas y regla de Barrow
Ejercicio 7
Encuentre la fórmula de una función que permita calcular el área comprendida entre el eje x y la gráfica de la función f(x), entre x=a y x=b, representada en el siguiente gráfico:
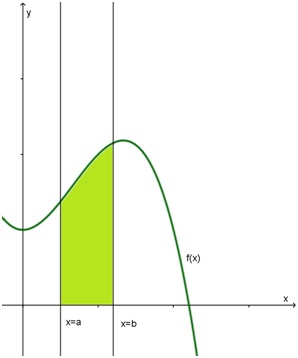
La resolución de este ejercicio, que es teórico, requiere encontrar la fórmula de una función, a la que se llamará A(x). En el siguiente video, se explica el procedimiento:
Por lo tanto, será:
\[ Área = \int^b_a f(x)dx = F(b) - F(a) \]
Este resultado, conocido como Regla de Barrow, es válido para funciones cuyas gráficas sean continuas y tomen valores positivos o nulos entre x=a y x=b.
La integral definida de una función es el resultado [un número] de la resta que aparece en el último miembro de la fórmula anterior. Es importante notar la diferencia con la integral indefinida (cuyo resultado es la fórmula de una función).
3.4.1. Área bajo una curva
Ejercicio 8
Calcule de dos maneras el área comprendida entre x=0 y x=2 y entre y=0 y la gráfica de
f(x) = 3x
En este ejercicio el área a calcular es la que aparece rosada en el siguiente gráfico:
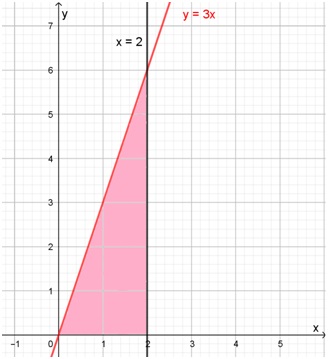
Como puede apreciarse se trata de un triángulo. Por eso, su área se puede calcular con la fórmula:
\[ \text{área del triángulo} = \frac{ \text{base x altura}}{2} \]
Su base es el segmento entre x=0 y x=2, es decir, mide 2. Su altura es el segmento vertical entre la imagen de 2 y y=0. La imagen de 2 es:
f(2) = 3 · 2 = 6
Por lo tanto, mide 6.
Y el área del triángulo resulta:
\[ \text{área del triángulo} = \frac{ \text{base x altura}}{2} = \frac{2 \cdot 6}{2} = 6 \]
El triángulo mide 6 unidades cuadradas.
Otra manera de calcular esta misma área es utilizando la Regla de Barrow:
\[ área = \int^2_0 f(x)dx = \int^2_0 3xdx = \frac{3}{2} x^2 \Big|^2_0 \]
En el último paso, se calculó la primitiva y se ubicó a continuación una barra vertical con los extremos de integración, para explicitar entre qué valores debe calcularse la integral definida. En el extremo inferior de la barra está el límite menor del área buscada. En el extremo superior, el límite mayor del área. En el próximo paso, se resuelve la resta entre ambos extremos:
\[ \frac{3}{2} x^2 \Big|^2_0 = \left( \frac{3}{2} \cdot 2^2 \right) -\left( \frac{3}{2} \cdot 0^2 \right) = 6 -0 = 6 \]
Se obtiene, por supuesto, el mismo valor del área que de la otra manera.
Ejercicio 9
Calcule el área comprendida entre x=2 y x=4 y entre el eje x y la gráfica de f(x) = x2 - 1
Para resolver este tipo de ejercicios es conveniente graficar la situación. En el siguiente diagrama, se sombreó la región cuya área hay que calcular:
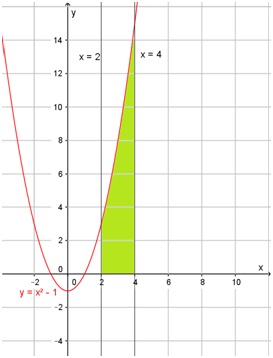
Como se trata de una función continua y toda la gráfica de f(x), entre x=2 y x=4 es positiva, se puede utilizar la Regla de Barrow para calcular el área:
\[ área = \int^4_2 f(x)dx = \int^4_2 (x^2+1)dx = \left( \frac{1}{3} x^3 + x \right) \Big|^4_2 \]
En este primer paso, se calculó la primitiva. Nuevamente, con la barra vertical del final, se expresa entre qué valores se calculará en área. Seguidamente, se reemplazan los extremos de integración en la función primitiva.
\[ área = \left( \frac{1}{3} x^3 + x \right) \Big| ^4_2 = \left( \frac{1}{3} \cdot 4^3 + 4 \right) - \left( \frac{1}{3} \cdot 2^3 + 2 \right) = \frac{64}{3} + 4 - \frac{8}{3} - 2 = \frac{62}{3} \]
NPor lo tanto, el área buscada mide 62/3 unidades cuadradas.
Es muy importante el uso de paréntesis.
Ejercicio 10
Calcule el área que se encuentra entre la gráfica de f(x) = x2 - 1 y el eje x.
Esta función es la misma que la del ejercicio anterior, pero cambian los extremos de integración. En el diagrama siguiente se sombreó la región cuya área hay que calcular:
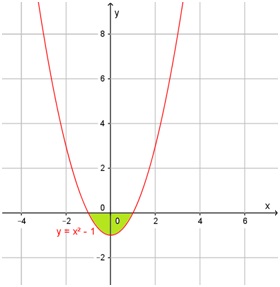
En este ejercicio hay dos problemas para solucionar. Por un lado, no se explicitan los extremos de integración. Por el otro, como la gráfica de la función toma valores negativos, será necesario realizar algunos cambios para poder utilizar la Regla de Barrow.
Se buscarán primero los extremos de integración. La región sombreada va desde uno de los puntos en los que la función interseca al eje x hasta el otro. De modo que dichos extremos son las raíces de la función. Para hallarlos, será necesario resolver la ecuación:
f(x) = 0
x2 - 1 = 0
\[ x = \sqrt[2]{1} \]
Entonces, los extremos de integración son x = -1 y x = 1.
Ahora, como el gráfico toma valores negativos, es necesario utilizar la función simétrica de f(x) respecto del eje x para el cálculo del área. En el siguiente gráfico se representaron f(x) en rojo, y su simétrica en verde. La fórmula de la función simétrica es:
\[ g(x) = -f(x) = -(x^2 - 1) = -x^2 + 1 \]
El área comprendida entre x = -1 y x = 1 entre la gráfica de f(x) y el eje es igual al área comprendida entre esos mismos extremos y la gráfica de g(x). Pero g(x) toma valores positivos en ese intervalo:
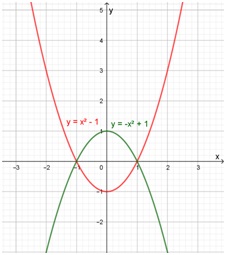
Entonces, el área buscada será:
\[ área = \int ^1_{-1} g(x)dx= \int ^1 _{-1} -(x^2 - 1) dx = \left[ - \left( \frac{1}{3} x^3 - x \right) \right] \Big| ^1 _{-1} \]
Solo restan resolver los cálculos:
\[ área = \left[ - \left( \frac{1}{3} x^3 - x \right) \right] \Big| ^1 _{-1} = \left[ - \left( \frac{1}{3} \cdot 1^3 - 1 \right) \right] - \left[ - \left( \frac{1}{3} \cdot (-1)^3 - (-1) \right) \right] \]
\[ área = \left[ - \left( - \frac{2}{3} \right) - \left( - \frac{2}{3} \right) \right] = \frac{4}{3} \]
Finalmente, el área buscada mide 4/3 de unidades cuadradas.
Es de destacar que es muy importante el uso de paréntesis en estos cálculos.
En los siguientes videos el profesor Julio Ríos resuelve integrales definidas.
<https://www.youtube.com/watch?v=jnXgBtY8Jac>
Encuentre el área comprendida entre:
- \( f(x) = -x^2 + 9x - 18 \) y el eje x.
- \( g(x) = \frac{12}{x+3} \) y entre x=3 y x=9.
Respuestas:
- Extremos de integración x=3 y x=6. Área=9/2 de unidades cuadradas.
- Área=8,318 unidades cuadradas.
3.4.2. Área entre curvas
Ejercicio 11
Calcule el área comprendida entre f(x) = x + 3 y g(x) = -x2 + 8x - 7
Para resolver este ejercicio es conveniente realizar un esquema de la situación. En el siguiente gráfico, se representaron ambas funciones y se sombreó el área que hay que calcular:
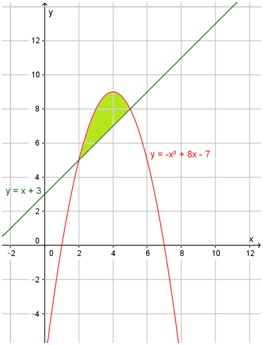
Como esta región sombreada no llega hasta el eje x, no se puede utilizar directamente la Regla de Barrow.
Pero el área sombreada se puede calcular como la resta entre las áreas de las siguientes regiones:
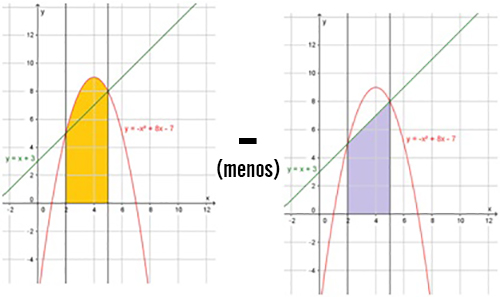
Es decir:
\[ \text{Área buscada} = \text{área naranja} - \text{área lila} = \int ^b_a g (x) dx - \int ^b _a f(x)dx \]
En esta fórmula a y b son las abscisas de los puntos de intersección entre las dos funciones.
Al aplicar las propiedades de las integrales, también se puede calcular como:
\[ \int ^b_a g (x) dx - \int ^b _a f(x)dx = \int^b_a [g(x) - f(x)] dx \]
Por lo tanto, el área entre dos curvas se puede calcular como la integral definida entre las abscisas de los puntos de intersección de dichas curvas, de la diferencia entre la función que limita por arriba y la que limita por abajo a la región entre ambas.
En el presente ejercicio falta encontrar las abscisas de los puntos de intersección. En esos puntos, es:
f(x) = g(x)
x + 3 = -x2 + 8x - 7
x + 3 + x2 - 8x + 7 = 0
x2 - 7x + 10 = 0
Resolviendo esta ecuación de segundo grado, se obtienen los dos resultados:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{7 \pm \sqrt{7^2 - 4 \cdot 1 \cdot 10}}{2 \cdot 1} \]
\[ x = 2 \ o \ x = 5 \]
Por lo tanto, las funciones se intersectan en los puntos de abscisas x=2 y x=5. Dichos puntos son: (2; 5) y (5; 8).
El área comprendida entre las funciones serán entonces:
\[ Área = \int ^5_2 [(-x^2 + 8x - 7)-(x+3)]dx = \int ^5_2 (-x^2 + 8x - 7 - x - 3) dx = \]
\[ = \int^5_2 (-x^2 + 7x - 10) dx = \left( - \frac{1}{3} x^3 + \frac{7}{2} x^2 - 10x \right) \Big| ^5_2 = \]
\[ = \left( - \frac{1}{3} \cdot 5^3 + \frac{7}{2} \cdot 5^2 - 10 \cdot 5 \right) - \left( \frac{1}{3} \cdot 2^3 + \frac{7}{2} \cdot 2^2 - 10 \cdot 2 \right) = \]
\[ = - \frac{25}{6} - \left( - \frac{26}{3} \right) = \frac{9}{2} \]
En este ejercicio se sabía que el borde superior de la región estaba formado por la función g(x) porque se había realizado el gráfico. Si no se dispone de la representación, para encontrar cuál de los gráficos de las dos funciones forma el borde superior, se elige una abscisa comprendida entre los dos extremos de integración. Por ejemplo, en este caso, podría ser x=3. Este valor se reemplaza en cada una de las dos funciones:
f(3) = x + 3 = 3 + 3 = 6
g(3) = -x2 + 8x - 7 = -32 + 8 · 3 - 7 = 8
Como g(3) > f(3), el borde superior de la zona cuya área hay que calcular es la función g(x).
Ejercicio 12
Calcule el área comprendida entre las funciones f(x) = -x + 8 y \( g(x) = \frac{24}{x+3} \)
Si bien es conveniente confeccionar un diagrama de la situación, aquí se resolverá directamente, para mostrar que también es posible resolver el ejercicio sin diagrama.
Como se trata de una región entre dos curvas, primero se buscan las abscisas de los puntos de intersección entre ambas funciones:
f(x) = g(x)
-x + 8 = \( \frac{24}{x+3} \)
(-x + 8) · (x + 3) = 24
-x2 + 8x - 3x + 24 = 24
-x2 + 5x = 0
x=0 o x=5
Por lo tanto, los extremos de integración serán x=0 y x=5.
Para hallar la función que forma el borde superior, se elige una abscisa intermedia a estos valores, por ejemplo, x=1 y se halla su imagen por cada una de las funciones:
f(1) = -1 + 8 = 7
\[ g(1) = \frac{24}{1+3} = 6 \]
Como f(1) > g(1), f(x) forma el borde superior. Por lo tanto, el área buscada es:
\[ Área = \int ^5_0 [f(x)- g(x)]dx = \int ^5_0 \left[ (-x + 8) - \left( \frac{24}{x+3} \right) \right] dx = \]
\[ = \int ^5_0 - x \ dx + \int ^5_0 8dx - \int^5_0 \frac{24}{x+3} dx \](1)
Para calcular la primitiva del tercer término, se utilizará la siguiente sustitución:
u = x + 3
\( u´= \frac{du}{dx} = 1 \) por lo tanto, du = dx
Entonces es:
\[ \int \frac{24}{x+3}dx = \int \frac{24}{x+3}du = 24 \cdot \int \frac{1}{u}du = 24 \cdot ln|u| + C = 24 \cdot ln|x+3| + C \]
Al reemplazar este resultado en (1) y calcular el resto de las primitivas queda:
\[ \int^5_0 -x \ dx + \int^5_0 8 dx - \int^5_0 \frac{24}{x+3} dx = \left( - \frac{1}{2} x^2 \right) \Big|^5_0 + 8x |^5_0 - 24 \cdot ln|x+3| |^5_0 \]
\[ = \left( - \frac{1}{2} \cdot 5^2 \right) - \left( - \frac{1}{2} \cdot 0^2 \right) + 8 \cdot 5 - 8 \cdot 0 - [24 \cdot ln|5+3| - (24 \cdot ln|0+3|)] = \]
\[ = - \frac{25}{2} - 0 + 40 - 0 - (24 \cdot ln \ 8 - 24 \cdot ln \ 3) \cong \frac{55}{2} - 23,54 = 3,96 \]
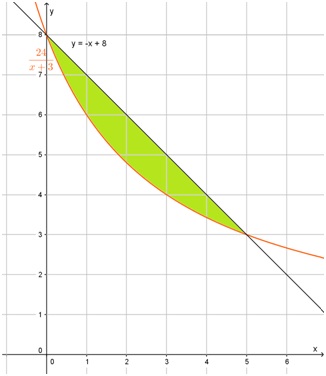
Por lo tanto, el área encerrada entre ambas funciones es de aproximadamente 3,96 unidades cuadradas.
En el siguiente gráfico se aprecia la situación y se confirman los resultados obtenidos analíticamente:
Ejercicio 13
Encuentre el área de la región comprendida entre el eje y, la recta y=2 y la función \( f(x) = \sqrt{x+1} - 1 \)
En el siguiente gráfico, se representó la situación y se sombreó la región cuya área hay que calcular:
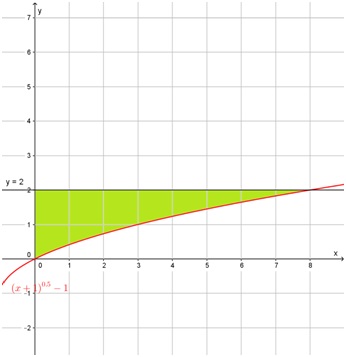
Esta región se puede considerar como comprendida entre la recta y=2 y la función f(x), entre x=0 y el punto de intersección entre las dos primeras funciones. La abscisa de ese punto se obtiene resolviendo la siguiente ecuación:
\[ 2 = \sqrt{x+1} - 1 \]
\[ 2 + 1 = \sqrt{x+1} \]
32 = x + 1
9 - 1 = x
x = 8
Por lo tanto, el área es:
\[ \int^8_0 [2 - (\sqrt{x+1} - 1)] dx = \int^8_0 (2 - (\sqrt{x+1} + 1) dx = \int^8_0 (3 - \sqrt{x+1}) dx = \]
\[ \int^8_0 3 dx - \int^8_0 \sqrt{x+1} dx \](1)
Para hallar la segunda primitiva, se realizará la siguiente sustitución:
u = x + 1
Así, \( u´= \frac{du}{dx} = 1 \)entonces du = dx
De este modo:
\[ \int \sqrt{x+1} dx = \int \sqrt{u} \ du = \int u^{1/2}du = \frac{1}{3/2} u ^{3/2} + C = \frac{2}{3} \cdot (x+1)^{3/2} + C \]
Cuando reemplazamos este resultado en (1) y resolvemos el primer término se tiene:
\[ Área = 3x |^8_0 - \left[ \frac{2}{3} \cdot (x+1)^{3/2} \right] \Big|^8_0 = \]
\[ = 3 \cdot 8 - 3 \cdot 0 - \left\lbrace \left[ \frac{2}{3} \cdot (8+1)^{3/2} \right] - \left[ \frac{2}{3} \cdot (0+1)^{3/2} \right] \right\rbrace = \]
\[ = 24 - 0 - \left( 18 - \frac{2}{3} \right) = \frac{20}{3} \]
Por lo tanto, el área buscada mide 20/3 de unidades cuadradas.
En el siguiente video <https://www.youtube.com/watch?v=0hs3v3lilT8> el profesor Julio Ríos calcula áreas entre curvas.
Encuentre el área entre:
- f(x) = -2 · x2 + 10 y g(x) = -x2 - 2 · x +2
- f(x) = -x2 + 7 y g(x) = x3 - 12x + 7
Respuestas:
- \( Área = \int^4_{-2} [f(x) - g(x)] dx = 36 \)
- La situación es la que se indica en el gráfico.
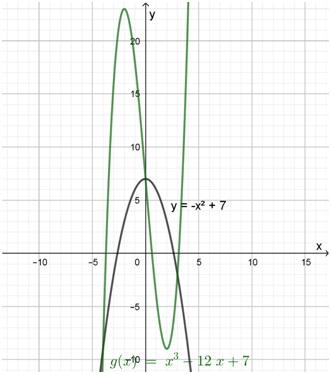
Como se puede apreciar, hay tres puntos de intersección entre las dos funciones, los que generan dos regiones. Sus áreas se calculan por separado:
\[ área = \int^0_{-4} [g(x) - f(x)] dx + \int^3_0 [f(x) - g(x)] dx = \]
\[ área = \left[ 0 - \left( - \frac{160}{3} \right) \right] + \left( \frac{99}{4} - 0 \right) = \frac{937}{12} \]
3.4.3. Aplicaciones económicas
Ejercicio 14
En el mercado de un cierto bien, las funciones de oferta y demanda vienen dadas por:
\[ D:q = \frac{90}{p} - 2 \]
\[ O:q = p - 1 \]
Se pide que encuentre el excedente del consumidor de este mercado.
En el siguiente video, se presenta el tema de Excedente del consumidor y se resuelve este ejercicio de aplicación económica.
Ejercicio 15
En el mercado de un cierto bien, las funciones de oferta y demanda vienen dadas por:
\[ D:p = - \frac{1}{2} \cdot q + 120 \]
\[ 0:p = - \frac{33000}{5q - 400} \]
Se pide que:
- Determine el precio y la cantidad de equilibrio.
- Calcule los excedentes del consumidor y del productor.
- Explique y calcule qué sucederá con el excedente del productor y del consumidor si este mercado se abre al comercio internacional, sabiendo que el precio más los impuestos será de $100.
Para hallar el precio y la cantidad de equilibrio, es necesario determinar el punto en el que las curvas de oferta y demanda se intersecan.
Analíticamente esto se hace igualándolas:
\[ D = 0 \]
\[ - \frac{1}{2} \cdot q + 120 = - \frac{33000}{5q - 400} \]
\[ \left( - \frac{1}{2} \cdot q + 120 \right) \cdot (5q - 400) = -33000 \]
\[ - \frac{5}{2} \cdot q^2 + 200 \cdot q + 600 \cdot q - 48000 + 33000 = 0 \]
\[ - \frac{5}{2} \cdot q^2 + 800 \cdot q - 15000 = 0 \]
Las dos soluciones para esta ecuación son q = 20 y q =300.
Para hallar el precio de equilibrio, se reemplazan estos valores en las funciones de oferta y demanda:
\[ D_{(20)}:p = - \frac{1}{2} \cdot 20 + 120 = 110 \] \[ 0_{(20)}:p = - \frac{33000}{5 \cdot 20 - 400} = 110 \]
\([ D_{(300)}:p = - \frac{1}{2} \cdot 300 + 120 = -30 \] \[ 0_{(20)}:p = - \frac{33000}{5 \cdot 300 - 400} = -30 \]
Como no tiene sentido económico un precio de -30, el punto de equilibrio de mercado es cuando se ofrecen y demandan 20 unidades al precio de 110.
En la página 71 de la cuarta edición del libro Economía: principios y aplicaciones, de Francisco Mochón y Víctor Alberto Beker (Buenos Aires: Mc Graw Hill Interamericana, 2008), se define al excedente del consumidor de la siguiente manera: “El excedente del consumidor, con relación a un bien determinado, es la diferencia entre la cantidad máxima que estaría dispuesto a pagar por el número de unidades que demanda de ese bien y la cantidad que realmente paga en el mercado.”
Gráficamente, corresponde al área entre la curva de demanda y el precio de mercado de dicho bien.
En la página 126 de esa misma obra, se define excedente del productor: “El excedente del productor (...) puede definirse como la cantidad que los productores reciben por un bien, menos lo que les cuesta producirlo. En términos gráficos, está representado por el área total situada debajo del precio y encima de la curva de oferta”.
La situación de este problema se puede representar gráficamente de la siguiente manera:
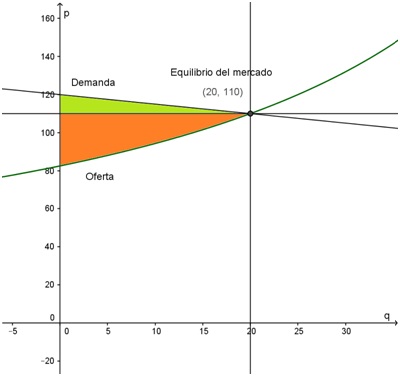
En este gráfico se sombreó en verde la zona que corresponde al excedente del consumidor y en color naranja la que representa el excedente del productor.
Se comenzará calculando el excedente del consumidor. Esa región tiene como límite superior a la función de demanda y como límite inferior a la recta correspondiente al precio de equilibrio p = 110. Los extremos de integración son q = 0 y la cantidad de equilibrio: q = 20. La variable es la cantidad q:
Excedente del consumidor \( = \int^{Qe}_0 [D_{(q)}- p_e]dq \)
Excedente del consumidor \( = \int^{20}_0 \left[ \left( - \frac{1}{2} q + 120 \right) - 110 \right] dq = \)
\[ = \int^{20}_0 \left( - \frac{1}{2} q + 10 \right) dq = \left( - \frac{1}{4} q^2 + 10q \right) \Big|^{20}_0 = \]
\[ = \left( - \frac{1}{4} \cdot 20^2 + 10 \cdot 20 \right) - \left( - \frac{1}{4} \cdot 0^2 + 10 \cdot 0 \right) = -100 + 200 - 0 = 100 \]
De modo que el excedente del consumidor es de 100 pesos por unidad.
Se calculará ahora el excedente del productor. En el gráfico es la zona pintada en color naranja, cuyo borde superior es el precio de equilibrio p = 110 y el borde inferior es la función de oferta. Los extremos de integración son los mismos que en el excedente del consumidor: q = 0 y la cantidad de equilibrio q = 20:
Excedente del productor \( = \int^{Qe}_0[p_e - 0_{(q)}] dq \)
Excedente del productor \( = \int^{20}_0 \left[ 110 - \left( - \frac{33000}{5q-400} \right) \right] dq = \)
\( = \int^{20}_0 \left( 110 + \frac{33000}{5q-400} \right) dq = \int^{20}_0 110 dq + \int^{20}_0 \frac{33000}{5q-400} dq \)(1)
Para resolver la segunda integral, se llamará u = 5q - 400 por lo que:
\[ u`= \frac{du}{dq} = 5 \to du = 5 dq \to \frac{du}{5} = dq \]
Al sustitur en la segunda integral es:
\[ \int \frac{33000}{5q - 400} dq = \int \frac{33000}{u} \frac{du}{5} = \int \frac{6600}{u} du = 6600 \int \frac{1}{u} du = \]
\[ =6600 \cdot ln|u| + C = 6600 \cdot ln|5q - 400| + C \]
Reemplazando este resultado en (1) y resolviendo la primera integral es:
Excedente del productor \( = [110 \cdot q + 6600 \cdot ln|5 \cdot q -400|] |^{20}_0 = \)
\( = [110 \cdot 20 + 6600 \cdot ln|5 \cdot 20 - 400| ] - [110 \cdot 0 + 6600 \cdot ln|5 \cdot 0 - 400| ] = \)
\( =(2200 + 6600 \cdot ln |-300|) - (0 + 6600 \cdot ln|-400|) \cong \)
\( \cong 39844,96 - 39543,67 = 301,29 \)
Por lo tanto, el excedente del productor es de $301,29 por unidad.
-
Si el mercado se abre al comercio internacional –como el precio más los impuestos es menor al precio de equilibrio del mercado local– se importarán algunas unidades de este producto.
La cantidad ofrecida por los productores locales vendrá dada por:
\[ 0_{(q)} : 100 = - \frac{33000}{5q-400} \]
\[ 100 \cdot (5q-400) = -33000 \]
\[ 5q - 400 = - \frac{33000}{100} = -330 \]
\[ 5q = -330 + 400 = 70 \]
\[ q = \frac{70}{5} = 14 \]
Por lo tanto, ante la apertura al comercio internacional, la producción local descenderá de 20 a 14 unidades.
Y las cantidades demandadas, como el precio es inferior, serán más. Se puede calcular según:
\[ D_{(q)}:100 = - \frac{1}{2} \cdot q + 120 \]
\[ 100 - 120 = -20 = - \frac{1}{2} \cdot q \]
\[ -20 \cdot \left( - \frac{2}{1} \right) = 40 = q \]
Es decir, se demandarán 40 unidades, 20 más que en la situación anterior. De ellas, 26 son importadas.
Gráficamente, puede observarse cómo, en la nueva situación, aumentó el excedente del consumidor y disminuyó el del productor:
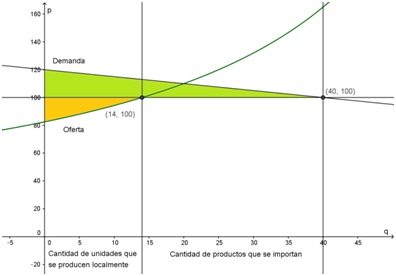
Para calcular los nuevos valores de los excedentes del productor y del consumidor, se pueden utilizar las primitivas encontradas en b), modificando el precio y los extremos de integración. Es importante notar que los extremos de integración son distintos en cada excedente:
Excedente del consumidor: = \( \int^{40}_0 \left[ \left( - \frac{1}{2} q + 120 \right) - 100 \right] dq = \)
\( = \left( - \frac{1}{4} \cdot 40^2 + 20 \cdot 40 \right) - \left( - \frac{1}{4} \cdot 0^2 + 20 \cdot 0 \right) = -400 + 800 - 0 = 400 \)
Excedente del productor = \( \int ^{14}_0 [100 - 0_{(q)}] dq = \)
\( = [100 \cdot 14 + 6600 \cdot ln|5 \cdot 14 - 400|] - [100 \cdot 0 + 6600 \cdot ln|5 \cdot 0 - 400|] \cong \)
\( = 1400 + 38274,01 - 39543,671 = 130,34 \)
Entonces, en esta nueva situación el excedente del consumidor es de $400 por unidad y el del productor de $130,34 por unidad. Como puede apreciarse, el excedente del consumidor aumentó más de lo que disminuyó el del productor.
Este tipo de resultados es el que se utiliza para justificar la conveniencia de “abrir los mercados”. Sin embargo, es importante notar que este análisis no tiene en cuenta cuáles pueden ser las repercusiones de una caída en la producción local. En este ejercicio se puede ver que, ante la apertura comercial, disminuye la cantidad de bienes que se producen localmente. Esto implicaría que haya cierre de empresas o despidos de personal, lo que llevaría a una modificación de la función de demanda. Como ninguna persona puede demandar si no tiene ingresos, se debe tener cuidado al generalizar conclusiones.
En los siguientes videos se explican los conceptos de excedente del productor y del consumidor.
<https://www.youtube.com/watch?v=vodtfrc-Gk4>
Ejercicio 16
En un cierto mercado, las funciones de oferta y demanda vienen dadas por:
\[ D:q = \frac{77}{p} - 3 \]
\[ 0:q = \frac{p-3}{2} \]
Se pide que:
- determine el precio y la cantidad de equilibrio.
- calcule el excedente del consumidor.
- grafique la situación
- Explique qué sucederá con los excedentes del productor y del consumidor si este mercado se abre al comercio internacional, sabiendo que el precio más los impuestos será de $15.
Para encontrar el punto de equilibrio de este mercado, se igualan ambas funciones:
\[ D = 0 \]
\[ q = \frac{77}{p} - 3 = \frac{p-3}{2} \]
\[ \left( \frac{77}{p}-3 \right) \cdot 2 = p - 3 \]
En este paso son muy importantes los paréntesis. Ahora se distribuye el producto:
\[ \frac{77}{p} \cdot 2 - 3 \cdot 2 = p-3 \]
\[ \frac{154}{p} - 6 = p-3 \]
\[ \frac{154}{p} = p-3+6 \]
\[ \frac{154}{p} = p+3 \]
Aquí, se multiplica por p, otra vez, con paréntesis:
154 = (p + 3) · p
Cuando se distribuye y ordena queda:
154 = p2 + 3p
0 = p2 + 3p - 154
Esta ecuación es de segundo grado. Para resolverla, se utiliza, por ejemplo, la fórmula de la resolvente:
\[ a = 1 \ \ \ b= 3 \ \ \ c=-154 \]
\[ p= \frac{-3 \pm \sqrt{3^2 - 4 \cdot 1 \cdot (-154)}}{2 \cdot 1} \]
Los dos resultados posibles son: p = -14 que no tiene sentido económico y por eso se descarta, y p = 11
Si el precio de equilibrio es $11, la cantidad de equilibrio se puede obtener en cualquiera de las dos funciones:
\[ D:q = \frac{77}{11} - 3 = 7 - 3 = 4 \]
La cantidad de equilibrio es: 4 unidades.
Como ya se vio en ejercicios anteriores, el excedente del consumidor se calcula mediante la siguiente fórmula:
\[ EC = \int^{QE}_0 (D-PE) dq \]
En este ejercicio, es necesario despejar p en la])
\[ q+3 = \frac{77}{p} \]
\[ (q+3) \cdot p = 77 \]
\[ p = \frac{77}{q+3} \]
Entonces, reemplazando los datos en la fórmula del excedente del consumidor es:
\[ EC = \int^4_0 \left( \frac{77}{q+3}-11 \right) dq \]
Para resolver esta integral definida, se separa en términos y en el primero se utiliza la siguiente sustitución: t = q + 3 por lo tanto dt = dq
\[ EC = \int^4_0 \left( \frac{77}{q+3}-11 \right) dq = \int^4_0 \left( \frac{77}{q+3} \right) dq - \int^4_0 11 \cdot dq = \]
\[ \int^4_0 \frac{77}{t} dt - 11 \cdot q|^4_0 = 77 \cdot \int ^4_0 \frac{1}{t} dt - (11 \cdot 4 - 11 \cdot 0) = \]
En el segundo término ya se resolvió la integral y falta hacer las cuentas. En el primero, resta integrar:
\[ 77 \cdot ln(t) |^4_0 - (44-0) = 77 \cdot ln(q+3) |^4_0 - 44 = \]
\[ =77 \cdot (ln7 - ln3) - 44 = \]
Para resolver este último cálculo se utiliza una calculadora científica que tenga logaritmos naturales:
= 77 · (1,9459 - 1,0986) - 44 = 21,2421
Por lo tanto, el excedente del consumidor es de $21,24 por unidad.
Como los gráficos de oferta y demanda tienen en el eje vertical a los precios, es necesario despejar p en ambas funciones. Ya se realizó en el caso de la demanda. Para la oferta es:
\[ O:q = \frac{p-3}{2} \]
\[ q \cdot 2 = p - 3 \]
\[ 2 \cdot q + 3 = p \]
Entonces, las funciones que se grafican son:
\[ D:p = \frac{77}{q+3} \]
\[ O:p = 2 \cdot q + 3 \]
En el siguiente gráfico, se representó a la oferta en color rojo y a la demanda en color verde. También se graficó el precio de equilibrio. En color celeste se pintó la región correspondiente al excedente del consumidor y en rosa el excedente del productor:
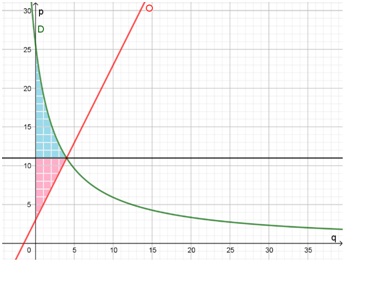
Si en el mercado internacional el precio de equilibrio más los impuestos es de $15, la situación sería la siguiente:
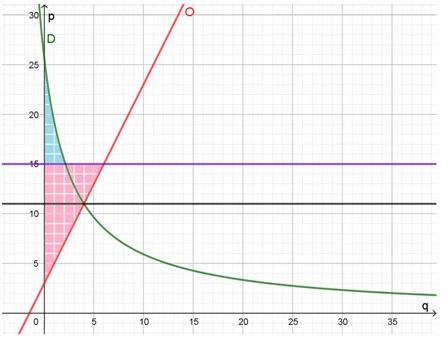
En el gráfico se puede apreciar cuánto disminuyó el excedente del consumidor y cuánto aumentó el del productor.
Para realizar este mismo análisis algebráicamente, es necesario calcular las nuevas cantidades demandadas y ofrecidas en el mercado interno.
Para la demanda es:
\[ q = \frac{77}{p} - 3 = \frac{77}{15} - 3 = 2,13 \ unidades \]
Para la oferta:
\[ q = \frac{p-3}{2} = \frac{15-3}{2} = 6 \ unidades \]/span>
La diferencia entre estos dos valores serán exportaciones.
El nuevo excedente del consumidor se calcula ahora:
\[ EC= \int ^{2,13}_0 \left( \frac{77}{q+3} - 15 \right) dq = \int^{2,13}_0 \left( \frac{77}{q+3} \right) dq - \int^{2,13}_0 15 \cdot dq = \]
\[ \int ^{2,13}_0 \frac{77}{t} dt - 15 \cdot q|^{2,13}_0 = 77 \cdot \int ^{2,13}_0 \frac{1}{t} dt - (15 \cdot 2,13 - 11 \cdot 0) = \]
\[ 77 \cdot ln(t)|^{2,13}_0 -(32-0) = 77 \cdot ln(q+3)|^{2,13}_0 - 32 = \]
\[ 77 \cdot (ln \ 5,13 - ln \ 3) - 32 = \]
Nuevamente se utiliza una calculadora científica que tenga logaritmos naturales:
= 77 · (1,6351 - 1,0986) - 32 = 9,3099
Como puede verse, el excedente del consumidor es mucho menos que en la situación a). Ahora es de $9,31 por unidad.
El excedente del productor será:
\[ EP = \int^6_0 [15 - 0_{(q)}] dq = \int^6_0 [15 - (2q+3)] dq = \]
\[ \int^6_0 [15 - 2q - 3)] dq == \int^6_0 (12-2q) dq = 12q -q^2 |^6_0 = \]
\[ = 12 \cdot 6 - 6^2 -(12 \cdot 0 -0^2) = 36 \]
Por lo tanto, el excedente del productor será de $36 por unidad.
En esta situación se podría pensar que se beneficia a la actividad del país, ya que se producen localmente 2 unidades más que sin comercio internacional. Sin embargo, sería necesario profundizar el análisis porque cae mucho el consumo interno. Si este mercado fuera de alimentos, ¿en qué situación queda la población?
El análisis matemático facilita el estudio de estas situaciones, pero no pueden sacarse conclusiones solo basadas en la matemática. La Economía no debe dejar de ser una Ciencia Social, aunque utilice herramientas matemáticas.
En cierto mercado, las funciones de oferta y de demanda vienen dadas por:
\[ O:p = \frac{5000}{q-500} \]
\[ D:p = 100 - \frac{1}{8} q \]
Se pide que:
- determine el precio y la cantidad de equilibrio,
- calcule el excedente del consumidor,
- grafique la situación y
- sin hacer cálculos, explique qué sucederá con el excedente del productor y del consumidor si este mercado se abre al comercio internacional, sabiendo que el precio más los impuestos será de $55.
Respuestas:
- Precio de equilibrio: $50, cantidad de equilibrio: 400 unidades. Hay otro punto de intersección de las funciones, pero corresponde a un precio negativo.
- El excedente del consumidor es de ·$30.000 por unidad.
Aquí se indcicó en rojo la oferta, en verde la demanda y se representó la recta del precio de equilibrio. También se puede ver el otro punto de intersección entre las funciones, que no se considera en este ejercicio porque no tiene sentido económico.
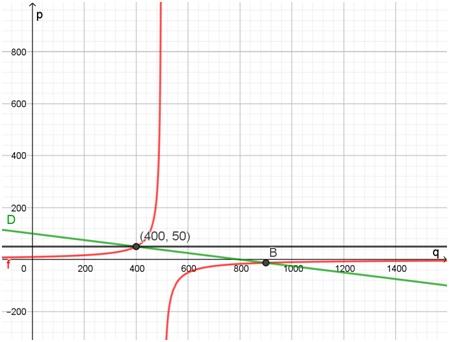
- Si el precio internacional fuera de $55, ganarían los productores de esta mercadería y perderían los consumidores. Se producirá más y se exportará, pero caerá el consumo interno.

