4. Sistemas lineales
Objetivos
- Reconocer y operar con matrices.
- Resolver sistemas de ecuaciones lineales, utilizando métodos matriciales.
- Resolver problemas de administración, utilizando sistemas de ecuaciones lineales.
4.1. Matrices
Ejercicio 1
Una empresa vende tres clases de televisores en cuatro locales. En la siguiente tabla, se indica la cantidad de televisores de cada clase que hay en cada sucursal:
|
|
TV clase 1 |
TV clase 2 |
TV clase 3 |
|
Local Sur |
2 |
5 |
4 |
|
Local Norte |
6 |
1 |
5 |
|
Local Este |
0 |
4 |
4 |
|
Local Oeste |
7 |
2 |
5 |
Con base en esta información, se pide que:
- Confeccione una matriz A con los datos, ubicando en las columnas los locales y en las filas las clases de televisor.
- Identifique e interprete el valor que se encuentra en las siguientes casillas: a21, a34, a13 y a22 .
- Interprete los números de la tercera columna.
- Responda: ¿en qué posición quedaron los datos correspondientes a los televisores clase 3 de la sucursal Este?
- Responda: ¿dónde se encuentran los datos sobre los televisores de clase 2?
Resolución
- Si se deben ubicar los datos correspondientes a los locales en columnas, es necesario reacomodar la tabla:
La casilla a21 es la casilla ubicada en la segunda fila, primera columna. En esa posición está la cifra 5, que indica que hay 5 televisores clase 2 en el local Sur.
En la posición a34 (tercera fila, cuarta columna) también hay un 5. Pero este significa que hay 5 televisores clase 3 en la sucursal Oeste.
En la posición a13 (primera fila, tercera columna) hay un 0; lo que indica que no hay televisores clase 1 en la sucursal Este.
En la posición a22 (segunda fila, segunda columna) hay un 1; significa que hay 1 televisor clase 2 en la sucursal Norte.
- Los datos de la tercera columna indican cuántos televisores de cada clase quedan en la sucursal Este.
- Los datos de los televisores de la clase 3 están en la tercera fila. Los de la sucursal Este, en la tercera columna. Entonces, la cantidad de televisores de clase 3 de la sucursal Este se encuentran en la posición a33. Son 4 televisores.
- Los datos de los televisores de clase 2 están en la segunda fila.
|
|
Local Sur |
Local Norte |
Local Este |
Local Oeste |
|
TV clase 1 |
2 |
6 |
0 |
7 |
|
TV clase 2 |
5 |
1 |
4 |
2 |
|
TV clase 3 |
4 |
5 |
4 |
5 |
Entonces, la matriz correspondiente es:
\[ 4 = \left( \begin{array}{cccc} 2 & 6 & 0 & 7\\ 5 & 1 & 4 & 2\\ 4 & 5 & 4 & 5\\ \end{array} \right) \]
4.1.1. Operaciones con matrices
Ejercicio 2
La empresa del ejercicio anterior reparte un cargamento de nuevos televisores entre sus locales según la siguiente matriz (que respeta el orden de la que se armó en el ejercicio 1):
\[ B = \left( \begin{array}{cccc} 1 & 0 & 9 & 0\\ 4 & 4 & 4 & 6\\ 2 & 1 & 3 & 3\\ \end{array} \right) \]
Se pide que:
- Encuentre la nueva matriz de distribución de televisores, después del reparto.
- Indique en qué sucursal hay más televisores clase 3 y de qué tipo son los televisores que más abundan en la sucursal Sur.
Resolución
Para realizar este ejercicio, es necesario hacer la suma de las matrices:
\[ A + B = \left( \begin{array}{cccc} 2 & 6 & 0 & 7\\ 5 & 1 & 4 & 2\\ 4 & 5 & 4 & 5\\ \end{array} \right) + \left( \begin{array}{cccc} 1 & 0 & 9 & 0\\ 4 & 4 & 4 & 6\\ 2 & 1 & 3 & 3\\ \end{array} \right) \]
El resultado de esta suma es otra matriz de 3 filas por 4 columnas, cuyos elementos se obtienen al sumar en cada posición:
\[ A + B = \left( \begin{array}{cccc} 2+1 & 6+0 & 0+9 & 7+0\\ 5+4 & 1+4 & 4+4 & 2+6\\ 4+2 & 5+1 & 4+3 & 5+3\\ \end{array} \right) \]
\[ A + B = \left( \begin{array}{cccc} 3 & 6 & 9 & 7\\ 9 & 5 & 8 & 8\\ 6 & 6 & 7 & 8\\ \end{array} \right) \]
Los televisores de clase 3 se encuentran en la tercera fila. En ella, la cifra más alta es 8 y se encuentra en la cuarta columna, que corresponde al local Oeste. Por lo tanto, es en el local Oeste en el que más cantidad de televisores de Clase 3 hay.
Los datos correspondientes a la sucursal Sur están en la primera columna. En ella, la cifra más alta es 9, y ocupa la segunda fila. Por lo tanto, en la sucursal Sur hay más televisores clase 2: 9 en total.
Ejercicio 3
Un mes después de la situación del ejercicio 2, las personas a cargo de los locales informaron a la casa central cuántos televisores de cada clase se vendieron. Con esa información, se armó la siguiente matriz (que respeta el orden que se viene utilizando):
\[ C = \left( \begin{array}{cccc} 3 & 5 & 6 & 7\\ 8 & 5 & 7 & 5\\ 2 & 5 & 7 & 8\\ \end{array} \right) \]
Confeccione una nueva matriz con la cantidad de televisores que quedan en cada sucursal al final de ese mes.
En este caso, a la matriz suma del ejercicio 2, se le debe restar la matriz C:
\[ A + B - C = \left( \begin{array}{cccc} 3 & 6 & 9 & 7\\ 9 & 5 & 8 & 8\\ 6 & 6 & 7 & 8\\ \end{array} \right) - \left( \begin{array}{cccc} 3 & 5 & 6 & 7\\ 8 & 5 & 7 & 5\\ 2 & 5 & 7 & 8\\ \end{array} \right) \]
\[ A + B - C = \left( \begin{array}{cccc} 0 & 1 & 3 & 0\\ 1 & 0 & 1 & 3\\ 4 & 1 & 0 & 0\\ \end{array} \right) \]
Ejercicio 4
El precio de los televisores de Clase 1 es de U$S 220, el de los de Clase 2 es de U$S 340 y el de los de Clase 3 es de U$S 400. Con estos datos, se pide que se calcule el ingreso de esta empresa por la venta de los televisores desglosado por local, según los datos del ejercicio anterior.
Los datos de las ventas están dados por la matriz \( C = \left( \begin{array}{cccc} 3 & 5 & 6 & 7\\ 8 & 5 & 7 & 5\\ 2 & 5 & 7 & 8\\ \end{array} \right) \). Para calcular el ingreso total se puede multiplicar esta matriz por la de precios de venta, ordenándolos adecuadamente.
En <https://www.vitutor.com/algebra/matrices/producto.html> se puede consultar cómo se define la multiplicación de matrices y sus propiedades.
Para multiplicar matrices, el número de columnas de la primera matriz debe coincidir con el número de filas de la segunda. Por eso, los precios se ordenarán de la siguiente manera:
P = (220 340 400)
De este modo, se puede multiplicar la matriz P, de 1 fila por 3 columnas, con la matriz C de 3 filas por 4 columnas. El resultado será una matriz, a la que se le llamará I, de 1 fila por 4 columnas.
Para realizar este cálculo, se propone la siguiente disposición:
|
\[ P \ x \ C \] |
\[ \left( \begin{array}{cccc} 3 & 5 & 6 & 7\\ 8 & 5 & 7 & 5\\ 2 & 5 & 7 & 8\\ \end{array} \right) \] |
|
\[ (220 \ \ 340 \ \ 400) \] |
\[ (i_{11} \ \ i_{12} \ \ i_{13} \ \ i_{14}) \] |
Según la definición de la matriz producto, el elemento i11 se calcula de acuerdo con la siguiente fórmula:
\[ i_{11} = \sum^3_{j=1} P_{1j} \cdot C_{j1} = P_{11} \cdot C_{11} + P_{12} \cdot C_{21} + P_{13} \cdot c_{31} \]
Con la disposición propuesta, ese cálculo queda “alineado” en el cruce de la fila 1 de la matriz P y la columna 1 de la matriz C:
|
\[ P \ x \ C \] |
\[ \left( \begin{array}{cccc} \bbox[#BABABA]{3} & 5 & 6 & 7\\ \bbox[#BABABA]{8} & 5 & 7 & 5\\ \bbox[#BABABA]{2} & 5 & 7 & 8\\ \end{array} \right) \] |
|
\[ ( \bbox[#BABABA]{220} \ \ \bbox[#BABABA]{340} \ \ \bbox[#BABABA]{400} ) \] |
\[ ( \bbox[#BABABA]{i_{11}} \ \ i_{12} \ \ i_{13} \ \ i_{14}) \] |
Resolviendo estos cálculos se obtiene el elemento
i11 = 220 · 3 + 340 · 8 + 400 · 2 = 4180
Este valor corresponde al ingreso obtenido en el Local Sur.
Para encontrar el valor del elemento i12 se “cruzan” la fila 1 de la matriz P con la columna 2 de la matriz C:
|
\[ P \ x \ C \] |
\[ \left( \begin{array}{cccc} 3 & \bbox[#BABABA]{5} & 6 & 7\\ 8 & \bbox[#BABABA]{5} & 7 & 5\\ 2 & \bbox[#BABABA]{5} & 7 & 8\\ \end{array} \right) \] |
|
\[ ( \bbox[#BABABA]{220} \ \ \bbox[#BABABA]{340} \ \ \bbox[#BABABA]{400} ) \] |
\[ ( 4180 \ \ \bbox[#BABABA]{i_{12}} \ \ i_{13} \ \ i_{14}) \] |
Los cálculos a resolver aquí son:
i12 = 220 · 5 + 340 · 5 + 400 · 5 = 4800
Por lo tanto, el ingreso por venta de televisores en el Local Norte fue de U$S 4800.
Al repetir el procedimiento, se encuentran los dos elementos que faltan en la matriz I:
|
\[ P \ x \ C \] |
\[ \left( \begin{array}{cccc} 3 & 5 & 6 & 7\\ 8 & 5 & 7 & 5\\ 2 & 5 & 7 & 8\\ \end{array} \right) \] |
|
\[ (220 \ \ 340 \ \ 400) \] |
\[ (4180 \ \ 4800 \ \ 6500 \ \ 6440) \] |
Por lo tanto, el ingreso por venta de televisores en el Local Este fue de U$S 6500 y en el Local Oeste fue de U$S 6440.
En <https://support.office.com/es-es/article/mmult-funci%C3%B3n-mmult-40593ed7-a3cd-4b6b-b9a3-e4ad3c7245eb> se explica cómo calcular el producto de dos matrices utilizando Excel.
4.1.2. Matrices especiales. Determinante de una matriz
Ejercicio 5
Con las matrices
\( A = \left( \begin{array}{ccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) \), \( B = \left( \begin{array}{ccc} -3 & 1 & -3\\ 1 & 3 & -5\\ 1 & -2 & 8\\ \end{array} \right) \) y \( C = \left( \begin{array}{ccc} 4 & 4 & 4\\ -4 & 2 & 4\\ -2 & -4 & -4\\ \end{array} \right) \)
realice los siguientes cálculos:
- \( 2 \times A = \)
- \( (A + B) \times C = \)
- \( C \times (A +B) = \)
- Calcule el determinante de las tres matrices.
- Encuentre la matriz X tal que A + 2 x X = C
La operación pedida corresponde a la multiplicación de un número por una matriz. En este caso, se multiplica cada uno de los elementos de la matriz por ese número:
\[ 2 \ \times \ A = 2 \ \times \left( \begin{array}{ccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) = \left( \begin{array}{ccc} 2 \times 1 & 2 \times 1 & 2 \times (-2)\\ 2 \times 0 & 2 & 2 \times 1\\ 2 \times (-1) & 2 \times (-2) & 2 \times 1\\ \end{array} \right) = \]
\[ 2 \ \times \ A = \left( \begin{array}{ccc} 2 & 2 & -4\\ 0 & 4 & 2\\ -2 & -4 & 2\\ \end{array} \right) \]
\[ (A + B) \times C = \left[ \left( \begin{array}{ccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) + \left( \begin{array}{ccc} -3 & 1 & -3\\ 1 & 3 & -5\\ 1 & -2 & 8\\ \end{array} \right) \right] \times C = \]
\[ = \left( \begin{array}{ccc} 1-3 & 1+1 & -2-3\\ 0+1 & 2+3 & 1-5\\ -1+1 & -2-2 & 1+8\\ \end{array} \right) \times \left( \begin{array}{ccc} 4 & 4 & 4\\ -4 & 2 & 4\\ -2 & -4 & -4\\ \end{array} \right) = \]
\[ = \left( \begin{array}{ccc} -2 & 2 & -5\\ 1 & 5 & -4\\ 0 & -4 & 9\\ \end{array} \right) \times \left( \begin{array}{ccc} 4 & 4 & 4\\ -4 & 2 & 4\\ -2 & -4 & -4\\ \end{array} \right) \]
Para resolver el último cálculo, se utilizará nuevamente la disposición del ejercicio anterior:
\[ (A+B) \ \times \ C\]
\[ \left( \begin{array}{ccc} 4 & 4 & 4\\ -4 & 2 & 4\\ -2 & -4 & -4\\ \end{array} \right) \]
\[ \left( \begin{array}{ccc} -2 & 2 & -5\\ 1 & 5 & -4\\ 0 & -4 & 9\\ \end{array} \right) \]
\[ \left( \begin{array}{ccc} -6 & 16 & 20\\ -8 & 30 & 40\\ -2 & -44 & -52\\ \end{array} \right) \]
Aquí, cada elemento de la matriz producto se obtiene multiplicando la fila de (A+B) por la columna de C. Por ejemplo, el resultado de la posición 3-2 se obtiene multiplicando cada elemento de la fila 3 de (A+B) por el correspondiente de la columna 2 de la matriz C:
\[ 0 \times 4 + (-4) \times 2 + 9 \times (-4) = 0 - 8 - 36 = -44 \]
\[ C \ \times (A+B) = C \ \times \ \left[ \left( \begin{array}{ccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) + \left( \begin{array}{ccc} -3 & 1 & -3\\ 1 & 3 & -5\\ 1 & -2 & 8\\ \end{array} \right) \right] = \]
\[ = \left( \begin{array}{ccc} 4 & 4 & 4\\ -4 & 2 & 4\\ -2 & -4 & -4\\ \end{array} \right) \times \left( \begin{array}{ccc} 1-3 & 1+1 & -2-3\\ 0+1 & 2+3 & 1-5\\ -1+1 & -2-2 & 1+8\\ \end{array} \right) = \]
\[ = \left( \begin{array}{ccc} 4 & 4 & 4\\ -4 & 2 & 4\\ -2 & -4 & -4\\ \end{array} \right) \times \left( \begin{array}{ccc} -2 & 2 & -5\\ 1 & 5 & -4\\ 0 & -4 & 9\\ \end{array} \right) \]
En este caso, las matrices a multiplicar son las mismas del ejercicio anterior, pero están cambiadas de orden. Entonces, en la disposición quedan intercambiadas:
|
\[ C \ \times \ (A+B)\] |
\[ \left( \begin{array}{ccc} -2 & 2 & -5\\ 1 & 5 & -4\\ 0 & -4 & 9\\ \end{array} \right) \] |
|
\[ \left( \begin{array}{ccc} 4 & 4 & 4\\ -4 & 2 & 4\\ -2 & -4 & -4\\ \end{array} \right) \] |
\[ \left( \begin{array}{ccc} -4 & 12 & 0\\ 10 & -14 & 48\\ 0 & -8 & -10\\ \end{array} \right) \] |
Es muy importante notar que el resultado obtenido no es igual que en el ejercicio anterior. Por ejemplo, el elemento en la posición 3-2, ahora se calcula:
\[ -2 \times 2 + (-4) \times 5 + (-4) \times (-4) = -4 - 20 +16 = -8 \neq -44 \]
El producto de matrices NO ES CONMUTATIVO. Por ese motivo es necesario prestar mucha atención al orden en el que se multiplican las matrices.
Estas matrices son de 3 x 3. Cada determinante se calculará por un método distinto, para ilustrar cómo hacerlo.
El determinante de A se hallará utilizando la fórmula:
\[ \left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array} \right] = \]
\[ = a_{11} \ a_{22} \ a_{33} \ + a_{12} \ a_{23} \ a_{31} \ + a_{13} \ a_{21} \ a_{32} \ - a_{11} \ a_{23} \ a_{32} \ - a_{12} \ a_{21} \ a_{33} \ - a_{13} \ a_{22} \ a_{31} \]
\[ det(A) = \left[ \begin{array}{ccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right] = \]
\[ = 1 \times 2 \times 1 + 1 \times 1 \times (-1) + (-2) \times 0 \times (-2) -1 \times (-2) \times 1 -1 \times 0 \times 1 \]
\[ - (-1) \times 2 \times (-2) = 2 - 1 + 0 - (-2) - 0 - 4 = -1 \]
Por lo tanto, el determinante de A es igual a -1.
El determinante de B se desarrollará por la primera columna:
\[ det(B) = \left[ \begin{array}{ccc} -3 & 1 & -3\\ 1 & 3 & -5\\ 1 & -2 & 8\\ \end{array} \right] = \]
\[ = (-3) \ \times \ (-1)^{1+1} \ \times \ |^3_{-2} \ ^{-5}_{ \ \ \ 8}| + 1 \ \times \ (-1)^{2+1} \ \times \ |^1_{-2} \ ^{-3}_{ \ \ \ 8}| \]
\[ + 1 \ \times \ (-1)^{3+1} \times |^1_3 \ ^{ \ \ \ -3}_{ \ \ \ -5}| = \]
\[ = -3 \times [3 \times 8 - (-2) \times (-5)] -1 \times [1 \times 8 - (-2) \times (-3)] + 1 \times [1 \times (-5) - 3 \times (-3)] = \]
\[ = -3 \times (24 - 10) - 1 \times (8 - 6) + 1 \times (-5 + 9) = \]
\[ = -3 \times 14 - 1 \times 2 + 1 \times (-14) = -42 - 2 + 4 = -40 \]
Finalmente, para calcular el determinante de C se utilizará la “regla de Sarrus”. En esta disposición, se vuelven a copiar las dos primeras filas de la matriz debajo de la última:
\[ det(C) = \left| \begin{array}{ccc} 4& 4 & 4\\ -4 & 2 & 4\\ -2 & -4 & -4\\ \end{array} \right| = \left| \begin{array}{ccc} 4& 4 & 4\\ -4 & 2 & 4\\ -2 & -4 & -4\\ 4& 4 & 4\\ -4 & 2 & 4\\ \end{array} \right| = \]
\[ = 4 \times 2 \times (-4) + (-4) \times (-4) \times 4 + (-2) \times 4 \times 4 - 4 \times 2 \times (-2) - 4 \]
\[ \times (-4) \times 4 - (-4) \times 4 \times (-4) = \]
\[ = -32 + 64 - 32 + 16 + 64 - 64 = 16 \]
Esta disposición facilita el cálculo. Pero es importante recordar que solo sirve para calcular determinantes de matrices de 3 x 3.
En <https://www.youtube.com/watch?v=u6Qk6xXTx6o> el Profesor Julio Ríos realiza una multiplicación de dos matrices, utilizando otra disposición.
En <https://www.youtube.com/watch?v=ZO0naBrmgj4> se explica cómo hallar el determinante de una matriz de 4 x 4.
En <https://www.youtube.com/watch?v=DPqgJQE24lU> se calcula un determinante, utilizando el método de Sarrus, pero copiando columnas en lugar de filas.
En este ejercicio, es necesario resolver una ecuación matricial:
\[ A + 2 \times X = C \]
Para resolverla, se puede restar, a cada miembro de la igualdad, la matriz A:
\[ A + 2 \times X - A = C - A \]
Al reordenar el primer miembro es:
\[ A - A + 2 \times X = C - A \]
Entonces es:
\[ \left( \begin{array}{ccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) - \left( \begin{array}{ccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) + 2 \ \times \ X =\]
\[ = \left( \begin{array}{ccc} 4& 4 & 4\\ -4 & 2 & 4\\ -2 & -4 & -4\\ \end{array} \right) - \left( \begin{array}{ccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) \]
Ahora, se efectúan los cálculos:
\[ \left( \begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array} \right) + 2 \ \times \ X = \left( \begin{array}{ccc} 3 & 3 & 6\\ -4 & 0 & 3\\ -1 & -2 & -5\\ \end{array} \right) \]
La primera matriz de esta expresión, con todos los elementos iguales a cero, se llama “matriz nula” y si se suma a cualquier otra matriz A, se vuelve a obtener A.
En <https://www.wikiwand.com/es/Matriz_cero> se puede consultar para más información sobre las matrices nulas.
Entonces, es
\[ \left( \begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array} \right) + 2 \ \times \ X = 2 \ \times \ X = \left( \begin{array}{ccc} 3 & 3 & 6\\ -4 & 0 & 3\\ -1 & -2 & -5\\ \end{array} \right) \]
Para hallar la matriz X se puede multiplicar, a la izquierda de cada miembro, por el número 1/2 :
\[ \frac{1}{2} \times \ 2 \ \times \ X = \frac{1}{2} \times \left( \begin{array}{ccc} 3 & 3 & 6\\ -4 & 0 & 3\\ -1 & -2 & -5\\ \end{array} \right) \]
\[ 1 \ \times \ X = X = \frac{1}{2} \times \left( \begin{array}{ccc} 3 & 3 & 6\\ -4 & 0 & 3\\ -1 & -2 & -5\\ \end{array} \right) \]
\[ X = \left( \begin{array}{ccc} 3/2 & 3/2 & 3\\ -2 & 0 & 3/2\\ -1/2 & -1 & -5/2\\ \end{array} \right) \]
Entonces, la matriz buscada es
\[ X = \left( \begin{array}{ccc} 3/2 & 3/2 & 3\\ -2 & 0 & 3/2\\ -1/2 & -1 & -5/2\\ \end{array} \right) \]
Ejercicio 6
Con las matrices \( A = \left( \begin{array}{ccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) \), \( B = \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{array} \right) \) y \( C = \left( \begin{array}{ccc} -4 & -3 & -5\\ 1 & 1 & 1\\ -2 & -1 & -2\\ \end{array} \right) \) realice los siguientes cálculos:
- \( A \times B = \)
- \( B \times A = \)
- \( A \times C = \)
- \( C \times A = \)
a) y b) Para resolver estos productos se utilizará la misma disposición que en ejercicios anteriores.
\[ A \ \times \ B \]
\[ \left( \begin{array}{cccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{array} \right) \]
\[ \left( \begin{array}{cccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) \]
\[ \left( \begin{array}{cccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) \]
Si se presta atención al resultado se notará que es igual a la matriz A.
Esto no es una casualidad. La matriz B de este ejercicio es la “matriz identidad” de 3 filas por 3 columnas. También llamada “matriz unidad”, es el elemento neutro de la multiplicación de matrices de esa dimensión. Y se simboliza con la letra I (i latina mayúscula).
Por ese motivo es que también \( B \times A = A \)
Para más información sobre la matriz identidad y sus propiedades, se puede consultar:
<https://www.matesfacil.com/matrices/matrices-especiales.html>
-
\[ A \ \times \ C \]
\[ \left( \begin{array}{cccc} -4 & -3 & -5\\ 1 & 1 & 1\\ -2 & -1 & -2\\ \end{array} \right) \]
\[ \left( \begin{array}{cccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right) \]
\[ \left( \begin{array}{cccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{array} \right) \]
Aquí se obtiene que \( A \times C = I \) la matriz identidad. Cuando el producto de dos matrices cuadradas es la matriz identidad se dice que ambas matrices son “inversas” y se anota con el exponente menos 1.
En este caso: \( C = A^{-1}. \)
Como C es la inversa de A, A es la inversa de C y su producto, cambiando el orden, también es la matriz identidad, como puede verificarse al realizar la multiplicación pedida.
\[ C \ \times \ A \]
\[ \left( \begin{array}{cccc} 1 & 1 & -2\\ 0 & 2 & 1\\ -1 & -2 & 1\\ \end{array} \right)\]
\[ \left( \begin{array}{cccc} -4 & -3 & -5\\ 1 & 1 & 1\\ -2 & -1 & -2\\ \end{array} \right) \]
\[ \left( \begin{array}{cccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{array} \right) \]
En <https://www.vitutor.com/algebra/matrices/inversa.html> se pueden consultar las propiedades de las matrices inversas y se explica cómo calcularlas por el método de Gauss, que se utilizará más adelante.
Siendo \( A = \left( \begin{array}{ccc} 1 & 4 & -1\\ 2 & 6 & 1\\ 0 & -1 & 2\\ \end{array} \right) \), \( B = \left( \begin{array}{ccc} 1 & 4 & 1\\ 3 & -2 & 3\\ 5 & 6 & 7\\ \end{array} \right) \) y \( C = \left( \begin{array}{ccc} 5 & -8 & 4\\ 1 & -1 & 7\\ -3 & -3 & 1\\ \end{array} \right) \) se pide que:
- Calcule el determinante de la matriz A.
- Realice los siguientes cálculos:
- \((A - B) \times C = \)
- \(C \times (B + A) = \)
Halle la matriz X que satisface la siguiente ecuación:
X + 2A - C = B
Respuestas:
- \( |A|= -1 \)
- \( (A-B) \ \times \ C= \left( \begin{array}{ccc} 6 & 6 & -2\\ 9 & 6 & 50\\ -17 & 62 & 74\\ \end{array} \right) \)
- \( C \ \times \ (B+A) = \left( \begin{array}{ccc} -10 & 28 & 4\\ 32 & 39 & 59\\ -16 & -31 & -3\\ \end{array} \right) \)
- \( X= \left( \begin{array}{ccc} 4 & -12 & 7\\ 0 & -15 & 8\\ 2 & 5 & 4\\ \end{array} \right) \)
4.2. Sistemas de ecuaciones
4.2.1. Sistemas de ecuaciones compatibles determinados
Ejercicio 7
En la fabricación de un producto X se utilizan 5 unidades del insumo A y 3 del B. En la fabricación del producto Y, se utilizan 2 unidades de A y 4 de B. Si se dispone de 71 unidades de A y 79 unidades del insumo B, calcule cuántos productos X y cuántos Y se pueden fabricar, utilizando la totalidad de los insumos disponibles.
Si hiciera falta producir 13 unidades de X y 3 de Y, ¿alcanzarían los insumos con los que se cuenta?
Para comenzar es importante preguntarse ¿qué hay que averiguar en este problema? Y asignar una incógnita a cada cantidad que hay que averiguar:
- cantidad del producto X a fabricar: x
- cantidad del producto Y a fabricar: y.
Conviene acomodar la información en una tabla:
| Insumos | ||
|
Productos |
X |
Y |
|
A |
5 |
2 |
|
B |
3 |
4 |
La restricción la impone la cantidad de insumos disponibles. Se puede agregar una columna con ese dato:
| Insumos | |||
|
Productos |
X |
Y |
Total |
|
A |
5 |
2 |
71 |
|
B |
3 |
4 |
79 |
Entonces, para el insumo A se tienen 71 unidades, que se pueden utilizar de la siguiente manera:
5 por cada producto X que se vayan a producir (en total sería por x) y 2 por cada producto Y (en total, sería por y).
De la misma manera, para el insumo B, se pueden utilizar 3 unidades por cada producto X y 4 por cada producto Y. Y en total se pueden gastar 79 unidades.
Es decir:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 5 \cdot x + 2 \cdot y = 71\\ 3 \cdot x + 4 \cdot y = 79 \end{array} \right. \end{equation}\]
La llave que abarca ambas ecuaciones significa que ambas deben tener la misma solución. Eso significa que forman un “sistema de ecuaciones”. Ahora solo resta resolver este sistema de ecuaciones. Por ejemplo, por sustitución. De la primera ecuación se puede despejar y:
\[ y = \frac{71 - 5 \cdot x}{2} = 35,5 - 2,5 \cdot x \](3)
Esta ecuación (3) se reemplaza en la segunda del sistema:
3 · x + 4 · (35,5 - 2,5 · x) = 79
3 · x + 142 - 10 · x = 79
-7 · x = 79 - 142 = -63
x = 9 (4)
Finalmente, reemplazando el resultado (4) en la ecuación (3), se obtiene:
y = 35,5 - 2,5 · 9 = 13
Por lo tanto, al utilizar la totalidad de los insumos disponibles, se pueden fabricar 9 unidades del producto X y 13 del producto Y.
-
Las ecuaciones que se utilizaron sirven para pensar esta parte, pero sin poner el resultado:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 5 \cdot x + 2 \cdot y =\\ 3 \cdot x + 4 \cdot y = \end{array} \right. \end{equation}\]
En esta parte, se conocen x e y, y falta ver si el stock disponible alcanza para lo que se necesita:
\[\begin{equation} \left\lbrace \begin{array}{ll} 5 \cdot 13 + 2 \cdot 3 = 65 + 6 = 71\\ 3 \cdot 13 + 4 \cdot 3 = 39 + 12 = 51 \end{array} \right. \end{equation}\]
Como se puede ver, fabricando 13 unidades de X y 3 de Y, alcanza la cantidad disponible del insumo A y sobran 28 unidades del insumo Y.
La idea de este ejercicio es ver que las ecuaciones \(\begin{equation} \left\lbrace \begin{array}{ll} 5 \cdot x + 2 \cdot y = 71\\ 3 \cdot x + 4 \cdot y = 79 \end{array} \right. \end{equation}\) se pueden considerar como la “frontera de posibilidades de producción”. En realidad sería:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 5 \cdot x + 2 \cdot y \le 71\\ 3 \cdot x + 4 \cdot y \ge 79 \end{array} \right. \end{equation}\]
Al graficar esta situación con Geogebra, se obtiene:
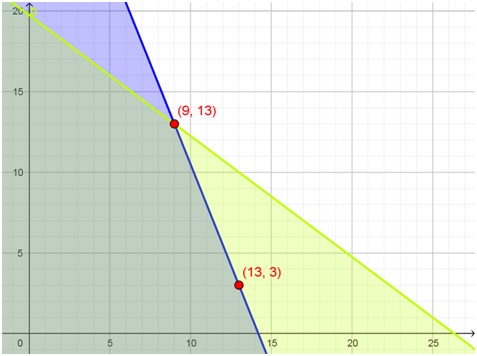
Por supuesto, solo vale el primer cuadrante, ya que tanto x como y representan “cantidades de productos” y, por lo tanto, solo toman valores positivos. Todos los puntos sombreados en dos colores (que se ve en verde) son posibles de producir con esta cantidad de insumos. Los de la “frontera” también se pueden producir, como el óptimo (la solución del sistema de ecuaciones que se obtuvo en la parte a del ejercicio), en el que no se desperdicia ningún insumo, pero también el caso del pedido de 13 unidades de X y de 3 de Y.
Ejercicio 8
Una compañía produce tres tipos de muebles para patios: sillas, mecedoras y sillones reclinables. Cada uno requiere de madera, plástico y aluminio, en las cantidades que se indican en la tabla siguiente. La compañía tiene en existencia 400 unidades de madera, 700 de plástico y 1500 de aluminio. Si se quiere utilizar todo el inventario, ¿cuántas sillas, mecedoras y sillones deberán fabricarse?
|
|
Madera |
Plástico |
Aluminio |
|
Silla |
1 unidad |
1 unidad |
2 unidades |
|
Mecedora |
1 unidad |
2 unidades |
3 unidades |
|
Sillón |
1 unidad |
2 unidades |
5 unidades |
Para resolver este problema es conveniente plantear un sistema de ecuaciones, en el que las incógnitas representan la información que se busca. Siempre es conveniente comenzar explicando qué es lo que se necesita calcular y asignarle una letra, que representa la incógnita que se quiere encontrar. En este caso, se requiere conocer:
- el número de sillas: s
- el número de mecedoras: m
- el número de sillones reclinables: r
que se pueden fabricar con la materia prima existente.
La cantidad de materia prima existente es la “restricción”: no se puede fabricar cualquier cantidad de estos productos, porque no se dispone de más materia prima. En el caso de la madera, hay en total 400 unidades. Por la información de la tabla, se sabe que hace falta 1 unidad de madera por cada silla, 1 por cada mecedora y una por cada sillón reclinable. Esto se puede sintetizar con la siguiente ecuación:
1 · s + 1 · m + 1 · r = 400
Pero la madera no es la única restricción. Además, hay solo 700 unidades de plástico, que se deben utilizar 1 por cada silla, 2 por cada mecedora y 2 por cada sillón reclinable:
1 · s + 2 · m + 2 · r = 700
Y con el aluminio, es:
2 · s + 3 · m + 5 · r = 1500
Estas tres ecuaciones deben tener la misma solución para hallar el resultado del problema. Esto se simboliza uniéndolas con una llave:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 1 \cdot s + 1 \cdot m + 1 \cdot r = 400\\ 1 \cdot s + 2 \cdot m + 2 \cdot r =700 \\ 2 \cdot s + 3 \cdot m + 5 \cdot r = 1500 \end{array} \right. \end{equation}\]
Este es un sistema de ecuaciones de tres ecuaciones con tres incógnitas.
Hay muchos métodos para resolverlo, como el de sustitución que se utilizó en el ejercicio anterior. Sin embargo, cuando la cantidad de incógnitas es mayor a dos, resulta complicado. Por eso, aquí se utilizará el método de Gauss, con la matriz ampliada.
En <https://www.vadenumeros.es/primero/sistemas-gauss.htm> se explica el método de Gauss.
Se puede consultar en: <https://matematica.laguia2000.com/general/metodo-de-gauss-jordan>
Este método está relacionado con el de Gauss JordanN , que se utilizará más adelante
La matriz ampliada es:
\[ \left( \begin{array}{ccccc} 1 & 1 & 1 & | & 400\\ 1 & 2 & 2 & | & 700\\ 2 & 3 & 5 & | & 1500\\ \end{array} \right) \]
Y se busca hacer 0 los elementos de las posiciones 2-1, 3-1 y 3-2.
Para hacer 0 las dos primeras posiones, que corresponden a la primera columna, se utilizará como “pivote” al 1 de la posición 1-1. Las operaciones a aplicar son:
F'2 = F2 - F1
F'3 = F3 - 2 · F1
\[ \left( \begin{array}{ccccc} 1 & 1 & 1 & | & 400\\ 1-1 & 2-1 & 2-1 & | & 700 - 400\\ 2-2 \cdot 1 & 3-2 \cdot 1 & 5-2 \cdot 1 & | & 1500-2 \cdot 400\\ \end{array} \right) = \left( \begin{array}{ccccc} 1 & 1 & 1 & | & 400\\ 0 & 1 & 1 & | & 300\\ 0 & 1 & 3 & | & 700\\ \end{array} \right) \]
Así quedó lista la primera columna.
Para que la segunda columna quede lista, falta hacer 0 el elemento 3-2. Para ello, se toma como “pivote” el 1 de la posición 2-2. (En este ejercicio ya hay un 1. Si no lo hubiera, se debería conseguir dividiendo toda la fila 2 por el elemento 2-2). Aquí la operación será:
F'3 = F3 - F2
\[ \left( \begin{array}{ccccc} 1 & 1 & 1 & | & 400\\ 0 & 1 & 1 & | & 300\\ 0 & 1-1 & 3-1 & | & 700-300\\ \end{array} \right) = \left( \begin{array}{ccccc} 1 & 1 & 1 & | & 400\\ 0 & 1 & 1 & | & 300\\ 0 & 0 & 2 & | & 400\\ \end{array} \right) \]
Esta última matriz ampliada está “subtriangulada” con ceros. Y equilave al siguiente sistema de ecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 1 \cdot s + 1 \cdot m + 1 \cdot r = 400 \ (1)\\ 1 \cdot m + 1 \cdot r =300 \ (2)\\ 2 \cdot r = 400 \ (3) \end{array} \right. \end{equation}\]
que se resuelve mucho más facilmente que el original:
De la ecuación (3), se deduce que \( r = \frac{400}{2} = 200 \). Cuando reemplazamos este resultado en la ecuación (2) obtenemos:
1 · m + 1 · 200 = 300
m = 300 - 200 = 100
Y con estos dos resultados en la ecuación (1), se halla la cantidad de sillas:
1 · s + 1 · 100 + 1 · 200 = 400
s = 400 - 100 - 200 = 100
Por lo tanto, para utilizar todo el inventario se deberán fabricar 100 sillas, 100 mecedoras y 200 sillones reclinables.
4.2.2. Sistemas de ecuaciones para hallar matrices inversas
Ejercicio 9
Encuentre la matriz inversa de \[ A = \left( \begin{array}{ccc} 1 & 1 & -3\\ -1 & 0 & 2 \\ 0 & 2 & -1\\ \end{array} \right) \]
La inversa de una matriz cuadrada A es otra matriz cuadrada A-1 tal que:
A x A-1 = A-1 x A = I
En esta última expresión I es la matriz identidad. En la multiplicación de matrices de 3 x 3 la matriz identidad, como ya se mencionara en ejercicios anteriores, es:
\[ I = \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1\\ \end{array} \right) \]
En general, la matriz identidad (también llamada “matriz unidad”) es una matriz cuadrada en la que sus elementos son
\( a_{ij} = 0 \text{ si } i \ne j \text{ y } a_{ij} = 1 \text{ si } i = j \)
Para hallar la matriz inversa de A se pueden plantear sistemas de ecuaciones, teniendo en cuenta el modo en que se multiplican las matrices. Continuamos con el esquema ya presentado para realizar la operación:
|
\[ A \ x \ A^{-1} \] |
\[ \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array} \right) \] |
|
\[ \left( \begin{array}{ccc} 1 & 1 & -3\\ -1 & 0 & 2\\ 0 & 2 & -1\\ \end{array} \right) \] |
\[ \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{array} \right) \] |
Entonces deberá ser:
1 · a11 + 1 · a21 + (-3) · a31 = 1 ecuación correspondiente al elemento i11 de la matriz identidad.
(-1) · a11 + 0 · a21 + 2 · a31 = 0 ecuación correspondiente al elemento i21 de la matriz identidad.
0 · a11 + 2 · a21 + (-1) · a31 = 0 ecuación correspondiente al elemento i31 de la matriz identidad.
Se obtiene así el siguiente sistema de ecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 1 \cdot a_{11} + 1 \cdot a_{21} + (-3) \cdot a_{31} = 1\\ (-1) \cdot a_{11} + 0 \cdot a_{21} + 2 \cdot a_{31} = 0\\ 0 \cdot a_{11} + 2 \cdot a_{21} + (-1) \cdot a_{31} = 0 \end{array} \right. \end{equation}\]
En el que las incógnitas son a11, a21 y a31, los elementos correspondientes a la primera columna de la matriz A-1 .
De este mismo modo, se obtiene el siguiente sistema de ecuaciones para hallar los elementos a12, a22 y a32 de la segunda columna de la matriz A-1:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 1 \cdot a_{12} + 1 \cdot a_{22} + (-3) \cdot a_{32} = 0\\ (-1) \cdot a_{12} + 0 \cdot a_{22} + 2 \cdot a_{32} = 1\\ 0 \cdot a_{12} + 2 \cdot a_{22} + (-1) \cdot a_{32} = 0 \end{array} \right. \end{equation}\]
Y, para hallar los elementos a13, a23 y a33 de la tercera columna de la matriz A-1, el sistema de ecuaciones es:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 1 \cdot a_{13} + 1 \cdot a_{23} + (-3) \cdot a_{33} = 0\\ (-1) \cdot a_{13} + 0 \cdot a_{23} + 2 \cdot a_{33} = 0\\ 0 \cdot a_{13} + 2 \cdot a_{23} + (-1) \cdot a_{33} = 1 \end{array} \right. \end{equation}\]
Si se presta atención a estos tres sistemas de ecuaciones, se notará que los tres tienen los mismos coeficientes, pero difieren los resultados. Para resolver cada uno de ellos, se puede proceder como en el ejercicio anterior, ampliando la matriz de coeficientes. Así, cada uno de los tres sistemas tienen las siguientes matrices ampliadas:
\[ \left( \begin{array}{ccccc} 1 & 1 & -3 & | & 1\\ -1 & 0 & 2 & | & 0\\ 0 & 2 & -1 & | & 0\\ \end{array} \right) \]
\[ \left( \begin{array}{ccccc} 1 & 1 & -3 & | & 0\\ -1 & 0 & 2 & | & 1\\ 0 & 2 & -1 & | & 0\\ \end{array} \right) \]
\[ \left( \begin{array}{ccccc} 1 & 1 & -3 & | & 0\\ -1 & 0 & 2 & | & 0\\ 0 & 2 & -1 & | & 1\\ \end{array} \right) \]
Se pueden resolver todos los sistemas de ecuaciones por separado o, como se hará aquí, se resuelven todos juntos, por el método de Gauss Jordan, para llegar directamente a la matriz inversa. Con ese fin, se escribe la matriz A ampliada con cada una de las columnas, en el orden correspondiente:
\[ \left( \begin{array}{ccccccc} 1 & 1 & -3 & | & 1 & 0 & 0\\ -1 & 0 & 2 & | & 0 & 1 & 0\\ 0 & 2 & -1 & | & 0 & 0 & 1\\ \end{array} \right) \]
Es importante observar que en este esquema, se tiene a la izquierda la matriz A y a la derecha la matriz identidad:
\[ (A | I) \]
partir de aquí se procederá a realizar operaciones con las filas para llegar a tener la matriz identidad a la izquierda. Y la matriz que quede a la derecha será la solución de los tres sistemas de ecuaciones, es decir, la matriz inversa que se busca:
\[ (I | A^{-1}) \]
Entonces, partiendo de:
\[ \left( \begin{array}{ccccccc} 1 & 1 & -3 & | & 1 & 0 & 0\\ -1 & 0 & 2 & | & 0 & 1 & 0\\ 0 & 2 & -1 & | & 0 & 0 & 1\\ \end{array} \right) \]
En la primera columna solo hace falta anular el elemento 2-1, porque ya hay un 1 en la posición 1-1 y un 0 en la posición 3-1. Por eso se hace:
F'2 = F2 + F1
\[ \left( \begin{array}{ccccccc} 1 & 1 & -3 & | & 1 & 0 & 0\\ 0 & 1 & -1 & | & 1 & 1 & 0\\ 0 & 2 & -1 & | & 0 & 0 & 1\\ \end{array} \right) \]
Así quedó lista la primera columna. Se sigue por la segunda, tomando como “pivote” el elemento 2-2. Por suerte, ya es un 1. Falta anular el elemento 1-2 y el 3-2. Para lograrlo, se hace:
F'1 = F1 - F2
F'3 = F3 - 2 · F2
\[ \left( \begin{array}{ccccccc} 1 & 0 & -2 & | & 0 & -1 & 0\\ 0 & 1 & -1 & | & 1 & 1 & 0\\ 0 & 0 & 1 & | & -2 & -2 & 1\\ \end{array} \right) \]
Ya están listas las dos primeras columnas. Para terminar, como el elemento 3-3 ya es un 1, solo faltan anular los elementos 1-3 y 2-3, para lo que se hace:
F'1 = F1 + 2 · F3
F'2 = F2 + F3
\[ \left( \begin{array}{ccccccc} 1 & 0 & 0 & | & -4 & -5 & 2\\ 0 & 1 & 0 & | & -1 & -1 & 1\\ 0 & 0 & 1 & | & -2 & -2 & 1\\ \end{array} \right) \]
Por lo tanto, la solución del primer sistema de ecuaciones es:
a11 = -4
a21 = -1 y
a31 = -2
Son los elementos de la primera columna de la matriz inversa, que aquí aparecen ordenados en su lugar, como sucede también con las soluciones de los otros dos sistemas de ecuaciones. Por lo tanto, la matriz inversa buscada es:
\[ A^{-1} = \left( \begin{array}{ccc} -4 & -5 & 2\\ -1 & -1 & 1 \\ -2 & -2 & 1\\ \end{array} \right) \]
Este resultado puede comprobarse, realizando la multiplicación \( A \times A^{-1} : \)
|
\[ A \ \times \ A^{-1} \] |
\[ \left( \begin{array}{ccc} -4 & -5 & 2\\ -1 & -1 & 1 \\ -2 & -2 & 1\\ \end{array} \right) \] |
|
\[ \left( \begin{array}{ccc} 1 & 1 & -3\\ -1 & 0 & 2\\ 0 & 2 & -1\\ \end{array} \right) \] |
\[ \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{array} \right) \] |
Ejercicio 10
Siendo \( A = \left( \begin{array}{ccc} 1 & 1 & -1\\ 2 & 2 & -1 \\ -2 & -1 & 1\\ \end{array} \right) \), \( B = \left( \begin{array}{ccc} -5 & -5 & 5\\ 2 & -2 & 1 \\ 0 & 3 & 1\\ \end{array} \right) \) y \( C = \left( \begin{array}{ccc} 1 & 2 & 1\\ 3 & -1 & -2 \\ -2 & 0 & 3\\ \end{array} \right) \) se pide que:
- Calcule la matriz inversa de A.
- Halle la matriz X para que A x X - B = C
En <https://www.educ.ar/recursos/70274/la-inversa-de-una-matriz-diferentes-metodos-de-obtencion> se explican diferentes maneras de encontrar una matriz inversa.
En este ejercicio, para hallar la inversa de esta matriz, se utilizará el método de los determinantes.
\[ A^{-1} = \frac{Adj(A^t)}{|A|} \]
Con base en esta fórmula, se calculará primero la matriz Adjunta de A Adj(A), cuyos elementos son determinantes. En general, para una matriz:
\[ A = \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array} \right) \]
La matriz adjunta se calcula de la siguiente manera:
\[ \large Adj(A) = \left( \begin{array}{ccc} |^{a_{22}}_{a_{32}} \ \ \ ^{a_{23}}_{a_{33}}| & - |^{a_{21}}_{a_{31}} \ \ \ ^{a_{23}}_{a_{33}}| & |^{a_{21}}_{a_{31}} \ \ \ ^{a_{22}}_{a_{32}}| \\ - |^{a_{12}}_{a_{32}} \ \ \ ^{a_{13}}_{a_{33}}| & |^{a_{11}}_{a_{31}} \ \ \ ^{a_{13}}_{a_{33}}| & -|^{a_{11}}_{a_{31}} \ \ \ ^{a_{12}}_{a_{32}}|\\ |^{a_{12}}_{a_{22}} \ \ \ ^{a_{13}}_{a_{23}}| & - |^{a_{11}}_{a_{21}} \ \ \ ^{a_{13}}_{a_{23}}| & |^{a_{11}}_{a_{21}} \ \ \ ^{a_{12}}_{a_{22}}|\\ \end{array} \right) \]
En este ejercicio es:
\[ |^{a_{22}}_{a_{32}} \ \ \ ^{a_{23}}_{a_{33}}| = |^{2}_{-1} \ \ \ ^{-1}_{\ \ \ 1}| = 2 \cdot 1 - 1 \cdot (-1) = 2 - 1 = 1 \]
\[ - |^{a_{21}}_{a_{31}} \ \ \ ^{a_{23}}_{a_{33}}| = - |^{2}_{-2} \ \ \ ^{-1}_{\ \ \ 1}| = - [2 \cdot 1 - (-2) \cdot (-1)] = -(2 - 2) = 0 \]
\[ |^{a_{21}}_{a_{31}} \ \ \ ^{a_{22}}_{a_{32}}| = |^{2}_{-2} \ \ \ ^{\ \ \ 2}_{-1}| = 2 \cdot (-1) - 2 \cdot (-2) = - 2 + 4 = 2 \]
\[ - |^{a_{12}}_{a_{32}} \ \ \ ^{a_{13}}_{a_{33}}| = - |^{1}_{-1} \ \ \ ^{-1}_{\ \ \ 1}| = -[ 1 \cdot 1 - (-1) \cdot (-1)] = - (1-1) = 0\]
\[ |^{a_{11}}_{a_{31}} \ \ \ ^{a_{13}}_{a_{33}}| = |^{1}_{-2} \ \ \ ^{-1}_{\ \ \ 1}| = 1 \cdot 1 - (-1) \cdot (-2) = 1-2 = -1 \]
\[ - |^{a_{11}}_{a_{31}} \ \ \ ^{a_{12}}_{a_{32}}| = |^{1}_{-2} \ \ \ ^{\ \ \ 1}_{-1}| = -[1 \cdot (-1) - 1 \cdot (-2)] = -(-1+2) = -1 \]
\[ |^{a_{12}}_{a_{22}} \ \ \ ^{a_{13}}_{a_{23}}| = |^{1}_{2} \ \ \ ^{-1}_{-1}| = 1 \cdot (-1) - (-1) \cdot 2 = (-1) +2 = 1 \]
\[ - |^{a_{11}}_{a_{21}} \ \ \ ^{a_{13}}_{a_{23}}| = - |^{1}_{2} \ \ \ ^{-1}_{-1}| = -[1 \cdot (-1) - (-1) \cdot 2] = -(-1+2) = -1 \]
\[ |^{a_{11}}_{a_{21}} \ \ \ ^{a_{12}}_{a_{22}}| = |^{1}_{2} \ \ \ ^{1}_{2}| = 1 \cdot 2 - 1 \cdot 2 = 2 - 2 = 0 \]
Al reemplazar estos resultados, se obtiene la matriz adjunta:
\[ Adj(A) = \left( \begin{array}{ccc} 1 & 0 & 2\\ 0 & -1 & -1\\ 1 & -1 & 0\\ \end{array} \right) \]
La matriz transpuesta de esta es:
\[ Adj(A)^t = \left( \begin{array}{ccc} 1 & 0 & 1\\ 0 & -1 & -1\\ 2 & -1 & 0\\ \end{array} \right) \]
Solo resta calcular el determinante de la matriz A para resolver el último cálculo. Dicho determinante se resolverá con la fórmula:
a11a22a33+ a12a23a31 + a13a21a32 - a11a23a32 - a12a21a33 - a13a22a31
En este caso es:
\[ |A| = 1 \cdot 2 \cdot 1 + 1 \cdot (-1) \cdot (-2) + (-1) \cdot 2 \cdot (-1) - 1 \cdot (-1) \cdot (-1) - 1 \cdot 2 \cdot 1 - (-1) \cdot 2 \cdot (-2) \]
\[ = 2 + 2 + 2 - 1 - 2 - 4 = -1 \]
\[ A^{-1} = \frac{Adj(A)^t}{|A|} = \frac{\left( \begin{array}{ccc} 1 & 0 & -1\\ 0 & -1 & -1\\ 2 & -1 & 0\\ \end{array} \right)}{-1} = \left( \begin{array}{ccc} -1 & 0 & 1\\ 0 & 1 & 1\\ -2 & 1 & 0\\ \end{array} \right) \]
Por lo tanto, la matriz inversa buscada es:
\[ A^{-1} = \left( \begin{array}{ccc} -1 & 0 & -1\\ 0 & 1 & 1\\ -2 & 1 & 0\\ \end{array} \right) \]
Si se deseara comprobar este resultado, se podría efectuar la multiplicación \( A \times A^{-1} \) y verificar que el resultado es la matriz identidad.
Aquí se pide resolver la ecuación matricial \( A \times X - B = C . \) Para ello se puede sumar en ambos miembros la matriz B:
\[ A \times X - B + B = C + B \]
Como se explicó en otro ejercicio, -B + B da como resultado la matriz nula, entonces es
\[ A \times X = C + B \]
Si esta fuera una ecuación de números reales, se podría dividir por A. Pero es importante notar que no está definida la división de matrices. Por eso, para resolver una ecuación matricial como esta, se utilizan matrices inversas. Como el producto de matrices NO ES conmutativo, es también importante fijarse de qué lado se multiplicará por la matriz inversa. Aquí, para que A-1 quede junto a la matriz A, se deben multiplicar a izquierda ambos miembros por la matriz inversa calculada en la parte a):
\[ A^{-1} \times A \times X = A^{-1} X (C + B) \]
Al agrupar en el primer miembro es:
\[ A^{-1} \times A \times X = (A^{-1} \times A) \times X = A^{-1} \times (C + B) \]
\[ I \times X = A^{-1} \times (C + B) \]
\[ X = A^{-1} \times (C + B) \]
Ahora, se resolverán los cálculos indicados:
\[ X = \left( \begin{array}{ccc} -1 & 0 & -1\\ 0 & 1 & 1\\ -2 & 1 & 0\\ \end{array} \right) \times \left[ \left( \begin{array}{ccc} 1 & 2 & 1\\ 3 & -1 & -2\\ -2 & 0 & 3\\ \end{array} \right) + \left( \begin{array}{ccc} -5 & -5 & 5\\ 2 & -2 & 1\\ 0 & 3 & 1\\ \end{array} \right) \right] \]
\[ X = \left( \begin{array}{ccc} -1 & 0 & -1\\ 0 & 1 & 1\\ -2 & 1 & 0\\ \end{array} \right) \times \left( \begin{array}{ccc} -4 & -3 & 6\\ 5 & -3 & -1\\ -2 & 3 & 4\\ \end{array} \right) \]
Finalmente,
\[ X = A^{-1} \ \times \ (C+B) \]
\[ C + B = \left( \begin{array}{ccc} -4 & -3 & 6\\ 5 & -3 & -1 \\ -2 & 3 & 4\\ \end{array} \right) \]
\[ A^{-1} = \left( \begin{array}{ccc} -1 & 0 & -1\\ 0 & 1 & 1\\ -2 & 1 & 0\\ \end{array} \right) \]
\[ \left( \begin{array}{ccc} 6 & 0 & -10\\ 3 & 0 & 3\\ 13 & 3 & -13\\ \end{array} \right) \]
Por lo tanto, la matriz buscada es:
\[ X = \left( \begin{array}{ccc} 6 & 0 & -10\\ 3 & 0 & 3\\ 13 & 3 & -13\\ \end{array} \right) \]
Halle la matriz X que satisface la siguiente ecuación matricial:
\[ X \ \times \ \left( \begin{array}{ccc} 2 & 2 & 2\\ 2 & 3 & -2\\ 0 & -1 & 2\\ \end{array} \right) + \left( \begin{array}{ccc} 0 & -1 & 1\\ 2 & 0 & 2\\ 1 & -1 & 6\\ \end{array} \right) = \left( \begin{array}{ccc} 6 & 6 & 3\\ 6 & 6 & -2\\ 7 & 6 & 6\\ \end{array} \right) \]
Respuesta: \( X = \left( \begin{array}{ccc} 2 & 1 & 0\\ 0 & 2 & 0\\ 1 & 2 & 1\\ \end{array} \right) \) En la resolución de este ejercicio es importante notar que se debe buscar la inversa de la matriz \( \left( \begin{array}{ccc} 2 & 2 & 2\\ 2 & 3 & -2\\ 0 & -1 & 2\\ \end{array} \right) \) y multiplicar a por esa matriz inversa a la derecha de cada miembro.
Ejercicio 11
Dado el sistema de ecuaciones:
\[ \begin{equation}
\left\lbrace
\begin{array}{ll}
y = 9 + 4z - 2x\\
x - 2y + 2z = -7\\
3x + 3z = 4y - 12
\end{array}
\right.
\end{equation}\]
Se pide que:
En este ejercicio, el sistema de ecuaciones ya está dado, y se pide una manera específica de resolverlo.
Para comenzar, hace falta reordenar el sistema, para poder encontrar la matriz asociada:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 2x + y - 4z = 9\\ x - 2y + 2z = -7\\ 3x - 4y + 3z = -12 \end{array} \right. \end{equation} \]
Por lo tanto, la matriz asociada al sistema es:
\[ A = \left( \begin{array}{ccc} 2 & 1 & -4\\ 1 & -2 & +2\\ 3 & -4 & 3\\ \end{array} \right) \]
Su determinante se puede calcular por la regla de Sarrus:
\[ |A| = \left| \begin{array}{ccc} 2 & 1 & -4\\ 1 & -2 & 2\\ 3 & -4 & 3\\ 2 & 1 & -4\\ 1 & -2 & 2\\ \end{array} \right| = \]
\[ = 2 \cdot (-2) \cdot 3 + 1 \cdot (-4) \cdot (-4) + 3 \cdot 1 \cdot 2 \]
\[ -[(-4) \cdot (-2) \cdot 3 + 2 \cdot (-4) \cdot 2 + 3 \cdot 1 \cdot 1 ] = \]
\[ = -12 + 16 + 6 - (24- 16 + 3) = 10 - 11 = -1 \]
Por lo tanto, el determinante de la matriz es igual a -1.
Se buscará ahora la matriz inversa. Para ello, se utilizará el método de Gauss Jordan:
\[ \left( \begin{array}{ccccccc} 2 & 1 & -4 & | & 1 & 0 & 0\\ 1 & -2 & 2 & | & 0 & 1 & 0\\ 3 & -4 & 3 & | & 0 & 0 & 1\\ \end{array} \right) \]
Para obtener un 1 en la posición 1-1, se puede dividir toda la fila por 2. Pero también se pueden cambiar de lugar las filas uno y dos. Aquí se prefiere hacer eso, para evitar trabajar con fracciones:
\[ F1 \leftrightarrow F2 \]
\[\left( \begin{array}{ccccccc} 1 & -2 & 2 & | & 0 & 1 & 0\\ 2 & 1 & -4 & | & 1 & 0 & 0\\ 3 & -4 & 3 & | & 0 & 0 & 1\\ \end{array} \right) \]
Ya hay un 1 en la posición 1-1. Este valor será el pivote para buscar un cero en la posición 2-1 y otro en la posición 3-1 para que quede lista la primera columna. Por eso, se hace:
F'2 = F2 - 2 · F1
F'3 = F3 -3 · F1
\[ \left( \begin{array}{ccccccc} 1 & -2 & 2 & | & 0 & 1 & 0\\ 2 - 2 \cdot 1 & 1-2 \cdot (-2) & -4-2 \cdot 2 & | & 1-2 \cdot 0 & 0-2 \cdot 1 & 0-2 \cdot 0\\ 3-3 \cdot 1 & -4 - 3 \cdot (-2) & 3-3 \cdot 2 & | & 0-3 \cdot 0 & 0-3 \cdot 1 & 1-3 \cdot 0\\ \end{array} \right) \]
\[ \left( \begin{array}{ccccccc} 1 & -2 & 2 & | & 0 & 1 & 0\\ 0 & 5 & -8 & | & 1 & -2 & 0\\ 0 & 2 & -3 & | & 0 & -3 & 1\\ \end{array} \right) \]
Para obtener el pivote de la segunda columna, hace falta un 1 en la posición 2-2. Para eso, se divide toda la fila por 5: F'2 = F2/5
\[ \left( \begin{array}{ccccccc} 1 & -2 & 2 & | & 0 & 1 & 0\\ 0 & 1 & -1,6 & | & 1 & -0,4 & 0\\ 0 & 2 & -3 & | & 0 & -3 & 1\\ \end{array} \right) \]
Para completar de ceros la columna 2, se hace: F'1 = F1 + 2 · F2 y F'3 = F3 - 2 · F2.
\[ \left( \begin{array}{ccccccc} 1 & 0 & -1,2 & | & 0,4 & 0,2 & 0\\ 0 & 1 & -1,6 & | & 0,2 & -0,4 & 0\\ 0 & 0 & 0,2 & | & -0,4 & -2,2 & 1\\ \end{array} \right) \]
Queda así lista la columna 2.
Ahora, se busca el pivote en la tercera columna. Para tener un 1 en la posición 3-3, se hace:
F'3 = F3/(0,2)
\[ \left( \begin{array}{ccccccc} 1 & 0 & -1,2 & | & 0,4 & 0,2 & 0\\ 0 & 1 & -1,6 & | & 0,2 & -0,4 & 0\\ 0 & 0 & 1 & | & -2 & -11 & 5\\ \end{array} \right) \]
Para completar con ceros el resto de la tercera columna, solo hace falta hacer:
F'1 = F1 + 1,2 · F3
F´2 = F2 + 1,6 · F3
\[ \left( \begin{array}{ccccccc} 1 & 0 & 0 & | & -2 & -13 & 6\\ 0 & 1 & 0 & | & -3 & -18 & 8\\ 0 & 0 & 1 & | & -2 & -11 & 5\\ \end{array} \right) \]
Por lo tanto, la matriz inversa buscada es:
\[ A^{-1} = \left( \begin{array}{ccc} -2 & -13 & 6\\ -3 & -18 & 8\\ -2 & -11 & 5\\ \end{array} \right) \]
Se puede comprobar que esta es la matriz inversa, realizando la multiplicación entre A-1 y la matriz A.
Encuentre la solución del sistema, utilizando el método de la matriz inversa.
Para resolver el sistema, conviene escribirlo primero como un producto de matrices:
\[ \left( \begin{array}{ccc} 2 & 1 & -4\\ 1 & -2 & 2\\ 3 & -4 & 3\\ \end{array} \right) \cdot \left( \begin{array}{c} x\\ y\\ z\\ \end{array} \right) = \left( \begin{array}{c} 9\\ -7\\ -12\\ \end{array} \right) \]
Para resolverlo, se multiplica a la izquierda de ambos miembros por la matriz inversa encontrada:
\[ \left( \begin{array}{ccc} -2 & -13 & 6\\ -3 & -18 & 8\\ -2 & -11 & 5\\ \end{array} \right) \cdot \left( \begin{array}{ccc} 2 & 1 & -4\\ 1 & -2 & +2\\ 3 & -4 & 3\\ \end{array} \right) \cdot \left( \begin{array}{c} x\\ y\\ z\\ \end{array} \right) = \left( \begin{array}{ccc} -2 & -13 & 6\\ -3 & -18 & 8\\ -2 & -11 & 5\\ \end{array} \right) \cdot \left( \begin{array}{c} 9\\ -7\\ -12\\ \end{array} \right) \]
Y se resuelven los productos en ambos miembros:
\[ \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{array} \right) \cdot \left( \begin{array}{c} x\\ y\\ z\\ \end{array} \right) = \left( \begin{array}{c} 1\\ 3\\ -1\\ \end{array} \right) \] \[ \left( \begin{array}{c} x\\ y\\ z\\ \end{array} \right) = \left( \begin{array}{c} 1\\ 3\\ -1\\ \end{array} \right) \]Por lo tanto, la solución del sistema de ecuaciones es
\[ \begin{equation} \left\lbrace \begin{array}{ll} x=1\\ y=3\\ z=-1 \end{array} \right. \end{equation} \]
En el siguiente video <https://www.youtube.com/watch?v=uBeHINQZnUU> se explica cómo calcular matrices inversas, utilizando Excel.
Ejercicio 12
Resuelva el siguiente sistema de ecuaciones, utilizando el método de Cramer:
\[ \begin{equation} \left\lbrace \begin{array}{ll} x+3y-z=-5\\ 2x + y + z=0\\ -4x + 4z =2y \end{array} \right. \end{equation} \]
Aquí se explica el método de Cramer y se presentan ejercicios resueltos:
Para resolver este sistema de ecuaciones hay que ordenarlo antes:
\[ \begin{equation} \left\lbrace \begin{array}{ll} x+3y-z=-5\\ 2x + y + z=0\\ -4x -2y + 4z = 0 \end{array} \right. \end{equation} \]
Ahora se reconocen las diferentes matrices que se utilizarán para resolverlo. La matriz de coeficientes es:
\[ A = \left( \begin{array}{ccc} 1 & 3 & -1\\ 2 & 1 & 1\\ -4 & -2 & 4\\ \end{array} \right) \]
Y su determinante es:
\[ |A| = 1 \cdot 1 \cdot 4 + 3 \cdot 1 \cdot (-4) + (-1) \cdot 2 \cdot (-2) - 1 \cdot 1 \cdot (-2) - 3 \cdot 2 \cdot 4 - (-1) \]
\[ \cdot 1 \cdot (-4) = 4 - 12 + 4 + 2 - 24 - 4 = -30 \]La matriz X que se obtiene reemplazando la columna de coeficientes de x de la matriz A por los términos independientes de las ecuaciones, es:
\[ X = \left( \begin{array}{ccc} -5 & 3 & -1\\ 0 & 1 & 1\\ 0 & -2 & 4\\ \end{array} \right) \]
Y su determinante:
\[ |X| = -5 \cdot 1 \cdot 4 + 3 \cdot 1 \cdot 0 + (-1) \cdot 0 \cdot (-2) - (-5) \cdot 1 \cdot (-2) - 3 \cdot 0 \cdot 4 \]
\[ - (-1) \cdot 1 \cdot 0 = -20 + 0 + 0 - 10 - 0 - 0 = -30 \]El valor de x se obtiene:
\[ x = \frac{|X|}{|A|} = \frac{-30}{-30} = 1 \]
De la misma manera se obtienen los valores de y y de z:
\[ Y = \left( \begin{array}{ccc} 1 & -5 & -1\\ 2 & 0 & 1\\ -4 & 0 & 4\\ \end{array} \right) \]
Y su determinante:
\[ |Y| = 1 \cdot 0 \cdot 4 + (-5) \cdot 1 \cdot (-4) + (-1) \cdot 2 \cdot 0 - 1 \cdot 1 \cdot 0 - (-5) \cdot 2 \cdot 4 - (-1) \]
\[ \cdot 0 \cdot (-4) = 0 + 20 + 0 - 0 + 40 - 0 = 60 \]Y el valor de y es:
\[ y = \frac{|Y|}{|A|} = \frac{60}{-30} = -2 \]
Finalmente,
\[ Z = \left( \begin{array}{ccc} 1 & 3 & -5\\ 2 & 1 & 0\\ -4 & -2 & 0\\ \end{array} \right) \]
Y su determinante:
\[ |Z| = 1 \cdot 1 \cdot 0 + 3 \cdot 0 \cdot (-4) + (-5) \cdot 2 \cdot (-2) - 1 \cdot 0 \cdot (-2) - 3 \cdot 2 \cdot 0 - (-5) \]
\[ \cdot 1 \cdot (-4) = 0 + 0 + 20 - 0 - 0 - 20 = 0 \]El valor de z es:
\[ z = \frac{|Z|}{|A|} = \frac{0}{-30} = 0 \]
Por lo tanto, el sistema de ecuaciones tiene como solución a:
\[ \begin{equation} \left\lbrace \begin{array}{ll} x=1\\ y=-2\\ z = 0 \end{array} \right. \end{equation} \]
Resuelva el siguiente problema, planteando un sistema de ecuaciones y resolviéndolo por el método que prefiera.
En un zoológico hay mamíferos, aves y serpientes. Calcule cuántos ejemplares de cada clase hay, sabiendo que en total hay 27 cabezas, 64 patas y el número de mamíferos es el doble que el de serpientes.
Se desea conocer el precio de 3 productos: café, té y cereales surtidos por un mismo proveedor. Se sabe que en el comercio A se pagaron $ 5870 por 8 kilos de café, 1 kg. de té y 2 kgs. de cereales. En el comercio B se pagaron $ 6070 por 5 kgs. de café, 7 de té y 3 de cereales y, finalmente en el comercio C se abonó $ 1970 por 2 kgs. de café, 1 de té y 2 de cereales. Calcule los precios de los productos de este proveedor.
Respuestas:
- Hay 10 mamíferos, 12 aves y 5 serpientes.
- El café cuesta $650 por kilo, el té $330 y los cereales $170.
4.2.3. Sistemas de ecuaciones en Economía
Ejercicio 13
Encuentre el punto de equilibrio de un mercado en el que las funciones de demanda y de oferta vienen dadas por:
D : q = 300 - 3p
O : q = 3p - 60
En el siguiente video, producido por la Universidad Nacional de Quilmes, se explica el concepto de curvas de demanda y de oferta y se representan esta últimas funciones:
Encontrar el punto de equilibrio de un mercado implica encontrar el precio para el cual todas las personas que estén dispuestas a pagar ese precio puedan adquirir todo lo que quieran de ese bien y que todas quienes quieran vender a ese precio, puedan hacerlo. Es decir, a ese precio se “vacía” el mercado. En ese precio, se igualan la oferta y la demanda. Por lo tanto, matemáticamente implica resolver el siguiente sistema de ecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{ll} q = 300 - 3p\\ q = 3p - 60 \end{array} \right. \end{equation} \]
Este es un sistema muy sencillo que se resuelve fácilmente por igualación. Como ambas cantidades son iguales, será:
300 - 3p = 3p - 60
300 + 60 = 3p + 3p
360 = 6p
\[ \frac{360}{60} = 60 = p \]Por lo tanto, el precio de equilibrio es de $60. A ese precio se demandan:
q = 300 - 3 · 60 = 180 - 60 = 120
120 unidades y también se ofrecen:
q = 3 · 60 - 60 = 180 - 60 = 120
120 unidades.
A este mismo resultado se puede llegar gráficamente. Como se explica en el video, en Economía se grafican los precios en el eje vertical. Por eso, se grafican las funciones inversas (aunque en Economía no se mencione este tema). Buscando las funciones inversas, se llega a que:
\[ D:p = 100 - \frac{q}{3} \] \[ O:p = \frac{q}{3} + 20 \]En el siguiente gráfico, confeccionado con Geogebra, se aprecia ambas funciones y el punto de equilibrio del mercado:
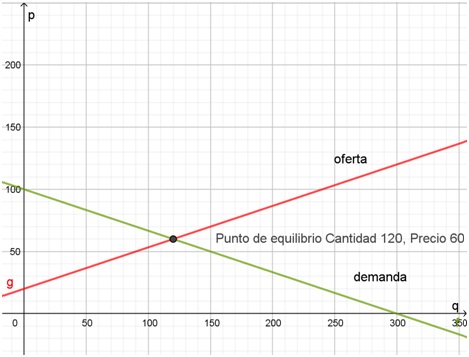
Los sistemas de ecuaciones con dos incógnitas pueden representarse gráficamente. Cuando la solución existe, es la intersección de las curvas que representan las ecuaciones del sistema. En este caso, corresponde al punto de equilibrio del mercado.
Encuentre el equilibrio de cierto mercado en el que las funciones de oferta y de demanda son:
\[ D:p = 1250 - \frac{25}{4}p \] \[ O:p = 25p - 2500 \]Respuesta: el punto de equilibrio de este mercado se logra cuando el precio es de $120 y se compran y venden 500 unidades.
4.2.4. Clasificación de sistemas de ecuaciones
Ejercicio 14
En la producción de cierto medicamento A se utilizan 5 unidades de la droga X y 7 de la Y. En la preparación de otro medicamento B, se requieren 15 unidades de la droga X y 21 de la Y. Si en total el laboratorio dispone de 1400 unidades de la droga X y 2240 de la Y, ¿cuántas unidades del medicamento A y cuántas del B se deberán fabricar para agotar el stock?
Las incógnitas de este problema son:
- a: cantidad de unidades del medicamento A
- b: cantidad de unidades del medicamento B.
La restricción correspondiente al insumo “droga X” se puede expresar por la ecuación:
5 · a + 15 · b = 1400
La restricción correspondiente al insumo “droga Y” se puede expresar por la ecuación:
7 · a + 21 · b = 2240
Entonces, el sistema de ecuaciones será:
\[ \begin{equation} \left\lbrace \begin{array}{ll} 5 \cdot a + 15 \cdot b = 1400 \\ 7 \cdot a + 21 \cdot b = 2240 \end{array} \right. \end{equation} \]
Que se puede resolver por cualquiera de los métodos ya estudiados.
Se utilizará el de Cramer, por su sencillez:
\[ a = \frac{|^{1400}_{2240} \ ^{15}_{21}|} {|^{5}_{7} \ ^{15}_{21}|} = \frac{-4200}{0} \]Claramente, no se puede dividir por cero. En este caso, significa que el sistema no tiene solución.
Cuando la matriz correspondiente a los coeficientes del sistema tiene un determinante igual a cero, el sistema de ecuaciones no tiene solución única. Si todos los determinantes correspondientes a las incógnitas también son nulos, el sistema es indeterminado, lo que significa que tiene infinitas soluciones. Pero, como en este caso, cuando por lo menos uno de esos determinantes no es cero, el sistema es incompatible, es decir, no tiene solución.
Gráficamente, se puede apreciar cuál es la situación:
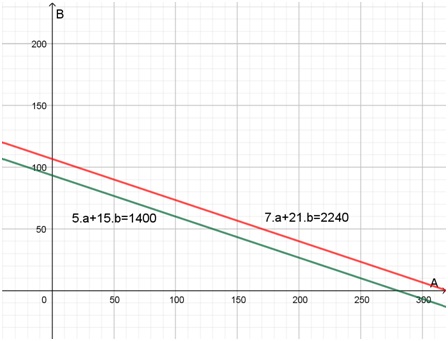
Las rectas que corresponden a la representación gráfica de las ecuaciones de este sistema son paralelas. Por eso no se intersecan y el sistema no tiene solución.
Sin embargo, respondiendo a la pregunta del problema, toda la región comprendida entre la recta verde (la ecuación 1) y los ejes cartesianos, son puntos posibles de producir. La recta verde es la “frontera de posibilidades de producción”. Toda la región sombreada en verde en el gráfico siguiente, confeccionado también con Geogebra, corresponde a combinaciones de los medicamentos A y B que se pueden fabricar con los insumos disponibles. Para agotar el stock se puede elegir cualquier punto sobre la recta borde. Por ejemplo, 280 medicamentos A y ninguno del B. O una unidad del medicamento A y 93 del B.
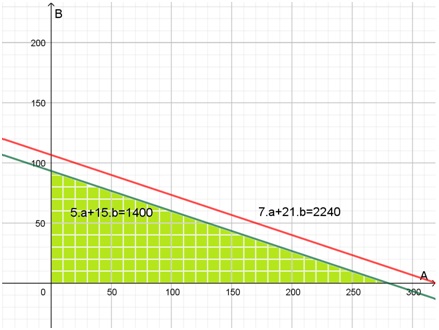
Ejercicio 15
Dado el sistema de ecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{lll} x + k \cdot y + 3 \cdot z= 12 \\ k \cdot z = - 7 + 2 \cdot x + y\\ 2 \cdot k \cdot z = 0 \end{array} \right. \end{equation} \]
Determine para qué valores de k resulta compatible determinado, para cuáles es compatible indeterminado y para cuáles es incompatible.
Si un sistema de ecuaciones lineales es compatible, el determinante de la matriz de coeficientes debe ser diferente a cero. Pero antes, es necesario ordenar y completar el sistema de ecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{lll} x + k \cdot y + 3 \cdot z= 12 \\ -2 \cdot x - y + k \cdot z = - 7 \\ 0 \cdot x + 0 \cdot y + 2 \cdot k \cdot z = 0 \end{array} \right. \end{equation} \]
Ahora sí, se calculará el determinante de la matriz de coeficientes, utilizando la regla de Sarrus.
\[ \left| \begin{array}{ccc} 1& k & 3\\ -2 & -1 & k\\ 0 & 0 & 2k\\ 1 & k & 3\\ -2 & -1 & 2k\\ \end{array} \right| = 1 \cdot (-1) \cdot 2k + (-2) \cdot 0 \cdot 3 + 0 \cdot k \cdot 2k \]
\[ -[3 \cdot (-1) \cdot 0 + k \cdot 0 \cdot 1 + 2k \cdot k \cdot (-2) ]= \]\[ =-2k + 0 + 0 - (0+0-4k^2) = 4k^2 - 2k \neq 0 \]
Para que este determinante no resulte igual a cero, deberá ser \( k \neq 0 \) o \( k \neq \frac{1}{2} \) que son los valores que anulan la expresión anterior (calculados, por ejemplo, utilizando la fórmula de la resolvente).
Por lo tanto, si k pertenece al conjunto \( \Re - \left\lbrace 0; \frac{1}{2} \right\rbrace \), el sistema de ecuaciones será compatible y determinado.
Para averiguar qué sucede cuando \( k= \frac{1}{2} \), se calculará el determinante correspondiente a la variable x, cuando k toma este valor.
\[ |X| = \left| \begin{array}{ccc} 12& 1/2 & 3\\ -7 & -2 & 1/2\\ 0 & 0 & 1\\ \end{array} \right| = -8,5 \neq 0 \]
Como hay al menos un determinante de coeficientes que es distinto de cero, el sistema será incompatible cuando \( k = \frac{1}{2} \) .
Falta averiguar qué sucede cuando k = 0. Con ese objetivo, se calcularán los determinantes correspondientes a todas las variables, cuando k toma este valor:
\[ |X| = \left| \begin{array}{ccc} 12& 0 & 3\\ -7 & -1 & 0\\ 0 & 0 & 0\\ \end{array} \right| = 0 \]
\[ |Y| = \left| \begin{array}{ccc} 1& 12 & 3\\ -2 & -7 & 0\\ 0 & 0 & 0\\ \end{array} \right| = 0 \]
\[ |Z| = \left| \begin{array}{ccc} 1& 0 & 12\\ -2 & -1 & -7\\ 0 & 0 & 0\\ \end{array} \right| = 0\]
Como todos los determinantes son nulos, el sistema es indeterminado cuando k = 0.
En resumen, todo lo dicho hasta aquí es:
Si k = 0, el sistema resulta indeterminado (infinitas soluciones).
Si \( k = \frac{1}{2} \), el sistema resulta incompatible (no tiene solución).
Si \( k \in \Re - \left\lbrace 0; \frac{1}{2} \right\rbrace \), el sistema es compatible determinado (tiene solución única).
Como este sistema de ecuaciones tiene tres incógnitas, no puede graficarse en un plano cartesiano.
Determine para qué valores de k, el siguiente sistema es compatible determinado, indeterminado o incompatible:
\[ \begin{equation} \left\lbrace \begin{array}{lll} k \cdot x + y + 7z = -4 \\ -5x + (k+3) \cdot y + z = -15 \\ y + 2z = -1 \end{array} \right. \end{equation} \]
Respuesta:
Si k = 2,5 o si k = -5, el sistema resulta incompatible (no tiene solución).
Si \( k \in \Re - \{-5;2,5 \} \), el sistema es compatible determinado (tiene solución única).
Ejercicio 16
Resuelva el siguiente sistema de ecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{lll} x + 3y = 11 - z \\ z + x = 3 + y \\ 2x + 6y = 22 - 2z \end{array} \right. \end{equation} \]
Antes de comenzar, es necesario ordenar el sistema. Así, se obtiene:
\[ \begin{equation} \left\lbrace \begin{array}{lll} x + 3y + z = 11 \\ x - y + z = 3 \\ 2x + 6y + 2z = 22 \end{array} \right. \end{equation} \]
Se resolverá utilizando la método de Gauss. Para ello, se escribe la matriz ampliada:
\[ \left( \begin{array}{ccccc} 1 & 3 & 1 & | & 11\\ 1 & -1 & 1 & | & 3\\ 2 & 6 & 2 & | & 22\\ \end{array} \right) \]Se toma como pivote el primer elemento de la primera fila y para anular el resto de la primera columna, se hace: F'2 = F2 - F1 y F'3 = F3 - 2 · F1 y se obtiene:
\[ \left( \begin{array}{ccccc} 1 & 3 & 1 & | & 11\\ 0 & -4 & 0 & | & -8\\ 0 & 0 & 0 & | & 0\\ \end{array} \right) \]
Así, la tercera fila se anuló completamente. Esto significa que el sistema de ecuaciones es indeterminado: no tiene solución única sino que tiene infinitas soluciones. A esta misma conclusión se podría haber llegado, analizando el sistema por la regla de Cramer. La ventaja de utilizar Gauss es que se va a poder llegar a obtener alguna solución posible. Con ese objetivo, se sigue trabajando con las dos filas que no son completamente nulas. Para buscar un pivote en la posición 2-2 , se divide toda la fila 2 por -4
\[ \left( \begin{array}{ccccc} 1 & 3 & 1 & | & 11\\ 0 & 1 & 0 & | & 2\\ 0 & 0 & 0 & | & 0\\ \end{array} \right) \]
Para conseguir un 0 en la posición 1-2, se hace: F'1 = F1 - 3 · F2
\[ \left( \begin{array}{ccccc} 1 & 0 & 1 & | & 5\\ 0 & 1 & 0 & | & 2\\ 0 & 0 & 0 & | & 0\\ \end{array} \right) \]
Reescribiendo esta matriz como un sistema de ecuaciones, queda:
\[ \begin{equation} \left\lbrace \begin{array}{lll} x + 0 \cdot y + z = 5 \\ 0 \cdot x + y + 0 \cdot z = 2 \\ 0 \cdot z + 0 \cdot y + 0 \cdot z = 0 \end{array} \right. \end{equation} \]
Es decir:
\[ \begin{equation} \left\lbrace \begin{array}{lll} x + z = 5 \\ y = 2 \\ 0 = 0 \end{array} \right. \end{equation} \]
Aquí se puede apreciar que todas las ternas que cumplan con las dos ecuaciones satisfacen el sistema de ecuaciones original. Por ejemplo:
\( \begin{equation} \left\lbrace \begin{array}{lll} x = 5 \\ y = 2 \\ z = 0 \end{array} \right. \end{equation} \) o \( \begin{equation} \left\lbrace \begin{array}{lll} x = 3 \\ y = 2 \\ z = 1 \end{array} \right. \end{equation} \) o \( \begin{equation} \left\lbrace \begin{array}{lll} x = 2 \\ y = 2 \\ z = 3 \end{array} \right. \end{equation} \)
En general, se pueden escribir todas las posibles soluciones como
\[ \begin{equation} \left\lbrace \begin{array}{lll} x = 5 - z \\ y = 2 \\ z = z \end{array} \right. \end{equation} \]
Y z puede tomar cualquier valor real.
Geométricamente ese sistema de ecuaciones equivale a una recta en el espacio. Pero eso excede al nivel de este curso.
Ejercicio 17
Resuelva el siguiente sistema de ecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{lll} x + y = 5 + z \\ x + z + 5 = 5y \\ 3x + 3y = 16 + 3z \end{array} \right. \end{equation} \]
Como siempre, primero se ordena el sistema:
\[ \begin{equation} \left\lbrace \begin{array}{lll} x + y - z = 5 \\ x - 5y + z = -5 \\ 3x + 3y -3z = 16 \end{array} \right. \end{equation} \]
La matriz ampliada es
\[ \left( \begin{array}{ccccc} 1 & 1 & -1 & | & 5\\ 1 & -2 & 1 & | & -5\\ 3 & 3 & -3 & | & 16\\ \end{array} \right) \]
Tomando como pivote el 1 que se encuentra en la posición 1-1, para anular toda la primera columna se hace: F'2 = F2 - F1 y F'3 = F3 - 3 · F1:
\[ \left( \begin{array}{ccccc} 1 & 1 & -1 & | & 5\\ 0 & -3 & 2 & | & -10\\ 0 & 0 & 0 & | & 1\\ \end{array} \right) \]
En este caso, la última fila corresponde a la siguiente ecuación:
0 · z + 0 · y + 0 · z = 1
Es decir 0 = 1
Esta situación es imposible. Por eso, este sistema de ecuaciones es incompatible, es decir, no tiene solución.
Encuentre la solución del siguiente sistema de ecuaciones:
\[ \begin{equation} \left\lbrace \begin{array}{lll} 2x + 3y - z = 4 \\ 3x + 4,5y - 1,5z = 6 \\ x + 2y - z = 5 \end{array} \right. \end{equation} \]
Respuesta: este sistema es indeterminado. Sus infinitas soluciones tienen la forma:
\[ \begin{equation} \left\lbrace \begin{array}{lll} x = -7 - z \\ y = 6 + z \\ z = z \end{array} \right. \end{equation} \]
Por ejemplo la terna \( \begin{equation} \left\lbrace \begin{array}{lll} x = -7 \\ y = 6 \\ z = 0 \end{array} \right. \end{equation} \) satisface el sistema.

