4.2. Vectores
En el trabajo con cada uno de los modelos de comportamientos físicos que serán aplicados en los programas de esta unidad se utilizarán vectores. El tipo de vectores a utilizar serán Euclidianos (por Euclides, claro), los cuales son entidades que tienen una determinada magnitud (o módulo) y una dirección. De esta manera, se pueden representar de manera efectiva fuerza, velocidad, dirección, aceleración, mediante su magnitud, o sea, cuánto de cada una de estas se aplica, y en qué dirección se aplica, y así poder generar entes que se mueven en un espacio en dos o tres dimensiones. En general, un vector se representa por una flecha, cuyo largo representa la magnitud y, hacia donde apunta, representa su dirección.
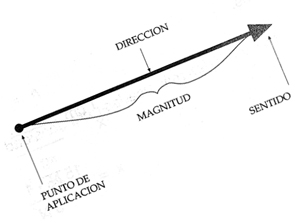
Aquí puede observarse su magnitud y dirección, y también se ve representado su sentido y punto de aplicación.
Fuente: gráfico creado para esta unidad.
Este vector contiene toda la información para ubicar y caracterizar la forma en que un objeto se presenta en un espacio,
y en este caso representa esta información en dos dimensiones, y por lo tanto, contendrá datos en las coordenadas X e Y.
Las operaciones entre vectores son diferentes a las que se realizan con números. A continuación, se verá cómo realizar
diferentes operaciones con vectores y cómo esas operaciones se representan en el entorno de Processing.
4.2.1. Operaciones matemáticas básicas con vectores
Como se indicó arriba, los vectores son muy útiles para describir las diferentes características físicas que tiene, por
ejemplo, una pelota dibujada en un Sketch en 2D. Esta pelota puede tener las siguientes características:
Ubicación x, ubicación y
Velocidad x, velocidad y
Es claro que para describir cada una de estas características es necesario hacerlo en las dimensiones X e Y que presenta
Processing. Si se quisiera generar un programa que mueva esta pelota por el Sketch, la siguiente sería la forma de
determinar cada una de estas variables sin la utilización de vectores:
//Ubicación en la coordenada x de la pelota
float x = 50;
//Ubicación en la coordenada y de la pelota
float y = 50;
//Velocidad en la coordenada x de la pelota
float Velx = 10;
//Velocidad en la coordenada y de la pelota
float Vely = 5;
Y así con cada una de las cualidades que se vayan agregando, como la aceleración, la fricción, o el viento que afectará
el movimiento de la pelota. Utilizando vectores dentro de Processing se puede simplificar la escritura y realizar
operaciones de una forma más sencilla. El mismo código arriba descrito puede reformularse de la siguiente manera:
//Este vector contiene la ubicación x e y
PVector ubicacion = new PVector(50, 50);
//Este vector contiene la velocidad en x e y
PVector velocidad = new PVector(10, 5);
Como se observa, para trabajar con un vector se utiliza el objeto PVector, el cual contiene los campos y métodos necesarios
para una correcta operación entre estos.
Entonces, es hora de pensar en una forma sencilla de mover esa pelota, utilizando los datos de ubicación y velocidad
que fueron escritos arriba. Para que la pelota se mueva en el tiempo, se debe actualizar su ubicación en X e Y en cada
cuadro de procesamiento de Processing. Esta actualización se produce en el loop draw(), por lo tanto, se deben ubicar
allí las funciones necesarias para realizar el movimiento y la actualización en cada vuelta del loop.
Pero ¿cómo el programa puede saber cuándo y cuánto la pelota debe moverse? La respuesta a esa pregunta está en
el valor de la velocidad que se indica en cada eje. La velocidad describe la relación entre la cantidad de movimiento
(en metros, centímetros o píxeles como este caso) en una determinada unidad de tiempo (en este caso los Frames o
cantidad de cuadros por segundo). Si se suma la velocidad establecida a la ubicación actual de la pelota, se producirá
entonces un movimiento específico que está directamente relacionado con una tasa de tiempo.
Por supuesto que se debe tener en cuenta que la ubicación de la pelota se actualizará en cada cuadro y que es necesario
guardar esta información en cada momento. La fórmula que describe este procedimiento es la siguiente:
ubicación = ubicación + velocidad
Utilizando las variables (sin los vectores) el problema se resolvería de la siguiente manera en ambos ejes:
//Se suma la velocidad a cada una de las coordenadas de cada eje
x = x + Velx;
y = y + Vely;
Utilizando vectores esto puede resolverse en una sola línea:
ubicación.add(velocidad);
Cada vector contiene métodos que resuelven diferentes tipos de operaciones. En este caso, se requería sumar al vector
ubicación el vector velocidad, y para eso se utilizó el método add.
De esta manera, se resolvió de forma sumamente fácil el movimiento de la pelota y además se aprendió cómo sumar
vectores. Un ejemplo práctico se presenta en el siguiente ejemplo complementario:
CAP5EjemploComplmentario1.pde
Actividad 1
A partir del ejemplo complementario anterior, generar un programa que simule la lluvia con, por lo menos, 20 gotas. Utilizar vectores para la simulación del movimiento.
A continuación, se revisarán algunos de los métodos que contienen los vectores y que permiten realizar operaciones entre estos.
4.2.2. Operaciones entre vectores disponibles en Processing
Como se indicó anteriormente, la forma de realizar operaciones entre vectores es diferente a la que se acostumbra
con números sin estas características. Por suerte los PVector`s de Processing contienen métodos para diferentes operaciones
que pueden ser realizadas directamente.
Los métodos que contienen los PVector de Processing y que permiten realizar operaciones varias son:
La palabra Vector que antepone a cada operación se utiliza solamente a modo ilustrativo. En la operatoria normal, en lugar de la palabra vector se pone el nombre del PVector con el cual se desea realizar la operación.
//Se define el objeto vector, que es utilizado luego en las operaciones
PVector Vector;
//Suma de vectores. Recibe como argumento otro PVector
Vector.add(PVector one);
//Resta de vectores. Recibe como argumento otro PVector.
Vector.sub(PVector one);
//Multiplicación. Multiplica el vector por un escalar. Recibe como argumento un número.
Vector.mult(float numero);
//División. Divide un vector por un escalar. Recibe como argumento un
//número.
Vector.div(float numero);
//Magnitud. Calcula la magnitud del vector.
Vector.mag();
//Magnitud. Configura la magnitud del vector. Recibe como argumento un //número.
Vector.setMag(float numero);
//Normalización. Normaliza el vector a 1. Lo convierte en un vector
//unidad.
Vector.normalize();
//Limitador. Limita la magnitud del vector. Recibe como argumento un
//número.
Vector.limit(float numero);
//Rotación. Calcula el ángulo de rotación del vector.
Vector.heading2D();
//Rotación. Rota el vector a un determinado ángulo. Recibe como
//argumento un número, el ángulo en radianes.
Vector.rótate(float angulo);
//Interpolación. Interpolación lineal entre un vector y otro. Recibe como
//argumento otro vector.
Vector.lerp(PVector one);
//Distancia. Calcula la distancia entre dos puntos, considerando al punto
//como un vector. Recibe como argumento otro vector
Vector.dist(PVector one);
//Ángulo. Calcula el ángulo entre dos vectores. Recibe como argumento
//otro vector.
Vector.angleBetwen(PVector one);
//Producto escalar. Calcula el producto escalar entre dos vectores. Recibe
//como argumento otro vector.
Vector.dot(PVector one);
//Producto cruzado de vectores. Recibe como argumento otro vector.
Vector.cross(PVector one);
//Aletoriedad. Configura un vector en 2D como un vector unidad con una
//dirección aleatoria.
Vector.random2D();
//Aleatoriedad. Configura un vector en 3D como un vector unidad con una
//dirección aleatoria.
Vector.random3D();
4.2.3 Vector de velocidad
Mediante el aprendizaje de las operaciones con vectores se puede comenzar a describir y programar algunos comportamientos
básicos que tienen que ver con el movimiento de objetos. Ya se observó que la velocidad de un objeto
se suma a la posición de dicho objeto para moverlo en un determinado espacio. Es el caso de la pelota que se mencionó
anteriormente. Dentro de Processing los pasos son secuenciales, primero se debe mover la pelota, o sea, sumarle
la velocidad a la posición y luego dibujar la pelota, que en este caso será mediante la función primitiva ellipse (la cual
aprendimos a usar al principio del curso). En el ejemplo complementario 1 se observa la resolución de este comportamiento
mediante operaciones comunes.
Se puede decir que el algoritmo funciona de la siguiente manera:
1- Suma la velocidad a la posición
2- Dibujo el objeto con la nueva posición
En código Processing utilizando vectores esto sería:
//Se suma la velocidad a la ubicación actual
ubicación.add(velocidad);
//Se dibuja la elipse que representa la pelota
ellipse(ubicación.x, ubicación.y, 40, 40);
Obsérvese cómo la ubicación de la elipse se determina mediante los campos internos del vector ubicación.
Si se unen todas las partes del código que se escribieron hasta este momento en el transcurso de la unidad y se suman
otras también importantes, se puede crear una clase que genere el movimiento de una elipse teniendo en cuenta el
uso de PVector, ubicación y velocidad. La clase estaría conformada entonces como se indica en el siguiente ejemplo:
//Se define la clase mover con sus campos y métodos básicos
class mover
{
//Se definen los vectores de ubicación y velocidad
Pvector ubicacion;
Pvector velocidad;
//Se define un método para actualizar la posición de la elipse
void actualizar()
{
ubicacion.add(velocidad);
}
//Otro método que muestra la elipse a partir de la posición actualizada
void mostrar()
{
stroke(0);
fill(175);
ellipse(ubicación.x, ubicación.y, 40,40);
}
}
Sería interesante poder agregar métodos que vayan dotando al programa de características interesantes. Por ejemplo,
darle al programa la capacidad de detectar cuándo la pelota ha salido por un lado de la pantalla, para aparecer del
otro lado y así dar la impresión de que la elipse se mueve en un entorno cerrado, como en el ejemplo complementario
1. Para este método, se utilizarán dos condicionales que evaluarán la posición de la elipse en cada frame y cuando
se haya sobrepasado alguno de los bordes, inicializará la posición x o y, haciendo que el movimiento continúe en el
extremo opuesto:
//Método que detecta bordes
void detectarBordes()
{
//Si la ubicación X de la pelota es mayor a la de la pantalla o
//menor a cero se determina la nueva posición
if(ubicacion.x > width)
{
ubicacion.x = 0;
}
else if(ubicacion.x < 0)
{
ubicacion.x = width;
}
//Se configura un comportamiento similar al anterior, pero en
//el eje Y
if(ubicacion.y > height)
{
ubicacion.y = 0;
}
else if(ubicacion.y < 0)
{
ubicacion.y = heigth;
}
}
4.2.4. Vector de velocidad
Hasta ahora la pelota que sirve de ejemplo se mueve a velocidad constante, pero en la vida real pocas veces sucede
esto, ya que en un entorno real existe también la aceleración. La aceleración, estrictamente hablando, es la tasa a la
cual varía la velocidad. Es claro que la aceleración afecta a la velocidad y esta a la ubicación de la elipse. En definitiva,
la aceleración definirá cómo cambia la velocidad con respecto al tiempo. Por lo tanto, la aceleración es un vector que
se le suma a la velocidad y cambia su magnitud.
En Processing esto se establece de la siguiente forma, primero actualizando la velocidad y luego, la ubicación:
velocidad.add(aceleracion);
ubicación.add(velocidad);
Lo interesante de esta forma de trabajar es que solamente con cambiar los valores de aceleración se afectan los valores
de ubicación y velocidad. La aceleración puede mantenerse constante, tomar valores aleatorios o estar afectada
por el movimiento del mouse, convirtiéndose en un efecto dinámico de una forma muy sencilla.
Al tratarse de un valor que se suma a la velocidad, en algún momento tal vez quiera limitarse su magnitud y por lo tanto
se debe utilizar un método que realiza esta acción, para que justamente los valores de velocidad no se desboquen.
En Processing se aplicará la operación de limitación para tal fin:
velocidad.limit(5);