
4.7. Modelado físico
La técnica de síntesis por modelado físico se basa en modelos matemáticos que simulan el comportamiento físico de
los instrumentos musicales.
Como parte de estas técnicas, nos detendremos en la simulación de las cuerdas punteadas –como la guitarra– para lo
cual utilizaremos un desarrollo conocido como algoritmo de Karplus-Strong.
Alexander Strong fue el inventor del algoritmo, y Kevin
Karplus formalizó el modelo matemático sobre el cual
se basa su funcionamiento. El instrumento así creado
fue denominado digitar (por digital guitar) por los autores,
y consiste en una breve banda de ruido a la cual se
le aplica un retardo seguido de un filtrado de agudos.
La salida de la señal retardada y filtrada reingresa nuevamente
en el circuito, de forma periódica, dando lugar
a un sonido de altura definida, similar al de una cuerda
pellizcada.
A fin de implementarlo, y según lo hemos descrito, deberemos recurrir a operaciones de retardo y de filtrado que desarrollaremos
en detalle posteriormente (en las Unidad 5 y Unidad 6, respectivamente). No obstante ello, emplearemos
los objetos de Pure Data que realizan estas tareas, adelantándonos al tratamiento más profundo de estos temas.
4.7.1. Generación de bandas de ruido centradas en torno a una frecuencia dada
La fuente de excitación del algoritmo, según mencionamos antes, está dada por una banda de ruido. La posibilidad
de modificar el ancho y la ubicación de la banda en el registro nos permite simular diferentes comportamientos del
instrumento, derivados del modo de ejecución. Una guitarra, por ejemplo, suena de forma diferente si pulsamos la
cuerda cerca del puente (elemento de sujeción de las cuerdas sobre la caja), o cerca del orificio de la caja de resonancia.
En el primer caso, el sonido producido es brillante y, bastante más opaco, en el segundo.
Para imitar este comportamiento vamos a partir del objeto rand~ que genera una señal de audio a partir de números
aleatorios. Por su inlet recibe la cantidad de números a generar por segundo y traza rampas entre ellos para calcular
los valores de las muestras intermedias. Mientras mayor es la cantidad de números al azar, más se aproxima el sonido
al ruido blanco. Si, en cambio, el número se hace más pequeño, el sonido resultante se asemeja a un ruido cada vez
más filtrado en agudos.
Cuando tratamos la modulación en anillo vimos que al multiplicar dos señales de audio se producía la convolución de sus
espectros. Podemos utilizar ese principio para continuar modelando la banda de ruido generada por rand~, desplazándola
en el registro de audio mediante una multiplicación con una señal sinusoidal. A través de este proceso, las
frecuencias de las componentes del ruido se suman y se restan a la frecuencia de la sinusoide, centrándose en torno
a ella. G.4.19. muestra la programación necesaria para alcanzar este propósito.
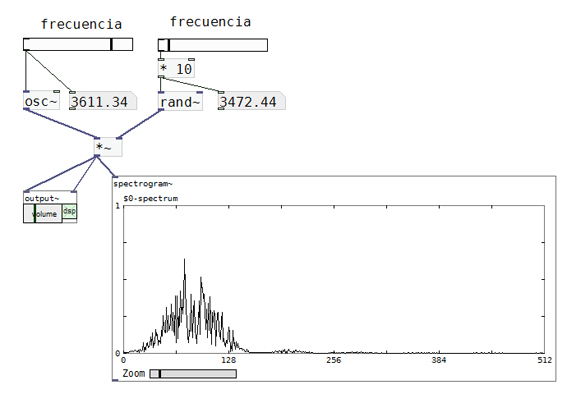
Según se aprecia en G.419. utilizamos el objeto denominado spectrogram~ para representar gráficamente el espectro de la señal resultante.
El patch “40-rand.pd” contiene la programación de la figura G.4.19. Experimente la generación de bandas de ruido, modificando la frecuencia del objeto rand~ y la frecuencia de la sinusoide producida por el oscilador.
El algoritmo de Karplus-Strong
El ruido que sirve de excitación –y que se compara con la acción de pulsar la cuerda– debe durar un tiempo idéntico
al del retardo a aplicar. Para ello, una envolvente generada con vline~ deja pasar la señal de ruido y la interrumpe
luego de una cantidad de milisegundos preestablecida. La señal retardada vuelve a ingresar en la línea de retardo
repetidamente, pero multiplicada cada vez por un valor inferior a 1, por lo cual, pasado cierto tiempo se extingue. En
las sucesivas repeticiones produce una señal periódica, que es percibida como un sonido tónico, y que decrece en
amplitud a medida que el tiempo transcurre. El tiempo de retardo equivale al período de la señal sintetizada y, por
lo tanto, es la inversa de la frecuencia (T = 1 / f , donde T es el tiempo que dura un ciclo, expresado en segundos, y f la
frecuencia del sonido).
Nótese, además, que luego del retardo, ubicamos un filtro pasabajos (este filtro elimina las componentes de mayor
frecuencia y deja pasar las más bajas), que actúa cada vez que la señal abandona la línea de retardo. Mediante este
recurso la señal no solo decrece en amplitud, sino que se torna más y más opaca con el paso del tiempo.
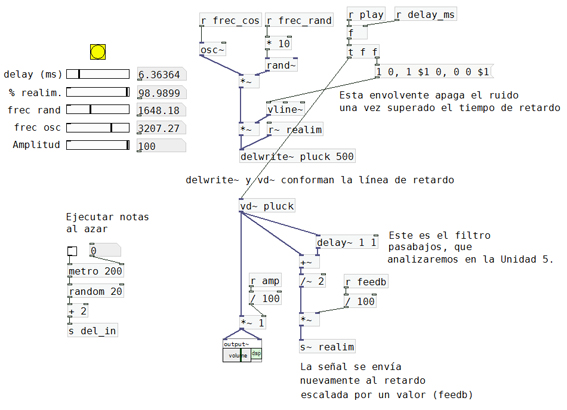
El patch “41-Karplus Strong básico.pd” contiene la programación de G.4.20. Es conveniente que luego de estudiar las unidades
SERRA, J. “Perspectivas actuales en la síntesis digital de sonidos musicales”, [EN LÍNEA].
En: Formats. Revista de Comunicación Audiovisual. Barcelona. Universidad Pompeu Fabra. 1997. Disponible en: <http://www.iua.upf.edu/formats/formats1/a07et.htm>
[Consulta: 23 de julio de 2013].
Actividad 1
a. Programar un patch que produzca sonidos no tónicos por síntesis aditiva cuyas
frecuencias se generen aleatoriamente.
b. Aplicar a cada componente una envolvente de dos pasos que también se genere
por medio del azar.
En el archivo “Respuesta Actividad 05.pd” encontrará una posible solución de este ejercicio.
Compare los resultados que obtuvo con los del archivo y anote las diferencias.
Actividad 2
Programar un patch de síntesis de sonido por frecuencia modulada, empleando tres
osciladores en cascada. Los dos primeros osciladores generan una FM simple, y la
salida se utiliza para modular a un tercer oscilador que produce la señal portadora.
En el archivo “Respuesta Actividad 06.pd” encontrará una posible solución de este ejercicio.
Compare los resultados que obtuvo con los del archivo y anote las diferencias.