7.2. La selección natural, desglosando el algoritmo genético
Una vez establecidas las características fundamentales de los algoritmos genéticos, es necesario describir los tres
núcleos principales de la teoría evolutiva de Darwin, los cuales serán implementados en los programas que se crearán
a partir del lenguaje Processing. Para emular la selección natural, parte de la teoría darwiniana, presente en la naturaleza,
deben existir estos tres elementos:
A partir de estas nociones se puede empezar a estudiar un algoritmo genético. En general, este se divide en dos partes:
un conjunto de condiciones de inicialización y un estado donde se repiten ciertas operaciones hasta llegar a la
respuesta correcta.
7.2.1. Crear una población y aplicar la teoría evolutiva
Para explicar cómo aplicar un algoritmo a un problema determinado se partirá del ejemplo que propone Danniel
Shiffman en su libro “Nature of Code”.
Shiffman utiliza una clásica suposición de la teoría de las probabilidades (teoría del mono infinito), que sostiene que
si tenemos determinada cantidad de monos golpeando las teclas de una máquina de escribir al azar, en un momento
y en un tiempo determinado, estos monos podrían escribir una obra de Shakespeare o, por lo menos una frase del
Bardo de Avon.
Esto parte de la idea de que al ejecutar teclas totalmente al azar, en un tiempo determinado, alguna de las combinaciones
que ejecutan los monos tiene que ser poder compararse a una frase legible. Es una idea un tanto divertida,
pero que sirve de ejemplo. Danniel Shiffman realiza una explicación magistral sobre cómo sería exactamente llegar a
esta combinación, pero no se presentará en este apartado.
El desarrollo de la teoría de los monos infinitos propuesta por Daniel Shiffman puede revisarse en:
Shiffman, D. (2006), “The nature of code-The evolution of code”, Daniel Shiffman, USA.
Como se dijo anteriormente, las poblaciones de individuos
representan soluciones a un determinado problema.
En este caso de los monos tipeadores, “la población”
son las posibles frases que estos escriban. En este contexto,
las frases son posibles cadenas de caracteres ya
que no todas tendrán un significado en algún idioma.
El problema aquí es cómo crear esta población, ya que
no se tiene una base de desde dónde partir. Para esto,
se utiliza la noción de variación que se estudió antes.
Por supuesto, el algoritmo genético, en su segunda
etapa, contempla la posibilidad de variar lo suficiente
los elementos de la población inicial como para encontrar
el resultado buscado.
Por lo tanto, para ser más específicos, se puede indicar
lo siguiente para empezar:
Se debe crear una población de elementos generados aleatoriamente.
Por ejemplo, si se desea llegar a la frase/palabra “Red” y se tiene
una población de tres frases/palabras: auto, música y polo.
Por supuesto, las tres palabras con sumamente variables, pero si
se trata de generar “Red” a partir de estas, es imposible, dado que
ninguna tiene alguna de las tres letras de esta solución. Esto da la
pauta de que en realidad no existe demasiada variedad en la población
como para obtener una generación donde la frase “Red”
aparezca como solución. Si, en realidad, se tuviera un población
de miles de frases, la probabilidad subiría ya que existiría una mayor
posibilidad de que alguno de los elementos de la población
tuviera una “r” como primer caracter, otra una “e” como segundo
caracter y una “d” como tercer caracter. Estas combinaciones aumentarían
la probabilidad de que una de las soluciones sea la
frase que se está buscando.
De esta manera, se puede empezar a trabajar con una población inicial, pero antes se deben definir algunas nociones
que dan entidad a una población.
En cuanto a los tipos de poblaciones en sí, se pueden tener diferentes escenarios, donde los elementos sean imágenes,
vehículos, partículas, etc. En cuanto a las poblaciones con las que se va a trabajar con los algoritmos genéticos,
se puede decir que cada miembro de la población tiene una especie de “ADN” virtual, el cual define un número determinado
de propiedades (las cuales, para continuar con la analogía, pueden llamarse “genes”) que describen cómo un
elemento dado se ve o se comporta.
A partir de esta idea, se pueden definir conceptos que provienen del campo de la genética, donde se realiza una distinción
importante entre la noción de genotipo y fenotipo. El genotipo de un elemento es el código genético en sí,
la composición de este código, lo que se transmite de generación en generación, y en el caso de un elemento creado
mediante un lenguaje de programación, es su información digital propia. El fenotipo es la manifestación física de esos
rasgos guardados en el código genético, el cual también es afectado por el ambiente y otros genes participantes.
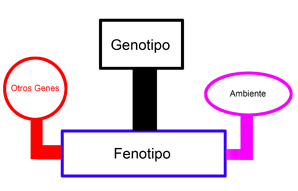
Fuente: gráfica creada para esta unidad.
Por lo tanto, esta distinción es fundamental dentro de los algoritmos genéticos que se diseñen. ¿Cuáles son los objetos
que van a ocupar el nuevo mundo que se crea? ¿Cómo se va a diseñar el genotipo de los objetos, o sea, la estructura
de datos que almacena las propiedades? ¿Cómo se va a diseñar el fenotipo del objeto, o sea, la expresión misma
de las variables y funciones?
Por supuesto, esto es algo que se realiza todo el tiempo cuando se programa, pero es muy interesante entenderlo de
esta manera para poder aplicar los algoritmos que se estudian aquí.
Un ejemplo interesante es el código de colores que maneja Processing y la representación en pantalla de ese color, el
primero configura el genotipo y el segundo el fenotipo del elemento. Uno es la información, el color que se elige mediante
una variable, y otro, la expresión, el color que se ve en pantalla, que depende del tipo de monitor que usemos,
o si se trata de una impresión en papel, etcétera.
El caso de las frases que escriben los monos en el ejemplo planteado es singular debido a que no existe una diferencia
entre el genotipo y el fenotipo, por lo cual, el ADN es la frase en sí mismo y la expresión de este ADN es cada uno de
los caracteres. Por lo tanto, la regla para crear una población inicial en este caso es sumamente sencilla: “Crear una
población de N elementos, cada una de estas con un ADN generado aleatoriamente”.
A partir de esta noción de población inicial hay que empezar a determinar y aplicar los principios de selección que
propone la teoría darwiniana. Para esto, se necesita evaluar cada miembro de la población y determinar cuáles miembros
pueden ser seleccionados para la siguiente generación de la población.
El proceso de selección puede dividirse en dos partes: la evaluación de la actitud y la creación de un grupo de reproducción.
Se crea, entonces, una función que produce un puntaje que describe la actitud de un miembro de la población con respecto a la solución del problema. Por supuesto, esto no sucede en la vida real, pero es una manera que se
tiene para crear el algoritmo de selección y obtener una solución óptima.
En el caso de las frases de los monos, se podría evaluar la cantidad de caracteres correctos que tiene una palabra y
otorgarle un puntaje por ello.
Una vez que se ha puesto un puntaje a cada miembro, se seleccionan los más adecuados para que sean padres y son
ubicados dentro del grupo de reproducción. Una vez que se está en esta instancia, se podría elegir a los dos mejores
puntajes (y de hecho sería muy simple de programar esta alternativa), pero esto produciría que la siguiente generación
no tenga mucha variación, lo que no sería positivo para generaciones futuras, impidiendo el proceso evolutivo.
La mejor solución es utilizar un método probabilístico, en este caso una especie de rueda de la fortuna. En este método
se otorga a cada miembro una sección en porcentaje de la rueda correspondiente al puntaje que obtuvo.
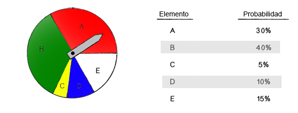
Fuente: gráfica creada para esta unidad.
En la figura se observa que el elemento B tiene el mayor porcentaje de la rueda y, por lo tanto, la mayor probabilidad
respecto de los demás elementos. Cada elemento tiene expresado su porcentaje de probabilidad y esto garantiza
que los elementos que tienen mayor puntaje tengan más posibilidades de reproducirse sin eliminar la variación que
pueden agregar los elementos con menos posibilidades.
Una vez que se tiene una estrategia de selección de elementos de una población, es necesario pensar cómo estos
elementos se reproducirán, teniendo en cuenta las nociones de que herencia que propone Darwin, donde las nuevas
generaciones reciben características de sus padres.
Existen varias estrategias para la reproducción. Por ejemplo, una de estas es la llamada reproducción asexual, donde
se elige uno de los padres y se realiza una copia idéntica de este. Sin embargo, la opción estándar que se utiliza en los
algoritmos genéticos, es tomar a los dos parientes y crear un sucesor de acuerdo con determinados pasos. En general,
se trabaja en dos pasos, en el primero se cruza parte de la información de los padres, en el segundo se genera una
mutación a partir del resultado anterior.
El cruce de la información entre los parientes, involucra crear un descendiente que tenga datos genéticos de ambos.
Por ejemplo, si se tienen las siguientes palabras:
Pariente A: ALAS
Pariente B: PELO
Se puede obtener un descendiente que tenga un 50 % de información de cada pariente, o se puede dar un porcentaje mayor a determinado elemento, o simplemente hacer que sea aleatoria la selección de material genético.
Ejemplos:
Pariente A Pariente B
ALAS PELO
Posibles descendientes
ALPE
ASLO
PLOA
En cuanto a la mutación, se parte de la creación de ADN que se produce del cruce anterior. Una vez obtenido este ADN
se realiza un proceso que agrega información a la nueva generación. Si bien con el cruce de información genética de
los parientes se tiene ya una variación, la mutación permite generar aún más elementos nuevos, lo que hace posible
que la evolución ocurra de una manera eficaz.
La mutación se piensa también en términos de porcentaje, donde se especifica qué cantidad de información genética
del elemento tiene probabilidades de cambiar. Una vez que se fija un porcentaje de mutación y se eligen los elementos,
estos cambian aleatoriamente, produciendo un heredero que cumple con las nociones que postuló Darwin.