6.2. Autómatas celulares (AC)
En la mayoría de los ejemplos que se revisaron con anterioridad, se creaban sistemas complejos donde los integrantes
de estos sistemas podían moverse por el entorno y cumplían ciertas reglas de la física, pero ninguno de estos integrantes
cambiaban sus características básicas con el correr del tiempo, no evolucionaban de ninguna manera. En este contexto,
los AC permiten generar sistemas complejos de muchos objetos y que estos varíen su estado con el correr del tiempo.
Además, este apartado funcionará como un adelanto del tema algoritmos genéticos que trataremos más adelante.
El desarrollo de los sistemas de autómatas celulares (AC) se atribuye generalmente a Stanislaw Ulam y a John von
Neumann, quienes realizaron sus investigaciones en los Laboratorios Nacionales de Los Álamos, en Nuevo México en
la década de 1940. Sin embargo, uno de los científicos más significativos que ha estudiado los autómatas celulares
fue Stephen Wolfram, quien en 2002 publicó uno de los trabajos más importantes sobre este tema, “A new Kind of
science”. Algunos ejemplos que se revisarán en esta unidad provienen de las teorías de Wolfram.
Texto aparte
El libro de Wolfram, “A new kind of science”, presentó, en su momento, muchas teorías controversiales, donde se estudia empírica y sistemáticamente los autómatas celulares aplicados a los sistemas informáticos.
En su definición básica, un AC es un modelo de objeto del tipo “Célula” con las siguientes características:
- Las células viven en una cuadrícula. Los sistemas que se crearán en este capítulo serán unidimensionales y bidimensionales,
pero los AC pueden existir en múltiples dimensiones si así se lo requiriera.
- Cada célula tiene un estado. El número de estados posibles es finito.
- Cada célula tiene una vecindad. O sea, cada célula está rodeada de células adyacentes, en general representadas
por una lista.
6.2.1. Autómata celular elemental
Para empezar a entender cómo se desarrolla un AC elemental, se presentará un ejemplo de simulación de un trabajo de Wolfram. Se puede pensar, en primera instancia, en cuál sería el AC más simple de construir. Sin lugar a dudas, se empieza con un AC unidimensional ya que contiene, de forma básica, todos los elementos que se indican como características de un AC. En este caso, se utilizará el CA de Wolfram, el cual presenta las siguientes características:

De esta manera, se tiene una línea de células con estados iniciales (por ahora elegidos de forma aleatoria) que tienen
dos vecinos cada uno. Si bien existen algunos que solo tienen un vecino, los de las puntas, no se hará foco en este
problema.
Una vez que se cumplen las reglas básicas es preciso tener en cuenta otras características de los autómatas celulares.
En primera instancia se debe saber que estos existen por un tiempo limitado, el cual se denomina “generación”. En
el ejemplo planteado arriba se tiene la generación original, la generación 0. El problema a resolver es saber cómo se
calcula el estado de las siguientes generaciones, con base en qué se realiza este cálculo, etcétera:

La fórmula que se utiliza para resolver este problema es la siguiente:
Estado de la CÉLULA en el tiempo t = f(Estado de los vecinos de la CÉLULA en el tiempo t-1)
Como se observa, el nuevo estado de una célula es una función de todos los estados de las células vecinas en el momento
previo o durante la generación actual.
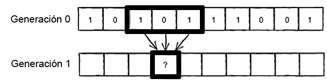
Fuente: gráfica creada para esta unidad.
En el mundo de los autómatas celulares existen muchas maneras de procesar los estados de un grupo de células. Se
ha visto en unidades anteriores cómo, mediante determinados algoritmos, se puede determinar el color de un píxel a
través del valor promedio de sus vecinos, por medio de las matrices de convolución, por ejemplo. También se podría
decir que el nuevo estado de una célula es la suma de los estados de sus vecinos.
A partir de esta libertad de elección, Wolfram encaró el diseño de una forma más sencilla. Tomó todas las posibles
combinaciones que podían existir entre estos píxeles y definió un resultado por cada combinación de forma anticipada.
Pensando un poco en qué cantidad de combinaciones se puede tener con tres células de dos estados, es fácil darse
cuenta de que se tiene un código binario de tres elementos y que en total pueden hacerse 8 combinaciones:
![]()
Una vez que se definen todas las posibles combinaciones, se necesita definir un valor para cada nuevo estado, el cual esté relacionado con una combinación. De esta manera, no está atado a una operación, sino a una decisión específica. Por ejemplo, se podría utilizar la siguiente relación entre combinación y estado nuevo:
![]()
Wolfram propone una primera generación donde, a partir de un sistema unidimensional de células impares, se tiene la siguiente generación 0:
![]()
Donde se observa claramente que todos los estados son 0, excepto el del medio.
Si se aplican las reglas anteriores a cada triada de células, se observa que la siguiente generación contendrá los siguientes
estados:
![]()
Las triadas significativas (donde realmente hay un cambio) se da en las inmediaciones del único 1 que existe en el sistema, y allí se produce el cambio. En las demás, cuando hay solo ceros, la siguiente generación serán ceros.
![]()
Si se utiliza el 0 como color blanco y el 1 como color negro se puede obtener un patrón de dibujo particular, aplicando las reglas de generación en generación. Por ejemplo, un sistema con una gran cantidad de células, y muchas generaciones, con este conjunto de reglas particulares puede observarse en la siguiente imagen:
negros ubicados mediante un autómata celular del tipo Wolfram
Fuente: imagen creada para esta unidad.
Esta forma se denomina “Triángulo de Sierpinski”, en honor al matemático polaco Waclaw Sierpinski, y se trata de un
patrón fractal, como los que se estudiaron en la unidad de sistemas.
Un set de reglas particular define un patrón particular, pero ¿cuántos patrones se pueden generar? O, siendo más
específicos ¿cuántas reglas diferentes se pueden obtener de un sistema donde las células presentan solo dos estados?
Si se piensa nuevamente en el código binario, es sencillo darse cuenta de que 8 resultados (8 bits) generarán 256
reglas diferentes. Por lo tanto, un sistema de autómatas celulares de estas características podrá generar 256 patrones.
El solo hecho de utilizar un conjunto de reglas no es garantía de que el patrón tenga características interesantes, pero
existen muchos patrones que sí lo hacen y también pueden verse en la naturaleza.
Una vez establecidas y estudiadas las reglas y procedimientos para crear autómatas celulares, se procederá a explicar
cómo utilizarlos dentro de un programa informático.
6.2.2. Programando un AC simple
Para empezar a trasladar las nociones anteriores a la programación de un AC, primero es importante establecer cómo
será la clase “AC” que defina los elementos y comportamientos de los mismos. En esta explicación se observará también
cómo se deben adaptar ciertas características de los AC dentro de la programación en sí.
Entonces, a continuación se observa la programación y explicación de cómo se conforma la clase AC.
En primera instancia, se definen los campos, el constructor de la clase:
Class AC
{
//Campos de la clase
//Un array de enteros que contiene las células
int[] celulas;
//Otro array que guarda las reglas
int[] setDeReglas;
//Constructor de la clase
AC()
{
//Se define el tamaño del array //células, tendrá el mismo tamaño
//como píxeles tiene la pantalla.
celulas = new int[width];
//Se llena directamente el set de
//reglas con una configuración arbitraria
setDeReglas = {0,1,0,1,1,0,1,0};
//Se establece la configuración de la
//generación 0 determinada por Wolfram,
//todas las células en 0 excepto la del medio
for (int i = 0; i < celulas.length; i++)
{
celulas[i] = 0;
}
celulas[celulas.length/2] = 1;
}
Una vez establecidas las características iniciales de la clase, se procede a determinar los diferentes métodos que establecen
las acciones comunes de los autómatas celulares de Wolfram, respetando las características detalladas en la
explicación previa. En principio hace falta un método que calcule la siguiente generación a partir de una generación
inicial y además un método que aplique las reglas establecidas. Por lo tanto, el siguiente es un método para evaluar
la siguiente generación de células:
void generador()
{
//Se crea un array donde se guardará la siguiente
//generación.
//Esto se hace para no sobrescribir el array original
//hasta que no se termine con el procesamiento.
int[] SiguienteGeneración = new int[celulas.length];
//Loop para determinar las vecindades de células para su procesamiento
//Nótese que el índice empieza en 1
for (int i = 1; i < celulas.length-1; i++)
{
int izquierda = celulas[i-1];
int centro = celulas[i];
int derecha = celulas[i+1];
//Apartir de esta información se calcula la siguiente
//generación mediante el método “reglas”
SiguienteGeneración[i] = reglas(izquierda, centro, derecha);
}
//Se iguala el array de células a la siguiente generación para seguir
//procesando
celulas = SiguienteGeneracion;
}
Para que el generador de nuevas generaciones funcione totalmente, se debe programar el método reglas. Existen
muchas formas de aplicar las reglas, pero tal vez la más sencilla es convertir las tríadas de números binarios en su equivalente
decimal e indexar el array de reglas. De esta forma, cualquier combinación posible tendrá un lugar en el array.
//Este método recibe tres enteros que corresponde a la célula central y sus
//dos vecinos los cuales combinados generan un código binario de 3 dígitos
int reglas (int a, int b, int c)
{
//Se guarda en una variable String los tres valores binarios para
//conformar un solo número binario de 3 dígitos
String s = “” + a + b + c;
//Una vez conformado el número binario de tres dígitos
//mediante la función Integer.parseInts se transforma el número
//binario en su equivalente entero, el cual puede servir fácilmente
//para indexar el array y devolver el resultado para la próxima
//generación
int index = Integer.parseInt(s,2);
return setDeReglas[index];
}
El siguiente ejemplo complementario permite observar cómo se
aplica esta clase para la creación de un sistema de autómatas celulares
del estilo Wolfram.
CAP6EjemploComplementario3.pde
Actividad 3
A partir del ejercicio complementario 3, construir un programa donde al hacer click en la pantalla, genera aleatoriamente un set de reglas para las nuevas generaciones de un autómata celular.
6.2.3. El juego de la vida
El paso siguiente en el trabajo con AC es pensar en sistemas bidimensionales. Se trata de sistemas un poco más
complejos debido a que cada célula tiene muchos más vecinos, pero que presenta una posibilidad de aplicación más
interesante.
Una de esas aplicaciones es el “Juego de la vida” de John Conway. Este juego permite justamente simular el mundo
natural mediante código y sistemas de dos dimensiones. El algoritmo que utiliza y la técnica de implementación proveen
una gran inspiración para generar simulaciones que exhiben las características comportamentales de sistemas
biológicos de reproducción.
A partir de la teoría desarrollada sobre los AC se puede aprender de qué forma funciona “El juego de la vida”.
En primera instancia, el sistema ya no tiene una línea de células, sino una matriz bidimensional. Como en cualquier AC
elemental los estados posibles son 0 o 1, los que representan, en este caso en particular, la “vida” (1) y “muerte” (0) de
una célula. Los vecinos de cada célula ahora son 9 y, por lo tanto, las posibilidades de combinación de estos vecinos
derivan en 512 reglas. Debido a que puede ser tedioso proponer 512 reglas directamente en el código del juego de
la vida, se define un conjunto de reglas de acuerdo con características generales del vecindario. En otras palabras, las
reglas variarán dependiendo de si el vecindario está superpoblado de células vivas o muertas o existe un balance.
Las reglas del juego son las siguientes:
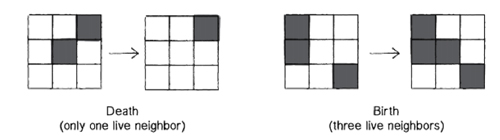
- “Muerte”: si una célula está viva, o sea su estado es 1, esta puede morir en las siguientes circunstancias:
- Superpoblación: si la célula tiene 4 o más vecinos vivos.
- Soledad: si la célula tiene uno o menos vecinos vivos.
- “Nacimiento”: si una célula está muerta, o sea su estado es 0, esta puede vivir si tiene exactamente tres vecinos
vivos (ni más ni menos).
- “Éxtasis”: en cualquier otro de los casos, el estado de la célula no cambia.
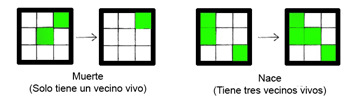
Fuente: gráfica creada para esta unidad.
A partir de estas reglas se puede comenzar a programar el juego en sí. Para esto, se comenzará a extender el modelo
de AC de Wolfram, utilizando arrays de dos dimensiones, como el siguiente:
//Se define un array de dos dimensiones
int[][] tablero = new int[columnas][filas];
También se inicializa cada célula del tablero en un estado aleatorio, 0 o 1:
for (int x=0; x<columnas; x++)
{
for (int y=0; y<filas; y++)
{
ActualGeneracion[x][y] = int(random(2));
}
}
Para procesar la siguiente generación, es necesario también un array bidimensional donde escribir el resultado del
análisis de cada célula y sus vecinos, y así obtener los nuevos estados. Entonces:
//Un array bidimensional
int[][] NuevaGeneracion = new int[columnas][filas];
Ahora, habría que recorrer las filas y columnas para ir calculando la nueva generación. Recorrer el array bidimensional
es sencillo porque se realiza con loops for, el nuevo desafío es generar el algoritmo que procese la información de la
vecindad para poder calcular la nueva generación de células.
En el caso del array unidimensional, uno podía indexar el array de células posicionándose en una de estas y sumando
y restando 1 al índice podía saberse el valor de las células vecinas. En este caso, no se tiene un índice simple, sino que
justamente se debe indexar la célula y sus vecinos en dos dimensiones. Por lo tanto, las direcciones en donde se debe
buscar el valor de los vecinos de una determinada célula son las siguientes:

Y, de esta manera, se soluciona fácilmente el indexado de una célula y sus vecinos dentro de un array bidimensional.
Debido a que en el juego de la vida lo importante reside en saber cuántos vecinos están vivos, será necesario tener
una variable que vaya registrando el valor de vida de cada vecino. Cada vez que se encuentre un vecino con valor 1,
esa variable se incrementará. Para aplicar esto a las vecindades de una célula determinada se deben utilizar los cálculos
de índices que se vieron anteriormente. El código de esto sería, entonces:
//Variable que guarda la cantidad de vecinos
int vecinos = 0;
//Vecinos de la fila de arriba de la célula
if (tablero[x-1][y-1] == 1) vecinos++;
if (tablero[x ][y-1] == 1) vecinos++;
if (tablero[x+1][y-1] == 1) vecinos++;
//Vecinos de la fila del medio de la célula, no se cuenta a sí misma
if (tablero[x-1][y] == 1) vecinos++;
if (tablero[x+1][y] == 1) vecinos++;
//Vecinos de la fila de debajo de la célula
if (tablero[x-1][y+1] == 1) vecinos++;
if (tablero[x ][y+1] == 1) vecinos++;
if (tablero[x+1][y+1] == 1) vecinos++;
Si bien esta es una forma didáctica de contar los vecinos vivos alrededor de una célula, en realidad no es una forma
práctica, debido a que un AC con más dimensiones sería muy trabajoso de implementar. Sería más efectivo en este
caso utilizar un loop for doble e ir indexando el array tablero de forma tal que se produzcan todas las operaciones. La
forma de hacer esto es la siguiente:
//Prestar atención a cómo se inicializan los índices de los loops para que
//cumplan todas las operaciones
for (int i = -1; i <= 1; i++)
{
for(int j = -1; j <=1; j++)
{
vecinos += board[x+1][y+j]
}
}
//Al final del loop sustraemos el valor de la célula central, debido a que no es
//un vecino
vecinos -= tablero[x][y];
Por último, se aplican dentro de los loops for las reglas preestablecidas del juego de la vida mediante condicionales,
calculando la nueva generación:
//Los puntos suspensivos indican que esta parte del código
//se inserta dentro de los loops for anteriores
…
if ((tablero[x][y] == 1) && (vecinos < 2)) NuevaGeneracion[x][y] = 0;
else if ((tablero[x][y] == 1) && (vecinos > 3)) NuevaGeneracion [x][y] = 0;
else if ((tablero[x][y] == 0) && (vecinos == 3)) NuevaGeneracion [x][y] = 1;
else NuevaGeneracion[x][y] = tablero[x][y];
}}
tablero = NuevaGeneracion;
Se puede observar el ejemplo completo de este juego de la vida
simple en el siguiente ejemplo complementario.
CAP6EjemploComplementario4.pde
Actividad 4
Implementar la teoría aquí desarrollada de “El juego de la vida”, de Conway, para construir un programa que establezca relaciones entre diferentes tipos de vehículos, según lo estudiado en la teoría de Reynolds. Se debe crear un medioambiente donde los vehículos circulen y mueran o se reproduzcan de la misma manera que en el juego original.
Conclusiones
En esta unidad se ha revisado la teoría básica de los agentes autómatas y los autómatas celulares, entidades que permiten
jugar un poco con las relaciones entre determinados elementos de un ecosistema.
Si bien existe infinidad de aplicaciones de autómatas celulares en muchos campos de la ciencia, también se pueden
encontrar ejemplos interesantes en el campo del arte. Tanto en la música como en el arte generativo en general se
han utilizado agentes autómatas de diversos tipos para generar obras de arte. Dos ejemplos claros de este uso puede
observarse en el trabajo del grupo argentino Biopus, conformado por Emiliano Causa y Matías Romero Costas.
Uno de estos trabajos es “Ecosistema Textual”, en donde el público puede enviar mensajes de texto para generar organismos
que se reproducen y mueren en un determinado ecosistema.
La otra, es la obra llamada “Coexistencia”, donde se plantea una naturaleza artificial donde el público puede generar
música en tiempo real al interactuar.
Lectura Obligatoria
Shiffman, D. (2012), “Capítulo 6. Autonomous Agents” en: Nature
of Code.
Shiffman, D. (2012), “Capítulo 7. Cellular Automata” en: Nature of
Code.
Del Castillo Waters, J. Y Rubio Torrente, G. (2008), “El juego de la vida
de Conway”, en Escuela superior de ingeniería informática. Universidad
de Castilla, España.
López Salinas, A. (2011), Introducción a la vida artificial y autómatas
celulares. Departamento de aplicación de microcomputadores,
Instituto de Ciencias, Universidad Autónoma de Puebla, México.

