5.3. Fractales
Un fractal es una forma geométrica fragmentada que puede ser dividida en partes, donde cada una de estas es una
copia reducida de la totalidad, denominándose esto autosimilaridad (self-similarity). Esta es la definición que su creador,
Benoit Mandelbrot, esgrimió en 1975 para definirlos, pudiendo utilizar los fractales para simular, por ejemplo, el
crecimiento de las ramas de los árboles y generando modelos similares a los reales.
A pesar de que en una primera aproximación se puede conseguir mediante fractales árboles totalmente simétricos,
los fractales no necesariamente deben tener esta topología. Los fractales que no son simétricos son denominados
fractales estocásticos, en contraposición a los fractales determinísticos. De los primeros se dice que el estado subsiguiente
está determinado tanto por las acciones predecibles del proceso como por elementos aleatorios. En los
determinísticos, el azar directamente no está involucrado en su desarrollo.
Existen técnicas, que se verán en este apartado, y definen estos dos comportamientos.
Si bien la autosimilitud es un rasgo clave de los fractales, es necesario aclarar esta característica. Si bien una línea puede
ser escalable fácilmente, no es un fractal, ya que estos se caracterizan por tener una estructura fina y compleja en
escalas pequeñas, y no puede ser descrita por la geometría euclidiana.
5.3.1. Recursividad
Otro rasgo importante de la geometría de los fractales es la recursión. Todo fractal tiene componentes recursivos. La recursividad permite realizar un número determinado de acciones una y otra vez, las cuales producen un nuevo evento, relacionado con el anterior, pero con un resultado diferenciado. Esto es relativamente sencillo de realizar en Processing, gracias a las herramientas para crear condicionales y loops que se estudiaron en unidades anteriores.
A continuación, un ejemplo de recursión en Processing, el cual realiza un acercamiento al trabajo
con fractales:
void setup()
{
size(400,400);
smooth();
}
void draw()
{
background(255);
//Se llama a una función que dibujará círculos recibe
//como argumento, la posición x, posición y, lado del //cuadrado inicial.
DibujarCirculos(width/2,height/2,200)
}
//Función que realiza el dibujo
void DibujarCirculos(float x, float y, float lado)
{
rect(x, y, lado, lado);
//Mediante este condicional se produce la recursividad
//como se observa se va reduciendo el tamaño de los cuadrados
//hasta cumplir el condicional
if(lado > 8)
{
DibujarCirculos(x + lado/2, y, lado/2);
DibujarCirculos(x - lado/2, y, lado/2);
DibujarCirculos(x, y + lado/2, lado/2);
DibujarCirculos(x, y - lado/2, lado/2);
}
}
5.3.2. El conjunto de Cantor
El conjunto de Cantor, llamado así por el aporte de Georg Cantor en 1883, es un conocido subconjunto fractal que se desarrolla entre el intervalo 0 y 1. La definición geométrica es que se trata de un conjunto de carácter recursivo que en cada una de sus recursiones elimina el segmento abierto correspondiente al tercio central de cada intervalo. Si se empieza por una línea, esta se iría segmentando de manera tal que generaría un patrón repetitivo, pero que, a la vez, va disminuyendo en el tiempo.
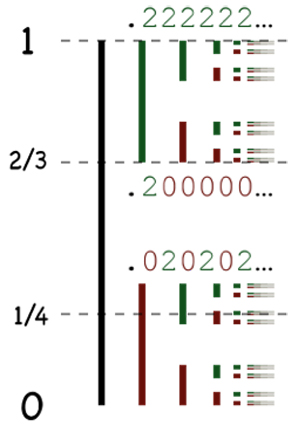
Fuente: http://commons.wikimedia.org/wiki/File:Cantor_base_3.svg
Como es de carácter recursiva, la estructura será similar a la lograda en el ejemplo anterior:
void cantor(float x, float y, float len)
{
//la recursión se detendrá cuando se llegue a un píxel
if (len >= 1)
{
line(x,y,x+len,y);
y += 20;
cantor(x,y,len/3);
cantor(x+len*2/3,y,len/3);
}
}
El secreto de esta función está en ir dividiendo las posiciones x e y por tercios, y así lograr la forma del conjunto de
cantor. Otro patrón fractal interesante de estudiar es la curva de Koch, la cual se desarrolla a continuación.
5.3.3. La curva Koch
Se ha observado arriba que mediante la recursión se puede generar fácilmente fractales. Sin embargo, esta forma de
hacerlo no permite accionar sobre los elementos que conforman el fractal de forma independiente.
Para lograr que un fractal posea esta característica, se puede utilizar la técnica de recursión combinada con ArrayList,
los cuales se estudiaron con anterioridad en los sistemas de partículas. Como ejemplo de aplicación de esta técnica se
va a trabajar con otro patrón fractal, la curva de Koch, llamada así por su descubridor Helge von Kotch, quien trabajó
con estos patrones en 1904.
La de Koch es una curva fractal continua, y su construcción más simple se realiza mediante un proceso iterativo que
se inicia partiendo un segmento de recta en tres partes e insertando dos más en el terceto del medio a manera de un
triángulo equilátero. Luego, se repite el proceso con cada línea que posee en el diseño, para volver a iterar el proceso
la cantidad de veces que se requiera.
La siguiente figura presenta una iteración sencilla de tres pasos:
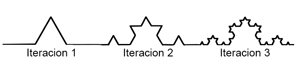
Fuente: gráfica creada para esta unidad.
Como se aclaró antes, la intención es que cada uno de los segmentos de la curva Koch sea independiente y, por lo
tanto, se debe asegurar el poder de cambiarlos de posición, rotarlos, cambiar su color, etc. Para esto, debemos tratar
cada segmento como un objeto separado, pero el problema reside en que la curva cambia con cada iteración y se
vuelve confuso guardar esa información. Para salvar este problema se trata a cada segmento como si fuera una línea
de una curva Koch. Cada una de estas líneas tendrá un punto de inicio y un punto final que se llamarán “a” y “b”, y los
cuales serán objetos Pvector.
Un ejemplo de cómo se puede armar la clase que dibuja cada línea Koch en Processing:
class LineaKoch
{
PVector inicio;
PVector final;
//Constructor
KochLine(PVector a, PVector b)
{
start = a.get();
end = b.get();
}
//Método para dibujar la línea
void mostrar()
{
//Borde negros
stroke(0);
//Se dibuja una línea de principio a fin
line(inicio.x, inicio.y, final.x, final.y);
}
}
Una vez que se tiene la clase, esta será utilizada en el programa principal a partir de un ArrayList, lo que permitirá generar muchos objetos LineaKoch:
//Esta ArrayList se utilizará para ir guardan los segmentos
ArrayList<LineaKoch> lineas;
//Configuración
void setup()
{
size(600, 300);
//Se define y asigna espacio para el ArrayList
lineas = new ArrayList<LineaKoch>();
//Se define un punto de inicio
PVector inicio = new PVector(0, 200);
//Se define un punto de final
PVector final = new PVector(width, 200);
//Se agrega una nueva línea al ArrayList líneas
lineas.add(new LineaKoch(inicio, final));
}
//Loop de dibujo
void draw()
{
background(255);
//Mediante este forma de loop, L toma cada uno de los
//elementos del ArrayList líneas y los recorre hasta que se
//terminan
for (LineaKoch L : lineas)
{
//Se ejecuta el método que muestra el elemento
//de la curva
L.mostrar();
}
}
Antes de continuar con el programa principal se debe escribir el algoritmo que contenga las reglas de la curva Koch, para que estas sean aplicadas a cada segmento individual. Para comenzar, se debe tener en claro que cada segmento individual se convertirá en cuatro segmentos individuales en cada una de las iteraciones, y estos cuatro segmentos suplantarán al segmento original, para luego aplicarse nuevamente las leyes de la curva en cada uno. Una simple figura aclarará la forma en que trabaja el algoritmo:

Fuente: gráfica creada para esta unidad.
Como se observa, también se debe tener en cuenta que la nueva curva estará conformada por los puntos a, b, c, d y
e. Estos puntos también deben ser contemplados en el algoritmo.
Para hacer esto, se empieza por crear una función que genere los segmentos a partir de los cinco puntos antes mencionados,
en este caso se llamará GeneradorKoch.
El siguiente ejemplo ilustra la función:
void GeneradorKoch()
{
//Un ArrayList llamado NuevaLinea que contenga objetos de la
//clase LineaKoch. Aquí se guardarán las nuevas líneas creadas
ArrayList NuevaLinea = new ArrayList<LineaKoch>();
//Se procesa cada línea del ArrayList líneas
for (LineaKoch L : lineas)
{
//Se generan los nuevos puntos de cada línea
//para esto debo tener las siguientes cinco //funciones
PVector a = L.kochA();
PVector b = L.kochB();
PVector c = L.kochC();
PVector d = L.kochD();
PVector e = L.kochE();
//Se agregan las nuevas líneas generadas a partir de las funciones que nos devuelven los puntos
NuevaLinea.add(new LineaKoch(a, b));
NuevaLinea.add(new LineaKoch(b, c));
NuevaLinea.add(new LineaKoch(c, d));
NuevaLinea.add(new LineaKoch(d, e));
}
//Ahora el ArrayList líneas toma el contenido del
//ArrayList NuevaLinea
lineas = NuevaLinea;
}
Lo único que faltaría para terminar de definir este programa que genera curvas Koch es definir cada una
de las funciones que crearán los nuevos puntos. A continuación, los ejemplos de código para cada una:
//El primer punto será el inicio.
PVector kochA()
{
return inicio.get();
}
//El segundo punto se encuentra a un tercio del total.
PVector kochB()
{
//Se genera un vector desde el inicio hasta el fin
PVector v = PVector.sub(inicio, fin);
//Se divide por 3
v.div(3);
//Se agrega al nuevo vector
v.add(start);
//Se retorna el vector que contiene al punto
return v;
}
//El tercer punto es el más complejo debido a que es el único que no está en
//línea con los otros.
PVector kochC()
{
//Se genera un vector que contenga el punto del inicio
PVector a = inicio.get();
//Luego se genera un vector de inicio a fin
PVector v = PVector.sub(end, start);
//Se divide por 3
v.div(3);
//Se agrega la línea al vector inicial. Ya tengo un vector de un /
/tercio del total desde el inicio al fin.
a.add(v);
//Se rota el punto v a 60 grados hacia arriba, que es el ángulo de
//los triángulos equiláteros utilizados en la curva Koch
v.rotate(-radians(60));
//Se suman ambos vectores, lo que da posición del punto C
a.add(v);
//Se devuelve el punto C
return a;
}
//El punto D está ubicado a 2/3 del punto de inicio
PVector kochD()
{
//Se genera un vector desde el inicio al final
PVector v = PVector.sub(inicio, final);
//Se multiplica el vector por 2/3
v.mult(2/3.0);
//Se suma el vector con el inicio y nos da el punto D
v.add(inicio);
//Se retorna el punto D
return v;
}
//El último punto es el mismo de la curva original
PVector kochE()
{
return final.get();
}
A partir de la función GeneradorCoch, se puede directamente generar todo desde el setup. Un
último ejemplo muestra este procedimiento:
ArrayList<LineaKoch> lineas;
void setup()
{
size(600, 300);
background(255);
lineas = new ArrayList<LineaKoch>();
//Vectores para los puntos de inicio y final
PVector inicio = new PVector(0, 200);
PVector final = new PVector(width, 200);
//Se agrega la línea original al ArrayList
lineas.add(new LineaKoch(inicio, final));
//Se iteran las reglas de la curva Coch arbitrariamente 5 veces
for (int i = 0; i < 5; i++)
{
GeneradorCoch();
}
}
Todos los métodos que se han estudiado para la generación de fractales hasta aquí son del tipo determinísticos. Para mostrar un ejemplo del tipo estocástico, en el siguiente apartado se estudiarán las estrategias para crear fractales del tipo árbol.
Actividad 3
Tomando los algoritmos para el desarrollo de fractales revisados en este apartado, generar un programa que combine el conjunto de Cantor y la curva Koch de tal manera que genere un dibujo que ocupe toda la ventana de visualización. La elección estética de qué características tendrá el dibujo es decisión del estudiante.
5.3.4. Árboles
En este apartado se examinarán algunas técnicas que generan fractales estocásticos, también llamados “no determinísticos”.
Para esto, se usará como ejemplo la relación entre un árbol y sus ramas, cuyo modelo de crecimiento puede
ser simulado mediante las siguientes reglas:
1- Dibujar una línea.
2- Al final de la línea (a) rotar hacia la izquierda y dibujar una línea más corta que la anterior y (b) rotar a la derecha y
dibujar una línea corta.
3- Repetir el paso 2 todas las veces que se desee.
Para generar una rotación dentro de Processing es necesario entender algunas funciones que este utiliza y que corresponden
al uso de una matriz de rotación, pushMatrix() y popMatrix(). Estas funciones permiten actuar sobre todos los elementos de un sketch o solamente sobre los elementos que se encuentren encerrados entre ellas, permitiendo rotarlos,
escalarlos y moverlos en dos dimensiones. Las funciones que pueden utilizarse para realizar estas acciones son:
translate(x, y): recibe como argumento el punto del plano donde se requiere transladar uno o un conjunto de objetos.
rotate(ang): recibe como argumento el ángulo de rotación (en radianes) de uno o un conjunto de objetos.
scale(s): recibe como argumento el porcentaje al cual se requiere escalar uno o un conjunto de objetos. El número 1
sería un 100 %.
Estas tres funciones, pueden afectar a uno o a un conjunto de objetos. Si se desea que solo afecte a un elemento del
sketch, se deben utilizar las funciones pushMatrix y popMatrix. Como se mencionó más arriba, estas expresiones limitan
el uso de las funciones descritas. Un ejemplo:
//Tamaño del lienzo
size(400,400);
//Comienzo de la transformación
pushMatrix();
//Se traslada lo que haya aquí dentro al medio del lienzo
translate(width/2, height/2);
//Se rota a un ángulo igual a PI/3
rotate(PI/3);
//Se dibuja un rectángulo que ya está trasladado y rotado
rect(0,0,50,50);
//Fin de la transformación
popMatrix();
//Se dibuja otro rectángulo
rect(100,200,50,50);
El primer rectángulo será afectado por la translación y rotación y el siguiente, no.
Luego de este ejemplo, se puede empezar a estudiar cómo se aplicaría el algoritmo de crecimiento de tres pasos que
se estudió más arriba. Para esto se escribirá una función que dibuje cada una de las ramas del árbol en forma recursiva
(igual que las curvas Coch).
Lo interesante de esta función es que se le pasa como argumento el largo inicial del tronco del árbol que se desea y
luego se va reduciendo el tamaño de las ramas que van ascendiendo (tal cual pasa en la vida real) de forma recursiva.
A continuación, el código de ejemplo y la explicación del mismo.
//Función para crear las ramas de un árbol, recibe el largo inicial del
//tronco del árbol.
void ramas(float largo)
{
//Primero se dibuja una línea en el punto inicial,
//apuntando hacia arriba (por eso -largo).
line(0, 0, 0, - largo);
//Se traslada la línea a su largo para que el tronco quede
//bien ubicado.
translate(0, - largo);
//Se disminuye el largo de la próxima generación de
//ramas, en este caso al 66 %.
largo *= 0.66;
//Este condicional permite que no se produzca un loop
//infinito. Cuando el largo es más chico que 2, se //termina la recursión.
if (largo > 2)
{
//Se aplica una rotación a cada rama por
//separado.
//Rama de la derecha
pushMatrix();
//Se rota un ángulo theta que en este caso se
//identifica como una variable global.
rotate(theta);
branch(largo);
popMatrix();
//Rama de la izquierda
pushMatrix();
//En este caso la rotación será negativa para que la rama vaya hacia la
//izquierda.
rotate(-theta);
branch(largo);
popMatrix();
}
}
De esta manera se puede crear un árbol completo mediante la aplicación de una sola función. Es interesante pensar que cada variable que actúa en este algoritmo puede tener un carácter dinámico, por lo que también se pueden crear árboles que cambien en el tiempo o mediante la interacción con el usuario. El siguiente ejemplo complementario que utiliza este algoritmo en conjunto con el mouse, permite entender la potencialidad de este tipo de curvas.
CAP5EjemploComplementario4.pde
Actividad 4
Aplicar al algoritmo de crecimiento la capacidad de indicar qué grosor tendrá cada rama. Puede ser de la manera natural, donde el grosor va disminuyendo con el crecimiento, o se pueden aplicar grosores irreales donde algunas ramas pueden ser más grandes que el tronco. En el programa resultante deben poder seleccionarse, por lo menos, tres posibilidades.
Actividad 5
En los ejemplos, el ángulo al que se rotan las ramas se mantiene fijo. Agregar al algoritmo de crecimiento la capacidad de que el ángulo de rotación de las ramas sea totalmente aleatorio.
Actividad 6
Mediante las nociones aprendidas en toda esta unidad, generar un sistema de partículas que tenga la capacidad de crear bosques a partir de la teoría de simulación de ramas estudiadas aquí.
Conclusiones
Los sistemas de partículas y fractales han sido y son herramientas sumamente utilizadas tanto en el arte en sí, como
en la industria de la animación, la cual va desde el cine hasta los videojuegos.
Sería sumamente amplio tratar de realizar un recorrido por las obras y recursos que conforman el mundo de los algoritmos
para estos sistemas. Sin embargo, una web sumamente interesante, donde se pueden revisar muchos trabajos
y además contiene código fuente de esos trabajos es formandcode.com, la página de Casey Reas (uno de los creadores
de Processing) y Chandler McWilliams (un artista sumamente destacado en su medio).
Se recomienda la sección de links donde aparecen las páginas de los principales artistas electrónicos de este momento.
Lectura Obligatoria
Shiffma n, D. (2012), “Capítulo 4. Particle Systems” en: Nature of Code.
Shiffman, D. (2012), “Capítulo 8. Fractals” en: Nature of Code.
.