6.3. Análisis espectral de la señal digital

Las señales digitales pueden ser representadas y analizadas espectralmente mediante un recurso matemático desarrollado por el físico-matemático Joseph Fourier en el siglo XIX. Este recurso, denominado matemáticamente transformada, se encarga de trocar la información espectral contenida en el dominio temporal al dominio de las frecuencias para obtener una mejor representación del aspecto analizado.

Según el teorema de Fourier:

El enunciado nos dice que si tomamos un ciclo de una señal periódica podemos obtener, mediante este procedimiento matemático, la amplitud y fase de cada uno de sus componentes, puesto que toda señal periódica puede ser entendida como un movimiento armónico complejo, es decir, la suma de infinitos movimientos sinusoidales en relación armónica.

El primer valor es llamado frecuencia fundamental (o primer armónico) y las sucesivas frecuencias son llamadas parciales armónicos (frecuentemente llamados de manera indistinta como parciales o armónicos).

La transformada de Fourier se encarga de realizar el procedimiento inverso. Dado un movimiento armónico complejo, nos dice cuáles son los componentes armónicos presentes y cuáles son sus amplitudes y fases.

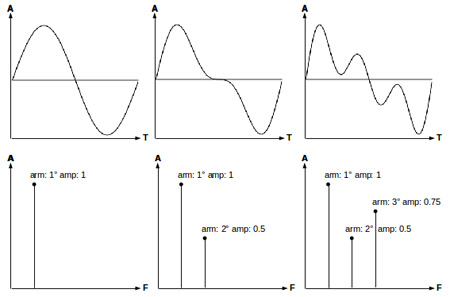
En los gráficos temporales (fila de arriba) los componentes armónicos se manifiestan en la forma de onda, la cual se vuelve más compleja a medida que se incrementa la cantidad de componentes. Sin embargo, es prácticamente imposible darse cuenta qué componentes están presentes y con qué amplitud. En los gráficos espectrales (fila de abajo), en cambio, se pueden apreciar claramente los componentes armónicos presentes y sus respectivas amplitudes.

La transformada de Fourier es una herramienta de análisis muy útil debido a que su forma de representar las cualidades internas de un sonido se relaciona de forma más directa con la manera en la que se percibe el sonido.

6.3.1. Transformada de Fourier discreta (DFT) e inversa (IDFT)

Matemáticamente, la Transformada de Fourier es un proceso continuo, es decir, que está definido para todos los valores sin importar qué tan pequeños o grandes puedan ser, y se basa además en la idealización matemática de un movimiento armónico cuya duración es infinita. Sin embargo, las señales digitales son discretas por definición y, por lo tanto, no pueden representar infinitos valores. Es por esto que en lugar de aplicarse la transformada continua se aplica la formulación matemática discreta del mismo proceso y pasa a llamarse en consecuencia Transformada Discreta de Fourier (DFT por sus siglas en inglés: Discrete Fourier Transform).

La transformada es un proceso reversible, esto quiere decir que si la aplicamos a una forma de onda y obtenemos los datos espectrales, con base en estos podemos volver a reconstruir la forma de onda original sin perder información.

Incluso es posible modificar el sonido empleando la representación espectral para luego reconstruirlo con estas modificaciones. Esto resulta útil para la construcción de ecualizadores gráficos (empleados para balancear espectralmente una señal), para filtrar o realzar componentes específicos del espectro o incluso para generar modificaciones espectrales que transformen las cualidades de la señal original en algo totalmente diferente.

6.3.2. Transformada de Fourier discreta rápida (FFT) e inversa (IFFT)

La DFT es un proceso matemático relativamente sencillo pero que implica el empleo reiterado de operaciones simples y la manipulación de una gran cantidad de datos y, por lo tanto, requiere cierta cantidad de recursos computacionales. Para poder efectuar la DFT de forma prácticamente útil se desarrolló un algoritmo que reduce la capacidad de cómputo necesaria y posibilita su cálculo en menor tiempo. A este algoritmo se los denomina Transformada Rápida de Fourier (FFT
por sus siglas en inglés: Fast Fourier Transform).

Sin embargo, lo que se gana en eficiencia se pierde en precisión. Para que el algoritmo pueda procesar los datos de forma rápida es necesario restringir los valores posibles de ciertos parámetros. Al ser un algoritmo digital que emplea el sistema binario, los tamaños de las ventanas de análisis están restringidos a las potencias de base 2, es decir 2¹ = 2; 2² = 4; 2³ = 8; 2⁴ = 16; etc. Esto restringe a su vez las posibles frecuencias de análisis que además de afectar la precisión
con la que se representa el espectro genera artefactos de análisis como se explica a continuación.

6.3.4. Parámetros básicos de la FFT

Tanto la FT como la DFT son procedimientos matemáticos que están definidos de manera general (o podría decirse ideal), esto quiere decir que no están acotados temporalmente. Sin embargo, en la práctica es necesario adoptar límites temporales puesto que los sonidos que podemos percibir, grabar y manipular son finitos. Es por esto que para aplicar la DFT mediante el algoritmo FFT es necesario definir ciertos parámetros.

El primer parámetro, que generalmente viene predefinido en la señal de audio almacenada digitalmente, es la frecuencia de muestreo. A mayor frecuencia de muestreo vamos a obtener una mayor precisión temporal en general.

El segundo parámetro que surge ya directamente en relación con el análisis de Fourier es el tamaño de la ventana de análisis. La ventana de análisis es un período temporal que se toma, en cantidad de muestras, de una porción de la señal a analizar. Se llama ventana por analogía al efecto visual que produce una ventana cuando se mira un paisaje desde dentro de una habitación, lo que podemos ver del horizonte está acotado a la imagen que podemos percibir a través de la pared.

La relación entre la frecuencia de muestreo y el tamaño de la ventana de análisis determina otro parámetro que es la frecuencia de análisis. La frecuencia de análisis es la frecuencia fundamental de la serie armónica (también referida como serie de Fourier) y corresponde al recíproco del período definido por la ventana de análisis. Si W es la cantidad de muestras que toma la ventana de análisis y R es la frecuencia de muestreo entonces T = W/R es el período de la ventana de análisis en segundos. Como la frecuencia y el período son inversos, la frecuencia de análisis resultante es f_a = 1/T. Si juntamos las operaciones en una sola ecuación y simplificamos nos queda f_a = 1/T = 1 / (W/R) = R/W.

 

La cantidad de componentes parciales (bins en inglés) que se pueden analizar es la mitad del tamaño de la ventana de análisis. Por ejemplo, 512/2 = 256 que van desde los 0 Hz hasta la frecuencia de Nyquist (R/2). De cada bin se puede obtener tanto la amplitud como la fase aunque el valor que se usa para graficar el espectro es solo la amplitud.

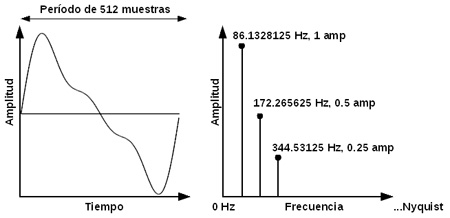
En el gráfico de la izquierda se muestra un período de un movimiento armónico complejo, compuesto de tres armónicos de amplitud decreciente (cada uno tiene la mitad de la amplitud del anterior), que dura exactamente 512 muestras con una frecuencia de muestreo de 44100 Hz. Esas 512 muestras son tomadas como la ventana de análisis de la FFT que da como resultado el gráfico de la derecha.

Preste especial atención a la “dominio” que es diferente en ambos casos. En el gráfico de la izquierda se representa la amplitud en función del tiempo mientras que en el gráfico de la derecha se representa la amplitud en función de la frecuencia (el tiempo está ausente puesto que se representa el espectro contenido en las 512 muestras de la ventana). Este es un ejemplo elaborado especialmente para demostrar cómo se pasa de un dominio a otro, en la práctica es poco probable que los valores coincidan exactamente.

6.3.5. Resolución en frecuencia y resolución temporal

Al incrementarse el tamaño de la ventana de análisis disminuye la frecuencia de análisis y, por lo tanto, la serie de Fourier crece a pasos más pequeños, siempre desde 0 Hz hasta la frecuencia de Nyquist. Esto produce una mayor resolución en frecuencia al costo de sacrificar la resolución temporal. Al ser más grande la ventana de análisis, el período de tiempo que pasa entre análisis consecutivos es mayor. Si por el contrario queremos una mayor resolución temporal, para poder ver como varía el espectro entre instantes pequeños, tendremos que achicar la ventana de análisis y perder resolución en frecuencia. Didácticamente, esto puede ser entendido de otra manera, como si el análisis de Fourier fuera el espectro promedio de una determinada cantidad de muestras. No obstante ello, como veremos más adelante, el análisis de Fourier presupone que la ventana de análisis es un período completo de un solo movimiento armónico.

Al emplear la FFT, los límites en el tamaño de la ventana están definidos de manera práctica entre 8 y 32768 muestras (entre 2³ y 2¹⁵), siendo las ventanas más usadas las de 256, 512, 1024 y 2048 muestras, según se prefiera mayor resolución temporal o de bandas de frecuencia. Sin embargo, la relación inversa entre resolución en frecuencia y resolución temporal es una característica intrínseca del análisis de Fourier que se explica mediante el principio de incertidumbre.

6.3.6. Artefactos de análisis y ventanas de suavizamiento

Como se dijo anteriormente, el análisis de Fourier presupone que la ventana de análisis es un período completo de un solo movimiento armónico. Esto implica que al analizar espectralmente fragmentos de señales complejas o que no coincidan con el período de análisis, los resultados no van a ser ideales.

Por una parte, la energía de los componentes en frecuencia del fragmento analizado que no coincidan exactamente con la serie de Fourier definida por la ventana de análisis, será distribuida en las bandas laterales. Esto genera “ruido visual” en la representación espectral. Por la otra, al reconstruir la señal mediante al IFFT, la energía distribuida en las bandas reconstruye de manera precisa la forma de onda original.

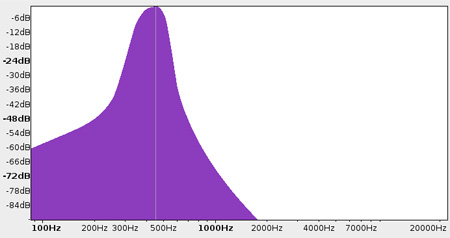
Análisis espectral de una sinusoide de 440 Hz generada a una frecuencia de muestreo de 44100 Hz, la amplitud (eje de las ordenadas) está medida en decibeles. La ventana de análisis utilizada es de 512 muestras. Como la frecuencia de la sinusoide no es múltiplo de la frecuencia de análisis, la energía se distribuye en las bandas laterales. La frecuencia de análisis es de 86.1328125 Hz y el múltiplo más cercano es 430.6640625 Hz.

Otro problema que surge al tomar arbitrariamente una parte de una señal para ser analizada es que se generan discontinuidades desde el punto de vista del análisis. Como la ventana de análisis entiende su contenido como si fuera un ciclo de una señal periódica, al recortar la señal mediante la ventana de análisis, el ciclo que se genera usualmente tiene un salto abrupto entre el final y el inicio que genera componentes espectrales agudos y ruido en el análisis.

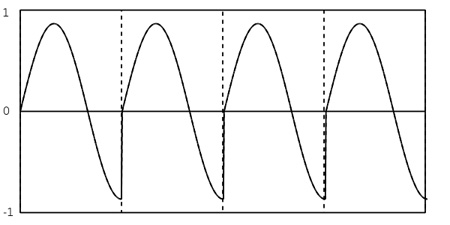
Para la transformada de Fourier es como si la información contenida en la ventana de análisis fuera un ciclo de una señal periódica y, por lo tanto, la señal que estaría analizando sería como la que se muestra. Las líneas punteadas delimitan la ventana de análisis que toma una cantidad de muestras que no coincide con el período de una señal sinusoidal. En la figura se repite la ventana de análisis cuatro veces para ilustrar la discontinuidad que se genera.

Para solucionar el problema de la discontinuidad que se produce al recortar una señal se aplican ventanas de suavizamiento. Las ventanas de suavizamiento son envolventes dinámicas que multiplican la señal capturada por la ventana de análisis antes de ser analizada. Estas envolventes hacen que los valores de amplitud próximos al inicio y al final de la forma de onda analizada sean coincidentes o que no se produzcan saltos abruptos.

Existen distintos tipos de ventanas de suavizamiento que hacen que disminuyan los artefactos de análisis de diversas maneras. Las más usadas se llaman Hanning, Hamming, Blackman y Blackman-Harris, en honor a sus creadores. También es común que los programas permitan usar una ventana de suavizamiento rectangular, lo que equivale a no usar ninguna ventana.

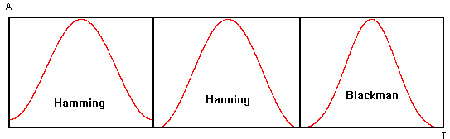
Distintas ventanas de suavizamiento de uso frecuente
Las ventanas Hanning y Blackman hacen que las muestras iniciales de la señal analizada sean cero, aunque similares son funciones distintas que alteran sutilmente los resultados del análisis. La ventana Hamming, a diferencia de las anteriores, no hace que las muestras iniciales y finales lleguen a cero.

6.3.7. Análisis de espectros cambiantes mediante ventanas deslizantes

Hasta ahora se ha visto el análisis espectral de pequeñas porciones de una señal. Si se quisiera analizar la evolución espectral de una señal de mayor duración sería necesario emplear sucesivas ventanas a medida que se avanza en la forma de onda. Se denomina a este recurso ventana deslizante y puede implementarse de varias maneras.

La manera más sencilla sería yuxtaponer sucesivas ventanas y sobre la base de esto ir analizando los cambios de ventana en ventana. De esta forma, la resolución temporal del análisis de cambios espectrales está determinada por la duración de la ventana.

Una técnica empleada para aumentar la resolución temporal sin disminuir el tamaño de la ventana es emplear ventanas solapadas, es decir, que la siguiente ventana de análisis se superponga con la ventana previa una cierta cantidad de tiempo. Esto hace que la duración del espectro “promedio” visualizado sea más pequeña y las muestras espectrales sucesivas estén más juntas.

El solapamiento se mide como factor (porcentaje de ventana solapada) puesto que el tamaño de la ventana de análisis deslizante puede ser variado. Un porcentaje de solapamiento típico es el 75%, quiere decir que la siguiente ventana de análisis comienza luego de transcurrido un cuarto de la ventana anterior. Por ejemplo, si N es el tamaño de la ventana en muestras, la siguiente ventana de análisis comenzará N/4 muestras después.

Para lograr resultados óptimos de análisis según la señal que se quiera analizar, es necesario realizar un compromiso entre el tamaño de la ventana de análisis y el factor de solapamiento. Ajustando adecuadamente estos parámetros se puede lograr una resolución aceptable tanto en tiempo como en frecuencia.

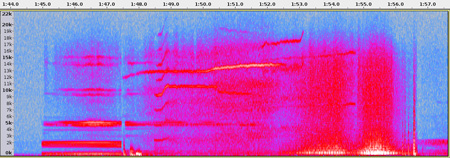
6.3.8. Gráficos de espectros

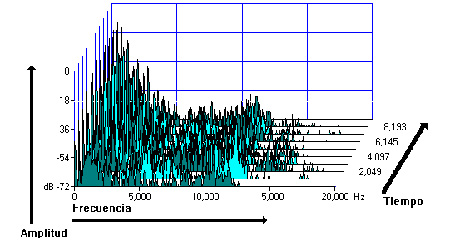
Los datos obtenidos mediante el análisis espectral con ventana deslizante se suelen representar gráficamente de dos maneras. Una forma es hacer un gráfico tridimensional, usualmente con el eje horizontal representando la frecuencia; el vertical, la amplitud; y el eje de profundidad, el tiempo. Otra forma de representar los datos es mediante el empleo de dos dimensiones espaciales, horizontal para el tiempo, vertical para las bandas espectrales y una tercera dimensión, que emplea una escala de colores o matices de grises, para representar la energía presente en cada banda. A este último tipo de representación se lo denomina espectrograma.

Ambas representaciones tienen sus ventajas y desventajas, el gráfico tridimensional es más preciso si se quieren visualizar los datos como funciones pero requiere mayor capacidad gráfica. Este es, tal vez, el más adecuado para observar variaciones rápidas del espectro en una señal que representa un solo sonido. Es más fácil ver la amplitud de cada componente espectral con relación a los demás.

En cambio, el espectrograma representa el espectro de una manera más tradicional en cuanto a la concepción de altura musical ya que muestra la frecuencia en función del tiempo. Esto hace que sea más fácil visualizar el recorrido de distintos componentes espectrales. Su principal desventaja es que, al emplear colores o matices para representar la amplitud, esta queda expresada con menor precisión.