5.9. Cuantización

Al muestrear una señal continua no solo se está discretizando su cualidad temporal (los valores sucesivos que se toman en cuenta) sino también los valores de amplitud, que serían los valores correspondientes al eje de las ordenadas cuando representamos la forma de onda. A este proceso se lo denomina cuantización de la señal. La cuantización, a diferencia del muestreo en frecuencia, no es reversible puesto que se pierde información respecto de la señal original que se transforma en ruido de cuantización como se verá a continuación.

5.9.1. Resolución en bits

La resolución en bits de una señal digital determina la precisión con que se representan estos valores de amplitud tomados por muestra. Define el rango dinámico, entendido como la distancia entre la amplitud máxima y mínima de la señal digitalizada según la cantidad de valores distintos que se puedan representar.

 

 

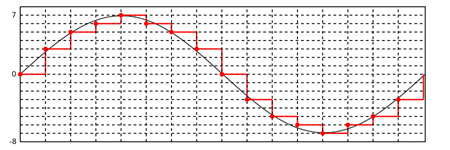
En la figura se muestra una señal continua en negro y superpuesta en rojo la misma señal pero cuantizada a un determinado período de muestreo. Mientras más lejano sea el recorrido de la señal continua con respecto a los puntos rojos de las líneas horizontales mayor será el error de cuantización.

 

Además del rango dinámico, el proceso de cuantización afecta la forma de onda resultante puesto que los infinitos valores de amplitud posibles en un señal continua son asignados a una cantidad finita de números binarios. Al transformar variaciones de voltaje (amplitud de una señal continua) en valores discretos (amplitud de una señal digital) se produce un redondeo. Los valores continuos que caen dentro del rango de dos valores discretos son asignados al valor discreto más próximo perdiéndose precisión en la representación de la amplitud. A mayor resolución en bits, mayor será la resolución con que se representan las variaciones de amplitud de la señal.

Según se redondee hacia arriba o hacia abajo, en comparación con la señal analógica, la señal digital resultante contiene pequeños saltos. La amplitud máxima de estos saltos está definida por la resolución en bits y equivale a la mitad de la amplitud representable entre dos valores (1 bit). La dirección de estos saltos no es previsible y depende de si el redondeo es ascendente o descendente. En el gráfico anterior se puede observar cómo los puntos rojos que representan el valor digital de la señal no coinciden exactamente con la señal analógica, quedando por arriba o por abajo, más o menos cerca del valor original. Estos saltos generan lo que se denomina ruido de cuantización, el cual acompaña las variaciones de amplitud de la señal y se vuelve audible en el procesos de conversión digital-analógica posterior.

5.9.2. Cuantización uniforme

Existen varias maneras de cuantizar una señal según como se distribuyan la cantidad de valores distintos, de manera uniforme o no uniforme, al representar la amplitud de una muestra. La cuantización uniforme distribuye de manera equidistante los distintos valores de amplitud posibles determinados por la resolución en bits. Esto hace que se tenga la misma resolución al representar tanto sonidos de alta como de baja amplitud.

5.9.3. Relación señal-error de cuantización

El ruido generado por el error de cuantización hace que la señal se distorsione más o menos según su amplitud. Para señales de muy baja amplitud el ruido de cuantización enmascara la señal representada. A este límite de enmascaramiento se le llama piso de ruido, toda señal cuya amplitud esté próxima a este se verá degrada por el proceso de cuantización. La relación entre el piso de ruido y la señal representada se denomina SQNR (por Signal to Quantization error Noise Ratio en inglés).

La relación SQNR es la que determina el rango dinámico de las señales que se pueden representar dentro de una resolución en bits determinada. Para determinar esta relación se emplea la siguiente fórmula: SQNR = 20 * log₁₀ 2ⁿ , siendo n la resolución en bits. Esta fórmula nos da el rango dinámico en dB y de ella podemos aproximar que cada un bit de precisión que se agrega a la resolución, el rango dinámico representable se incrementa en 6dB aproximadamente. Por esto último podemos simplificar de manera práctica, y decir que SQNR = 6dB * n, siendo n nuevamente la cantidad de bits. La resolución estándar de un CDA es de 16 bits lo que da un rango dinámico aproximado de 96dB.

La SQNR es una proporción que relaciona el ruido de cuantización con la amplitud de la señal representada, en el caso anterior sería con una señal de amplitud máxima. Pero si queremos saber cuál es la SQNR para señales de menor amplitud podemos usar la fórmula aproximada: SQNR = 6dB * n + S, donde S es la amplitud efectiva en cantidad de dB_fs. Por ejemplo, si tenemos una señal a -18dB_fs y una resolución de 16 bits la relación señal/ruido de esta señal en particular sería SQNR = 6dB * 16 + (-18) = 96dB - 18 = 72dB. Esto es útil para saber cuán degradada puede estar una señal grabada a cierta amplitud puesto que si el nivel de grabación fue muy bajo, luego no será posible amplificarla sin aumentar también el ruido de cuantización.

5.9.4. Cuantización no-uniforme

En relación con el desarrollo de las telecomunicaciones fueron desarrolladas dos técnicas de cuantización no lineal implementadas en las normas Mu-Law y A-Law. Ambas son versiones ligeramente distintas de un mismo procedimiento de conversión analógica–digital no lineal empleado para luego comprimir las señales de audio a ser transmitidas. Estas técnicas emplean en el proceso de muestreo una mayor resolución para representar los valores de amplitud cercanos a cero (de la cantidad de bits disponibles se emplean más para representar valores pequeños) y una menor resolución para los valores de amplitud cercanos al máximo.

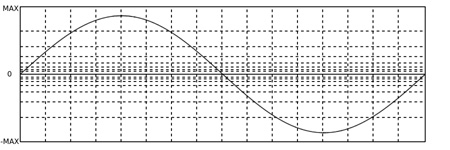
La grilla de líneas puenteadas esquematiza el proceso de cuantización no lineal en relación con una señal de gran amplitud.

La distribución de los valores de amplitud de una señal cuantizada de esta manera no es pareja a lo largo del rango dinámico. Tener un mayor grado de precisión para los componentes de baja amplitud implica menor precisión para los componentes de mayor amplitud. La cuantización no lineal disminuye el ruido de cuantización en bajas amplitudes, donde es más audible, pero lo incrementa cuando la señal es de mayor amplitud. Esto es preferible puesto que los sonidos de mayor amplitud tienden a enmascarar el ruido de cuantización. Sin embargo, el desarrollo de esta técnica de cuantización se basa en que las señales de voz hablada se desarrollan comúnmente a valores de baja amplitud, lo que permite tener una buena calidad de sonido para el rango dinámico de la voz hablada y, a la vez, permitir la codificación de sonidos de mayor amplitud.

5.9.5. Dithering

El ruido de cuantización “acompaña” espectralmente a la señal digitalizada según varíe su amplitud. Esto hace que se generen bandas de ruido a medida que la energía de la señal disminuye y produce un efecto, preceptivamente muy notable, denominado distorsión armónica.

Para evitar este fenómeno se usa el dithering que consiste en aplicar ruido blanco de baja amplitud antes de la conversión analógica-digital, lo que hace que el error de cuantización no varíe espectralmente junto con las variaciones de la señal de entrada. El ruido blanco hace que el error de cuantización adquiera una función de distribución de probabilidades uniforme sin importar las características de la señal de entrada esto es lo que garantiza que no se produzca una distorsión variable que sería mucho más audible.

El dithering también hace que los efectos del ruido de cuantización sean menos notorios puesto que al generar un ruido estacionario constante, e igual para todo el rango dinámico, el piso de ruido se vuelve mucho menos perceptible.