
5.7. Teorema de Nyquist
Mediante una señal temporalmente discreta no es posible representar infinitos
valores de frecuencias altas porque no es posible tomar muestras a períodos infinitamente
pequeños. Por lo tanto, la frecuencia más alta que se puede representar
depende de la frecuencia de muestreo que se emplee para discretizar la señal.
El teorema de Nyquist define formalmente cuál es la frecuencia máxima que se
puede representar digitalmente a determinada frecuencia de muestreo, a esta
frecuencia máxima se la denomina frecuencia de Nyquist.
La frecuencia de Nyquist (N) equivale a N = SR/2 y define que para una determinada
SR, la máxima frecuencia que se puede representar es la mitad de SR. Por
ejemplo, a una SR de 44100 Hz, la máxima frecuencia que se puede representar
es 44100/2 = 22050 Hz. Si se quisieran muestrear o generar frecuencias mayores
a la frecuencia de Nyquist se genera un fenómeno denominado aliasing.
El teorema de Nyquist sostiene que un movimiento oscilatorio se puede representar
con un mínimo de dos muestras, una para el semiciclo positivo y otra para
el negativo.
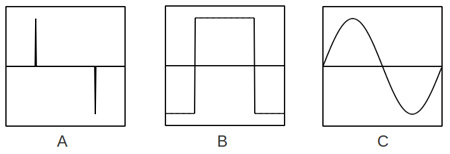
En los gráficos A, B y C de la figura se muestra solo un ciclo de un movimiento
sinusoidal a frecuencia de Nyquist. Dos muestras discretas de un ciclo en A,
convertidas en una función continua en B que luego de pasar por el filtro pasa
bajos, dan como resultado la forma de onda en C.
Digitalmente podría parecer que la forma de onda que se está representando
es una onda cuadrada, sin embargo al pasar por el filtro pasa bajos luego de la
conversión digital-analógica, todos los componentes que estén por sobre la frecuencia
de Nyquist se eliminan dando como resultado una sinusoide.