
2.2. Presión dinámica e intensidad de las ondas acústicas
Antes de tratar en detalle los aspectos perceptivos de las señales acústicas, se verán algunas unidades de medición de sus atributos físicos.
2.2.1. Relación entre amplitud, presión e intensidad acústica
La amplitud del movimiento de un cuerpo que vibra y produce una onda sonora
es directamente proporcional a la presión e intensidad acústica que esta produce.
La amplitud del movimiento de las moléculas en las ondas sonoras, en
la escala del mínimo audible al umbral del dolor, es de 10-11 (0.00000000001)
metros a 10-5 (0.00001) metros.
Como resulta complicado medir la amplitud del movimiento en las moléculas, dadas
las ínfimas dimensiones de este, se toman habitualmente como referencia
las nociones de presión dinámica e intensidad.
2.2.2. Presión estática
La presión es una fuerza ejercida sobre una superficie. Cuando no cambia (o lo hace muy levemente en intervalos de tiempo muy grandes), se considera presión estática. Por ejemplo, la presión estática media de la atmósfera terrestre es de 101.300 Pa (1.013 hectopascales).
2.2.3. Presión dinámica
Dado que una onda sonora produce cambios de presión en el medio (habitualmente,
el aire) a intervalos temporales de su frecuencia, se considera que produce
presión dinámica. Estos cambios de presión son positivos o negativos (mayores
o menores que la presión promedio de la atmósfera, por ejemplo). La presión
dinámica producida por las ondas sonoras se mide con micrófonos sensibles a
presión, tomando como referencia máxima 20 Pa y mínima 20 micropascales.
En términos de acústica, es habitual medir la presión y la intensidad de las ondas
sonoras en unidades que se denominan decibeles (dB).
Vivimos habitualmente en el fondo de un océano de aire... La atmósfera es el gran lienzo en el que la música es pintada. Toda vez que una perturbación interrumpe el reposo de la atmósfera, las noticias” del evento son propagadas hacia afuera en todas las direcciones a la velocidad del sonido… si esa perturbación mecánica es causada por oscilaciones que están en el rango aproximado de 20 a 20000 por segundo, la perturbación resultante puede ser potencialmente detectada a través de nuestro sentido de la audición, asumiendo que las oscilaciones sean suficientemente fuertes como para ser oídas y suficientemente débiles como para no dañar nuestro mecanismo de audición (Moore, 1990: 340-341).
Cuando los Decibeles se usan para la medición de presión sonora, se los denomina
dB SPL (del inglés, Sound Pressure Level, Nivel de Presión Sonora). La relación entre
la presión de las ondas sonoras medida en dB SPL y en Pascales es la siguiente:
Presión = 20 * log10(p/pr). [Db SPL]
En donde p es la presión y pr =20 micropascales (20 Pa / 1000000), ambas
indicadas en Pascales.
La escala de dB SPL va de 0 dB (Umbral de Audición) a 120 dB (Umbral del dolor). Se corresponde mejor con nuestra percepción de la sonoridad (variaciones de presión proporcionales generan sensaciones de variación de sonoridad equivalentes) y reduce notablemente el enorme rango numérico que implica expresar la presión en Pascales.
Texto aparte
La denominación de Decibel proviene de la unidad denominada Belio (Bell, en inglés) en honor a su inventor, el físico inglés Alexander Graham Bell (1847-1922). Un Decibel es la décima parte de un Belio. Se considera una unidad relativa, dado que expresa la relación entre dos magnitudes, una de referencia y la que se quiere medir. No se usa únicamente en acústica, sino también en electricidad.
Para convertir presión en Pa a dB y en dB a Pa se pueden usar las siguientes
fórmulas:
xdB = 20*Log10(xpa/xpref)
xPa = (10 (xdB /20))*0.00002

Obsérvese que a cada 6 dB de aumento o disminución, corresponde un cambio de la presión dinámica del doble o la mitad, respectivamente.
2.2.4. Potencia e intensidad acústica
La potencia acústica es la cantidad de energía acústica transferida por unidad de
tiempo y se mide en unidades denominadas Watts.
P= DE/Dt Watts
P= ΔE/Δt Watts
La letra griega Δ (Delta) se suele usar, por convención, para indicar una diferencia
entre dos magnitudes. En este caso, dos medidas de energía sucesivas
tomadas en un intervalo de tiempo.
La intensidad acústica es la potencia que atraviesa un área. Se mide en W/m2.
I= P/A Watts/m2
En donde A es el área o superficie afectada por la potencia P.
I= P/A Watts/m2
La intensidad acústica de una onda progresiva plana es proporcional al cuadrado de su presión dinámica. Por lo que, tanto intensidad y presión dinámica, como potencia, son maneras de medir la energía asociada a una onda acústica.
20Pa de presión dinámica (umbral del dolor), equivalen a una intensidad de 1 W/m2 y 20μPa
(micropascales, umbral de audibilidad) equivalen a 10-12 W/m2.
De manera análoga a la presión dinámica, la intensidad se puede medir en dB
SIL (del Inglés, Sound Intensity Level, Nivel de Intensidad Sonora), de acuerdo
con la siguiente ecuación:
xdB = 10*Log10(I/Iref) ) (dB SIL)
Donde Iref=10-12 W/m2
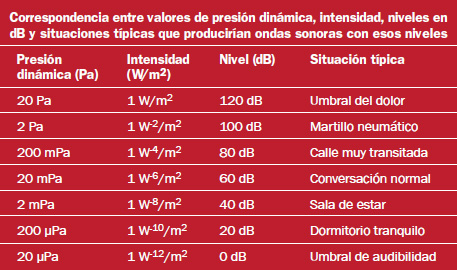
En la siguiente tabla (Basso, 2006) se pueden ver varios valores de presión dinámica e intensidad acústica en Pa y W/m2 respectivamente, relacionados con su valor expresado
en dB SPL y dB SIL, y con las situaciones típicas que generan las ondas
sonoras de tales niveles.
Actividad 1
a) Usando las fórmulas que se han provisto en esta sección, convierta
diversos valores de presión sonora en Pa a dB SPL y viceversa.
b) Derive las fórmulas necesarias para convertir valores de intensidad
acústica en dB SIL a W/m2.
Miyara, F. (2013), “Capítulo 3”, en: Ruido, Arte y Sociedad. UNR Editora, Rosario.