1.6. Suma de ondas senoidales

Cuando se suman dos ondas senoidales se suma la energía de cada una y como resultado se obtiene la combinación de las dos ondas.

Para simplificar, nos concentraremos en la representación de la forma de onda e imaginaremos dos sinusoides. A intervalos regulares de tiempo evaluaremos la energía de cada onda, las sumaremos y obtendremos el nuevo valor de elongación de la sumatoria de las dos ondas. Entonces, la suma de las dos ondas será el resultado de la suma algebraica de la energía de cada una de estas, evaluada a intervalos regulares de tiempo.

1.6.1. Suma de ondas senoidales cuya resultante es otra senoidal

Para que la suma de dos sinusoides dé como resultado otra sinusoide, es necesario que ambos componentes tengan la misma frecuencia.

Suma de sinusoides de igual frecuencia, amplitud y fase
La resultante es otra sinusoide de igual frecuencia, fase y el doble de amplitud.

 

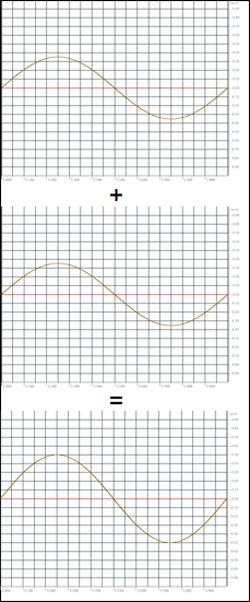
Suma de sinusoides de igual frecuencia, fase y distinta amplitud
La resultante es otra sinusoide de igual frecuencia, fase y la suma de sus amplitudes.

 

Suma de sinusoides de igual frecuencia, amplitud y distinta fase
Si la diferencia de fase es cercana a 0º, la amplitud resultante será próxima al doble. Por el contrario, si la diferencia de fase es cercana a 180º, la amplitud resultante será cercana a cero.

Suma de sinusoides de igual frecuencia y amplitud, pero con fases distintas
La resultante es otra sinusoide de igual frecuencia, la amplitud será la suma de las amplitudes y la fase el promedio de las fases.

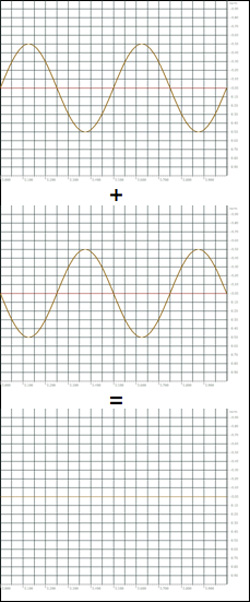
Suma de sinusoides de igual frecuencia y amplitud, pero en oposición de fase
La resultante será una línea recta o silencio.

1.6.2. Suma de ondas senoidales cuya resultante es una onda compleja

Todos los tipos de ondas que no sean senoidales se denominan ondas complejas. El Teorema de Fourier, que se desarrollará en profundidad en la Unidad 6, muestra que podemos descomponer a las ondas complejas como suma de ondas simples o senoidales de frecuencia, amplitud y fase determinadas.

Si las frecuencias de los componentes de una onda compleja son múltiplos enteros de la sinusoide de frecuencia más baja, la onda resultante será periódica o armónica.

Si las frecuencias de los componentes de una onda compleja no son múltiplos enteros de la sinusoide de frecuencia más baja, la onda resultante será aperiódica o inarmónica.

Espectro de frecuencias
Podemos definir al espectro de una onda como la distribución de su energía en función de la frecuencia.

La representación de la forma de onda y del espectro son dos posibles visualizaciones de las características de una misma onda. En la forma de onda vemos representada la amplitud en función del tiempo, y en el espectro de frecuencias, la amplitud en función de la frecuencia.

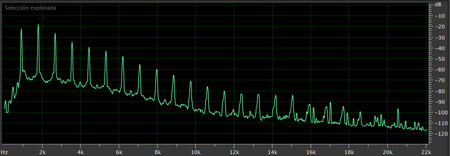
Se puede representar gráficamente la distribución de energía de una onda en un momento dado por medio de un espectro de frecuencias o espectrograma. Consiste en representar la amplitud en función de la frecuencia en un par de ejes, vertical para la amplitud y horizontal para la frecuencia. Gracias a esta representación, podemos visualizar la descomposición de una onda compleja como la suma de ondas senoidales de frecuencia y amplitud determinadas.

Ondas complejas periódicas
Una onda periódica de frecuencia f se puede descomponer como una suma de sinusoides cuyas frecuencias serán f, 2f, 3f, 4f, 5f, etc. A la frecuencia f se la denomina fundamental y es la que determina la altura percibida. A los otros componentes se los denomina armónicos superiores y se encuentran en una relación de múltiplos enteros con la fundamental.

Si tenemos una onda compleja cuya fundamental es de 440 Hz la podemos representar como la suma de armónicos con amplitudes y fases determinadas, cuyas frecuencias serán:

(f ) 440 Hz + (f 2) 880 Hz + (f 3) 1.320 Hz + (f 4) 1.760 Hz + (f 5) 2.200 Hz, etcétera.

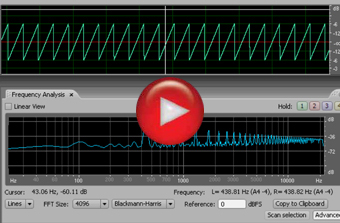
Onda diente de sierra
La onda diente de sierra es una onda periódica generada artificialmente en la que la amplitud de sus armónicos decrece proporcionalmente con el número de armónico.

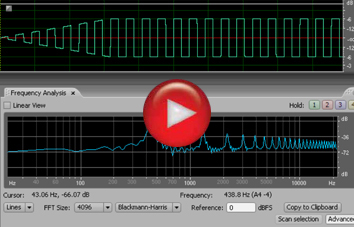
Onda cuadrada
La onda cuadrada se obtiene sumando solo los armónicos impares, y su amplitud decrece proporcionalmente con el número de armónico.

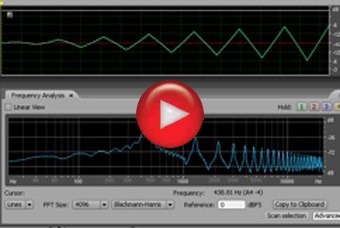
Onda triangular
La onda triangular se obtiene sumando solo los armónicos impares, y su amplitud decrece proporcionalmente con el cuadrado del número de armónico.

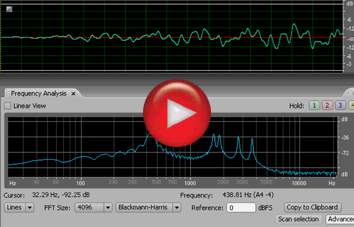
Ondas complejas aperiódicas
A las ondas complejas cuyas componentes no forman parte de una serie armónica se las denomina aperiódicas. Estas ondas producen sonidos que no definen altura.

1.6.3. Batidos o pulsaciones

Un caso particular de suma de ondas periódicas simples o complejas que no están en relación armónica es el que se conoce como batidos o pulsaciones. Este fenómeno se produce a partir de la suma de ondas periódicas cuyas frecuencias sean levemente distintas, sin superar los 20hz de diferencia. El resultado de dicha suma será otra onda del mismo tipo, cuya frecuencia será el promedio de las frecuencias originales. Su amplitud no será constante, sino que variará periódicamente en el tiempo a una frecuencia igual a la diferencia de las frecuencias originales.

Los músicos aprovechan este fenómeno para afinar sus instrumentos. Se toma un tono de referencia, por ejemplo el La de 440 hz que da un diapasón, se toca la misma nota en el instrumento a afinar, y mientras se escuchen batidos entre los dos sonidos, estos estarán desafinados. Entonces, es necesario subir o bajar la afinación del instrumento hasta que los batidos desaparezcan.