
10.3. Cadenas de Markov
Las cadenas de Markov son el resultado de un proceso aleatorio que depende de un análisis estadístico, realizado
previamente sobre el conjunto de valores posibles.
A fin de ejemplificar este proceso, vamos a utilizar un fragmento musical muy conocido: la melodía de la “Oda a la
Alegría” de Ludwig van Beethoven, que forma parte de su Novena Sinfonía.
Las notas de la melodía, en el orden en que aparecen, son las siguientes:
MI-FA-SOL-SOL-FA-MI-RE-DO-DO-RE-MI-MI-RE
MI-FA-SOL-SOL-FA-MI-RE-DO-DO-RE-MI-RE-DO
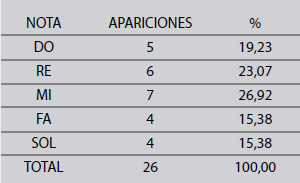
Podríamos decir, en términos estadísticos, que la nota Mi aparece 7 veces en un total de 26 notas. Significa que el
porcentaje de recurrencia de esa nota sobre el total es de aproximadamente un 27 % (7 x 100 / 26). La nota SOL, por
su parte, aparece 4 veces, y el porcentaje de aparición es del 15,3 %. La tabla siguiente ilustra los porcentajes para
cada caso:
El patch de G.10.5. muestra cómo generar eventos aleatorios de acuerdo con una probabilidad. Mediante el objeto Uzi producimos 100 bangs, uno a continuación de otro y generamos 100 números al azar entre 0 y 99. Más abajo, observamos a varios objetos moses, que van a clasificar a los números generados aleatoriamente. A moses ingresa un valor, si ese valor es menor que el argumento, sale por la izquierda, y si es mayor o igual, sale por la derecha. Con el primer moses estamos separando números entre 0 y 18, y entre 19 y 99, o sea que lo que sale por la izquierda, representa el 19 % del total. El segundo moses separa el 23 % del resto, vale decir, ingresan números entre 19 y 99, y por la izquierda salen los números entre 19 y 41 (23 posibilidades), y así siguiendo. Los subpatches de la parte inferior (PD +) suman la cantidad de eventos ocurridos para cada nota. Y así es como asignamos a cada nota una probabilidad de aparición diferente.

La programación del patch de G.10.5. se encuentra en el archivo “76-porcentaje de probabilidad.pd”.
El patch también nos sirve para comprobar si la probabilidad se cumple o no. Ejecutando el programa repetidas veces
podemos observar que, en un número alto de casos, los porcentajes coinciden con la cantidad de eventos registrados.
Podríamos continuar esta idea y generar 26 notas al azar, pero dando a cada nota una probabilidad diferente. Y a
este proceso de considerar probabilidades particulares para cada elemento del conjunto se lo denomina cadena de
Markov de orden cero.
También podría resultar interesante considerar, no solo la cantidad de apariciones de cada nota en la melodía, sino
analizar para cada una de ellas cuáles son sus sucesoras. Podemos escribir en la primera fila de una tabla las notas
que suceden a DO, y qué cantidad de veces. En la segunda fila lo mismo para RE, y así siguiendo, como se observa a
continuación:
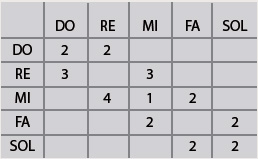
La nota DO es seguida dos veces por la misma nota y otras dos veces por RE, por ejemplo. Por lo cual, la posibilidad
que los sucesores de DO sean DO o RE, es del 50 % para cada caso. La nota RE es seguida 3 veces por DO y tres veces
por MI, con iguales porcentajes.
Este análisis nos podría servir para determinar las posibilidades que posee cada nota de ser sucesora de la nota anterior.
En algunos casos vemos que la tabla está vacía, como en el caso de SOL, que nunca es seguida por DO, ni por RE,
ni por MI, por lo cual, la posibilidad de que algo de esto ocurra es nula. Y, en otros casos, la posibilidad de que a una
nota la siga otra podría ser del 100 %, si bien eso no sucede con la “Oda a la Alegría”.
El patch siguiente (G.10.6.) corresponde a un secuenciador muy básico, capaz de almacenar notas de una melodía y
sus duraciones, y reproducirlas en cualquier momento. Los mensajes que contienen a las notas y las duraciones son
leídos secuencialmente por objetos zl con el argumento nth. Este secuenciador nos permite escuchar la “Oda a la
Alegría” y nos va a servir para analizar auditivamente las variantes que obtengamos al utilizar las cadenas de Markov.
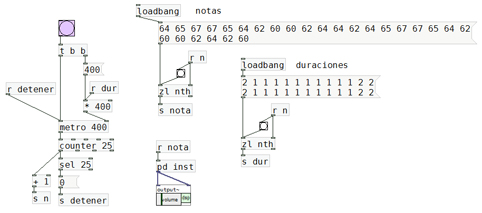
La programación del patch de G.10.6. se encuentra en el archivo “77-secuenciador.pd”.
A partir del análisis estadístico que realizamos de la melodía de la “Oda a la Alegría” intentaremos obtener nuevas versiones,
considerando las probabilidades de que a cada nota la sucedan las mismas que ocurren en el modelo. Al proceso
que vamos a realizar lo denominamos “proceso de Markov de primer orden”. De lo explicado se desprende que si
considerásemos un número mayor de sucesores, por ejemplo dos, el proceso sería de segundo orden, y así siguiendo.
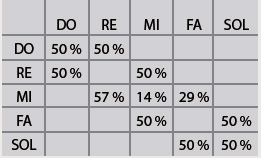
Volviendo a la tabla anterior, vamos ahora a expresar la probabilidad de cada sucesor en porcentajes.
El patch de G.10.7. implementa las cadenas de Markov con el propósito de lograr variaciones de la melodía tomada
como modelo.
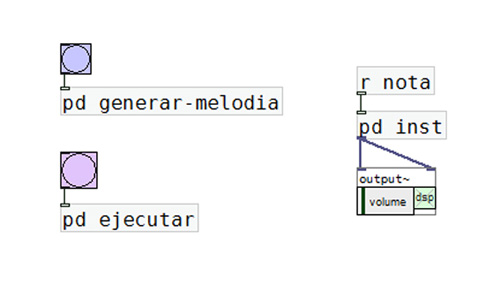
Para comenzar generamos la melodía, y luego la interpretamos, utilizando el secuenciador antes visto.
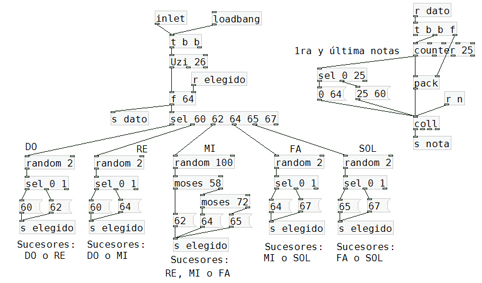
G.10.8. muestra el subpatch de generación melódica. Se trata de un algoritmo recursivo, en el cual se elige un sucesor para
la primera nota, se almacena, y esa nueva nota reingresa en el circuito para buscar su propio sucesor. Las notas se guardan
en un objeto coll, que recibe un mensaje con un número de orden (en nuestro caso 0 a 25) seguido del número de la nota a
guardar. Para recuperar el dato solo se necesita enviar a este objeto el número de orden y devuelve la nota.
Los sucesores son elegidos teniendo en cuenta el análisis estadístico del modelo que resumimos en la tabla anterior.
Finalmente, la primera y última notas se modifican para que sean un MI y un DO, respectivamente, pues dan mayor
sensación de inicio y final.
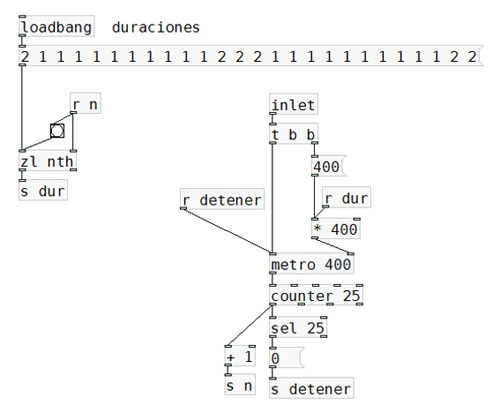
El subpatch de secuenciación es similar al que programamos anteriormente. La diferencia reside en que no extraemos
las notas de la melodía de una lista, sino del objeto coll donde fueron almacenadas.
La programación del patch de G.10.7. se encuentra en el archivo “78-cadenas de Markov.pd”.
Romero Costas, M. (2008), “Algoritmos evolutivos y artes genético” en: Revista de Investigación Multimedia Nro. 2. IUNA, Buenos Aires, pp. 41-49.
Causa, E. y Sosa, A. (2008), “La computación afectiva y el arte interactivo” en: Revista de Investigación Multimedia Nro. 2. IUNA, Buenos Aires, pp. 51-60.
Actividad 1
a. Proyecte y desarrolle un trabajo final de cierta complejidad. El programa, realizado
en PD, puede estar destinado al procesamiento de audio en tiempo real, o bien
a la síntesis del sonido.
b. Puede, además, orientar su proyecto a la realización de una instalación sonora,
que capture sonidos circundantes y los procese, o bien, que las transformaciones
sean realizadas por los mismos espectadores, utilizando sensores de algún tipo.