7.3. Aplicaciones de la FFT en el procesamiento de sonido

La Transformada Rápida de Fourier resulta de gran utilidad en el desarrollo de técnicas de síntesis y transformación del sonido. La operación sobre los datos espectrales nos permite modificar puntual o globalmente la amplitud o la fase de cada componente del análisis, y lograr así resultados muy interesantes.

7.3.1. Crossover

Un crossover es un tipo de circuito utilizado en los baffles, que divide la señal de audio en bandas, cada una de ellas dirigida a un parlante distinto. La banda grave se destina a un parlante desarrollado para reproducir graves, los medios a otro, y así.

Vamos a programar un crossover espectral que corte con total precisión en determinado armónico de la fundamental de análisis, separando los graves, para reproducirlos con el parlante izquierdo, y los agudos con el derecho.

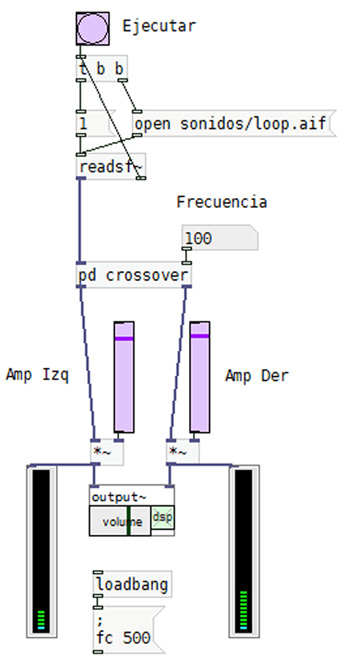
G.7.12. muestra la pantalla principal. Al subpatch de procesamiento ingresa la señal del archivo de audio a reproducir y el valor de frecuencia donde deseamos producir el corte. A las salidas tendremos las señales dirigidas a cada parlante. Agregamos sliders para controlar la amplitud de cada canal y poder escuchar a uno de ellos silenciando al otro.

La amplitud de la señal puede visualizarse mediante vúmetros, programados como abstracciones, con el nombre vu~. El subpatch de procesamiento realiza la FFT de la señal de entrada (ver G.7.13.) empleando una ventana Hanning que multiplica a cada bloque. Las funciones de ventana se encuentran en la librería Windowing.

Los resultados de la FFT se van a dividir en dos ramas y cada una de ellas, luego de un simple procesamiento, va convertirse nuevamente en forma de onda mediante la FFT inversa. Pero en este caso, para calcular la FFT no utilizaremos los objetos fft~ e ifft~, sino rfft~ y rifft~. Estas versiones solo calculan la parte positiva del espectro y rellenan con ceros la parte negativa.

Por debajo de estos objetos, observamos una división por N, dado que las amplitudes están escaladas, y nuevamente la aplicación de la ventana Hanning suavizando las discontinuidades producidas por el proceso.

La parte superior derecha del programa selecciona qué componentes del espectro van a pasar al canal izquierdo y cuáles al derecho, poniendo en cero aquellas que se destinan al canal contrario.

A un objeto expr~ ingresan por la izquierda los números de armónico de la fundamental de análisis, y por la derecha, el número de armónico donde deseamos cortar, calculado a partir de una frecuencia especificada por el usuario.

Para calcular el índice de frecuencia k dada la frecuencia f, utilizamos la siguiente fórmula, ya estudiada:

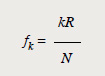
Pero en este caso, vamos a despejar k, pues f es dato:

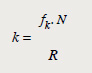
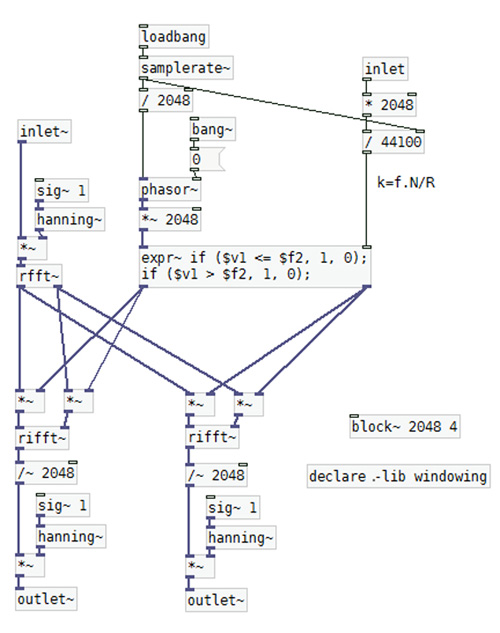
El objeto expr~ incluye dos condicionales if separados por punto y coma. Este tipo de sintaxis produce dos outlets, uno para cada condición. El primero pregunta si el número de armónico actual es menor o igual que el especificado por el usuario. De ser cierto, envía un 1 por la izquierda, y si es falso un 0. El otro condicional hace lo contrario y envía el dato por la derecha. Multiplicar luego por 1 equivale a dejar pasar, y por 0, a anular la señal.

Una última cuestión a considerar es la forma de especificar el tamaño del bloque. Al objeto block~ le agregamos otro argumento (el número 4) que indica un solapamiento de las ventanas de análisis, lo cual va arrojar resultados más precisos.

 

7.3.2. Ecualizador gráfico por FFT

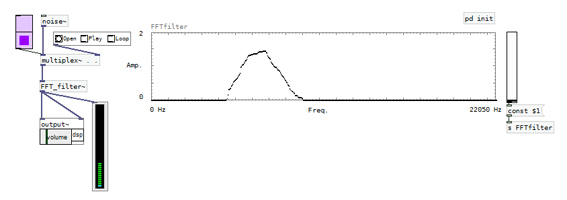
La siguiente aplicación es un ecualizador gráfico espectral de 512 bandas.

Para especificar la amplitud de cada banda utilizamos una tabla de 512 posiciones, donde cada posición representa a un slider de ajuste de la amplitud de la banda.

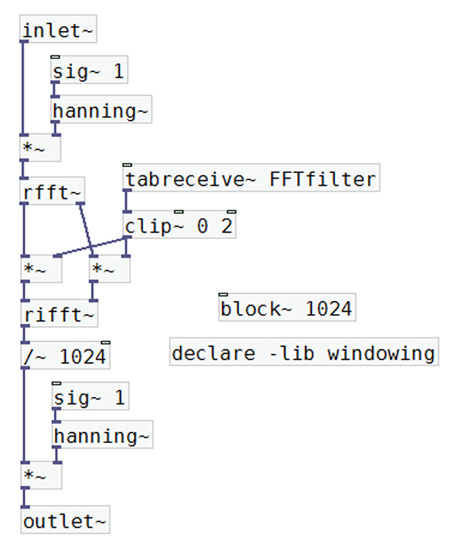
La abstracción donde se realiza el procesamiento está representada en G.7.15. La entrada de audio es multiplicada por una ventana Hanning, al igual que la salida.

Cada bloque es de 1024 muestras. El objeto tabreceive~ lee la tabla a frecuencia de muestreo, de manera tal que las 512 posiciones son leídas dos veces por bloque. En ambos casos, los valores de amplitud de la tabla multiplican a los valores a y b de la FFT, que por ser real (objeto rfft~) tienen ceros en las amplitudes que corresponden a las frecuencias negativas del espectro, o sea en los últimos 512 pares de valores.

El objeto clip~ mantiene el rango de los valores provenientes de la tabla entre 0 y 2. Esto resulta necesario dado que, por errores de PD, es posible que el usuario dibuje fuera del cuadro de la tabla, generando así valores mayores o menores a lo esperado, de forma involuntaria.

 

 

7.3.3. Síntesis cruzada

La síntesis cruzada resulta de la multiplicación de dos espectros. La multiplicación se realiza muestra a muestra, por lo cual, si la amplitud de una componente está en cero, anula a la misma componente del otro espectro.

El proceso en sí mismo se denomina “convolución simple de amplitud”, pero como ha sido ampliamente utilizado en la producción de sonidos, conforma una técnica de síntesis llamada “síntesis cruzada”.

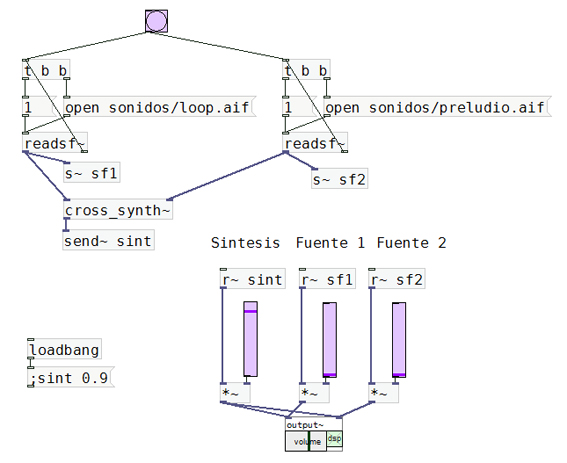
G.7.16. muestra la pantalla principal del programa. Las señales de dos archivos de sonido ingresan en la abstracción, y sale el producto de la síntesis. Mediante sliders es posible escuchar el resultado, o bien cada una de las fuentes por separado, para compararlos:

G.7.17. muestra la abstracción que realiza la síntesis.

Los valores a y b de un espectro son multiplicados por la amplitud calculada del segundo espectro. Si bien podríamos haber calculado las amplitudes de ambos espectros y luego multiplicarlas, esta forma es más eficiente y ahorra bastante proceso.

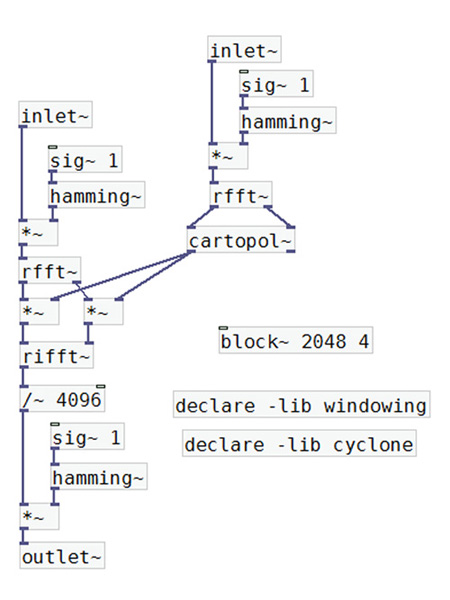
Para calcular las amplitudes del segundo espectro no utilizamos el teorema de Pitágoras, sino un objeto que realiza el proceso directamente. Al objeto cartopol~ ingresan los valores a y b de la FFT, y este devuelve la amplitud por la izquierda y la fase de la componente por la derecha.