
7.2. Comprobaciones teóricas
De acuerdo con lo visto hasta el momento, el objeto de PD que implementa la Transformada Rápida de Fourier, va a
devolver N pares de valores (a y b), de los cuales la primera mitad corresponde a la parte positiva del espectro.
Los pares contienen la amplitud y la fase de las componentes.
Para extraer la amplitud debo aplicar el teorema de Pitágoras, y la amplitud que obtendré estará escalada por N/2; lo cual significa que si analizo una componente de amplitud 1, de una señal de 256 muestras, el algoritmo de la FFT indicará una amplitud 128.
Para conocer la frecuencia de las componentes debo dividir R y N y multiplicar por el número de par. Este último es un
dato fácil de conocer, ya que los pares salen ordenados de 0 hasta N - 1, y puedo contarlos.
Todas las frecuencias de las componentes calculadas son múltiplos de la frecuencia menor, llamada “fundamental de análisis”.
Entendido esto, estamos en condiciones de comprobar los fundamentos teóricos de la FFT, mediante el patch de
G.7.4., que analizaremos a continuación.
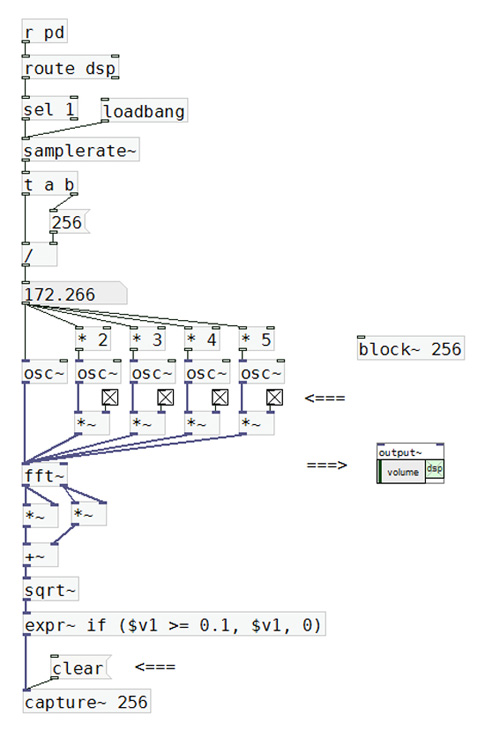
El patch “57-comprobación FFT.pd” contiene la programación de G.7.5.
El programa comienza recibiendo un mensaje que PD envía cada vez que se enciende o apaga el procesamiento de
audio, y que es “dsp 1” o “dsp 0”. El objeto route, al tener inscripto el argumento dsp, reconoce el término y devuelve
lo que sigue en el mensaje, o sea, el 1 o el 0. De estos dos posible valores, el objeto select elige el 1 y envía un bang.
Vale decir que lo realizado hasta el momento nos sirve para detectar cuándo el usuario del programa enciende el
procesamiento de audio.
El mensaje bang que ocurre al encender el procesamiento ingresa a un objeto samplerate~, que reporta la frecuencia
de muestreo (R). Este procedimiento suele utilizarse cuando el proceso depende de la frecuencia de muestreo, pues,
si el usuario cambia esa variable, los resultados pueden ser impredecibles.
Por otra parte, debemos informar a PD la cantidad de muestras que queremos analizar o, mejor dicho, el tamaño de
la ventana de análisis; pues, una vez que termine con un bloque de datos seguirá analizando el resto de la señal que
ingresa al objeto. Para determinar N, o sea el tamaño de la ventana o bloque, utilizamos el objeto block~.
Conocidos ahora R y N, podremos calcular la frecuencia fundamental de análisis, realizando R/N.
En la figura se observa que la frecuencia fundamental de análisis para una frecuencia de muestreo de 44.100 Hz, y
una ventana de 256 muestras, es de 172.266 Hz. Esta frecuencia será la primera que intentará encontrar en la señal a
analizar, siguiendo por sus armónicos (344.5, 689, 1378.1, etcétera).
Según se observa, con el oscilador ingresando al objeto fft~ queremos comprobar si detecta la amplitud de una simple
sinusoide cuya frecuencia es la fundamental de análisis.
A los pares de datos a y b que salen del objeto fft~ les aplicamos el teorema de Pitágoras, es decir, los elevamos al
cuadrado, los sumamos, y hallamos la raíz cuadrada con sqrt~.
Finalmente, guardamos los primeros 256 valores de amplitud en una tabla, mediante el objeto capture~ de la librería
Cyclone. Cada vez que enviamos el mensaje clear se rellena la tabla y podemos ver los resultados haciendo clic sobre
el objeto.
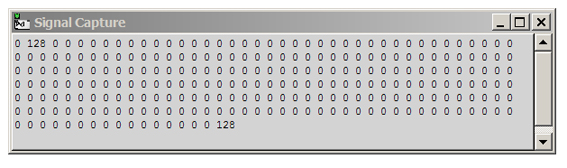
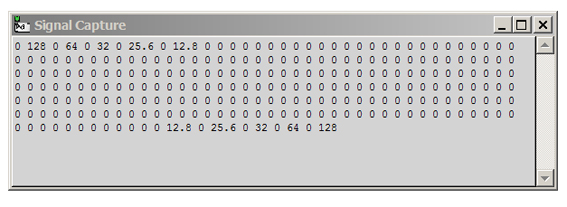
Observando la tabla de G.7.5. vemos que se inicia con un 0, que corresponde a la amplitud para 0 Hz, que en nuestro
caso no nos interesa.
El segundo número es la amplitud de la frecuencia fundamental de análisis. Da el valor 128, que debe interpretarse
como la amplitud multiplicada por N y dividida por 2, o sea 1.
Los valores restantes dan 0, lo cual es correcto pues no hay otras componentes presentes en la señal, salvo el 128
que aparece al final de la tabla, que es la versión negativa (en espejo) de la frecuencia fundamental de análisis. Según
dijimos antes, de los 256 números presentes nos interesan particularmente los 128 primeros, que reflejan la parte
positiva del espectro.
Antes del objeto capture~ observamos un objeto denominado expr~, que permite realizar cálculos sobre las muestras
de una señal de audio. Mediante un condicional if, preguntamos si la muestra que ingresa, almacenada en la variable
$v1 es mayor o igual a 0,1. Si la condición se cumple, la enviamos a la salida, pero si no se cumple, enviamos un 0 en su
lugar. La función de esta parte del programa es eliminar números extremadamente pequeños con muchos decimales
que, a causa de cuestiones de precisión en el cálculo del algoritmo de la FFT, ocupan espacio innecesario en la tabla
y complican su lectura.
7.2.1. Análisis de una señal compleja
Analizaremos ahora un patch similar en el que ingresaremos una señal compleja, sintetizada a partir de los cinco primeros
armónicos. Puede verse la programación en G.7.6.
El objeto fft~ recibe las muestras de una señal periódica, cuya frecuencia fundamental coincide con la frecuencia
fundamental de análisis.
Todas las componentes tienen la misma amplitud y su salida no está atenuada, por lo cual, el valor es 1.
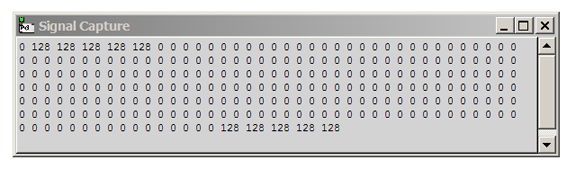
El patch “58-comprobación FFT con armónicos.pd” contiene la programación de G.7.6.
En la tabla generada por capture~ podemos apreciar, luego de la amplitud de 0 Hz, los cinco valores iguales que
corresponden a los cinco primeros armónicos de la fundamental de análisis, y la simetría de la parte negativa del
espectro (G.7.7.).
7.2.2. Índices de frecuencia
Finalmente, para concluir con esta comprobación de resultados de la Transformada, vamos a obtener el número de
armónico que corresponde a cada par de valores calculado por el objeto fft~
G.7.8. muestra el patch de análisis, modificado para sintetizar los cinco primeros armónicos impares con amplitudes
decrecientes, y una representación gráfica muy simple del espectro.
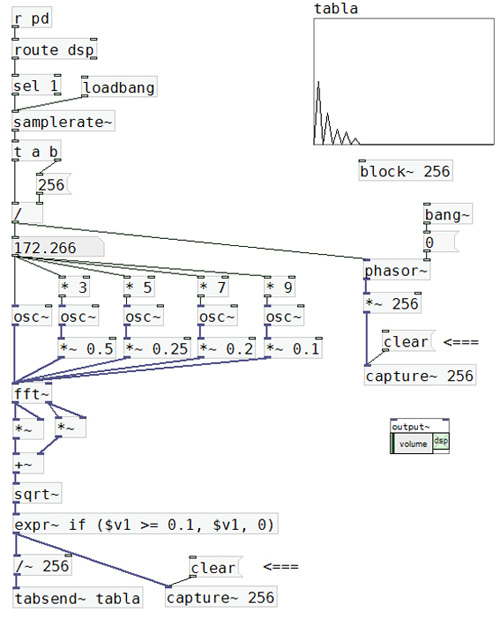
El patch “59-FFT y número de armónico.pd” contiene la programación de G.7.8.
En la tabla de captura de las amplitudes se observa que los resultados obtenidos son coherentes con los datos de la señal sintetizada.
Para generar los números de armónico utilizamos un objeto phasor~, a la frecuencia fundamental de análisis. Como
sabemos, este objeto produce una rampa cíclica entre 0 y 1, pero si multiplicamos su salida por N, podremos obtener
números enteros entre 0 y ese valor.
Estos números deben estar sincronizados con los pares de valores que salen de la FFT; por lo cual, utilizamos un objeto
bang~ que emite un mensaje bang cada vez que da comienzo un nuevo bloque de la Transformada. Este mensaje
dispara, a su vez, un mensaje con un 0, que ingresa al inlet de fase del objeto phasor~, forzando el inicio de la rampa
en alineación con el bloque (ver la tabla en G.7.10.).
7.2.3. Interpretación de los resultados de la FFT
Analizados varios ejemplos, cabe preguntarse qué sucede si ingresamos a la FFT una sinusoide cuya frecuencia no es
múltiplo de la fundamental de análisis.
Supongamos que la señal de entrada es una sinusoide cuya frecuencia se encuentra justo entre la fundamental de
análisis y su segundo armónico. Eso significa que en N muestras, la sinusoide no entró un número entero de veces,
sino una vez y media.
La Transformada de Fourier espera encontrar un solo ciclo de una señal infinitamente periódica, y en este caso va a
devolver varios armónicos, pues la forma de un ciclo y medio no es la que corresponde a una sinusoide, sino a una
onda compleja.
Aún sabiendo que la señal ingresada como dato es una sinusoide, el análisis arroja resultados distintos al esperado,
registrando amplitud en las frecuencias vecinas. Por esta razón, notamos que los resultados de la Transformada de
Fourier requieren de cierta interpretación.
Empleando el patch de G.7.4. generamos una señal sinusoidal de 258.4 Hz, o sea 1.5 veces mayor a la fundamental
de análisis. Los resultados obtenidos se aprecian en G.7.11. Vemos amplitud en 0 Hz, en la fundamental de análisis
(65.19), más en el segundo armónico (93.13) y también en los restantes. Si bien podemos intuir dónde se encuentra la
componente, los datos no lo revelan con tanta claridad.
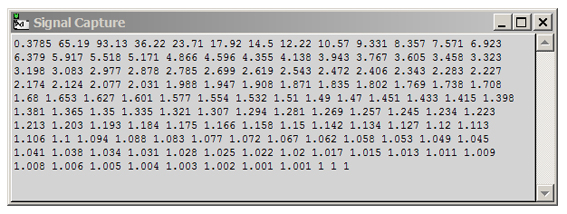
A los pequeños valores de amplitud que aparecen en la mayoría de las componentes del ejemplo se los suele denominar
“artefactos de análisis”. Existe una forma de disminuir los artefactos, creando un pequeño fade-in al comienzo de
la señal de N muestras a analizar, y un pequeño fade-out al finalizar. Y una manera efectiva de llevarlo a la práctica es
multiplicando la señal por una función de N muestras, con forma de campana, similar a la que utilizamos para suavizar
las transiciones en la síntesis granular.
Esas funciones poseen nombres propios, tales como Hamming, Hanning, Blackman, etc., y cada una presenta ciertas
particularidades.
