7.1. Aspectos teóricos de la Transformada Discreta de Fourier

La Transformada Discreta de Fourier es una herramienta matemática que, aplicada al campo de conocimiento que aquí tratamos. Nos permite calcular el espectro de una forma de onda. Contrariamente, utilizando su inversa, podemos obtener la forma de onda si conocemos el espectro (ver figura G.7.1.).

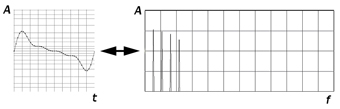
Esta herramienta resulta sumamente útil, pues nos sirve para analizar espectralmente una señal de audio, y realizar procesos y transformaciones que no serían posibles operando directamente sobre las muestras de la forma de onda.

Para entender el principio de funcionamiento de la Transformada Discreta de Fourier vamos a comenzar tratando de extraer la amplitud de un ciclo de una señal conocida, por medios matemáticos.

7.1.1. Relación entre el movimiento oscilatorio armónico y el movimiento circular uniforme

Sabemos que experimentamos la sensación sonora a partir de movimientos oscilatorios, y que la complejidad del movimiento determina la complejidad del sonido escuchado. El sonido más simple es el sonido puro, y lo determina un movimiento oscilatorio simple, que es un movimiento de ida y vuelta alrededor de un punto de equilibrio (similar al que realiza un péndulo).

Para poder predecir la amplitud que tendrá un movimiento oscilatorio simple en un momento determinado, podemos recurrir a un sistema análogo, formado por un móvil que se desplaza en una trayectoria circular a velocidad constante.

Si ubicamos un objeto en el borde de una bandeja giradiscos, por ejemplo, e iluminamos sobre un costado, podremos observar la proyección (sombra) del objeto sobre la pared. El movimiento oscilatorio proyectado, desarrollado en el tiempo, puede representarse a través de una sinusoide (ver G.7.2.).

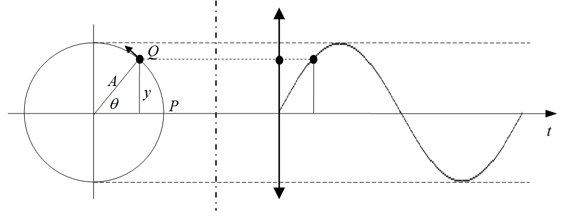
Esta analogía resulta útil para predecir la amplitud del movimiento oscilatorio en un momento determinado. Para conocerlo, basta calcular el valor de y, utilizando la definición de la función seno.
sin ø = y/A
y = A. sin ø

Debemos tener presente que en los medios digitales el tiempo no es una variable continua, sino discreta, y está representado a través de muestras.

Si consideramos, por ejemplo, una señal sinusoidal periódica x(n) con amplitud máxima 1, cuyo ciclo está representado por 8 muestras, el valor de amplitud de cada muestra es 0, 0.707, 1, 0.707, 0, -0.707, -1 y 0.707 (G.7.3.).

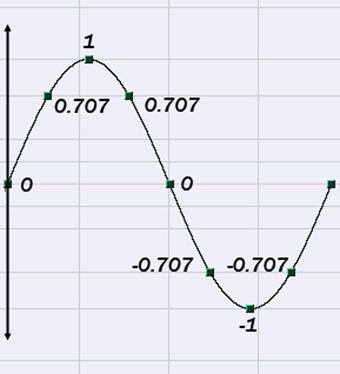
Para 0º en el sistema análogo, y vale 0 de amplitud, para 45º vale 0.707, para 90º vale 1, etc. Pero para aquellos ángulos cuyo seno vale 0.707, o -0.707, vamos a utilizar una expresión más adecuada, debido a que el seno de 45º tiene infinitos decimales.

sin 45º = 0.707… = 2/2 = 1/2

7.1.2. Obtención de la amplitud de un ciclo de una sinusoide

Supongamos ahora que no conocemos la amplitud máxima de nuestra sinusoide, pero deseamos averiguarla realizando un cálculo sobre sus muestras, que podríamos representar así:

1 1 1 1
x(n) = 0, A, A, A, 0, - A, - A, - A
2 2 2 2

Podríamos comenzar por sumarlas, para ver si obtenemos algún resultado.

1 1 1 1
0 + A + A + A + 0 - A - A - A = 0
2 2 2 2

Pero vemos que la suma da 0, lo cual es bastante lógico debido a que ambos hemiciclos son opuestos, tienen forma similar, pero signo contrario.

Veamos qué sucede si, en cambio, elevamos el valor de cada muestra al cuadrado y luego las sumamos:
A A A A A
0 + + A + + 0 + + A + = 4A = N
2 2 2 2 2

Al sumar, notamos que nos da 4 veces la amplitud, lo cual parece incorrecto. Pero si realizamos la misma operación sobre otras sinusoides, con distinta cantidad de muestras por ciclo, vemos que la amplitud siempre está multiplicada por el número de muestras (N), y divido por 2. De esta manera, hemos podido extraer la amplitud de una sinusoide por medios puramente matemáticos.

7.1.3. El principio de funcionamiento de la Transformada de Fourier

Una vez que se logró obtener la amplitud de una sinusoide, partiendo del valor de sus muestras, odemos hallar el modo de calcular la amplitud de las componentes sinusoidales que se encuentran en una señal compleja.

Para lograr este objetivo, la Transformada de Fourier multiplica a las muestras de la señal a analizar por las muestras de sinusoides de distintas frecuencias. Si la sinusoide por la que multiplico se encuentra dentro de la señal compleja, los valores de las muestras se elevan al cuadrado, y al sumarlos dan un número distinto de cero.

Se trata de un procedimiento de prueba y error, en el cual voy buscando a través de un repertorio de sinusoides cuál de ellas puede estar contenida en la forma de onda a analizar.

 

7.1.4. Frecuencia fundamental de análisis

Si el procedimiento se basa en probar sinusoides de distinta frecuencia cabe preguntarse por dónde comenzar, cuántas utilizar, a qué frecuencia finalizar.

De acuerdo con lo que Fourier expresa, una onda compleja infinitamente periódica, siempre puede ser descompuesta en sinusoides de frecuencias cuyos valores son múltiplos. Por ello, si analizamos un ciclo de una señal compleja de N muestras, solamente deberemos multiplicarla por sinusoides de frecuencias múltiplos, de las cuales, la menor es llamada “fundamental de análisis”.

Para averiguar la frecuencia de la fundamental de análisis, simplemente debemos dividir la cantidad de muestras que entran en un segundo (R o frecuencia de muestreo), por la cantidad de muestras contenidas en un ciclo de la onda a analizar (N). Como el resto de las sinusoides son múltiplos de ella, podemos expresar la frecuencia de cada componente del siguiente modo:

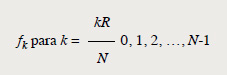
donde f_k es la frecuencia del armónico k (k = 0, 1, 2, 3, etc.), R es la frecuencia de muestreo y N es la cantidad de muestras a analizar.

La transformada multiplica la señal a analizar por la frecuencia fundamental de análisis y continúa con sus armónicos, hasta llegar a la frecuencia de muestreo.

Si bien estamos acostumbrados a ver solamente la parte positiva del espectro, en rigor, la Transformada calcula la parte positiva hasta una frecuencia igual a la mitad de la frecuencia de muestreo y luego continúa en forma decreciente con la parte negativa, que es simétrica a la positiva y, por lo tanto, redundante a los efectos prácticos.

Así como la forma de onda está muestreada en el tiempo, el espectro también lo está, pero en frecuencia. La cantidad de muestras que posee el espectro es equivalente a la cantidad de muestras de la señal analizada, pero solo la mitad se encuentra en el eje positivo de frecuencias.

7.1.5. La sinusoide compleja

Según vimos, la Transformada multiplica la señal a analizar por distintas sinusoides. Pero, en realidad, ocurre que la señal se multiplica por una sinusoide y luego por una cosinusoide de igual frecuencia. A esa combinación se la denomina “sinusoide compleja”, y el nombre se relaciona obviamente con los números complejos. Al resultado obtenido al multiplicar por la cosinusoide se lo denomina “parte real” (a), y a la multiplicación por la sinusoide, “parte imaginaria” (b).

7.1.6. Transformada Rápida de Fourier

La Transformada Rápida de Fourier (o FFT por Fast Fourier Transform) es un algoritmo computacional que implementa de forma veloz la Transformada Discreta de Fourier.

El único requerimiento que presenta la FFT es que el número de muestras a analizar (N) debe ser potencia de 2.

El objeto de PD que implementa la Transformada Rápida devuelve un par de valores de amplitud para cada frecuencia, los cuales resultan de multiplicar a la señal de entrada por la cosinusoide y la sinusoide.

A partir de esos valores podemos determinar la amplitud y la fase de cada componente. Dado que no vamos a realizar procesos que empleen la fase de las componentes, no nos vamos a referir al modo de extraerla. Pero en el caso de las amplitudes, dados a y b (parte real e imaginaria), debemos aplicar la siguiente fórmula, que proviene del teorema de Pitágoras:

donde Ak es la amplitud del armónico k de la fundamental de análisis, ak es la parte real de la amplitud del armónico k, y b_k es la parte imaginaria.